2. 中南大学地球科学与信息物理学院, 湖南 长沙 410083
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
随着测量理论与技术的发展,测量平差的对象已从过去的单一同类观测扩展为同类不同精度,或不同类多源观测,通过多源数据融合可以获取更全面、更有效的信息,产生比单一信息源更精确、更可靠的信息[1-3]。然而,多源观测有不同的函数模型和随机模型,如边角网平差、导线网平差、地面网与空间网联合平差、水准网与重力网联合平差、不同空间网联合平差等[4-6]。另外,多源数据融合也会出现一些关于函数模型和随机模型的先验信息,如参数间往往存在固有的几何关系,构成函数模型约束,参数也可能存在某些先验随机信息,构成随机模型约束[7]。例如,多GNSS系统间存在互操作参数,具有系统性或缓变特性,因此可以通过最初若干历元求得的互操作参数作为先验的随机约束信息,参与后续的互操作参数解算。这些不同的模型,不同的先验信息给多源数据融合带来了挑战。在大地测量中(如复测网),为了融合多源观测数据,获取最优估计值,许多学者提出了联合平差方法,此类方法大多需要知道各类观测量的准确先验方差,从而确定各类融合数据的权[8-12]。在无法准确知道各类观测量的先验方差时,可以采用方差分量估计的方法对方差进行估计后再计算权值,如Helmert方差估计和最小范数二次无偏估计(MINQUE),由于随机约束信息并不能保证能够进行方差估计,因此本文不讨论此类方法。有学者直接提出了迭代求权值方法[10-12],但是迭代重加权最小二乘法是参数的一种非线性估计,其协方差阵计算困难,无法对其进行精度评估。在数学上,许多学者把多源观测数据看成是在新观测得到的样本信息上加上一些先验的随机约束信息[13-16],文献[17—19]研究了这类问题,提出了混合估计。由于附加信息和样本信息在估计过程中作用是不均等的,文献[20]在混合估计的基础上,提出了加权混合估计。这些算法大多注重于算法的效率和估计的优良性,不能直接用于大地测量数据处理。本文综合了大地测量中各种异方差多源观测模型和联合平差方法,利用带有随机约束的线性模型理论,建立了新的加权平差准则,平衡先验约束和观测信息对参数估计的影响,分析了加权混合估计的统计性质,扩展了已有的加权混合方法,提出了权的最优化选择方法,使得加权混合估计方法能有效应用于大测量数据处理。
1 带有随机约束的平差模型与加权混合估计对于平差模型
 (1)
(1)
式中,L为n维观测向量;A是n×m的设计矩阵;秩(A)=m;X =[x1 x2 … xm]T为m维未知向量;Δ为n维随机误差向量;ΣΔ为协方差矩阵;Δ~N(0,ΣΔ);ΣΔ=σΔ2 PΔ-1;PΔ=σΔ2 ΣΔ-1;σΔ2为单位权方差。
式(1)中的X是没有任何约束的,但在一些实际问题中,往往要求X满足某种约束条件,如X是非负的,或X满足某个线性等式约束。文献[18]提出了混合回归模型,将线性约束HX = c随机化得到随机化约束
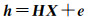 (2)
(2)
式中,h是p维随机向量;H是p×m矩阵;e是服从正态分布的p维随机误差向量,它的期望为0,协差阵为Σe=σe2Pe-1,即e~N(0,Σe)。Δ与e是独立的。这样就形成了带有随机约束的平差模型
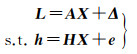 (3)
(3)
其参数估计为
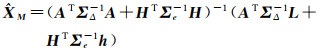 (4)
(4)
由式(4)可以看出,随机约束下混合估计形式上只需要在无约束最小二乘估计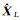


现假定ΣΔ=σΔ2PΔ-1,Σe=σe2Pe-1,其中,PΔ、Pe为已知的权矩阵,则式(4)可以写为
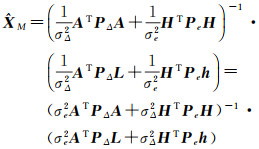 (5)
(5)
其协方差为
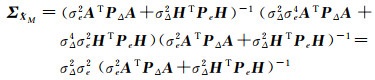 (6)
(6)
令S=ATPΔA,由矩阵公式(A+BCD)-1=A-1-A-1B(C-1+DA-1B)DA-1,有
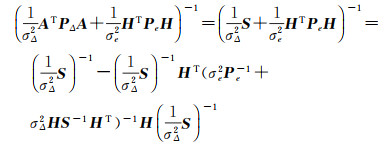
所以

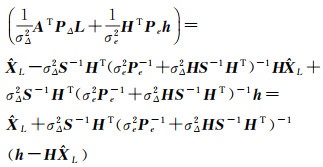 (7)
(7)
在随机约束式(2)中,当σe2=0时,约束条件式(2)可以转换为非随机约束h = HX,由式(7)可知其解为
 (8)
(8)
显然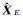
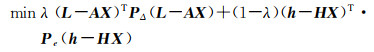
其中,0≤λ≤1。利用拉格朗日求极限的方法,可以求得
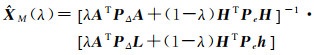 (9)
(9)
若λ=1,加权混合估计退化为最小二乘估计;若λ=1/2,加权混合估计退化为普通的最小二乘混合估计。当0.5 < λ < 1时,它表示赋予样本信息的权重高于先验信息;反之,权重0 < λ < 0.5表示赋予先验信息的权重高于样本信息。在式(5)中,若σΔ2和σe2已知,令λ=σe2/(σΔ2+σe2),则式(9)也可以化成式(5)的形式,这时权值λ由单位权方差σΔ2和σe2确定。若假设新的观测信息比先验信息“更准确”,就会有0.5 < λ=σe2/(σΔ2+σe2) < 1。设
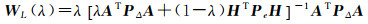 (10)
(10)
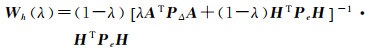 (11)
(11)
由式(9)有
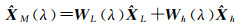 (12)
(12)
由于有WL(λ)+Wh(λ)=I,I为单位矩阵,故可以将
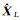
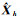
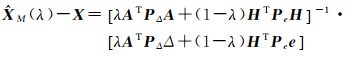 (13)
(13)
而E(ATPΔΔ)=0,E(HTPee)=0,有E(

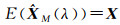 (14)
(14)
由式(13)和式(14)可以计算混合估计
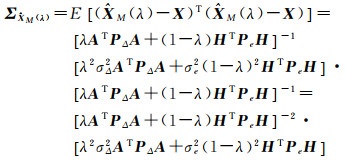 (15)
(15)
在前面的讨论中,假定单位权方差σΔ2和σe2是已知的,但在测绘工程实际中它们未必知道,或者虽已知,但不准确。若单位权方差σΔ2未知,而σe2已知文献[18-19]建议用单位权方差σΔ2的最小二乘估计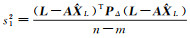

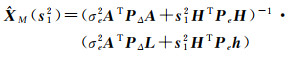 (16)
(16)
令PA=A(ATPΔA)-1ATPΔ,有L-A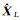
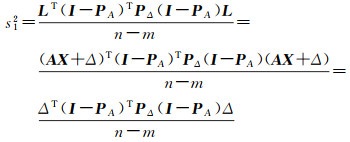 (17)
(17)
显然


由于σΔ2、σe2都未知,不能采用式(5)来计算
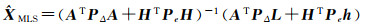 (18)
(18)
其协方差可由式(19)近似计算
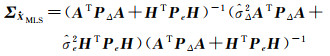 (19)
(19)
式中,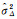
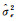
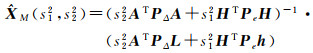 (20)
(20)
由式(20),有
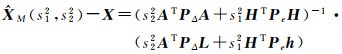 (21)
(21)
而E(ATPΔΔ)=0,E(HTPee)=0,有E[ 




加权混合估计方法沿承了经典最小二乘估计的优良特性,是异质传感器数据融合比较理想方法,然而在大地测量实践中, σΔ2、σe2往往是未知的, 无法准确知道加权混合估计中的权,为了得到近似的加权混合估计,采用迭代重加权混合估计方法。迭代重加权法的本质就是为了给σΔ2、σe2较精确的估计,因此,首先利用s12和s22作为σΔ2、σe2的初始估计值
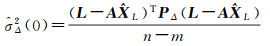 (22)
(22)
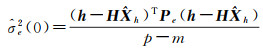 (23)
(23)
然后,进行迭代循环
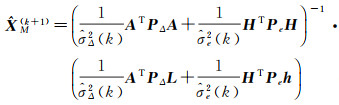 (24)
(24)
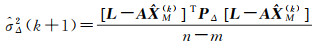 (25)
(25)
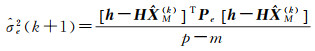 (26)
(26)
直到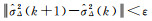
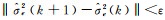
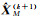
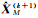
前面的分析说明迭代重加权混合估计方法解决σΔ2、σe2未知时的参数估计问题,却无法进行精度评估,现提出一种最优权计算方法。其基本思路是:把权当作一个非随机变量,先通过迭代方法求出σΔ2、σe2的估计,然后利用加权混合估计均方误差矩阵,求均方误差的极小值从而得到最优的权值,进而得到这组权值下的最小二乘估计,以此作为参数估计结果。设加权混合估计为
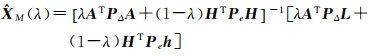 (27)
(27)
式中,权λ是一个非随机变量,λ∈[0, 1]。由于,对于一般的参数向量θ的一个估计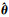
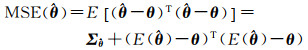 (28)
(28)
此处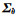
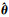
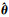
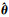
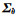

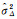
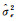

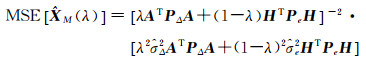 (29)
(29)
建立优化模型
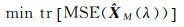 (30(a))
(30(a))
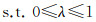 (30(b))
(30(b))
tr(M)为矩阵M的求迹函数,解优化问题式(30),可计算出最优权值λ*,然后代入式(27)可以得到混合估计
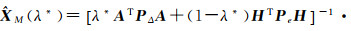
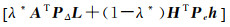 (31)
(31)
对于优化模型式(30)的解算,可在λ满足式(30(b))的条件下,直接利用的搜索算法,λ从0开始到1止,通过增量Δλ(如Δλ=0.001),逐步遍历搜索得到使MSE[

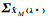
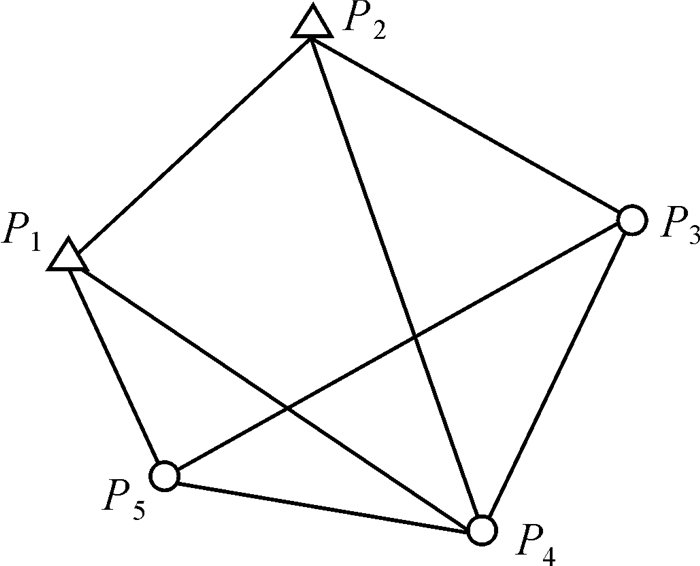
如图 1所示的网形,P1、P2为已知点,其坐标分别为(47 502.285, 61 113.496)和(48 013.013, 61 625.845),为了便于分析比较,算例中的点P3、P4、P5的真实坐标假设已知(见表 1)。假设有两类观测值,都是利用真实坐标计算,再加上得到的:第1类是两点间的GPS基线向量观测值(只取二维),其噪声Δ为高斯噪声,单位权方差为σΔ2=0.1 m2,权阵为PΔ,其观测向量和设计矩阵见表 2;第2类是边长观测值,其噪声e为高斯噪声,单位权方差为σe2=0.4 m2,权阵为Pe,其观测向量和设计矩阵见表 2,其中,权矩阵PΔ和Pe为对角矩阵,它们分别为
PΔ=diag(1.214 8, 1.115 9, 1.912 3, 1.810 6, 1.242 7, 1.217 6, 1.647 3, 1.576 9, 2.185 7, 1.965 3, 1.528 5, 1.353 4, 1.248 3, 1.194 4)
Pe=diag(2.677 2, 1.925 0, 2.235 8, 2.488 8, 2.962 5, 0.183 3, 1.305 9)
|
| 图 1 三角网形 Fig. 1 Triangulation net |
| 点名 | 真实坐标 | 近似坐标 | |||||
| P3 | P4 | P5 | P3 | P4 | P5 | ||
| x/m | 48 521.134 | 48 089.412 | 47 797.210 | 48 521.151 | 48 089.398 | 47 797.234 | |
| y/m | 61 103.829 | 60 618.187 | 60 588.498 | 61 103.810 | 60 618.270 | 60 588.590 | |
| L | A | |||||
| -0.094 6 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0.000 4 | 0 | 0 | 0 | 1 | 0 | 0 |
| -0.057 7 | 0 | 0 | 0 | 0 | 1 | 0 |
| -0.047 5 | 0 | 0 | 0 | 0 | 0 | 1 |
| -0.096 6 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0.129 0 | 0 | 1 | 0 | 0 | 0 | |
| 0.103 8 | 0 | 0 | 1 | 0 | 0 | 0 |
| -0.010 8 | 0 | 0 | 0 | 1 | 0 | 0 |
| -0.028 1 | -1 | 0 | 1 | 0 | 0 | 0 |
| -0.105 7 | 0 | -1 | 0 | 1 | 0 | 0 |
| -0.062 2 | -1 | 0 | 0 | 0 | 1 | 0 |
| -0.074 2 | 0 | -1 | 0 | 0 | 0 | 1 |
| -0.081 8 | 0 | 0 | -1 | 0 | 1 | 0 |
| -0.079 9 | 0 | 0 | 0 | -1 | 0 | 1 |
利用上面的观测数据和设计矩阵,可以建立带有随机约束的平差模型式(3),分别用最小二乘估计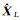
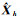

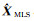


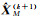

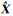
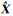
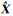
| h | H | |||||
| 0.065 9 | 0 | 0 | 0.764 4 | -0.644 8 | 0 | 0 |
| 0.116 6 | 0 | 0 | 0 | 0 | 0.489 9 | -0.871 8 |
| 0.026 3 | 0.697 5 | -0.716 6 | 0 | 0 | 0 | 0 |
| -0.026 1 | 0 | 0 | 0.075 6 | -0.997 1 | 0 | 0 |
| 0.011 0 | 0.664 5 | 0.747 3 | -0.664 5 | -0.747 3 | 0 | 0 |
| 3.318 3 | 0.814 7 | 0.579 8 | 0 | 0 | -0.814 7 | -0.579 8 |
| -0.036 7 | 0 | 0 | 0.994 9 | 0.101 1 | -0.994 9 | -0.101 1 |
| Xtrue | 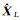 |
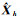 |
 |
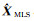 |
 (s12) (s12) |
 (s12, s22) (s12, s22) |
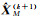 |
 (λ*) (λ*) |
| -0.017 0 | -0.017 2 | 0.240 5 | 0.013 5 | 0.070 3 | -0.014 9 | -0.016 6 | -0.016 7 | -0.016 7 |
| 0.019 0 | 0.092 9 | 0.131 4 | 0.086 0 | 0.087 3 | 0.092 2 | 0.092 7 | 0.092 7 | 0.092 7 |
| 0.014 0 | -0.005 0 | 0.038 0 | 0.008 7 | 0.029 9 | -0.003 9 | -0.004 7 | -0.0048 | -0.004 8 |
| -0.083 0 | 0.002 0 | 0.085 4 | -0.002 9 | 0.004 4 | 0.001 4 | 0.001 8 | 0.0018 | 0.001 8 |
| -0.024 0 | -0.072 5 | -0.266 5 | -0.070 8 | -0.079 3 | -0.072 2 | -0.072 4 | -0.0725 | -0.072 5 |
| -0.092 0 | -0.035 3 | -0.435 3 | -0.066 1 | -0.124 6 | -0.037 6 | -0.035 9 | -0.035 8 | -0.035 8 |
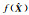 |
0.018 6 | 0.284 5 | 0.014 7 | 0.024 3 | 0.018 1 | 0.018 5 | 0.018 5 | 0.018 5 |
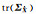 |
0.166 7 | 2.454 7 | 0.144 1 | 0.612 1 | — | — | — | 0.010 4 |
算法分析:
(1) 由于在观测向量L中,观测数n较大,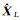
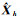
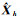
(2) 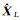
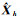

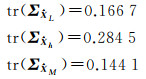
另外,从表 4中的偏差平方和也可以看出
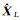
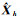
一般情形下都会有
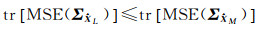
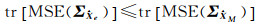
即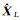
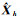

(3) 当σΔ2和σe2已知时,普通混合估计


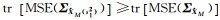
(4) 当σΔ2和σe2未知时,扩展最小二乘估计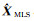

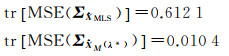
由于最小二乘估计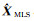


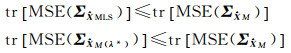
(5) 迭代重加权法解决了σΔ2、σe2未知时的参数估计问题,但是,迭代的每一步估计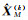
(6) 

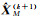




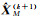

联合平差的原理和方法与线性模型中的混合估计理论是一致的,异质观测、前期观测都可以看成是一种随机约束。大地测量中各种异方差多源观测模型进行融合需要进行混合估计,由于附加信息和样本信息在估计过程中作用是不均等的,本文在混合估计理论的基础上,分析了加权混合估计中权值对参数估计的影响,虽然它们的估计效率在数学上已有大量的研究成果,一般都优于最小二乘算法,但用于测量平差算法还存在缺陷。本文综合分析了数学上现有的多种权的选择方法,提出了一个最优化权选择方法,可以使加权混合估计方法更有效地应用于大测量数据处理。
| [1] |
杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505-510. YANG Yuanxi. Concepts of comprehensive PNT and related key technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505-510. DOI:10.11947/j.AGCS.2016.20160127 |
| [2] |
杨元喜, 曾安敏. 大地测量数据融合模式及其分析[J]. 武汉大学学报(信息科学版), 2008, 33(8): 771-774. YANG Yuanxi, ZENG Anmin. Fusion modes of various geodetic observations and their analysis[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 771-774. |
| [3] |
杨元喜. 多源传感器动、静态滤波融合导航[J]. 武汉大学学报(信息科学版), 2003, 28(4): 386-388, 396. YANU Yuanxi. Kinematic and static filtering for multi-sensor navigation systems[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 386-388, 396. |
| [4] |
张正禄. 监测大区域地壳垂直形变的重复精密重力和水准测量联合平差模型[J]. 测绘学报, 1986, 15(3): 208-216. ZHANG Zhenglu. Repeated precise gravity and leveling combined adjustment model for monitoring vertical crustal deformation in large regions[J]. Acta Geodaetica et Cartographica Sinica, 1986, 15(3): 208-216. DOI:10.3321/j.issn:1001-1595.1986.03.006 |
| [5] |
周忠谟, 晁定波. GPS空间基线向量网与地面控制网的联合平差模型[J]. 武汉测绘科技大学学报, 1987, 12(2): 20-28. ZHOU Zhongmo, CHAO Dingbo. The combined adjustment model for GPS space baseline vector network and terrestrial control network[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1987, 12(2): 20-28. |
| [6] |
杨沾吉, 於宗俦, 于正林, 等. GPS水准、天文重力水准与重力大地水准面多种数据联合处理的研究[J]. 武汉测绘科技大学学报, 1996, 21(4): 330-337. YANG Zhanji, YU Zongchou, YU Zhenglin, et al. A study of combined data processing with GPS leveling, astrogravimetric leveling and gravimetric geoid[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996, 21(4): 330-337. |
| [7] |
杨元喜, 曾安敏, 景一帆. 函数模型和随机模型双约束的GNSS数据融合及其性质[J]. 武汉大学学报(信息科学版), 2014, 39(2): 127-131. YANG Yuanxi, ZENG Anmin, JING Yifan. GNSS data fusion with functional and stochastic model constraints as well as property analysis[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 127-131. |
| [8] |
张朝玉, 陶本藻, 时晋. 多类观测量联合平差中方差分量估计的序贯算法[J]. 大地测量与地球动力学, 2005, 25(3): 34-38. ZHANG Chaoyu, TAO Benzao, Shi Jin. Sequential algorithm on variance component estimation in joint adjustment of various observations[J]. Journal of Geodesy and Geodynamics, 2005, 25(3): 34-38. |
| [9] |
成英燕, 程鹏飞, 顾旦生, 等. 联合平差中的方差分量估计问题的探讨[J]. 测绘科学, 2005, 30(2): 51-54. CHENG Yingyan, CHENG Pengfei, GU Dansheng, et al. Variance component's estimation in the combined adjustment[J]. Science of Surveying and Mapping, 2005, 30(2): 51-54. DOI:10.3771/j.issn.1009-2307.2005.02.015 |
| [10] |
独知行, 欧吉坤, 靳奉祥, 等. 联合反演模型中相对权比的优化反演[J]. 测绘学报, 2003, 32(1): 15-19. DU Zhixing, OU Jikun, JIN Fengxiang, et al. Optimization inversion of the relative weight ratio λ in the joint inversion models[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 15-19. DOI:10.3321/j.issn:1001-1595.2003.01.004 |
| [11] |
王乐洋, 许才军, 张朝玉. 一种确定联合反演中相对权比的两步法[J]. 测绘学报, 2012, 41(1): 19-24. WANG Leyang, XU Caijun, ZHANG Chaoyu. A two-step method to determine relative weight ratio factors in joint inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 19-24. |
| [12] |
刘长建, 吴洪举, 黄勇. 一种调整两类观测值权比的新方案[J]. 测绘通报, 2006(9): 47-48, 68. LIU Changjian, WU Hongju, HUANG Yong. A new scheme for adjusting weight ratio of two kinds of observations[J]. Bulletin of Surveying and Mapping, 2006(9): 47-48, 68. DOI:10.3969/j.issn.0494-0911.2006.09.013 |
| [13] |
王松桂. 线性模型的理论及其应用[M]. 合肥: 安徽教育出版社, 1987. WANG Songgui. The theory and application of linear model[M]. Hefei: Anhui Education Press, 1987. |
| [14] |
王松桂, 范永辉. Panel模型中两步估计的优良性[J]. 应用概率统计, 1998, 14(2): 177-184. WANG Songgui, FAN Yonghui. Optimality of two-stage estimator in Panel models[J]. Chinese Journal of Applied Probability and Statistics, 1998, 14(2): 177-184. |
| [15] |
邬吉波, 杨虎. 回归系数的加权混合估计与最小二乘估计的相对效率[J]. 应用概率统计, 2015, 31(1): 11-19. WU Jibo, YANG Hu. The relative efficiency of weighted mixed estimator with respect to least squares estimator in linear regression model[J]. Chinese Journal of Applied Probability and Statistics, 2015, 31(1): 11-19. DOI:10.3969/j.issn.1001-4268.2015.01.002 |
| [16] |
陈玉蓉. 回归系数的混合估计与最小二乘估计的两种相对效率[J]. 数学杂志, 2007, 27(1): 83-87. CHEN Yurong. Two kinds of relative efficiencies of mixed estimator with respect to LS estimator in linear regression model[J]. Journal of Mathematics, 2007, 27(1): 83-87. DOI:10.3969/j.issn.0255-7797.2007.01.016 |
| [17] |
DURBIN J. A note on regression when there is extraneous information about one of the coefficients[J]. Journal of the American Statistical Association, 1953, 48(264): 799-808. DOI:10.1080/01621459.1953.10501201 |
| [18] |
THEIL H, GOLDBERGER A S. On pure and mixed statistical Estimation in economics[J]. International Economic Review, 1961, 2: 65-78. DOI:10.2307/2525589 |
| [19] |
THEIL H. On the use of incomplete prior information in regression analysis[J]. Journal of the American Statistical Association, 1963, 58(302): 401-414. DOI:10.1080/01621459.1963.10500854 |
| [20] |
SCHAFFRIN B, TOUTENBURG H. Weighted mixed regression[J]. Zeitschrift fur Angewandte Mathematik und Mechanik, 1990, 70(6): T735-T738. |
| [21] |
李广云. 混合估计及其应用[J]. 勘察科学技术, 1993(1): 44-46. LI Guangyun. Mixed estimation and its application[J]. Site Investigation Science and Technology, 1993(1): 44-46. |
| [22] |
KAKWANI N C. Note on the unbiasedness of a mixed regression estimator[J]. Econometrica, 1968, 36(3-4): 610-611. |



