2. 中国航天员科研训练中心, 北京 100094;
3. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG), 北京 100029;
4. 61741部队, 北京 100094;
5. 61540部队, 北京 100029
2. The National Key Laboratory of Human Factors Engineering, Beijing 100094, China;
3. The State Key Laboratory of Numerical Modeling for Atmosphere Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China;
4. Troops 61741, Beijing 100094, China;
5. Troops 61540, Beijing 100029, China
60~100 km为低电离层高空范围,该高空范围内的电子密度较小、空气密度较大,对高频无线电波传播具有比较大的影响,甚至会导致无线电通信的中断;同时,该高度区域内的电子密度变化,常常会影响低频、甚低频无线电导航及定位系统的精度。随着以无线电测量为主要手段的遥感遥测及卫星导航的广泛应用,研究电离层时空物理特性及其建模和预测显得越来越重要。
目前,在高度60~100 km区域,常用的电离层垂直探测仪无法探测它,卫星、探空气球也无法到达该高度区域,且卫星探测的空间分辨率较低(千米量级),虽然探空火箭可以探测该高度区域,但价格不菲,不利于进行长期连续性探测,难以取得连续性资料。中频雷达可以长期地、连续地进行探测,从而得到连续性资料,但同样因为价格昂贵,只能在少数研究单位进行,因此,已有的高度60~100 km范围内电子密度观测数据不能较好地满足业务需求。为解决该问题,大量学者通过构建电离层经验模型补偿观测数据缺失的问题,并对所构建的电离层模型性能、精度等特征进行了一系列研究,取得了大量成果[1-4]。目前,最具代表性、应用广泛的电离层经验模型是由国际空间委员会(Committee On Space Research, COSPAR)和国际无线电联盟(International Union of Radio Science, URSI)共同发起的项目——国际参考电离层模型(International Reference Ionosphere,IRI)[5-6]。该模型通过利用卫星资料、探空火箭资料及非相干散射雷达等观测数据,同时引入太阳活动、地磁指数,并融合多个大气模型,在给定年份、日期、时间、地理(磁)纬度和经度等要素情况下,能够较为准确地描述全球范围内特定时间和地点的电离层形态变化。目前,IRI模型已广泛应用于电离层形态学和空间工程电波修正等研究[7],国内外专家针对该模型做了大量的工作[8-21],取得一系列重要成果。例如,文献[17]探讨了国际参考电离层模型IRI输出参数与测高仪垂测数据的相关性,并进一步分析了COSMIC掩星和IRI模型在不同地方时高估或低估垂测参数的分布特征;文献[18]提出将电离层薄层高度作为约束条件对IRI模型确定的电子密度峰值高度的均值进行参数约束估计,得到一种改进的电离层模型算法,并利用Swarm卫星GPS观测数据对其进行验证;文献[20]利用IRI模型分析了电离层薄层高度的时空变化规律,提出了基于应用中STEC的电离层改正误差分析理论,分析了电离层薄层高度变化的相关影响。
基于高度60~100 km范围内的电子密度观测数据不能较好地满足日益增长的业务需求,且IRI2016作为目前最新的国际参考电离层模型,因此,统计该模型电子密度精度特征具有重要的实际意义。本文以2014—2016年廊坊中频雷达电子密度资料为基准,通过利用偏差、绝对差、相关系数、相对偏差、Lomb-Scargle周期图方法,对IRI2016模型电子密度在中纬度地区60~100 km高度范围内的精度进行统计分析。其中,本文研究所用廊坊中频雷达、IRI2016模型电子密度资料的时间分辨率为1 h、空间分辨率为2 km;在使用IRI2016模型输出电子密度时,该模型的可选外部辅助参数值(如F10.7,AP指数等)均为默认值,从而初步得到IRI2016模型在中纬度60~100 km高度的精度特征。
1 资料简介及方法 1.1 IRI模型国际参考电离层模型是标准经验预报模型,它是IRI工作组从1960年开始,在空间研究委员会和国际无线电科学联合会的资助下,利用全球180多个地面观察站的观测数据建立起来的,其中IRI2016为目前最新版本。IRI模型成型于1975年,其数据主要来源于地面、卫星和火箭探测,主要描述了海拔高度50~1500 km范围内平静地磁场条件下非极区电离层各特征参量(电子密度、离子温度、电子温度、TEC最大值等)的平均值,给出较好的全球电离层形态,其电子密度单位为“个/m3”。IRI模型相对复杂,但电离层改正精度较高,在无线电通信等领域得到广泛应用[22]。
1.2 廊坊中频雷达在2009年5月,中国科学院空间科学与应用研究中心在廊坊安装了一部可重部署的中频雷达,其主要参数见表 1,所得到的电子密度单位为“个/cm3”,因此,对IRI2016模型电子密度精度分析之前,需先将电子密度单位统一,本文统一为“个/cm3”。
| 探测模式 | SAM |
| 坐标 | (39.4°N,116.7°E) |
| 探测高度/km | 60~100 |
| 探测物理量 | 风场、电子密度 |
| 峰值功率/KW | ~64 |
| 工作频率/MHz | 1.99 |
| 高度分辨率/km | 2 |
| 时间分辨率/min | 4 |
| 相干积累个数 | 32(白天),16(晚上) |
| 脉冲重复频率/Hz | 80(白天),40(晚上) |
1.3 方法
IRI2016模型与中频雷达之间电子密度的偏差、绝对差、相关系数和相对偏差计算公式如下
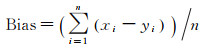 (1)
(1)
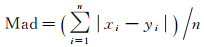 (2)
(2)
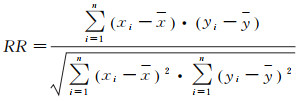 (3)
(3)
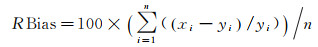 (4)
(4)
式中,Bias为偏差;Mad为绝对差; RR为相关系数; RBias为相对偏差;n为样本数,x和y分别代表IRI2016模型电子密度、中频雷达电子密度,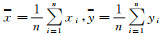
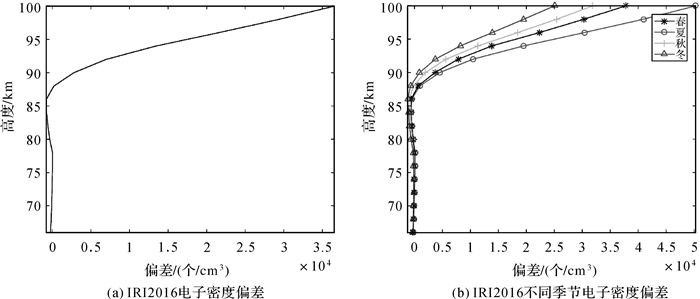
IRI2016模型与中频雷达之间的电子密度偏差、不同季节电子密度偏差随高度变化特征如图 1所示。在图 1(a)中,偏差在高度60~86 km内变化不大,且以负值为主,随后开始转化为正值,且随高度增加,偏差值越大,并在高度100 km达到最大值;在高度60~100 km的偏差值范围为-797.894 5(86 km)~3.655 0×104(个/cm3)(100 km),平均值为5.976 4×103(个/cm3);IRI2016模型与中频雷达之间电子密度偏差特征与季节有关(图 1(b)),其中的春、夏、秋、冬分别为3—5月、6—8月、9—11月、12—2月(下同),不同季节的偏差在高度60~86 km均以负值为主、且相差不大;而在高度88~100 km以正值为主、且随高度增加而快速增大(此时,不同季节之间的偏差值开始出现明显差异特征,同一高度层的偏差值从小到大分别为冬季、秋季、春季和夏季)。在高度60~100 km,春季、夏季、秋季、冬季的偏差值范围分别为“-587.725 5(84 km)~3.776 3×104(个/cm3)(100 km)”、“-580.117 9(84 km)~5.027 6×104(个/cm3)(100 km)”、“-929.749 2(86 km)~3.188 0×104(个/cm3)(100 km)”、“-1.197 9×103(86 km)~2.501 7×104(个/cm3)(100 km)”,平均值分别为6.331 8×103(个/cm3)、8.628 8×103(个/cm3)、5.071 9×103(个/cm3)、3.647 2×103(个/cm3)。
|
| 图 1 2014—2016年IRI2016模型与中频雷达之间电子密度偏差及不同季节电子密度偏差的垂直廓线 Fig. 1 The vertical profile of electron density deviation, electron density deviation in different seasons between IRI2016 model and MF radar during 2014—2016 |
2.2 绝对差
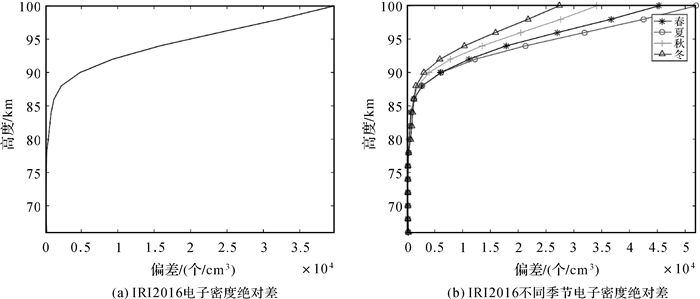
图 2描述了IRI2016模型与中频雷达之间的电子密度绝对差、不同季节电子密度绝对差随高度变化特征。从图 2(a)可看出,高度60~86 km内的绝对差变化不大,随高度增加呈现出缓慢减小、缓慢增大的变化趋势特征,而在高度88~100 km范围内随高度增加而快速增大,在100 km达到最大值;绝对差在高度60~100 km的值范围为147.134 3(70 km)~3.970 6×104(个/cm3)(100 km),平均值为7.357 3×103(个/cm3)。类似偏差,不同季节的电子密度绝对差随高度增加同样存在差异,且高度越高,差异特征越明显,在高度100 km的差异最明显(图 2(b)),在高度60~86 km,不同季节之间的电子密度绝对差均随高度增加均呈现出缓慢减小、缓慢增大变化趋势特征,但差异不大;而在高度88~100 km,不同季节之间的电子密度绝对差均随高度增加而快速增大,且可以明显看出同一高度层的绝对差依小到大均为冬季、秋季、春季、夏季。在高度60~100 km,春季、夏季、秋季、冬季的电子密度绝对差值范围分别为“153.760 0(70 km)~4.525 5×104(个/cm3)(100 km)”、131.025 9(70 km)~5.190 3×104(个/cm3)(100 km)、“124.698 7(72 km)~3.411 0×104(个/cm3)(100 km)”、“158.578 6(72 km)~2.732 7×104(个/cm3)(100 km)”,平均值分别为8.392 6×103(个/cm3)、9.612 4×103(个/cm3)、6.318 6×103(个/cm3)、5.076 4×103(个/cm3);从上述分析可知,偏差、绝对差的最大值均出现在顶层(100 km),但最小值均未出现在底层(60 km)。
|
| 图 2 2014—2016年IRI2016模型与中频雷达之间的电子密度绝对差及不同季节电子密度绝对差的垂直廓线 Fig. 2 The vertical profile of electron density absolute difference, electron density absolute difference in different seasons between IRI2016 model and MF radar during 2014—2016 |
2.3 相关系数
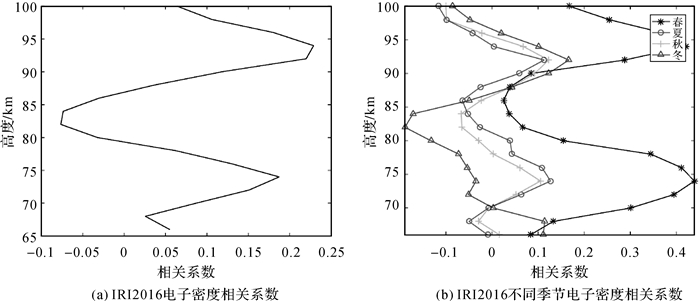
IRI2016模型与中频雷达之间的电子密度相关系数、不同季节电子密度相关系数值随高度变化特征如图 3所示。在图 3(a)中,高度80~86 km范围内为负相关,其他高度范围为正相关,但相关系数值较小(最大值不超过0.25),与偏差、绝对差随高度变化特征不同,相关系数随高度增加呈现出增大、减小的交替变化特征;在高度60~100 km的相关系数值范围为-0.076 6(82 km)~0.228 9(94 km),平均值为0.079 9。从图 3(b)可明显看出,不同季节之间的电子密度相关系数值随高度增加存在明显差异,但呈现出较一致的增大、减小交替变化特征;在高度60~100 km,春季、夏季、秋季、冬季的相关系数值范围分别为“0.025 3(86 km)~0.438 8(74 km)”、“-0.116 3(100 km)~0.127 0(74 km)”、“-0.099 9(100 km)~0.122 8(92 km)”和“-0.188 9 (82 km)~0.166 5(92 km)”,平均值分别为0.223 2、0.003 6、0.006 8和-0.011 4;从上述分析可看出,不同季节的电子密度相关系数值在整个高度层均较小,最大值不超过0.45,且在某些高度层均存在负值。
|
| 图 3 2014—2016年IRI2016模型与中频雷达之间电子密度相关系数及不同季节电子密度相关系数的垂直廓线 Fig. 3 The vertical profile of electron density correlation coefficient, electron density correlation coefficient in different seasons between IRI2016 model and MF radar during 2014—2016 |
2.4 相对偏差
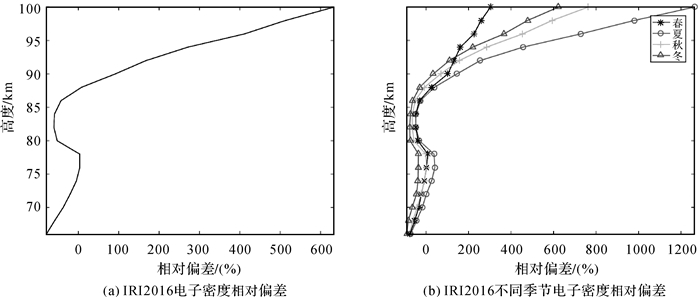
IRI2016模型与中频雷达之间的电子密度相对偏差、不同季节电子密度相对偏差随高度变化特征如图 4所示。在图 4(a)中,相对偏差在高度60~86 km内变化不大,且以负值为主,而在高度88~100 km范围内随高度增加而快速增大,且均为正值,在高度100 km达到最大值;在整个高度范围内,相对偏差的值范围为-79.261 1%(60 km)~632.734 4%(100 km),平均值为93.600 2%;不同季节之间的电子密度相对偏差随高度变化存在较明显差异(图 4(b)),其中,在高度60~90 km,各高度层的相对偏差值由小到大依次均为夏季、春季、秋季、冬季;当高度超过90 km时,随着高度增大,不同季节的相对偏差均快速增大,且均为正值,此时各高度层上的相对偏差值由小到大依次分别为春季、冬季、秋季、夏季,与高度60~90 km存在一定差异。在整个高度范围内,春季、夏季、秋季、冬季的相对偏差值范围分别为-76.310 1%(66 km)~303.333 0%(100 km)、-73.077 6%(66 km)~1.262 4×103%(100 km)、-79.220 7%(66 km)~762.542 3 (100 km)、-90.458 4%(66 km)~622.691 6% (100 km),平均值分别为47.800 1%、204.749 5%、103.599 1%、62.142 8%,由小到大依次分别为春季、冬季、秋季、夏季。
|
| 图 4 2014—2016年IRI2016模型与中频雷达之间电子密度相对偏差及不同季节电子密度相对偏差的垂直廓线 Fig. 4 The vertical profile of electron density relative deviation, electron density relative deviation in different seasons between IRI2016 model and MF radar during 2014—2016 |
3 不同地磁、太阳活动条件的IRI2016模型精度特征
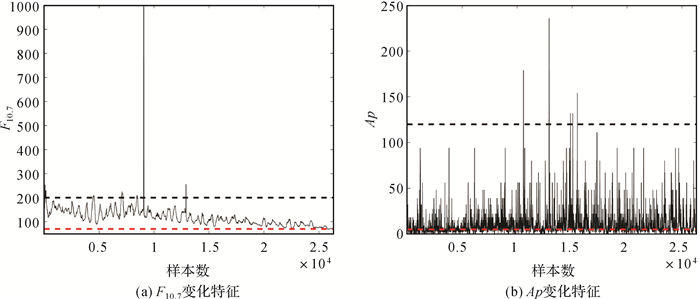
为反映不同地磁、太阳活动条件下的IRI2016模型精度特征,基于文献[23],本文将太阳活动分为太阳活动低年(F10.7≤70)、太阳活动高年(F10.7≥200);地磁条件分为磁宁静(Ap≤5)、磁暴(Ap≥120)。图 5为2014—2016年(时间分辨率为1 h) F10.7和Ap的变化特征,其中,横坐标样本数,共有26 304个(即:24×(365+365+ 366)),图 5(a)中的粗黑虚线、粗红虚线分别代表F10.7=200、F10.7=70,图 5(b)中则分别代表Ap=120、Ap=5;针对2014—2016年的F10.7和Ap变化特征,本文按地磁条件、太阳活动分为4类,分别为①F10.7≤70,Ap≤5,总样本数为60;②F10.7≤70,Ap≥120,总样本数为0;③F10.7≥200,Ap≤5,总样本数为150;④F10.7≥200,Ap≥120,总样本数为3。由于②的样本数为0、④的样本数仅为3,下面仅针对①、③条件情况下的IRI2016模型电子密度精度特征进行研究。
|
| 图 5 2014—2016年F10.7和Ap随时间变化特征 Fig. 5 F10.7 and Ap variation with time during 2014—2016 |
3.1 在F10.7≤70,Ap≤5条件下
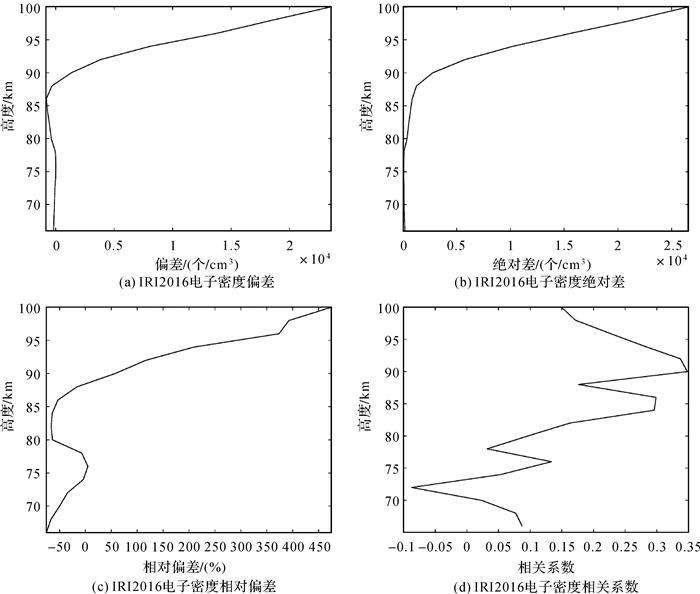
在2014—2016年,共有60个样本满足F10.7≤ 70,Ap≤5条件,在该太阳活动、地磁条件下,IRI2016模型与中频雷达之间电子密度的偏差、绝对差、相对偏差和相关系数随高度变化特征如图 6所示。其偏差在高度60~88 km以负值为主,且随高度变化较小,随后开始转化为正值,且随高度增加而快速增大(图 6(a)),在高度60~100 km的偏差值范围为-816.143 6(86 km)~ 2.356 5×104(100 km)(个/cm3),平均值为3.665 2× 103(个/cm3);绝对差随高度增加呈现出减小、增大、快速增大特征(图 6(b)),在高度60~100 km的值范围为73.464 1(74 km)~2.656 8× 104(100 km)(个/cm3),平均值为4.822 8×103(个/cm3);类似图 6(a),相对偏差在高度60~88 km以负值为主,随后转变为正值,且随高度增加而快速增大(图 6(c)),在高度60~100 km的值范围为-75.495 8%(66 km)~474.793 7%(100 km),平均值为62.667 8%;相关系数值在高度60~100 km以正值为主,其最大值不超过0.35,在某些高度层为负值(图 6(d)),中高层的相关系数值大于相应的中低层,在整个高度范围内的相关系数值范围为-0.087 1(72 km)~ 0.348 1(90 km),平均值为0.158 8。通过对图 5与图 1—图 4进行对比,可看出在F10.7≤70,Ap≤5条件下的IRI2016模型电子密度精度更高。
|
| 图 6 在F10.7≤70, Ap≤5条件下,2014—2016年IRI2016模型与中频雷达之间电子密度的偏差、绝对差、相对偏差和相关系数随高度变化特征 Fig. 6 Under the F10.7≤70, Ap≤5 conditions, the altitude variations of electron density deviation, electron density absolute difference, electron density relative deviation and electron density correlation coefficient between IRI2016 model and MF radar during 2014—2016 |
3.2 在F10.7≥200,Ap≤5条件下
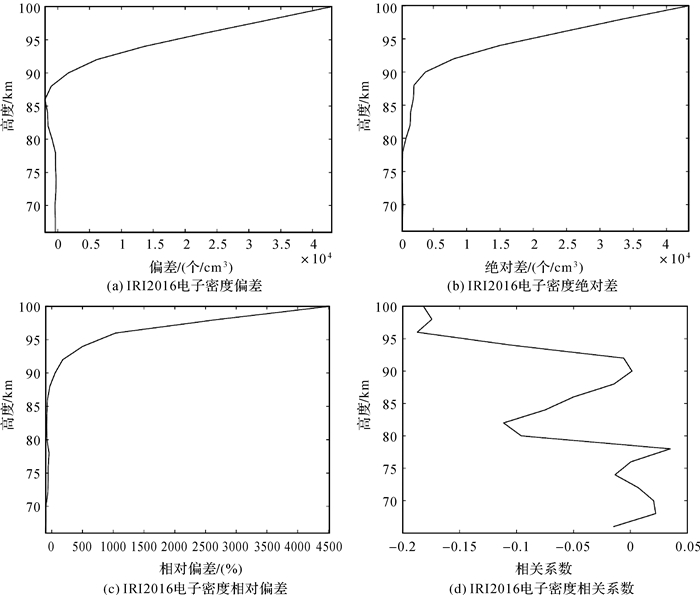
在2014—2016年,共有150个样本满足F10.7≥200,Ap≤5条件,在该太阳活动、地磁条件下,IRI2016模型与中频雷达之间电子密度的偏差、绝对差、相对偏差和相关系数随高度变化特征如图 7所示。类似图 6,其偏差同样在高度60~88 km以负值为主,且随高度变化不大(图 7(a)),在高度90~100 km均为正值,随高度增加而快速增大,在高度60~100 km的偏差值范围为-1.994 4×103(86 km)~4.301 8×104(100 km)(个/cm3),平均值为6.175 5×103(个/cm3);其绝对差同样随高度增加呈现出减小、增大、快速增大的变化特征(图 7(b)),在高度60~100 km的值范围为323.195 5~4.336 6×104(个/cm3),平均值为7.686 5×103(个/cm3);相对偏差在高度60~88 km以负值为主,随后转变为正值,且随高度增加而快速增大(图 7(c)),在高度60~100 km的值范围为-101.907 9%(66 km)~4.513 8×103%(100 km),平均值为449.398 1%;与图 6(d)不同,图 7(d)中的相关系数值在高度60~100 km以负值为主,最大值不超过-0.2,在中低层的某些高度层存在正值,在整个高度范围内的相关系数值范围为-0.187 2(96 km)~0.035 0 (78 km),平均值为-0.052 4。通过对图 7与图 6、图 1—图 4进行对比可以看出,在F10.7≥200,Ap≤5条件下的IRI2016模型电子密度精度最低。
|
| 图 7 在F10.7≥200,Ap≤5条件下,2014—2016年IRI2016模型与中频雷达之间电子密度的偏差、绝对差、相对偏差和相关系数随高度变化特征 Fig. 7 Under the F10.7≥200, Ap≤5 conditions, the altitude variations of electron density deviation, electron density absolute difference, electron density relative deviation and electron density correlation coefficient between iri2016 model and MF radar during 2014—2016 |
4 频谱特征
利用Lomb-Scargle周期图方法可分析某一高度层的大气频谱特征。该方法[24-25]分析序列数据中的频谱分布特征具有独特优势,一方面可以给出分辨率比1/T(T为序列数据的跨度)更精细的功率谱,另一方面可以对不均匀采样数据进行直接处理,最大程度地给出原数据的谱信息。该特点使得Lomb-Scargle周期图方法非常适用于对含有缺测数据的资料进行谱分析,因此该方法的应用十分广泛[26-28]。通过上述分析结果可知,IRI2016模型与中频雷达之间的电子密度存在较明显差异,且差异特征与高度密切相关,为进一步认识IRI2016模型与中频雷达电子密度之间的差异特征,本文采用Lomb-Scargle周期图法对中频雷达、IRI2016模型电子密度数据(高度分别为82、84、86、88、90、92 km)进行频谱分析,并得频谱特征进行对比研究。
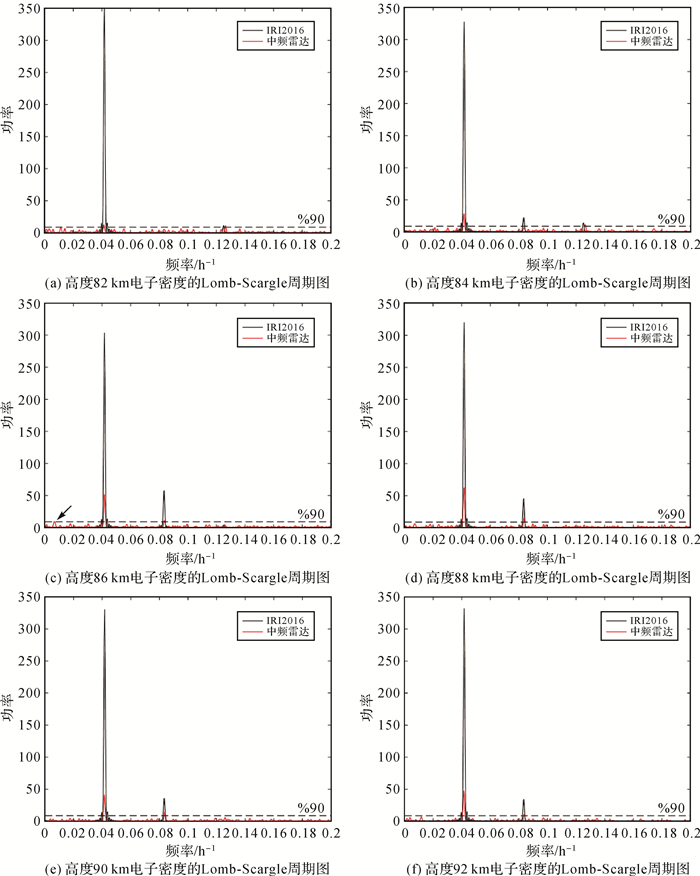
图 8为IRI2016模型、中频雷达电子密度分别在高度82、84、86、88、90和92 km的Lomb-Scargle周期图特征。从图 8可明显看出,IRI2016模型和中频雷达电子密度在82 km均显著(通过90%显著性检验,下同)含有准全日潮汐波、准8 h重力波。在84 km,IRI2016模型显著含有准全日潮汐波、准半日潮汐波和准8 h重力波,而中频雷达电子密度在此高度层未显著含有准半日潮汐波;在86~92 km,IRI2016模型、中频雷达电子密度均显著地含准全日潮汐波、准半日潮汐波,无准8 h重力波。另外,从图 8(c)中还可发现,中频雷达电子密度在86 km还显著含有周期为6.218 9日行星波(对应的功率谱值为9.445 2,见图 8(c)中黑箭头指向),而IRI2016模型在82~92 km均未显著含有该类行星波。
|
| 图 8 IRI2016模型、中频雷达电子密度在高度82、84、86、88、90、92 km的Lomb-Scargle周期图结果(图中虚线为90%显著性检验) Fig. 8 Lomb-Scargle periodiagram of electron density at 82、84、86、88、90、92 km for IRI2016 model and MF radar (the dashed line is 90% significant test) |
表 2给出了IRI2016模型、中频雷达电子密度在高度82、84、86、88、90、92 km显著含有的准全日潮汐波、准全日潮汐波、准8 h重力波周期及功率谱值。结合图 8和表 2可看出:①对于功率谱值,IRI2016模型的准全日潮汐波功率谱值随高度增加呈现出减小、增大的趋势特征,准半日潮汐波功率谱则呈现出增大、减小的趋势特征;而中频雷达的准全日潮汐波、准半日潮汐波功率谱在高度82~88 km均呈现出随高度增加而增大特征,在高度88~92 km随高度增加呈现出减小趋势;②对于周期,IRI2016模型、中频雷达显著含有的准全日潮汐波周期在高度84~88 km一致(均为23.98 h),但在高度82 km、90~92 km存在一定差异,其中,IRI2016模型的准全日潮汐波周期维持不变(23.98 h),而中频雷达的准全日潮汐波周期均改变为24.15 h;IRI2016模型、中频雷达显著含有的准半日潮汐波和准8 h重力波周期,在高度82~92 km均随高度增加而维持不变,其中,IRI2016模型的准半日潮汐波、准8 h重力波周期分别为11.99 h、7.99 h,而中频雷达的准半日潮汐波、准8 h重力波周期均分别为11.93 h、7.91 h,即IRI2016模型与中频雷达显著含有的准半日潮汐波、准8 h重力波周期存在一定差异;③从图 8及表 2中的功率谱值特征可看出,对于IRI2016模型、中频雷达电子密度,其各高度层均为准全日潮汐波功率谱值最大,表明准全日潮汐波在各高度层电子密度变化中均起主要作用;对于中频雷达,准8 h重力波在高度82~84 km电子密度变化中起次要作用,其他高度层为准半日潮汐波起次要作用;而对于IRI2016模型,准8 h重力波在82 km电子密度变化中起次要作用,其他高度层均为准半日潮汐波起次要作用。
| 高度/km | 准全日潮汐波 | 准半日潮汐波 | 准8 h重力波 | ||||||||||||||
| 中频雷达 | IRI2016模型 | 中频雷达 | IRI2016模型 | 中频雷达 | IRI2016模型 | ||||||||||||
| 功率 | 周期 | 功率 | 周期 | 功率 | 周期 | 功率 | 周期 | 功率 | 周期 | 功率 | 周期 | ||||||
| 82 | 12.34 | 24.15 | 348.70 | 23.98 | — | — | — | — | 11.14 | 7.91 | 11.32 | 7.99 | |||||
| 84 | 27.72 | 23.98 | 327.45 | 23.98 | — | — | 22.15 | 11.99 | 11.09 | 7.91 | 13.90 | 7.99 | |||||
| 86 | 51.43 | 23.98 | 303.35 | 23.98 | 10.58 | 11.93 | 57.74 | 11.99 | — | — | — | — | |||||
| 88 | 62.13 | 23.98 | 319.87 | 23.98 | 15.02 | 11.93 | 45.38 | 11.99 | — | — | — | — | |||||
| 90 | 41.23 | 24.15 | 330.13 | 23.98 | 14.45 | 11.93 | 35.79 | 11.99 | — | — | — | — | |||||
| 92 | 47.58 | 24.15 | 331.47 | 23.98 | 11.04 | 11.93 | 34.08 | 11.99 | — | — | — | — | |||||
5 讨论与结论
IRI国际参考电离层模型已广泛应用于电离层形态学、空间工程电波修正等一系列研究。目前,IRI2016为最新的国际参考电离层模型,针对IRI2016模型电子密度在中纬度60~100 km高度范围内的精度研究较少,本文以2014—2016年廊坊中频雷达电子密度资料为基准,以偏差、绝对差、相关系数、相对偏差、Lomb-Scargle周期图方法,对IRI2016模型电子密度在中纬度地区60~100 km高度范围内的精度特征进行定量统计分析,得到主要结论如下:
(1) IRI2016模型电子密度偏差、绝对差与高度和季节存在紧密关系。其偏差和绝对差在高度60~90 km变化较小、在高度90~100 km随高度增加而快速增大;需注意的是,虽然偏差、绝对差的最大值均出现在顶层(100 km),但最小值均未出现在底层(60 km)。
(2) IRI2016模型电子密度相关系数值在高度60~100 km内均较小,且在某些高度层存在负相关,其变化特征与季节有关,随高度增加呈现出增大、减小的交替变化特征(与偏差、绝对差特征不同),在高度60~100 km,不同季节的电子密度相关系数由小到大依次分别为夏季、秋季、冬季、春季。
(3) IRI2016模型电子密度相对偏差在高度60~86 km内变化不大,且以负值为主;随后开始转变为正值,且随高度增加而快速增大;类似于偏差、绝对差和相关系数,相对偏差随高度变化特征同样与季节有关;在高度60~100 km,不同季节的相对偏差由小到大依次分别为春季、冬季、秋季、夏季。
(4) IRI2016模型电子密度精度与太阳活动、地磁条件有关,在F10.7≤70,Ap≤5条件下的IRI2016模型电子密度精度偏高,而在F10.7≥200,Ap≤5条件下的IRI2016模型电子密度精度偏低。
(5) Lomb-Scargle周期图结果表明,在高度82~92 km范围内的某些高度层,IRI2016模型与中频雷达电子密度显著含有的波动种类存在一定差异,即使在某些高度层含有同一类型波,但波功率谱、波周期也会存在一定差异。在高度82~92 km的IRI2016模型、中频雷达电子密度变化特征中,准全日潮汐波均起主要作用;对于中频雷达,准8 h重力波在高度82~84 km起次要作用,其他高度层为准半日潮汐波起次要作用;而对于IRI2016模型,准8 h重力波在82 km电子密度变化中起次要作用,其他高度层均为准半日潮汐波起次要作用。
关于IRI2016模型电子密度存在偏差较大、相关性较弱的原因,一方面是由于IRI模型是在大量的探测数据和大气理论知识基础上,发展起来的半经验参考电离层模型,所得电子密度反映的是月均值统计特征;且IRI模型电子密度的精度受太阳活动、地磁条件较大影响(例如,磁暴会导致电离层中电子数剧增),本文IRI2016模型电子密度均为在宁静状态条件下得到的数据结果,而廊坊中频雷达资料则反映了真实太阳活动、地磁条件下电子密度实时的时变化特征。另一方面,从中频雷达、IRI2016模型电子密度频谱特征可看,两者资料之间显著含有的波功率谱值、波周期存在一定差异,这种差异同样会影响IRI2016模型电子密度精度;由于对高度60~100 km大气动力机制认识不够,且在该高度范围内历史数据较少、精度较低;同时,IRI2016模型作为经验参考电离层模型,不能像气象业务中应用的数值预报模式可以每日利用全球观探测等实况资料进行更新模式初始场,导致其对存在较快速变化的电子密度无法较好地刻画出来。例如,2016年11月14日11—13时(北京时)的中频雷达、IRI2016模型电子密度变化特征(图略),在11—13时,中频雷达电子密度呈现出快速增大、快速减小的变化趋势特征,但IRI2016模型电子密度在11—13时表现为一致增大特征;对于时分辨率的中频雷达、IRI2016模型电子密度资料,该种特征,同样会对其精度产生重大影响,导致其准确率较低、相关性弱等特征。
在IRI2016模型外部可选辅助参数值均为默认值的情况下,本文利用中频雷达电子密度,对IRI2016模型电子密度的精度特征进行了初步分析;后续将针对IRI2016模型外部可选辅助参数值为实际值时,进一步对IRI2016模型电子密度的精度特征进行更深入分析,从而更多、更好地认识IRI2016模式电子密度精度特征。
| [1] |
王斐, 吴晓莉, 周田, 等. 不同Klobuchar模型参数的性能比较[J]. 测绘学报, 2014, 43(11): 1151-1157. WANG Fei, WU Xiaoli, ZHOU Tian, et al. Performance comparison between different Klobuchar model parameters[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1151-1157. DOI:10.13485/j.cnki.11-2089.2014.0176 |
| [2] |
刘宸, 刘长建, 冯绪, 等. 适用于不同尺度区域的Klobuchar-like电离层模型[J]. 测绘学报, 2016, 45(S2): 54-63. LIU Chen, LIU Changjian, FENG Xu, et al. Klobuchar-like ionospheric model for different scales areas[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 54-63. DOI:10.11947/j.AGCS.2016.F026 |
| [3] |
王宁波, 袁运斌, 李子申, 等. 不同NeQuick电离层模型参数的应用精度分析[J]. 测绘学报, 2017, 46(4): 421-429. WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Performance analysis of different NeQuick ionospheric model parameters[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 421-429. DOI:10.11947/j.AGCS.2017.20160400 |
| [4] |
袁运斌, 霍星亮, 张宝成. 近年来我国GNSS电离层延迟精确建模及修正研究进展[J]. 测绘学报, 2017, 46(10): 1364-1378. YUAN Yunbin, HUO Xingliang, ZHANG Baocheng. Research progress of precise models and correction for GNSS ionospheric delay in China over recent years[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1364-1378. DOI:10.11947/j.AGCS.2017.20170349 |
| [5] |
BILITZA D. International reference ionosphere 2000[J]. Radio Science, 2001, 36(2): 261-275. |
| [6] |
BILITZA D, ALTADILL D, ZHANG Yongliang, et al. The international reference ionosphere 2012-a model of international collaboration[J]. Journal of Space Weather and Space Climate, 2014, 4: A07. DOI:10.1051/swsc/2014004 |
| [7] |
黄智, 袁洪. 磁赤道地区2007-2013年COSMIC掩星反演和国际参考电离层模型输出结果分析[J]. 地球物理学报, 2016, 59(7): 2333-2343. HUANG Zhi, YUAN Hong. An analysis of ionospheric characteristic parameters retrieved from COSMIC and IRI at Jicamarca during the period of 2007-2013[J]. Chinese Journal of Geophysics, 2016, 59(7): 2333-2343. |
| [8] |
蔡红涛, 马淑英, SCHLEGEL K. 高纬电离层气候学特征研究-EISCAT雷达观测及与IRI模式的比较[J]. 地球物理学报, 2005, 48(3): 471-479. CAI Hongtao, MA Shuying, SCHLEGEL K. Climatologic characteristics of high-latitude ionosphere-EISCAT observations and comparison with the IRI model[J]. Chinese Journal of Geophysics, 2005, 48(3): 471-479. DOI:10.3321/j.issn:0001-5733.2005.03.002 |
| [9] |
方涵先, 翁利斌, 杨升高, 等. IRI、NeQuick和Klobuchar模式比较研究[J]. 地球物理学进展, 2012, 27(1): 1-7. FANG Hanxian, WENG Libin, YANG Shenggao, et al. The research of IRI、NeQuick and Klobuchar models[J]. Progress in Geophysics, 2012, 27(1): 1-7. |
| [10] |
BILITZA D, REINISCH B W. International reference ionosphere 2007:improvements and new parameters[J]. Advances in Space Research, 2008, 42(4): 599-609. DOI:10.1016/j.asr.2007.07.048 |
| [11] |
OLADIPO O A, ADENIYI J O, RADICELLA S M, et al. Variability of the ionospheric electron density at fixed heights and validation of IRI-2007 profile's prediction at Ilorin[J]. Advances in Space Research, 2011, 47(3): 496-505. DOI:10.1016/j.asr.2010.09.021 |
| [12] |
蔡超军, 黄江, 邓柏昌, 等. IRI-2007预测TEC在广州地区的适用性分析[J]. 空间科学学报, 2013, 33(3): 277-285. CAI Chaojun, HUANG Jiang, DENG Baichang, et al. Applicability analysis of IRI-2007 in predicting TEC over Guangzhou region[J]. Chinese Journal of Space Science, 2013, 33(3): 277-285. |
| [13] |
KENPANKHO P, SUPNITHI P, NAGATSUMA T. Comparison of observed TEC values with IRI-2007 TEC and IRI-2007 TEC with optional f0F2 measurements predictions at an equatorial region, Chumphon, Thailand[J]. Advances in Space Research, 2013, 52(10): 1820-1826. DOI:10.1016/j.asr.2013.08.012 |
| [14] |
张啸, 闻德保, 汤佳明. 国际电离层模型磁暴模式的适用性分析[J]. 导航定位学报, 2015, 3(3): 89-94. ZHANG Xiao, WEN Debao, TANG Jiaming. The applicability analysis of international reference ionosphere in storm mode[J]. Journal of Navigation and Positioning, 2015, 3(3): 89-94. |
| [15] |
万德焕, 黄江, 邓柏昌, 等. 基于IRI-2012模型广州地区f0F2实测与预测的对比分析[J]. 空间科学学报, 2015, 35(2): 166-177. WAN Dehuan, HUANG Jiang, DENG Baichang, et al. Comparison of f0F2 between observation and the prediction based on IRI-2012 over Guangzhou[J]. Chinese Journal of Space Science, 2015, 35(2): 166-177. |
| [16] |
刘桢迪, 方涵先, 翁利斌, 等. 基于CHAMP、GRACE和COSMIC掩星数据的全球电离层hmF2建模研究[J]. 地球物理学报, 2016, 59(10): 3555-3565. LIU Zhendi, FANG Hanxian, WENG Libin, et al. Global model of ionospheric hmF2 based on CHAMPE, GRACE and COSMIC radio occultation[J]. Chinese Journal of Geophysics, 2016, 59(10): 3555-3565. DOI:10.6038/cjg20161003 |
| [17] |
黄智, 袁洪. 磁赤道地区2007-2013年COSMIC掩星反演和国际参考电离层模型输出结果分析[J]. 地球物理学报, 2016, 59(7): 2333-2343. HUANG Zhi, YUAN Hong. An analysis of ionospheric characteristic parameters retrieved from COSMIC and IRI at Jicamarca during the period of 2007-2013[J]. Chinese Journal of Geophysics, 2016, 59(7): 2333-2343. |
| [18] |
田英国, 郝金明, 于合理, 等. LEO卫星单频精密定轨电离层模型改进算法[J]. 测绘学报, 2016, 45(7): 803-809. TIAN Yingguo, HAO Jinming, YU Heli, et al. Improved ionospheric model algorithm for LEO satellite single-frequency precise orbit determination[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 803-809. DOI:10.11947/j.AGCS.2016.20150628 |
| [19] |
赵玲, 周杨, 薛武. GIM和IRI2012模式在中国地区的时空变化和扰动分析[J]. 地球物理学进展, 2016, 31(5): 2048-2055. ZHAO Ling, ZHOU Yang, XUE Wu. Temporal and spatial variation and perturbation analysis for China with GIM and IRI2012 model[J]. Progress in Geophysics, 2016, 31(5): 2048-2055. |
| [20] |
刘宸, 刘长建, 鲍亚东, 等. 电离层薄层高度对电离层模型化的影响[J]. 空间科学学报, 2018, 38(1): 37-47. LIU Chen, LIU Changjian, BAO Yadong, et al. Effects of ionosphere shell height on ionospheric modeling[J]. Chinese Journal of Space Science, 2018, 38(1): 37-47. |
| [21] |
赵海生, 徐朝辉, 高敬帆, 等. 电离层中性气体释放的早期试验效应研究[J]. 物理学报, 2018, 67(1): 019401. ZHAO Haisheng, XU Zhaohui, GAO Jingfan, et al. Early time effects produced by neutral gas ionospheric chemical release[J]. Acta Physica Sinica, 2018, 67(1): 019401. |
| [22] |
章红平.基于地基GPS的中国区域电离层监测与延迟改正研究[D].上海: 中国科学院上海天文台, 2006. ZHANG Hongping. Study on monitoring ionosphere and correcting ionospheric delay in China by ground-based GPS[D]. Shanghai: Shanghai Astronomic Observatory, Chinese Academy of Sciences, 2006. http://cdmd.cnki.com.cn/Article/CDMD-80022-2006109504.htm |
| [23] |
纪巧, 马瑞平, 徐寄遥. 不同太阳活动及地磁条件下的电导率分布变化[J]. 地球物理学报, 2006, 49(5): 1235-1242. JI Qiao, MA Ruiping, XU Jiyao. Variations of the ionospheric conductivity with different solar activities and geomagnetic conditions[J]. Chinese Journal of Geophysics, 2006, 49(5): 1235-1242. DOI:10.3321/j.issn:0001-5733.2006.05.001 |
| [24] |
PRESS W H, TEUKOLSKY S A, VETTERLING W T, et al. Spectral analysis of unevenly sampled data[M].Numerical Recipes in FORTRAN. 2nd ed. New York: Cambridge University Press, 1992: 569-577.
|
| [25] |
SCARGLE J D. Studies in astronomical time series analysis. Ⅱ, Statistical aspects of spectral analysis of unevenly spaced data[J]. Astrophysical Journal, 1982, 263: 835-853. DOI:10.1086/160554 |
| [26] |
YI Fan. Short-term variability and temporary structures of tides and mean wind in the polar summer mesosphere[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2001, 63(8): 749-757. DOI:10.1016/S1364-6826(01)00005-0 |
| [27] |
JIANG Guoying, XIONG Jiangang, WAN Weixing, et al. The 16-day waves in the mesosphere and lower thermosphere over Wuhan (30.6°N, 114.5°E) and Adelaide (35°S, 138°E)[J]. Advances in Space Research, 2005, 35(11): 2005-2010. DOI:10.1016/j.asr.2005.03.011 |
| [28] |
丁楠, 张皓晶, 张雄, 等. 蝎虎天体OJ287中等时标光变的周期特性研究[J]. 物理学报, 2015, 64(13): 139801. DING Nan, ZHANG Haojing, ZHANG Xiong, et al. A study of the middle time-scale periodic behavior of light curve of BL Lac object OJ287[J]. Acta Physica Sinica, 2015, 64(13): 139801. DOI:10.7498/aps.64.139801 |



