近年来,随着无人机平台技术的发展与成熟,基于无人机倾斜多视影像的三维重建成为摄影测量和计算机视觉领域的研究热点。与LiDAR(light detection and ranging)相比,多视三维重建的性价比更高、平台移动性更灵活,因此被广泛地应用于电力巡检、林业调查、城区规划等领域。多视三维重建的主要步骤包括:空中三角测量、影像密集匹配、三维表面重建及多视纹理映射。其中,多视纹理映射旨在根据影像信息和三维表面模型结构特征,选择三角面元的最佳可见纹理,形成附有纹理信息的三维模型。
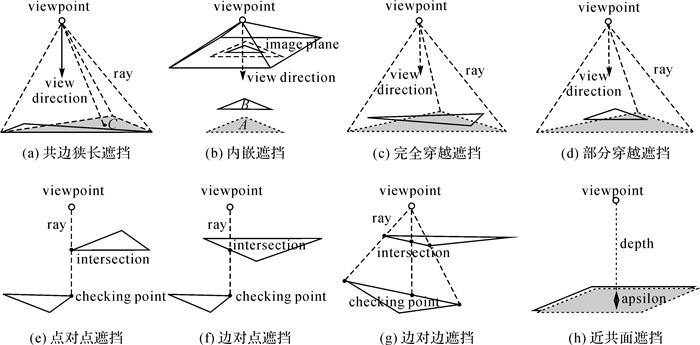
基于多视影像重建的三维表面模型具有结构复杂、面元密集,并存在较多自遮挡区域的特点,因此,必须进行可见性检测,防止非可见纹理映射到模型表面,影响纹理模型的质量。但是,可见性检测目前并没有受到足够的重视。文献[1]在纹理映射的过程中忽略了可见性检测。文献[2]引入隐藏点剔除算法[3](hidden point removal, HPR),用于判定面元f在给定影像视角V下的可见性:若f的重心C位于模型顶点集和V组成的凸包内,则f可见;否则,f不可见。然而,HPR初衷是解决离散点集的可见性问题,无法适用于具有邻接拓扑关系的三角网模型(如图 1(a)所示,虽然阴影面元的重心C在当前视点下可见,但该面元是被遮挡的)。文献[4]采用一种投影距离判别法来辨识可见性:若一面元A同时满足两个条件(①3个顶点的投影位于另一面元B的投影区域内;②到视点V的距离大于B到V的距离),则该面元不可见;否则,其可见。然而,使用这种算法会将图 1(b)中的A识别为可见面元。
|
| 图 1 三维表面模型中的遮挡情形(可见面元用实线绘制,不可见面元用虚线绘制) Fig. 1 Occlusion situations in 3D surface |
目前,文献[5-11]使用光线追踪算法[12-15]和Z缓冲区算法[16-22]解决多视纹理映射的可见性问题。光线追踪算法的基本原理为:从视点V向三维表面模型上的一点P发射光线L,若L在到达P之前与模型产生了碰撞,则P为不可见点;否则,P为可见点[23]。文献[6]利用光线碰撞检测开源库[24]对面元的3个顶点进行可见性检测,若3顶点均可见则该面元可见。但是,有限顶点的可见性并不能保证整体面元的可见性(如图 1(a)(c)(d)中,虽然阴影面元的3个顶点在当前视点下均可见,但整体面元实际不可见)。为了解决上述问题,在可见性检测中必须提高光线追踪的密度。但是,高采样密度将导致时间开销呈指数级增长。尽管对模型构建层级树状索引[12-13, 15]可以提高光线追踪的效率,但是当模型中存在较多与坐标轴平行的面元时,索引结构带来的提升并不显著[25]。另外,当碰撞的交点恰好位于顶点、边上时(如图 1(e)-(g)所示),可见面元又会被识别为不可见面元。Z缓冲区算法的基本思想为:设dp为点P到视点V的距离,lp为P经过透视变换后存储在Z缓冲区中的深度;若dp≤lp,则P可见;否则,不可见。Z缓冲区算法的本质是基于透视变换将三维模型的连续可见性问题转化为二维投影平面上的离散可见性问题[23, 26]。因此,当且仅当投影后面元的内部像素均满足dp≤lp时,该面元方可识别为可见面元。当多视影像数据大、三维表面模型面元密集时,基于逐像素检测面元可见性的效率会很低。为了减少采样次数,文献[5, 21]降低了Z缓冲区的分辨率。但是,这种方案会导致Z缓冲区储存的深度无法正确地反映模型的空间分布,从而降低了可见性检测的精度。
由于浮点数有限精度带来的误差[27],基于光线追踪算法和Z缓冲区算法的可见性检测,需要人工设定一个微小偏差来消除误差[9, 25]。但是,固定的偏差并不能适用于复杂模型[20]:如果偏差过大将导致不可见点被识别为可见点;反之,可见点会被识别为不可见点[19]。同时,当待检测点位于近共面的平面上时(如图 1(h)所示),人工指定的偏差造成的负面影响更为严重。
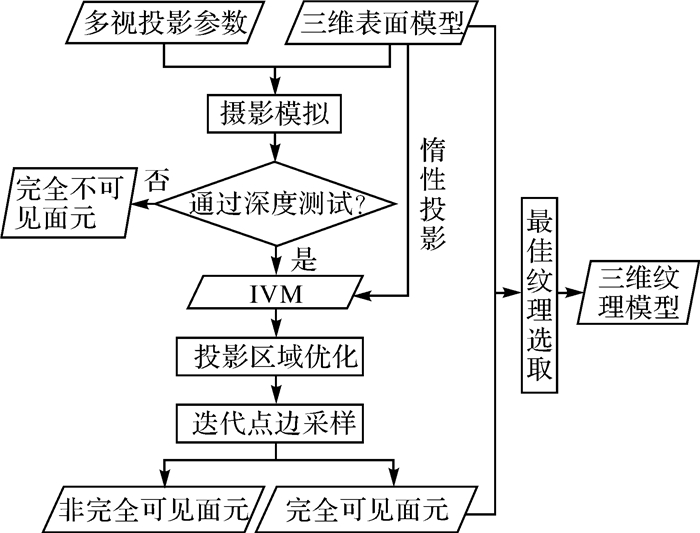
针对多视纹理映射中的可见性检测问题,本文基于图形学渲染管道提出一种快速、准确的可见性检测方案。其最大贡献为:在无需设定偏差的前提下实现可见性检测。首先,本文设计了一种基于着色器编程的摄影模拟方案。在模拟的过程中,每张影像视角下的完全不可见面元会被深度测试自动排除,可见面元经过光栅后形成IVM。IVM具有3条空间属性(轻量性、一致性和连续性)。基于这3条属性,面元可见性可以被准确地检测。然后,对投影到IVM上的面元执行投影区域优化。与其他相关文献[5, 7-10]相比,本文首次将投影区域优化考虑到基于像素进行可见性检测的过程中,这对可见性检测的精度具有显著的促进作用。其次,在可见性分类阶段,提出惰性投影和迭代点边采样算法来减少处理的面元数和采样次数。最后,在检测出每张影像视角下的完全可见面元后,笔者根据完全可见面元之间的拓扑关联构建马尔科夫随机场[28]并使用图割算法[29, 30]选择最佳纹理。图 2为本文算法的框架流程。
|
| 图 2 多视纹理映射中无需设定偏差的快速可见性检测 Fig. 2 Fast visibility detection without specifying biases in multi-view texture mapping |
1 多视纹理映射中无需设定偏差的快速可见性检测 1.1 IVM生成
本节围绕图形渲染管道的主要环节,详细阐述IVM的生成过程。主要步骤包括:首先,在顶点着色器中根据影像投影参数实现透视变换;然后,利用线性边界函数[31](linear edge function, LEF)栅格化投影后的二维面元;最后,在片元着色器中将可见面元的索引记录在帧缓冲区对象(frame buffer object,FBO)。
1.1.1 基于着色器编程的摄影模拟文献[32]将影像的内外方位元素转换为固定渲染管道(fixed rendering pipeline,FRP)中的模型视图矩阵、投影矩阵及视口变换矩阵,以此实现摄影模拟。然而,当像主点不位于影像中心时,基于固定渲染管道模拟的影像存在明显的离心投影偏移。因此,本文设计了一种基于着色器编程的摄影模拟方案。
在计算机视觉领域,给定一无畸变影像的投影参数,则从三维空间向二维影像平面变换的数学关系可以表达为
 (1)
(1)
式中,R为旋转矩阵;S为成像位置;(fxfy)为以像素为单位的焦距长度;(cx, cy)为像主点位置。在计算机图形学中,三维到二维的透视变换可以表达为
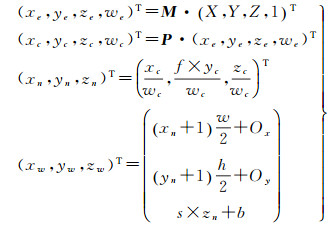 (2)
(2)
在式(2)中,M为将物方坐标(X, Y, Z, 1)T变换到视觉坐标(xe, ye, ze, we)T的矩阵;P为将视觉坐标变换为剪裁坐标(xc, yc, zc, wc)T的矩阵;(xn, yn, zn)T为归一化设备坐标(normalized device coordinate,NDC)。当成像视口的起点位于左下角时,f=1;当成像视口的起点位于左上角时,f=-1;(xw, yw, zw)T为投影后的窗口坐标,其中xw、yw代表像素在视口中的位置,zw代表像素深度;s和b为深度控制系数,在默认情况下s=b=0.5;(Ox, Oy)代表视口起点在设备上下文中的位置,默认情况下(Ox, Oy)位于原点0, 0处;(w, h)为视口大小。
顶点着色器的主要任务之一是生成剪裁坐标。联合式(1)和式(2),将式(1)中的像素坐标
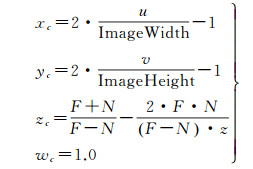 (3)
(3)
在式(3)中,wc被归一化为1.0,以提高后续透视变换的效率;视口大小(w, h)用影像大小代替;zc根据投影矩阵P中远近截面参数(F,N)形成的视椎体进行计算,详细原理参见文献[33]。
1.1.2 基于线性边界函数的光栅化经过透视投影后,三角面元在光栅化阶段被离散化为像素。光栅化的主要任务有两点:①进行覆盖测试,即确定二维面元所占的像素区域;②确定每个像素的属性值。由于其简洁高效性,线性边界函数LEF成为光栅化过程的经典算法。其数学表达形式为
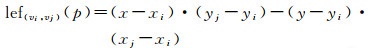 (4)
(4)
式中,(vi, vj)代表由顶点vi和vj组成的边;(x*, y*)代表顶点v*的位置;(x, y)代表待检测像素p的位置。如图 3所示,给定一顶点按逆时针排列的三角面元,像素p与三角面元一边的位置关系可以通过LEF的值进行判定:

|
| 图 3 基于LEF的三角面元栅格化 Fig. 3 LEF-based triangle rasterization |
(1) 若lef(vi, vj)(p) < 0,则p位于边(vi, vj)的左侧;
(2) 若lef(vi, vj)(p)=0,则p位于边(vi, vj)上;
(3) 若lef(vi, vj)(p)>0,则p位于边(vi, vj)的右侧。
因此,当且仅当lef(v0, v1)(p)、lef(v1, v2)(p)以及lef(v2, v0)(p)均小于0时,像素p位于面元内部。那么,p所在的位置将被栅格化。
光栅化不仅需要将矢量面元离散化为像素,还需要计算像素所在位置的属性值f。根据当前像素p在三角面元中的重心坐标(λ0, λ1, λ2),f可以通过线性插值求得
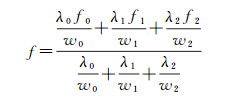 (5)
(5)
式中,(f0, f1, f2)为三顶点处的属性值;(w0, w1, w2)为三顶点处的剪裁坐标。像素p的重心坐标λ0, λ1, λ2)可以通过LEF计算得到
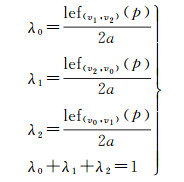 (6)
(6)
式中,a代表三角面元的有符号面积。
1.1.3 基于索引缓冲区的IVM生成光栅阶段生成的像素被送入片元着色器,在片元着色器中可以对像素属性(颜色、深度、法向量等)进行编辑。片元着色器执行结束后,逐片元操作(per-fragment operation)开始启动,在这一阶段深度测试(depth test)会过滤掉不可见像素,保留可见像素。最终,将可见像素送入目标帧缓冲区。目前,有多种类型的帧缓冲区。其中,包括深度帧缓冲区、模板帧缓冲区,以及颜色缓冲区。文献[5, 9]使用深度缓冲区存储可见像素到视点的距离,并制作形成深度图,作为可见性检测的参照。
为了避免基于深度图检测可见性时指定的偏差,本文使用关联在FBO上的离屏纹理对象构建索引缓冲区。经过深度测试后,索引缓冲区记录可见面元的索引值。特别地,本文算法在片元着色器中打开早期深度测试[33](early fragment tests),从而保证传入片元着色器的像素为可见面元对应的像素。渲染结束后,从索引缓冲区中返回渲染结果,形成IVM。因为完全不可见面元所对应的像素已经被排除,IVM中仅记录完全可见面元和非完全可见面元所对应的像素。
IVM具有以下3条空间属性,如下所述。在不设定偏差的前提下,利用这3条空间数据可以实现完全可见面元和非完全可见面元的分类。
(1) 轻量性:IVM仅记录可见面元的信息;
(2) 一致性:面元在IVM中的可见性与在三维表面模型中保持一致;
(3) 连续性:对于任一完全可见面元,其内部像素的索引值保持不变;否则,该面元为非可见面元(如图 4所示,其中红色区域代表非完全可见面元所占的像素,绿色区域代表完全可见面元所占的像素)。

|
| 图 4 IVM的空间连续性 Fig. 4 The continuity of IVMs |
1.2 投影区域优化
基于图形渲染管道对三维模型进行透视投影后,面元的投影区域需要进一步优化。其主要原因包括两点:第一,对于具有邻接关系的面元,公共边上的像素归属需要用某一准则进行判定;第二,光栅化过程中存在误差,误差的存在会导致面元投影区域发生改变。
1.2.1 公共边上的像素归属对于中心位于邻接面元公共边e上的像素p,lefe(p)=0对左右两面元均成立。对于这类像素,三维渲染引擎在光栅化阶段会使用某一既定准则将其指定给其中一个面元,以保证渲染一致性。左上准则[34](top-left rule, TLR)是Direct3D中解决公共边上像素归属的依据。TLR中有两个重要的概念:上边界(top edge, TE)和左边界(left edge, LE)。假定给定一顶点按逆时针排列的三角面元t,(s, d)为t的一边(s为起点,d为终点)。那么,
(1) 如果sy=dy并且dx < sx,则(s, d)为t的上边界。
(2) 如果sy>dy,则(s, d)为t的左边界。
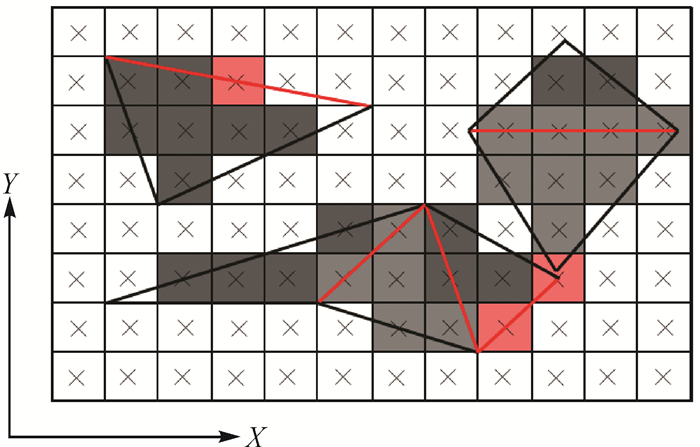
如图 5所示,TLR的判定准则为:中心位于公共边上的像素p属于左边界或者顶边界所在的面元。
|
| 图 5 基于TLR对公共边上的像素归属进行判定 Fig. 5 Juding the affiliation of the pixels on shared edges based on LEF |
1.2.2 栅格化误差
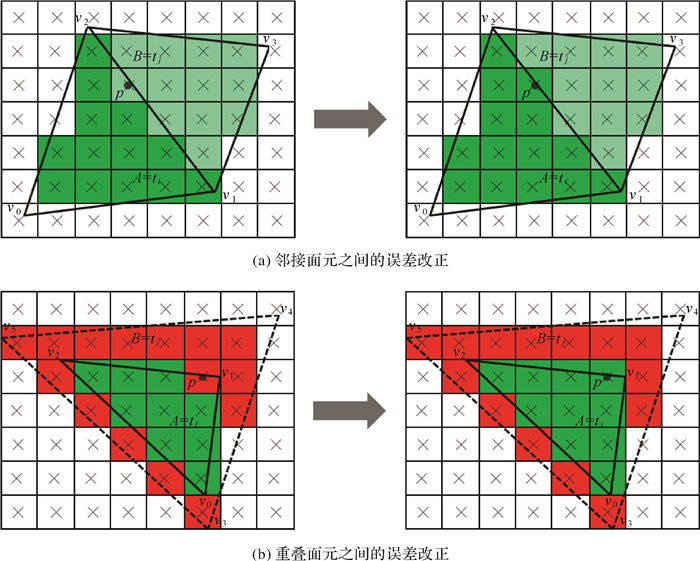
由于图形渲染管道使用的单精度浮点数精度有限,导致光栅化阶段覆盖测试无法准确地定位出面元的投影区域,从而形成栅格化误差。尽管栅格化误差对可视化效果的影响很小,但是其在基于像素的可见性检测中不容忽视。如图 6所示,栅格化误差指本应属于面元A的内部像素被错误地划归为面元B的信息。栅格化误差一般出现在面元的边界周围。研究发现,栅格化误差的程度最大可接近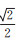
|
| 图 6 栅格化误差改正 Fig. 6 Rasterization error correction |
1.2.3 投影区域优化
综合1.2.1节和1.2.2节所述,本文提出一种基于栅格化准则(LEF、TLR)和像素深度的投影区域优化算法PCR,来恢复可见面元的空间连续性。
算法1:投影区域优化。
输入:给定一可见三角面元ti(i代表ti在三维表面模型上的面元索引),p*代表被ti的一边穿过的像素,vp代表p的属性值,di代表在ti平面内像素p到视点的深度。
输出:ti正确的投影区域
function PCR (ti):
foreach p∈p* do
if p∈ti and vp≠i then
j←vp
if 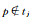
vp←i
else if di < dj then
vp←i
end if
end if
end foreach
end function
上述算法包含以下几步:
(1) 依次遍历ti每一边所对应的像素p*, 使用LEF和TLR判断当前像素p是否属于ti:若p不属于ti,则继续判断下一个像素;否则,转步骤(2);
(2) 判断p的属性值vp是否等于ti的面元索引值i:若相等,转步骤(1);否则,转步骤(3);
(3) 取vp所对应的三角面元tj,使用LEF和TLR判断p是否属于tj:若不属于,说明p所在的位置存在栅格化误差,将p的属性值vp修改为面元ti的索引值i(如图 6(a)所示);否则,转步骤(4);
(4) 根据影像投影参数分别插值计算出像素p在ti平面、tj平面的深度di,dj,比较di,dj:若di < dj说明p所在的位置存在栅格化误差,将p的属性值vp修改为面元ti的索引值i(如图 6(b)所示);否则,转步骤(1)。
1.3 可见性分类为了提高可见性分类的效率,本文提出惰性投影LP和迭代点边采样IVES来减少处理面元的数量以及采样次数。
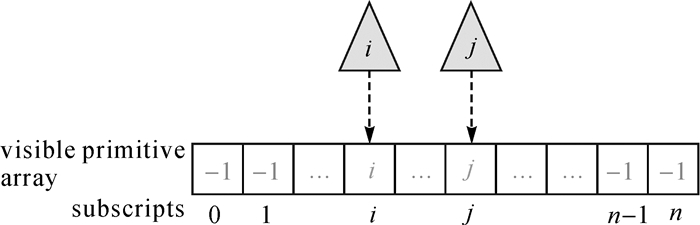
1.3.1 惰性投影目前,相关研究在执行可见性检测之前,会根据影像的投影参数执行反向面元剔除和视截体筛选,减少面元的处理数量。然而,经过反向面元剔除和视截体筛选后仍存在较多的完全不可见面元。为了避免处理这些完全不可见面元,本文利用着色器存储缓冲对象(shader storage buffer object,SSBO),记录可见面元的索引值。由于打开了早期深度测试,因此只有可见面元所对应的像素信息传入片元着色器。SSBO可以看成是显存上的一段连续数组,笔者将可见像素所对应的面元索引值记录在数组下标的相应位置(如图 7所示)。当某一视角下的影像模拟完成后,从显存中读取SSBO所保存的信息,仅仅将这些可见面元投影到IVM上,从而避免了对完全不可见面元的处理。
|
| 图 7 通过SSBO记录可见面元的索引 Fig. 7 Recording visible faces' indexes in a shader storage buffer object |
1.3.2 迭代点边采样
逐像素判断面元可见性是目前的主流方法,其按某一扫描方向顺序遍历面元投影区域的所有像素。如果非完全可见面元的像素按照图 8所示排列时,扫面线算法在最坏的情况下需要遍历20个像素,才能辨识出非完全可见面元。本文提出的迭代点边采样IVES,仅需遍历2个像素就能识别出非完全可见面元。结合IVM的空间连续性,本节给出IVES的推导过程。

|
| 图 8 基于扫描线算法顺序遍历面元投影区域内的像素 Fig. 8 Traversing the pixels of one primitive's projection area in order based on scanning line |
将一可见面元投影到IVM,若其是完全可见面元,则必满足以下3个必要条件:
(1) 顶点可见性条件(vertex visibility condition, VVC):三顶点处的像素拥有一致的索引值;
(2) 边界可见性条件(edge visibility condition, EVC):三边上的像素拥有一致的索引值;
(3) 区域可见性条件(region visibility condition, RVC):每个子区域内的像素拥有一致的索引值。
换句话说,如果某一可见面元不满足以上任一条件,则其为非完全可见面元。在图 9(a)中,完全可见面元满足VVC,而非完全面元不满足VVC;在图 9(b)中,完全可见面元满足EVC,而非完全可见面元不满足EVC;在图 9(c)中,完全可见面元满足RVC,而非完全可见面元不满足RVC。另外,根据流体表面模型的空间结构特征,笔者给出以下推论:
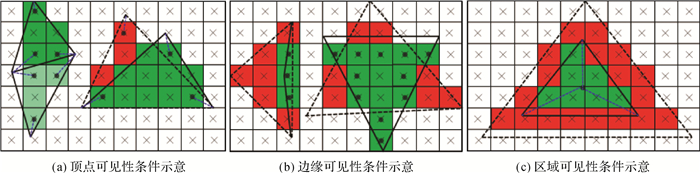
|
| 图 9 完全可见面元满足的3个必要条件 Fig. 9 The three requirements satisfied by a fully visible face |
点边采样推论(vertex-edge sampling, VES):给定流体表面模型上的某一面元f,如果f满足VVC和EVC,则f为完全可见面元。即对于流体模型中的面元,仅仅需要采样顶点和边上的像素,就可判定其可见性。
兼顾非流体表面模型中的遮挡情形,本文将上述3个必要条件进行整合形成迭代点边采样IVES。图 10展示了IVES的框架和含义,其伪代码如下。
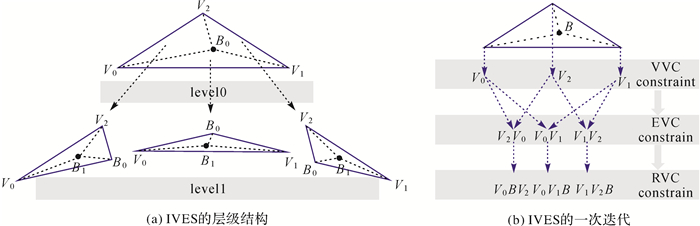
|
| 图 10 IVES框架 Fig. 10 The framework of IVES |
算法2:迭代点边采样。
输入:令B为可见面元f的重心,fv代表f为完全可见面元,pv代表f为非完全可见面元,emp代表f内部的所有像素都已被处理,sub(f)→{f0, f1, f2}为根据B将f划分为3个子区域。
输出:面元f的可见性
function IVES (f):
f←fv
if f 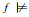
f←pv
return
end if
if 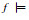
return
else do
sub (f)→{f0, f1, f2}
IVES (fi)
end if
end function
1.4 基于图割优化选取最佳纹理多视纹理映射的目的是从多视影像中选取三维表面模型面元的最佳纹理。考虑到空间连续性,邻接面元的纹理最好来源于同一张影像。因此,多视纹理映射可以看成基于马尔科夫随机场的多标签分类问题。
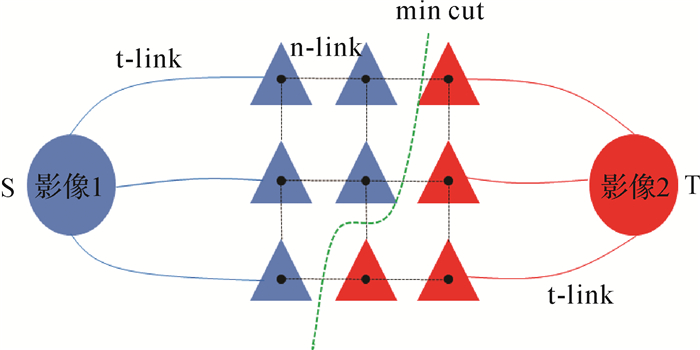
在得到每张影像的完全可见面元后,根据面元之间的拓扑邻接关系构建标签图G(V, E)。如图 11所示,G(V, E)由顶点V和边E组成,其中左右两个终端节点为图的源点S和汇点T,代表两类不同的标签;其余中间节点代表完全可见面元。节点之间通过t-link和n-link边连接。t-link为连接终端节点与中间节点的边,边上的权重代表中间节点被指定为不同标签的概率;n-link为连接中间节点的边,边上的权重代表邻接面元被指定为同一标签的概率。多标签分类问题本质是求解一组标签集和实现最大化后验概率(maximum a posteriori,MAP),其等价于最小化后验能量函数[35]。在计算机视觉中,图割是最小化能量函数的经典算法[36]。本文采用文献[6]中的方法构建能量函数
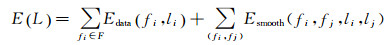 (7)
(7)
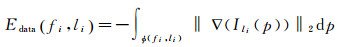 (8)
(8)
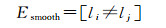 (9)
(9)
|
| 图 11 基于面元之间的邻接关系构建标签图 Fig. 11 The labeled graph based on adjacent primitives |
式中,数据项Edata通过Sobel算子求得影像li的梯度,并累加面元fi投影区域(fi, li)内的像素梯度获取;平滑项Esmooth通过potts模型来计算。利用alpha-expansion[29]最小化E(L),求得完全可见面元的最佳纹理标签。
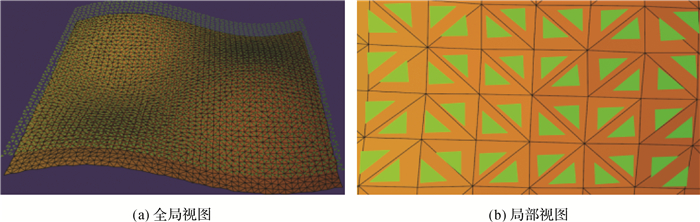
2 试验与分析 2.1 精度分析本文设计了3组试验数据A、B和C,用于论证算法的精度。如图 12(a)所示,每一组试验数据包含上下两层结构相同的三角网。在每一组试验数据中,上下两层三角网之间的距离不断递增(A、B、C中上下两层的距离依次为0.01,1.0和100)。给定一正射视点V,则在3组数据中,上层三角网中的面元都是完全可见面元,而下层三角网中的面元都是非完全可见面元(如图 12(b)所示)。
|
| 图 12 合成模型 Fig. 12 Synthetic models |
表 1-表 3为Z缓冲区算法、光线追踪算法和本文算法可见性检测的精度统计。其中vis代表完全可见面元的数量,occ代表被遮挡面元的数量,acc代表检测精度,e代表Z缓冲区算法和光线追踪算法中指定的人工偏差。在表 3中,n代表执行投影区域优化之前的检测精度;y代表执行投影区域优化后的检测精度。对比表 1-表 3,可以看出,Z缓冲区算法和光线追踪算法的精度受限于人工指定的偏差:如果指定的偏差过小,很多可见面元会被误识别为不可见面元;若偏差过大,不可见面元会被误识别为可见面元。本文提出的无偏差指定的可见性检测算法,在执行投影区域优化后,其精度可以达到100%。
| A | B | C | |||||||||||
| e | vis | occ | acc/(%) | e | vis | occ | acc/(%) | e | vis | occ | acc/(%) | ||
| 0.001 56~0.1 | 9603 | 1 | 50.01 | 0.003~0.1 | 9603 | 1 | 50.01 | 7.81e-4~0.1 | 4735 | 4869 | 99.30 | ||
| 7.81e-4 | 9592 | 12 | 50.00 | 0.001 56 | 4718 | 4886 | 99.13 | 3.91e-4 | 4324 | 5280 | 95.02 | ||
| 3.91e-4 | 8331 | 1273 | 50.26 | 7.81e-4 | 4711 | 4893 | 99.05 | 1.95e-4 | 3585 | 6019 | 87.33 | ||
| 1.95e-4 | 7051 | 2553 | 49.86 | 3.91e-4 | 4140 | 5464 | 93.11 | 9.77e-5 | 3175 | 6429 | 83.06 | ||
| 9.77e-5 | 6272 | 3332 | 49.98 | 1.95e-4 | 3512 | 6092 | 86.57 | 4.88e-5 | 2934 | 6670 | 80.55 | ||
| 4.88e-5 | 5915 | 3689 | 50.11 | 9.77e-5 | 3136 | 6468 | 82.65 | 2.44e-5 | 2812 | 6792 | 79.28 | ||
| 2.44e-5 | 5750 | 3854 | 50.10 | 4.88e-5 | 2916 | 6688 | 80.36 | ||||||
| 1.22e-5 | 2789 | 6815 | 79.04 | 2.44e-5 | 2813 | 6791 | 79.29 | 1.22e-5 | 2747 | 6857 | 78.60 | ||
| 1.22e-5 | 2768 | 6836 | 78.82 | ||||||||||
| 模型A | 模型B | 模型C | |||||||||||
| e | vis | occ | acc/(%) | e | vis | occ | acc/(%) | e | vis | occ | acc/(%) | ||
| 0.012 5~0.1 | 9604 | 0 | 50.00 | 1.95e-4~0.1 | 4802 | 4802 | 100.00 | 1.95e-4~0.1 | 4802 | 4802 | 100.00 | ||
| 1.95e-4~0.006 | 4802 | 4802 | 100.00 | 9.77e-5 | 4763 | 4841 | 99.59 | 9.77e-5 | 4753 | 4851 | 99.49 | ||
| 9.77e-5 | 4774 | 4830 | 99.70 | 4.88e-5 | 4233 | 5371 | 94.08 | 4.88e-5 | 4168 | 5436 | 93.40 | ||
| 4.88e-5 | 4342 | 5262 | 95.21 | 2.44e-5 | 3077 | 6527 | 82.04 | 2.44e-5 | 3190 | 6414 | 83.22 | ||
| 2.44e-5 | 3327 | 6277 | 84.64 | 1.22e-5 | 2080 | 7524 | 71.66 | 1.22e-5 | 2147 | 7457 | 72.36 | ||
| 1.22e-5 | 2346 | 7258 | 74.43 | ||||||||||
| A | B | C | |||||||||||
| PCR | vis | occ | acc/(%) | PCR | vis | occ | acc/(%) | PCR | vis | occ | acc/(%) | ||
| n | 4736 | 4868 | 99.31 | n | 4717 | 4887 | 99.11 | n | 4734 | 4870 | 99.29 | ||
| y | 4802 | 4802 | 100.00 | y | 4802 | 4802 | 100.00 | y | 4802 | 4802 | 100.00 | ||
2.2 效率分析
本文利用43张多视影像(图 13)重建的三维表面模型(图 14)分析算法效率。对比表 4-表 6的统计结果可知,在惰性投影的辅助下,本文算法处理的面元总数相较于其他两种算法减少了近1/3;在IVES的作用下,采样次数相较于其他两种算法下降了近2200万。并且,使用VES时的采样次数可以进一步减少。对于表 4-表 6的统计结果,以下3个方面需要注意:①当e=0.000 01时,Z缓冲区算法的采样次数和时间比本文方法更少,主要因为此时指定的e过小,导致很多可见面元仅仅在被采样数个像素后就被标识为不可见面元;②Z缓冲区算法的时间消耗随着e的增加而增长,主要因为随着e的增大,越来越多的像素被判别为可见像素,需要更多的采样次数方能判定面元的可见性;③光线追踪算法的时间消耗随着e的增加而逐渐减少,主要因为虽然较大的e会使得采样次数增加,但是光线追踪算法所需的时间主要花费在空间查找中,即越大的e会降低遍历空间索引中非叶节点的次数[24],从而加快达到叶节点的速度。本文算法在兼顾精度的前提下,效率更高。

|
| 图 13 用于三维重建的部分影像 Fig. 13 Part of images used in 3D reconstruction |

|
| 图 14 三维表面模型 Fig. 14 3D surface |
| e | 处理的面元数 | 采样次数 | 时间消耗/s |
| 0.000 01 | 14 514 510 | 186 659 322 | 20.54 |
| 0.000 1 | 14 514 510 | 269 039 318 | 26.90 |
| 0.001 | 14 514 510 | 295 725 638 | 29.28 |
| 0.01 | 14 514 510 | 303 479 553 | 29.52 |
| e | 处理的面元数 | 采样次数 | 时间消耗/s |
| 0.000 01 | 14 514 510 | 263 249 353 | 1 666.48 |
| 0.000 1 | 14 514 510 | 263 421 883 | 1 622.45 |
| 0.001 | 14 514 510 | 265 066 824 | 1 248.05 |
| 0.01 | 14 514 510 | 295 846 279 | 706.68 |
| 采样类型 | 处理的面元数 | 采样次数 | 时间消耗/s |
| IVES | 10 230 279 | 246 995 434 | 28.47 |
| VES | 10 230 279 | 194 294 149 | 24.73 |
2.3 纹理模型对比
本文使用两个数据集验证所提算法在多视纹理映射中的优越性。第1个数据集是ISPRS和EuroSDR提供的基础数据集,其对应的纹理模型如图 15(a)所示,本文将其命名为M1模型;第2个数据集为武汉大学校园的倾斜影像,其对应的纹理模型如图 15(b)所示,本文将其命名为M2模型。

|
| 图 15 基于本文方法生成的纹理模型 Fig. 15 Textured models based on the proposed method |
图 16-图 19是M1对应的纹理细节区域。其中图 16为没有执行可见性检测时的纹理效果,因此靠右的两张截图其纹理质量很差;左侧的截图纹理效果较好,这是由于对应的区域是一平面结构,不包含复杂的遮挡情况,通过投影参数就可获取正确的可见纹理。图 17验证了本文的投影区域优化对纹理映射的有效性。在投影区域优化后,纹理模型的质量得到明显提升,纹理错位、扭曲以及接缝等问题均被消除。对比图 16和图 17(b),可以看出,高精度的可见性检测对纹理映射的质量具有显著的促进作用。图 18和图 19分别是使用Z缓冲区算法和光线追踪算法进行可见性检测后的纹理效果,可以看出,由于受到人工偏差的影响,无法实现精确的可见性检测,导致纹理模型中存在较多瑕疵。图 20-图 22为本文算法与商业软件ContextCapture和开源软件MVE-Texturing的对比结果,其中上面一行的纹理结果对应于M1,下面一行的纹理结果对应于M2。可以看出基于本文算法生成的纹理模型相较于其他两者,具有更高的保真度和结构完整性。

|
| 图 16 没有执行可见性检测时的纹理细节 Fig. 16 Detail texturing without visibility tests |

|
| 图 17 基于本文算法的纹理细节 Fig. 17 Detail texturing based on the proposed method |

|
| 图 18 基于Z缓冲区算法的纹理细节 Fig. 18 Detail texturing based on the Z-buffer algorithm |

|
| 图 19 基于光线追踪算法的纹理细节 Fig. 19 Detail texturing based on the ray-tracing algorithm |

|
| 图 20 ContextCapture的纹理细节 Fig. 20 Detail texturing generated by ContextCapture |

|
| 图 22 本文方法的纹理细节 Fig. 22 Detail texturing of the proposed method |
3 总结
针对多视纹理映射的可见性检测问题,本文提出一种无需设定偏差的快速解决方案。首先,本文设计了一种基于着色编程的摄影模拟算法,保证生成的IVM没有离心投影偏移。其次,基于矢量栅格化准则和像素深度对IVM中的面元投影区域进行优化,显著地提高了可见性检测的精度。然后,提出惰性投影和迭代点边采样算法,减少处理面元的数量和像素采样次数,提高了可见性检测的效率。最后,基于图割算法选择最佳可见纹理,生成逼真的三维纹理模型。利用人工合成的数据和真实遥感影像进行试验,结果表明,本文方法的精度和效率优于经典的主流算法。基于本文算法,后面将从可见性拣选、路径规划、阴影图生成和空间相交检测等方面进行进一步的应用研究。
| [1] |
FRUEH C, SAMMON R, ZAKHOR A. Automated texture mapping of 3D city models with oblique aerial imagery[C]//Proceedings of the 2nd International Symposium on 3D Data Processing, Visualization and Transmission. Thessaloniki, Greece: IEEE, 2004: 396-403.
|
| [2] |
XU Lin, LI E, LI Jianguo, et al. A general texture mapping framework for image-based 3D modeling[C]//Proceedings of the 2010 IEEE International Conference on Image Processing. Hong Kong, China: IEEE, 2010: 2713-2716.
|
| [3] |
KATZ S, TAL A, BASRI R. Direct visibility of point sets[J]. ACM Transactions on Graphics, 2007, 26(3): Article No. 24.
|
| [4] |
PAGÉS R, BERJÓN D, MORÁN F, et al. Seamless, static multi-texturing of 3D meshes[J]. Computer Graphics Forum, 2015, 34(1): 228-238. DOI:10.1111/cgf.12508 |
| [5] |
ZHANG Weilong, LI Ming, GUO Bingxuan, et al. Rapid texture optimization of three-dimensional urban model based on oblique images[J]. Sensors, 2017, 17(4): 911. DOI:10.3390/s17040911 |
| [6] |
WAECHTER M, MOEHRLE N, GOESELE M. Let there be color! Large-scale texturing of 3D reconstructions[C]//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: Springer, 2014: 836-850.
|
| [7] |
PINTUS R, GOBBETTI E, CALLIERI M, et al. Techniques for seamless color registration and mapping on dense 3D models[M]//MASINI N, SOLDOVIERI F. Sensing the Past. Geotechnologies and the Environment, vol 16.[S.l.]: Springer, 2017: 355-376.
|
| [8] |
BAUMBERG A. Blending images for texturing 3D models[C]//Proceedings of the British Machine Vision Conference. Cardiff, UK: BMVA Press, 2002: 38.1-38.10.
|
| [9] |
BERNARDINI F, MARTIN I M, RUSHMEIER H. High-quality texture reconstruction from multiple scans[J]. IEEE Transactions on Visualization and Computer Graphics, 2001, 7(4): 318-332. DOI:10.1109/2945.965346 |
| [10] |
CALLIERI M, CIGNONI P, CORSINI M, et al. Masked photo blending:mapping dense photographic data set on high-resolution sampled 3D models[J]. Computers & Graphics, 2008, 32(4): 464-473. |
| [11] |
ROCCHINI C, CIGNONI P, MONTANI C, et al. Multiple textures stitching and blending on 3D objects[C]//Proceedings of the 10th Eurographics Workshop on Rendering. Granada, Spain: The Eurographics Association, 1999.
|
| [12] |
WEGHORST H, HOOPER G, GREENBERG D P. Improved computational methods for ray tracing[J]. ACM Transactions on Graphics, 1984, 3(1): 52-69. DOI:10.1145/357332.357335 |
| [13] |
GLASSNER A S. Space subdivision for fast ray tracing[J]. IEEE Computer Graphics and Applications, 1984, 4(10): 15-24. DOI:10.1109/MCG.1984.6429331 |
| [14] |
FRANKLIN W R, CHANDRASEKHAR N, KANKANHALLI M, et al. Efficiency of uniform grids for intersection detection on serial and parallel machines[C]//Proceedings of the New Trends in Computer Graphics. Berlin, Heidelberg: Springer, 1988: 288-297.
|
| [15] |
YU B T W, YU W W H. Image space subdivision for fast ray tracing[C]//Proceedings of the SPIE's International Symposium on Optical Science, Engineering, and Instrumentation. Denver, CO, United States: SPIE, 1999.
|
| [16] |
GREENE N, KASS M, MILLER G. Hierarchical Z-buffer visibility[C]//Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques. Anaheim, CA: ACM, 1993: 231-238.
|
| [17] |
WAND M, FISCHER M, PETER I, et al. The randomized z-buffer algorithm: interactive rendering of highly complex scenes[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2001: 360-370.
|
| [18] |
WILLIAMS L. Casting curved shadows on curved surfaces[J]. ACM SIGGRAPH Computer Graphics, 1978, 12(3): 270-274. DOI:10.1145/965139.807402 |
| [19] |
ANNEN T, MERTENS T, SEIDEL H P, et al. Exponential shadow maps[C]//Proceedings of the Graphics Interface. Windsor, Ontario, Canada: ACM, 2008: 155-161.
|
| [20] |
DOU H, YAN Y J, KERZNER E, et al. Adaptive depth bias for shadow maps[C]//Proceedings of the 18th meeting of the ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games. San Francisco, California: ACM, 2014: 97-102.
|
| [21] |
李明, 张卫龙, 范丁元. 城市三维重建中的自动纹理优化方法[J]. 测绘学报, 2017, 46(3): 338-345. LI Ming, ZHANG Weilong, FAN Dingyuan. Automatic texture optimization for 3D urban reconstruction[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 338-345. DOI:10.11947/j.AGCS.2017.20160467 |
| [22] |
张春森, 张卫龙, 郭丙轩, 等. 倾斜影像的三维纹理快速重建[J]. 测绘学报, 2015, 44(7): 782-790. ZHANG Chunsen, ZHANG Weilong, GUO Bingxuan, et al. Rapidly 3D texture reconstruction based on oblique photography[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 782-790. DOI:10.11947/j.AGCS.2015.20140341 |
| [23] |
FLORIANI L, MAGILLO P. Algorithms for visibility computation on terrains:a survey[J]. Environment & Planning B:Planning & Design, 2003, 30(5): 709-728. |
| [24] |
GEVA A. ColDet 3D collision detection[EB/OL].[2013-05-20]. https://sourceforge.net/projects/coldet.
|
| [25] |
WAECHTER C, KELLER A. Quasi-monte carlo light transport simulation by efficient ray tracing: United States, 7952583[P]. 2011-05-31.
|
| [26] |
BITTNER J, WONKA P. Visibility in computer graphics[J]. Environment & Planning B:Planning & Design, 2003, 30(5): 729-755. |
| [27] |
PERSSON E, STUDIOS A. Creating vast game worlds: experiences from Avalanche Studios[C]//Proceedings of the ACM SIGGRAPH 2012 Talks. Los Angeles, California, USA: ACM, 2012: Article No. 32.
|
| [28] |
SZELISKI R, ZABIH R, SCHARSTEIN D, et al. A comparative study of energy minimization methods for markov random fields[C]//European Conference on Computer Vision. Berlin Heidelberg: Springer, 2006: 16-29.
|
| [29] |
BOYKOV Y, VEKSLER O, ZABIH R. Fast approximate energy minimization via graph cuts[C]//Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra, Greece: IEEE, 1999: 377-384.
|
| [30] |
KOLMOGOROV V, ZABIH R. What energy functions can be minimized via graph cuts?[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(2): 147-159. |
| [31] |
PINEDA J. A parallel algorithm for polygon rasterization[C]//Proceedings of the 15th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1988: 17-20.
|
| [32] |
张祖勋, 苏国中, 郑顺义, 等. OpenGL成像机理及其与摄影测量方位元素的相关分析[J]. 武汉大学学报(信息科学版), 2004, 29(7): 570-574. ZHANG Zuxun, SU Guozhong, ZHENG Shunyi, et al. Relating OpenGL imaging process with exterior and interior parameters of photogrammetry[J]. Geomatics and Information Science of Wuhan University, 2004, 29(7): 570-574. |
| [33] |
SEGAl Mark, AKELEY Kurt. The opengl graphics system: a specification (Version 4.5)[EB/OL].[2017-06-29]. https://www.khronos.org/registry/OpenGL/specs/gl/glspec45.core.pdf.
|
| [34] |
DAVIDOVIČ T, ENGELHARDT T, GEORGIEV I, et al. 3D rasterization: a bridge between rasterization and ray casting[C]//Proceedings of the Graphics Interface 2012. Toronto, Ontario, Canada: ACM, 2012: 201-208.
|
| [35] |
LI S Z. Markov random field models in computer vision[C]//Proceedings of the European Conference on Computer Vision. Berlin, Heidelberg: Springer, 1994: 361-370.
|
| [36] |
GREIG D M, PORTEOUS B T, SEHEULT A H. Exact maximum A Posteriori estimation for binary images[J]. Journal of the Royal Statistical Society:Series B (Methodological)s, 1989, 51(2): 271-279. DOI:10.1111/j.2517-6161.1989.tb01764.x |




