遥感卫星区域覆盖分析能力作为衡量遥感卫星应用效能的重要指标,对任务规划、星座设计、观测数据获取、侦察与反侦察等任务都具有重要意义[1-3]。遥感卫星区域覆盖分析的主要任务是计算给定时间范围内卫星对地面区域的覆盖率、覆盖次数、总覆盖时间、平均覆盖时间、最大覆盖间隔和平均覆盖间隔等区域覆盖参数,常用方法主要有解析法、网格点法和几何运算法。解析法[4]基于卫星和地球的几何关系获取计算覆盖面积的解析公式,其主要针对单颗卫星覆盖区域被地面区域包含的情况,无法有效解决多卫星多地面目标区域的问题。网格点法[5-6]根据卫星覆盖的网格数计算覆盖率等各项参数,仿真软件STK[6]使用该方法计算卫星覆盖率。该方法的计算效率和精度受网格大小影响较大。几何运算方法[7-9]通过卫星覆盖区域与地面区域之间的并运算获取覆盖多边形,并得到相关参数。该方法精度较高,但仅适用于瞬时覆盖分析,只能获取总覆盖率,无法获取覆盖次数等参数,且效率较低。文献[10]提出基于多边形布尔运算的卫星区域覆盖分析法,能够有效计算覆盖分析参数,但未考虑卫星或传感器姿态变化,且无法给出卫星区域覆盖的准确时间范围。21世纪地理空间科学与应用要求能够提供实时应对高并发请求的在线服务[11]和基于星载的实时计算服务[12-13],但在面对多星多地面区域的覆盖分析时,所述算法或者计算量大,或者效率较低,或者无法给出全面的卫星区域覆盖分析结果,尤其当遥感卫星发生机动后,无法及时获取卫星变轨事件对后续地面覆盖的影响。现阶段已经开始从基于地面的数据处理转移到基于星载计算机的数据处理,但是由于星载计算机平台的体积、功耗等受到了严格的限制,处理能力有限,更加凸显了面临的处理效率问题。同时,上述算法存在分析结果表达效果不理想、无法有效降低数据认知难度等问题。STK等商业应用软件虽然能够提供相关的分析功能,但是无法提供即时有效地在线服务。同时,由于商业软件的版权与价格因素,导致其使用代价较大。
针对以上问题,为保证计算的效率与精度,并降低对结果的认知难度,本文提出一种遥感卫星区域覆盖实时分析方法与可视化服务。首先,提出一种多模式判断策略,将扩充外接矩形(extended bounding rectangle,EBR)、卫星覆盖区域和卫星瞬时覆盖最大跨度直线[10] 3种判断策略组合为多模式判断策略,精确获取传感器任意指向下的遥感卫星区域覆盖详细参数;然后,按照卫星数量和时间范围实时分割不断产生的计算任务,构建基于时间序列的数据实时处理方案;最后,计算结果以数据流的方式通过虚拟三维地球进行实时可视化,为分析和评估遥感卫星应用效能提供一种高效的计算与可视化方式的同时,也为后续相关的数据分析需求提供可借鉴的高性能实时处理与可视化方案。
1 基于多判断策略的参数快速获取方法 1.1 算法原理遥感卫星区域覆盖参数计算较为复杂,是影响计算效率的主要原因之一[14-15]。卫星运行的一个周期内,卫星覆盖区域仅存在有限时间与地面区域相交或包含,而避免其余时间段卫星覆盖区域的计算,能够较好地提高效率。
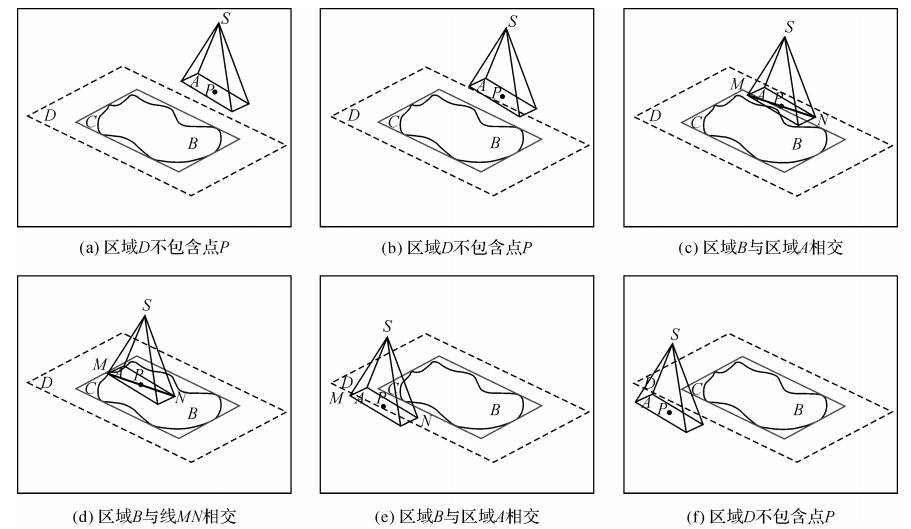
平面坐标系中的空间关系易于判断,因此本文约定参与空间关系判断的点、线和面均转换到平面坐标系下,并且不考虑高程因素的影响。同时,遥感卫星存在多种成像方式,本文以矩形锥体成像模型为例,其他成像方式可借鉴此方法。如图 1所示,区域A为卫星覆盖区域,点P为传感器中心线与地球椭球的交点,虚线为点P运动轨迹,点M和点N为点P运动轨迹两侧距离虚线最远的两点,MN即为卫星瞬时覆盖最大跨度直线,区域B为地面区域,区域C为地面区域最小外接矩形(minimum bounding rectangle,MBR),区域D为地面区域的MBR向4个方向扩充一定角度形成的EBR。
本文算法原理为:计算区域A在地球椭球上对应的最大圆心角αmax,αmax在卫星运行的整个周期内仅需计算一次。使用αmax对地面区域的MBR在4个方向上进行扩充,即可得到地面区域的EBR,即区域D。图 1(a)和(b)中,当区域D不包含点P时,区域A和区域B相离,进行下一时刻计算;否则,计算区域A,并判断与区域B的空间关系。图 1(c)中,当区域A与区域B包含或相交时,计算直线MN。图 1(d)中,若直线MN与区域B相交,区域A与区域B必定包含或相交,因此无需计算区域A,此时记录直线MN端点坐标,用于后续参数计算。图 1(e)中,当直线MN与区域B相离,重新开始计算区域A,并判断区域A与区域B是否包含或相交。图 1(f)中,当区域A与区域B相离时,重新开始计算点P,并判断区域D是否包含点P。
|
| 图 1 算法原理 Fig. 1 Algorithm principle |
1.2 算法执行流程
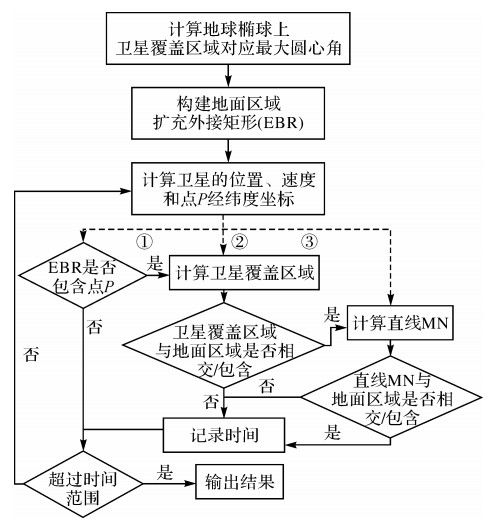
基于算法原理,本文通过不同情况下执行不同的判断策略来实现算法的流程。如图 2所示,编号①、②和③为种判断策略,通过控制各个步骤的执行与否来实现对3种判断策略的选择执行。定义未进行姿态机动的卫星本体坐标系为O-XYZ,进行姿态机动后的卫星本体坐标系为O-X′Y′Z′,算法具体执行过程如下:
|
| 图 2 算法流程 Fig. 2 Algorithm flowchart |
步骤1 数据准备。根据卫星的轨道参数和姿态变化,计算卫星覆盖区域对应的最大圆心角αmax,并获取地面区域的EBR。此EBR能够确保当传感器中心线与地球椭球的交点P不在EBR内时,卫星覆盖区域与地面区域相离。
步骤2 计算卫星的位置、速度和传感器中心线与地球椭球交点P的经纬度坐标。
步骤3 依据判断①,如果地面区域的EBR包含点P,执行步骤4;否则,执行步骤6。
步骤4 依据判断②,计算卫星覆盖区域,如果卫星覆盖区域与地面区域相交或包含,不再执行步骤3,并执行步骤5;否则,允许执行步骤3,并执行步骤6。
步骤5 依据判断③,如果直线MN与地面区域相交,不再执行步骤4,记录点M和点N坐标,并执行步骤6;否则,允许执行步骤4,并执行步骤6。执行该步骤的前提是卫星覆盖区域与地面区域相交或包含,因此无论直线MN与地面区域是否相交,均需记录时间。
步骤6 判断当前时间是否超过计算时间范围。若超过计算时间范围,则输出结果;否则,返回执行步骤2。
基于以上流程,步骤4在部分时间段内不被执行,避免了计算卫星地面覆盖区域。因此,在保证精度的前提下,能够实现遥感卫星区域覆盖分析参数计算效率的提高。同时,通过直线MN构建精确的覆盖多边形,能够一次性获取覆盖率、覆盖次数、总覆盖时间、平均覆盖时间、最大覆盖间隔和平均覆盖间隔等参数。
1.3 构建扩充外接矩形在遥感卫星的运行周期内,必定存在一个角度αmax,使得卫星覆盖区域在地球椭球上对应的最大圆心角不超过αmax。然而,卫星本体的姿态机动会导致αmax计算变得复杂,因此为了简化计算的同时保证精度,本文提出一种计算αmax的特殊方法。
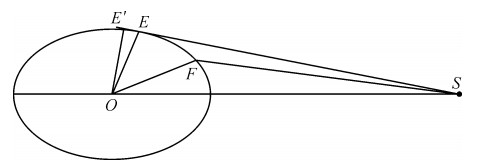
如图 3所示,某一时刻t,S为卫星,E和F为卫星覆盖范围在切面图下与地球椭球的两个交点,
|
| 图 3 卫星地面覆盖区域切面 Fig. 3 Sectional view of satellite's area coverage |
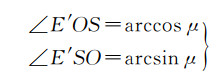 (1)
(1)
式中,μ=OE′/OS。在△FOS中,通过式(2)和式(3)分别获取∠FSO和∠OFS
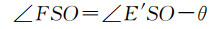 (2)
(2)
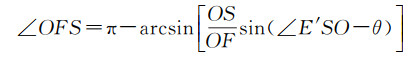 (3)
(3)
结合式(1)、式(2)、式(3),可得
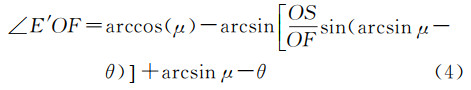 (4)
(4)
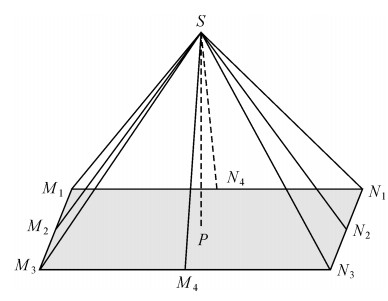
式(4)求导可得∠E′OF对OE′单调递减,对OS、OF和θ单调递增。由于OE′>Eminor,OF≤Emajor,OS≤Omajor,Emajor=6 378 137.0 m为地球椭球半长轴,Eminor=6 356 752.314 2 m为地球椭球短半轴,Omajor为卫星远地点与地心的距离。为方便计算,令OE′=Eminor,OF=Emajor,OS=Omajor。如图 4所示,在矩形椎体传感器模型,水平半角θH=∠M4SP,垂直半角
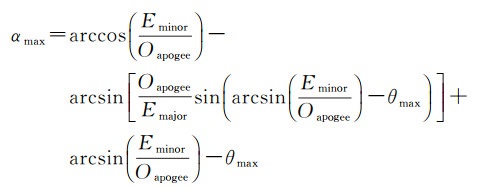 (5)
(5)
|
| 图 4 矩形椎体模型 Fig. 4 Rectangular cone model |
使用αmax对地面区域的MBR 4个方向进行扩充,可得地面区域的EBR。
1.4 确定覆盖区域相关点线面如图 4所示,点M1为卫星覆盖区域边界上的点,点P为传感器中心线与地球椭球交点。根据θH和θV,可以坐标系O-XYZ下的向量SP1和SM1。以SM1为例,当卫星本体姿态随俯仰角pitch、偏航角yaw和滚动角roll中的一个或多个发生变化时,通过空间关系变换,获取SM1在J2000坐标系下的矢量为
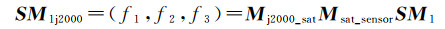 (6)
(6)
式中,Μsat_sensor为O-XYZ与O-X′Y′Z′之间的变换矩阵Mj2000_sat=[XTYTZT]通过卫星在J2000坐标系下的位置(xsat, ysat, zsat)和速度(vxsat, vysat, vzsat)获取。通过SM1j2000与卫星位置构造直线方程,并与地球椭球方程联合求解,即可得到卫星覆盖区域的点M1坐标,组成卫星覆盖区域的其余点可依此法获取。当获取组成卫星覆盖区域的点集合之后,转换为平面坐标系下经纬度坐标,即可构建卫星覆盖区域。
当遥感卫星传感器为矩形锥体成像模型时,卫星地面覆盖区域在点P轨迹线两侧距离该轨迹线最远的两点为矩形两条对角线之一的两个端点,即点M1和N3或点M3和N1。这两个端点的轨迹构成卫星地面覆盖区域的覆盖带,因此,在考虑偏航角yaw的情况下,直线MN确定方法如下
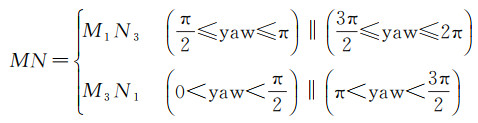 (7)
(7)
为了提供更好的认知效果,需要将计算结果及时高效的可视化,故本文采用一种“动态可视化语言+流式计算引擎”结合的实时流计算与可视化方案来实现遥感卫星区域覆盖参数的高效计算和实时可视化。
2.1 动态可视化语言CZML虚拟三维地球已经成为融合、分析与展示不同时空尺度下空间信息的标准方式[16-18],并且存在多种表示和交换空间数据的国际标准,如KML[19]、GML[20]、CityGML[21]等。其中,大部分虚拟三维地球采用KML(keyhole markup language)实现空间目标的分析和可视化,但KML在表示动态目标时,存在效率低和无法处理网络环境下实时变化的流式数据的问题。CZML(cesium markup language)作为一种基于JSON的描述动态目标的标记语言,可以通过数据分组实现高效、增量的流式数据传输,能够很好地应对基于网络的、实时的、数据驱动的可视化和分析[22],是一种在基于网络的虚拟三维地球中表达和分析动态目标的有效手段[23-24]。
在CZML格式数据中,一个目标的所有属性信息存储在一个Packet中,一个Packet能够被分割为大小不等的多个Packet,各个Packet能够依据数据流进行组合。使用CZML格式传递数据,能够很好地通过控制数据的多少来保证单次数据计算和传输的时效性,遥感卫星对地观测场景的CZML数据格式如下
[{//地面区域Packet
″id″:″AreaTarget/AreaTarget1″,
″polygon″:{地面区域数据}
},
{//卫星信息Packet
″id″:″Satellite/ZIYUAN_3-2″,
″path″:{轨道绘制数据},
″model″:{卫星模型数据},
″position″:{位置相关数据},
″orientation″:{姿态相关数据}
},
{//传感器信息Packet
″id″:″Satellite/ZIYUAN_3-2/Sensor/Sensor2″,
″parent″:″Satellite/ZIYUAN_3-2″, //所在卫星
″agi_rectangularSensor″:{传感器参数},
″orientation″:{姿态相关数据}
}]
其中包括了地面区域Packet、卫星Packet和传感器Packet。由于不同的Packet计算消耗时间不同,因此,可将每个Packet单独分别进行数据传输和可视化。
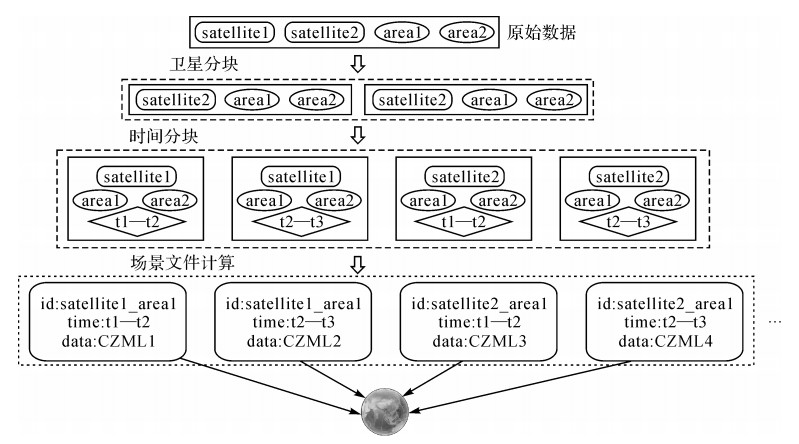
2.2 实时流计算与可视化大数据处理方面存在很多优秀的技术与框架,如Apache Hadoop、Apache Spark、Apache Flink、Apache Storm等[24]。其中,Apache Hadoop无法满足实时的计算任务与需求[26-27],Apache Storm仅支持流处理[27],Apache Spark基于批处理来模拟[28],而Apache Flink则完全基于流处理,并通过流处理来模拟批处理。因此,Apache Flink通过一套方案实现流数据处理和批数据处理,能够更好地满足科研工作者的需求[29-30]。本文算法基于Apache Flink的实时流计算流程如图 5所示,具体流程为:
(1) 外部计算任务输入到卫星分块模块中,被分解为单颗卫星与所有地面区域的组合,即〈satellite1, area1, area2〉、〈satellite2, area1, area2〉等。
(2) 在时间分块模块中,数据根据计算的时间范围被分解为单颗卫星、所有地面区域与特定时间段的组合,即〈satellite1, area1, area2, t1—t2〉、〈satellite1, area1, area2, t2—t3〉等。
(3) 在场景文件计算模块中,使用本文算法进行计算,生成单卫星、单地面区域与特定时间段情况下的CZML数据文件,即图 5中的CZML1、CZML2、CZML3等,任意CZML完成计算,即发送至虚拟三维地球,由虚拟三维地球进行可视化。
|
| 图 5 实时计算与可视化 Fig. 5 Real-time calculation and visualization |
3 试验与分析 3.1 试验数据与测试硬件环境
本文试验平台操作系统为Ubuntu 16.04 LTS,处理器为Intel Core i7-6700HQ 2.60 GHz,8核,内存为16 GB;Apache Flink版本为1.7.0;STK版本为11.2.0。本文试验数据选用3颗遥感卫星和两个地面区域,具体信息如表 1所示,其中,地面区域数据为相应点的经度和纬度坐标,地面区域1为(89.358 4°, 31.303 9°), (89.211 7°, 27.345°), (95.516 8°, 27.149 5°), (95.565 7°, 30.961 8°);地面区域2 (-110.60°, 43.32°), (-104.75°, 42.83°), (-104.15°, 45.85°), (-104.45°, 49.13°), (-109.68°, 50.54°), (-110.18°, 46.94°), 卫星坐标计算步长为1 s,卫星地面覆盖区域通过采集8个点构建而成。时间范围为2018-12-01 T00:00:00至2018-12-11 T00:00:00。
| 类别 | 参数 | |
| 资源三号2星 | 轨道根数 | 1 41556U 16033A 18360.16266073.00000446 00000-0 23037-4 0 9996 2 41556 97.4159 75.2737 0003224 104.0789 336.3495 15.21266840142925 |
| 传感器参数 | θH=1°,θV=3°,pitch=10°,yaw=10°,roll=10° | |
| 高分5号 | 轨道根数 | 1 43461U 18043A 18360.11744794-.00000015 00000-066166-5 0 9996 2 43461 98.1459 296.8281 0000886 308.5684 51.5438 14.57785406 33726 |
| 传感器参数 | θH=2°,θV=5°,pitch=20°,yaw=10°,roll=20° | |
| WorldView4 | 轨道根数 | 1 41848U 16067A 18360.22122525.00001879 00000-0 22607-3 0 9999 2 4184897.8946 75.8578 0001575 8.2585 351.8677 14.85111481114924 |
| 传感器参数 | θH=3°,θV=3°,pitch=20°,yaw=30°,roll=20° |
3.2 计算结果对比与分析
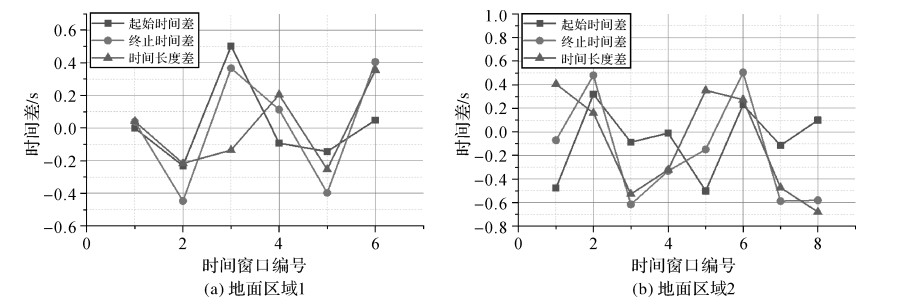
基于测试数据,采用本文算法和商业软件STK获取卫星覆盖区域与地面区域相交或包含的起止时间,并计算覆盖时间长度。通过对比,获取本文算法与STK计算结果的起始时间差、终止时间差和时间长度差结果分别如图 6、图 7和图 8所示。可以看出,本文算法与STK计算结果之间,起始时间差和终止时间差的变化范围均小于1 s,表明本文算法结果接近STK计算结果,具有较高的精度,能够满足遥感卫星区域覆盖分析精度的需求。
|
| 图 6 本文算法与STK计算结果的差值(资源三号2星) Fig. 6 Differences between calculation results of the method in this paper and STK (ZY3-02) |
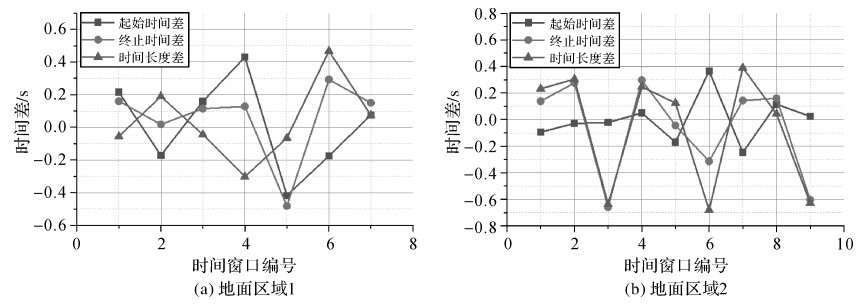
|
| 图 7 本文算法与STK计算结果的差值(高分5号) Fig. 7 Differences between calculation results of the method in this paper and STK (GF5) |
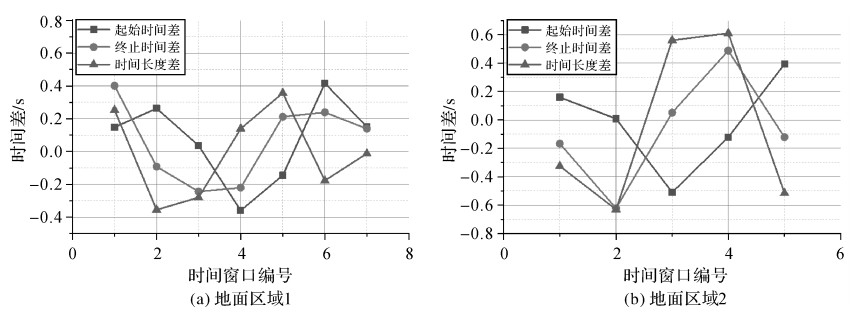
|
| 图 8 本文算法与STK计算结果的差值(WorldView 4) Fig. 8 Differences between calculation results of the method in this paper and STK (WorldView 4) |
为比较覆盖率,设置STK中地面区域网格划分单位为0.05°。通过STK中的覆盖分析,获取去除重叠部分之后的总覆盖率,与本文算法结果对比见表 3。通过对比可得,本文算法结果与STK分析结果差异较小,能够满足实际需求。
| 结果对比 | 资源三号2星覆盖率 | 高分5号覆盖率 | WorldView4覆盖率 | |||||
| 地面区域1 | 地面区域2 | 地面区域1 | 地面区域2 | 地面区域1 | 地面区域2 | |||
| STK结果 | 39.71 | 40.30 | 69.85 | 90.81 | 73.94 | 68.62 | ||
| 本文结果 | 39.70 | 40.16 | 69.83 | 90.82 | 73.92 | 68.88 | ||
3.3 计算结果效率对比与分析
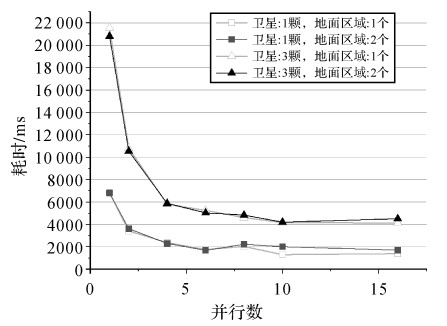
为验证采用多判断策略与流式计算协作的加速策略的合理性,通过设定不同数据量和算法并行数测试效率。表 4为加速策略耗时对比,结果表明,采用并行数为8的流式计算和判断策略结合能够获取超过6倍的加速比。图 9所示为不同计算并行数的耗时对比,结果表明,当数据量一定时,算法并行数越多,分割后的每份数据量越少,因此计算耗时越低;当算法并行数一定时,计算耗时与卫星数量成正比,符合预期,而地面区域的数量对计算耗时影响较小,原因是数据被分解为单颗卫星与所有地面区域的组合,针对不同的地面区域,卫星相关参数仅需计算一遍。当并行数超过8,即运行平台CPU核数时,计算耗时降低缓慢,甚至有所上升,主要是因为数据分割、传递和计算队列切换等操作导致。因此,算法最佳并行数应不大于运行平台CPU核数。
| 数据 | 无多判断策略 | 多判断策略 | 流式计算(并行数为8)+多判断策略 |
| 卫星:1颗,地面区域:1个 | 13 192 | 8579 | 2025 |
| 卫星:1颗,地面区域:2个 | 14 012 | 8725 | 2223 |
| 卫星:3颗,地面区域:1个 | 38 679 | 27 162 | 4604 |
| 卫星:3颗,地面区域:2个 | 38 821 | 27 295 | 4828 |
|
| 图 9 不同算法并行数计算耗时对比 Fig. 9 Comparison of computation time with different parallel numbers |
3.4 分析结果实时可视化展示
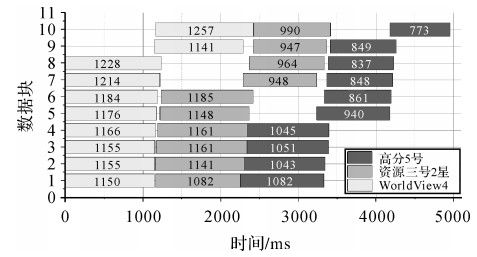
计算结果可视化能够有效地提高对数据的认知和理解,本文采用开源的三维虚拟地球Cesium[21-22],通过流式计算,实现计算结果的分块实时可视化。本文算法中,按照1天步长将计算时间2018-12-01 T00:00:00至2018-12-11 T00:00:00均分,计算并行数为8。图 10为测试数据的流式计算时间线,矩形中的数据为耗时长度,每一块数据均能够在完成计算后构建CZML数据文件并在三维虚拟地球中完成可视化。
|
| 图 10 流式计算时间线 Fig. 10 Timeline of stream computing |
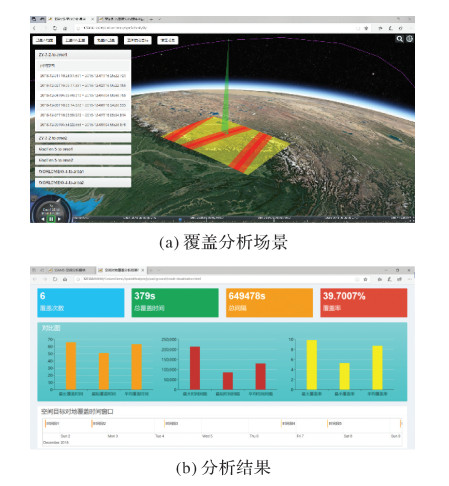
图 11为资源三号2星对地面区域1进行区域覆盖分析的可视化效果,图 11(a)为区域覆盖分析演示场景,包括卫星位置、传感器、地面区域、传感器覆盖区域和覆盖时间列表,图 11(b)为遥感卫星区域覆盖分析结果,包括覆盖次数、总覆盖时间、覆盖时间总间隔、覆盖率、空间目标对地覆盖时间窗口等信息。
|
| 图 11 场景与结果可视化 Fig. 11 Visualization of scenarios and results |
4 结语
空间对地观测任务中数据和计算量的增长,导致遥感卫星区域覆盖分析面临着不同的问题和挑战。探索能够同步兼顾精度和效率,并且能够有效辅助认知的方法,具有重要的研究意义。本文针对当前遥感卫星区域覆盖分析效率与表达方面的不足,提出基于流式计算的遥感卫星区域覆盖实时分析与可视化服务。通过不同判断策略的组合,提高了传感器任意指向下遥感卫星区域覆盖分析的计算效率,并获取了完整的遥感卫星区域覆盖分析参数;结合流式处理技术与虚拟三维地球,实现了分析结果的实时可视化。选取了3颗卫星和两个地面区域作为试验数据,通过对比计算结果,验证了本文算法在计算精度上的可靠性;通过构建不同数量卫星与地面区域的组合,并对比在不同并行数下的计算耗时,证明了本文方法具有较高的计算效率;最后通过计算结果的流式可视化,实现计算结果的分批增量可视化,改善了可视化的体验效果。作为在线服务,能够满足不同用户的需求,而无须考虑使用商业软件等带来的各种问题;提出的流式实时分析方案也可以应用到基于星载计算机的实时分析中。本文方案为后续相关分析提供了一种有益的借鉴,也为开展其他方面的分析与计算提供了参考。
| [1] |
王慧林, 邱涤珊, 黄小军, 等. 面向区域覆盖的电子侦察卫星规划方法研究[J]. 兵工学报, 2011, 32(11): 1365-1372. WANG Huilin, QIU Dishan, HUANG Xiaojun, et al. Research on schedule technique for area-detecting electronic reconnaissance satellite[J]. Acta Armamentarii, 2011, 32(11): 1365-1372. |
| [2] |
徐青, 姜挺, 周杨, 等. 空间态势感知信息支持系统的构建[J]. 测绘科学技术学报, 2013, 30(4): 424-432. XU Qing, JIANG Ting, ZHOU Yang, et al. Construction of space situational awareness information support system[J]. Journal of Geomatics Science and Technology, 2013, 30(4): 424-432. |
| [3] |
吕亮, 赵英豪, 徐青, 等. 一种遥感卫星连续过境区域快速判定方法[J]. 测绘科学技术学报, 2018, 35(2): 165-169, 174. LÜ Liang, ZHAO Yinghao, XU Qing, et al. A rapid method for determining continuous transit area of remote sensing satellite[J]. Journal of Geomatics Science and Technology, 2018, 35(2): 165-169, 174. |
| [4] |
张润.基于重访周期的对地侦察小卫星星座设计[D].西安: 西安电子科技大学, 2012. ZHANG Run. Design of the ground reconnotired minisat constellation based on revisit cycle[D]. Xi'an: Xidian University, 2012. |
| [5] |
马吉康.通信卫星组网仿真系统的设计与实现[D].北京: 北京邮电大学, 2008. MA Jikang. The design and implementation of simulation system of telecommunication satellite network[D]. Beijing: Beijing University of Posts and Telecommunications, 2008. |
| [6] |
刘华俊, 蔡波, 朱庆. 一种成像卫星区域覆盖的自适应规划方法[J]. 武汉大学学报(信息科学版), 2017, 42(12): 1719-1724. LIU Huajun, CAI Bo, ZHU Qing. Self-adaptive planning method of imaging reconnaissance satellites area coverage[J]. Geomatics and Information Science of Wuhan University, 2017, 42(12): 1719-1724. |
| [7] |
沈欣, 李德仁, 姚璜. 一种面向成像任务规划的光学遥感卫星成像窗口快速预报方法[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1468-1471. SHEN Xin, LI Deren, YAO Huang. A fast algorithm for imaging time window prediction of optical satellites considering J_2 perturbation for imaging mission scheduling[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1468-1471. |
| [8] |
汪荣峰. 空间态势可视化与分析技术[M]. 北京: 国防工业出版社, 2017: 360-377. WANG Rongfeng. Visualization and analysis technology of space situation[M]. Beijing: National Defense Industry Press, 2017: 360-377. |
| [9] |
吴晓洋.基于几何拓扑的遥感卫星高精度对地覆盖分布式算法研究与应用[D].开封: 河南大学, 2016. WU Xiaoyang. Research and application on remote sensing satellite high-precision to cover the distributed algorithm based on the geometric topology[D]. Kaifeng: Henan University, 2016. |
| [10] |
汪荣峰. 基于多边形布尔运算的卫星区域覆盖分析算法[J]. 装备学院学报, 2016, 27(2): 83-87. WANG Rongfeng. Analysis algorithm for satellite regional coverage based on polygonal Boolean operation[J]. Journal of Equipment Academy, 2016, 27(2): 83-87. |
| [11] |
范协裕.空间云计算平台集群服务与矢量数据并行处理研究[D].北京: 中国科学院大学, 2013. FAN Xieyu. Research on technologies of cluster service and parallel vector data processing for spatial cloud computing platform[D]. Beijing: University of Chinese Academy of Sciences, 2013. |
| [12] |
王密, 张致齐, 董志鹏, 等. 高分辨率光学卫星影像高精度在轨实时云检测的流式计算[J]. 测绘学报, 2018, 47(6): 760-769. WANG Mi, ZHANG Zhiqi, DONG Zhipeng, et al. Stream-computing based high accuracy on-board real-time cloud detection for high resolution optical satellite imagery[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(6): 760-769. DOI:10.11947/j.AGCS.2018.20170618 |
| [13] |
WANG Mi, ZHANG Zhiqi, DONG Zhipeng, et al. Stream-computing of high accuracy on-board real-time cloud detection for high resolution optical satellite imagery[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 50-59. DOI:10.11947/j.JGGS.2019.0206 |
| [14] |
卢万杰, 徐青, 蓝朝桢, 等. 卫星对地覆盖时间窗口实时计算方法[J]. 地球信息科学学报, 2019, 21(11): 1689-1698. LU Wanjie, XU Qing, LAN Chaozhen, et al. A real-time calculation method for satellite ground coverage time window[J]. Journal of Geo-Information Science, 2019, 21(11): 1689-1698. |
| [15] |
LU Wanjie, XU Qing, LAN Chaozhen, et al. Microservice-based platform for space situational awareness data analytics[J]. International Journal of Geo-information Science, 2020, 1(1): 1-22. |
| [16] |
BLASCHKE T, DONERT K, GOSSETTE F, et al. Virtual globes:serving science and society[J]. Information, 2012, 3(3): 372-390. DOI:10.3390/info3030372 |
| [17] |
DE PAOR D G, DORDEVIC M M, KARABINOS P, et al. Exploring the reasons for the seasons using Google earth, 3D models, and plots[J]. International Journal of Digital Earth, 2017, 10(6): 582-603. DOI:10.1080/17538947.2016.1239770 |
| [18] |
LÜ Liang, XU Qing, LAN Chaozhen, et al. Sino-InSpace:A digital simulation platform for virtual space environments[J]. ISPRS International Journal of Geo-Information, 2018, 7(9): 373. DOI:10.3390/ijgi7090373 |
| [19] |
Open Geospatial Consortium. OGC KML 2.3[EB/OL].[2015-08-04]. http://docs.opengeospatial.org/is/12-007r2/12-007r2.html.
|
| [20] |
TONG X H. Modeling cadastral spatial features based on geography markup language in GIS:a case study in Shanghai[J]. Journal of Environmental Informatics, 2005, 6(2): 103-110. |
| [21] |
GRÖGER G, PLÜMER L. CityGML-interoperable semantic 3D city models[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2012, 71: 12-33. |
| [22] |
ZHU Liangfeng, WANG Zhongliang, LI Zhiwen. Representing time-dynamic geospatial objects on virtual globes using CZML-Part I:overview and key issues[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 97. DOI:10.3390/ijgi7030097 |
| [23] |
ZHU Liangfeng, LI Zhiwen, WANG Zhongliang. Representing time-dynamic geospatial objects on virtual globes using CZML-Part Ⅱ:impact, comparison, and future developments[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 102. DOI:10.3390/ijgi7030102 |
| [24] |
KUMAR K, LEDOUX H, STOTER J. Dynamic 3D visualization of floods: case of the Netherlands[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Delft, The Netherlands: [s.n.], 2018, XLII-4/W10: 83-87.
|
| [25] |
代明竹, 高嵩峰. 基于Hadoop、Spark及Flink大规模数据分析的性能评价[J]. 中国电子科学研究院学报, 2018, 13(2): 149-155. DAI Mingzhu, GAO Songfeng. Framework performance evaluation based on Hadoop, Spark and Flink large-scale data analysis[J]. Journal of CAEIT, 2018, 13(2): 149-155. |
| [26] |
VERMA A, MANSURI A H, JAIN N. Big data management processing with Hadoop MapReduce and Spark technology: a comparison[C]//Proceeding of 2016 Symposium on Colossal Data Analysis and Networking. Indore, India: IEEE, 2016: 1-4.
|
| [27] |
MARCU O C, COSTAN A, ANTONIU G, et al. Spark versus Flink: understanding performance in big data analytics frameworks[C]//Proceeding of 2016 IEEE International Conference on Cluster Computing. Taipei, China: IEEE, 2016: 433-442.
|
| [28] |
LOPEZ M A, LOBATO A G P, DUARTE O C M B. A performance comparison of open-source stream processing platforms[C]//Proceeding of 2016 IEEE Global Communications Conference. Washington, DC: IEEE, 2016: 1-6.
|
| [29] |
CARBONE P, KATSIFODIMOS A, EWEN S, et al. Apache FlinkTM:stream and batch processing in a single engine[J]. Bulletin of the IEEE Computer Society Technical Committee on Data Engineering, 2015, 36(4): 28-38. |
| [30] |
倪政君, 夏哲雷. Flink的并行Apriori算法设计与实现[J]. 中国计量大学学报, 2018, 29(2): 175-180. NI Zhengjun, XIA Zhelei. Design and implementation of the parallel Apriori algorithm on Flink platforms[J]. Journal of China University of Metrology, 2018, 29(2): 175-180. |



