2. 中国科学院大学, 北京 100049;
3. 上海华测导航技术股份有限公司, 上海 201799
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai Huace Navigation Technology Co., Ltd., Shanghai 201799, China
进入21世纪,网络RTK(real-time kinematic)技术和精密单点定位技术(precise point positioning, PPP)日趋成熟并得到广泛应用,定位精度可达到分米级甚至厘米级[1-3]。但网络RTK技术仍存在覆盖范围受限于参考网内部、数据通信负担大等缺陷,而PPP的主要问题在于首次收敛和重收敛时间比较长。文献[4]提出了PPP-RTK的概念,并利用参考站坐标已知的优势,解算出实时状态的空间参数和各种误差参数,通过误差建模等手段将改正信息播发给用户,实现用户在服务区域内的实时精密单点定位。PPP-RTK亟须解决的问题是模糊度的快速固定问题,文献[5]提出利用已有的CORS网增强PPP的方法来解决非差模糊度快速固定的难题,实现了PPP-RTK的定位原型。文献[6]提出利用全球电离层模型约束PPP达到缩短初始化时间的目的,但初始化时间仍需15 min左右。目前IGS已经向用户提供实时轨道和钟差产品(http://www.rtigs.org),但基于其产品实现3~5 min内的快速收敛仍具有一定的难度[7]。
实现PPP-RTK技术需要高精度的卫星轨道和钟差,在此基础上,利用区域或者全球的IGS参考站数据解算出卫星的相位偏差,实现PPP快速模糊度固定,缩短定位收敛时间[8]。近年来,PPP-RTK技术从采用无电离层组合观测值向采用非差非组合观测数据发展。非差非组合技术通过约束电离层和对流层参数,能进一步加快PPP的收敛速度[9]。相对于将观测噪声放大了近3倍的传统无电离层组合PPP模型,非差非组合PPP避免了因为观测量的组合形式引起的噪声放大情况[10]。文献[11-13]对非差非组合PPP模型进行深入研究,并在精确提取斜路径电离层总电子含量和分离站星DCB等方面取得应用,其提取的STEC精度较高,定位可靠性强,分离的卫星DCB误差少于0.1 ns。文献[14]从数学推导上证明UofC模型与非组合模型两者是等价的,均优于传统的无电离层组合,而附加电离层约束的非组合模型能有效提高模糊度的固定率。文献[15]对105个MGEX测站分别进行多系统非差非组PPP单频和双频解算,结果表明,多系统非差非组合PPP的收敛时间比单GPS系统缩短60%以上。
基于非差非组合的PPP-RTK技术的区域高精度定位,关键在于区域电离层误差和对流层误差改正模型的构建。对于区域电离层模型的研究,一些国家和地区建立了本地的广域差分增强系统,如美国的WAAS利用动态网格模型可以改正中纬度用户端约80%电离层延迟[16-17]。文献[18]利用相位平滑伪距的方法解求卫星DCB并提取电离层,试验对山东地区采用球谐模型进行电离层建模,获得与CODE解算VTEC差值均方根1.22 TECU、STD为0.93 TECU的结果。文献[19]利用非差非组合PPP提取电离层,采用天顶总电子含量多项式模型进行区域电离层建模,模型拟合效果可达2 TECU左右。在区域对流层建模研究方面,文献[20]利用Bernese估算香港参考站数年的天顶对流层,建立了符合香港地区的精密对流层改正模型,新模型精度比Saastammoinen模型提高了2~3倍。文献[21]利用区域CORS参考站数据实时解算参考站天顶对流层参数,通过数学模型内插出流动站天顶对流层参数以达到加快PPP模糊度固定和缩短收敛时间的效果,试验表明,在平缓地区可达到10 mm以内的内插精度。文献[22]改进了传统BP神经网络对区域进行精密对流层建模,在拟合和预报精度上分别为7.83、8.52 mm。文献[23]基于数年的气象数据分析了对流层的投影误差,并提出了更高精度两步估计法估计对流层湿延迟。
以上大部分的研究都是基于无电离层组合观测数据,本文提出了基于非差非组合的PPP区域电离层模型和区域ZTD对流层模型,并应用于PPP-RTK大气改正系统,建立了相应的数据服务系统。该方法基于非差非组合PPP函数模型,通过坐标约束和模糊度固定的方法从区域跟踪网观测数据中提取出电离层延迟值和ZTD对流层延迟。电离层建模采用星间单差多项式模型消除接收机硬件延迟对电离层建模的影响,对流层延迟由于不包含硬件延迟则使用非差建模。为适应实时需求,采用短时建模方式,每个历元生成一套电离层模型和对流层参数。用户端接收来自服务端的大气模型参数,采用大气参数约束的方法以实现实时快速高精度PPP-RTK定位。
1 非差非组合PPP大气延迟提取在非差非组合精密单点定位函数模型中,将斜路径电离层延迟和天顶对流层延迟等大气延迟参数作为待估量保留在观测方程中,PPP在解求其他参数的同时估计大气延迟参数,观测方程见式(1)
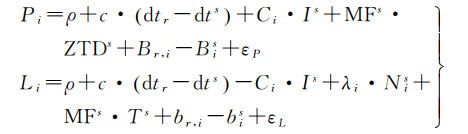 (1)
(1)
式中,P表示伪距原始观测值;L表示相位原始观测值;下标i表示卫星的频率号;上标s为卫星号;ρ为地卫的几何距离;c表示光速常数;dtr表示接收机的钟差;dts表示卫星的钟差;Ci表示电离层延迟参数系数,当i=1时,Ci=1, 当i=2时,Ci=f12/f22,f表示频率;I表示在卫星第一频点的斜路径方向上的电离层延迟;MF表示对流层从测站天顶方向到卫星斜路径方向上的投影函数;T表示测站天顶方向对流层延迟;N表示相位模糊度;Br表示接收机端的硬件延迟;Bs表示卫星端的硬件延迟;br表示接收机端的相位延迟;bs表示卫星端的相位延迟;εP、εL分别代表伪距观测量和相位观测量的观测噪声。
在非差非组合PPP中,卫星钟差使用的无电离层组合的钟差产品,需要进行硬件延迟修正。修正后的钟差记为 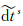
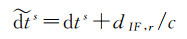 (2)
(2)
同理,由于接收机硬件延迟可被接收机钟差所吸收,得到新的接收机钟差参数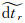
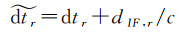 (3)
(3)
式中
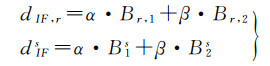 (4)
(4)
式中,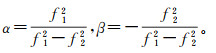
将式(2)、式(3)、式(4)代入式(1)中,得到式(5)
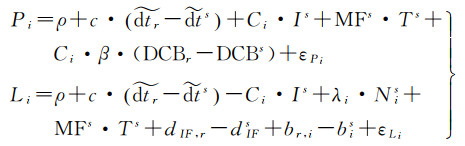 (5)
(5)
式中,DCBr=Br, 1-Br, 2,DCBs=B1s-B2s。
由于DCBr、DCBs参数与电离层参数、相位模糊度参数线性相关,参数之间无法分离,因此,式(5)可以改写为式(6)
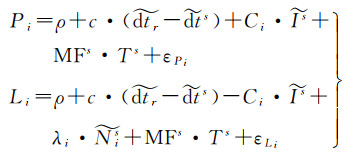 (6)
(6)
分别记为等效电离层参数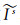
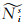
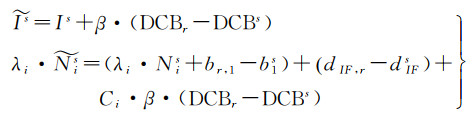 (7)
(7)
基于式(6),服务端的跟踪站坐标精确已知,可以对观测方程中的站坐标进行约束。对模糊度进行部分固定的策略,进一步提高参数的解算精度。当非差非组合PPP收敛一段时间后,服务端提取的等效电离层延迟和天顶对流层延迟精度很高,提取的大气参数可以作为大气建模的原始观测值。
2 区域大气改正模型 2.1 星间单差电离层改正模型针对区域卫星斜路径电离层延迟的特点,构建斜路径电离层延迟为参考点经纬度到卫星穿刺点经纬度差值的函数,对每颗卫星模型可表达为式(8)
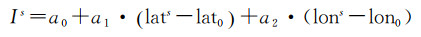 (8)
(8)
式中,Is为斜路径电离层延迟值;lats、lons为卫星穿刺点纬度、经度;lat0、lon0为参考点纬度、经度;a0、a1、a2为各项系数。
由于式(8)是基于每颗卫星的模型,卫星端的硬件延迟能被常数项a0所吸收。由式(7)可知,通过非差非组合PPP提取的斜路径电离层延迟中既含有接收机端的硬件延迟又含有卫星端的硬件延迟, 因此接收机端的硬件延迟不能被模型参数吸收。为消除其影响,选定一个卫星作为参考卫星,对非差非组合PPP提取的等效电离层延迟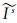
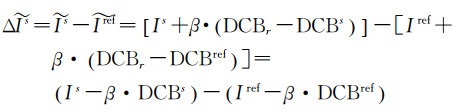 (9)
(9)
式中,上标ref为参考卫星。
在式(9)中,接收机端的硬件延迟被消除掉后,式(8)的模型变成星间单差电离层延迟,见式(10)
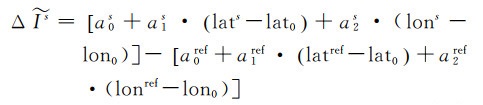 (10)
(10)
对于式(9)、式(10),由于不同测站和不同的卫星系统的DCBr不同,故卫星s与ref必须是同一测站同一卫星系统,即基于该模型解算时必须为每一个测站的每一个卫星系统选定一颗参考星。服务端建模可以选择卫星系统中高度角最高的卫星作为参考星。
2.2 对流层改正模型同样地,对流层的改正模型仍可以采用式(8)的表达形式进行建模。由于对流层不存在色散效应,也不存在设备的硬件延迟的影响,不需要对每颗卫星单独处理,也不需要进行星间单差建模。采用天顶对流层建模的形式,将所有卫星斜路径上的对流层延迟值投影到参考点天顶方向上进行建模,其模型函数如式(11)
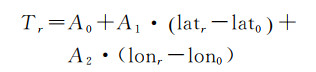 (11)
(11)
式中,Tr为天顶对流层延迟;A0、A1、A2为各项系数。
在服务端网络跟踪站足够的情况下(4个以上),单个历元即可完成电离层和对流层改正模型参数的计算,不需要进行法方程的叠加。但受限于网络参数播发的压力,实际可以按照需求拉长播发间隔。
3 用户端大气延迟参数约束用户端可以通过网络或其他方式接收服务端播发的大气延迟参数。基于星间单差电离层模型的系数、卫星穿刺点经纬度以及参考点经纬度,用户利用式(10)拟合出卫星的等效斜路径电离层延迟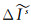
 (12)
(12)
式中,等式的左边中,上标表示卫星号,下标表示卫星的频率;ΔĨ表示模型拟合的电离层虚拟观测值;T表示模型拟合的天顶对流层虚拟观测值;在等式的右边中,u表示坐标参数系数矩阵;s表示伪距和载波相位观测值的钟差系数,是一个元素均为1的2n×1的矩阵;MFs表示对流层从天顶方向到斜路径方向的投影矩阵;C表示电离层参数的系数矩阵;D表示伪距和相位的模糊度系数;0表示零矩阵;x表示坐标参数矩阵;dt表示接收机钟差参数;T表示接收机天顶对流层参数;Ĩ为等效斜路径电离层参数矩阵;N表示卫星模糊度参数矩阵;εp、εL、εΔĨ、εT分别表示伪距、相位、电离层虚拟观测值和天顶对流层观测值的观测噪声;QP、QL、QΔĨ、QT分别表示伪距、相位、电离层单差虚拟观测值和天顶对流层虚拟观测值的方差;K表示电离层参数的约束系数矩阵,是卫星与参考卫星的单差观测方程的系数矩阵,以最后一颗(第n颗)卫星为参考星,若去掉全为0的行和列后为K′,则可得式(13)
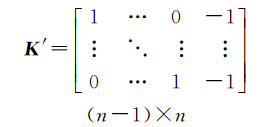 (13)
(13)
由式(12)可知,用户端相位和伪距的观测方程与式(5)相同,用户端的解算策略依然与服务端保持一致。用户端参数的误差项与服务端解算的参数误差项有很高的的相似性,使得用户端与服务端两者具有很高的自洽性,从而使得用户端的参数可以快速分离,达到快速收敛的目的。
4 试验分析基于以上模型和定位算法,开发了非差非组合PPP-RTK数据处理系统。系统包括服务端及用户端两个处理模块。服务端主要利用连续观测站数据进行非差非组合PPP,在每个观测站上提取高精度电离层、对流层等大气延迟值,并在此基础上,构建区域的电离层和对流层模型。服务端计算得到模型参数后,对电离层和对流层参数按照RTCM3的格式进行编码,利用网络或者卫星等方式向用户进行信息播发。用户接收到实时数据流后,进行电文解析获取改正参数和模型参数,并基于式(12)进行实时PPP定位解算。
对以上算法模型和软件进行测试,选取上海市的8个连续跟踪CORS站的实时数据作为系统服务端的数据源,搭建区域服务系统。选取上海CORS网的两个站作为用户站(CH51、CH52),进行实时非差非组合伪动态PPP定位,在服务端跟踪站网选择另一区域(上海西虹桥北斗产业园SCHC)进行实时动态PPP-RTK用户端试验。伪动态PPP试验时间从2019年10月16日6时到2019年10月18日6时,用户端两个站每10 min重新启动进行重新收敛测试,实时动态PPP试验时间为2020年6月24日11时。试验中,服务端的建模采样间隔为5 s,用户端的观测数据采样间隔为1 s。服务端使用的跟踪站相邻距离普遍在20~60 km,用户端测试站与服务端跟踪站普遍在30~60 km。服务端跟踪站(外围)、用户端实时伪动态测试站(CH51、CH52)及用户端实时动态测试站(三角标志)分布见图 1。

|
| 图 1 试验区域及测站分布 Fig. 1 Experimental area and station distribution |
首先采用上海华测导航技术股份有限公司开发的CORSPPP2010程序进行服务端大气延迟值提取。该软件包含了实时钟差计算模块和实时的宽窄巷相位偏差UPD(uncalibrated phase daley)估计模块,并配套相关的网络播发参数功能。另外,针对PPP-RTK服务,上海华测导航技术股份有限公司还提供实时的轨道产品。钟差、UPD及卫星轨道实时产品都是基于分布全球的100多个跟踪站的数据解算得到,不同产品用到的跟踪站稍有区别,针对国内的用户需求,其中UPD产品国内跟踪站超过40个。服务端UPD产品基于小数偏差估计[25]得到,其基本思想为基于MW组合观测值计算宽巷的浮点解模糊度,利用小数偏差估计解得宽巷UPD与固定的宽巷模糊度,然后使用L1、L2实数模糊度组合成无电离层模糊度,并将其重构为宽巷模糊度与窄巷模糊度的线性组合,最后将宽巷模糊度代入该线性组合,再利用小数偏差估计方法得到窄巷UPD。本文在CORSPPP2010的基础上,按照上述大气模型开发了区域大气模块。用户端的定位程序为上海华测导航技术股份有限公司配套的SWASPPP程序,其核心算法与CORSPPP2010保持一致,能接收来自服务端播发的卫星钟差、卫星轨道、相位偏差UPD和大气模型参数等信息,并在用户端加入基于大气参数约束的PPP实时定位模块。
在卫星模糊度参数固定方面,服务端和用户端均采用相同的部分相位模糊度固定的策略。两套程序对GPS、Galileo和BDS系统卫星都进行了模糊度固定,由于GLONASS系统采用的是频分多址的模式,没有对GLONASS系统卫星进行模糊度固定,只进行卡尔曼滤波浮点解解算。基于宽巷模糊度波长较长易于固定的特性,服务端和用户端程序的固定策略是对卫星两个频率的相位观测值组成宽巷、窄巷模糊度,先固定宽巷模糊度,再固定窄巷模度。卫星相位模糊度固定需要先进行接收机端和卫星端的相位偏差校正恢复其整周特性。接收机端的相位偏差可以通过选定一个参考卫星进行星间单差进行消除,卫星端的相位偏差则通过服务端的UPD模块的UPD产品进行修正。对于浮点解小数部分较小的宽巷模糊度可直接取整,其他浮点解则采用LAMBDA[26]搜索法得到。获得宽巷模糊度的单差浮点解以及整周模糊度的单差值后,可与L1、L2的单差浮点模糊度组成观测方程,进行滤波更新,得到更加精确的L1、L2单差浮点模糊度。通过UPD产品,对L1、L2的窄巷UPD进行修正,同样利用LAMBDA搜索法得到L1对应的N1单差模糊度整周解。根据宽巷单差整周模糊度和N1单差模糊度即可确定N2单差整周模糊度。同理,模糊度固定后,对其他参数进行更新。
为适应大气的实时快速变化,本文试验的服务端的大气模型均采用单历元建模,但受限于播发频率,每1 min播发一次大气参数。
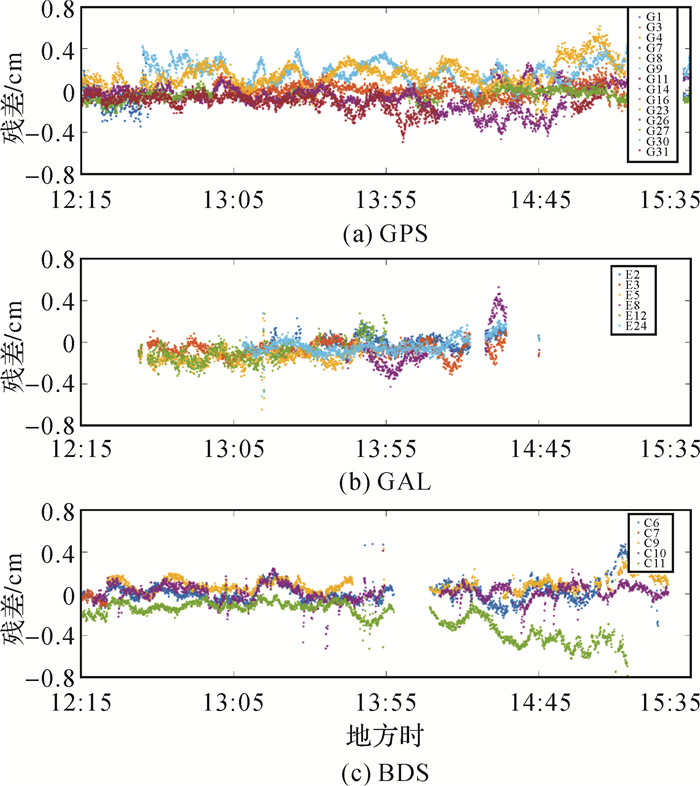
4.1 大气模型内符合精度在电离层建模完成后每颗卫星得到3个模型参数,对流层在整个区域可解得3个模型参数。计算得到的模型参数可以拟合出实时的电离层延迟和对流层延迟,通过拟合值与提取值的比较可计算出模型的内符合精度。计算电离层内符合精度时,对于不同的卫星系统,均选择该卫星系统高度角最高的卫星作为参考卫星。由于建模使用的观测值为已固定模糊度的卫星的大气延迟值,因此参与建模的卫星中不包含GLONASS系统。电离层活动在午间更活跃,本文对GPS、Galileo及BDS 3个系统在此期间的结果进行分析,其单差内符合序列见图 2。图中Galileo和BDS系统部分时段出现中断是由于在该时间段内模糊度没有固定。其他时段和其他卫星的序列与示例类似。从序列中可以看出不同系统的卫星残差相当,大部分都在5 mm以内,Galileo系统相对较稳定,但未表现出系统间模型效果的明显差异。
|
| 图 2 不同卫星系统电离层残差序列 Fig. 2 Ionospheric residual sequences of different satellite systems |
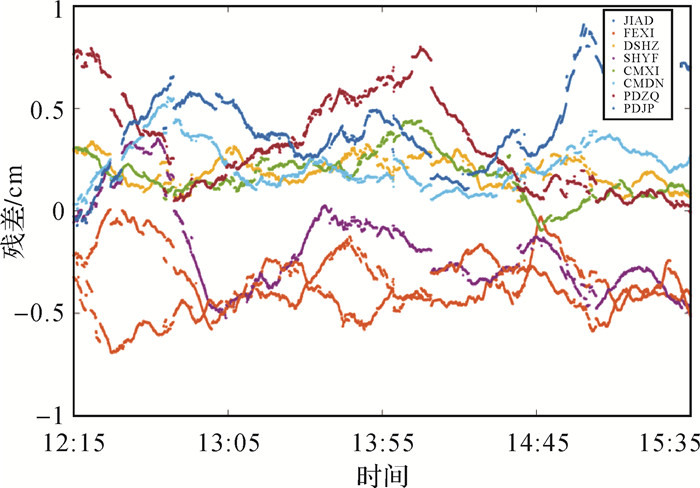
计算对流层时,由于一个测站只有一个天顶对流层参数,把模型拟合的天顶对流层与服务端提取的天顶对流层投影到斜路径作差,得到观测路径对流层延迟残差见图 3。由图 3可知,不同站点的对流层残差序列都在1 cm内,所有测站的残差序列都不是0均值序列,但所有测站总体呈现0均值序列。造成该结果的原因是由于不同测站与参考点位置的天顶投影误差引起的,但由于测站围绕参考中心分布,所以所有测站残差序列呈现0均值分布。
|
| 图 3 不同测站对流层残差序列 Fig. 3 Tropospheric residual sequences at different stations |
统计GPS、Galileo和BDS 3个系统的电离层及对流层延迟的均方根误差(root mean squared error,RMSE),其定义见式(14)
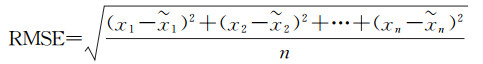 (14)
(14)
式中,x1、x2、…、xn表示观测值;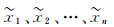
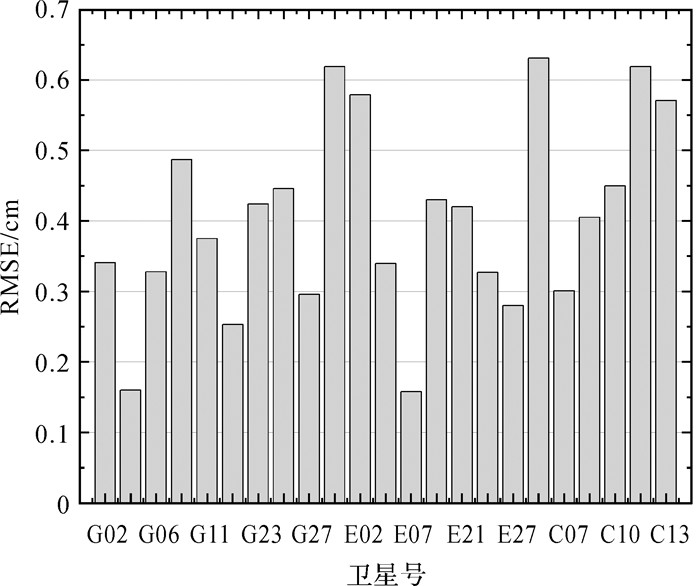
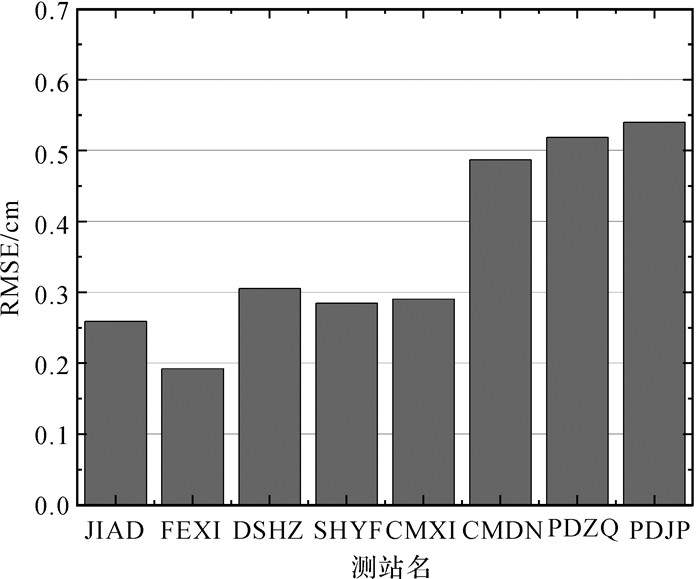
以JIAD测站为例,2019年11月20日12时到22时部分卫星电离层延迟的RMSE统计情况见图 4,其他测站和未列出卫星情况相似。8个跟踪站在12时到22时的天顶方向对流层的RMSE统计情况见图 5。
|
| 图 4 每颗卫星电离层模型内符合RMSE Fig. 4 Internal RMSE of ionospheric model for each satellite |
|
| 图 5 对流层模型内符合RMSE Fig. 5 Internal RMSE of troposphere model of different stations |
图 4和图 5中,所有卫星的电离层延迟RMSE均小于7 mm,所有测站天顶对流层的RMSE均在6 mm以内。由图 2到图 5可以看出,本文建立的电离层模型、对流层模型与非差非组合PPP提取的大气参数有很好的拟合效果,说明了模型的有效性。此外,由于目前用于对比的电离层、对流层公开产品达不到本文提取参数的精度,因此没有采用外部第3方产品进行外符合精度校验。
4.2 实时非差非组合伪动态PPP收敛测试用户端通过网络接收到服务端的轨道、钟差、UPD、大气参数后,可进行实时动态定位。其中接收的大气模型参数可以按照式(12)、式(13)进行约束。根据上文可以看出无论是电离层模型还是对流层模型,基本都可以达到毫米级的拟合效果。理论上,若通过非差非组合PPP提取的大气延迟值无误差,则模型最后的使用精度亦可以达到毫米级,在用户端约束定权时,可以使用毫米级的方差约束。但无论通过何种方法提取大气延迟值,无可避免地存在提取误差,故实际的模型精度不能直接采用内符合精度。本文采用经验常数定权的方法给约束的虚拟观测方程定权,其定权方案见式(15)
 (15)
(15)
式中,Wion为电离层虚拟观测值的权;Wtrop为对流层虚拟观测值的权。
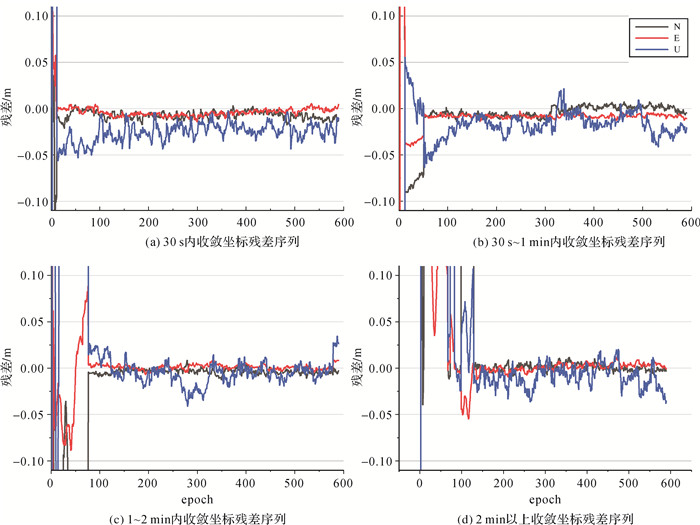
试验时间从2019年10月16日6时到2019年10月18日6时,将CH51、CH52作为用户端进行非差非组合伪动态PPP定位,测试首次收敛时间。以上海华测导航技术股份有限公司长期连续监测定位的测站的站坐标作为每个测站的坐标真值,以CH51的4个典型时段为例,其动态坐标与真值差值在NEU 3个方向上的时间序列见图 6。
|
| 图 6 CH51站附加大气参数约束获取的动态坐标与真值差值序列 Fig. 6 Kinematic coordinates time series of CH51 with ionosphere/troposphere constraint |
在图 6中,图 6(a)为30 s内收敛的情况、图 6(b)为1 min内收敛的情况、图 6(c)、图 6(d)分别为2 min内和2 min以外的收敛情况。图中由于纵坐标的显示尺度问题,部分曲线未能显示完全。在实际统计中,绝大部分首次收敛时间和收敛后的稳定性如图 6(a)所示,其NEU 3个方向均在30 s内收敛到0.05 m,且收敛后较稳定;图 6(b)相较于图 6(a),3个方向收敛相对较慢,尤其是U方向较差,收敛后U方向也有起伏。图 6(c)、图 6(d) 3个方向收敛都较慢,主要有可能因为定权方案不是最优导致的,最优的定权方案仍需继续研究。
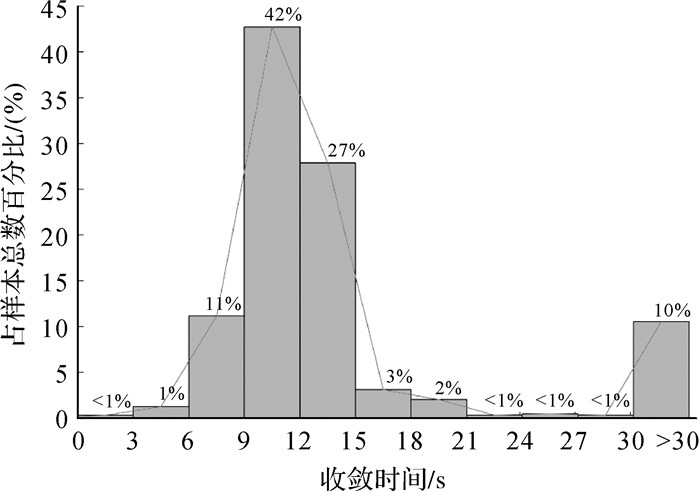
为验证约束模型的效果,对CH51、CH52两个用户站进行多次试验,在试验期间每10 min重新启动进行重新收敛,共获得646组统计数据。由于电离层和对流层对定位结果影响不同,电离层延迟对坐标水平方向定位影响较大,而对流层一般对坐标高程影响较大。设定坐标水平方向误差小于0.05 m和三维位置误差小于0.10 m为阈值,若连续120个历元内误差不超过阈值则认为首次收敛完成。对所有以上646组结果进行收敛性统计,其中,坐标水平方向收敛时间超过30 s的占了约10%,最长的收敛时间为400 s;三维位置收敛时间超过30 s的占了约13%,最长的收敛时间为442 s。平面坐标收敛情况见图 7及表 1,三维位置收敛情况见图 8及表 2。
|
| 图 7 水平方向收敛时间概率分布 Fig. 7 Convergence time probability distribution in the horizontal direction |
| 收敛时间 | 数目 | 百分比/(%) |
| 30 s内 | 576 | 89.16 |
| 1 min内 | 593 | 91.80 |
| 2 min内 | 620 | 95.98 |
| 2 min以上 | 26 | 4.02 |
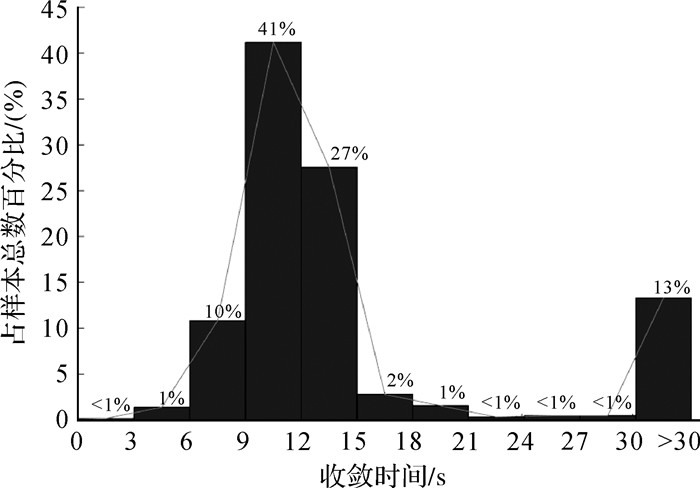
|
| 图 8 三维坐标收敛时间概率分布 Fig. 8 Convergence time probability distribution in three-dimensional direction |
| 收敛时间 | 数目 | 百分比/(%) |
| 30 s内 | 557 | 86.22 |
| 1 min内 | 573 | 88.70 |
| 2 min内 | 603 | 93.34 |
| 2 min以上 | 43 | 6.66 |
由图 7及图 8可以看出,无论是水平方向统计还是三维方向统计,30 s内收敛占了大部分时段。由表 1可知,大部分(89.16%)的试验组在30 s内收敛到水平0.05 m,91.80%的试验组在1 min内收敛。整体而言,绝大多数(95.98%)可在2 min内收敛。由表 2可知,附加大气改正模型约束的非差非组合动态PPP中,三维坐标30 s内收敛的时段有557个、1 min内收敛的有573个、2 min内收敛的有603个、仅43个时段收敛时间超过2 min,分别占648个时段总数的86.22%、88.70%、93.34%和6.66%。
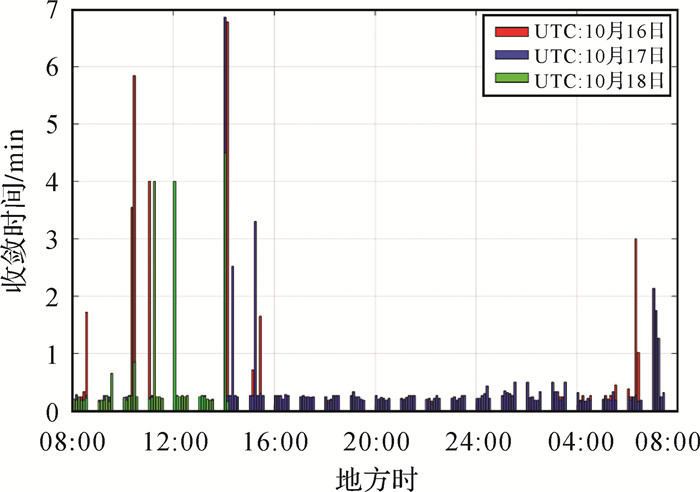
从统计结果上看,水平方向和三维方向分别有10%、13%左右的试验组结果超过30 s,以CH51三维方向PPP结果为例,对该站的不同试验组的收敛时间和开始启动时间进行统计,见图 9。
|
| 图 9 CH51收敛时间 Fig. 9 Convergence time of CH51 |
由图 9可以看出,从16:00到次日05:00收敛都在30 s内,效果不佳时段主要集中在白天电离层活跃时段,尤其是下午14:00附近,由于该时间段电离层在一天中最活跃,相对其他时段,该时段附近的定位试验中部分试验组的收敛性较差,收敛时间相对较长。针对上述现象,本文认为原因主要由两个方面引起:一方面由于电离层存在白天活跃晚上平静的特点,所以呈现出晚上的总体收敛效果要好于白天;另一方面,由于本文采用了常数定权方法,与大气的时空变化无关,没有顾及不同地方不同时段的模型精度的差异,所以部分拟合效果并不是最优。
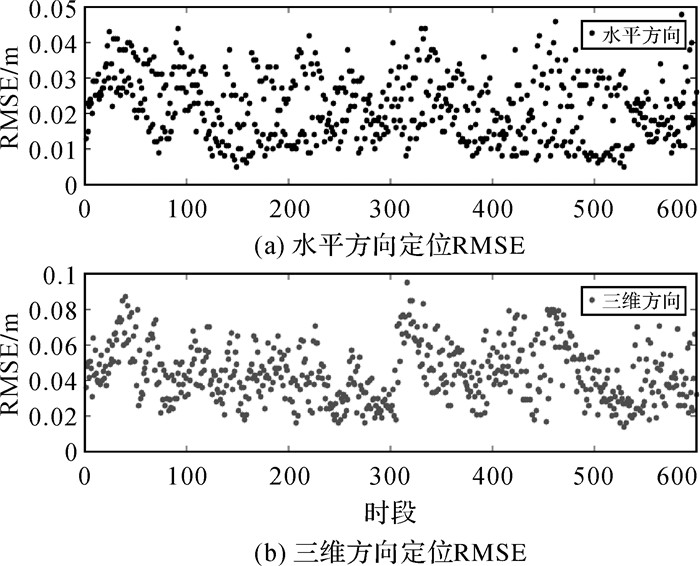
在实际应用中,用户除了关注PPP的收敛速度外,收敛后的精度也是另一个重要关注的指标。对以上所有试验进行收敛后的精度统计,计算试验收敛后水平方向以及三维方向的定位RMSE。对每个试验统计的结果表明用户端PPP试验收敛后水平方向RMSE如图 10所示,大部分分布在1~4 cm,三维方向总体分布在2~8 cm。对所有试验进行归并统计得到的水平方向RMSE为2.35 cm,三维方向RMSE为4.63 cm,精度统计见图 10。
|
| 图 10 水平及三维方向定位RMSE Fig. 10 Horizontal and three-dimensional positioning RMSE |
在定位当中,大气约束对模糊度的固定有着很大的影响,模糊度的首次固定时间、固定成功率也反映了大气模型的效果。本文对各个试验的首次模糊度固定时间进行统计(见表 3)。统计表明,所有试验的首次固定时间均大于等于10 s,30 s内实现首次固定占了较大比例(95.51%),统计结果见表 3。
| 首次固定时间/s | 数目 | 百分比/(%) |
| 10~15 | 405 | 62.69 |
| 15~20 | 189 | 29.26 |
| 20~30 | 23 | 3.56 |
| >30 | 29 | 4.49 |
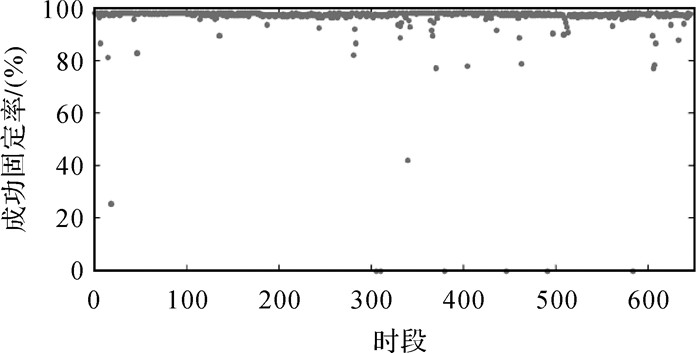
模糊度固定是否可靠、正确对最终的参数估计影响巨大,为确保模糊度固定正确,需要对其进行检核,试验采用以下检核手段:①设定一定的ratio阈值,模糊度的ratio值必须大于该阈值。②bootstrap检验。③设定模糊度残差阈值,不能有大的残差。④多历元一致性检核。在滤波过程中连续多个历元最优解是否一致。⑤浮点解一致性检核,浮点解参数历元之间应该是平滑的。经过这些检核可认为模糊度固定是可靠的,对模糊度的成功固定率进行统计,结果见图 11。
|
| 图 11 模糊度固定率 Fig. 11 Fixed rate of ambiguity |
图中大部分(93.34%)时段试验的模糊度固定率在95%以上。对所有试验进行统计,得到总体的模糊度固定率为95.97%。
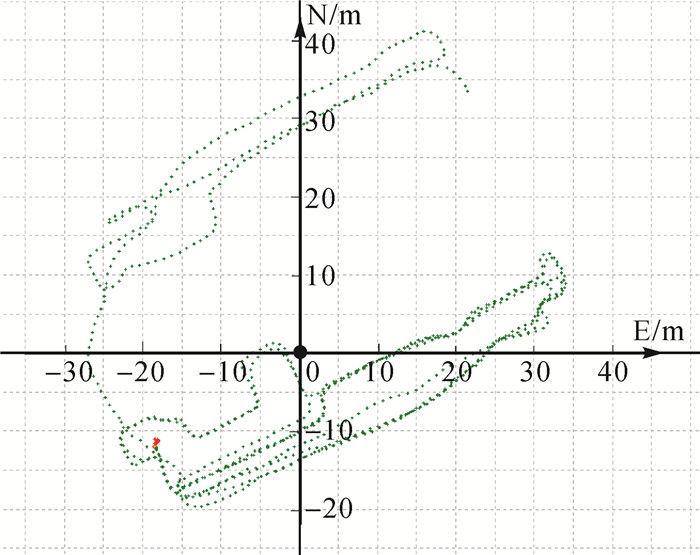
4.3 实时动态试验上述结论是基于伪动态实时定位试验,为验证模型在实时动态定位中的效果,进行动态用户端PPP-RTK试验。动态试验于2020年6月24日上午在上海青浦区的上海西虹桥北斗产业园区内进行,运动速度为约1 m/s,其动态轨迹见图 12,其中红色的点代表PPP浮点解结果,绿色的点代表模糊度固定的结果。
|
| 图 12 用户端PPP-RTK动态试验运动轨迹 Fig. 12 Trajectory of PPP-RTK real-time experiment |
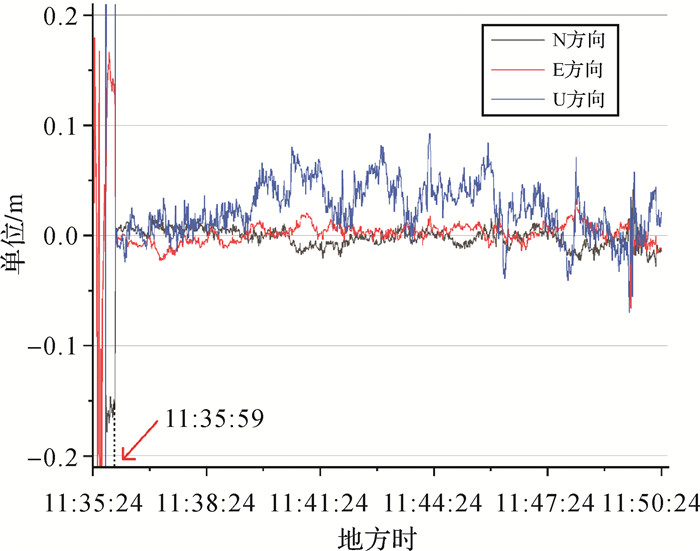
以RTK解算结果作为坐标参考标准对用户端PPP-RTK的试验结果进行检核,得到PPP-RTK定位结果与RTK定位结果的差值序列见图 13。
|
| 图 13 PPP-RTK实时动态定位结果与RTK定位结果在NEU方向的差值序列 Fig. 13 Coordinate residuals between PPP-RTK and RTK positions in NEU direction |
试验从11:35:24开始,开始数个历元PPP-RTK模糊度未固定执行的是PPP浮点解策略,误差较大。11:35:59实现了载波相位模糊度首次固定,与4.2中情况类似,水平方向和垂直方向在模糊度定后均稳定收敛。对PPP-RTK定位结果的模糊度固定率、首次固定时间以及以RTK的定位结果作为参考标准的收敛后的精度进行统计,结果见表 4。从动态试验的结果(表 4)中可以看出首次收敛时间、水平方向和三维方向的定位精度都与前面静态试验结果一致。
| 首次固定(收敛)时间/s | 模糊度固定率/(%) | 固定(收敛)后水平方向RMSE/cm | 固定(收敛)后三维方向RMSE/cm |
| 36 | 96.1 | 1.13 | 3.21 |
5 结论
本文服务端利用非差非组合PPP的手段提取斜路径电离层延迟和天顶对流层,对每颗卫星进行斜路径上的单差建模,对参考点的天顶方向进行对流层建模。试验采用分布在上海的7个测站作为服务端的跟踪站,两个测站作为用户端测试站验证模型的精度与用户端应用非差非组合动态PPP的效果,并进行了实时动态PPP试验验证,结论如下。
(1) 以非差非组合PPP提取的电离层延迟和对流层延迟为基准,得到两种模型的内符合RMSE均在1 cm内。
(2) 附加大气模型约束的用户端非差非组合动态PPP的水平和三维方向收敛时间可以大幅度缩短,其中三维方向收敛中:30 s内收敛、1 min内收敛和2 min内收敛的试验时段分别占比为86.22%、88.70%、93.34%,大气模型约束效果明显。
(3) 实时的测试数据结果表明:电离层模型在加速非差非组合动态PPP的水平方向收敛上起到了一个非常明显的作用;整体附加大气改正模型约束对PPP三维方向上快速收敛也可以达到与水平方向相当的水平。
(4) 附加大气约束后,模糊度的平均固定率为95.59%,收敛后水平方向、三维方向定位RMSE分别为2.35、4.63 cm。
(5) 实时动态试验中,用户首次收敛时间为36 s,收敛后水平方向、三维方向定位RMSE分别为1.13、3.21 cm。与前面采用固定站统计结果相当,表明论文模型算法有较好的实用效果。
针对以上数据,尝试采取了考虑时空变化的大气参数约束模型,定位性能没有明显改进。因此针对电离层活跃时期的电离层约束的定权策略值得进一步探讨。
| [1] |
黄丁发, 周乐韬, 刘经南, 等. 基于Internet的VRS/RTK定位算法模型及实验研究[J]. 武汉大学学报(信息科学版), 2007, 32(3): 220-224, 228. HUANG Dingfa, ZHOU Letao, LIU Jingnan, et al. Internet based VRS/RTK positioning algorithm and experiment[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 220-224, 228. |
| [2] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [3] |
GENG J, TEFERLE F N, MENG X, et al. Towards PPP-RTK:ambiguity resolution in real-time precise point positioning[J]. Advances in Space Research, 2011, 47(10): 1664-1673. DOI:10.1016/j.asr.2010.03.030 |
| [4] |
WVBBENA G, SCHMITZ M, BAGGE A. PPP-RTK: precise point positioning using state-space representation in RTK networks[C]//Proceedings of the 18th Technical Meeting. Long Beach, California, USA: Institute of Navigation, 2005: 2584-2594.
|
| [5] |
LI Xingxing, ZHANG Xiaohong, GE Maorong. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution[J]. Journal of Geodesy, 2011, 85(3): 151-158. DOI:10.1007/s00190-010-0424-0 |
| [6] |
LI Xingixing, GE Maorong, ZHANG Hongping, et al. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning[J]. Journal of Geodesy, 2013, 87(5): 405-416. DOI:10.1007/s00190-013-0611-x |
| [7] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407. ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1399-1407. |
| [8] |
张润涛.基于局域参考站的PPP-RTK定位技术研究[D].郑州: 信息工程大学, 2017. ZHANG Runtao. Technology research of the PPP-RTK based on the local reference station[D]. Zhengzhou: Information Engineering University, 2017. |
| [9] |
ZHANG Shoujian, LI Jiangcheng, ZHAO Lei. An improved method to accelerate the convergence of PPP-RTK with sparse CORS stations' augmentation[C]//Proceedings of 2015 China Satellite Navigation Conference. Berlin, Heidelberg: Springer, 2015, 340: 129-140.
|
| [10] |
闫伟, 袁运斌, 欧吉坤, 等. 非组合精密单点定位算法精密授时的可行性研究[J]. 武汉大学学报(信息科学版), 2011, 36(6): 648-651. YAN Wei, YUAN Yunbin, OU Jikun, et al. Feasibility of precise timing with uncombined PPP[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 648-651. |
| [11] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099. ZHANG Baocheng. Study on the theoretical methodology and applications of precise point positioning using undifferenced and uncombined GNSS data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099. DOI:10.13485/j.cnki.11-2089.2014.0155 |
| [12] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of slant total electron content and satellite-receiver's differential code biases with uncombined precise point positioning technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. |
| [13] |
张宝成, 欧吉坤, 李子申, 等. 利用精密单点定位求解电离层延迟[J]. 地球物理学报, 2011, 54(4): 950-957. ZHANG Baocheng, OU Jikun, LI Zishen, et al. Determination of ionospheric observables with precise point positioning[J]. Chinese Journal of Geophysics, 2011, 54(4): 950-957. |
| [14] |
李博峰, 葛海波, 沈云中. 无电离层组合、Uofc和非组合精密单点定位观测模型比较[J]. 测绘学报, 2015, 44(7): 734-740. LI Bofeng, GE Haibo, SHEN Yunzhong. Comparison of ionosphere-free, UofC and uncombined PPP observation models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 734-740. DOI:10.11947/j.AGCS.2015.20140161 |
| [15] |
LOU Yidong, ZHENG Fu, GU Shengfeng, et al. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models[J]. GPS Solutions, 2016, 20(4): 849-862. DOI:10.1007/s10291-015-0495-8 |
| [16] |
EL-ARINI M B, CONKER R S, ALBERTSON T W, et al. Comparison of real-time ionospheric algorithms for a GPS wide-area augmentation system (WAAS)[J]. Navigation, 1994, 41(4): 393-414. DOI:10.1002/j.2161-4296.1994.tb01887.x |
| [17] |
PRASAD N, SARMA A D. Ionospheric time delay estimation using IDW grid model for GAGAN[J]. Journal of Indian Geophysical Union, 2004, 8(4): 319-327. |
| [18] |
从建锋, 刘智敏, 陈汉林. 山东区域电离层模型的建立及精度评估[J]. 测绘科学, 2020, 45(1): 48-53. CONG Jianfeng, LIU Zhimin, CHEN Hanlin. Establishment and accuracy assessment of regional ionospheric model in Shandong province[J]. Science of Surveying and Mapping, 2020, 45(1): 48-53. |
| [19] |
申健, 赵文, 安向东. 基于非组合精密单点定位的区域电离层建模[J]. 测绘地理信息, 2019, 44(6): 31-34. SHEN Jian, ZHAO Wen, AN Xiangdong. Regional ionosphere modeling based on non-combined precise point positioning[J]. Journal of Geomatics, 2019, 44(6): 31-34. |
| [20] |
戴吾蛟, 陈招华, 匡翠林, 等. 区域精密对流层延迟建模[J]. 武汉大学学报(信息科学版), 2011, 36(4): 392-396. DAI Wujiao, CHEN Zhaohua, KUANG Cuilin, et al. Modeling regional precise tropospheric delay[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 392-396. |
| [21] |
张小红, 朱锋, 李盼, 等. 区域CORS网络增强PPP天顶对流层延迟内插建模[J]. 武汉大学学报(信息科学版), 2013, 38(6): 679-683. ZHANG Xiaohong, ZHU Feng, LI Pan, et al. Zenith troposphere delay interpolation model for regional CORS network augmented PPP[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6): 679-683. |
| [22] |
肖恭伟, 欧吉坤, 刘国林, 等. 基于改进的BP神经网络构建区域精密对流层延迟模型[J]. 地球物理学报, 2018, 61(8): 3139-3148. XIAO Gongwei, OU Jikun, LIU Guolin, et al. Construction of a regional precise tropospheric delay model based on improved BP neural network[J]. Chinese Journal of Geophysics, 2018, 61(8): 3139-3148. |
| [23] |
FAN Haopeng, SUN Zhongmiao, ZHANG Liping, et al. A two-step estimation method of troposphere delay with consideration of mapping function errors[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 76-84. |
| [24] |
ZHOU Feng, DONG Danan, LI Pan, et al. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning[J]. GPS Solutions, 2019, 23(3): 59. DOI:10.1007/s10291-019-0852-0 |
| [25] |
ZHOU Feng, DONG Danan, LI Weiwei, et al. GAMP:An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations[J]. GPS Solutions, 2018, 22(2): 33. DOI:10.1007/s10291-018-0699-9 |
| [26] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D].武汉: 武汉大学, 2013. LI Xingxing. Rapid ambiguity resolution in GNSS precise point positioning[D]. Wuhan: Wuhan University, 2013. |
| [27] |
TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment:a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1): 65-82. |



