2. 香港理工大学土地测量及地理资讯学系, 香港 999077;
3. 湖北科技学院资源环境科学与工程学院, 湖北 咸宁 437100;
4. 深圳市水务规划设计院股份有限公司, 广东 深圳 518000;
5. 中南大学地球科学与信息物理学院, 湖南 长沙 410083;
6. 中国科学院精密测量科学与技术创新研究院, 湖北 武汉 430077
2. Department of Land Surveying and Geo-informatics, the Hong Kong Polytechnic University, Hongkong 999077, China;
3. School of Resources and Environment Science and Engineering, Hubei University of Science and technology, Xianning 437100, China;
4. Shenzhen Water Planning and Design Institute Company Limited, Shenzhen 518000, China;
5. School of Geosciences and Info-physics, Central South University, Changsha 410083, China;
6. Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430077, China
Sentinel-1卫星TOPS模式影像由于多普勒中心在方位向的快速变化导致其方位线(azimuth lines)具有时变信号特性,干涉时要求方位向配准精度达到0.001个像素,否则相邻Burst影像干涉图之间将出现相位跳变[1]。然而Sentinel-1卫星精密轨道精度约为5 cm,依据SAR影像配准理论,几何配准理论精度约为0.005个像素(置信度为68.3%),尚无法满足方位向配准精度要求,需要在几何配准的基础上进一步采用增强谱分集(enhanced spectral diversity)对残余偏移量进行估计[2-4]。增强谱分集是Burst模式影像进行谱分集配准的特殊形式,处理时无须对影像进行过采样,具有计算效率高、配准精度高等优势。目前研究人员已经从数学角度证明了Sentinel-1卫星增强谱分集配准极限精度(Cramer-Rao lower bound,CRLB)精度优于0.001像素[5]。因此可认为增强谱分集配准是Sentinel-1卫星影像干涉处理的关键[6-7]。
增强谱分集算法产生已有20余年,主要是利用非零多普勒中心引起的线性相位成分差异计算配准误差,从而实现Burst模式影像的高精度配准。但由于数据可获取性以及技术成熟性(如时间同步),Burst模式影像一直未能成为InSAR领域主要的数据源,增强谱分集理论在相当长的一段时期未得到发展和完善,致使该算法在数据处理流程、参数估计等方面目前依然缺乏严格的理论指导[8]。目前各种InSAR软件提供的增强谱分集数据处理策略也存在差异,操作时则主要依赖于处理者的经验,难以对其规范化。概括起来,增强谱分集配准主要面临两方面的挑战:①影像相干性偏低条件下的增强谱分集配准可能无法达到预期配准精度;②增强谱分集实际数据处理时不可避免地受到其他信号的干扰,如地表方位向形变、电离层效应,甚至是极端天气条件下的水汽变化[9-13]。为了确保Sentinel-1卫星时序影像干涉处理时增强谱分集配准的精度和可靠性,文献[14-16]提出了利用影像干涉对组合形成的增强谱分集冗余观测量进行联合平差的优化处理方案。上述多基线配准方案尽管整体上提升了配准精度,但可能会削弱高相干条件下的影像干涉对配准精度。因此Sentinel-1卫星时序处理仍需要寻找更为有效的配准方案,以确保海量影像干涉配准处理的规范化、自动化。
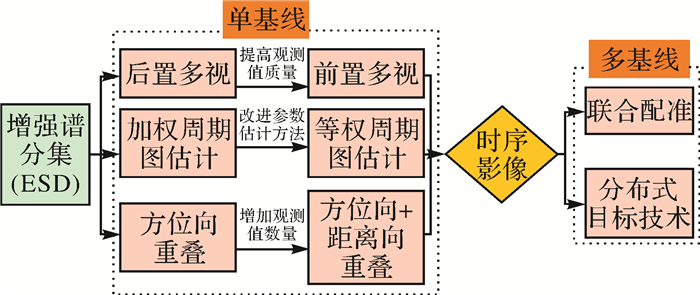
鉴于增强谱分集配准尚存在不足,本文提出拟从5个方面改善Sentinel-1卫星增强谱分集配准的优化方法,如图 1所示。首先在单基线条件下,调整增强谱分集多视处理方法,提高观测值质量;增加距离向增强谱分集,增加观测值数量;残余偏移量等权估计方法升级为加权估计,优化参数估计方案。然后在单基线配准的基础上再次进行多基线配准,或者利用(分布式目标)DS技术优化干涉图,以提高配准精度。基于上述思路,本文基于增强谱分集原理分别讨论相应的改进方案。
|
| 图 1 增强谱分集优化内容 Fig. 1 Generic flowchart of advanced coregistration methods for enhanced spectral diversity |
1 增强谱分集及其优化技术
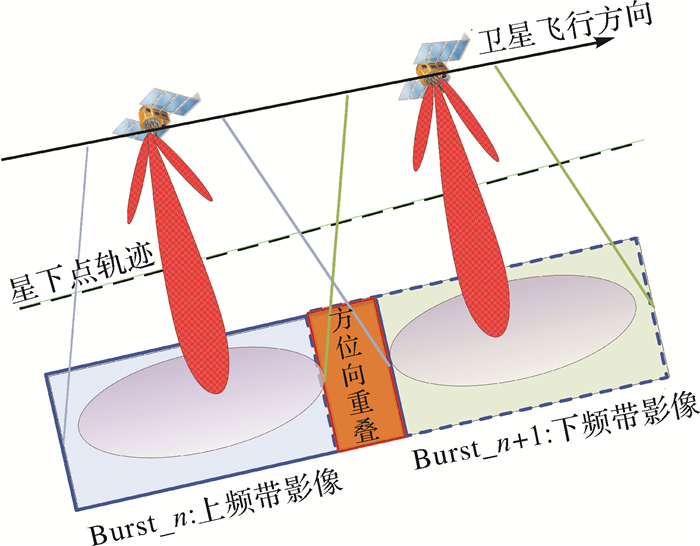
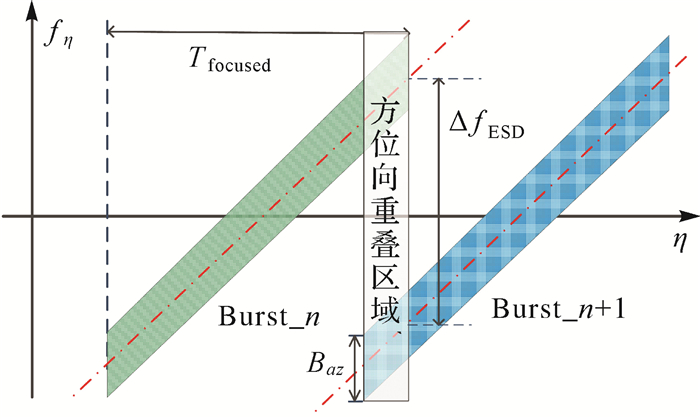
目前Sentinel-1卫星TOPS模式影像主要选用方位向重叠区域进行增强谱分集处理,与谱分集相比,增强谱分集并没有降低上、下频带影像的多普勒带宽,对应的几何模型如图 2所示[17]。重叠区域Burst_n对应的多普勒中心为正值,因此称之为上频带影像;而Burst_n+1对应的多普勒中心频率为负值,则称为下频带影像;Burst_n与Burst_n+1生成的干涉图分别称为上频带干涉图和下频带干涉图。与图 2对应的Burst影像方位向频谱如图 3所示,横轴表示方位时间η,纵轴表示多普勒频率fη。
|
| 图 2 方位向增强谱分集几何模型 Fig. 2 Geometry configuration of enhanced spectral diversity |
|
| 图 3 方位向增强谱分集中的Burst方位向频谱 Fig. 3 Time frequency diagram of two consecutive burst in azimuth sketching ESD |
图 3中Burst方位向重叠区域的多普勒中心基线ΔfESD远高于多普勒带宽Baz,增强谱分集配准CRLB精度σESD为[18]
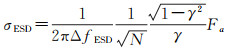 (1)
(1)
式中,Fa为影像方位向采样频率;γ表示影像相干性;N为重叠区域分辨率单元数量。Sentinel-1卫星影像方位向重叠度约为10%,多普勒中心基线最高可达5000 Hz,由式(1)可知其CRLB精度在低相干条件下也优于0.001像素。当进行实际数据处理时,为了确保残余偏移量的无偏估计,增强谱分集配准接近其CRLB精度,本文拟对增强谱分集处理流程进行以下改进:①采用前置多视进行增强谱分集处理;②基于CRLB公式对方位向增强谱分集进行加权估计;③基于CRLB公式对距离向增强谱分集进行加权估计。
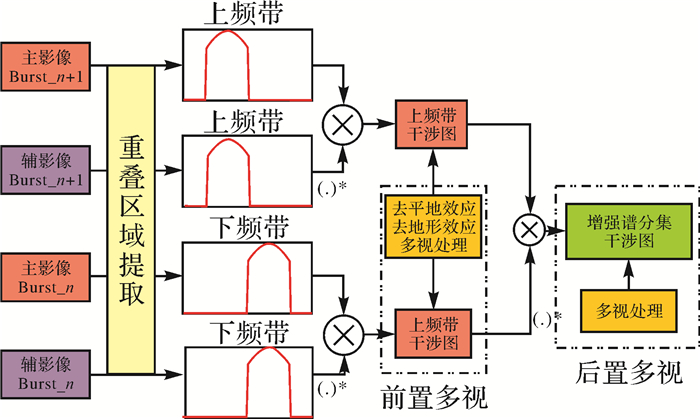
1.1 增强谱分集多视顺序调整增强谱分集通过重叠区域上、下频带干涉图的差分干涉相位估计影像残余偏移量,其结果易受到干涉图噪声的干扰。尽管增强谱分集未像谱分集一样进行子带分解处理,多普勒带宽依然保持不变,但增强谱分集干涉图需经过两次干涉生成,在同等相干条件下,其噪声水平远高于常规干涉图。多视处理具有低通滤波特性,可以有效提高SAR影像信噪比,因此为了提高增强谱分集偏移量估计精度,一般需要对增强谱分集所涉及的干涉图进行多视处理。增强谱分集通过上、下频带干涉图再次干涉得到谱分集干涉图,根据多视处理对象的差异,如图 4所示,增强谱分集多视处理分为前置多视(early-multilooking)和后置多视(late-multilooking)。
|
| 图 4 增强谱分集前置多视处理流程 Fig. 4 Process flow of the early-multilooking ESD |
后置多视处理对象为增强谱分集干涉图,前置多视处理对象为常规干涉图,即上、下频带干涉图,其数学表达式如式(2)和式(3)所示[19]
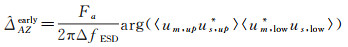 (2)
(2)
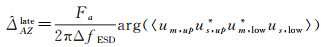 (3)
(3)
式中, 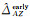
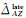
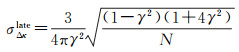 (4)
(4)
增强谱分集后置多视CRLB精度σESDlate由式(4)推导出
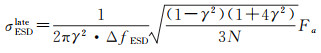 (5)
(5)
假设Sentinel-1卫星影像方位向重叠区域多普勒中心基线为4500 Hz,方位向重叠区域大小为115×24 500像素,依据上述参数根据式(1)和式(5)可以得到不同相干条件下增强谱分集前置多视和后置多视的理论配准精度,如图 5所示。其中横轴表示影像相干系数,纵轴表示偏移量估计的标准差,图 5结果表明可以看出前置多视配准精度整体上高于后置多视,特别在低相干条件下,前置多视的优势更为明显。两者配准精度的信噪比如式(6)所示[21]

|
| 图 5 增强谱分集前置多视和后置多视配准精度 Fig. 5 Azimuth co-registration accuracy of early multi-looking and late multi-looking for the ESD |
 (6)
(6)
当影像相干系数为0.1时,根据式(6)可以计算得到前置多视比后置多视配准精度平均高15 dB,因此增强谱分集应选择前置多视配准处理,以确保Sentinel-1影像配准精度优于0.001像素。
尽管前置多视理论上配准精度较高,但其处理对象——上、下频带干涉图存在平地效应和地形效应,干涉图条纹密集,如果直接对上、下频带干涉图进行多视处理将导致有效信息丢失[21-23]。为确保前置多视配准结果准确,本文对增强谱分集处理流程进行调整,在对上下频带干涉图多视处理前增加去平地效应、去地形效应处理,式(2)应调整为
 (7)
(7)
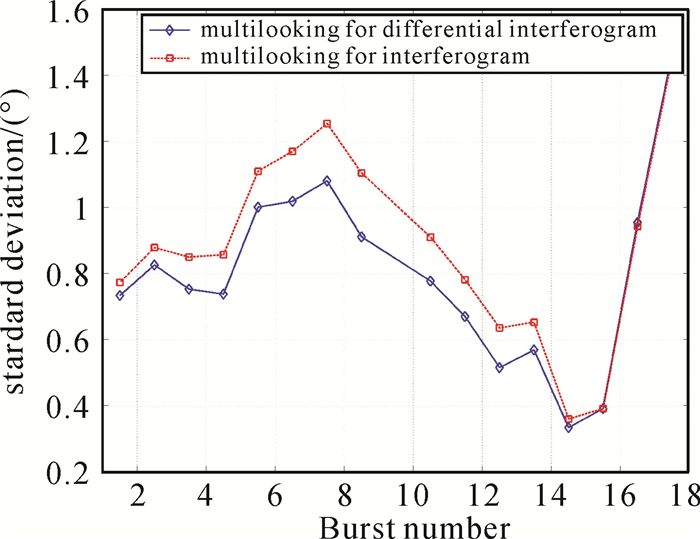
式中,ϕflat表示平地效应相位;ϕtopo表示地形效应相位。为了验证前置多视处理时去平地和地形效应处理对增强谱分集结果的影响,本文选取覆盖陕西省和内蒙古自治区113轨道的Sentinel-1A影像为试验数据,如图 6所示,影像覆盖区域属于风沙草滩地貌,人口密度较低,人工建筑较少,雷达影像后向散射特性以分布式目标(distributed scatterers, DS)为主,适合本文增强谱分集配准多视处理算法的验证。影像由两个Frame组成,本文则基于影像零多普勒时间对其进行方位向拼接,形成由54个Burst组成的长条带影像。以影像2017-10-02和影像2018-03-19组成的干涉对为例,分别对上下频带干涉图和上下频带差分干涉图进行多视处理,其增强谱分集结果如图 7和图 8所示。图 7为Burst影像增强谱分集相位直方图对比结果,图 7(a)为差分干涉图多视结果,相位分布较为集中,图 7(b)为干涉图直接多视后的结果,其相位分布较为分散。理论上增强谱分集相位分布应为干涉图相位分布的卷积,图 7(a)中相位分布直方图更加匀称,与理论相契合[25]。如果对比子测绘带中18个Burst的增强谱分集相位均方差(如图 8所示),可以发现上、下频带差分干涉图多视处理后增强谱分集相位标准差相对较小,而干涉图因多视信息丢失,导致增强谱分集干涉图相位噪声增大,增加了偏移量估计的不确定性。上述试验表明,增强谱分集前置多视需对上下频带干涉图进行去平地效应和去地形效应处理才能实现Sentinel-1卫星影像的高精度配准。但与后置多视相比,额外的去平地、去地形处理将导致前置多视计算效率偏低。因此高相干影像干涉对配准处理依然可以选择使用后置多视方案。

|
| 图 6 研究区域与卫星覆盖范围 Fig. 6 Study area location and Sentinel-1 data coverage |

|
| 图 7 增强谱分集相位直方图 Fig. 7 Histograms of measured ESD phases |
|
| 图 8 增强谱分集干涉图相位标准差 Fig. 8 Standard deviation of the measured ESD phases |
1.2 基于加权周期图的影像偏移量估计
Sentinel-1卫星影像上、下频带成像间隔一般小于3 s,视角差异约为1.2°,根据图 2所示的增强谱分集几何模型可知,这一差异在对流层内引起的上、下频带视线最大距离约为250 m,此时大气效应处于强相关状态,对增强谱分集干涉图相位的影响可忽略不计,因此增强谱分集干涉图中理论上只存在失相干噪声ϕnoise[26-28]。Sentinel-1卫星轨道基线受到严格控制,Burst零多普勒影像方位向重叠区域持续时间大约0.3 s,通常认为几何配准处理后每个像素对应的残余偏移量是相同的。增强谱分集干涉图相位ϕESD与残余偏移量ΔAZ之间的关系如式(8)所示
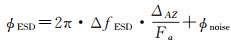 (8)
(8)
鉴于增强谱分集干涉图统计模型缺失,通常认为失相干噪声为零对称分布,理论上不会对增强谱分集相位产生系统性的误差,DLR等研究单位一般通过周期图方法对几何配准后的残余偏移量ΔAZ进行优化估计,如式(9)所示
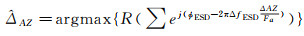 (9)
(9)
式中,R表示周期图实部值,影像偏移量即对应于周期图谱实部最大值,式(9)也可视为每个像素相同权重下的LCV(least circular variance)估计。鉴于雷达影像中每个像素噪声水平存在差异,理论上加权处理才能实现残余偏移量的无偏估计,但如何加权目前这方面研究尚无明确结论。本文拟根据式(1)中的增强谱分集CRLB精度代之以中误差,并以此为依据对每个相位观测值加权处理,式(9)则转化为
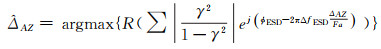 (10)
(10)
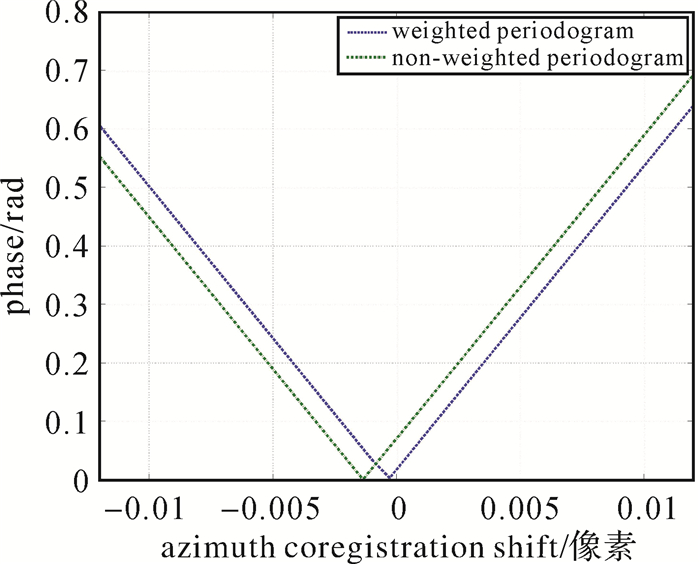
由于方位向重叠区域中增强谱分集多普勒中心基线基本一致,所以式(10)未考虑其对每个像素相位权重产生的影响。加权周期图估计方法理论上可以更准确地估计出影像配准的残余偏移量,假设多普勒中心基线为4000 Hz,方位向采样频率为486 Hz,残余偏移量为零,本文通过模拟均匀场景下的SAR影像增强谱分集相位对比分析等权和加权周期图估计方法精度的差异,并分别基于加权周期图和等权周期图进行偏移量估计,如图 9所示。其中横轴表示方位向偏移量,纵轴为周期图相位值,其相位最小值即对应偏移量估计结果。从图 9中可以看出,与等权周期图相比,加权周期图估计结果更接近于模拟的零残余偏移量,因此可认为加权周期图更能准确估计出偏移量。在实际应用中,当Burst重叠影像覆盖森林、水域等失相干区域时,其增强谱分集观测量不足,采用加权周期图参数方法可以确保影像偏移量估计的准确性。
|
| 图 9 加权与等权周期图估计方法差异 Fig. 9 Comparison between weighted and nonwei-ghted periodogram |
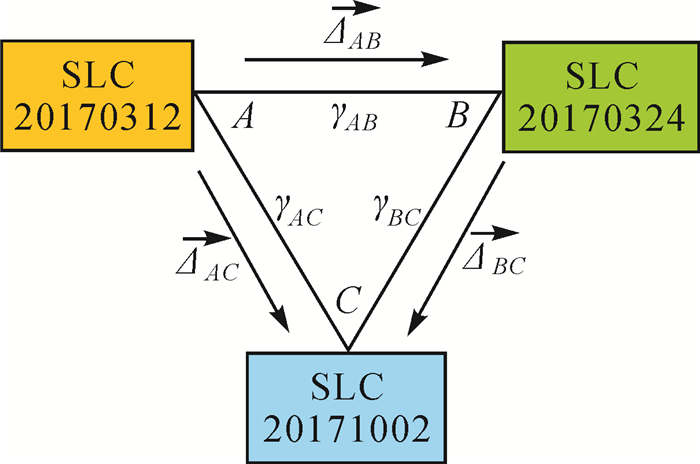
增强谱分集理论上是配准精度最高的方案,但数据处理时难以直接评估其具体配准精度[31]。根据式(1)可知,相干系数越高,增强谱分集的配准精度也越高。因此本文通过影像组合生成的干涉对相干性差异来检测配准谱分集配准精度,即通过高相干影像组合来检验低相干影像组合的增强谱分集配准精度,具体方法如图 10所示:本文选取图 6所示研究区域的113轨道Sentinel-1影像A、B、C,对应的拍摄时间分别为2017-03-12、2017-03-24、2017-10-02,影像A、B作为辅影像,分别与主影像C在精密轨道条件下进行几何配准和增强谱分集配准,分别得到重采样后的辅影像Res_A和Res_B。主影像C和重采样的辅影像Res_A、Res_B组合生成干涉影像对A_B、A_C、B_C,其对应的残余偏移量ΔAB、ΔAC、ΔBC符合以下关系
|
| 图 10 增强谱分集配准精度检验原理 Fig. 10 Demonstration of coregistration accuracy verification of enhanced spectral diversity |
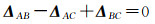 (11)
(11)
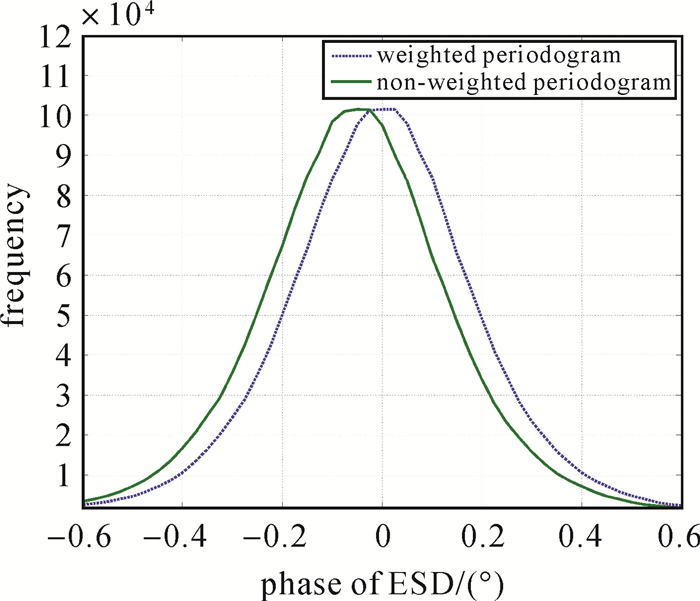
根据式(11)可知,影像干涉对之间的残余偏移量理论上闭合差为零。如果干涉对A_C或者干涉对B_C配准误差较大,必然导致干涉对A_B配准误差较大。由于A、B影像时间基线只有12天,相干性γAB远大于γAC、γBC,由式(1)可知,其增强谱分集配准精度相对较高,可检验主影像C与辅影像A、B的配准结果。基于这一思路,本文对比周期图等权与加权估计条件下A、B影像组合生成的增强谱分集相位分布结果,如图 11所示,可以看出加权估计对应的相位分布更接近于零对称,由式(8)可知,零对称意味着残余偏移量ΔAB接近于零。由上述试验结果可知,尽管依据CRLB公式加权方案未必最优,但已经足以表明增强谱分集加权估计时配准精度更高。
|
| 图 11 短时间基线干涉对加权与等权周期图估计方法差异 Fig. 11 Comparison between weighted and non-weighted periodogram for short temporal baseline |
1.3 距离向增强谱分集
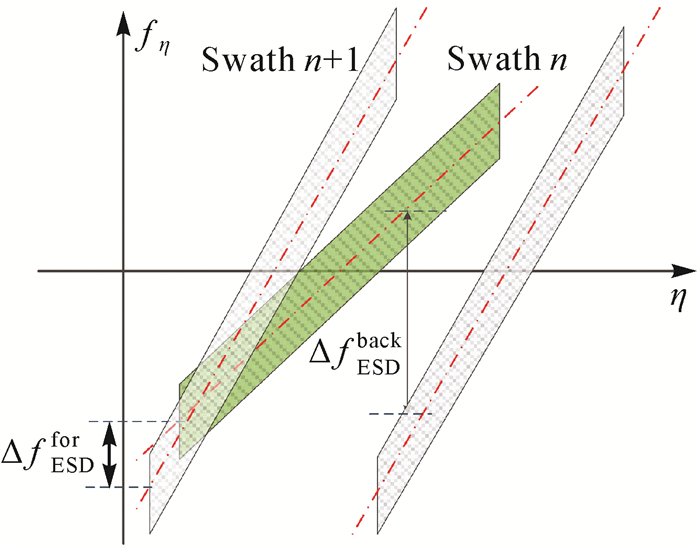
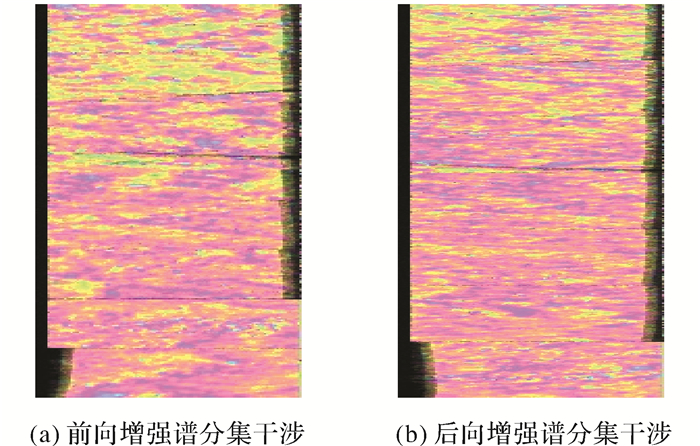
为了得到精度和可靠性均较高的偏移量估计结果,本文进一步利用相邻子测绘带间的距离向重叠区域进行配准,以增加增强谱分集观测相位数量[32]。Sentinel-1卫星在扫描成像过程中雷达波束依次在3个子测绘带间依次进行切换成像,聚集影像中每个Burst一般与相邻子测绘带中连续的两个Burst重叠,如图 12所示,分别为前向重叠和后向重叠,因此距离向增强谱分集可分为前向增强谱分集和后向增强谱分集。由于不同子测绘带的雷达波束旋转角速度不同,重叠区域多普勒中心基线一直在发生变化,其多普勒频谱如图 13所示,前向重叠多普勒中心基线ΔfESDfor一般小于200 Hz,后向重叠多普勒中心基线ΔfESDback约为4000 Hz。尽管Sentinel-1卫星每个子测绘带成像时发射的脉冲带宽并不相同,但聚焦过程中通过转换采样率使得子测绘带聚焦影像距离向采样频率相同,每个Burst聚焦影像均可按照零多普勒时间严格排列,相邻子测绘带间的重叠区域和多普勒中心基线可直接根据像素的零多普勒时间进行计算[33]。本文依然选用图 6所示研究区域的Sentinel-1影像利用距离向增强谱分集处理,其中影像干涉对(2017-08-15—2017-08-03)对应的前、后向增强谱分集干涉图如图 14所示,可以看出其干涉图与方位向增强谱分集一样受到失相干噪声的干扰,也需要采用周期图方法进行偏移量估计。

|
| 图 12 Sentinel-1A/B卫星TOPS影像Burst重叠区域 Fig. 12 Schematic representation of the overlapping areas bet-ween adjacent bursts in the Sentinel-1A/B system |
|
| 图 13 距离向增强谱分集的Burst方位向频谱 Fig. 13 Time frequency diagram of three adjacent Burst in range sketching the ESD approach |
|
| 图 14 增强谱分集干涉 Fig. 14 Differential interferometric phase of the ESD of bea-mwise forward and backward in overlapping areas |
由于多普勒中心基线ΔfESDfor和ΔfESDback在重叠区域发生较大变化,如果采用1.2节提出的加权周期图估计方法,需要在式(1)的基础上,顾及多普勒中心基线变化引起的像素权重差异,此时残余偏移量估计公式应调整为
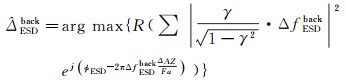 (12)
(12)
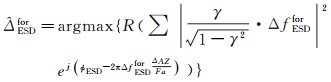 (13)
(13)
式中,
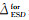
|
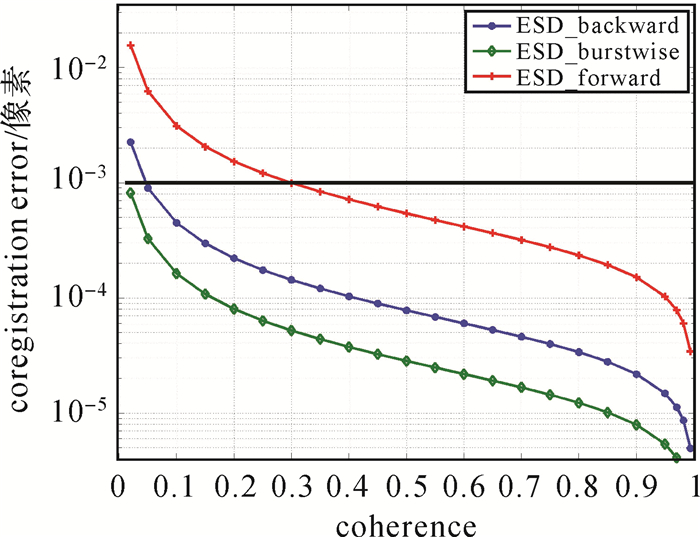
| 图 15 增强谱分集在前向、后向、方位向差异重叠区域精度差异 Fig. 15 Coregistration accuracy of the ESD for beamwise for-ward, backward, burstwise in overlapping areas |
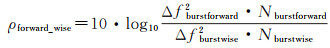 (14)
(14)
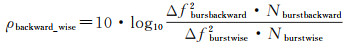 (15)
(15)
根据式(14)和式(15)可以看出,距离向增强谱分集估计精度在低相干条件下无法满足配准精度要求,需要进一步与方位向增强谱分集配准结果融合。当相干系数为0.1时,方位向增强谱分集估计精度高于前向增强谱分集30 dB,高于后向增强谱分集9 dB。如果它们与方位向增强谱分集联合使用,理论上对应的权值比分别为1:945和1:7.5。由于前向增强谱分集估计的残余偏移量权重过低,本文进行数据处理时仅将后向增强谱分集与方位向增强谱分集联合使用,相当于将方位向重叠区域增加13%,配准精度理论上可以提升6%。当方位向重叠区域为低相干区域时(如水域),该方法可以通过增加增强谱分集观测量以弥补相干系数过低对配准精度的影响。后向增强谱分集联合方位向增强谱分集配准精度检验依然需要通过高相干影像干涉对组合检验低相干影像组合的增强谱分集配准效果,由于试验方法在1.2节中已经阐述,为了避免重复,本文不再表述该试验过程和结果。
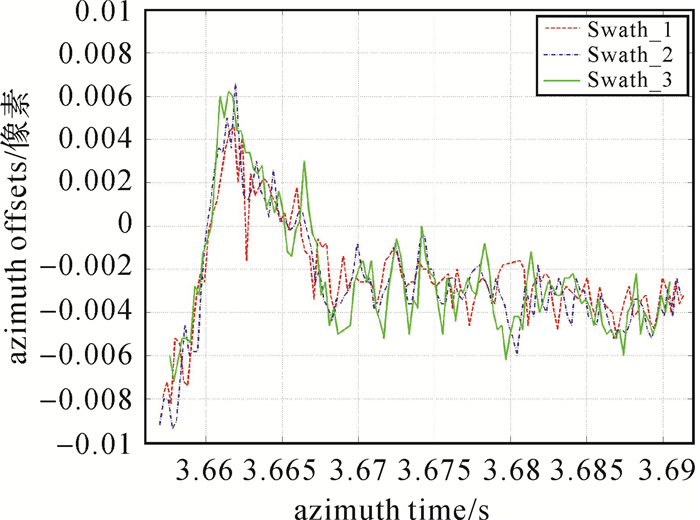
2 时序影像配准由于残余偏移量主要是由主辅影像的相对轨道切向误差引起的,可以利用卫星轨道误差的空间连续性对方位向上的增强谱分集估计结果进行多项式拟合,以提高增强谱分集估计精度[34-35]。Sentinel-1卫星影像干涉配准一般采用上述方案,也称之为单基线配准方案, 上文所述的改进方案均是基于单基线配准方案完成的。单基线配准计算效率较高,但存在诸多局限性。当参与处理的Burst数量过少时,难以确保多项式拟合准确;而Burst数量过多时,轨道误差的空间相关性逐渐减弱,残余偏移量变化规律将无法按照多项式进行拟合。图 16为Sentinel-1卫星142轨道影像连续126个Burst方位向残余偏移量分布,影像自南向北跨度达到1500 km,增强谱分集估计的残余偏移量变化趋势已难以进行多项式拟合,此时单基线配准已无法满足其干涉处理的需要。为了进一步提高影像配准精度,本文在单基线配准的基础上拟利用干涉对组合再次进行多基线配准,通过时间维和空间维的约束条件对增强谱分集估计结果进行平差处理。另外本文也提出利用分布式目标技术优化增强谱分集估计结果的方案,将时序DS-InSAR技术引入Sentinel-1卫星时序影像的配准处理中,可有效提高原始差分干涉图质量,间接提高了增强谱分集的估计精度。
|
| 图 16 增强谱分集估计的残余偏移量分布 Fig. 16 Azimuth shifts retrieved by ESD for three subswath |
2.1 增强谱分集多基线配准
增强谱分集多基线配准即是利用影像多基线组合构成的增强谱分集冗余观测量进行联合平差处理,以提高增强谱分集估计精度[36]。本文在单基线配准基础上再次进行多基线配准,假设有n+1景影像选取其中一景作为主影像,单基线配准处理后得到n景重采样后的辅影像RSLC,然后在此基础上进行多基线配准,即主影像联合重采样的辅影像进行多基线组合,得到m景干涉图,并进行增强谱分集处理,得到相应的m组残余偏移量,最后依据式(16)所示的相位闭合关系进行平差处理。如果以n+1景影像的残余偏移量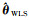
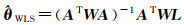 (16)
(16)
 (17)
(17)
增强谱分集联合平差处理类似于秩亏水准自由网平差,其中矩阵A∈Rm×(n+1),矩阵中每一行对应一个影像干涉对,其中主影像对应矩阵元素+1,辅影像对应-1,如式(17)所示。假定i、j分别为影像编号,且1≤i, j≤n+1,ϕij表示影像序列中影像i与影像j的常规差分干涉相位,对应的增强谱分集估计的偏移量为Δij,L∈Rm×1为多基线配准时干涉对组合的残余偏移量Δij组成列向量,通常表示为
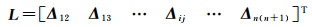 (18)
(18)
式中,W∈Rm×m为残余偏移量列向量相对应的权阵,由于雷达影像之间存在相干性,增强谱分集估计结果之间并不独立,因此式(16)需顾及残余偏移量L之间的相关性。鉴于相干系数必然存在估计误差,协方差矩阵将会产生非正定的问题[37-39],本文退而求其次,忽略干涉图之间的相关性,直接假定残余偏移量相互独立,其权重可以根据式(1)推导出,如式(19)所示
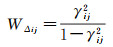 (19)
(19)
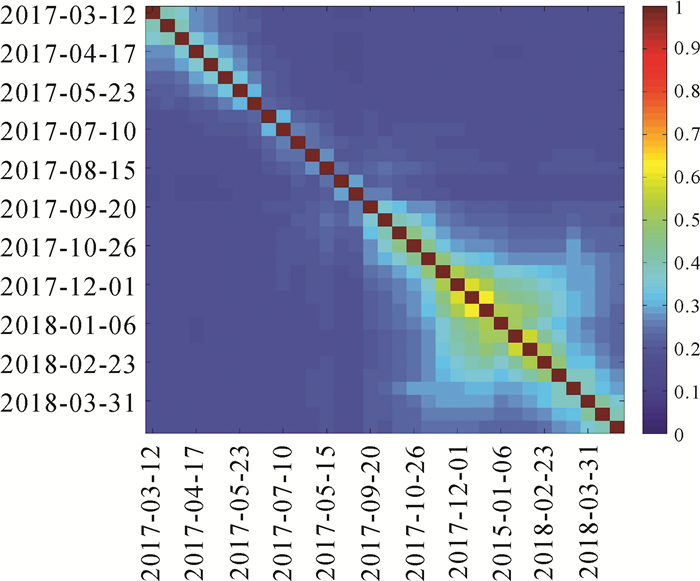
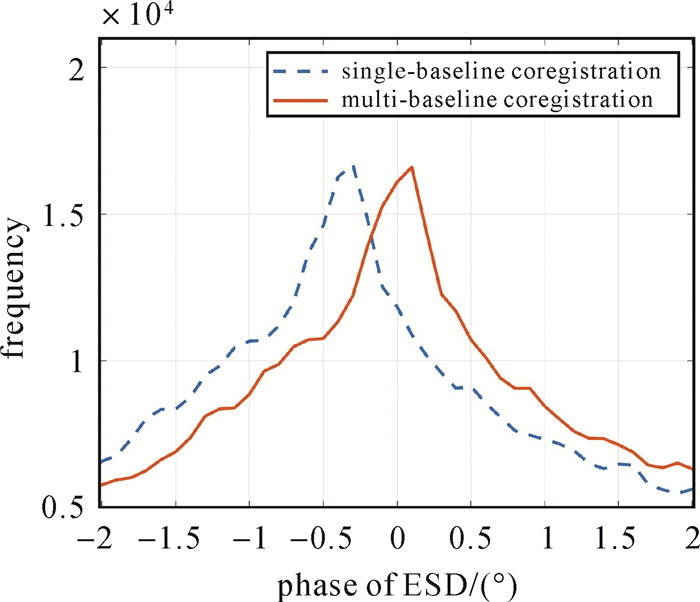
依据上述理论,本文选择覆盖图 6所示区域的33景Sentinel-1影像集进行干涉时序处理试验,其时空基线分布如图 17所示,参考主影像为2017-10-02。这些影像经过单基线配准处理后,再次进行多基线组合,共组成528个影像干涉对,对应的相干系数矩阵如图 18所示。本文处理数据时依据式(19)所示的加权方案解算式(16),得到每个辅影像相对于主影像的残余偏移量。试验结果发现多基线配准前后影像(2017-10-02)与影像(2017-04-17)之间的残余偏移量达到0.002像素,如图 19所示,多基线配准后增强谱分集相位直方图频率最大值对应相位更接近于零,表明多基线配准后残余偏移量更小,实施多基线配准可以优化单基线配准结果,进一步提高配准精度。InSAR时序处理通常面临新影像不断累积更新的问题,为了实现地表连续、动态形变监测,避免配准处理重复计算,本文建议采用序贯平差的方法解算多基线配准下的残余偏移量。

|
| 图 17 影像基线分布 Fig. 17 Baseline plot for Sentinel-1 acquisition |
|
| 图 18 干涉图对应的相干系数 Fig. 18 Absolute values of coherence matrices estimated from the interferogram |
|
| 图 19 单基线配准与多基线配准相对应的增强谱分集相位直方图 Fig. 19 Histograms of the measured ESD phases between direct ESD and joint retrieved shifts |
2.2 基于DS-InSAR技术的增强谱分集配准
本文拟引入DS-InSAR中的同质滤波技术和Phase-Linking技术进行增强谱分集处理,以提高增强谱分集干涉图质量,进而实现多基线条件下影像配准精度的提高。DS-InSAR技术主要通过分析时间维样本统计属性的相似程度,选取散射特性相同的像素进行同质滤波,并根据相位闭合原理(phase triangulation)对其缠绕相位进行phase-linking处理,以提高干涉图相位质量[40-43]。与常规的差分干涉图相同,增强谱分集干涉图也满足相位闭合原理[44]。假设Sentinel-1卫星A、B、C三景影像进行组合干涉,并进行增强谱分集处理,相应的增强谱分集相位由式(20)进行表示
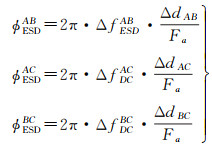 (20)
(20)
式中,多普勒中心基线为ΔfDCAB、ΔfDCAC、ΔfDCBC,理论上增强谱分集多普勒中心基线基本上一致,即ΔfDCAB≈ΔfDCAC≈ΔfDCBC,几何配准后的残余偏移量ΔdAB、ΔdAC、ΔdBC依然符合式(21)
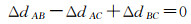 (21)
(21)
由式(21)可知,增强谱分集相位依然符合相位闭合原理,如式(22)所示
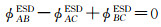 (22)
(22)
根据式(22)可知,增强谱分集也适用DS-InSAR技术优化其干涉图相位。本文首先对上下频带差分干涉图进行同质目标滤波。然后采用phase_linking算法对相干目标缠绕相位进行时间维相位平差处理。其中影像干涉对(2017-10-02—2018-04-24)中Burst8影像上频带差分干涉图处理结果如图 20所示,对比图 20(a)和(b)可以直观看出DS-InSAR技术有效提高了差分干涉图质量。最后本文对上、下频带差分干涉图再次干涉处理,得到增强谱分集干涉图,并与原始增强谱分集相位分布进行对比,如图 21所示,可以明显看出DS-InSAR技术处理后的增强谱分集干涉图相位集中度相对较高,证明引入该技术确实降低了增强谱分集干涉图相位方差,可以有效提高偏移量估计精度。

|
| 图 20 DS技术得到的差分干涉图与原始差分干涉图对比 Fig. 20 Comparison between original differential inter-ferogram and estimated differential interferogram by DS technique |

|
| 图 21 基于DS-InSAR技术处理后的增强谱分集相位直方图与原始增强谱分集对比 Fig. 21 Histograms of the measured residual ESD phases between original differential interferogram and estimated differential interferogram by DS-InSAR technique |
3 结论
本文针对Sentinel-1卫星干涉配准的需要,首先对单基线条件下的增强谱分集估计影像偏移量算法进行了改进,通过增加观测量、采用前置多视、优化参数估计等方法,提高增强谱分集估计精度;然后在单基线配准的基础上,针对时序影像利用干涉组合形成的增强谱分集多余观测量进行联合平差,或引用DS-InSAR技术以进一步提高增强谱分集配准的精度和可靠性。增强谱分集多基线配准与基于DS-InSAR技术的增强谱分集配准本质上是一致的,均是利用影像组合信息计算影像之间的残余偏移量,理论上两种方法的配准精度相同,时序处理时可根据需要选择其中一种方法。
本文尽管采用一系列措施提高Sentinel-1卫星影像配准精度,但增强谱分集干涉图统计模型的缺失导致平差处理时残余偏移量难以获得最优估计值,因此增强谱分集理论依然需要进一步完善,确保时序Burst模式影像能够实现低相干条件下的高精度配准。
| [1] |
PRATS P, SCHEIBER R, ZAN F D. Sentinel-1 InSAR performance study with TOPS data[C]//SEOM INSARAP Workshop. Frascati, Italy: ESA-ESRIN, 2014.
|
| [2] |
PETER H, JÄGGI A, FERNÁNDEZ J, et al. Sentinel-1A-first precise orbit determination results[J]. Advances in Space Research, 2017, 60(5): 879-892. DOI:10.1016/j.asr.2017.05.034 |
| [3] |
TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping applications using automatic SAR imaging[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 27-37. |
| [4] |
吴文豪, 周志伟, 李陶, 等. 精密轨道支持下的哨兵卫星TOPS模式干涉处理[J]. 测绘学报, 2017, 46(9): 1156-1164. WU Wenhao, ZHOU Zhiwei, LI Tao, et al. A study of sentinel-1 TOPS mode co-registration[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1156-1164. DOI:10.11947/j.AGCS.2017.20160352 |
| [5] |
YAGVE-MARTÍNEZ N, PRATS-IRAOLA P, GONZÁLEZ F R, et al. Interferometric processing of Sentinel-1 TOPS data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2220-2234. DOI:10.1109/TGRS.2015.2497902 |
| [6] |
QIN Yuxiao, PERISSIN D, BAI Jing. A common "stripmap-like" interferometric processing chain for tops and ScanSAR wide swath mode[J]. Remote Sensing, 2018, 10(10): 1504. DOI:10.3390/rs10101504 |
| [7] |
META A, PRATS P, STEINBRECHER U, et al. First TOPSAR interferometry results with TerraSAR-X[C]//FRINGE. Frascati Italy: DLR, 2007.
|
| [8] |
WEGMVLLER U, WERNER C, STROZZI T, et al. Sentinel-1 IWS mode support in the GAMMA Software[C]//Proceedings of the Asia-Pacific Conference on Synthetic Aperture Radar (APSAR). Singapore: IEEE, 2015: 23-27.
|
| [9] |
YAGUE-MARTINEZ N, RODRÍGUEZ-GONZÁLEZ F, BALSS U, et al. TerraSAR-X TOPS, ScanSAR and WideScanSAR interferometric processing[C]//EUSAR. Berlin, Germany: VDE, 2014.
|
| [10] |
XU Bing, LI Zhiwei, FENG Guangcai, et al. Continent-wide 2-D co-seismic deformation of the 2015 mw 8.3 Illapel, Chile earthquake derived from Sentinel-1A data:correction of azimuth co-registration error[J]. Remote Sensing, 2016, 8(5): 376. DOI:10.3390/rs8050376 |
| [11] |
SCHEIBER R, JÄGER M, PRATS-IRAOLA P, et al. Speckle tracking and interferometric processing of TerraSAR-X TOPS data for mapping nonstationary scenarios[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(4): 1709-1720. DOI:10.1109/JSTARS.2014.2360237 |
| [12] |
GOMBA G, GONZÁLEZ F R, DE ZAN F. Ionospheric phase screen compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 223-235. DOI:10.1109/TGRS.2016.2604461 |
| [13] |
GOMBA G, PARIZZI A, DE ZAN F, et al. Toward operational compensation of ionospheric effects in SAR interferograms:the split-spectrum method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1446-1461. |
| [14] |
YAGUE-MARTINEZ N, DE ZAN F, PRATS-IRAOLA P. Coregistration of interferometric stacks of Sentinel-1 TOPS data[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(7): 1002-1006. DOI:10.1109/LGRS.2017.2691398 |
| [15] |
FATTAHI H, AGRAM P, SIMONS M. A network-based enhanced spectral diversity approach for tops time-series analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 777-786. DOI:10.1109/TGRS.2016.2614925 |
| [16] |
DE ZAN F, PRATS-IRAOLA P. Joint coregistration of SAR images with an application to TerraSAR-X TOPS mode datasets[C]//Proceedings of Living Planet Symposium. Edinburgh, UK: ESA, 2013.
|
| [17] |
RODRIGUEZ-CASSOLA M, PRATS-IRAOLA P, DE ZAN F, et al. Doppler-related distortions in TOPS SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(1): 25-35. |
| [18] |
PRATS-IRAOLA P, SCHEIBER R, MAROTTI L, et al. TOPS interferometry with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3179-3188. DOI:10.1109/TGRS.2011.2178247 |
| [19] |
DE ZAN F, PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M. The theoretical performance of different algorithms for shift estimation between SAR images[C]//12th European Conference on Synthetic Aperture Radar (EUSAR). Aachen, Germany: VDE, 2018.
|
| [20] |
DE ZAN F, PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M. On the dependence of delta-k efficiency on multilooking[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1745-1749. DOI:10.1109/LGRS.2015.2424272 |
| [21] |
PRATS-IRAOLA P, YAGUE-MARTINEZ N, WOLLSTADT S, et al. Demonstration of the applicability of 2-look burst modes in non-stationary scenarios with TerraSAR-X[C]//Proceedings of the 11th European Conference on Synthetic Aperture Radar. Hamburg, Germany: VDE, 2016.
|
| [22] |
SICA F, COZZOLINO D, VERDOLIVA L, et al. The offset-compensated nonlocal filtering of interferometric phase[J]. Remote Sensing, 2018, 10(9): 1359. DOI:10.3390/rs10091359 |
| [23] |
DAVIDSON G W, BAMLER R. Multiresolution phase unwrapping for SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 163-174. DOI:10.1109/36.739150 |
| [24] |
GOEL K. Advanced stacking techniques and applications in high resolution SAR interferometry[D]. Munich: Technical University of Munich, 2014.
|
| [25] |
SCHEIBER R, MOREIRA A. Coregistration of interferometric SAR images using spectral diversity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2179-2191. DOI:10.1109/36.868876 |
| [26] |
DING Xiaoli, LI Zhiwei, ZHU Jianjun, et al. Atmospheric effects on InSAR measurements and their mitigation[J]. Sensors, 2008, 8(9): 5426-5448. DOI:10.3390/s8095426 |
| [27] |
YAGUE-MARTINEZ N. Burst-mode wide-swath SAR interferometry for solid earth monitoring[D]. Raumfahrt: DLR-Microwaves and Radar Institute, 2019.
|
| [28] |
吴文豪.哨兵雷达卫星TOPS模式干涉处理研究[D].武汉: 武汉大学, 2016. WU Wenhao. TOPS interferometry with Sentinel-1[D]. Wuhan: Wuhan University, 2016. |
| [29] |
BAMLER R. Interferometric stereo radargrammetry: absolute height determination from ERS-ENVISAT interferograms[C]//IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120). Honolulu, HI: IEEE, 2000: 742-745.
|
| [30] |
WANG Yuanyuan, ZHU Xiaoxiang. Robust estimators for multipass SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 968-980. DOI:10.1109/TGRS.2015.2471303 |
| [31] |
BAMLER R, EINEDER M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 151-155. DOI:10.1109/LGRS.2004.843203 |
| [32] |
SAKAR N, BRCIC R, GONZALEZ F R, et al. An advanced co-registration method for TOPSAR interferometry[C]//Proceedings of 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Milan, Italy: IEEE, 2015.
|
| [33] |
吴文豪, 张磊, 李陶, 等. 基于几何配准的多模式SAR影像配准及其误差分析[J]. 测绘学报, 2019, 48(11): 1439-1451. WU Wenhao, ZHANG Lei, LI Tao, et al. Coregistration scheme and error analysis of multi-mode SAR image based on geometric coregistration[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(11): 1439-1451. DOI:10.11947/j.AGCS.2019.20180440 |
| [34] |
META A, PRATS P, STEINBRECHER U, et al. First TOPSAR image and interferometry results with TerraSAR-X[J]. American Heart Journal, 2008, 36(6): 943-949. |
| [35] |
MANCON S, GUARNIERI A M, GIUDICI D, et al. On the phase calibration by multisquint analysis in TOPSAR and stripmap interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 134-147. DOI:10.1109/TGRS.2016.2598686 |
| [36] |
DE ZAN F. Coherent shift estimation for stacks of SAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1095-1099. DOI:10.1109/LGRS.2011.2157079 |
| [37] |
JIANG Mi, DING Xiaoli, LI Zhiwei. Hybrid approach for unbiased coherence estimation for multitemporal InSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2459-2473. DOI:10.1109/TGRS.2013.2261996 |
| [38] |
WANG Yuanyuan, ZHU Xiaoxiang. Robust estimators for multipass SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 968-980. DOI:10.1109/TGRS.2015.2471303 |
| [39] |
ANSARI H, DE ZAN F, BAMLER R. Sequential estimator:toward efficient InSAR time series analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5637-5652. DOI:10.1109/TGRS.2017.2711037 |
| [40] |
GUARNIERI A M, TEBALDINI S. On the exploitation of target statistics for SAR interferometry applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(11): 3436-3443. DOI:10.1109/TGRS.2008.2001756 |
| [41] |
FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks:SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460-3470. DOI:10.1109/TGRS.2011.2124465 |
| [42] |
赵超英, 王宝行. SAR干涉图降噪的稳健协方差矩阵分解法[J]. 测绘学报, 2019, 48(1): 24-33. ZHAO Chaoying, WANG Baohang. SAR interferogram denoising based on robust covariance matrix decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(1): 24-33. DOI:10.11947/j.AGCS.2019.20170394 |
| [43] |
SUN Qishi, JIANG Liming, JIANG Mi, et al. Monitoring coastal reclamation subsidence in Hong Kong with distributed scatterer interferometry[J]. Remote Sensing, 2018, 10(11): 1738. DOI:10.3390/rs10111738 |
| [44] |
CAO Ning, LEE H, JUNG H C. A phase-decomposition-based PSInSAR processing method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1074-1090. DOI:10.1109/TGRS.2015.2473818 |



