2. 同济大学测绘与地理信息学院, 上海 200092;
3. 中国卫星导航系统管理办公室, 北京 100034
2. College of Surveying and Geo-Informatics, Tongji University, Shanghai 200092, China;
3. China Satellite Navigation Office, Beijing 100034, China
最优参数估计、精度评定和质量控制都必须采用正确的观测值随机模型(方差-协方差阵)。线性(或线性化)高斯-马尔可夫观测模型为
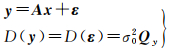 (1)
(1)
式中,y为n维观测向量;x是t维参数向量;A为列满秩的设计矩阵;观测白噪声ε对应的协因数阵为Qy;σ02为单位权方差因子。通过分析最小二乘(LS)估值、验后方差估值和质量控制涉及的整体检验统计量来简要阐述随机模型的重要性。
取任意正定对称矩阵P作为权矩阵进行LS平差,得LS估值及其协方差阵[1]为
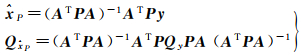 (2)
(2)
验后单位权方差
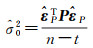 (3)
(3)
以及质量控制通常涉及的整体检验统计量[2]
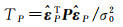 (4)
(4)
式中,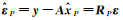
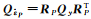
(1) 容易证明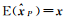
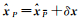
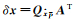
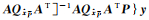
(2) 分析验后单位权方差的无偏性。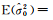
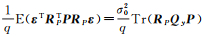
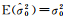
(3) 当取P为权阵时,容易证明E(TP)=q,从而采用自由度为q的卡方分布χ2(q)进行检验;但当取P为权阵时,则E(TP)=q+Tr(RPQyδP)。此时若依然采用χ2(q)检验,必然导致检验结果出现偏差,即可能将错误模型判为正确,将正确模型判为错误。
以上3点充分阐述了随机模型的重要性,换句话说,方差-协方差分量估计(variance component estimation, VCE)在测量数据处理中占有与参数估计同等重要的地位。在实际应用中,应该采用VCE确定观测值正确的协方差阵,对高精度GNSS应用也不例外。已有诸多采用VCE精化GNSS随机模型的研究[3-6],取得了良好的效果。文献[7]提出了根据卫星高度角定权模型;文献[8]在GPS基线解算中,采用MINQUE方法同时估计协方差阵,改善了基线结果;文献[9—10]先后采用超短基线和中长基线GPS数据,分析了不同接收机的不同类型观测值精度及其与高度角的关系,时间相关性以及不同类型观测值之间的交叉相关性;文献[11]提出了一种基于移动窗口实时估计双差观测值先验协方差阵的方法,改善了动态定位结果。此外,针对北斗二号卫星,文献[12]详细评估了不同接收机3类卫星的随机特性,并分析了精化的随机模型对定位结果和评定指标,以及质量控制涉及的整体检验、w-检验和最小可探测粗差的影响机制[13]。
北斗三号系统已于2018年12月向全球用户提供基本导航服务[14],文献[15]表明联合北斗二号和三号卫星能有效改善定轨、RTK和PPP效果,但该结果是基于经验随机模型得到的。由于北斗三号卫星的信号体制、硬件和信号质量相对北斗二号均有显著提升[16],若简单地采用北斗二号信号的随机模型或者经验随机模型,将必然影响北斗定位的精度和可靠性。因此,本文基于短基线单差观测模型,假设不同频率、不同卫星的相位和伪距观测精度不同,任意频率之间的交叉相关性不同,不同频率的相位和伪距观测值在不同时间间隔上的时间相关性不同,深入地分析了北斗GEO、IGSO和MEO卫星随机特性,为精化不同接收机的随机模型提供理论支撑。
1 短基线BDS单差观测模型由于短基线站间单差能消除卫星钟差和有效消除大气误差的影响,且无需参考卫星从而不会引入数学相关性等优点,通常被用于分析GNSS观测值随机特性。忽略短基线对流层、电离层等误差的影响,则跟踪s颗卫星的单历元三频BDS单差观测方程为
 (5)
(5)
式中,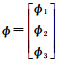
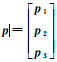
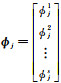
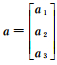
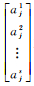
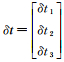
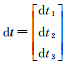
显然,钟差δt和模糊度a的系数阵满足线性组合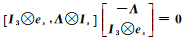
 (6)
(6)
式中,zj为第j个频率的双差模糊度,具有整数特性。消除秩亏后,得到满秩单差观测方程
 (7)
(7)
式中,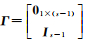
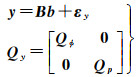 (8)
(8)
式中,y=[ϕT pT]T表示基线和双差整周模糊度改正后的单历元观测值;设计矩阵B=I6⊗es对应6个未知钟差参数b=[δtT, dtT]T;Qy为高斯白噪声εy的方差协方差(VC)矩阵,Qϕ和Qp分别表示单差相位和伪距观测值的VC矩阵。连续K个历元的单差观测方程为
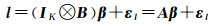 (9)
(9)
式中,l=[y1T, y2T, …, yKT]T,β=[b1T, b2T, …, bKT]T,下标K表示历元。
2 待估VC矩阵及其求解策略本文旨在充分剖析北斗GEO、IGSO和MEO 3类卫星三频相位和伪距观测值的随机特性,包括精度及其与高度角的关系、交叉相关性、时间相关性等,需要合理确定待估VC矩阵。为分析不同频率、3类卫星的相位和伪距精度,对每颗卫星引入方差元素;为分析任意两个频率间的交叉相关系数,对三频相位和伪距分别引入3个交叉相关系数;为分析不同时间间隔、不同频率相位和伪距时间相关性,对K个历元的每个频率伪距和相位观测值分别引入(K-1)个时间相关系数。下文首先给出单历元待估VC矩阵,然后引入时间相关系数,导出K个历元的待估VC矩阵。
2.1 单历元待估VC矩阵假设不同频率、每颗卫星的相位和伪距观测值的方差不同,任意两个频率间的相位和伪距的交叉相关系数不同。则单历元相位观测值的VC矩阵为
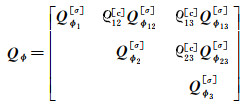 (10)
(10)
式中,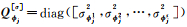
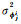
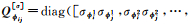
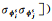
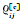
在静态观测较短的时间内,卫星高度角和观测环境变化微小,可认为这段时间内所有单个历元的待估VC矩阵相同。但多历元的待估VC矩阵将引入时间相关系数,对任意两个历元间隔的所有频率的伪距和相位观测值分别引入时间相关系数,则连续K个历元观测值的待估VC矩阵为
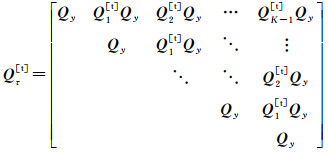 (11)
(11)
式中,间隔为τ的两个历元观测值的时间相关矩阵
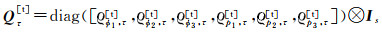 (12)
(12)
式中,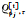
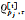
如引言所述,随机模型的确定采用VCE方法。自Helmert利用残差估计分类观测数据方差分量的无偏估计开始,许多学者对VCE理论作了深入的研究[17-19]。先后提出了最小范数二次无偏估计(MINQUE)[20]、最优不变二次无偏估计(BIQUE)[21]、极大似然估计、贝叶斯估计[22]、最小二乘估计等。文献[23]指出,所有的方差分量估计的本质是采用等效残差信息估计观测值本身的二阶中心距,尽管不同方法推导的出发点不同,但得到的估计公式是等价的。
将VC矩阵表示为待估元素的线性函数
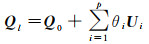 (13)
(13)
式中,Q0表示VC矩阵的已知部分,例如在迭代中固定的部分元素;θi为待估方差和相关系数元素,对应已知的系数矩阵Ui,总共有p个待估元素。由于不同的VCE方法是等价的,省去推导直接给出VCE法方程[23]
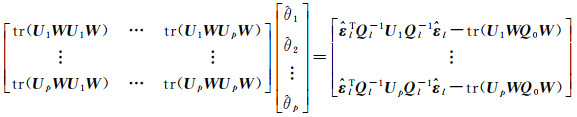 (14)
(14)
式中,W=Ql-1R=Ql-1-Ql-1B(BTQl-1B)-1BTQl-1。由于式(14)中左右两侧都包含了未知VC矩阵Ql,因此VCE需要迭代计算。给定待估方差、交叉相关系数和时间相关系数的初值,可确定初始VC矩阵Ql和W矩阵,从而迭代计算未知数[12]。
与传统评估GNSS随机特性的文献[7, 8, 24]不同,本文构造的待估VC矩阵能充分估计每颗卫星、每个频率、每类观测值的精度,任意频率间的交叉相关系数,以及不同频率任意历元间隔的时间相关系数,因此导致待估未知元素较多。设K个历元连续跟踪s颗卫星的三频相位和伪距数据,则总共有6s+6K个待估元素,其中6s个观测值方差、6个交叉相关系数和6(K-1)个时间相关系数。根据方差分量估计性质[25],同时估计所有未知数可能导致结果不稳定,甚至出现负方差或者没有实际意义的相关系数。因此,本文采用分步估计策略[12]:
(1) 忽略交叉相关性和时间相关性,估计每颗卫星每个频率相位和伪距观测值精度,并用于高度角建模;
(2) 将第(1)步求得的观测值精度视为已知,求解相位和伪距的交叉相关系数;
(3) 固定前两步求得的观测值精度和交叉相关系数,求解相位和伪距的时间相关系数。
注意,由于前两步估计都不同程度地忽略相关性信息,因此当相关性较显著时,将会影响到观测值精度的估计结果,因此建议对这3步骤进行迭代计算。
3 测试与分析采用上海站采集的2019年1月14日的北斗观测数据,接收机型号为天宝alloy,采样间隔1s,共7200个历元,北斗二号GEO/IGSO/MEO卫星为B1[B1I]、B2[B2I]、B3[B3I]频率上的伪距和相位,北斗三号IGSO/MEO卫星为B1[B1C]、B2[B2a]、B3[B3I]频率上的伪距和相位。北斗三号GEO卫星尚未可用。截止高度角为10°,基线长度约为4.866m。
3.1 观测值精度与交叉相关性基于式(9),短基线两端采用同类型接收机,对于每个历元来说,不同卫星对应不同的高度角,需要单颗卫星的观测值残差来分析观测值精度与卫星高度角的关系。由于高度角在短时间内的变化较小,连续观测n个历元,可得到卫星j的非差相位观测值精度。
在以往的GNSS解算过程当中,高度角加权模型通常采用下式的经验模型
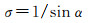 (15)
(15)
式中,σ为标准差。这种高度角模型过于简单,并不能很好地体现观测值精度与高度角的关系,尤其是忽略了北斗GEO/IGSO/MEO 3种类型卫星观测值精度与高度角关系的差异。本文通过不同类型卫星观测值与高度角的趋势关系,对以下3种高度角加权模型当中的系数进行拟合,得到符合北斗卫星特性的模型
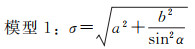 (16)
(16)
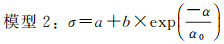 (17)
(17)
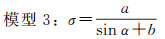 (18)
(18)
式中,α表示卫星高度角;a、b、α0为待拟合的系数。
表 1、表 2分别给出了北斗二号和北斗三号各类卫星观测值精度及交叉相关性,加粗数字的为北斗三号的结果。其中对角线元素表示观测值的精度,非对角线元素表示交叉相关性。表 1的测试结果表明,北斗三号卫星在不同频率上的伪距和相位的精度都优于北斗二号卫星。对于北斗三号卫星,3个频率伪距精度几乎相当,B3频率上的伪距精度略微优于B1和B2频率上的伪距精度。表 2的测试结果表明,北斗三号MEO卫星B3频率上相位的精度优于B2频率上的相位精度,但差于B1频率上的相位精度。对于Alloy接收机,北斗二号B1频率上相位观测值与B2、B3频率上相位观测值之间存在的一定程度的相关性,其他类型观测值之间的交叉相关性不明显。由此可知,不同类型观测值之间的交叉相关性与观测值类型和接收机都相关。
| 观测类型 | B1伪距/m | B2伪距/m | B3伪距/m | B1相位/mm | B2相位/mm | B3相位/mm |
| B1伪距 | 0.177 | 0.030 | -0.046 | 0.018 | -0.013 | 0.011 |
| 0.131 | -0.006 | -0.039 | 0.009 | -0.012 | 0.006 | |
| B2伪距 | 0.116 | 0.051 | -0.014 | 0.015 | 0.023 | |
| 0.113 | 0.010 | 0.008 | 0.014 | 0.021 | ||
| B3伪距 | 0.099 | 0.008 | 0.011 | 0.005 | ||
| 0.097 | 0.015 | 0.011 | 0.020 | |||
| B1相位 | 1.567 | 0.558 | 0.565 | |||
| 1.478 | 0.013 | 0.011 | ||||
| B2相位 | 1.848 | 0.644 | ||||
| 1.755 | 0.010 | |||||
| B3相位 | 1.790 | |||||
| 对称 | 1.631 |
| 北斗系统 | 卫星 | B1伪距/m | B2伪距/m | B3伪距/m | B1相位/mm | B2相位/mm | B3相位/mm |
| 北斗二号 | GEO | 0.171 | 0.102 | 0.075 | 1.386 | 1.538 | 1.561 |
| IGSO | 0.146 | 0.081 | 0.072 | 0.986 | 1.094 | 1.102 | |
| MEO | 0.123 | 0.078 | 0.061 | 0.944 | 1.037 | 1.035 | |
| 北斗三号 | IGSO | 0.101 | 0.087 | 0.085 | 1.009 | 1.061 | 1.101 |
| MEO | 0.093 | 0.069 | 0.061 | 0.933 | 0.979 | 0.968 |
3.2 观测值精度与高度角
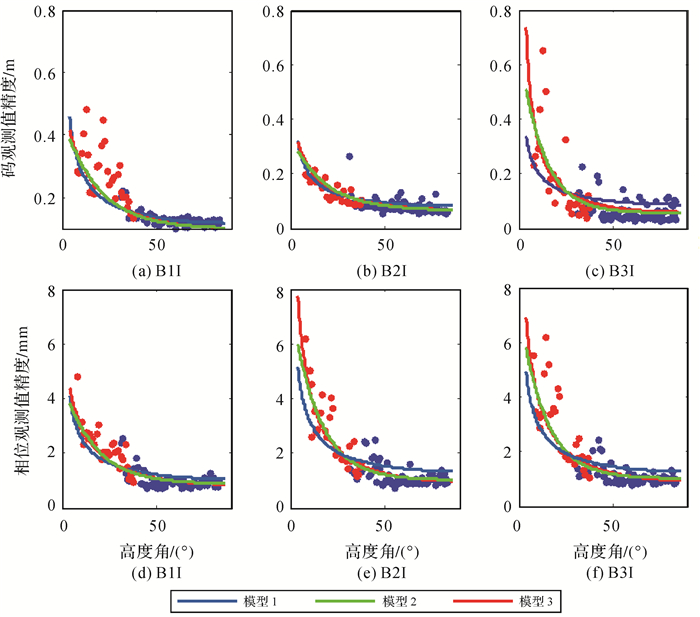
图 1给出了北斗二号B1和B2频率上伪距与相位观测值精度与高度角的关系,不同颜色表示不同卫星。所有类型观测值都与卫星高度角呈明显相关性,即高度角越高,观测精度越好,但不同类型的观测值,精度与高度角的关系不尽相同。表 3和表 4分别给出了北斗二号和北斗三号各个频率上的伪距与相位观测值的高度角加权模型拟合结果和拟合误差。模型2对各个频率上的伪距观测值的拟合误差最小;3种模型对相位观测值的拟合效果基本相当,拟合误差小于1mm。不同观测值的高度角相关程度和加权模型系数各不相同,所以,运用统一的随机模型定权的方法并不科学。
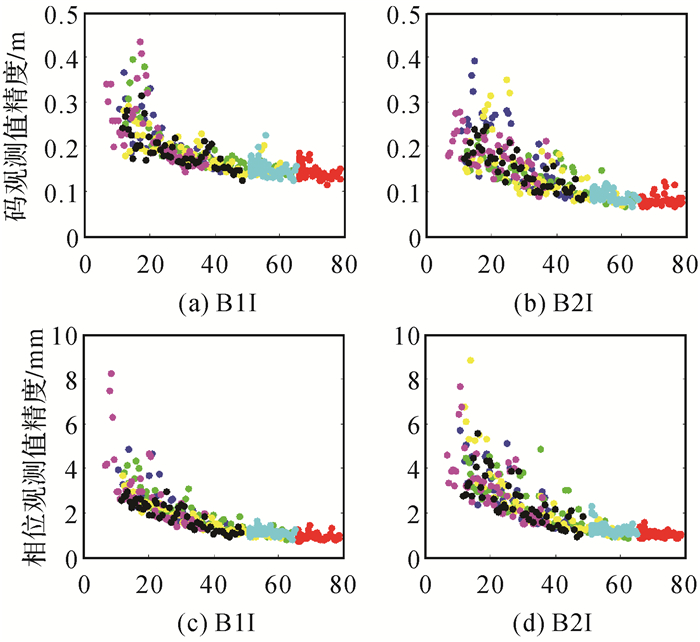
|
| 图 1 精度与高度角关系 Fig. 1 The correlations between satellite elevation and precision |
| 模型1 | 模型2 | 模型3 | ||
| B1伪距 | 拟合结果 | 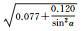 |
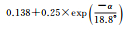 |
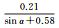 |
| 拟合误差 | 0.033 | 0.029 | 0.031 | |
| B2伪距 | 拟合结果 | 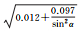 |
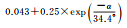 |
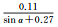 |
| 拟合误差 | 0.038 | 0.032 | 0.035 | |
| B3伪距 | 拟合结果 | 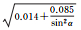 |
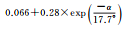 |
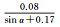 |
| 拟合误差 | 0.067 | 0.065 | 0.066 | |
| B1相位 | 拟合结果 | 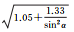 |
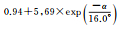 |
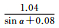 |
| 拟合误差 | 0.57 | 0.43 | 0.45 | |
| B2相位 | 拟合结果 | 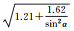 |
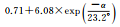 |
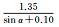 |
| 拟合误差 | 0.83 | 0.66 | 0.70 | |
| B3相位 | 拟合结果 | 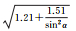 |
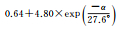 |
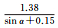 |
| 拟合误差 | 0.71 | 0.60 | 0.63 |
| 模型1 | 模型2 | 模型3 | ||
| B1伪距 | 拟合结果 | 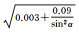 |
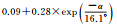 |
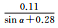 |
| 拟合误差 | 0.03 | 0.03 | 0.03 | |
| B2伪距 | 拟合结果 | 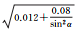 |
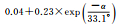 |
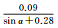 |
| 拟合误差 | 0.03 | 0.02 | 0.03 | |
| B3伪距 | 拟合结果 | 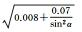 |
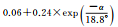 |
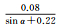 |
| 拟合误差 | 0.05 | 0.04 | 0.05 | |
| B1相位 | 拟合结果 | 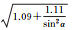 |
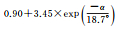 |
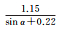 |
| 拟合误差 | 0.46 | 0.42 | 0.44 | |
| B2相位 | 拟合结果 | 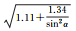 |
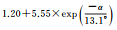 |
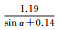 |
| 拟合误差 | 0.75 | 0.52 | 0.63 | |
| B3相位 | 拟合结果 | 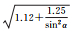 |
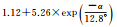 |
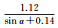 |
| 拟合误差 | 0.63 | 0.60 | 0.60 |
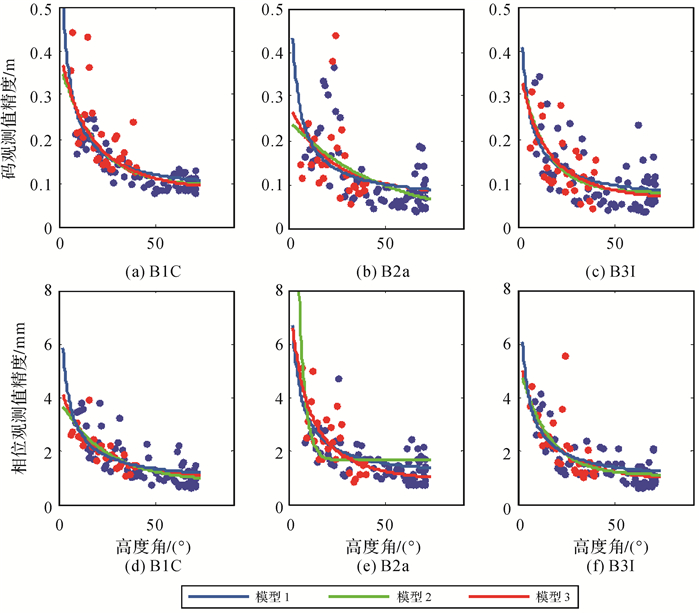
图 2至图 6分别给出了北斗二号GEO、IGSO和MEO 3类卫星和北斗三号IGSO和MEO卫星在各个频率上的伪距和相位观测值精度与高度角的关系。不同颜色表示不同卫星。GEO卫星相对于地球静止,所以高度角集中在几个高度角值附近,但也明显可以看出,高度角高时的精度优于低高度角的精度。北斗二号和北斗三号的IGSO卫星和MEO卫星的精度都与高度角明显相关,高度角越高,精度越好,但可以看出,不同观测值类型的相关程度并不相同。

|
| 图 2 北斗二号GEO卫星伪距/相位精度与高度角关系 Fig. 2 The correlation between BeiDou-2 GEO satellites code/phase precision and elevation |

|
| 图 3 北斗二号IGSO卫星伪距/相位与高度角关系 Fig. 3 The correlation between BeiDou-2 IGSO satellites code/phase precision and elevation |
|
| 图 4 北斗二号MEO卫星伪距/相位与高度角关系 Fig. 4 The correlation between BeiDou-2 MEO satellites code/phase precision and elevation |
|
| 图 5 北斗三号IGSO卫星伪距/相位与高度角关系 Fig. 5 The correlation between BeiDou-3 IGSO satellites code/phase precision and elevation |

|
| 图 6 北斗三号MEO卫星伪距/相位与高度角关系 Fig. 6 The correlation between BeiDou-3 MEO satellites code/phase precision and elevation |
3.3 观测值的时间相关性
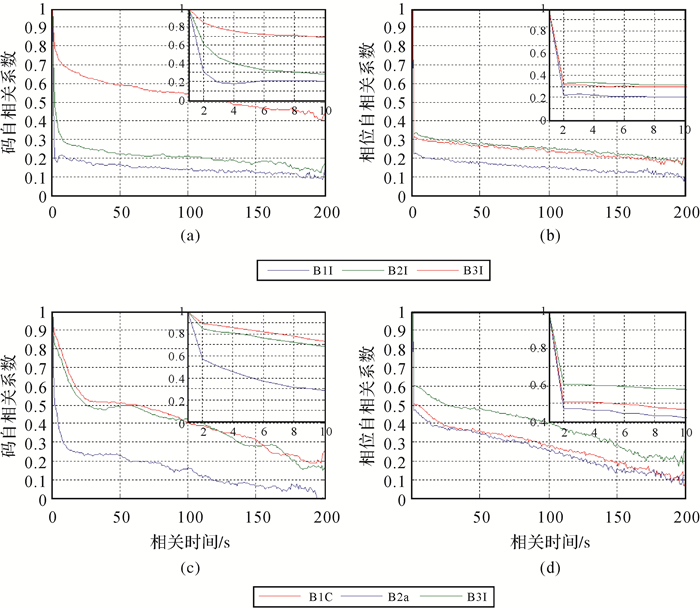
图 7给出了北斗各类观测值在前200s的时间相关性。每个子图右上方的小图代表各类观测值前10s的时间相关性。其中图 7(a)和图 7(b)分别表示北斗二号卫星码和相位观测值的时间相关性;图 7(c)和图 7(d)分别表示北斗三号卫星码和相位观测值的时间相关性。在图 7(a)和图 7(b)中,B1I、B2I频率上伪距和相位观测值的自相关系数从1开始迅速减小,最后稳定在0.1左右;B3I频率上伪距和相位观测值的自相关系数分别从1开始迅速减小至0.4和0.2左右趋于稳定。在图 7(c)和图 7(d)中,B1C、B2a和B3I频率上伪距和相位观测值的自相关性较北斗二号观测值几乎相当。B3I和B1C频率上伪距观测值的自相关系数则从1开始逐渐减小至0.2左右;B2a频率上伪距观测值的自相关系数则从1开始逐渐减小至零;B2a和B1C频率上相位观测值从1迅速下降至0.1左右;B3I频率上相位观测值从1迅速下降至0.2左右。由此可见,各类观测值的时间相关性确实存在,有些甚至不可忽略,不同类型观测值的时间相关性相差较大,在合理确定方差-协方差矩阵和实现高精度定位时应予以考虑。
|
| 图 7 北斗观测值时间相关性 Fig. 7 The temporal correlation coefficients of BDS observations |
3.4 随机模型对基线精度的影响
根据文献[12, 26],在考虑时间相关性的前提下,由K个历元计算的基线精度公式如下
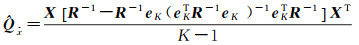 (19)
(19)
式中,X是K个历元的基线解构成的矩阵,X=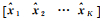
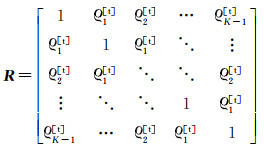 (20)
(20)
基线的理论精度可以通过单历元解算基线向量,然后平均K个历元基线方差得到,即
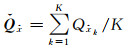 (21)
(21)
给定K=30,对北斗二号和北斗三号联合解算,通过式(19)和式(21)分别计算基线精度。图 8给出了随机模型对基线精度的影响。其中经验模型由式(15)给出。显然,采用估计的随机模型计算的基线精度在N、E和U 3个方向与理论精度比较吻合,而采用经验随机模型计算的基线精度则小于理论值。换句话说,在数据处理中采用不准确的随机模型将导致基线精度过于乐观且不切实际。
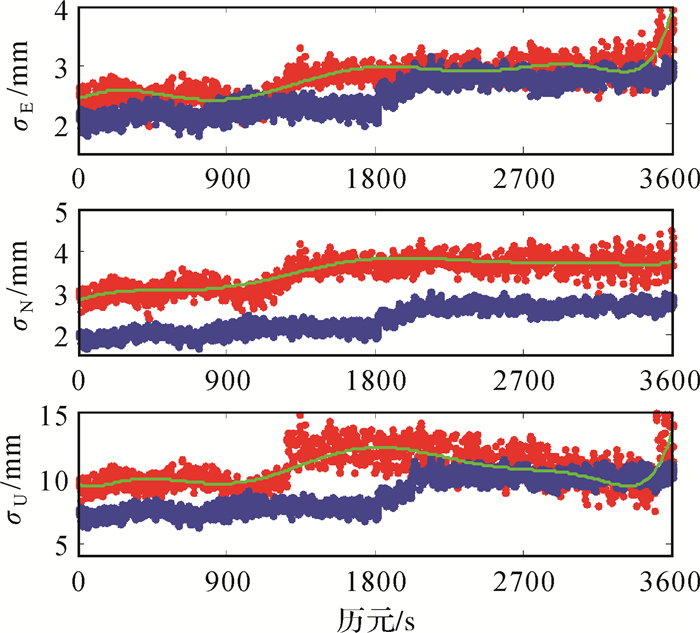
|
| 图 8 随机模型对基线精度的影响 Fig. 8 Impact of BDS stochastic model on baseline precisions |
3.5 随机模型对可靠性的影响
此部分分析随机模型对可靠性的影响,主要分析整体检验统计量。根据式(4),采用估计的随机模型和经验随机模型单历元解算模糊度固定解的整体检验统计量,如图 9所示。
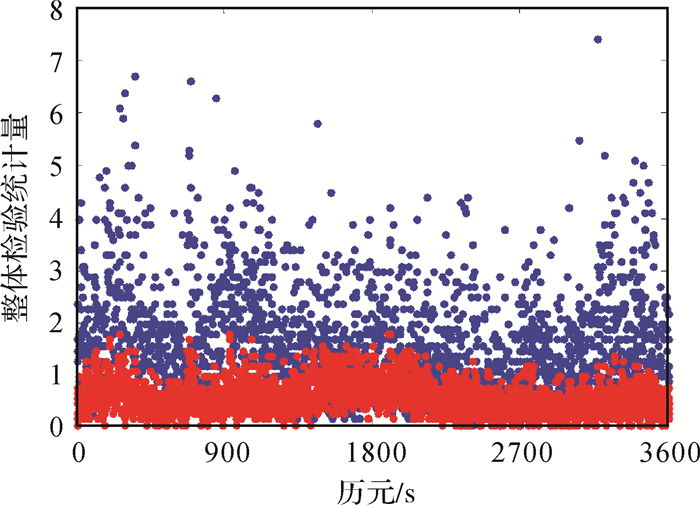
|
| 图 9 随机模型对整体检验统计量的影响 Fig. 9 Impact of BDS stochastic model on overall tests |
如果随机模型很好地描述了观察值的随机特性,则整体统计量的期望等于1。从图 9中可以看出,估计的随机模型计算的统计量确实总体上接近1,但是经验随机模型计算的统计量存在明显偏差。对所有历元总体检验统计量的结果取均值列于表 5。结果表明,计算出的均值越接近1,说明采用的随机模型更准确地描述观测值的随机特性。表 5中同样给出了在显著性水平α=0.05情况下整体检验统计量的弃真概率。显然估计的随机模型的弃真概率远小于经验随机模型。因此,采用恰当的随机模型可以降低对模型的弃真概率。
| 统计量平均值 | 弃真概率/(%) | |||
| 估计随机模型 | 经验随机模型 | 估计随机模型 | 经验随机模型 | |
| 1.01 | 2.56 | 6.21 | 78.65 | |
4 结论
本文基于短基线单差观测模型,采用方差分量估计的方法估计不同频率、不同卫星的相位和伪距观测值精度,任意频率之间的交叉相关性以及不同频率的相位和伪距观测值在不同时间间隔上的时间相关性。随后采用估计的随机模型分析了对基线精度和整体检验统计量的影响。通过对北斗观测数据的分析研究,得到如下结论:
(1) 北斗用户接收机采集北斗二号和北斗三号的各类卫星观测信息的精度都与高度角相关,北斗三号卫星在不同高度角加权模型的拟合误差都优于北斗二号,其中拟合误差最小的模型为高度角指数加权函数,因此在实际数据处理中建议采用高度角指数加权模型。
(2) 北斗二号的各类卫星B1频率上相位观测值与B2、B3频率上相位观测值之间存在一定程度的相关性,在数据处理过程中需要顾及相位观测值之间的相关性。北斗三号卫星相位观测值相关性不明显。
(3) 北斗二号和北斗三号的各类卫星伪距与相位观测值不相关,不同频率的相位和伪距之间相关性较小,实际数据处理中可忽略;北斗二号和北斗三号伪距和相位观测值的时间相关性较明显,需在接收机研制和数据处理中关注。
(4) 采用恰当的随机模型计算的基线精度与理论值符合较好,解算的基线精度更客观。在整体检验统计量计算中,采用估计的随机模型和经验模型分析表明,采用估计的随机模型可以减少弃真概率。
| [1] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993. YANG Yuanxi. Robust estimation and its applications[M]. Beijing: Bayi Publishing House, 1993. |
| [2] |
TEUNISSEN P J G. Testing theory:an introduction[M]. 2nd ed. Delft: Delft University Press, 2006.
|
| [3] |
AMIRI-SIMKOOEI A R, ZANGENEH-NEJAD F, ASGARI J. Least-squares variance component estimation applied to GPS geometry-based observation model[J]. Journal of Surveying Engineering, 2013, 139(4): 176-187. |
| [4] |
TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-squares variance component estimation[J]. Journal of Geodesy, 2008, 82(2): 65-82. |
| [5] |
AMIRI-SIMKOOEI A R, TEUNISSEN P J G, TIBERIUS C C J M. Application of least-squares variance component estimation to GPS observables[J]. Journal of Surveying Engineering, 2009, 135(4): 149-160. |
| [6] |
TIBERIUS C C J M, KENSELAAR F. Estimation of the stochastic model for GPS code and phase observables[J]. Survey Review, 2000, 35(277): 441-454. |
| [7] |
EUELER H J, GOAD C C. On optimal filtering of GPS dual frequency observations without using orbit information[J]. Bulletin Géodésique, 1991, 65(2): 130-143. |
| [8] |
WANG Jinling, STEWART M P, TSAKIRI M. Stochastic modeling for static GPS baseline data processing[J]. Journal of Surveying Engineering, 1998, 124(4): 171-181. |
| [9] |
LI Bofeng, SHEN Yunzhong, XU Peiliang. Assessment of stochastic models for GPS measurements with different types of receivers[J]. Chinese Science Bulletin, 2008, 53(20): 3219-3225. |
| [10] |
李博峰, 沈云中, 楼立志. GPS中长基线观测值随机特性分析[J]. 武汉大学学报(信息科学版), 2010, 35(2): 176-180. LI Bofeng, SHEN Yunzhong, LOU Lizhi. Analysis of the stochastic characteristics for medium and long base line GPS measurements[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 176-180. |
| [11] |
何海波, 杨元喜. GPS观测量先验方差-协方差矩阵实时估计[J]. 测绘学报, 2001, 30(1): 42-47. HE Haibo, YANG Yuanxi. Real-time estimation of a prior variance-covariance for GPS observations[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 42-47. DOI:10.3321/j.issn:1001-1595.2001.01.009 |
| [12] |
LI Bofeng. Stochastic modeling of triple-frequency BeiDou signals:estimation, assessment and impact analysis[J]. Journal of Geodesy, 2016, 90(7): 593-610. |
| [13] |
LI Bofeng, ZHANG Lei, VERHAGEN S. Impacts of BeiDou stochastic model on reliability:overall test, w-test and minimal detectable bias[J]. GPS Solutions, 2017, 21(3): 1095-1112. |
| [14] |
YANG Yuanxi, GAO Weiguang, GUO Shuren, et al. Introduction to BeiDou-3 navigation satellite system[J]. Navigation, 2019, 66(1): 7-18. |
| [15] |
ZHANG Zhiteng, LI Bofeng, NIE Liangwei, et al. Initial assessment of BeiDou-3 global navigation satellite system:signal quality, RTK and PPP[J]. GPS Solutions, 2019, 23(4): 111. |
| [16] |
YANG Yuanxi, MAO Yue, SUN Bijiao. Basic performance and future developments of BeiDou global navigation satellite system[J]. Satellite Navigation, 2020, 1(1): 1-8. |
| [17] |
HELMERT F. Die Ausgleichung nach der Methode der kleinsten quadrate[J]. Auflage, Verlagvon BG Teubner, Leipzig/Berlin, 1907. |
| [18] |
王新洲, 刘经南, 陶本藻. 稳健最优不变二次无偏估计[J]. 武汉测绘科技大学学报, 1995, 20(3): 240-245. WANG Xinzhou, LIU Jingnan, TAO Benzao. Robust best invariant quadratic unbiased estimation[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995, 20(3): 240-245. |
| [19] |
於宗俦. Helmert型方差-协方差分量估计的通用公式[J]. 武汉测绘科技大学学报, 1991, 16(2): 8-17. YU Zongchou. The general formulas of Helmert type for estimating variance and covarince components[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1991, 16(2): 8-17. |
| [20] |
RAO C R. Estimation of variance and covariance components-MINQUE theory[J]. Journal of Multivariate Analysis, 1971, 1(3): 257-275. |
| [21] |
KOCH K R. Parameter estimation and hypothesis testing in linear models[M]. Berlin: Springer-Verlag, 1988.
|
| [22] |
朱建军. 方差分量的Bayes估计[J]. 测绘学报, 1991, 20(1): 1-6. ZHU Jianjun. Bayes estimation of the components of variance[J]. Acta Geodaetica et Cartographica Sinica, 1991, 20(1): 1-6. |
| [23] |
李博峰, 沈云中, 楼立志. 基于等效残差的方差-协方差分量估计[J]. 测绘学报, 2010, 39(4): 349-354, 363. LI Bofeng, SHEN Yunzhong, LOU Lizhi. Variance-covariance component estimation based on the equivalent residuals[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 349-354, 363. |
| [24] |
BONA P. Precision, cross correlation, and time correlation of GPS phase and code observations[J]. GPS Solutions, 2000, 4(2): 3-13. |
| [25] |
XU Peiliang, LIU Jingnan. Variance components in errors-in-variables models:estimability, stability and bias analysis[J]. Journal of Geodesy, 2014, 88(8): 719-734. |
| [26] |
LI Bofeng, ZHANG Zhetao. Several kinematic data processing methods for time-correlated observations[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(4): 1-9. |



