全球导航卫星系统(global navigation satellite system, GNSS)经过40多年的发展,在国民经济和国防建设中发挥了越来越重要的作用,成为国家空间信息基础设施的重要组成部分[1]。由于GNSS卫星信号属于L波段非常适合于反演地球表面环境,GNSS反射测量(GNSS-reflectometry, GNSS-R)技术应运而生,成为遥感和导航领域的研究热点。
国内外学者已经开展了一系列GNSS-R技术研究,如海面测高[2]、海面风场监测[3]、潮位监测[4]、雪深反演[5]、土壤湿度反演[6-7]等。近年来有学者研究利用GNSS-R技术探测海面目标。通常采用前向散射的几何配置生成围绕镜面散射点的延迟-多普勒图(delay-Doppler map, DDM)进行目标探测[8-10]。在DDM中,如果被探测目标不是恰好处于镜面散射点区域,则镜面散射点区域的海杂波能量强于目标回波,不利于目标信号的检测[11]。即便海杂波被有效地抑制,由于DDM图通常呈现为“马蹄形”,目标的位置也会变得不明确[12]。此外,GNSS-R技术用于目标探测的空间分辨率较低,为千米级[10]。因此,传统的GNSS-R技术并不太适合于海面目标探测。
从雷达技术的角度,GNSS卫星可被视为非合作的机会照射源,可与地表接收机构成天-地无源双基地雷达系统用于探测目标(以下简称GNSS无源雷达系统)。相比于传统的基于前向散射的GNSS-R技术,GNSS无源雷达系统采用后向散射的几何配置。在该几何配置下,海杂波的能量能够得到一定的抑制,目标的位置变得明确,空间分辨率也会得到改善。相比于传统的主动式雷达,GNSS无源雷达系统不需要沉重的发射设备,只需接收设备便可感知目标散射的GNSS信号。因此,该系统具有低成本、小体积、隐蔽性强、抗电子侦察、无辐射污染等优点[13]。随着无线电技术的发展,许多无线电信号源已经被用于构建无源雷达系统,例如FM[14]、DAB/DVB[15]、GSM[16]、WIFI[17]等。这些无源雷达系统大都采用地基照射源,信号的覆盖范围有限。相比于其他种类的无源雷达系统,GNSS卫星星座群(例如GPS、GLONASS、Galileo和北斗[18])带来的全球信号覆盖甚至包括极地地区,使得GNSS无源雷达系统的应用范围更广。特别是在缺乏其他信号覆盖的公开海域或者沿海岸地区,GNSS无源雷达可用于海上监视。文献[19]首先利用E5a Galileo卫星作为机会照射源开展了海面目标探测试验。试验结果表明了采用GNSS卫星作为机会照射源构建无源雷达的可行性。此外,GNSS无源雷达系统还可以做相干定位[20]、运动参数估计[21]、目标跟踪和目标成像等,具有不错的研究发展前景。
由于GNSS卫星距离地面的高度达到20000km,地表的GNSS信号能量较低。再经过目标的二次散射,目标回波能量变得微弱,常淹没在背景噪声和干扰信号之中。因此,GNSS无源雷达系统作目标探测的关键在于累积目标回波能量和抑制干扰信号。本文以GPS卫星作为机会照射源构建GPS天-地无源双基地雷达系统,将海面船只的运动轨迹看作是合成孔径等效于岸边固定的接收机以同样的速度沿反方向运动,提出利用SAR成像技术来累积目标回波能量和抑制干扰信号的方法。首先分析了目标运动过程中的双基地几何关系。然后,对SAR成像技术——距离多普勒算法(range-Doppler algorithm,RDA)[22]进行了适当的修改,实现对目标回波能量压缩聚集和抑制干扰信号。最后,使用相位梯度自聚焦算法(phase gradient autofocus,PGA)[23-24]作自聚焦处理进一步聚集目标回波能量。为了验证本文方法,现场试验采集了多组数据。结果表明,本文方法能够同时聚集多个目标回波能量,精确地估计目标到接收机的距离,并能判断目标的移动方向。
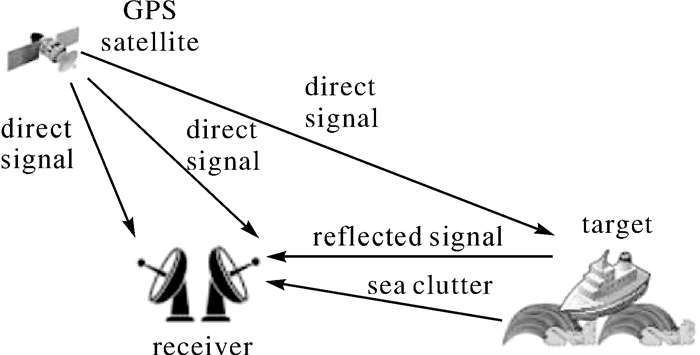
1 双基地几何分析图 1给出了GPS天-地无源双基地雷达系统探测海面移动目标的示意图。图中,岸边的GPS接收机包含两个通道,分别为参考通道和监视通道。参考通道的天线对准天空接收卫星发射的GPS直达波作为参考信号。监视通道的天线则指向海面接收目标反射的GPS信号。除了目标回波和背景噪声外,监视通道内的信号还包括干扰信号,例如直达波和海杂波。干扰信号及其旁瓣的能量强度往往高于目标回波,会给目标探测带来一定的困难。
|
| 图 1 GPS天-地无源双基地雷达探测海面目标 Fig. 1 GPS-based space-surface passive bistatic radar for maritime target detection |
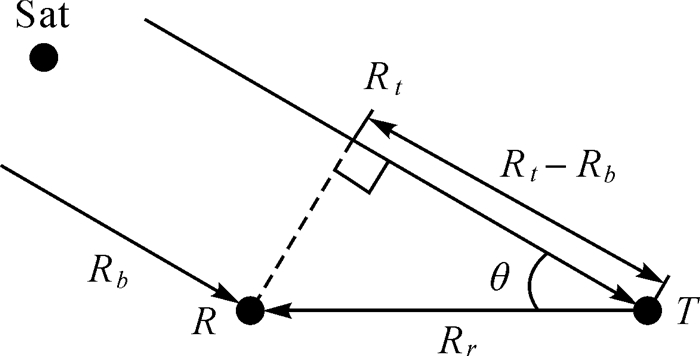
图 2对图 1的双基地几何关系作了抽象简化。为了简便起见,假定接收机R和目标T处在相同的高度。由于GPS卫星到地表的距离要远远大于目标到接收机的距离,图 2中卫星到接收机的直线和卫星到目标的直线接近于平行。因此,结合三角函数关系,双基地距离[25]表示为
 (1)
(1)
|
| 图 2 GPS天-地无源双基地雷达侧视图 Fig. 2 The side view diagram of GPS-based space-surface passive bistatic radar |
式中,Rb和Rt分别表示卫星到接收机的距离(基线距离)和卫星到目标的距离;Rr表示目标到接收机的距离;θ表示双基地角。文献[26]指出当双基地角在0°到90°之间,如果基线距离满足Rb≥0.82(Rt+Rr)或Rb≥4.56Rbi时,Rr的误差将小于10%。实际上,基线距离要远远大于5倍的双基地距离,而且本文采用的是后向散射的几何配置满足θ < 90°。所以,可以安全地使用式(1)来表示Rbi与Rr之间的关系。然而,式(1)不能直观地反映双基地距离随目标运动的变化。因此,在图 3和图 4中,将结合目标的运动轨迹进一步分析双基地角θ和目标到接收机距离Rr。
|
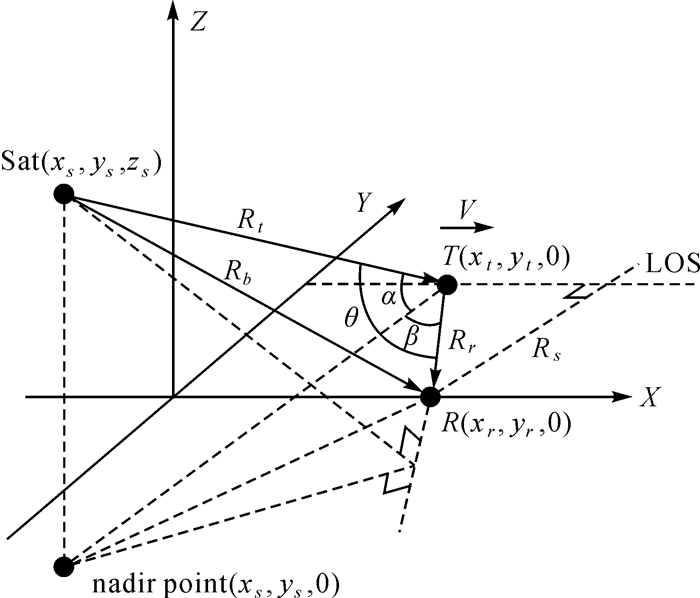
| 图 3 GPS天-地无源双基地雷达三维示意 Fig. 3 The 3D view diagram of GPS-based space-surface passive radar |
|
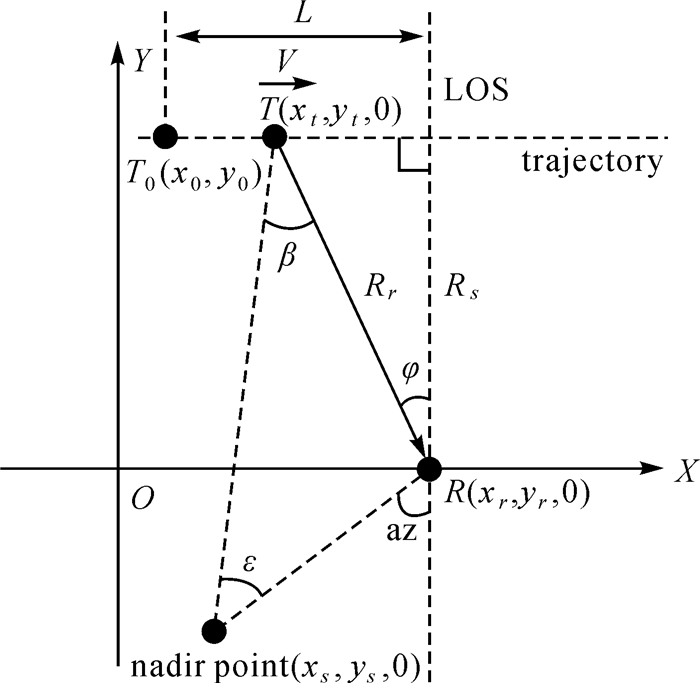
| 图 4 GPS天-地无源双基地雷达俯视图 Fig. 4 The top view diagram of GPS-based space-surface passive radar |
图 3为双基地几何的三维示意图。图中,点目标T自左向右移动穿过接收机天线视线(line of sight, LOS)方向(假设目标始终处在接收机天线3dB波束角照射范围内)。通过在图 3中添加必要的辅助线,不难得到如下关系
 (2)
(2)
利用三角函数关系简化式(2),双基地角表示为
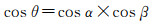 (3)
(3)
式中,α是卫星高度角;β是由接收机、目标和卫星星下点构成的顶角。图 4的俯视图给出了β角的关系
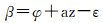 (4)
(4)
式中,φ=cos-1(Rs/Rr)是接收机天线相位中心对目标的斜视角;Rs表示目标到接收机的垂直距离;az称为本地卫星方位角,该角度可由实际的卫星方位角与接收机天线视线方位角计算得到(试验部分会结合具体的试验场景给出计算公式);ε是星下点到目标与星下点到接收机的直线间夹角,由于星下点到接收机或者目标的距离依然远远大于目标到接收机的距离,ε可以忽略不计。结合式(3)和式(4),双基地角表示如下
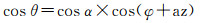 (5)
(5)
图 4中目标的运动轨迹垂直于接收机天线视线方向,Rr代表的目标到接收机距离可以记为
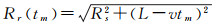 (6)
(6)
式中,tm∈[0, 2L/v]表示观测时间(也可称为慢时间);L=[xr-x0]表示合成孔径长度的一半;v表示目标的移动速度。将式(5)、式(6)代入式(1)并整理,得到在观测时间内双基地距离为
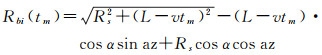 (7)
(7)
同理,如果图 4中的目标自右向左移动,双基地距离则变为
 (8)
(8)
式(7)、式(8)表明,当目标的运动方向不同时,对应的双基地距离表示式也不相同。需要注意的是,图 4仅显示了星下点在接收机天线视线方向左侧的例子。如果星下点位于右侧并且目标依然自左向右运动,双基地距离表达式则变成式(8),反之,则为式(7)。本节基于双基地几何关系推导的双基地距离表达式将用于下文的回波信号处理。
2 回波信号处理 2.1 信号同步无源雷达系统处理目标回波通常需要直达波作为参考信号。但是,参考通道接收的GPS直达波能量很低,仅-30dB[27],淹没在背景噪声中。这样的直达波不能直接用于回波信号处理,需要做信号同步。文献[28]讨论了信号同步在GNSS无源雷达系统中的重要性。所谓的信号同步就是从含有噪声的GPS直达波中提取码相位、载波相位、载波多普勒、导航电文等观测量,再利用这些观测量生成接近于无噪声的直达波作为参考信号。本文采用软件接收机系统来捕获和跟踪GPS直达波,从而可以实时地提取观测量信息。该软件接收机基于文献[29]开发。文献[30]已经利用软件接收机做了基于GNSS-R的形变监测研究,表明了软件接收机系统的有效性和可靠性。
以本文选用的GPS L1信号为例,将观测量生成的参考信号表示为雷达信号格式且忽略信号的幅值和初相
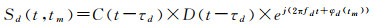 (9)
(9)
式中,t∈[0, PRI]表示快时间,PRI表示脉冲重复间隔(即C/A码持续时间为1ms);tm∈[0, T]表示慢时间,T是整个观测时长;C(·)表示C/A码;D(·)表示导航电文;e(·)表示复载波信号。φd(·)、fd和τd分别表示载波相位、载波频率和码延迟。同理,假设只有一个目标,监视通道内的目标回波表示为
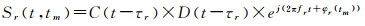 (10)
(10)
式中,φr(·)、fr和τr则分别表示回波信号的载波相位、载波频率和伪码延迟。
2.2 距离向压缩上文生成的参考信号将作为距离向匹配滤波器与目标回波作互相关处理,即为距离向压缩[31]。互相关处理表示为
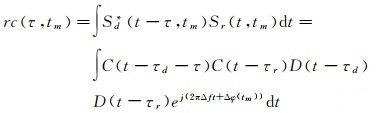 (11)
(11)
式中,*表示取共轭;τ表示码偏移;Δf表示快时间域两路信号的载波频率差;Δφ(tm)表示慢时间域两路信号的相位差。需要指出的是:①D(t-τd)D(t-τr)乘积为1,因为在6000km范围内参考信号与目标回波的导航电文相同[31];②Δf→0,因为相比于卫星的运动速度,目标速度在快时间域引起的载波多普勒变化几乎忽略不计;③Δφ(tm)消除了大气延迟、接收机钟差和振荡器漂移等误差相位,仅剩由双基地距离产生的传播延迟相位,因为接收机和目标上方的大气延迟误差几乎相同以及接收机双通道共用时钟和本地振荡器。综上,式(11)经过积分后表示为
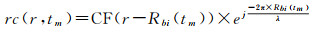 (12)
(12)
式中,r=τ×c表示双基地距离门单元;c表示光速;Rbi(tm)表示为式(7)或式(8)的双基地距离(取决于目标运动方向);CF(·)表示互相关函数包络;λ表示载波波长。由式(12)可知,互相关函数包络与慢时间存在耦合。对于宽带高距离向分辨率的主动式雷达,这种耦合会导致互相关函数包络沿慢时间维度分散在若干个距离门单元上,即所谓的距离徙动。然而,本文采用的GPS L1信号C/A码带宽为1.023MHz,对应的距离向分辨率约为150m。在粗糙的距离向分辨率下,距离徙动可以忽略[32],即式(12)的互相关函数包络对齐在同一个距离门单元(如果选用距离向分辨率更高的Galileo E5a/b或GPS L5信号,可以采用keystone变换[33]消除距离徙动)。利用互相关函数包络所在的双基地距离门单元可以估计目标到接收机的垂直距离。令式(7)或式(8)中L-vtm=0,则Rs表示为
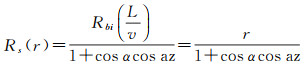 (13)
(13)
式(13)中的卫星高度角α和本地卫星方位角az均可方便获取,例如卫星星历数据或者由软件接收机解算。垂直距离Rs将用于下文的方位向匹配滤波器生成以及转换双基地距离为单基地距离方便获取目标到接收机距离。
2.3 方位向压缩距离向压缩会给目标回波带来一定的能量增益,但是目标回波可能依然淹没在背景噪声和干扰信号中。本文将船只的运动轨迹看作是合成孔径等效于岸边固定的接收机以同样的速度沿反方向运动,在慢时间维度上进一步压缩目标回波能量,即为方位向压缩。方位向压缩的原理是利用方位向匹配滤波器执行卷积运算去除目标回波相位中的调制相位项。卷积运算在频率域上具有较高的执行效率。因此,本文首先在频率域中推导方位向匹配滤波器的解析表达式,然后执行方位向压缩,最后讨论方位向匹配滤波器的生成和PGA补偿相位误差。
对式(12)沿慢速时间tm作傅里叶变换得到
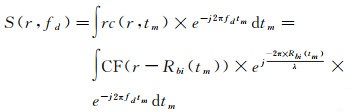 (14)
(14)
式中,fd∈-PRF/2, PRF/2表示频率分量;PRF表示脉冲重复频率(即上文中PRI的倒数)。式(14)的解析表达式难以直接求得,利用驻定相位原理[22]近似求解
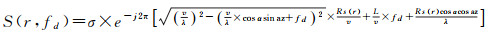 (15)
(15)
或
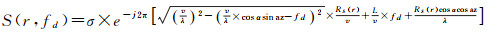 (16)
(16)
式中,σ表示频谱的幅值。式(15)、式(16)分别为式(7)、式(8)表示的不同运动方向的目标回波频谱解析式。观察式(15)、式(16)可知,指数相位中的第1项为调制相位,后两项分别为线性项和常数项。根据上述方位向压缩原理可知,方位向匹配滤波器即为调制相位项的共轭形式
 (17)
(17)
或
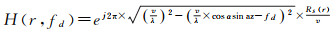 (18)
(18)
式(17)、式(18)表明当目标的运动方向不同时,对应的方位向匹配滤波器也不相同。换句话说,通过方位向匹配滤波器可以判断目标的移动方向(在试验部分给出具体实例)。
随后,将式(15)、式(17)相乘或者式(16)、式(18)相乘消除调制相位项,再执行逆傅里叶变换,从频率域回到慢时间域便可完成方位向压缩
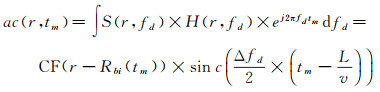 (19)
(19)
式中,Δfd表示多普勒频率带宽,其最大的带宽表示为
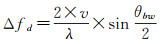 (20)
(20)
式中,θbw表示接收机天线3dB波束角。以上方位向压缩只考虑单个点目标的情况。实际情况下,船只目标可看作是若干个散射点集合。在整个慢时间域中,散射点回波的多普勒频率带宽相同,但是到达同一多普勒频率的时刻不同。因此,式(19)可扩展为N个散射点
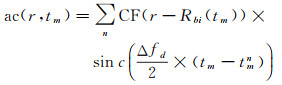 (21)
(21)
式中,∑·表示所有散射点集合而不是求和;tmn=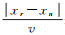
未知的目标速度同样影响方位向匹配滤波器的生成。为了解决这个问题,首先利用观测海域内过往船只的速度统计出一个经验速度值。距离向压缩后,在各个距离门上,根据式(17)或式(18)生成相应的方位向匹配滤波器作方位向压缩,探测所有可能存在的移动目标。显然,经验速度与目标的真实速度不一定匹配,方位向压缩后会存在相位误差产生散焦效应。然而,本文仅关心目标回波能量聚集而不是成像。因此,可以利用PGA自聚焦算法[34]补偿相位误差,将能量聚集到特显点上提高目标回波能量。最后,图 5给出了GPS天-地无源双基地雷达探测海面移动目标的信号处理基本流程。
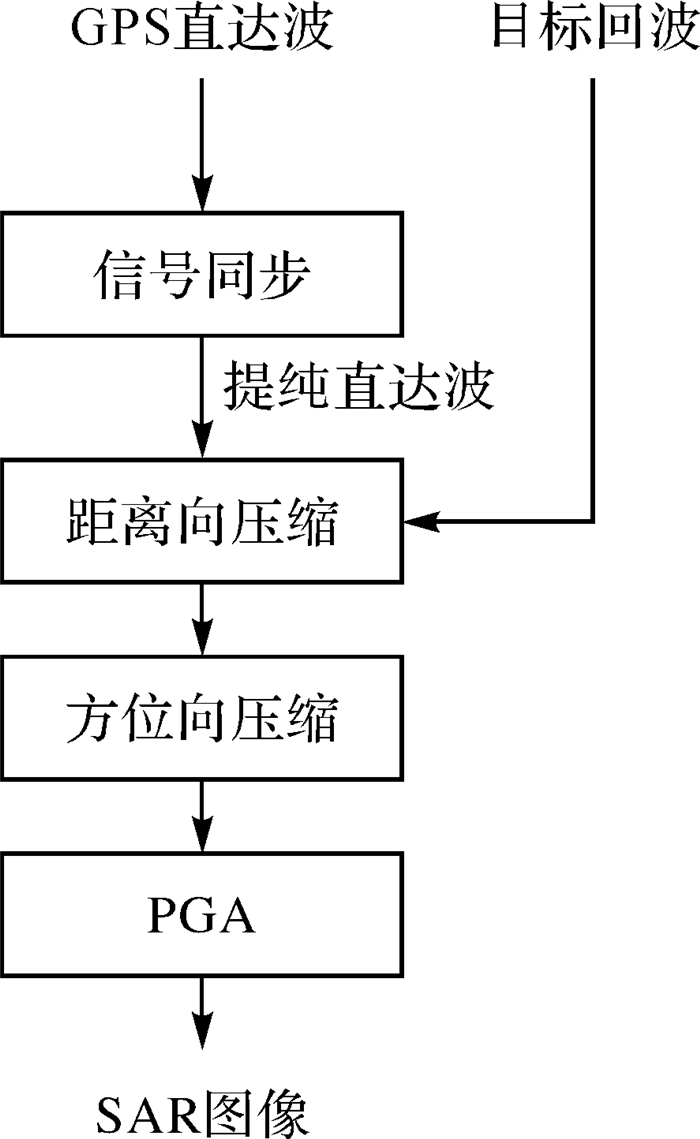
|
| 图 5 GPS天-地无源双基地雷达探测海面移动目标的信号处理流程 Fig. 5 Signal processing chain of GPS-based space-surface passive bistatic radar for maritime target detection |
3 试验验证 3.1 试验准备
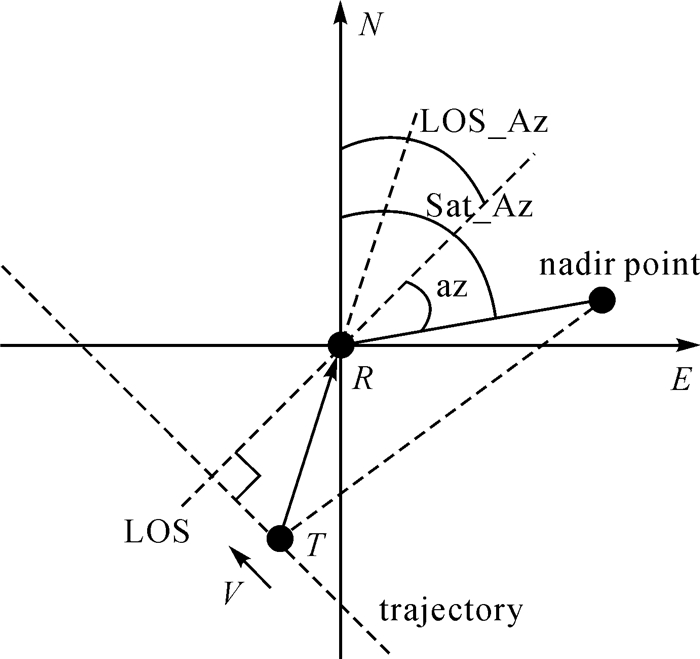
为了验证本文方法,在香港数码港海滨公园做了海面船只探测试验。图 6(a)为双通道GPS接收机前端,它的参考通道和监视通道分别连接图 6(b)的圆天线和方天线。在图 6(b)中,圆天线指向天空接收GPS直达波,方天线朝向海面收集船只回波信号。试验以船舶自动识别系统(automatic identification system, AIS)提供的船只信息(包括船舶名称、尺寸、航速、轨迹等)作为真值。图 7为现场试验的俯视图示意,以正东方向作为横轴和正北方向作为竖轴,接收机R位于坐标系原点。图中的GPS卫星方位角和接收机天线视线方位角可计算式(4)定义的本地卫星方位角。由图中角度关系可知,本地卫星方位角为
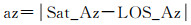 (22)
(22)

|
| 图 6 双通道GPS接收机前端与天线 Fig. 6 Dual-channel GPS receiver front-end and antennas |
|
| 图 7 真实实验试验俯视图 Fig. 7 The top view of the real scene |
式中,Sat_Az代表GPS卫星方位角;LOS_Az等于方天线视线方位角减去180°。最后,试验的一些基本配置列在表 1中用于信号处理。
| 参数名称 | 参数值 |
| GPS载波频率/MHz | 1575.42 |
| GPSC/A码频率/MHz | 1.023 |
| GPS脉冲重复频率/Hz | 1000 |
| 接收机采样率/MHz | 16.368 |
| 观测时间/s | 120 |
| 雷达天线LOS方位角/(°) | 239.7 |
| 经验速度/(m/s) | 5 |
| PGA最大迭代次数 | 4 |
3.2 试验结果与分析
现场采集了若干组试验数据,选取其中4组为代表,验证本文方法。表 2列出了每组试验船只的AIS信息包括船舶名称、尺寸、平均速度和到岸边接收机的垂直距离,以及选取的GPS卫星信息包括PRN、高度角和方位角。图 8给出了4艘船只的照片。需要补充的是,目标到岸边接收机的垂直距离是由AIS提供的目标轨迹点坐标和接收机坐标计算得到。由于GPS的距离向分辨率较差,表 2中给出的米级精度足够作为真值参考。
| 船舶名称 | 船舶尺 寸/m |
平均 速度 /(m/s) |
到岸边 直线距 离/m |
PRN/高度 角(°)/方 位角(°) |
| NAVIOS AMARILLO | 260×32 | 5.05 | 1450 | 22/20/48 |
| NEW OCEAN 3 | 48×18 | 4.28 | 360 | 11/18/51 |
| WAN HAI 506 | 269×32 | 4.94 | 1660 | 3/40/68 |
| ST BLUE | 199×32 | 6.54 | 840 | 22/32/68 |

|
| 图 8 海面船只照片 Fig. 8 The optical photographs of four vessels on the ocean surface |
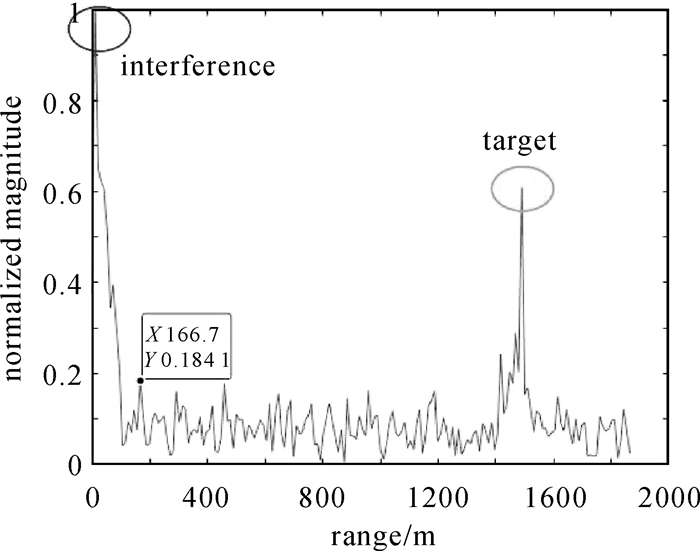
图 9为经过本文方法处理后的4组试验结果。从图 9可以看出,每幅图像上都有明显的区别于背景噪声的亮斑存在。这些亮斑对应海面船只反射的GPS信号,说明了本文方法的有效性。再利用适当的阈值操作(如恒虚警率检测)便可从背景噪声中提取出目标回波信号。监视通道内的干扰信号,例如海杂波和直达波,可能会被误认为是目标信号。然而,经过信号处理后,杂乱的海杂波能量被扩散掉,淹没在背景噪声中。而直达波的能量虽然有一定的衰减,但其能量强度可能依然远高于目标回波(图 10)。由于直达波的主瓣及其副瓣能量主要集中在离接收机较近的距离(大约为150m的距离范围)。因此,图 9中去除了小于150m的距离。目标回波能量成为图 9中归一化的能量最大值。此外,在图 9(d)中可以看到两个亮斑处在不同的距离门单元上。这两个亮斑对应图 8(d)中的两艘船,其中,方框内货船位于远处,圆框内的小船位于近处(小船没有提供其AIS信息)。本组试验结果表明本文方法可以探测多个目标。

|
| 图 9 海面船只SAR图像 Fig. 9 SAR images of four vessels on the ocean surface |
|
| 图 10 range轴截面图中的干扰信号和目标信号 Fig. 10 Interference signal and target signal in the range cross-section |
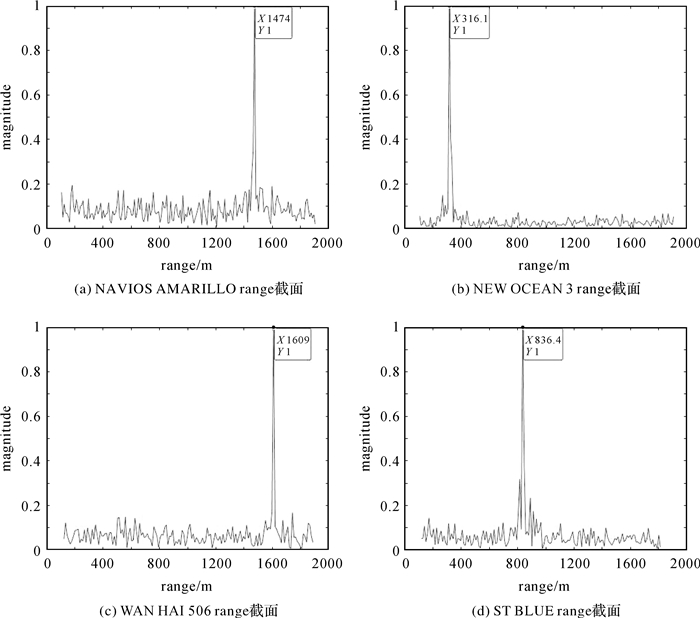
为了进一步验证本文方法,图 11显示了图 9的range轴截面图并标注了目标回波主瓣对应的距离值,即估计的目标到接收机垂直距离。表 3列出了估计的垂直距离、真值距离以及平均误差。可以看出4组试验的平均误差远小于GPS L1信号的距离向分辨率(约150m),说明了本文方法估计距离的精确性。
|
| 图 11 4组试验结果的range截面 Fig. 11 Range cross-sections of four group results |
| 估计垂直距离 | 真值距离 | 平均误差 |
| 1474 | 1450 | |
| 316.1 | 360 | 30.625 |
| 1609 | 1660 | |
| 836.4 | 840 |
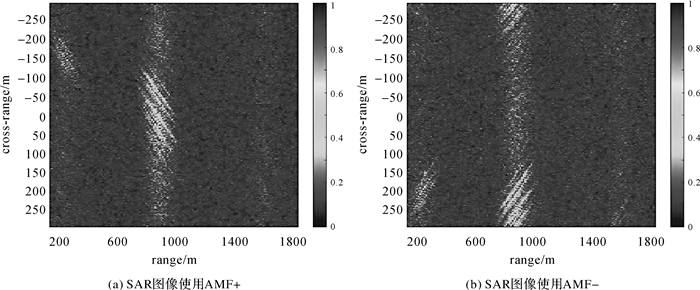
前文指出可以通过方位向匹配滤波器来判断目标的移动方向。这里以第4组试验感兴趣船只ST BLUE为例来说明。用式(17)(标记为AMF+)和式(18)(标记为AMF-)分别生成图 12(a)和(b)。需要注意的是,因为自聚焦算法能消除相位误差导致无法对比两种方位向匹配滤波器的成像结果,所以图 12(a)和(b)是自聚焦处理前的图像。对比两幅图像可以明显看到,图 12(b)中的亮斑被分割成了两个部分。原因在于使用了错误的方位向匹配滤波器导致目标回波能量散焦。因此,图 12(a)使用的式(17)为正确的方位向匹配滤波器。结合表 1的接收机天线视线方位角和表 2第4组试验选取的GPS卫星方位角可知,GPS卫星星下点处在接收机天线视线方向的左侧,与图 4显示恰好一致。由先前的推导可知,图 4中自左向右移动的目标对应的方位向匹配滤波器为式(17)。综上,可推断船只ST BLUE应该是自左向右移动,这与图 8(d)中的箭头指向相一致。
|
| 图 12 两个方位向匹配滤波器成像结果 Fig. 12 SAR images of two azimuth matched filters |
4 结语
本文研究利用GPS卫星作为非合作的机会照射源,与地面接收机共同构成天-地无源双基地雷达系统探测海面移动目标。由于目标反射的GPS信号能量微弱,常淹没在背景噪声和干扰信号之下,目标探测的核心在于累积目标回波能量和抑制干扰信号。本文将海面船只的运动轨迹作为合成孔径,利用SAR成像技术来聚集目标回波能量,使其能量强度高于背景噪声和干扰信号。为了验证本文方法,现场试验采集了多组数据。试验结果表明:①图像中可以看到区别于背景噪声的目标信号且能同时显示多个目标,说明了本文方法的有效性;②估计的目标到接收机垂直距离与真值距离的平均误差远小于距离向分辨率,说明该方法估计距离的精确性;③本文方法还能够初步判断目标的移动方向。
本文方法是为移动目标成像做准备。如果能估计出目标的运动速度,则可以成像移动目标,从而有机会估计船只的长度甚至识别船只。因此,下一步的工作将是研究估计目标的运动速度。此外,本文仅考虑了目标做平稳运动且运动轨迹垂直于接收机天线视线方向的情况。因此,后续还需考虑运动状况更为复杂的目标探测。
基于导航卫星的无源雷达系统不仅可以探测移动目标,还可以做目标相干定位、运动参数估计、目标跟踪和目标成像等,具有不错的研究和应用前景。随着我国北斗卫星导航定位系统完成全球组网,可以发展基于北斗卫星的无源雷达系统。因为北斗信号的伪码带宽范围优于传统的GPS L1波段,对应的距离向分辨率更高,更有利于雷达目标的探测和定位等。
| [1] |
杨东凯, 张其善. GNSS反射信号处理基础与实践[M]. 北京: 电子工业出版社, 2012. YANG Dongkai, ZHANG Qishan. GNSS reflected signal processing:fundamentals and applications[M]. Beijing: Electronics Industry Press, 2012. |
| [2] |
MARTIN-NEIRA M, CAPARRINI M, FONT-ROSSELLO J, et al. The PARIS concept:an experimental demonstration of sea surface altimetry using GPS reflected signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 142-150. |
| [3] |
路勇, 杨东凯, 熊华钢, 等. 基于GNSS-R的海面风场监测系统研究[J]. 武汉大学学报(信息科学版), 2009, 34(4): 470-473, 503. LU Yong, YANG Dongkai, XIONG Huagang, et al. Study of ocean wind-field monitoring system based on GNSS-R[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 470-473, 503. |
| [4] |
张双成, 南阳, 李振宇, 等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016, 45(9): 1042-1049. ZHANG Shuangcheng, NAN Yang, LI Zhenyu, et al. Analysis of tide variation monitored by GNSS-MR[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1042-1049. DOI:10.11947/j.AGCS.2016.20150498 |
| [5] |
王泽民, 刘智康, 安家春, 等. 基于GPS和北斗信噪比观测值的雪深反演及其误差分析[J]. 测绘学报, 2018, 47(1): 8-16. WANG Zemin, LIU Zhikang, AN Jiachun, et al. Snow depth detection and error analysis derived from SNR of GPS and BDS[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 8-16. DOI:10.11947/j.AGCS.2018.20160644 |
| [6] |
SÁNCHEZ N, ALONSO-ARROYO A, MARTÍNEZ-FERNÁNDEZ J, et al. On the synergy of airborne GNSS-R and Landsat 8 for soil moisture estimation[J]. Remote Sensing, 2015, 7(8): 9954-9974. |
| [7] |
邹文博, 张波, 洪学宝, 等. 利用北斗GEO卫星反射信号反演土壤湿度[J]. 测绘学报, 2016, 45(2): 199-204. ZOU Wenbo, ZHANG Bo, HONG Xuebao, et al. Soil moisture retrieval using reflected signals of Beidou GEO satellites[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 199-204. DOI:10.11947/j.AGCS.2016.20150135 |
| [8] |
刘池莉, 严颂华, 陈泽强, 等. 基于星载GNSS-R延迟-多普勒图的海面目标探测[J]. 科学技术与工程, 2018, 18(17): 250-256. LIU Chili, YAN Songhua, CHEN Zeqiang, et al. Ocean surface target detection using GNSS-R delay-Doppler map[J]. Science Technology and Engineering, 2018, 18(17): 250-256. |
| [9] |
孙启明, 张波, 刘建华, 等. GNSS-R岸基平台海面溢油面积探测方法[J]. 导航定位学报, 2019, 7(2): 88-95. SUN Qiming, ZHANG Bo, LIU Jianhua, et al. Detection method of oil spill areas on GNSS-R shore platform[J]. Journal of Navigation and Positioning, 2019, 7(2): 88-95. |
| [10] |
DI SIMONE A, PARK H, RICCIO D, et al. Sea target detection using spaceborne GNSS-R delay-Doppler maps:theory and experimental proof of concept using TDS-1 data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(9): 4237-4255. |
| [11] |
DI SIMONE A, BRACA P, MILLEFIORI L M, et al. Ship detection using GNSS-reflectometry in backscattering configuration[C]//Proceedings of 2018 IEEE Radar Conference (RadarConf18). Oklahoma City: IEEE, 2018: 1589-1593.
|
| [12] |
CLARIZIA M P, BRACA P, RUF C S, et al. Target detection using GPS signals of opportunity[C]//Proceedings of the 18th International Conference on Information Fusion (Fusion). Washington, DC: IEEE, 2015: 1429-1436.
|
| [13] |
HOWLAND P. Editorial:passive radar systems[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(3): 105-106. |
| [14] |
HOWLAND P E, MAKSIMIUK D, REITSMA G. FM radio based bistatic radar[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(3): 107-115. |
| [15] |
PALMER J E, HARMS H A, SEARLE S J, et al. DVB-T passive radar signal processing[J]. IEEE transactions on Signal Processing, 2013, 61(8): 2116-2126. |
| [16] |
任晓航, 魏平. 基于GSM的被动雷达系统信号处理技术研究[J]. 中国电子科学研究院学报, 2011, 6(5): 499-502. REN Xiaohang, WEI Ping. Direct signal cancellation of GSM based passive radar system[J]. Journal of CAEIT, 2011, 6(5): 499-502. |
| [17] |
庄旭昇, 汪玲, 高瑾, 等. 一种基于WiFi信号的运动目标无源雷达成像方法[J]. 雷达学报, 2014, 3(6): 694-701. ZHUANG Xusheng, WANG Ling, GAO Jin, et al. Passive radar imaging of moving targets using WiFi signals[J]. Journal of Radars, 2014, 3(6): 694-701. |
| [18] |
曾添, 隋立芬, 贾小林, 等. 风云3C增强北斗定轨试验结果与分析[J]. 测绘学报, 2017, 46(7): 824-833. ZENG Tian, SUI Lifen, JIA Xiaolin, et al. Results and analysis of BDS precise orbit determination with the enhancement of Fengyun-3C[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 824-833. DOI:10.11947/j.AGCS.2017.20170033 |
| [19] |
MA H, ANTONIOU M, PASTINA D, et al. Maritime moving target indication using passive GNSS-based bistatic radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 115-130. |
| [20] |
MA Hui, ANTONIOU M, STOVE A G, et al. Maritime moving target localization using passive GNSS-based multistatic radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4808-4819. |
| [21] |
ANTONIOU M, MA H, STOVE A G, et al. Target velocity estimation with multistatic GNSS-based radar[C]//Proceedings of the 19th International Radar Symposium (IRS). Bonn: IEEE, 2018: 1-7.
|
| [22] |
CUMMING I G, WONG F H. Digital processing of synthetic aperture radar data[M]. Boston: Artech House Press, 2005.
|
| [23] |
WAHL D E, EICHEL P H, GHIGLIA D C, et al. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-835. |
| [24] |
BRISKEN S, MARTORELLA M, MATHY T, et al. Motion estimation and imaging with a multistatic ISAR system[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 1701-1714. |
| [25] |
ZUO Rui. Bistatic synthetic aperture radar using GNSS as transmitters of opportunity[D]. Birmingham: University of Birmingham, 2012.
|
| [26] |
杨振起, 张永顺, 骆永军. 双(多)基地雷达系统[M]. 北京: 国防工业出版社, 1998. YANG Zhenqi, ZHANG Yongshun, LUO Yongjun. Bistatic (multistatic) radar systems[M]. Beijing: National Defense Industry Press, 1998. |
| [27] |
ANTONIOU M, CHERNIAKOV M. GNSS-based bistatic SAR:A signal processing view[J]. EURASIP Journal on Advances in Signal Processing, 2013, 2013(1): 98. |
| [28] |
ANTONIOU M, CHERNIAKOV M, MA Hui. Space-surface bistatic synthetic aperture radar with navigation satellite transmissions:a review[J]. Science China Information Sciences, 2015, 58(6): 1-20. |
| [29] |
BORRE K, AKOS D M, BERTELSEN N, et al. A software-defined GPS and galileo receiver:a single-frequency approach[M]. Boston: Springer Science & Business Media Press, 2007.
|
| [30] |
YANG Yang, ZHENG Yu, YU Wenkun, et al. Deformation monitoring using GNSS-R technology[J]. Advances in Space Research, 2019, 63(10): 3303-3314. |
| [31] |
ZENG Zhangfan. Passive bistatic SAR with GNSS transmitter and a stationary receiver[D]. Birmingham: University of Birmingham, 2013.
|
| [32] |
ANTONIOU M, SAINI R, CHERNIAKOV M. Results of a space-surface bistatic SAR image formation algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3359-3371. |
| [33] |
PERRY R P, DIPIETRO R C, FANTE R L. SAR imaging of moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 188-200. |
| [34] |
RICHARDS M A. Fundamentals of radar signal processing[M]. Dallas: Tata McGraw-Hill Education Press, 2005.
|


