2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着GNSS接收机硬件技术和软件算法的不断提高,使用载波相位观测值获得厘米级甚至亚厘米级的定位精度成为现实[1],并在形变监测、地壳运动监测及精密工程测量中得到了广泛应用。GNSS载波相位观测值是以天线相位中心(antenna phase center, APC)为测量点获得的。而在定位数据处理观测模型中的坐标是以天线参考点(antenna reference point, ARP)为基准[2]。由于天线本身的特性, 天线相位中心在水平方向、垂直方向上与ARP都存在偏差,即天线相位偏差,在垂直方向上最大可达分米量级,直接影响定位结果中的高程分量。如果不顾及此项改正,基线高程方向误差最大可达分米量级[3-5]。
目前,IGS发布最新的IGS14.ATX相位中心模型文件中给出了大部分测地型天线GPS/GLONASS等系统的改正值,但尚未发布BDS改正值。虽然不同的载波频率,其相位中心不同,但是BDS的B1/B2频率和GPS L1/L2频率较为接近,近些年针对BDS的天线相位中心改正通常采用GPS的公布值来近似代替。随着我国北斗三代在2018年底完成基本系统建设[6-7],BDS用户越来越广泛,有必要对BDS进行天线相位中心标定。本文借助机械臂可以控制天线自由旋转、并在短时间内实现全方位GNSS观测的特性,采用历元间差分的方法对TRM59800天线包括GPS L1/L2和BDS B1I/B2I/B3I等多个频点的相位中心进行了标定。
1 天线相位中心偏差(PCO)和天线相位中心变化(PCV)概述天线相位中心(APC)分为两个部分:天线相位中心偏差(PCO)和天线相位中心变化(PCV)[8]。如图 1所示,PCO定义为由ARP指向接收信号的平均相位中心在天线固定坐标系(antenna-fixed coordinate system,AFCS)中的三维坐标矢量,用NEU(北东天)表示。PCV定义为瞬时相位中心到PCO的距离标量,一般随入射高度角θ和方位角α变化[3]。几乎所有高精度GPS天线的PCV受方位角影响很小,它主要受高度角变化影响。
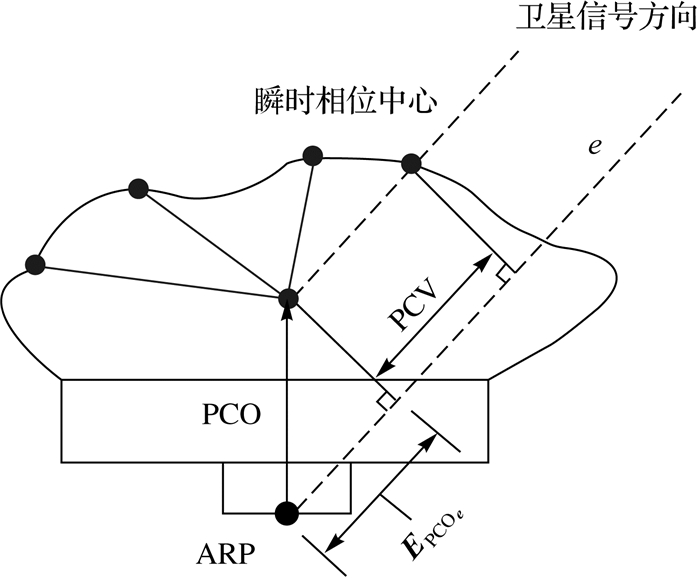
|
| 图 1 天线相位中心偏差和天线相位中心变化 Fig. 1 Antenna phase center offset and antenna phase center variation |
天线相位中心改正对观测值的影响Δ由PCO在信号方向e上的投影E与PCV之和组成[9]
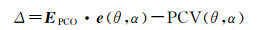 (1)
(1)
式中,负号是因为根据IGS天线模型文件交换格式中的定义[10],PCV对距离量的改正为正, 其与PCO在卫星视线上的投影符号相反所致。PCO测量方法有旋转天线法、交换天线法、完全流动观测法和相对参考天线的双差相位观测法等[11]。这些方法需要观测时间较长,流程较为烦琐,而且只能求解PCO,无法解算随高度角和方位角的变化而变化的PCV。
PCV的测量方法相比于PCO要复杂很多,因为PCV不仅与信号频率有关,而且还随信号的强弱以及方向而变化。因此精确标定PCV必须多次重复测量。对于GNSS天线,目前有效的标定方法分别是微波暗室测量法、相对现场标定和机器人标定方法[12], 其对比见表 1。微波暗室测量法设备昂贵,测量过程复杂,不宜推广;相对现场标定方法假定参考天线的PCV为零,PCO为已知值,因此会产生系统误差;传统机器人标定方法是在室外开阔无遮挡的环境中标定,在短基线的一端安置天线相位中心己知的天线,另一端在自动机器人上安装待测天线,第1天机器人通过按照一定的步长进行旋转测量采集数据。根据GPS卫星星座在连续两个恒星日内相同时刻的空间分布相同的特性,第2天在同一恒星时将被测天线初始方向旋转某角度(如果接收机天线在两个恒星日内保持天线方向不变,则多路径和PCV均被消除)进行同样的测量。然后利用这些观测值, 解算出用于拟合PCV模型的球谐函数系数。在IGS相位中心改正模型文件中,超过一半的接收机天线是用机器人校准得到的[9-10]。但是,由于BDS系统GEO/IGSO/MEO卫星轨道周期不同,该方法对北斗系统并不适用,每次标定并不能充分利用每颗卫星的数据,且标定时间长。针对上述问题,本文采用历元间差分的方法[13],借助机械臂可以快速旋转方向并能在短时间内获取天线半球空间的GPS/BDS观测数据的特点,采集均匀覆盖半球的数千个方向观测值进行测量。由于不同方向的观测值蕴含了天线旋转所引起的PCO和PCV变化信息,因此采用历元间差分模型既可以削弱多路径又能实现对PCO和PCV的同步标定。
| 类型 | 微波暗室测量 | 相对现场校准 | 机器人绝对标定 |
| 实际GNSS信号 | 否 | 是 | 是 |
| 快速旋转天线 | 是 | 否 | 是 |
| 多路径 | 不存在 | 存在 | 历元差分消除 |
| 天线覆盖范围 | 覆盖半球 | 极有限区域 | 覆盖半球 |
2 机械臂相位中心绝对标定估计模型
在设计观测模型时,本文采用已知基线法[14],在已知坐标的超短基线上进行同步观测,主站放置型号已知的参考天线,待测站上由机械臂连接待标定天线。
2.1 数学模型记基准天线B对i星的单频载波相位观测方程
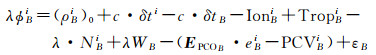 (2)
(2)
式中, ϕBi为卫星的载波相位观测值;λ为波长;(ρBi)0为天线ARP到卫星的几何距离;δti为卫星钟差;δtB为接收机钟差;IonBi、TropBi分别为电离层延迟和对流层延迟;NBi为B测站对应i卫星的整周模糊度;WB为地基相位缠绕误差[15];e为卫星信号矢量在AFCS下的单位矢量;εB为多路径和观测噪声。同理待标定天线C的观测方程为
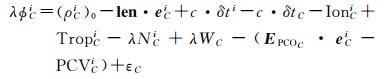 (3)
(3)
如图 2,与基准站不同的是,待测站方程中还包括了机械臂的固定旋转轴点F到待测天线ARP点的转动臂长在卫星矢量上的投影l=len·eCi改正。
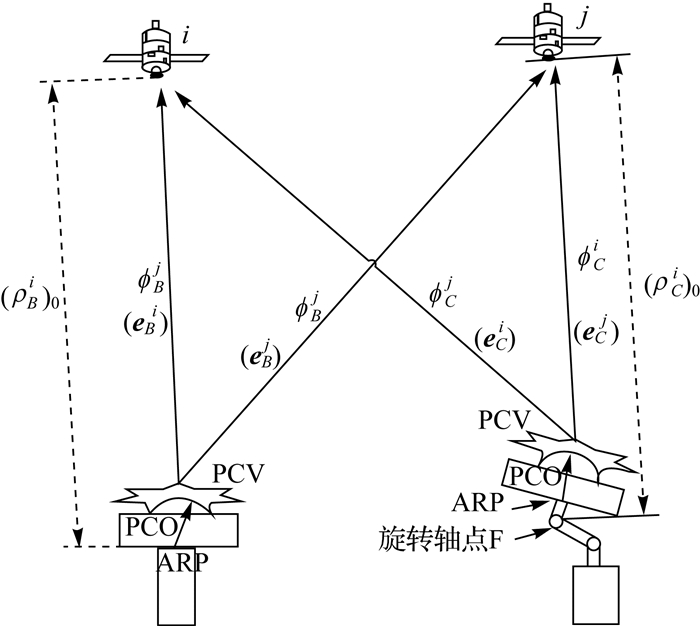
|
| 图 2 双差模型 Fig. 2 Double difference model |
为了消除卫星和接收机钟差,在星间和测站间组成双差模型。在超短基线下,对流层和电离层误差项也将被消除,并将基准站天线的已知PCO和PCV改正(或当基准站天线未知时其PCO和PCV的影响可以通过历元间(< 10 s)差分消除[9])。则双差方程为
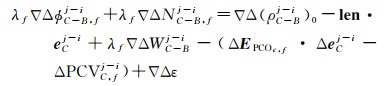 (4)
(4)
式中,∇ΔϕC-Bj-i=(ϕCj-ϕBj)-(ϕCi-ϕBi);∇ΔNC-Bj-i为双差模糊度;ΔPCVCj-i=PCVCj-PCVCi;eCj-i=eCj-eCi;f=B1, B2, B3。将已知坐标的几何距离、机械臂长、相位缠绕改正后,鉴于在天线旋转过程中卫星升降频繁,因此本模型中的模糊度采用单历元固定的策略[16-19],避免了天线快速转动引起的周跳对参数估计的影响。
在式(4)中,PCV量级在毫米至厘米量级,测地型天线PCO根据天线尺寸不同,其U分量从数厘米至分米级不等。利用短时间的静态基线解算与已知基线比较可以得到初始PCO分量,故可以用最小二乘解算得到精度较高的浮点解,然后基于LAMBDA算法单历元固定双差模糊度。在分别固定3个频点的双差模糊度后,则单个频率的相位双差残差为
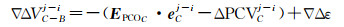 (5)
(5)
由于天线在快速转动和摆动,在相邻的两个历元间(< 10 s),多路径噪声可以视为相同,因此通过历元间求差可以有效消除多路径。最终得到历元差分观测方程为
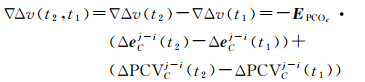 (6)
(6)
对于待标定天线C,天线在相邻观测历元进行了旋转,因此∇Δv(t2, t1)的变化包含了PCO和PCV的变化信息。
第1阶段求解PCO。根据前文所述PCO可以视为是APC的平均值,因此在解算PCO的过程中首先忽略PCV项,记∇Δv(t2)-∇Δv(t1)为L(t2, t1), 得到历元间差分观测方程为
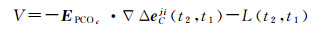 (7)
(7)
根据大量卫星矢量双差和历元差数据,将式(7)中的矢量展开为分量形式,利用最小二乘求解得到PCO的NEU 3个分量。记∇ΔeCji(t2, t1)的N、E、U分量分别为∇ΔeNji、∇ΔeEji、∇ΔeUji,则误差方程的矩阵形式为
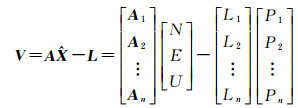 (8)
(8)
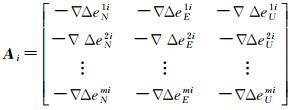 (9)
(9)
式中,A、L矩阵的下标代表参考星;P阵为权阵,其形式见2.2节随机模型。最后根据最小二乘原理求解
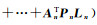
第2阶段估计PCV。待得到PCO估计值后,将其值作为已知值消去,则历元差残差可写为
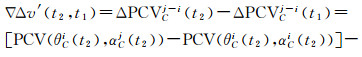
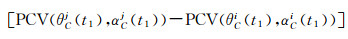 (10)
(10)
为了获得均匀覆盖半球的PCV模型,可以采用多项式拟合和球谐函数拟合。当只考虑卫星高度角的影响时,采用四阶多项式拟合效果最佳[3]。当同时考虑高度角和方位角时,可采用文献[20]提出的相位中心变化球谐函数(式11),利用最小二乘反算系数Anm和Bnm
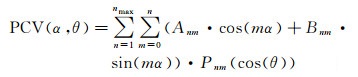 (11)
(11)
式(10)是4项球谐函数的代数和,因此消除了0阶项,在构造设计矩阵时,需要从n=1开始。此外,为了满足PCV在天顶处值为零的定义,需要附加约束条件: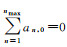
对于原始相位观测量,通常采用卫星高度角定权[21-22],这是基于低高度角卫星受大气影响较大、天线极化较弱、信噪比较低故而观测量的先验方差设置较大的先验假设。在本文天线旋转时,低高度卫星虽然受大气影响较大,但可能会接近天线的天顶方向,此时极化强度可能会大于高度角较高的卫星,因此本文采用高度角和信噪比混合模型[23],且将截止高度角提高到25°来削弱大气的影响。设载波相位观测量为Φ,E为单位阵, σ0为单位权中误差。对于BDS系统的3种类型卫星GEO/IGSO/GEO MEO,σ0分别取为0.003、0.003、0.009 m[24],则m颗卫星非差观测值的方差协方差阵为Dϕ=σ02Em。设TSD为单差算子,TDD为双差算子,在超短基线中,可认为同一卫星对A、B两站等权,即DϕA=DϕB, 故根据误差传播律可得到一个历元两个测站同时观测m颗卫星的单差观测量先验方差协方差矩阵DΔϕ和双差观测量先验方差协方差矩阵D∇Δϕ分别为
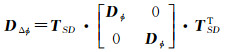 (12)
(12)
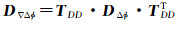 (13)
(13)
若不考虑不同观测历元观测量的相关性,测站A、B同时观测m颗卫星n个历元的双差观测量的方差协方差阵为
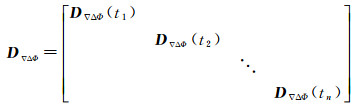 (14)
(14)
设三差算子为TTD,则m颗卫星n个历元的三差观测量的方差协方差阵为[25]
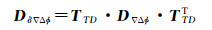
则2.1节数学模型中的权阵P=Dδ∇Δϕ-1。
3 标定策略在2.1节的数学模型中,需要对所有项进行时空统一转换。对于接收机时钟和机械臂控制器时间需要进行同步;对于在不同坐标框架下的矢量,需要统一归算到天线坐标系下。
(1) 时间同步。机械臂控制器由PC控制,其旋转到每一个位置均会输出此位置的起始时间、结束时间、天线高度角和方位角等信息。但是此输出时间是PC系统时间,精度较差,而接收机观测数据的时间是GPST时。为了实现接收机时间和PC输出时间同步,本文采用串口通信的方式,通过接收机串口读取时间戳来校正PC系统时间, 校正间隔为30 s,校正精度 < 0.1 s。
(2) 测站坐标。为了得到基准站天线ARP和机械臂旋转轴点的毫米级先验坐标,利用已知天线先进行24 h同步观测。对参考站和测试站进行PPP和基线解算,最终得到毫米级的先验坐标矢量。
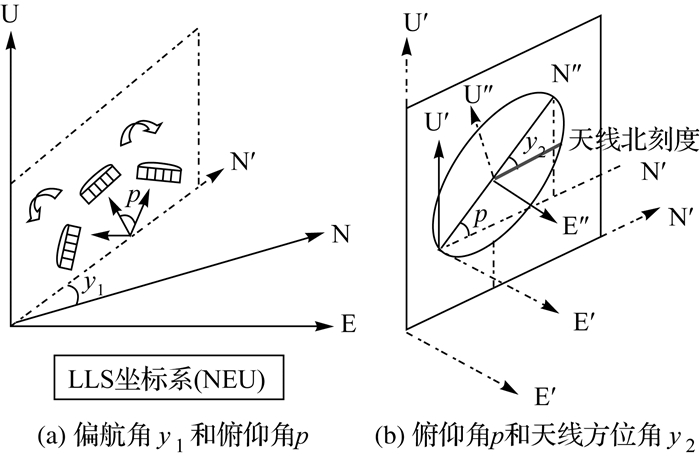
(3) 当地水平坐标系与天线固定坐标系转换。在上述模型中,卫星矢量是以天线固定坐标系(AFCS)为参考。在WGS-84坐标系下得到的站星矢量经转化后可以归算到当地水平坐标系(local level system,LLS)下。由LLS再转换到AFCS需要3步旋转。如图 3所示,第1个旋转角是机械臂安装固定后其Y轴与LLS北方向的夹角,记为偏航角y1。如图 4所示,第2个旋转角是天线的高度角,记为俯仰角p。第3个旋转角是机械臂控制的天线旋转方位角,在图 4中是天线北刻度与N″的夹角y2。经过3步旋转即可得到卫星矢量在AFCS系下的矢量e。上述旋转涉及的旋转矩阵如下
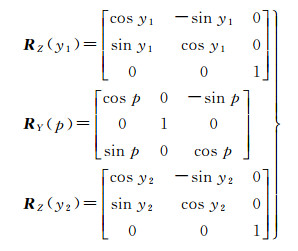
|
| 图 3 机械臂旋转 Fig. 3 Robot rotation |
|
| 图 4 坐标旋转 Fig. 4 Coordinate rotation |
(4) 机械臂运动方式。鉴于PCV由球谐函数表达,其自变量为方位角和高度角,因此天线应该在这两个维度分别旋转。第1步,外循环为高度角,机械臂绕其固定轴点倾斜旋转;内循环为方位角,天线绕其自转轴旋转;此过程为分离出方位角变化对PCV的影响。第2步,外循环为方位角,内循环为高度角。此过程为分离出高度角变化对PCV的影响。天线在旋转过程中,某些时刻卫星不可避免地会接近0°角入射。为避免信号在经过物体边缘处发生衍射效应,此时应将该颗卫星剔除。
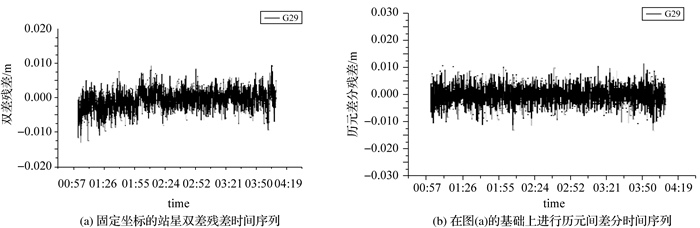
(5) 历元差分消除多路径效果。为了验证历元间差分对多路径消除效果,本文采集了采样率为1 Hz的3 h静态数据。固定先验坐标后G29的双差残差如图 5(a)。从图 5(b)的时间序列可以看出,历元间差分有效削弱了图 5(a)中2:00的波动趋势,呈现白噪声分布。
|
| 图 5 多路径时间序列 Fig. 5 Multipath time series |
4 实例与结果 4.1 标定过程
试验选取了两台Trimble R9接收机和两个Trimble 59800扼流圈天线。首先进行了24 h的水平静态测量,由于天线类型相同,因此在未获得天线PCO改正信息的情况下利用Bernese解算同样可以获得毫米级的基线坐标矢量,解算得到的基线长度约为3.597 m, 验后中误差ENU分别为0.2、0.2、0.4 mm。然后在2018年DOY 132—136进行了标定试验(见图 6)。每次标定过程采样率设置为1 Hz,持续时间约为3 h。天线固定坐标系截止高度角根据北斗/全球卫星导航系统(GNSS)测量型天线性能要求及测试方法[26]中的相位中心偏差测试方法设定为5°。

|
| 图 6 标定现场 Fig. 6 Calibration site |
分析图 7可以发现,相较于静态观测卫星轨迹只能覆盖有限的区域,使用精密旋转机械臂控制待测天线其卫星轨迹分布均匀覆盖天线半球,能在数小时内得到几千个不同方向上的观测值分布。
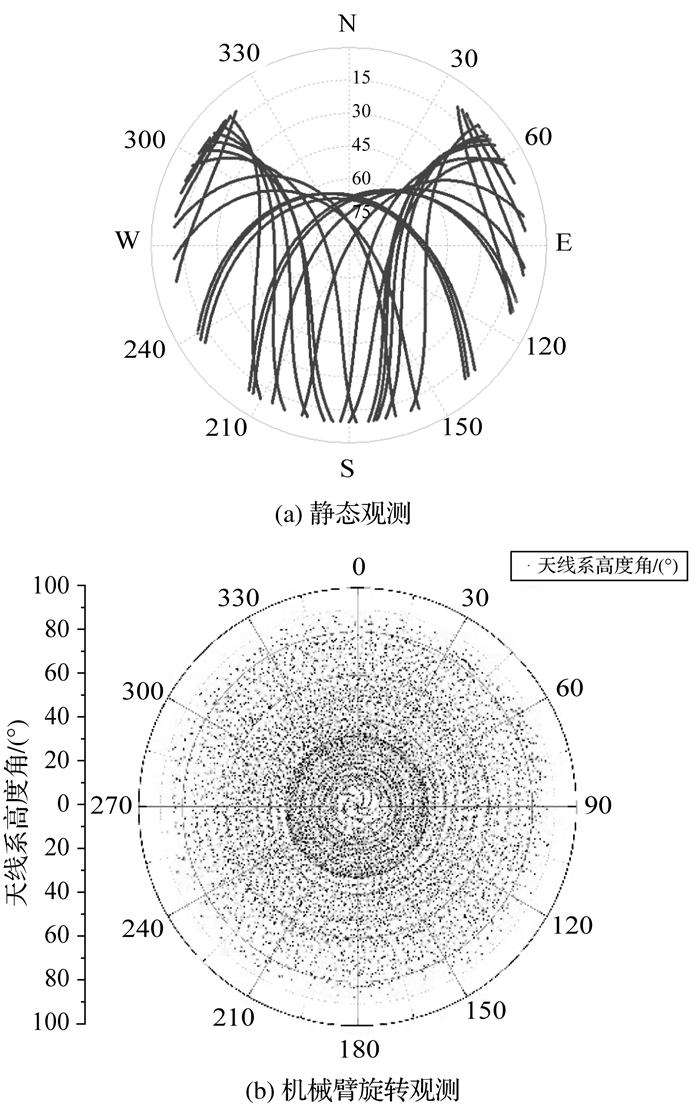
|
| 图 7 静态观测情况下和利用机械臂观测的数据分布对比 Fig. 7 Comparison of data distribution between static observation and observation with robotic arm |
4.2 标定结果 4.2.1 PCO估计结果
为了验证标定流程和算法,本文首先对Trimble 59800的L1/L2两个频点进行标定,并与IGS发布的结果进行比较。连续5 d的观测数据计算得到的Trimble 59800的GPS PCO估计值见表 2。其中横向两组NEU是基准站分别用已知和未知型号天线的标定结果。综合表 2数据可以看出,待测天线PCO标定结果几乎不依赖于主站天线PCO改正信息。GPS PCO两个频率标定值STD小于0.5 mm,其与IGS发布值的RMS小于1 mm。
| mm | |||||||||||||||||||||||||||||
| GPS L1频率PCO | |||||||||||||||||||||||||||||
| 项目 | 基准站天线型号已知 | 基准站天线型号未知 | |||||||||||||||||||||||||||
| North | East | Up | North | East | Up | ||||||||||||||||||||||||
| DOY 132 | 0.63 | 1.18 | 90.39 | 0.56 | 1.09 | 90.33 | |||||||||||||||||||||||
| DOY 133 | 0.43 | 0.90 | 89.90 | 0.48 | 0.95 | 89.84 | |||||||||||||||||||||||
| DOY 134 | 1.20 | 0.62 | 89.63 | 1.11 | 0.64 | 89.67 | |||||||||||||||||||||||
| DOY 135 | 0.95 | 0.98 | 90.34 | 0.90 | 1.05 | 90.17 | |||||||||||||||||||||||
| DOY 136 | 0.76 | 0.25 | 89.68 | 0.72 | 0.26 | 89.63 | |||||||||||||||||||||||
| IGS标定值 | 1.04 | 0.70 | 89.51 | 1.04 | 0.70 | 89.51 | |||||||||||||||||||||||
| 平均值 | 0.79 | 0.79 | 89.99 | 0.75 | 0.80 | 89.93 | |||||||||||||||||||||||
| RMS | 0.36 | 0.33 | 0.58 | 0.37 | 0.33 | 0.50 | |||||||||||||||||||||||
| STD | 0.26 | 0.32 | 0.32 | 0.23 | 0.31 | 0.28 | |||||||||||||||||||||||
| GPS L2频率PCO | |||||||||||||||||||||||||||||
| 项目 | 基准站天线型号已知 | 基准站天线型号未知 | |||||||||||||||||||||||||||
| North | East | Up | North | East | Up | ||||||||||||||||||||||||
| DOY 132 | 0.14 | -0.21 | 116.56 | 0.10 | -0.28 | 116.49 | |||||||||||||||||||||||
| DOY 133 | 0.02 | 0.18 | 116.26 | -0.01 | 0.13 | 116.27 | |||||||||||||||||||||||
| DOY 134 | -0.25 | 0.59 | 116.89 | -0.22 | 0.64 | 116.88 | |||||||||||||||||||||||
| DOY 135 | 0.54 | -0.05 | 117.08 | 0.62 | -0.13 | 117.20 | |||||||||||||||||||||||
| DOY 136 | 0.26 | 0.40 | 116.76 | 0.27 | 0.35 | 116.69 | |||||||||||||||||||||||
| IGS标定值 | 0.12 | 0.00 | 117.13 | 0.12 | 0.00 | 117.13 | |||||||||||||||||||||||
| 平均值 | 0.14 | 0.18 | 116.71 | 0.15 | 0.14 | 116.71 | |||||||||||||||||||||||
| RMS | 0.29 | 0.34 | 0.51 | 0.28 | 0.36 | 0.53 | |||||||||||||||||||||||
| STD | 0.29 | 0.32 | 0.31 | 0.28 | 0.33 | 0.32 | |||||||||||||||||||||||
然后本文对待测天线的BDS 3个频点进行了标定。连续5 d的观测数据计算得到的BDS PCO估计值见表 3—表 5。综合表 3—表 5数据可以看出,BDS 3个频率的STD均在1 mm以内,三维平均值分别为0.36、0.25、0.31 mm。北斗PCO在NE方向基本为零,没有明显偏心,在U方向达到分米量级。对比待测天线的GPS标定值,北斗PCO B1I/B2I的U分量与GPS L1/L2的差值分别为1.2、-0.6 mm。
| mm | |||||||||||||||||||||||||||||
| 项目 | North | East | Up | ||||||||||||||||||||||||||
| DOY 132 | 0.44 | -0.73 | 88.30 | ||||||||||||||||||||||||||
| DOY 133 | 0.36 | 0.21 | 87.84 | ||||||||||||||||||||||||||
| DOY 134 | -0.09 | -0.52 | 88.93 | ||||||||||||||||||||||||||
| DOY 135 | 0.21 | 0.16 | 89.06 | ||||||||||||||||||||||||||
| DOY 136 | 0.22 | 0.08 | 87.91 | ||||||||||||||||||||||||||
| 平均值 | 0.23 | -0.16 | 88.41 | ||||||||||||||||||||||||||
| STD | 0.18 | 0.39 | 0.51 | ||||||||||||||||||||||||||
| mm | |||||||||||||||||||||||||||||
| 项目 | North | East | Up | ||||||||||||||||||||||||||
| DOY 132 | -0.03 | -0.5 | 118.57 | ||||||||||||||||||||||||||
| DOY 133 | 0.26 | -0.09 | 118.98 | ||||||||||||||||||||||||||
| DOY 134 | -0.12 | -0.13 | 117.90 | ||||||||||||||||||||||||||
| DOY 135 | 0.32 | -0.2 | 118.31 | ||||||||||||||||||||||||||
| DOY 136 | 0.47 | -0.16 | 118.79 | ||||||||||||||||||||||||||
| 平均值 | 0.18 | -0.22 | 118.51 | ||||||||||||||||||||||||||
| STD | 0.22 | 0.15 | 0.38 | ||||||||||||||||||||||||||
| mm | |||||||||||||||||||||||||||||
| 项目 | North | East | Up | ||||||||||||||||||||||||||
| DOY 132 | -0.20 | -0.40 | 111.44 | ||||||||||||||||||||||||||
| DOY 133 | 0.31 | -0.17 | 112.12 | ||||||||||||||||||||||||||
| DOY 134 | 0.32 | -0.22 | 112.72 | ||||||||||||||||||||||||||
| DOY 135 | 0.09 | -0.15 | 111.39 | ||||||||||||||||||||||||||
| DOY 136 | 0.31 | 0.27 | 111.69 | ||||||||||||||||||||||||||
| 平均值 | 0.17 | -0.13 | 111.87 | ||||||||||||||||||||||||||
| STD | 0.20 | 0.22 | 0.50 | ||||||||||||||||||||||||||
4.2.2 PCV拟合结果
首先,按照四阶多项式拟合,即只拟合出GPS两个频点PCV值与卫星高度角(天顶距)之间的关系。由图 8可以看出,PCV的变化趋势随着天顶距增大(高度角降低)而先减小后增大。在低高度角处,最大可达到厘米量级。与IGS发布的拟合值比较(图中黑线)计算得到L1和L2的RMS分别为0.4、0.6 mm。
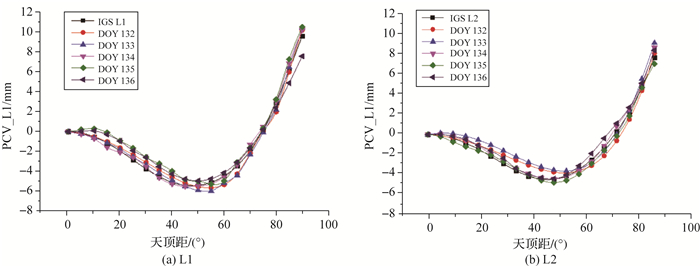
|
| 图 8 GPS拟合随天顶距变化的PCV Fig. 8 GPS fitting PCV with zenith |
其次,采用方位角和高度角描述相位中心变化的8阶5次球谐函数拟合PCV值,采用多天解的平均系数反算格网点的PCV值,并与IGS发布的格网值做差,得到的结果如图 9所示。从中可以看出,极坐标系中天顶距小于75°时,大部分格网点数值小于1.5 mm;在75°~90°时,即卫星在低高度角处拟合差值最大达到了2 mm。
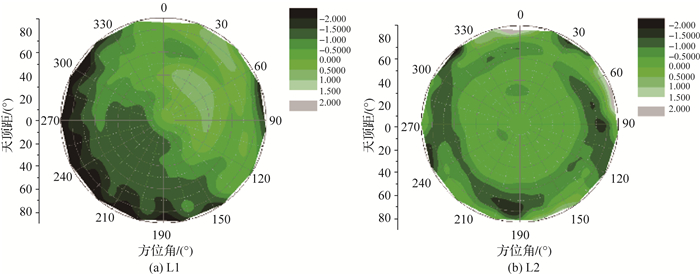
|
| 图 9 拟合格网点PCV与IGS格网点PCV差值 Fig. 9 Difference between the fitted PCV and IGS grid point PCV |
基于上述GPS拟合结果,本文对BDS 3个频点的PCV值也进行了球谐函数拟合,其多天拟合的格网值平均偏差和STD统计见表 6,3个频点均在2 mm以内。利用平均系数拟合的PCV在图 10中以三维图展示。图中水的坐标轴分别代表天顶距和方位角,纵轴代表PCV值。
| mm | |||||||||||||||||||||||||||||
| 项目 | BDS PCV多天格网值统计 | ||||||||||||||||||||||||||||
| B1 | B2 | B3 | |||||||||||||||||||||||||||
| PCV格网值平均偏差 | 0.63 | 0.57 | 0.34 | ||||||||||||||||||||||||||
| PCV格网值STD | 1.46 | 1.65 | 1.28 | ||||||||||||||||||||||||||
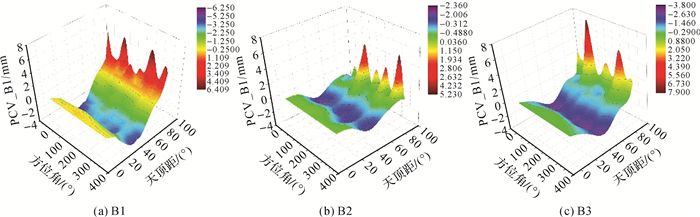
|
| 图 10 BDS球谐函数拟合PCV Fig. 10 BDS spherical harmonic function fitting PCV |
由图 10可以看出,BDS PCV的变化趋势和GPS同样呈现随着天顶距增大(高度角降低)而先减小后增大的波谷形状。在45°左右,3个频点最小可分别达到-4.1、-1.9、-2.7 mm。在天顶距达到90°时,3个频点最大可分别达到5.7、5.1、7.8 mm。方位角变化对BDS PCV整体影响较小,在天顶距大于85°时,其波动性较大,峰值-峰值最大达到了5.6 mm。
5 总结与讨论本文利用机械臂对GPS两个频点和BDS 3个频点的载波相位信号进行了天线相位中心及其变化标定。试验结果表明,GPS标定结果与IGS发布值符合较好,其RMS小于1 mm;对于本文测定的TRM59800天线,BDS PCO在水平方向无明显偏心,其均值接近于0;在U方向上随着频率的增加而减小:B2I最大,B3I次之,B1I最小,且B1I/B2I的U分量较GPSL1/L2的差值分别为1.2 mm和-0.6 mm。在不考虑方位角时,BDS PCV随高度角变化曲线呈现波谷形状,其范围均在-5~8 mm。在同时考虑方位角和高度角的情况下,利用球谐函数拟合曲面,多天拟合的格网值平均偏差和STD均在2 mm以内。试验结果表明在同一个高度角下,方位角对PCV数值影响甚微,其浮动大多均在1 mm以内,在低高度角处拟合值波动较大,峰值-峰值最大达到了5.6 mm。分析其原因是在球谐函数拟合时缺少下半球拟合数据,造成了低高度角拟合不稳定。在实际定位解算中,由于卫星截止高度角通常设为10°以上,因此低高度角PCV数据对定位影响可以忽略。基于上述结果可以看出对于高精度毫米级的静态测量,用GPS的相位中心改正参数直接代替BDS相位中心参数会带来微小误差。
随着今后北斗三代卫星的普及应用,笔者将对北斗三代卫星的新信号体制B1C和B2a信号进行标定;同时对于本文算法进一步优化,提高估计精度和拟合稳定性。
| [1] |
BÖDER V, MENGE F, SEEBER G, et al. How to deal with station dependent errors-new developments of the absolute field calibration of PCV and phase-multipath with a precise robot[C]//Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City: ION, 2001.
|
| [2] |
张成军. 基于测量机器人的GPS天线相位中心影响检测法[J]. 测绘通报, 2010(3): 7-9. ZHANG Chengjun. Calibration of influence of GPS antenna phase center based on robot[J]. Bulletin of Surveying and Mapping, 2010(3): 7-9. |
| [3] |
沙文东. GNSS天线相位中心偏差标定方法研究[D].北京: 中国科学院大学, 2015. SHA Wendong. A study on the calibration method of GNSS antenna phase center variation[D]. Beijing: University of Chinese Academy of Sciences, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2961991 |
| [4] |
马德强. GNSS接收机天线相位中心误差改正方法研究[D].西安: 长安大学, 2014. MA Deqiang. Study on the correction method of GNSS receiver antenna phase center error[D]. Xi'an: Chang'an University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014070895.htm |
| [5] |
KOUBA J.A guide to using international GNSS service (IGS) products[EB/OL]. (2009-04-23)[2019-01-15]. http://igscb.jpl.nasa.gov/igscb/resource/pubs/usingigsproductsver21.pdf.
|
| [6] |
中国卫星导航系统管理办公室.北斗卫星导航系统发展报告(3.0版)[R].Beijing: 中国卫星导航系统管理办公室, 2018. China Satellite Navigation Office. Development of BeiDou navigation satellite system (version 3. 0)[R]. Beijing: China Satellite Navigation Office, 2018. |
| [7] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学:地球科学, 2018, 48(5): 584-594. YANG Yuanxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system:data analysis based on BDS-3 demonstration system[J]. Science China Earth Sciences, 2018, 48(5): 584-594. |
| [8] |
DASH R, LUTZ S, WALSER P, et al. Bernese GNSS software version 5.2[M].Bern: University of Bern, Bern Open Publishing, 2015.
|
| [9] |
BILICH A L, MADER G L. GNSS absolute antenna calibration at the national geodetic survey[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR, 2010: 1369-1377.
|
| [10] |
ROTHACHER M, SCHMID R. ANTEX: the antenna exchange format (version 1.4)[EB/OL]. (2015-04-12)[2019-01-20].ftp://igs.org/pub/station/general/antex14.txt.
|
| [11] |
李晓波, 王小亚, 任金卫. GNSS天线相位中心偏差与变化精确标定方法研究[J]. 天文学进展, 2012, 30(4): 501-517. LI Xiaobo, WANG Xiaoya, REN Jinwei. Research on calibration methods of GNSS antenna phase center offsets and variations[J]. Progress in Astronomy, 2012, 30(4): 501-517. |
| [12] |
WILLI D, KOCH D, MEINDL M, et al. Absolute GNSS antenna phase center calibration with a robot[C]//Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation. Miami: [s.n.], 2018: 3909-3926.
|
| [13] |
WVBBENA G, SCHMITZM. Automated absolute field calibration of GPS antennas in real-time[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation.Salt Lake City: [s.n.], 2000.
|
| [14] |
李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009. LI Zhenghang, ZHANG Xiaohong. New techniques and precise data processing methods of satellite navigation and positioning[M]. Wuhan: Wuhan University Press, 2009. |
| [15] |
董大南, 陈俊平, 王解先. GNSS高精度定位原理[M]. 北京: 科学出版社, 2018. DONG Danan, CHEN Junping, WANG Jiexian. GNSS high precision positioning principle[M]. Beijing: Science Press, 2018. |
| [16] |
伯恩哈德·霍夫曼·韦伦霍夫, 赫伯特·利希特内格尔, 埃尔马·瓦斯勒.全球卫星导航系统: GPS, GLONASS, Galileo及其他系统[M].北京: 测绘出版社, 2009. HOFMANN-WELLENHOF B, LICHTENEGGER H, WASLE E. GNSS-global navigation satellite systems: GPS, GLONASS, Galileo & more[M]. Beijing: Surveying and Mapping Press, 2009. |
| [17] |
刘炎炎, 叶世榕, 江鹏, 等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(2): 209-213. LIU Yanyan, YE Shirong, JIANG Peng, et al. Instantaneous ambiguity resolution of short baselines using BeiDou triple frequency observations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 209-213. |
| [18] |
范建军, 王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报, 2007, 36(1): 43-49. FAN Jianjun, WANG Feixue. A method for GNSS three frequency ambiguity resolution based on short baselines[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 43-49. DOI:10.3321/j.issn:1001-1595.2007.01.008 |
| [19] |
唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报(信息科学版), 2005, 30(5): 444-446. TANG Weiming, SUN Hongxing, LIU Jingnan. Ambiguity resolution of single epoch single frequency data with baseline length constraint using LAMBDA algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 444-446. |
| [20] |
ROTHACHER M, SCHAER S, MERVART L, et al. Determination of antenna phase center variations using GPS data[R]//The 1995 IGS Workshop. Potsdam: IGS, 1995.
|
| [21] |
高成发, 赵毅, 万德钧. GPS载波定位中双差观测值权的合理确定[J]. 测绘科学, 2005, 30(3): 28-32. GAO Chengfa, ZHAO Yi, WAN Dejun. The weight determination of the double difference observation in GPS carrier phase positioning[J]. Science of Surveying and Mapping, 2005, 30(3): 28-32. DOI:10.3771/j.issn.1009-2307.2005.03.007 |
| [22] |
徐鹏. 基于卫星高度角的GPS观测量随机模型分析[J]. 现代测绘, 2012, 35(5): 6-7, 10. XU Peng. Analysis of the stochastic model of GPS observation based on satellite elevation[J]. Modern Surveying and Mapping, 2012, 35(5): 6-7, 10. DOI:10.3969/j.issn.1672-4097.2012.05.002 |
| [23] |
GAO Chengfa, WU Fei, CHEN Weirong, et al. An improved weight stochastic model in GPS precise point positioning[C]//Proceedings of 2011 International Conference on Transportation, Mechanical, and Electrical Engineering. Changchun, China: IEEE, 2011: 629-632.
|
| [24] |
李盼. GNSS精密单点定位模糊度快速固定技术和方法研究[D].武汉: 武汉大学, 2016. LI Pan. Research on methodology of rapid ambiguity resolution for GNSS precise point positioning[D]. Wuhan: Wuhan University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10486-1016113506.htm |
| [25] |
李学逊. GPS载波相位观测值的线性组合及其相关性分析[J]. 测绘通报, 1994(3): 10-15. LI Xuexun. Linear combination and correlation analysis of GPS carrier phase observation[J]. Bulletin of Surveying and Mapping, 1994(3): 10-15. |
| [26] |
中国卫星导航系统管理办公室.北斗/全球卫星导航系统(GNSS)测量型天线性能要求及测试方法: BD 420003-2015[S].北京: 中国卫星导航系统管理办公室, 2015. China Satellite Navigation Office.Performance requirements and test methods for BeiDou/global navigation satellite systems (GNSS) geodetic antenna: BD 420003-2015[S]. Beijing: China Satellite Navigation Office, 2015. |



