2. 武汉大学地理信息系统教育部重点实验室, 湖北 武汉 430079
2. Key Laboratory of Geographic Information Systems, Ministry of Education, Wuhan University, Wuhan 430079, China
元胞自动机(CA)作为一种离散的动力学模型, 在模拟复杂非线性问题上具有独特优势[1], 并在图像分割[2]、林火蔓延[3]和土地利用变化[4]等领域得到广泛应用。自文献[5-6]在20世纪70年代首次将CA模型引入城市研究中以来, 城市研究成为CA应用的热门领域, 特别是在城市扩展模拟中[7-11]。这些研究表明自下而上的CA模型能够通过简单的转换规则来模拟复杂的地理演变过程, 为地理时空分析提供技术手段[12]。CA模型的基本框架由5个部分组成, 包括元胞和元胞空间、元胞状态、转换规则、邻域和元胞时间, 其中转换规则的确定是CA模型的关键[13], 是研究对象在时空过程中变化的依据。在城市扩展CA中, 转换规则和空间驱动要素具有紧密的联系, 但如何从空间驱动要素中提取规律和特征, 构建合理的转换规则, 模拟空间驱动因素对城市扩展的影响仍是一个具有挑战性的问题。目前, 应用较为广泛的转换规则获取思路主要有两种:一种是空间驱动要素权重参数的优化, 另一种是采用人工智能算法提取规则。获取空间驱动要素权重参数的方法中, 最为常见的是逻辑回归方法[14], 但该方法只能提取线性规则, 难以实现对城市扩展的精确模拟。随着计算机技术的快速发展, 更多参数优化方法被应用于CA模型, 如遗传算法[15-16]、粒子群优化算法[17]、随机森林算法[18]、BBO算法[19-20]等, 这些算法较逻辑回归能挖掘空间变量间相互作用的非线性特征, 反映出更真实的城市扩展过程。提取转换规则的人工智能算法中, 一般有人工神经网络[21]、核学习机[22]、支持向量机[23-24]等。这些方法可提取空间变量与城市扩展演变间的非线性规律, 实现复杂的地理演变模拟, 取得了较优的模拟结果。随着计算机科学的快速发展, 人工智能算法在CA中的应用逐渐广泛和深入。
虽然线性与非线性的多种方法均在CA模型转换规则构建中得到应用, 但这些方法都是基于单个元胞的信息挖掘来构建转换规则的。即使在规则中有邻域约束对元胞的邻域特征进行表达, 由于元胞的变化不仅受到相邻元胞状态的影响, 还受到相邻元胞的空间变量信息影响, 因此不考虑邻域元胞的变量信息特征, 难以实现更为精准的演变模拟。基于此, 文献[25]采用卷积神经网络提取区域特征挖掘转换规则, 取得了较好的模拟结果。但是在应用卷积神经网络方法挖掘区域转换规则时, 卷积核的尺寸、数量和网络的层数都会影响模型的学习能力和结果质量, 若卷积核尺寸过大, 容易忽略区域的局部特征, 而尺寸过小, 则会提取出大量冗余信息, 从而导致模型最终提取的特征存在差异[26-29]。因此, 为了更全面地表达地理模拟中的区域特征, 更精确地获取CA模型的转换规则, 需要利用多结构卷积神经网络实现多尺度区域特征的提取。
针对以上问题, 本文提出一种基于多结构卷积神经网络的城市扩展CA模型, 通过设计能挖掘不同区域特征的网络结构, 组合不同尺度和数目的卷积核, 提高模型的稳定性和准确性, 实现对区域演变特征的多尺度提取。卷积神经网络提取区域特征的优势归结于卷积层, 通过在卷积层中设计各类不同大小和数目的卷积核来提取多尺度规则, 并将多尺度的规则耦合入新的神经网络进行训练是多结构卷积神经网络的核心思想。一般来说, 随着卷积核数量的增加以及网络层数的增加, 卷积神经网络模型的学习能力也会随之增强, 但训练耗时会成倍增加, 甚至会出现过拟合问题。本文应用的多结构卷积神经网络由于各个网络可单独训练, 避免过拟合问题, 且计算量接近单级网络, 参数量和计算量的增加并不显著, 具有较强的可应用性。基于多结构卷积神经网络的CA模型不仅实现了元胞区域特征信息规则的挖掘, 还将多尺度下的区域特征规则进行训练耦合, 充分考虑了CA模拟地理演变过程的区域效应和尺度效应, 使CA模型转换规则的挖掘提取更为完善, 进一步提高了CA模型的模拟应用能力。
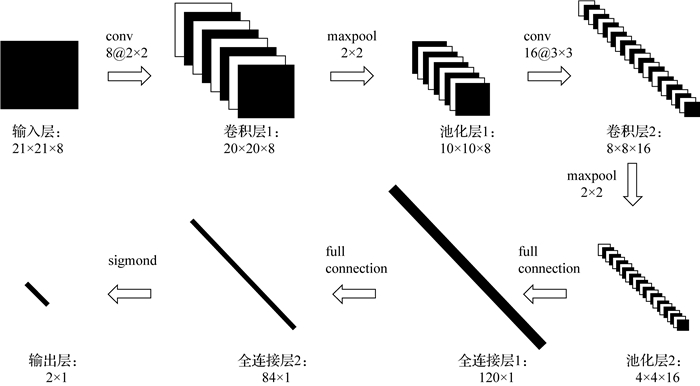
1 基于多结构卷积神经网络的城市扩展CA模型 1.1 卷积神经网络卷积神经网络(CNN)是一种深度前馈人工神经网络, 是针对图像识别和分类而设计的深度学习方法, 主要由输入层、隐含层和输出层组成。其中隐含层包含特征提取层和分类层, 特征提取层通常包括多个卷积层和池化层, 分类层由一层或者两层全连接层组成, 如图 1所示。
|
| 图 1 卷积神经网络结构 Fig. 1 The structure of CNN |
1.1.1 卷积层
卷积层是卷积神经网络的核心, 目的是从输入变量中获取特征。在卷积层中可通过各类卷积核, 完成对输入变量特征的提取, 低级卷积核可识别初级特征, 高级卷积核可识别高级特征。其数学表达式为
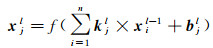 (1)
(1)
式中, xil-1是作为第l层卷积层的第i维输入变量;kjl和bjl分别是第l层卷积层中第j个卷积核组的权重向量和偏置项;xjl是第l层卷积层中第j个卷积核组对应的输出变量;n是第l层卷积层输入变量的总维数;f(·)为非线性激活函数。
1.1.2 池化层卷积层操作完成后, 参数量级虽已得到降低, 但数据量仍然很大, 故采用池化层来降低数据维度并避免过拟合。在池化过程中, 由于数据特征的平移不变性, 即使损失部分数据, 统计量仍能描述区域特征。其数学表达式为
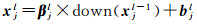 (2)
(2)
式中, xjl-1是作为第l层池化层的第j维输入变量;βjl和bjl分别是第l层池化层中第j维变量的乘法偏置项和加法偏置项;xjl是第l层池化层中第j维输出变量;down(·)表示池化函数。典型的池化操作包括最大值池化和均值池化。
1.1.3 全连接层经过多次卷积和池化操作后, 综合所提取的特征输入全连接层, 全连接层的每个结点都与上层所有结点相连, 以获取全局特征信息, 数学表达式为
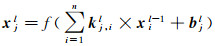 (3)
(3)
式中, xil-1是作为第l层全连接层输入变量的第i个神经元;xjl是第l层全连接层输出变量的第j个神经元;kj, il是输入变量的第i个神经元到输出变量第j个神经元的权重;bjl是第l层全连接层输出变量第j个神经元的偏置项;n是第l层全连接层输入变量的神经元总数。
1.2 MSCNN-CA模型 1.2.1 多结构卷积神经网络由于卷积神经网络模型的学习能力高度依赖于卷积核的尺寸和大小等参数, 细微的调整也会对结果造成较大影响[30], 降低模型特征提取的稳定性。因此, 多结构卷积神经网络模型中耦合了多种网络结构, 对不同网络结构的提取特征进行综合, 以提高模型的稳定性和准确性, 其模型框架如图 2所示。模型的主体部分为特征提取层, 它由多个具有针对性的网络结构组成。在该层中, 通过对同一组数据进行训练, 得到不同尺度的区域特征高维向量, 并将其输送至全连接层, 以综合全局特征信息, 在特征级联层中采用神经网络的级联结构, 将多个高维特征向量级联为模型最终的特征向量, 最后将该特征向量输入到分类器得到输出结果。
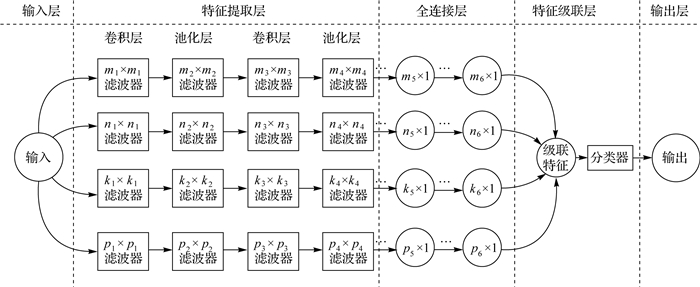
|
| 图 2 MSCNN模型网络结构 Fig. 2 The structure of MSCNN |
1.2.2 城市扩展CA模型
城市扩展CA模型由5个基本部分组成, 分别是元胞与元胞空间、元胞状态、邻域、时间和转换规则。其中转换规则是模型的核心, 一般由4个部分组成, 包括土地开发适宜性、邻域约束、限制性约束和随机扰动, 其中土地开发适宜性的计算方法是CA模型改进的重点[31-32]。本文引入多结构卷积神经网络模型来计算多尺度区域特征下的土地开发适宜性, 建立了如图 3所示的MSCNN-CA模型。依据MSCNN-CA模型的结构, 非城市用地转换为城市用地的概率(P)可用数学方法表示为
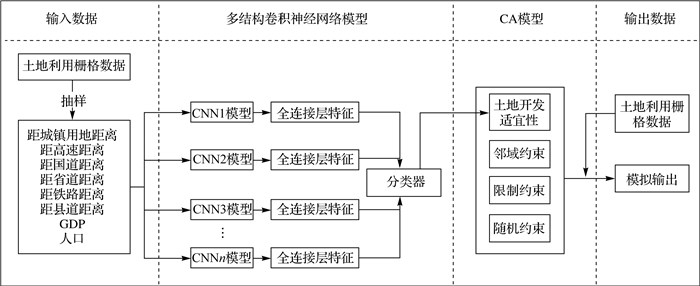
|
| 图 3 MSCNN-CA模型框架 Fig. 3 The frame of MSCNN-CA |
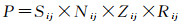 (4)
(4)
式中, Sij为基于多结构卷积神经网络模型计算的元胞(i, j)的土地开发适宜性;Nij为元胞(i, j)受其周围元胞影响的邻域约束, 本文采用3×3大小的摩尔型邻域, Nij即为中心元胞周围8个元胞中城市元胞所占的比率;Zij为元胞(i, j)所处空间位置受到的全局限制约束, 本文以水域作为限制因素, 当元胞(i, j)为水域时, Zij=0, 否则, Zij=1;Rij代表元胞(i, j)状态发生变化过程中的不确定性, Rij=1+(-ln(α))k, 其中α为0-1的随机数, k为控制随机强度的参数, 本文中k=2。
2 模型应用 2.1 研究区武汉是湖北省省会、中部六省唯一的副省级市和超大城市, 中国中部地区的中心城市, 长江经济带核心城市, 包括主城区和汉南区、蔡甸区、东西湖区、黄陂区、新洲区、江夏区6个远城区;上海是我国的直辖市之一、国家中心城市、超大城市, 国际经济、金融、贸易、航运、科技创新中心和综合交通枢纽, 首批沿海开放城市, 共辖16个市辖区。近10年来, 武汉土地城镇化发展水平呈快速发展的态势, 主要扩展区域集中在主城区, 而上海市已经进入土地城镇化的后期阶段, 城市扩展的速度有所减缓, 主要扩展区域集中在浦东新区, 因此本文选取武汉市的主城区和上海市的浦东新区两个处于土地城镇化不同发展阶段的区域作为试验区, 用来验证MSCNN-CA模型的合理性。试验区的位置与范围如图 4所示。
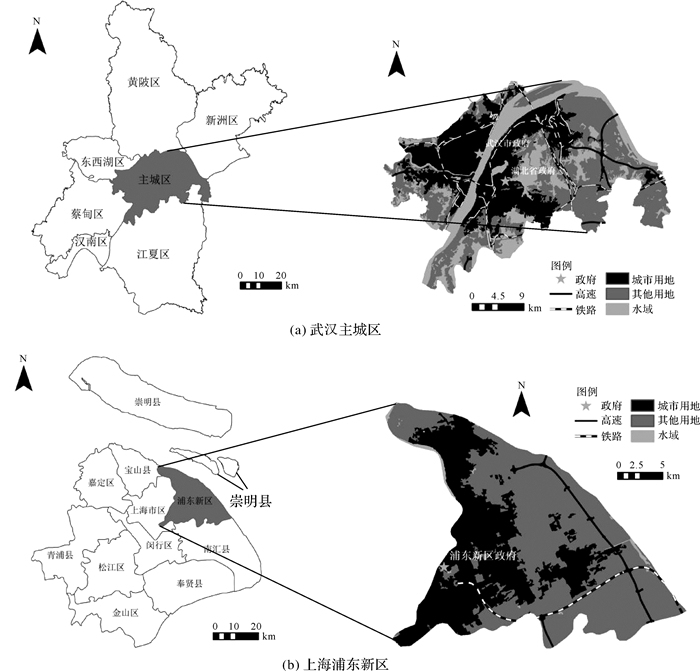
|
| 图 4 试验区位置与范围 Fig. 4 Location of the research area |
2.2 数据来源和处理
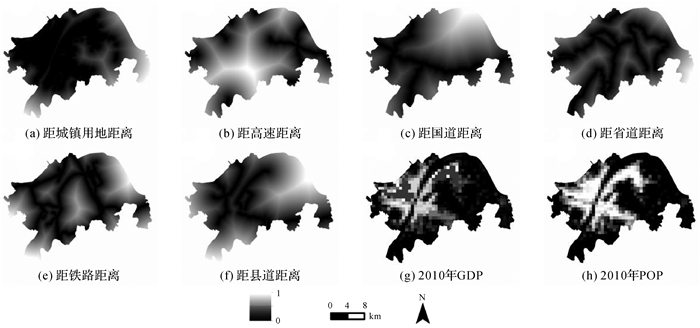
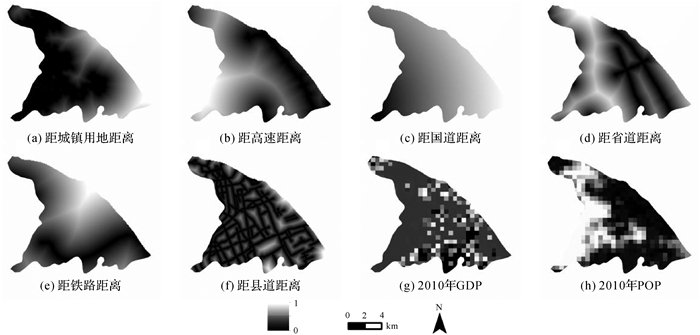
本研究所用的数据包括土地利用栅格数据, 道路矢量数据以及人口和GDP栅格数据。其中, 2005年、2015年两个时期的1:10万比例尺30 m×30 m土地利用栅格数据、行政区划矢量数据、道路数据、人口和GDP公里网格数据, 来源于中国科学院资源环境科学数据中心。利用空间矢量数据计算其欧氏距离栅格作为驱动因素。本文选取8个空间距离变量, 分别为:距城镇用地距离、距高速距离、距国道距离、距省道距离、距铁路距离、距县道距离、2010年GDP、2010年人口数据。对各个距离变量进行欧氏距离计算, 并将其数据归一化, 两个试验区的变量如图 5、图 6所示。
|
| 图 5 武汉主城区空间变量数据 Fig. 5 Spatial data of the main urban zone of Wuhan |
|
| 图 6 上海浦东新区空间变量数据 Fig. 6 Spatial data of Pudong New District of Shanghai |
2.3 模型训练和参数确定
采样窗口大小是MSCNN-CA模型中重要的参数。根据文献[23]对窗口大小的敏感性分析可知, 采样窗口的大小会影响模型的模拟精度和运行效率。当窗口大小在20~75内时模拟效果最佳, 虽然模拟精度随着随窗口大小的增加有所提高, 但运行效率随之降低。本文为验证模型可行性, 且综合考虑到计算量和邻域信息, 选取采样窗口大小为21×21, 共有8个空间变量, 因此网络的输入为21×21×8。
网络结构的设计是多结构卷积神经网络构建的核心。本文参考深度学习中的LeNet-5模型, 结合本文变量窗口大小, 设计了3个不同较浅层次的卷积神经网络模型, 分别为CNN1、CNN2和CNN3模型, 见表 1。CNN1模型中, 卷积层1由8个2×2大小的卷积核组成, 卷积步长为1, 池化层1过滤器大小为2×2, 步长为2, 采用平均池化下采样的方式;卷积层2由16个3×3大小的卷积核组成, 卷积步长为1, 池化层2过滤器大小为2×2, 步长为2, 采用最大池化下采样的方式;全连接层1将特征矩阵拉伸为大小为120×1的一维特征向量, 全连接层2再次对特征向量进行抽象降维, 得到大小为84×1的一维特征向量。类似的, 分别针对卷积核的数量和卷积核的尺寸大小设计了CNN2模型和CNN3模型, CNN2模型卷积层1的卷积核尺寸为4×4, 卷积层2的卷积核为2×2;CNN3模型卷积层1的卷积核寸为6×6, 卷积层2的卷积核为2×2。
| 网络 | C1 | S1 | C2 | S2 | F1 | F2 |
| CNN1 | 8@2×2 | 8@2×2 | 16@3×3 | 16@2×2 | 120 | 84 |
| (20×20) | (10×10) | (8×8) | (4×4) | |||
| CNN2 | 8@4×4 | 8@2×2 | 16@2×2 | 16@2×2 | 120 | 84 |
| (18×18) | (9×9) | (8×8) | (4×4) | |||
| CNN3 | 8@6×6 | 8@2×2 | 16@3×3 | 16@2×2 | 120 | 84 |
| (16×16) | (8×8) | (6×6) | (3×3) |
由于简单结构的CNN模型难以表现数据分布特征, 故在数据组合之前通过加深各自的网络深度, 得到精度和效率均较高的模型结构, 从而保证基础模型能够提取区域内足够丰富的变量信息。加深网络深度的方式为增加卷积核的数目, 以CNN1为例, CNN1.1为在CNN1的基础上加倍卷积核的数目, 将卷积层1的卷积核变为16, 卷积层2的卷积核变为32, CNN1.2为在CNN1.1的基础上加倍卷积核的数目, 将卷积层1的卷积核变为32, 卷积层2的卷积核变为64;然后选择表现较优的网络深度, 组合3个网络结构来达到提高模型挖掘区域内变量信息的能力, 各个模型的训练精度和运行时间见表 2。
| 试验区 | 网络结构 | 精度/(%) | 运行时间/s | 网络结构 | 精度/(%) | 运行时间/s | 网络结构 | 精度/(%) | 运行时间/s |
| 武汉主城区 | CNN1 | 99.1 | 27.9 | CNN2 | 99.2 | 33.2 | CNN3 | 98.5 | 36.8 |
| CNN1.1 | 99.3 | 78.6 | CNN2.1 | 99.4 | 82.5 | CNN3.1 | 99.1 | 90.8 | |
| CNN1.2 | 99.4 | 254.1 | CNN2.2 | 99.5 | 229.5 | CNN3.2 | 99.4 | 250.9 | |
| 上海浦东新区 | CNN1 | 98.5 | 24.7 | CNN2 | 98.6 | 31.1 | CNN3 | 98.0 | 33.1 |
| CNN1.1 | 98.8 | 70.5 | CNN2.1 | 98.8 | 77.7 | CNN3.1 | 98.5 | 82.4 | |
| CNN1.2 | 99.1 | 210.0 | CNN2.2 | 99.1 | 218.5 | CNN3.2 | 99.1 | 221.5 |
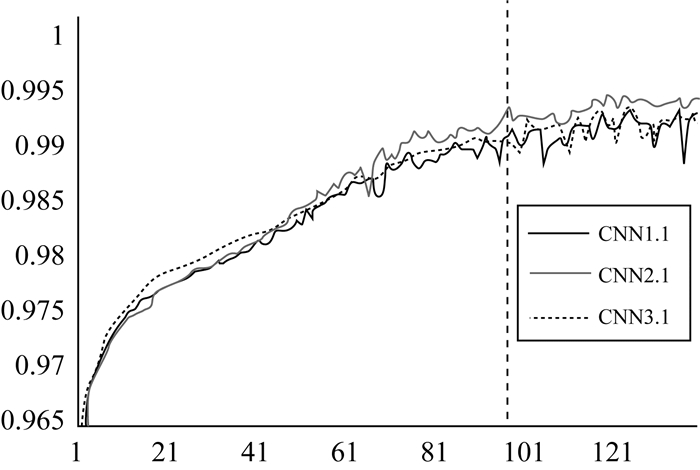
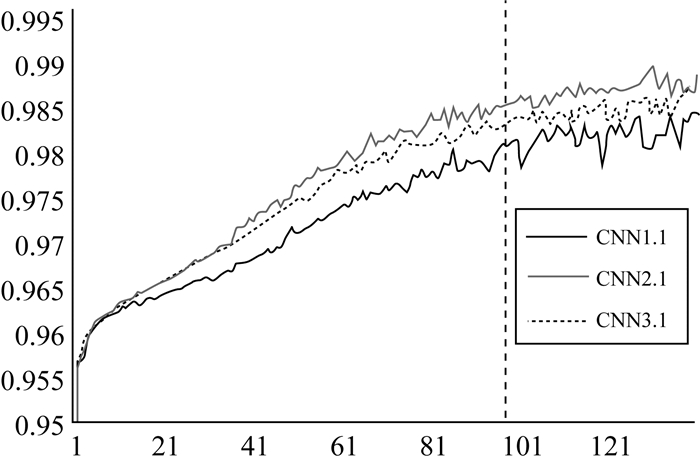
从模型测试的结果来看, 在网络较浅时, 可以通过加深网络的深度来达到加强模型挖掘转换规则的能力, 但随着网络深度的不断增加, 训练时间也大量增加。从试验结果来看, 当第1层卷积核数目为16, 第2层卷积核数目为32时, 模型平均精度为98.7%, 迭代一次平均运行时间为76.8 s, 模型在精度和效率的综合表现最佳, 因此选择此深度构建多结构卷积神经网络。此外, 3个CNN模型的其他参数相同, 学习率为1, 惯性系数为0.5, 每次训练图像个数为50, 经试验发现模型至少迭代100次才能收敛。为了保证模型的精度和效率, 将模型的训练次数设置为110次, 武汉主城区和上海浦东新区的训练曲线图如图 7、图 8所示。
|
| 图 7 武汉主城区训练曲线 Fig. 7 Training curve of the main urban zone of Wuhan |
|
| 图 8 上海浦东新区训练曲线 Fig. 8 Training curve of Pudong New District of Shanghai |
首先构建样本数据集, 将2005年土地利用数据和2015年土地利用数据做叠加运算, 将2005年的非城市用地区域分为0和1。0表示2005—2015年期间未转变为城市用地, 1表示2005—2015年期间转变为城市用地, 最后兼顾效率和精度, 分别按10%的比例随机采样。其中武汉主城区每个空间变量包括5000幅标签为城镇用地的图像和30 000幅标签为非城镇用地的图像, 得到35 000个大小为21×21×8的样本;上海浦东新区每个空间变量包括5000幅标签为城镇用地的图像和30 000幅标签为非城镇用地的图像, 得到35 000个大小为21×21×8的样本。在两类图像中各随机选取80%的空间变量数据作为训练集, 对模型进行训练, 剩余20%的样本作为测试集用来评价模型的精度。然后经过模型的训练和验证, 选取3个CNN模型的第2层全连接层F2级联为一个高维特征。最后, 文献[22]表明SVM分类器在处理不同驱动要素之间的非线性关系时有更好的表现, 从而在地理演变模拟时能获得更高的准确性, 因此本文选取SVM作为最终的分类器, 通过SVM中的核函数将级联后的高维特征拉伸为-1和1的二分类指数(1表示元胞可能转变为城市元胞, -1表示元胞未转变为城市元胞), 得到最终城市元胞的土地开发适宜性, 并结合邻域约束、限制约束和随机扰动的影响, 构建转换规则, 计算元胞由非城市向城市元胞转换的概率。
2.4 试验结果与分析本文选取Kappa系数、FoM(figure of merit)值、命中率h(表示模拟为城市元胞且实际为城市元胞的数目占元胞总数的比例)和错误率m(表示模拟为非城市元胞但实际为城市元胞的数目占元胞总数的比例)来评价MSCNN-CA的模拟结果。其中Kappa系数与FoM值的计算公式如下
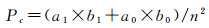 (5)
(5)
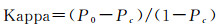 (6)
(6)
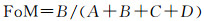 (7)
(7)
式中, P0是指模拟正确的栅格数量占总栅格数量的比例, 为观察一致性;Pc为期望一致性;栅格总数为n;实际栅格中为城市用地的数目为a1;实际为非城市用地的栅格数为a0;模拟栅格中为城市用地的数目为b1;模拟为非城市用地的栅格数为b0;A是实际土地利用类型发生变化但模拟结果中土地利用类型不变的错误区域;B是实际和模拟结果中土地利用类型都发生变化的正确区域;C是实际土地利用类型发生变化但模拟结果中土地利用类型预测错误的区域(在本研究中, 由于本文只模拟非城镇用地的转变, 因此C为0);D是实际土地利用类型不变但模拟结果中土地利用类型发生变化的错误区域。
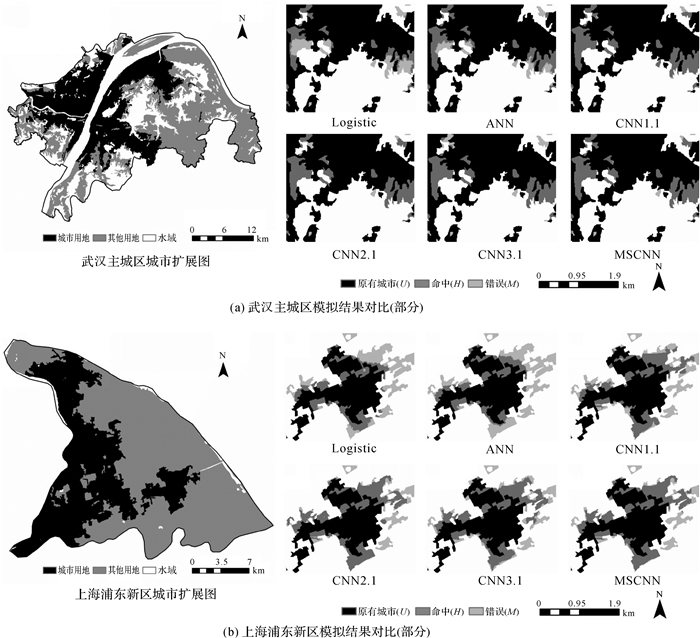
表 3是两个试验区各个模型模拟的精度指标对比。首先, 与逻辑回归和神经网络相比, 3个单一结构的CNN-CA模型在4个指标上都有不同程度的提高, 特别是FoM指数, 在武汉主城区提高了23.3%~29.4%, 在上海浦东新区提高了20.3%~28.5%。说明与传统方法基于单个元胞的信息挖掘来构建转换规则相比, 提取区域特征构建转换规则的CA模型考虑了CA模拟地理演变过程的区域效应, 从而能有效提高城市扩展的模拟精度。其次, MSCNN-CA模型与3个单一结构的CNN-CA模型相比, 在FoM指标上也有所改善, 在武汉主城区提高了0.8%~4.8%, 在上海浦东新区提高了2.8%~7.8%。说明多结构卷积神经网络可优化单结构卷积神经网络挖掘转换规则的能力, 耦合多尺度区域特征构建转换规则可提高模型的模拟精度。并且, MSCNN-CA模型在城市扩展模拟中都有着更高的命中率(h)和更低的错误率(m), 如图 9所示, 更能直观地突出MSCNN-CA模型的模拟优势, 其中, U表示模拟初期城市元胞, H表示模拟为城市元胞且实际为城市元胞, M表示模拟为非城市元胞但实际为城市元胞。与其他方法相比, MSCNN-CA模型模拟的新增城市元胞更加集聚, 更贴近真实的地理分布状态。因此可知, 网络结构的多样性, 对于丰富转换规则的特征信息, 准确提取区域内的非线性特征, 提高CA模型的模拟能力具有重要意义。
| 试验区 | 指标 | Logistic | ANN | CNN1.1 | CNN2.1 | CNN3.1 | MSCNN |
| 武汉主城区 | Kappa | 0.862 6 | 0.869 2 | 0.942 1 | 0.949 2 | 0.942 8 | 0.950 8 |
| FoM | 0.380 8 | 0.401 5 | 0.634 8 | 0.674 3 | 0.638 5 | 0.682 2 | |
| h/(%) | 4.21 | 4.37 | 4.99 | 5.21 | 5.01 | 5.24 | |
| m/(%) | 2.59 | 2.43 | 1.81 | 1.59 | 1.79 | 1.56 | |
| 上海浦东新区 | Kappa | 0.808 4 | 0.822 4 | 0.909 8 | 0.922 5 | 0.914 2 | 0.930 5 |
| FoM | 0.402 3 | 0.433 6 | 0.636 9 | 0.687 2 | 0.660 9 | 0.714 6 | |
| h/(%) | 6.12 | 6.45 | 7.42 | 8.01 | 7.87 | 8.19 | |
| m/(%) | 4.53 | 4.20 | 3.23 | 2.64 | 2.78 | 2.46 |
|
| 图 9 模拟结果对比 Fig. 9 The comparison of simulation results |
3 结论
本文提出基于多结构卷积神经网络构建城市扩展CA模型, 并以武汉市主城区和上海市浦东新区两个典型区域来验证所构建的模型优势。对比发现, 相比传统CA模型, 多结构卷积神经网络CA模型能够有效提高城市扩展模拟的精度, 更真实地反映城市扩展空间演变过程;相比单结构的卷积神经网络CA模型, 多结构卷积神经网络CA模型继承了传统卷积神经网络模型通过提取区域特征来挖掘转换规则的能力, 同时还考虑到不同尺度下提取到规则特征的差异性, 将多尺度下提取到的区域特征规则进行耦合, 充分考虑了CA模拟地理演变过程尺度效应, 因此模型的稳定性和模拟结果准确性有所提升, 且参数量和计算并没有显著增加, 具有较强的可应用性。
本文通过组合不同网络结构的CNN模型, 使城市扩展CA模型在模拟精度上的表现有所提高, 表明区域特征信息及其尺度特征对CA模型转换规则构建具有较强影响, 卷积神经网络在城市地理研究领域的应用潜力仍有待挖掘。篇幅所限, 本文对多结构卷积神经网络的网络结构设计仍存在需改进的地方, 人为选取模型参数存在一定的主观性, 如何更加科学的构建卷积神经网络的多结构层次是未来有待研究的问题。
| [1] |
王海军, 邓羽, 张文婷, 等. 利用元胞自动机和遗传算法的Voronoi图生成[J]. 武汉大学学报(信息科学版), 2010, 35(7): 778-781. WANG Haijun, DENG Yu, ZHANG Wenting, et al. Generation of Voronoi diagram based on genetic algorithms and cellular automata[J]. Geomatics and Information Science of Wuhan University, 2010, 35(7): 778-781. |
| [2] |
王海军, 张文婷, 贺三维, 等. 利用元胞自动机和模糊C均值进行图像分割[J]. 武汉大学学报(信息科学版), 2010, 35(11): 1288-1291. WANG Haijun, ZHANG Wenting, HE Sanwei, et al. An image segmentation method based on cellular automata and fuzzy C-means[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1288-1291. |
| [3] |
王海军, 张文婷, 陈莹莹, 等. 利用元胞自动机作用域构建林火蔓延模型[J]. 武汉大学学报(信息科学版), 2011, 36(5): 575-578. WANG Haijun, ZHANG Wenting, CHEN Yingying, et al. Fire spreading model based on CA scope[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5): 575-578. |
| [4] |
张利, 周亚鹏, 门明新, 等. 基于不同种类生态安全的土地利用情景模拟[J]. 农业工程学报, 2015, 31(5): 308-316. ZHANG Li, ZHOU Yapeng, MEN Mingxin, et al. Land use scenario simulation with different types of ecological security[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(5): 308-316. |
| [5] |
COUCLELIS H. Cellular worlds:a framework for modeling micro-macro dynamics[J]. Environment and Planning A:Economy and Space, 1985, 17(5): 585-596. |
| [6] |
COUCLELIS H. From cellular automata to urban models:new principles for model development and implementation[J]. Environment and Planning B:Planning and Design, 1997, 24(2): 165-174. |
| [7] |
王海军, 夏畅, 刘小平, 等. 大尺度和精细化城市扩展CA的理论与方法探讨[J]. 地理与地理信息科学, 2016, 32(5): 1-8. WANG Haijun, XIA Chang, LIU Xiaoping, et al. Theoretical and methodological perspectives of fine-scale urban expansion cellular automata for the large regions[J]. Geography and Geo-information Science, 2016, 32(5): 1-8. |
| [8] |
WHITE R, ENGELEN G. Cellular automata as the basis of integrated dynamic regional modelling[J]. Environment and Planning B:Planning and Design, 1997, 24(2): 235-246. |
| [9] |
WHITE R, ENGELEN G. Cellular automata and fractal urban form:a cellular modelling approach to the evolution of urban land-use patterns[J]. Environment and Planning A:Economy and Space, 1993, 25(8): 1175-1199. |
| [10] |
BATTY M, XIE Y. From cells to cities[J]. Environment and Planning B:Planning and Design, 1994, 21(7): 531-538. |
| [11] |
WU Fulong. SimLand:a prototype to simulate land conversion through the integrated GIS and CA with AHP-derived transition rules[J]. International Journal of Geographical Information Science, 1998, 12(1): 63-82. |
| [12] |
LI Xia, YEH A G O. Modelling sustainable urban development by the integration of constrained cellular automata and GIS[J]. International Journal of Geographical Information Science, 2000, 14(2): 131-152. |
| [13] |
王鹤, 曾永年. 城市扩展极限学习机模型[J]. 测绘学报, 2018, 47(12): 1680-1690. WANG He, ZENG Yongnian. Urban expansion model based on extreme learning machine[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(12): 1680-1690. DOI:10.11947/j.AGCS.2018.20170586 |
| [14] |
WU Fulong. Calibration of Stochastic cellular automata:the application to rural-urban land conversions[J]. International Journal of Geographical Information Science, 2002, 16(8): 795-818. |
| [15] |
CAO Kai, HUANG Bo, LI Manchun, et al. Calibrating a cellular automata model for understanding rural-urban land conversion:a Pareto front-based multi-objective optimization approach[J]. International Journal of Geographical Information Science, 2014, 28(5): 1028-1046. |
| [16] |
LIU Yan, FENG Yongjiu, PONTIUS JR R G. Spatially-explicit simulation of urban growth through self-adaptive genetic algorithm and cellular automata modelling[J]. Land, 2014, 3(3): 719-738. |
| [17] |
FENG Yongjiu, LIU Yan, TONG Xiaohua, et al. Modeling dynamic urban growth using cellular automata and particle swarm optimization rules[J]. Landscape and Urban Planning, 2011, 102(3): 188-196. |
| [18] |
BIAU G. Analysis of a random forests model[J]. Journal of Machine Learning Research, 2012, 13(4): 1063-1095. |
| [19] |
王海军, 夏畅, 张安琪, 等. 利用生物地理学优化算法获取城市扩展元胞自动机模型参数[J]. 武汉大学学报(信息科学版), 2017, 42(9): 1323-1329. WANG Haijun, XIA Chang, ZHANG Anqi, et al. Calibrating urban expansion cellular automata using biogeography-based optimization[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1323-1329. |
| [20] |
LI Xia, CHEN Guangzhao, LIU Xiaoping, et al. A new global land-use and land-cover change product at a 1-km resolution for 2010 to 2100 based on human-environment interactions[J]. Annals of the American Association of Geographers, 2017, 107(5): 1040-1059. |
| [21] |
刘小平, 黎夏. 从高维特征空间中获取元胞自动机的非线性转换规则[J]. 地理学报, 2006, 61(6): 663-672. LIU Xiaoping, LI Xia. Retrieving CA nonlinear transition rule from high-dimensional feature space[J]. Acta Geographica Sinica, 2006, 61(6): 663-672. |
| [22] |
杨青生, 黎夏. 基于支持向量机的元胞自动机及土地利用变化模拟[J]. 遥感学报, 2006, 10(6): 836-846. YANG Qingsheng, LI Xia. Cellular automata for simulating land use changes based on support vector machine[J]. Journal of Remote Sensing, 2006, 10(6): 836-846. |
| [23] |
HE Jialv, LI Xia, YAO Yao, et al. Mining transition rules of cellular automata for simulating urban expansion by using the deep learning techniques[J]. International Journal of Geographical Information Science, 2018, 32(10): 2076-2097. |
| [24] |
姚相坤, 万里红, 霍宏, 等. 基于多结构卷积神经网络的高分遥感影像飞机目标检测[J]. 计算机工程, 2017, 43(1): 259-267. YAO Xiangkun, WAN Lihong, HUO Hong, et al. Airplane object detection in high resolution remote sensing imagery based on multi-structure convolutional neural network[J]. Computer Engineering, 2017, 43(1): 259-267. |
| [25] |
陈超, 齐峰. 卷积神经网络的发展及其在计算机视觉领域中的应用综述[J]. 计算机科学, 2019, 46(3): 63-73. CHEN Chao, QI Feng. Review on development of convolutional neural network and its application in computer vision[J]. Computer Science, 2019, 46(3): 63-73. |
| [26] |
余东行, 郭海涛, 张保明, 等. 级联卷积神经网络的遥感影像飞机目标检测[J]. 测绘学报, 2019, 48(8): 1046-1058. YU Donghang, GUO Haitao, ZHANG Baoming, et al. Aircraft detection in remote sensing images using cascade convolutional neural networks[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(8): 1046-1058. DOI:10.11947/j.AGCS.2019.20180471 |
| [27] |
崔卫红, 熊宝玉, 张丽瑶. 多尺度全卷积神经网络建筑物提取[J]. 测绘学报, 2019, 48(5): 597-608. CUI Weihong, XIONG Baoyu, ZHANG Liyao. Multi-scale fully convolutional neural network for building extraction[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(5): 597-608. DOI:10.11947/j.AGCS.2019.20180062 |
| [28] |
WANG Haijun, HE Sanwei, LIU Xingjian, et al. Simulating urban expansion using a cloud-based cellular automata model:a case study of Jiangxia, Wuhan, China[J]. Landscape and Urban Planning, 2013, 110(1): 99-112. |
| [29] |
XIA Chang, WANG Haijun, ZHANG Anqi, et al. A high-performance cellular automata model for urban simulation based on vectorization and parallel computing technology[J]. International Journal of Geographical Information Science, 2018, 32(2): 399-424. |
| [30] |
XIA Chang, ZHANG Anqi, WANG Haijun, et al. Modeling urban growth in a metropolitan area based on bidirectional flows, an improved gravitational field model, and partitioned cellular Automata[J]. International Journal of Geographical Information Science, 2019, 33(5): 877-899. |
| [31] |
FENG Yongjiu, LIU Yan, BATTY M. Modeling urban growth with GIS based cellular automata and least squares SVM rules:a case study in Qingpu-Songjiang area of Shanghai, China[J]. Stochastic Environmental Research and Risk Assessment, 2016, 30(5): 1387-1400. |
| [32] |
门计林, 刘越岩, 张斌, 等. 多结构卷积神经网络特征级联的高分影像土地利用分类[J]. 武汉大学学报(信息科学版), 2019, 44(12): 1841-1848. MEN Jilin, LIU Yueyan, ZHANG Bin, et al. Land use classification based on multi-structure convolution neural network features cascading[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1841-1848. |



