多路径误差由卫星直射信号和反射、衍射信号等同时进入接收机天线并产生干涉效应造成,对于载波相位观测量而言理论上最大可达波长的1/4[1-2],是影响GPS数据处理精度和可靠性的一种主要误差源[3-5]。为削弱多路径误差,可将站址尽量选择在空旷平坦的观测环境[6],避免附近存在强反射环境或强辐射源;或者选用抗多路径误差的硬件,例如为天线加装扼流圈或抑径板[7-8];除了上述方法外,还可从数据处理算法上对其进行误差建模[9-10]。恒星日滤波SF(sidereal filtering)是一种目前应用较为广泛的多路径误差削弱方法[11-13],其理论基础在于当接收机天线与周围环境保持不变时,测站多路径效应主要与卫星信号传播方向的变化相关,利用卫星运行轨道的周日重复特性对多路径误差进行分离,并以此改正后续天的观测量,达到削弱多路径误差的目的[14-18]。
与利用卫星运动轨道的重复特性进行多路径误差建模相比,在空间域对测站处的多路径误差进行描述同样是削弱其影响的一种有效的解决方案。文献[19-20]根据观测值建立了基于接收机天线的多路径环境图表。文献[21]则进一步提出了利用半天球模型进行多路径误差消除的方法,当测站间存在共视卫星经过半天球上的某个格网点周边时,将此卫星的站间单差模糊度固定解所对应观测值残差求平均,在削弱噪声影响的同时保留低频多路径效应并对其进行模型化。不过该方法需采用接收机时钟同步的一机多天线观测模式,其应用距离受线缆传输时信号衰减等硬件条件的限制。
1 半天球格网点模型对于某一波长的卫星信号,其多路径误差受反射系数、反射信号入射角及天线相对反射物位置关系的影响[22]。若天线与周围环境的位置关系保持不变,则主要由于信号传播方向改变引起反射信号的传播路径变化,其入射角和反射系数会产生相应的改变,最终影响观测信号中存在的多路径效应。
基于多路径效应在空间域的以上特性,本文提出了一种多路径误差半天球格网点模型MHGM(multi-point hemispherical grid model),以接收机天线相位中心为球心建立半天球,并将高度角、方位角分别作为半天球的纬度和经度对其进行划分。认为在以天线为载体的半天球坐标系中,同一信号频率下的多路径效应只与卫星所处高度角和方位角有关,与信号观测时间和卫星编号无关。
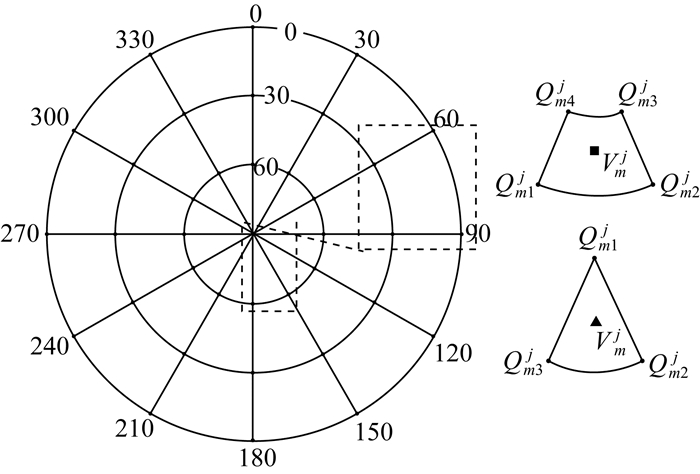
1.1 模型参数化对各测站处的半天球模型以高度角作为纬度,方位角作为经度进行格网点划分。格网点纬度圈的最小值设为B0,格网点纬度圈的最大值设为B1。格网点经度按照方位角的范围值设置为0°~360°。此外,还在天顶处设置一个格网点参数。格网点在纬度和经度方向的划分间隔为d,d取值越小,模型中待估参数越多,对计算机内存资源消耗越多,但对测站处的多路径误差描述也越精细。反之,模型资源消耗更少,但对测站处的多路径误差描述越简略。以下给出一组测站处的格网点划分实例(B0=0°,B1=60°,d=30°),其中格网点处需设定相应的待估模型参数。
1.2 模型解算对于测站m、n与卫星j、k间任意一组模糊度固定解对应的双差观测值残差s,构建相关待估格网点参数对应的法方程。测站m与卫星j间的多路径误差涉及格网模型上的4个点Qm1j、Qm2j、Qm3j和Qm4j(卫星j的高度角在B0和B1之间)或3个点Qm1j、Qm2j和Qm3j(卫星j的高度角大于B1时)。
若卫星j信号传播方向在半天球上的穿刺点与半天球格网点参数间位置关系如图 1右侧上方图例所示,黑色圆点表示格网点参数,正方形点表示卫星j的信号传播在站m上的半天球模型中的穿刺点位置,同时也对应半天球格网点模型的模型参数计算值Vmj。假定4个格网点参数Qm1j、Qm2j、Qm3j和Qm4j对应的经纬度坐标分别为(b1, l1)、(b1, l2)、(b2, l2)、(b2, l1),Vmj对应的经纬度坐标为(b, l),则Vmj处的模型参数计算值可通过双线性内插方法表达如下
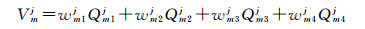 (1)
(1)
|
| 图 1 半天球格网点划分 Fig. 1 Distribution of hemispherical grid points |
式中,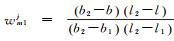
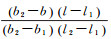
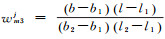
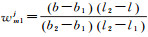
若卫星j信号传播方向在半天球上的穿刺点与半天球格网点参数间位置关系如图 1右侧下方图例所示。假定3个格网点参数Qm1j、Qm2j和Qm3j对应的经纬度坐标分别为(b1, l1)、(b2, l2)、(b2, l3),则三角形点表示的穿刺点Vmj处的模型参数计算值可通过平面内插方法[23-24]表达如下
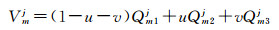 (2)
(2)
式中,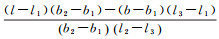
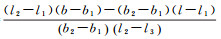
类似的,可建立测站m与卫星k间、测站n与卫星j间、测站n与卫星k间模型参数计算值Vmk、Vnj、Vnk的表达式,则双差观测值残差s可由上述模型参数计算值表达如下
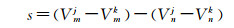 (3)
(3)
利用观测方程(3)构建相关格网点参数对应的法方程,并通过法方程叠加的方式实现不同测站卫星对、不同时段观测数据的融合解算。此外,还可通过对格网点参数间加入相关性约束,以及利用格网点参数绝对值应小于1/4波长的特性,进一步加强模型解算结果的精度和可靠性。
2 试验及结论 2.1 试验设计于2018年年积日DOY226-233,在武汉大学教学实验大楼顶楼开展验证分析。测试时布设了A、B、C 3个测站,其中A测站的西方向和B测站的东方向均安装了金属挡板,用于模拟强多路径观测环境,测站C未加装挡板,为正常的观测环境。测站相互间位置关系及周围观测环境如图 2所示。

|
| 图 2 测站间位置关系及周围观测环境 Fig. 2 Spatial relationship between stations and surrounding observation environment |
利用上述3个站精确已知的测站坐标,本次试验采用2018年DOY228-232的L1频率观测数据进行多路径误差建模,并分析了对2018年DOY233观测数据进行多路径误差改正的有效性。为论证不同时长观测数据对多路径误差建模的影响,测试中分别采用1~5 d的数据建立MHGM模型,模型参数中格网点纬度圈的最小值B0设置为5°,格网点纬度圈的最大值B1设置为85°,格网点在纬度和经度方向的划分间隔d设置为2°。同时,本文还给出了未进行多路径误差建模,以及采用传统SF方法进行多路径误差建模的结果进行对比分析。试验中的具体解算策略见表 1。
| 策略 | 建模方法 | 2018年年积日 | |
| 建模数据 | 测试数据 | ||
| N | - | - | 233 |
| S | SF | 232 | 233 |
| M1 | MHGM | 232 | 233 |
| M2 | MHGM | 231-232 | 233 |
| M3 | MHGM | 230-232 | 233 |
| M4 | MHGM | 229-232 | 233 |
| M5 | MHGM | 228-232 | 233 |
表 1的各个策略中,N策略为不进行任何多路径误差改正的情况下对2018年年积日DOY233数据进行处理;S策略是在使用SF方法进行多路径误差改正的情况下处理DOY233数据;M1~M5策略均是在使用本文提出的MHGM方法进行多路径误差改正的情况下处理DOY233数据。由于GPS卫星轨道重复周期为一个恒星日,因此SF方法的建模数据来源为DOY232数据。由于MHGM方法可进行多天叠加建模,在验证多天叠加改善效果并与传统的SF方法进行对比的同时可用于评估最优的叠加建模天数。
2.2 结果分析依据表 1的数据解算策略,图 3给出了A、B、C 3个测站各颗卫星在模糊度固定时段内的L1频率非差观测值残差,并按照星下点轨迹的方式进行展示。当未进行多路径误差改正时,A(N)、B(N)、C(N)的结果表明此时各颗卫星的非差观测值残差均相对较大。尤其是在A、B站加装挡板的位置,即A(N)左侧、B(N)右侧区域多路径影响尤为明显,出现了多组观测值残差偏大的现象。在使用SF方法进行多路径误差修正时需顾及卫星的轨道重复周期提前量,本次试验中设定轨道重复周期为一个恒星日,对应提前量为236s[11, 12, 25]。由A(S)、B(S)、C(S)的结果可知此时L1观测值所受多路径效应得到了有效削弱,但由于上述轨道重复周期提前量的存在导致DOY233部分时段观测数据无法进行多路径误差削弱。如A(S)、B(S)、C(S)中虚框所示,星下点轨迹存在端部残差值偏大的现象(简称为“末端效应”)。当采用本文提出的MHGM方法时,如A(M1)、B(M1)、C(M1)所示,即使仅采用前1 d的观测数据进行建模,卫星观测时段端部残差值偏大现象也能得到有效削弱,且整体而言对多路径误差改正的有效性要优于传统SF方法。当采用前2 d或3 d的观测数据进行建模时,MHGM方法的建模有效性可得到进一步提升,基本不存在卫星观测时段端部残差值偏大的现象。对比M3~5这3种策略下A、B、C 3个测站的非差观测值残差结果可以发现,其多路径误差的改善效率差异不大。分析认为,这是由于GPS的卫星轨道周期重复周期约为1 d,利用临近2~3 d的观测数据即可对GPS观测数据中所受多路径误差影响进行有效建模。限于文章篇幅,图 3仅给出了N、S、M1及M3策略下3个站的非差观测值残差结果。

|
| 图 3 A、B、C测站非差观测值残差的星下点分布图 Fig. 3 Satellite zero-differenced observation residuals at stations A, B and C |
为定量化给出本文提出的MHGM方法较SF方法的改进效果,并评估利用1~5 d观测数据进行多路径误差建模其有效性的差异。
表 2给出了7种处理策略下DOY233全部双差模糊度固定时段其观测值残差的RMS均值统计结果。如同样采用前一天观测数据进行多路径误差建模,MHGM方法的改正效果略优于SF方法,多路径误差的平均改善率由64.3%提升至68.6%。当采用之前2 d及以上观测数据进行多路径误差建模时,MHGM方法的改善率差异不大,平均在73.9%左右,较传统SF方法的改善率平均提升26.9%。
| 策略 | RMS平均 值/cm | 对比N策略的 提升/(%) | 对比S策略的 提升/(%) |
| N | 1.073 | - | - |
| S | 0.383 | 64.3 | - |
| M1 | 0.337 | 68.6 | 12.0 |
| M2 | 0.297 | 72.3 | 22.4 |
| M3 | 0.276 | 74.3 | 28.0 |
| M4 | 0.277 | 74.2 | 27.8 |
| M5 | 0.276 | 74.2 | 27.9 |
多路径误差改正最终目的是为了提升精密定位精度,为评估上述两种方法的有效性,分别统计了采用MHGM方法和SF方法进行多路径误差改正后对定位结果的影响。试验中固定测站C,按实时动态相对定位模式求解测站A、B的三维坐标,其中MHGM方法使用M3策略进行多路径误差建模。静态数据的动态定位模式结果RMS统计见表 3。
| mm | |||||||||||||||||||||||||||||
| 策略 | RMS | ||||||||||||||||||||||||||||
| A | B | ||||||||||||||||||||||||||||
| 平面 | 高程 | 平面 | 高程 | ||||||||||||||||||||||||||
| N | 5.51 | 10.18 | 4.95 | 9.61 | |||||||||||||||||||||||||
| S | 1.59 | 3.45 | 2.54 | 4.37 | |||||||||||||||||||||||||
| M3 | 1.53 | 2.60 | 1.81 | 3.38 | |||||||||||||||||||||||||
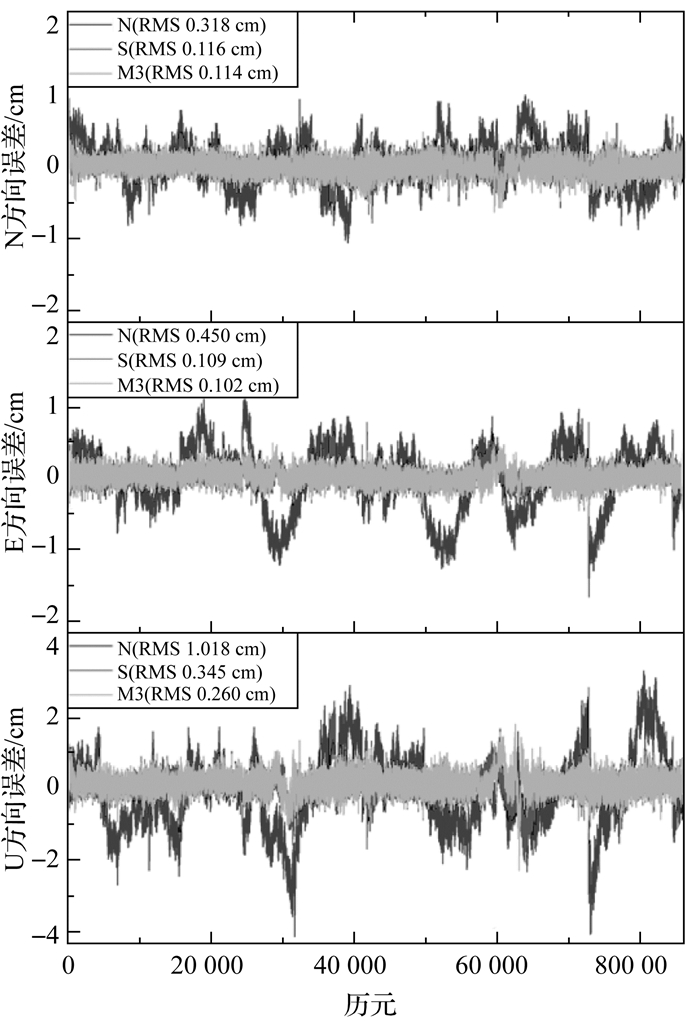
未进行多路径误差改正时,由于测站A、B均加装了挡板以模拟强多路径环境,因此定位精度较差。A、B两个测站的平面定位精度分别为5.51、4.95 mm,高程定位精度分别为10.18、9.61 mm。当采用SF方法进行多路径误差改正后,A、B两个测站的定位精度得到了明显改善,分别达到了平面1.59、2.54 mm,高程3.45、4.37 mm,三维定位精度的改善率分别高达67.2%和53.2%。当采用本文提出的MHGM方法进行多路径误差建模时,两测站A、B的定位精度分别提升至平面1.53、1.81 mm,高程2.60、3.38 mm,较SF方法在测站A、B的高程方向上能得到24.6%和22.7%的改善,在平面方向上其改善率也分别能达到3.8%和28.7%。为展示N、S、M2这3种处理策略对不同时刻对定位结果的影响,图 4给出了A站在N、E、U方向上的实时动态定位误差序列。
|
| 图 4 测站A的实时动态定位误差序列 Fig. 4 Real-time dynamic positioning error sequence of station A |
与SF方法相比,本文提出的MHGM方法除了在多路径误差改善效果上得到一定提升外,还可有效展现测站周边存在的多路径误差干扰情况。图 5给出了采用M3策略时的测站处MHGM模型半天球建模结果,分别为俯视、西侧和东侧视角的效果图。从俯视图中可见A(M3)的左侧、B(M3)的右侧区域存在较大面积的模型值偏高现象,进一步从A测站西侧、B测站东侧视图中可见视图底部存在明显且连续的“异常”区域,该现象出现的位置与金属挡板的架设方位相吻合,体现出挡板对测站A、B处造成的多路径误差影响。基于MHGM模型的上述特性,该模型不但可在数据解算时用于削弱测站处存在的多路径误差影响,还可进一步在测站环境评估时对测站周边可能存在的多路径误差源进行方位确定,对从物理意义上消除多路径误差源的影响给出一定的指导性意见。

|
| 图 5 采用M3策略时的测站处MHGM模型结果 Fig. 5 MHGM modeling results at stations using strategy M3 |
3 结论
本文提出了一种利用半天球格网点模型削弱测站多路径误差影响的新方法。该方法对以测站天线相位中心为球心的半天球进行格网点划分,通过格网点的参数化描述,实现测站处多路径误差建模。在格网点参数估计过程中,以不同时段、不同卫星对的模糊度固定解对应的双差观测值残差作为输入信息,得到整体一致的各测站处半天球格网点模型。
与半天球模型MHM(multipath hemispherical map)采用一机多天线硬件条件下的站间单差观测值残差进行建模相比,由于本文方法直接采用双差观测值残差对多路径误差建模,无须使用特定的接收机设备即可较为简便地应用于现有GPS网解数据处理过程,且测站间距离也不受硬件条件限制。
与SF方法相比,当仅采用前一天观测数据进行多路径误差建模时,MHGM方法的改正效果略优于传统SF方法,且有效解决了SF方法中卫星轨道重复周期提前量导致的“末端效应”,双差观测值残差的RMS平均改善率由64.3%提升至68.6%。当采用之前2 d或更多天观测数据按照MHGM方法进行多路径误差建模时,双差观测值残差的RMS均值改善率基本一致,平均在73.9%左右,较传统SF方法的效果平均提升26.9%。因此在采用MHGM方法模型化测站处GPS多路径效应时,建议至少采用前2~3 d的观测数据进行建模。与SF方法相比,在高程方向上能够得到近24%的改善,平面方向上的改善率也可达到16%。模型改正后的定位效果有显著提升,对于静态观测数据,按实时动态相对定位处理模式可获得平面精度约1.7 mm,高程精度约3.0 mm的定位结果。此外,本文提出的MHGM方法除了在多路径误差改善效果上得到一定提升外,还能有效展现测站周边存在的多路径误差干扰情况,这对于从物理意义上消除多路径误差源的影响可起到一定的指导性意见。
| [1] |
HOFMANN-WELLENHOF B, LICHTENEGGER H, WASLE E. GNSS-global navigation satellite systems:GPS, GLONASS, Galileo, and more[M]. Vienna: Springer, 2008.
|
| [2] |
黄声享, 李沛鸿, 杨保岑, 等. GPS动态监测中多路径效应的规律性研究[J]. 武汉大学学报(信息科学版), 2005, 30(10): 877-880. HUANG Shengxiang, LI Peihong, YANG Baocen, et al. Study on the characteristics of multipath effects in GPS dynamic deformation monitoring[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 877-880. |
| [3] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [4] |
钟萍, 丁晓利, 郑大伟. CVVF方法用于GPS多路径效应的研究[J]. 测绘学报, 2005, 34(2): 161-167. ZHONG Ping, DING Xiaoli, ZHENG Dawei. Study of GPS multipath effects with method of CVVF[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 161-167. DOI:10.3321/j.issn:1001-1595.2005.02.013 |
| [5] |
周晓卫, 戴吾蛟, 朱建军, 等. HVF方法在GPS多路径效应研究中的应用[J]. 大地测量与地球动力学, 2007, 27(1): 107-111. ZHOU Xiaowei, DAI Wujiao, ZHU Jianjun, et al. HVF method and its application in the study on GPS multipath effects[J]. Journal of Geodesy and Geodynamics, 2007, 27(1): 107-111. |
| [6] |
袁林果, 黄丁发, 丁晓利, 等. GPS载波相位测量中的信号多路径效应影响研究[J]. 测绘学报, 2004, 33(3): 210-215. YUAN Linguo, HUANG Dingfa, DING Xiaoli, et al. On the influence signal multipath effects in GPS carrier phase surveying[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 210-215. DOI:10.3321/j.issn:1001-1595.2004.03.005 |
| [7] |
范晓燕, 周乾. GPS测量中多路径效应研究综述[J]. 工程地球物理学报, 2010, 7(3): 382-386. FAN Xiaoyan, ZHOU Qian. Review of multipath effects in GPS measurement[J]. Chinese Journal of Engineering Geophysics, 2010, 7(3): 382-386. |
| [8] |
钟萍, 丁晓利, 郑大伟, 等. 一种基于交叉证认技术的自适应小波变换及其在削减GPS多路径误差中的应用[J]. 测绘学报, 2007, 36(3): 279-285. ZHONG Ping, DING Xiaoli, ZHENG Dawei. An adaptive wavelet transform based on cross-validation and its application to mitigate GPS multipath effects[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 279-285. DOI:10.3321/j.issn:1001-1595.2007.03.007 |
| [9] |
MEINDL M, SCHAER S, HUGENTOBLER U, et al. Tropospheric gradient estimation at CODE:results from global solutions[J]. Journal of the Meteorological Society of Japan, 2004, 82(1B): 331-338. DOI:10.2151/jmsj.2004.331 |
| [10] |
LAU L, MOK E. Improvement of GPS relative positioning accuracy by using SNR[J]. Journal of Surveying Engineering, 1999, 125(4): 185-202. DOI:10.1061/(ASCE)0733-9453(1999)125:4(185) |
| [11] |
GENRICH J F, BOCK Y. Rapid resolution of crustal motion at short ranges with the global positioning system[J]. Journal of Geophysical Research, 1992, 97(B3): 3261-3269. DOI:10.1029/91JB02997 |
| [12] |
BOCK Y, NIKOLAIDIS R M, DE JONGE P J, et al. Instantaneous geodetic positioning at medium distances with the Global Positioning System[J]. Journal of Geophysical Research, 2000, 105(B12): 28223-28253. DOI:10.1029/2000JB900268 |
| [13] |
NIKOLAIDIS R M, BOCK Y, DE JONGE P J, et al. Seismic wave observations with the Global Positioning System[J]. Journal of Geophysical Research, 2001, 106(B10): 21897-21916. DOI:10.1029/2001JB000329 |
| [14] |
RAGHEB A E, CLARKE P J, EDWARDS S J. GPS sidereal filtering:coordinate- and carrier-phase-level strategies[J]. Journal of Geodesy, 2007, 81(5): 325-335. DOI:10.1007/s00190-006-0113-1 |
| [15] |
CHOI K, BILICH A, LARSON K M, et al. Modified sidereal filtering:implications for high-ate GPS positioning[J]. Geophysical Research Letters, 2004, 31(22): 608-623. |
| [16] |
陈德忠, 叶世榕, 刘炎炎, 等. 基于观测值域的GPS多路径误差应用分析[J]. 武汉大学学报(信息科学版), 2014, 39(2): 147-151. CHEN Dezhong, YE Shirong, LIU Yanyan, et al. Applied analysis of GPS multipath errors based on observation domain[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 147-151. |
| [17] |
郑彬, 周宁, 欧钢. 基于恒星日滤波的PPP多径误差消除研究[J]. 大地测量与地球动力学, 2014, 34(3): 178-182. ZHENG Bin, ZHOU Ning, OU Gang. Study on elimination of multipath error in PPP based on sidereal filtering[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 178-182. |
| [18] |
ZHONG Ping, DING Xiaoli, YUAN Linguo, et al. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines[J]. Journal of Geodesy, 2010, 84(2): 145-158. DOI:10.1007/s00190-009-0352-z |
| [19] |
COHEN C E, PARKINSON B W. Mitigating multipath error in GPS based attitude determination[C]//Proceedings of Guidance and Control 1991. Washington D C: NASA, 1991: 53-68.
|
| [20] |
FUHRMANN T, LUO Xiaoguang, KNÖPFLER A, et al. Generating statistically robust multipath stacking maps using congruent cells[J]. GPS Solutions, 2015, 19(1): 83-92. DOI:10.1007/s10291-014-0367-7 |
| [21] |
DONG D, WANG M, CHEN W, et al. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map[J]. Journal of Geodesy, 2016, 90(3): 255-262. DOI:10.1007/s00190-015-0870-9 |
| [22] |
ELÓSEGUI P, DAVIS J L, JALDEHAG R T K, et al. Geodesy using the Global Positioning System:the effects of signal scattering on estimates of site position[J]. Journal of Geophysical Research, 1995, 100(B6): 9921-9934. DOI:10.1029/95JB00868 |
| [23] |
ZOU Xuan, WANG Yawei, DENG Chenlong, et al. Instantaneous BDS+GPS undifferenced NRTK positioning with dynamic atmospheric constraints[J]. GPS Solutions, 2018, 22(1): 17. DOI:10.1007/s10291-017-0668-8 |
| [24] |
WÜBBENA G, BAGGE A, SEEBER G, et al. Reducing distance dependent errors for real-time precise DGPS applications by establishing reference station networks[C]//Proceedings of the 9th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1996). Kansas City: Institute of Navigation, 1996: 1845-1852.
|
| [25] |
BOCK Y, PRAWIRODIRDJO L, MELBOURNE T I. Detection of arbitrarily large dynamic ground motions with a dense high-rate GPS network[J]. Geophysical Research Letters, 2004, 31(6): L06604. |



