空间分布模式是一种重要空间结构特征,建筑物空间分布模式识别是城市空间结构研究和地图自动综合研究的一个重要问题[1]。学者们基于人类视觉格式塔认知准则,考虑空间邻近、几何相似、分布连续等特征,采用聚类分析方法识别建筑物的空间分布模式,开展了一系列研究,大致归纳为3类。①基于划分聚类的方法。这类方法将建筑物抽象为空间点实体,将建筑物聚类简化为点聚类。如文献[2]采用SOM(self-organizing map)实现对建筑物的初步聚类,进而提出行列扫描方法对初始聚类结果进行优化获得建筑物聚类。文献[3]利用k-means算法识别建筑物聚类。这类方法只考虑了建筑物间的空间邻近性,忽略了建筑物形状、大小等几何特征的相似性。②基于分裂的方法。该类方法首先将所有建筑物视为一个聚簇,然后采取自上而下的分裂思想逐级划分为子簇[4-9]。如文献[4]提出一种基于最小生成树剪枝策略的聚集模式识别算法,根据建筑物间最小距离构建最小生成树,并通过局部长边删除操作生成连通子图,以此作为聚类结果。文献[5]综合考虑建筑物间距离、相对大小和方向提出视觉距离度量,根据视觉距离构建最小生成树,采用分裂的策略识别分布模式。该类方法可以考虑建筑物多维特征(如方向、大小等),且可以识别任意形状的分布模式[7-8],如线型分布、格网分布等。③基于聚合的方法。采取自下而上的聚合思想实现建筑物合并成簇[1, 10-11]。如文献[1, 10]结合城市形态学和格式塔认知准则,综合考虑建筑物的面积、形状和方向相似性,通过量化建筑物间的多因子相似性实现建筑物的逐层合并。文献[3]将建筑物抽象为一种图,综合考虑空间相似性进行图化简以实现建筑物聚类,在空间和几何上取得较好的效果。该类方法可以看作分裂的逆过程,在聚类过程中也可以使用机器学习方法识别特定类型的空间分布模式[11]。
综上所述,现有方法主要从空间邻近、几何形态相似等建筑物的空间几何特征进行分布模式识别[12],而没有充分顾及建筑物的功能语义特征,聚类结果难以支持建筑物语义层次的聚合操作的需求。建筑物的功能语义特征是人类在使用过程中对建筑物赋予的特定社会属性,是体现建筑物差异性的一种重要指标[13],也是建筑物综合过程中需要考虑的一个重要因素。因此,识别建筑物分布模式时,不仅要考虑建筑物的空间几何特征(即空间邻近性、几何相似性),还需要充分考虑建筑物的功能语义特征,从而可以更全面地刻画建筑物间的关联关系,由此获得的建筑物分布模式也更符合人类空间认知[5]。为此,本文采用空间-语义分治策略,提出一种顾及建筑物功能语义特征的空间分布模式识别方法,发掘空间邻近和功能语义相似的建筑物聚群,以更好地辅助建筑物地图综合,分析城市结构,识别建筑物用地功能区域和实现建筑物群场景的智能理解。
1 研究策略空间邻近性和功能语义相似性是人类认知建筑物聚集模式的两个重要因素[14]。为此,本文采用空间-语义分治策略,先考虑建筑物的空间位置邻近性(即建筑物间的最小距离)约束进行聚类,获得建筑物的空间分布模式和建筑物间的空间邻近关系;在此基础上,根据建筑物的功能语义相似性约束进行再次聚类,获得对建筑物的初步聚类结果;最后,依据簇内相似性与簇间差异性对初步聚类结果进行整体优化,获得建筑物最终的聚类结果。
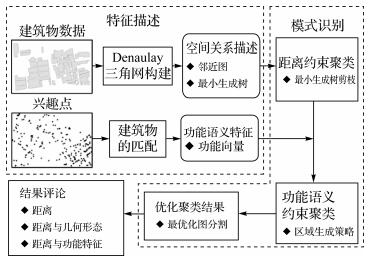
在建筑物的空间邻近性度量方面,本文通过构建Delaunay三角网描述建筑物空间邻近关系,以建筑物间最小距离为度量构建最小生成树,识别空间邻近的建筑物聚类。在建筑物功能语义特征描述方面,一方面,受传统地理空间数据采集手段限制,一般地图数据中,建筑物的功能语义描述信息很难获取;另一方面,由于城市建设不断发展,一些建筑物的功能语义属性也发生着快速变化。POI(point of interest,兴趣点)数据是目前获取建筑物语义信息的最直接、最广泛的一种数据来源,已经被广大学者广泛采用[15]。因此,本文采用POI数据来确定建筑物的功能属性特征。为了从POI数据中提取建筑物功能语义特征,通过建立POI与建筑物的匹配关系,将POI的语义信息与建筑物进行关联,实现建筑物功能语义特征的识别与提取。本文方法同时考虑建筑物空间邻近性和功能相似性,采用空间-语义分治策略进行建筑物聚类,并根据组间差异大和组内差异小的原则对聚类结果进行优化。本文采用的总体研究策略如图 1所示。
|
| 图 1 本文采取的研究策略 Fig. 1 The strategy for identifying building aggregation patterns |
2 顾及建筑物功能语义特征的空间分布模式识别方法 2.1 基于Delaunay三角网的建筑物空间邻近关系度量及优化
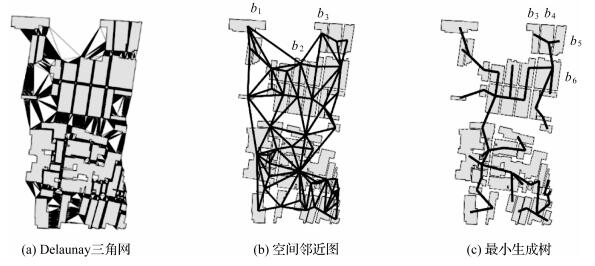
给定建筑物群数据集,采用约束Delaunay三角网构建邻近关系。具体地,通过边界点内插结点的形式对建筑物群转化为点群表达,并以此构建Delaunay三角网[9, 16],如图 2(a)所示。构造空间邻近图对Delaunay三角网进行简化表达,将建筑物b抽象为结点,若建筑物之间存在三角网的边,则结点间存在邻接边,进而得到一个建筑物空间邻近图,如图 2(b)所示。由于在空间分布非均匀区域,空间邻近图中存在明显不一致的长边,如图 2(b)中边b1b2,需要将这些不一致的长边进行剔除。最小生成树(minimum spanning tree,MST)是Delaunay三角网的一个子图,仅将最邻近实体连接,可以对建筑物间空间邻近关系进行更加准确的描述,在建筑物分布模式识别方面已得到广泛应用[4-5, 7-9, 17]。为此,本文采用两建筑物边界点之间最短欧氏距离来定义空间邻近图中边的权值,进而利用Prim算法在空间邻近图基础上构建最小生成树[18],如图 2(c)所示。其中,对于任一建筑物bi,若存在建筑物bj与bi通过最小生成树中的边相连,则将bj与bi定义为空间互邻近,记为bj↔bi。如图 2(c)所示,b3↔b4, b4↔b5, b4↔b6。
|
| 图 2 基于Delaunay三角网的建筑物空间邻近关系表达 Fig. 2 Spatial proximity relationships of buildings based on Delaunay triangulation |
2.2 建筑物功能语义特征提取与相似性度量
城市建筑物是提供人们从事各种行为活动的场所,一般在建设前预先设计好功能用途,但是大多地理数据库中通常没有表示这类功能信息,尤其是城市快速发展变化可能导致一些建筑物的功能特征也会发生改变。为此,学者们利用辅助数据对建筑物功能语义的提取开展了相关研究,如文献[19]提出结合航空遥感影像和地理信息数据的方法识别建筑物的功能语义。这类方法是通过观察与分析建筑物的物理特征(波谱特征)获取推断建筑物分类,没有考虑城市中人的活动与建筑物之间的内在联系。当前,城市各种类型POI数据为感知城市建筑物功能语义属性提供了新的数据源。不同于遥感影像,城市POI数据有很强的对空间位置实体描述的能力,并且城市大部分POI的载体都是建筑物,能够从人类活动的角度描述城市建筑物功能语义。因此,可以通过与建筑物关联的POI的空间分布特征进行分析与推断建筑物不同的功能类型[20-23],如文献[15]利用兴趣点分布进行建筑物功能类型的划分[15]。由于POI点包含了许多类别信息,为了更好地识别建筑物功能语义特征,本文首先根据高德地图对POI的分类标准,将POI划分为住宅、住宿、政府、医疗、休闲、生活、科技文化、金融、购物、企业、餐饮11种语义类型。在此基础上,为了度量建筑物间功能语义特征的相似性,定义了建筑物的功能向量等特征描述指标,具体描述为:
定义1 建筑物功能向量: 假设共有N类兴趣点分布于研究区域,那么任意建筑物bi或建筑物群Ci的功能类型可以通过一个N维向量进行描述,表达为
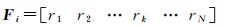 (1)
(1)
式中,rk为落入bi的第k类兴趣点的数目与第k类兴趣点总数的比值。这里,N=11。
定义2 建筑物功能相似度: 给定两个建筑物bi和bj(或建筑物群Ci和Cj),采用向量余弦来描述两个建筑物之间的功能相似度,表达为
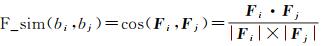 (2)
(2)
式中,Fi、Fj分别为建筑物bi、bj的功能向量;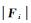
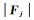
实际上,城市的乡村或郊区地区可能会存在缺少POI数据的问题,导致无法获取建筑物分类。通常情况下,城市乡村或郊区的建筑物功能较为单一,通过基于空间邻近关系的聚类分析则可得到建筑物的空间分布模式。对于建筑物分布紧凑且功能类型复杂的城区,不仅需要采用基于空间邻近关系的聚类分析,还需要顾及建筑物功能语义特征进行精确划分,从而使得识别的结果可以反映城市建筑物的复杂分布结构和用地功能。
2.3 建筑物分布模式识别 2.3.1 基于空间邻近关系的聚类本文采用基于分裂的思想,以建筑物间最短距离为度量构建连接建筑物的最小生成树,通过不断删除最小生成树中不一致的长边,形成建筑物的初步聚类。具体地,首先,删除最小生成树中权值最大的边,从而将原始建筑物群分裂为两个子群;然后,以每个子群为分析对象,采用删除最大边策略进行迭代剪枝。在每次删除最小生成树长边时,都需要对子群中建筑物空间分布同质性进行判别,如果获得的建筑物子群满足空间分布同质性要求,则停止对该子群进行分裂操作。建筑物空间分布同质性定义为:
定义3 空间分布同质性: 记建筑物最小生成树的边长方差为σ,若分裂后获得的子树边长标准差σ1λ1σ,则认为该子建筑物群具有空间分布同质性。其中,调节参数λ1取值为[0, 1]。
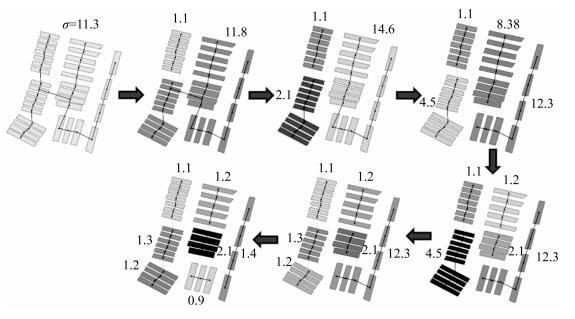
如果经过最小生成树剪枝获得的所有子群满足空间分布同质性,则停止聚类操作。图 3显示了一个建筑物群的最小生成树迭代剪枝过程示例。图中,初始最小生成树(MST)的边长标准差σ=11.3,给定λ1=0.3,通过分裂聚类策略,依次剪去权值最大的边,图中标注的数值为各子树边长的标准差。通过迭代剪枝,最终获得7个子建筑物聚群。
|
| 图 3 最小生成树剪枝 Fig. 3 Pruning process of the minimum spanning tree |
2.3.2 顾及空间邻近和功能语义特征相似性的建筑物聚类
采用分裂策略的聚类操作可以获得建筑物的空间聚群和建筑物间的空间邻近关系。进而,需要在每个建筑物聚群中考虑相邻建筑物间的功能语义特征的相似性。本文借鉴文献[24-25]提出的基于多约束的空间聚类思想,引入直接功能相似与间接功能相似的概念。
定义4 直接功能相似: 对于建筑物b1、b2,如果二者之间有边相连,且其功能相似度F_sim(b1,b2)λ2,则称建筑物b1、b2直接功能相似,其中λ2为设置的直接相似度阈值。
定义5 间接功能相似: 对于建筑物集合S={b1, b2, …, bi},如果功能相似度F_sim(S, {bi+1}≥λ3,则称S与bi+1间接功能相似,其中λ3为设置的间接相似度阈值。
顾及功能语义特征约束聚类时,首先选取建筑物空间聚群中的一个建筑物b,记为聚簇{b};进而,以{b}为初始种子,采用区域生长策略,寻找与{b}相邻的所有同时满足与其直接功能相似和间接功能相似的建筑物,并将其合并到聚簇{b}中。重复以上过程,直到没有相邻的建筑物可并入,聚簇的区域生长过程停止。从其他未并入任何聚簇的建筑物中选取一个建筑物作为新的聚簇,重复以上过程,直到所有建筑物被归入某个簇时,整个聚类过程终止。
2.3.3 最优化图分割在采用分治策略的聚类过程中,空间邻近性与功能相似性之间很可能会存在冲突,并且与空间邻近图相比,最小生成树对建筑物空间邻近关系的表达存在局限性。为使聚集模式识别结果更合理,需要将以上获得的初始聚类结果置于空间邻近图中进行优化。
定义6 边界点: 给定最小生成树剪枝聚类获得的任一簇Ci,若Ci中某建筑物bi在Delaunay三角网中与其他任一簇Cj中的建筑物bj存在相连关系,则称bi和bj分别为其各自所在簇的边界点,分别记为bpi和bpj。
对于簇Ci和Cj,同时考虑空间距离和功能语义特征的差异,可将Ci和Cj间的差异度表达为
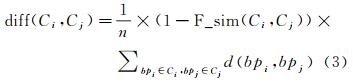 (3)
(3)
式中,n表示连接Ci和Cj的边数;d表示建筑物间最短欧氏距离;F_sim(Ci, Cj)表示簇间的功能相似度。假设将边界点bpi从其原有隶属簇Ci中移除,同时将bpi与其相邻簇Cj合并,变化后的Ci、Cj分别记为C′i、C′j。对于簇间差异度变化值gain=diff(Ci, Cj)-diff(C′i, C′j):若gain < 0,则认为边界点的重新分配使簇间差异增大,即重分配后的划分结果更合理,接受该分配;否则,拒绝该重分配。此外,若边界点与多个簇邻接,通过循环分析选取最优重分配;若边界点为孤立点,当diff(Ci, Cj)小于给定阈值ε时,将该建筑物并入邻接簇。采用该重分配原则对所有边界点进行循环判别分析,直至建筑物聚类结果稳定时优化过程结束。
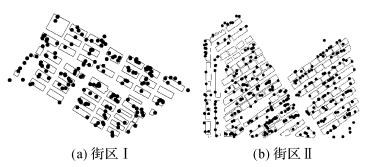
3 试验分析 3.1 试验1 3.1.1 试验数据为验证本文方法在保持功能语义特征相似性方面的合理性和有效性,将本文方法与顾及建筑物空间距离的方法(简称空间距离法)[4]以及同时顾及空间距离和几何形态的方法(简称空间-几何耦合法)[3]进行对比分析。采用深圳市两个街区的建筑物数据和兴趣点分布数据进行试验分析。其中,建筑物轮廓数据来自2018年的1:2000比例尺的地形图;兴趣点数据提取自2018年高德地图。两个街区的建筑物群以及兴趣点的空间分布如图 4所示,其中街区Ⅰ包含48个建筑物和281个兴趣点,街区Ⅱ包含115个建筑物和346个兴趣点。两个街区内的兴趣点分布广泛,可以满足街区内建筑物的功能语义特征提取需要。
|
| 图 4 街区建筑物与POI分布 Fig. 4 Spatial distributions of buildings and POIs in the two blocks |
根据高德地图POI分类编码(https://lbs.amap.com/api/webservice/download),对研究区内POI点进行分类,主要分为住宅、住宿、政府、医疗、休闲、生活、科技文化、金融、购物、企业、餐饮等11种类型。通过计算POI到各建筑物的最短距离,将各POI依据一定容差距离与建筑物进行匹配,由于POI数据和建筑物轮廓数据均存在误差,将POI与建筑物匹配时,可能会出现两种错误:①POI实际不在建筑物中,但错误地将两者匹配;②POI实际在建筑物中,但错误地认为两者不匹配。因而需要确定一个容差距离,使得在匹配后出现这两种错误的概率最小。对于这个问题,可以使用统计分析或专家经验法来确定此容差距离。这里取容差距离为5 m,如果POI到所有建筑物的最短距离大于5 m,则将该POI剔除。如果存在未匹配到POI的建筑物,则根据越邻近越相似准则,考虑建筑物周围其他建筑物的功能语义特征,采取中位数的方式对该无POI匹配的建筑物的功能语义特征进行估计。
将建筑物功能语义特征描述为11维的特征向量,为了对建筑物语义功能类型进行直观地可视化,首先采用k-means算法对所有建筑物的功能向量进行聚类。选择最合适的聚类数为6(即将试验数据中所有建筑物依据功能向量进行聚类后分为6大类,每一类表示功能属性相似的建筑物,同类建筑物的功能差异较小,不同类的建筑物功能差异较大)。据此,将建筑物的功能类型分为6大类,同类建筑物之间的POI类型占比差异较小:第1类建筑物的POI分布主要为生活服务和公司企业;第2类建筑物的POI分布主要为住宅和公司企业;第3类建筑物的POI分布主要为公司企业;第4类建筑物的POI分布中主要为政府机构及社会团体;第5类建筑物的POI分布主要为医疗服务;第6类建筑物的POI分布相对均匀、混合度较高。由此可见,公司企业类POI在这两个街区中分布比较多。考虑到本文旨在研究建筑物的空间分布模式,给建筑物分类只是为了体现建筑物间功能语义特征的相对差异,以体现所划分的建筑物群内部功能的差异,因而不讨论各类建筑物的具体类别。
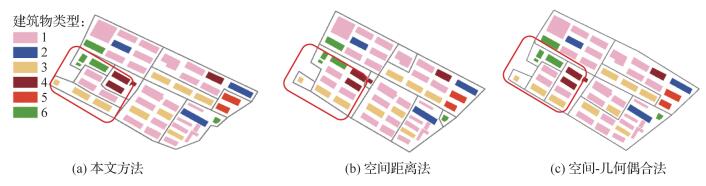
3.1.2 试验结果试验中,本文方法的λ1、λ2和λ3参数均设置为0.5;对于空间距离法,其聚类参数距离阈值设为1 m,p1和p2分别设为1.2和2[4];对于空间-几何耦合法的参数设置,根据文献[3]将距离、连接、大小和形状的权重分别设为0.4、0.05、0.5和0.05,相似性阈值设为0.7。图 5、图 6为两个街区建筑物空间分布模式(聚簇结构)的识别结果。对比可以发现,空间距离法和空间-几何耦合法仅满足建筑物空间位置和几何形状的约束,无法划分类似图 5圈出的整齐排布但功能不同的区域,且会多余地分割类似图 6圈出的空间距离相对较大但功能一致的区域。本文方法在顾及空间位置约束的情况下,尽可能地保持了建筑物群内部功能的一致性。
|
| 图 5 街区Ⅰ的聚集模式识别结果 Fig. 5 Recognition results of buildings in Block Ⅰ by the three methods |

|
| 图 6 街区Ⅱ的聚集模式识别结果 Fig. 6 Recognition results of buildings in Block Ⅱ by the three methods |
为了定量分析不同建筑物聚类算法的聚类结果质量,本文采用聚类分析中常用的一种相对评价指标(即轮廓系数)对3种方法的聚类结果进行定量评价[3]。轮廓系数表达为
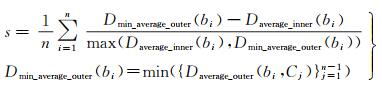 (4)
(4)
式中,n为建筑物数目;Daverage_inner(bi)表示建筑物bi与簇内其他建筑物间距离平均值;针对不包含bi的簇Cj,Daverage_outer(bi, Cj)表示bi与Cj内建筑物间距离平均值;Dmin_average_outer(bi)表示bi与所有不包含bi的簇间距离的最小值。Daverage_inner(bi)和Dmin_average_outer(bi)的作用是对聚类结果的簇内凝聚度和簇间分离度进行量化。轮廓系数越大,表明簇内建筑物越相似且簇间建筑物差异越大,即聚类结果越合理。
为分析空间关系、几何形态和功能类型对建筑物聚类识别结果的影响,将分别从以下3个角度定义建筑物间距离,具体描述为:
(1) 空间欧氏距离:D1=d,其中d为建筑物间最短欧氏距离。
(2) 融合空间关系和几何形态的距离:D2=Cs·Co·d,其中Cs和Co分别表示建筑物面积和主方向差异绝对值[5]。
(3) 融合空间关系和功能类型的距离:D3=(1-F_sim(bi, bj))·d,其中F_sim(bi, bj)为建筑物间的功能相似性。
将距离分别表示为D1、D2和D3,从3个角度计算聚类结果的轮廓系数,结果列于表 1。本文方法与现有方法相比:①如果仅从空间关系角度评价,本文方法的聚类效果略低于空间距离法,因为本文方法聚类时加入了功能特征,所以存在过度分割的情况;②从空间关系和几何形态角度评价,空间-几何耦合法的聚类效果略微提升,但是3种方法的聚类效果差别不大;③从空间关系和功能类型角度评价,本文方法结果则明显优于其他两种方法(其他方法对街区Ⅰ的聚类轮廓系数不超过0.25,街区Ⅱ不超过0.1,而本文方法分别为0.33和0.22)。在识别建筑物的分布模式时,本文方法能够更好地保持建筑物群内部功能语义特征的相似性,一定程度上满足地图语义聚合的深层需求。
| 评价角度 | 采用方法 | (试验1)轮廓系数s | (试验2)轮廓系数s | ||
| 街区Ⅰ | 街区Ⅱ | A区(市中心) | B区(城郊) | ||
| 空间关系 | 空间距离法 | 0.25 | -0.05 | 0.11 | 0.34 |
| 空间-几何耦合法 | 0.16 | -0.10 | 0.7 | 0.26 | |
| 本文方法 | 0.17 | -0.11 | 0.5 | 0.31 | |
| 空间距离法 | 0.24 | -0.02 | 0.06 | 0.24 | |
| 空间关系-几何形态 | 空间-几何耦合法 | 0.22 | 0.05 | 0.09 | 0.27 |
| 本文方法 | 0.22 | -0.04 | 0.02 | 0.23 | |
| 空间距离法 | 0.21 | 0.01 | -0.05 | 0.13 | |
| 空间关系-功能类型 | 空间-几何耦合法 | 0.15 | -0.09 | -0.11 | 0.08 |
| 本文方法 | 0.33 | 0.22 | 0.16 | 0.26 | |
3.2 试验2 3.2.1 试验数据
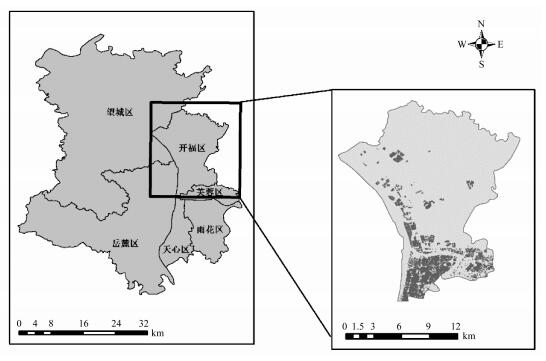
采用长沙市开福区作为试验区(图 7)进行试验分析,验证本文方法的适用性和有效性。其中,建筑物轮廓数据来自Open Street Map(OSM)上下载提取的建筑物,区域内共包含10 490个建筑物;兴趣点数据提取来自2018年高德地图,在研究区域内兴趣点分布较广泛。通过计算POI到各建筑物的最短距离,将各POI依据5 m误差与建筑物进行匹配,如果POI到所有建筑物的最短距离大于5 m,则将该POI剔除。对于未匹配到POI的建筑物,根据越邻近越相似准则,并考虑建筑物周围其他建筑物的功能语义特征,采取中位数的方式对该无POI匹配的建筑物的功能语义特征进行估计。
|
| 图 7 试验区域 Fig. 7 The study area |
具体地,根据高德地图POI分类编码将研究区内POI分为住宅、住宿、政府、医疗、休闲、生活、科技文化、金融、购物、企业、餐饮等11种类型,因而可将建筑物功能语义特征描述为11维的特征向量。为了对建筑物语义功能类型进行直观地可视化,采用k-means算法对所有建筑物的功能向量进行聚类。通过计算轮廓系数指标确定最合适的聚类数为5,将建筑物的功能类型分为5大类:第1类建筑物的POI分布主要为公司企业和金融服务,总体分布较平均;第2类建筑物的POI分布主要为公司企业和政府机构;第3类建筑物的POI分布主要为住宅和餐饮服务;第4类建筑物的POI分布中主要为购物;第5类建筑物的POI分布主要为住宅和购物。
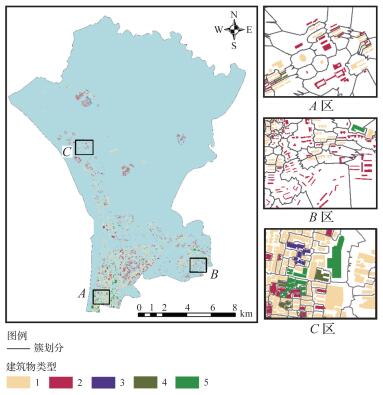
3.2.2 试验结果图 8为本文方法识别结果。其中,不同的建筑物聚类用黑色实线进行了分割。为了说明本文方法的有效性,分别选取了市中心(A)、城郊(B)和乡村(C)3个不同情境区域进行分析。
|
| 图 8 本文方法对研究区的聚集模式识别结果 Fig. 8 Recognition results of buildings in experimental area by the proposed methods |
(1) A区属于长沙市中心,其中建筑物分布较密集和紧凑,同时因为城市中心区域内建筑物的功能类型分布比较不均匀,有多功能类型建筑物的混合区域。通过本文方法可以发现这些功能混合的建筑物聚集区域,并将这些功能混合的建筑物进行剥离,形成功能类型相似的建筑物聚簇,使得建筑物聚簇内部保持一致的功能类型,有利于区分城市不同功能类型建筑物的空间分布特征。
(2) B区属于长沙市的城郊,建筑物的分布比市中心稍稀疏,同时城市郊区内的建筑物功能趋于均匀(如居住小区、工业园区等),局部区域的建筑物具有相一致的功能类型。从试验结果可以发现,本文方法很好地将这些建筑物在空间上较为整齐地划分为功能一致的建筑物群。
(3) C区属于长沙市区边缘的乡村,人口分布较少,建筑物分布稀疏,在村庄等区域会有较集中的建筑物分布。由于乡村的建筑物大多属于居住类型,建筑物空间位置邻近性是影响建筑物聚集效应认知的重要因素。从试验结果可以发现,本文方法对于建筑物功能类型较为单一的情形,仍然能够对建筑物进行较好地聚类。
进而,针对建筑物分布复杂的市中心、城郊区域,对比分析了空间距离法[4]、空间-几何偶合法[3]和本文方法识别建筑物聚簇的结果。其中空间距离法的参数设置为距离阈值设为1 m,p1和p2分别设为1.2和2[4];空间-几何耦合法的参数设置为距离、连接、大小和形状的权重分别设为0.4、0.05、0.5和0.05[3]。类似试验1,本文通过轮廓系数评价建筑物聚类结果质量见表 1。
可以发现:①对于区域A和B,当考虑建筑物聚簇内部的功能类型一致性时,本文方法结果优于其他方法,而单纯考虑空间关系、几何形态相似性时,本文方法聚类结果质量低于其他方法,主要原因在于本文方法聚类时加入了功能特征,相对而言存在一些过分割的情况;②在城市中心区域,建筑物分布紧凑、几何形状复杂和功能类型混杂,3种方法在识别A区(市中心)的建筑物分布模式时,轮廓系数都分别小于B区(城郊);③对于市中心的建筑物,功能分布复杂,然而本文方法顾及了功能特征,将在空间关系和几何形态评价上略差于现有方法,但在市区中,影响人们生活和出行更多的是建筑物的功能语义特征,本文方法在顾及功能类型的评价上远高于现有方法;④对于城郊的建筑物,功能较为单一,功能特征对聚类的影响减弱,导致本文方法在空间关系和几何形态评价上和现有方法相差不大。
4 结语空间特征和功能语义特征是人类认知建筑物聚群的两个重要特征。本文从人类认知角度出发,采用空间-语义分治策略,提出一种顾及空间邻近和功能语义相似双重约束的建筑物空间分布模式识别方法。首先,利用泛在POI数据识别与提取建筑物的功能语义特征;进而通过Delaunay三角网构建建筑物空间邻近关系,并依据建筑物间最短距离构建最小生成树聚类,形成建筑物的空间聚簇。在此基础上,考虑建筑物间的功能语义特征相似性,识别出空间邻近且功能语义特征相似的建筑物聚群。试验结果表明,本文方法识别的建筑物聚集模式符合人类对建筑物群的视觉认知和语义聚合结果。本文方法可应用于高层语义层次的建筑物多尺度聚合、分析与识别建筑物用地功能区域等。进一步的研究工作将主要集中在融合多源地理空间数据,实现建筑物群场景的智能理解与综合。
| [1] |
YAN Haowen, WEIBEL R, YANG Bisheng. A multi-parameter approach to automated building grouping and generalization[J]. Geoinformatica, 2008, 12(1): 73-89. DOI:10.1007/s10707-007-0020-5 |
| [2] |
程博艳, 刘强, 李小文. 一种建筑物群智能聚类法[J]. 测绘学报, 2013, 42(2): 290-294, 303. CHENG Boyan, LIU Qiang, LI Xiaowen. Intelligent building grouping using a self-organizing map[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 290-294, 303. |
| [3] |
WANG Wanyi, DU Shihong, GUO Zhou, et al. Polygonal clustering analysis using multilevel graph-partition[J]. Transactions in GIS, 2015, 19(5): 716-736. DOI:10.1111/tgis.12124 |
| [4] |
REGNAULD N. Contextual building typification in automated map generalization[J]. Algorithmica, 2001, 30(2): 312-333. DOI:10.1007/s00453-001-0008-8 |
| [5] |
艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报, 2007, 36(3): 302-308. AI Tinghua, GUO Renzhong. Polygon cluster pattern mining based on gestalt principles[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 302-308. DOI:10.3321/j.issn:1001-1595.2007.03.011 |
| [6] |
DENG Min, LIU Qiliang, CHENG Tao, et al. An adaptive spatial clustering algorithm based on delaunay triangulation[J]. Computers, Environment and Urban Systems, 2011, 35(4): 320-332. DOI:10.1016/j.compenvurbsys.2011.02.003 |
| [7] |
WEI Zhiwei, GUO Qingsheng, WANG Lin, et al. On the spatial distribution of buildings for map generalization[J]. Cartography and Geographic Information Science, 2018, 45(6): 539-555. DOI:10.1080/15230406.2018.1433068 |
| [8] |
ZHANG Xiang, AI Tinghua, STOTER J, et al. Building pattern recognition in topographic data: examples on collinear and curvilinear alignments[J]. GeoInformatica, 2013, 17(1): 1-33. |
| [9] |
ZHANG Xiang, AI Tinghua, STOTER J, et al. Characterization and detection of building patterns in cartographic data: two algorithms[C]//Proceedings of the 14th International Symposium on Spatial Data Handling. Berlin: Springer, 2012: 93-107.
|
| [10] |
LI Zhilin, YAN Haowen, AI Tinghua. Automated building generalization based on urban morphology and Gestalt theory[J]. International Journal of Geographical Information Science, 2004, 18(5): 513-534. DOI:10.1080/13658810410001702021 |
| [11] |
ZHANG Liqiang, DENG Hao, CHEN Dong, et al. A spatial cognition-based urban building clustering approach and its applications[J]. International Journal of Geographical Information Science, 2013, 27(4): 721-740. DOI:10.1080/13658816.2012.700518 |
| [12] |
DENG Min, TANG Jianbo, LIU Qiliang, et al. Recognizing building groups for generalization: a comparative study[J]. Cartography and Geographic Information Science, 2018, 45(3): 187-204. DOI:10.1080/15230406.2017.1302821 |
| [13] |
刘慧敏, 邓敏, 樊子德, 等. 地图上居民地空间信息的特征度量法[J]. 测绘学报, 2014, 43(10): 1092-1098. LIU Huimin, DENG Min, FAN Zide, et al. A characteristics-based approach to measuring spatial information content of the settlements in a map[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1092-1098. DOI:10.13485/j.cnki.11-2089.2014.0154 |
| [14] |
LI Zhilin. Algorithmic foundation of multi-scale spatial representation[M]. Boca Raton: Taylor & Francis Group, 2007: 122-125.
|
| [15] |
CHEN Yimin, LIU Xiaoping, LI Xia, et al. Delineating urban functional areas with building-level social media data: a dynamic time warping (DTW) distance based k-medoids method[J]. Landscape and Urban Planning, 2017, 160: 48-60. DOI:10.1016/j.landurbplan.2016.12.001 |
| [16] |
TSAI V J D. Delaunay triangulations in TIN creation: an overview and a linear-time algorithm[J]. International Journal of Geographical Information Systems, 1993, 7(6): 501-524. DOI:10.1080/02693799308901979 |
| [17] |
WU Bin, YU Bailang, WU Qiusheng, et al. An extended minimum spanning tree method for characterizing local urban patterns[J]. International Journal of Geographical Information Science, 2018, 32(3): 450-475. DOI:10.1080/13658816.2017.1384830 |
| [18] |
PRIM R C. Shortest connection networks and some generalizations[J]. The Bell System Technical Journal, 1957, 36(6): 1389-1401. DOI:10.1002/j.1538-7305.1957.tb01515.x |
| [19] |
DU Shihong, ZHANG Fangli, ZHANG Xiuyuan. Semantic classification of urban buildings combining VHR image and GIS data: an improved random forest approach[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 105: 107-119. DOI:10.1016/j.isprsjprs.2015.03.011 |
| [20] |
YUAN Jing, ZHENG Yu, XIE Xing. Discovering regions of different functions in a city using human mobility and POIs[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing: ACM, 2012: 186-194.
|
| [21] |
刘菊, 许珺, 蔡玲, 等. 基于出租车用户出行的功能区识别[J]. 地球信息科学学报, 2018, 20(11): 1550-1561. LIU Ju, XU Jun, CAI Lin, et al. Identifying functional regions based on the spatio-temporal pattern of taxi trajectories[J]. Journal of Geo-information Science, 2018, 20(11): 1550-1561. |
| [22] |
谷岩岩, 焦利民, 董婷, 等. 基于多源数据的城市功能区识别及相互作用分析[J]. 武汉大学学报(信息科学版), 2018, 43(7): 1113-1121. GU Yanyan, JIAO Limin, DONG Ting, et al. Spatial distribution and interaction analysis of urban functional areas based on multi-source data[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1113-1121. |
| [23] |
蒋云良, 董墨萱, 范婧, 等. 基于POI数据的城市功能区识别方法研究[J]. 浙江师范大学学报(自然科学版), 2017, 40(4): 398-405. JIANG Yunliang, DONG Moxuan, FAN Jing, et al. Research on identifying urban regions of different functions based on POI data[J]. Journal of Zhejiang Normal University (Natural Sciences), 2017, 40(4): 398-405. |
| [24] |
刘启亮, 邓敏, 石岩, 等. 一种基于多约束的空间聚类方法[J]. 测绘学报, 2011, 40(4): 509-516. LIU Qiliang, DENG Min, SHI Yan, et al. A novel spatial clustering method based on multi-constraints[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 509-516. |
| [25] |
刘启亮.自适应空间聚类方法研究[D].长沙: 中南大学, 2011. LIU Qiliang. A methodology of adaptive spatial clustering analysis[D]. Changsha: Central South University, 2011. |





