2. 93658部队, 北京 100061;
3. 北京航空航天大学自动化科学与电气工程学院, 北京 100191
2. Troops 93658, Beijing 100061, China;
3. School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China
地图投影是建立地球椭球面(或球面)与地图平面之间坐标映射关系的数学方法,作为地图中不可或缺的要素之一,地图投影在描述和研究地理以及地理信息相关问题与现象的过程中至关重要[1-4]。
按照可展曲面的不同,地图投影可以分为圆柱投影、圆锥投影、方位投影、伪圆柱投影、伪圆锥投影等不同类型[2, 5]。由于地球曲面的不可展性,在地图投影的过程中,会不可避免地发生变形。按照投影变形特征,地图投影可以分为等角投影、等积投影、等距投影等类型[2, 6]。
等角投影和等积投影是两类重要的地图投影方式。等角投影保持地图上各点在各方向的比例相同,即能够保留局部的形状;等积投影则保持地图要素的面积不变。不存在既等角又等积的地图投影[1]。
地图投影有其数学结构和计算上的复杂性[7],研究地图投影的变形是地图制图领域的关键问题之一[8]。考虑制图区域内的地图变形,将不可避免的变形控制在可以接受的范围之内,可以避免由于使用不恰当的地图投影导致变形量过大的问题,同时也能为地图的选择和设计提供依据[9-14]。与此同时,地图投影变形也是地球格网化剖分中的重要研究问题[15-20]。
底索指标(Tissot’s indicatrices)是一种直观的地图投影变形衡量方法。该方法将微分圆[21]变换到投影平面上,投影之后的微分(正)圆通常会变成长短轴不等的椭圆。底索椭圆能够反映地图投影的距离拉伸、面积变化、形状变化等多个特征[1],但底索椭圆只反映椭圆所在位置的变形,而不是地图投影全部位置的变形。此外,底索椭圆只能表示椭圆圆心位置无限小区域的地图投影变形,而不是整个椭圆区域的变形,即底索椭圆可能导致误读等问题的出现[22]。这些不足导致底索指标在应用上存在一定的局限性。
利用地图投影的微分性质能够研究地图投影的变形[23]。基于微分的方法依据地图投影正解公式的偏导数,计算得到长度、面积或形状变形系数[24]。微分指标是一种传统的方法,但该指标计算过程相对复杂(需要进行偏导数的计算),且要求被评估的地图投影具有连续可微的正解公式。对于直接球面剖分(direct spherical subdivision)方法,其构造是通过递归的方式进行的,不存在任意等级格网的通用构造公式,即不存在连续的地图投影公式。文献[25]给出的结果也表明直接球面剖分的互补比率均值指标并不连续,因此微分指标在使用中也存在应用受限的问题。面积变形系数也可以根据球面微圆的边界参数方程,对球面微圆所在区域进行数值积分求得[25],但计算过程也较复杂,且积分运算一般不存在统一的形式。
本文拟提出一种不依赖于微分或积分运算的大圆面积指标,用于计算地图投影的面积变形系数,同时在文献[25]中提出的小圆指标(即互补比率均值指标)基础上简化得到大圆形状指标,用于计算地图投影的形状变形系数。基于大圆面积指标和大圆形状指标,结合随机采样方法,本文将针对不同类型的地图投影,开展评估、比较和分析,验证指标的有效性,并分析地图投影的质量。分析结果表明,大圆指标能够有效降低小圆指标和微分指标的计算量,并能够有效地评估地图投影质量。
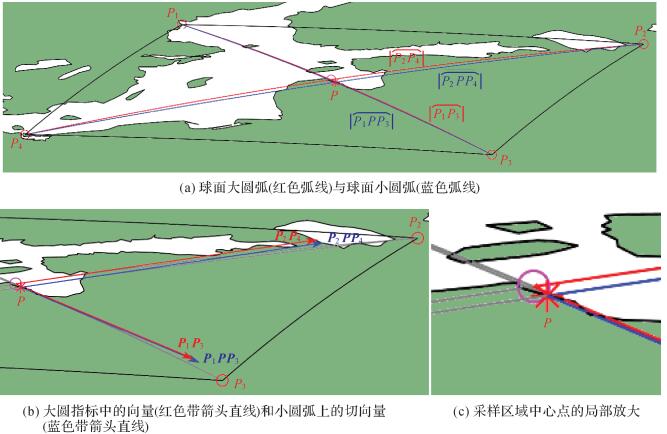
1 不依赖微分计算的地图变形指标 1.1 互补比率均值互补比率均值(averaged ratio between complementary profiles)[25]ρcs(文献[25]中以ρCP表示)是一种评价球面格网形状变形的方法,该指标由两项构成。为了区分小圆指标[25](带有上标s)与本文中的大圆意义下指标(带有上标g),本文中以ρcs表示文献[25]中的ρCP,其计算公式为
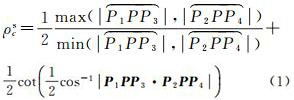 (1)
(1)
式中,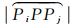

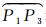

|
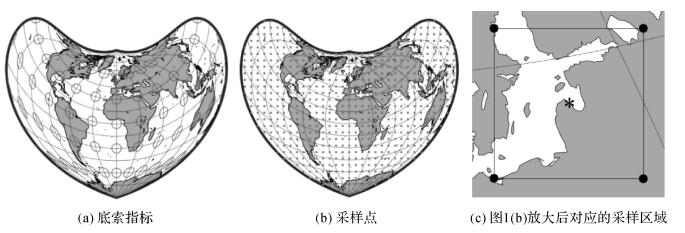
| 图 2 彭纳投影的底索指标和采样点 Fig. 2 Tissot's indicatrices of Bonne projection and sample points of Bonne projection |
小圆指标[25]需要计算两个球面小圆弧长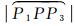
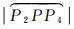
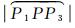
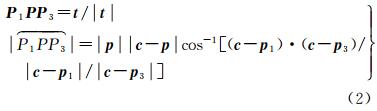 (2)
(2)
式中,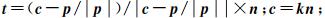
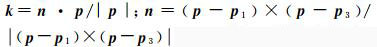
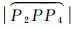
文献[25]利用互补比率均值,着重分析和比较了球面离散格网(而非地图投影)的质量。本文基于互补比率均值和球面大圆弧,适当地简化互补比率均值指标,同时提出一种不依赖于微分计算的面积变形指标(见1.2节),并检验形状变形指标和面积变形指标对评价地图质量的有效性。
1.2 基于大圆弧的形状变形指标与面积变形指标等角特征和等积特征是评估地图投影变形的两个独立的方面。本节将分别给出用于评估地图投影形状变形和面积变形的指标,关于两个指标的算例分析将在第2节中给出。
首先,本文针对文献[25]提出的小圆形状变形指标(式(1))进行简化,由式(3)给出球面大圆意义下的互补比率均值定义
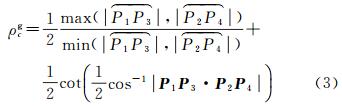 (3)
(3)
式中,
大圆指标需要计算两个球面大圆弧长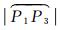
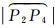
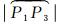
 (4)
(4)
对比式(2)与式(4),两指标中计算两次弧长和两次向量的开销列于表 1中。
| 指标 | 乘法运 算次数 |
除法运 算次数 |
点积运 算次数 |
叉积运 算次数 |
求模长 次数 |
三角函 数运算 次数 |
| 小圆指标 | 10 | 19 | 4 | 4 | 13 | 2 |
| 大圆指标 | 2 | 8 | 0 | 0 | 2 | 2 |
| 注:向量与标量相乘算做3次乘法运算;向量除以标量算做3次除法运算。 | ||||||
小圆形状变形指标的计算过程涉及较多的向量运算(点积、叉积、单位化等),而大圆形状变形指标运算过程相对简洁。根据表 1的结果,相较于小圆指标,大圆指标能够大大降低计算的复杂度。
本文以球面大圆弧长(或小圆弧长)和向量(或小圆上的切向量)为基础,进一步提出一种衡量面积变形的小圆面积变形指标ρsA和大圆面积变形指标ρgA。ρsA和ρgA的计算依赖于采样区域在球面上的面积As和Ag。关于采样区域的定义见第2节,As和Ag分别由式(5)和式(6)给出
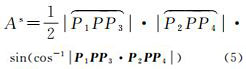 (5)
(5)
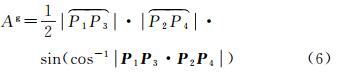 (6)
(6)
小圆面积变形指标ρsA和大圆面积变形指标ρgA的计算公式为
 (7)
(7)
 (8)
(8)
式中,S1表示单个采样区域在投影平面上的面积。由于采样区域为正方形,故S1=b2,b为采样区域边长。
本节给出的这些指标相比微分指标具有简捷的形式(见第2节算例分析中的比较)。此外,式(3)、式(4)、式(6)和式(8)采用大圆指标的形式,大圆指标相比小圆指标更为简捷。
2 地图投影变形的计算与分析算例 2.1 彭纳投影的投影公式本节以具体的地图投影(彭纳投影)为例,给出评估地图投影形状变形和面积变形的过程。彭纳投影是一种等积伪圆锥投影,其正解公式[24]为
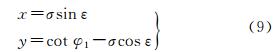 (9)
(9)
式中, σ和ε为中间变量, 其公式为
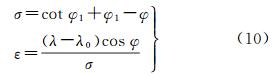 (10)
(10)
式中,φ表示纬度;λ表示经度;φ1为标准纬线;λ0为中央子午线。
彭纳投影的反解公式[24]为
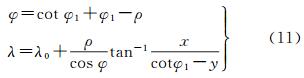 (11)
(11)
式中,中间变量
给定彭纳投影的正反解公式,本文取标准纬线为30°N(φ1=30°),中央子午线为本初子午线(λ0=0°)作为后续计算的条件。
对于等积投影,其底索指标为面积相同的(椭)圆,如图 2(a)所示。在标准纬线和中央子午线上,底索指标显示为大小相同的(正)圆,表明彭纳投影只在这些区域没有(形状和面积)变形。在其他位置,底索椭圆能够反映彭纳投影的形状变形。
2.2 大圆指标的计算为了使用小圆或大圆指标(见本节)以及微分指标(见2.3节)对彭纳投影的变形进行分析。首先应在地图投影平面上进行等间隔的采样,得到一系列的采样点,如图 2(b)所示,共有624个采样点。为了清晰地展示采样点,图 2中仅使用了较少数量的采样点。
给定采样点(图 2(c)中黑色圆点)后,将相邻的4个采样点所组成的正方形区域记为1个采样区域,(图 2(c)中正方形框)。对于每个采样区域,需要计算中心点(图 2(c)中心位置的黑色星号)的投影坐标。
为了后续计算过程在表述上的方便,记4个采样点或采样区域中心点的投影坐标为(xp, yp)(中心点坐标只在计算小圆指标时被使用),将(xp, yp)代入式(11),得到采样点或中心点的经纬度坐标(φp, λp),再根据式(12)将(φp, λp)转换到单位球面上,得到笛卡尔坐标(Xp, Yp, Zp)
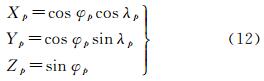 (12)
(12)
将采样点和中心点的笛卡尔坐标代入式(1)(或式(3))可得到形状变形指标,代入式(7)(或式(8))可得到面积变形指标,使用大圆指标(式(3)和式(8))无须计算中心点坐标。
2.3 微分指标的计算已知彭纳投影的正解公式(式(9)),分别对纬度φ和经度λ求偏导,得到式(13)
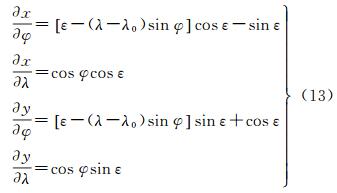 (13)
(13)
将每个投影区域中心点坐标的经纬度值(φp, λp)代入式(13),得到偏导数值,再将偏导数值代入式(14),得到a′和b′
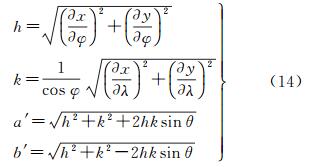 (14)
(14)
式中
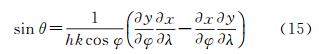 (15)
(15)
随后,由a′和b′的值可以计算出最大缩放系数a和到最小缩放系数b的数值(式(16))
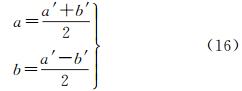 (16)
(16)
a与b的比值ρd=a/b表征点(φp, λp)位置的形状变形,a与b的乘积ρA=ab表征点(φp, λp)位置的面积变形。
根据本节的分析,微分方法计算相对复杂,且要求存在连续可微的投影变换公式。
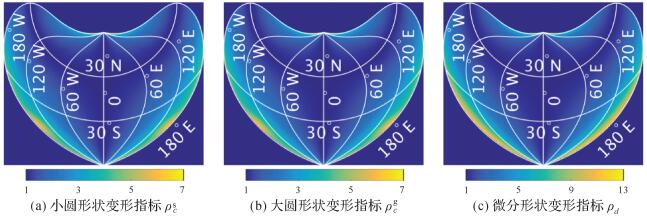
2.4 不依赖微分计算的指标与微分指标的比较按照不依赖微分计算的指标(ρcg和ρcs)和基于微分方法(ρd)得到的形状指标分布如3图所示,图中共计算了106个采样区域。图 3中的结果表明ρcg和ρcs有相近的分布,且在中央子午线和标准纬线附近,彭纳投影的变形程度较低,远离这些区域时,变形程度增加。该结果与按照底索指标给出的彭纳投影特征相符合。
|
| 图 3 彭纳投影的形状变形分布 Fig. 3 Distribution of shape distortions of Bonne projection |
为衡量ρcg与ρcs之间的一致性,本文采用皮尔森积矩相关系数PPMCC(x, y)计算两个变量x与y之间的相关性。PPMCC(x, y)=cov(x, y)/σx/σy,cov(x, y)表示x和y的协方差,σx和σy分别为x和y的标准差。PPMCC(x, y)是介于-1与1之间的值,PPMCC(x, y)=1表示x和y完全正相关,PPMCC(x, y)=-1表示x和y完全负相关,PPMCC(x, y)=0表示x和y不相关。
表 2中给出了在不同采样区域数目的条件下ρcs与ρcg的一致性结果。由表 2可知,随着采样点数目的增加,ρcs与ρcg的一致性随之提高,并向1收敛。因此,在采样点足够多的情况下,完全能够用ρcg替代ρcs替代。在下文中,不再计算小圆指标,所有分析和评估的过程均使用大圆指标。
| 采样区域数目 | PPMCC(ρsc, ρgc) |
| 102 | 0.998 920 27 |
| 103 | 0.999 871 23 |
| 104 | 0.999 948 89 |
| 105 | 0.999 995 80 |
| 106 | 0.999 999 34 |
接下来,需要定量衡量指标的ρcg与ρd之间的一致性。在106个采样区域的情况下,ρcg和ρd的范围分别为[1, 6.424 2]和[1, 12.217 1],给定ρcg的范围,分析对应的采样区域范围,得到ρcg与ρd之间的PPMCC值列于表 3中。
| ρcg的范围 | 采样区域的覆盖率/(%) | PPMCC(ρcg, ρd) |
| ρcg < 2 | 69.4 | 0.995 24 |
| ρcg < 4 | 95.5 | 0.992 59 |
| ρcg < 6 | 99.9 | 0.988 40 |
| ρcg < 8 | 100 | 0.988 48 |
由表 3可知,ρcg与ρd的一致性较高,尤其是在ρcg较小的采样区域,两者的一致性更好。因此,小圆或大圆指标能够较好地替代微分指标,衡量地图投影的形状变形。
接下来考虑彭纳投影的面积变形特性。由于彭纳投影是等积投影(没有面积变形),经过计算,其微分指标ρA≡1,这与等积投影的特性相符。进一步计算得到ρgA≈1。由于ρA≡1,若使用PPMCC指标分析ρgA与ρA的一致性,则会出现cov(ρgA, ρA)=0,σρA=0,此时PPMCC中分母为0,无法计算PPMCC的值。
为了能够定量衡量ρgA与1的接近程度,本文使用ρgA的均值μAg,用于衡量ρgA与1的接近程度,使用ρgA的变异系数χAg,用于衡量ρgA的分散(或集中)程度,式(17)给出了χAg的计算公式
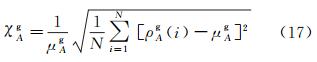 (17)
(17)
式中,N为采样区域数目。
经过计算,对于彭纳投影,本文提出ρgA的均值μAg=1.000 018 6,变异系数χAg=0.000 86,即对于彭纳投影,大圆面积指标与1之间的误差不超过0.02‰,其变异系数值不超过0.9‰。
本节使用大圆指标对彭纳投影进行了定量分析,通过比较,大圆变形指标与微分变形指标结果具有较好的一致性。为了更加全面地验证大圆指标的有效性,下文将利用该指标全面评估不同类型的地图投影。
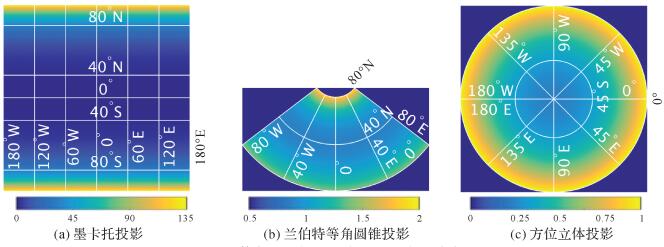
3 不同类型地图投影质量评估 3.1 等角地图投影的变形本节将评估3种等角地图投影——墨卡托投影(属于圆柱投影)、兰伯特等角圆锥投影(属于圆锥投影)和方位立体投影(属于方位投影)。由于在接近两极的区域,墨卡托投影存在较为严重的面积变形,且在通常情况下,墨卡托投影并不用来表示两极附近的区域,因此对于墨卡托投影,本文只评估纬度小于85°的区域。兰伯特等角圆锥投影取标准纬线为20°N和60°N,中央子午线为0°,评估范围为纬度介于0°与80°N之间,经度小于80°的区域。方位立体投影取南极点为中心点,评估范围是南半球区域。
对于上述3种等角投影,经过计算ρcs≡1,ρcg≡1,且ρd≡1。进一步分析,对于等角地图投影,任一点的ρcs、ρcg和ρd均为常数1。因此,使用ρcg能够很好地衡量等角地图投影的等角特性。
图 4中给出了3种等角投影的ρgA分布特性,若ρgA偏离1,表示存在面积变形。由于ρgA和ρA具有相近的分布特征,因此图 4中只给出了ρgA的分布。由图 4可知在高纬度区域,墨卡托投影存在较为严重的面积变形,兰伯特等角圆锥投影在靠近80°N的区域面积变形较大,方位立体投影在靠近南极的区域面积变形较大。
|
| 图 4 等角地图投影的大圆面积变形分布 Fig. 4 Distribution of great circle arcs based indicator of area distortions of some conformal map projections |
进一步计算ρgA与ρA的一致性,得到两者的PPMCC值列于表 4中。表中计算结果考虑了约106个采样区域(即使调整采样点间距,也只能使采样区域数目近似为106,但无法保证严格等于106)。
| 地图投影 | 采样区域数目 | PPMCC(ρgA, ρA) |
| 墨卡托投影 | 999 996 | 1注 |
| 兰伯特等角圆锥 | 1 000 000 | 1-1.11×10-16 |
| 方位立体投影 | 999 972 | 1注 |
| 注:在给定16位小数精度的情况下,结果为1。 | ||
根据表 4中的结果,对于3种等角地图投影,ρgA能够替代ρA衡量地图投影的面积变形特征。
3.2 等积地图投影的变形本节将对10种等积地图投影进行评价,包括3种圆柱投影(兰伯特圆柱投影、贝尔曼圆柱投影和高尔-彼得斯投影)、一种圆锥投影(阿尔伯斯投影)、一种方位投影(兰伯特等积方位投影)、一种改良的方位投影(汉麦尔-埃托夫投影)、两种伪圆柱投影(摩尔维特投影和正弦曲线投影)和两种伪圆锥投影(彭纳投影和Bottomley投影),其中,彭纳投影已在第2节进行了详细分析。3种圆柱投影的评估范围是纬度小于85°的区域。阿尔伯斯投影取标准纬线为20°N和60°N,中央子午线为0°,评估范围为纬度介于65°S与85°N之间,经度小于80°的区域。兰伯特等积方位投影取南极点为中心点,评估范围是南半球区域。其余5种投影的评估范围为全球。
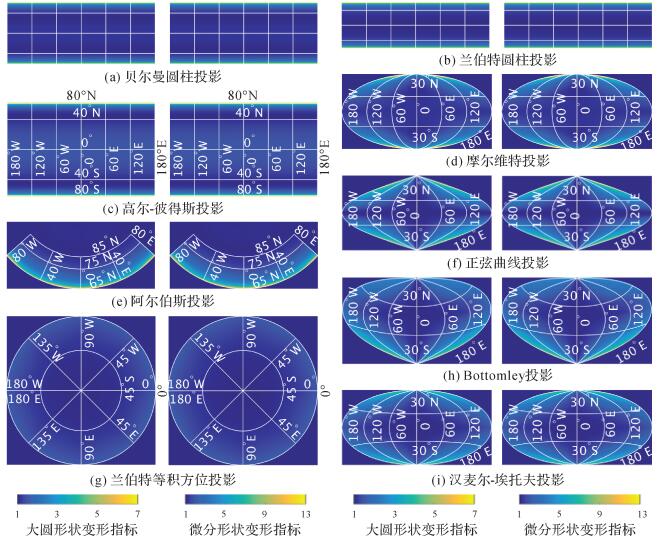
图 5给出了被评估等积投影的ρcg指标与ρd指标的分布情况,进一步计算得到形状变形指标之间的PPMCC值列于表 5中。图 5只对3种圆柱投影中的高尔-彼得斯投影进行了经纬度值的文字标注(经度线之间的间隔为60°,纬度线之间的间隔为40°),另外两种圆柱投影的经纬度间隔与之相同。
|
| 图 5 等积地图投影的形状变形分布 Fig. 5 Distribution of indicators of shape distortions for some equal-area map projections |
| 地图投影 | 采样区域数目 | PPMCC(ρgc, ρd) |
| 彭纳投影 | 1 000 000 | 0.988 48 |
| 兰伯特圆柱投影 | 999 236 | 1.000 00 |
| 贝尔曼圆柱投影 | 999 700 | 1.000 00 |
| 高尔-彼得斯投影 | 1 000 692 | 1.000 00 |
| 阿尔伯斯投影 | 999 998 | 0.991 15 |
| 兰伯特等积方位投影 | 999 972 | 0.992 04 |
| 摩尔维特投影 | 999 992 | 0.997 49 |
| 正弦曲线投影 | 1 000 004 | 0.996 41 |
| Bottomley投影 | 1 000 002 | 0.989 66 |
| 汉麦尔-埃托夫投影 | 999 992 | 0.997 68 |
根据图 5和表 5中的结果,ρcg与ρd具有相似的分布和较好的一致性(彭纳投影和Bottomley投影的PPMCC值大于0.988 4,阿尔伯斯投影和兰伯特等积方位投影的PPMCC值大于0.991 1,其余地图投影的PPMCC值均大于0.996 4)。
等积投影能够保持地图要素的面积不变,为了验证这一特征,接下来使用不同的面积变形指标对被评估的地图投影进行计算。经过计算,对于上述等积投影的ρA≡1,ρgA≈1。为了衡量本文提出的ρgA指标评估等积投影的有效性(与1的接近程度),分别计算ρgA的均值和变异系数,计算结果列于表 6中。
| 地图投影 | μgA | χgA |
| 彭纳投影 | 1.000 018 6 | 0.000 856 |
| 兰伯特圆柱投影 | 1.000 001 8 | 0.000 003 |
| 贝尔曼投影 | 1.000 001 6 | 0.000 003 |
| 高尔-彼得斯投影 | 1.000 001 5 | 0.000 003 |
| 阿尔伯斯投影 | 0.999 996 4 | 0.000 030 |
| 兰伯特等积方位投影 | 0.999 999 8 | < 0.000 001 |
| 摩尔维特投影 | 1.000 058 9 | 0.002 311 |
| 正弦曲线投影 | 1.000 034 0 | 0.001 218 |
| Bottomley投影 | 1.000 018 4 | 0.001 072 |
| 汉麦尔-埃托夫投影 | 1.000 004 6 | 0.000 417 |
表 6中的结果表明,ρgA的均值μAg与1之间的偏差小于0.06‰,ρgA的变异系数χAg小于3‰。由此可见,对于被评估的等积投影,ρgA能够较好地替代ρA衡量地图投影的面积变形特征。
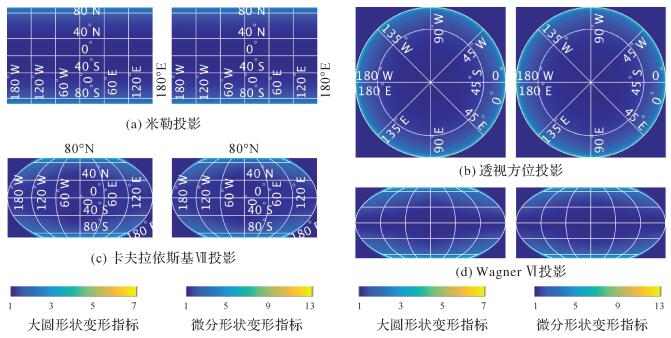
3.3 任意投影的变形本节将针对4种任意投影,分析其形状变形和面积变形特征,其中透视方位投影取南极点为中心点,评估范围是南半球区域。米勒投影(属于圆柱投影)和另外两种伪圆柱投影(卡夫拉依斯基Ⅶ投影和Wagner Ⅵ投影)虽然能够表示全球的范围,但这3种投影在高纬度区域,会存在较大的变形,因此对于这3种投影,只评估纬度小于85°的区域。
图 6和图 7给出了被评估任意地图投影的ρcg分布和ρgA分布,图中的卡夫拉依斯基Ⅶ投影和Wagner Ⅵ投影的经纬度网格线具有相同的间隔(经度线之间的间隔为60°,纬度线之间的间隔为40°)。
|
| 图 6 任意地图投影的形状变形分布 Fig. 6 Distribution of indicators of shape distortions for some arbitrary map projections |

|
| 图 7 任意地图投影的面积变形分布 Fig. 7 Distribution of indicators of area distortions for some arbitrary map projections |
为验证任意地图投影的形状变形指标和面积变形指标的有效性,表 7给出了大圆指标与微分指标的PPMCC值。根据表 7中的结果,对于被评估的任意地图投影,ρgA能够替代ρA衡量地图投影的面积变形(PPMCC值大于1-5×10-7),ρcg也能够在一定程度上较好地表征地图投影的形状变形(PPMCC值大于0.988)。
| 地图投影 | 采样区域 数目 |
PPMCC (ρgc, ρd) |
PPMCC (ρgA, ρA) |
| 米勒投影 | 1 000 384 | 1-6.3×10-13 | 1-2.0×10-12 |
| 透视方位投影 | 999 972 | 0.988 03 | 1-4.8×10-7 |
| 卡夫拉依斯基Ⅶ投影 | 999 996 | 0.996 96 | 1-1.3×10-10 |
| Wagner Ⅵ投影 | 1 000 268 | 0.997 46 | 1-1.8×10-10 |
3.4 地图投影变形指标质量评估小结
根据本节对不同地图投影变形指标的计算结果,大圆形状变形指标ρcg以及大圆面积变形指标ρgA与微分指标之间(ρd或ρA)的一致性结果如下:对于等角投影(见3.1节),ρcg≡1;对于等积投影(见3.2节),ρgA的均值和ρA的均值之间的偏差小于0.06‰;对于非等角投影(见3.2节和3.3节),PPMCC(ρcg, ρd)>0.988;对于非等积投影(见3.1节和3.3节),PPMCC(ρgA, ρA)>1-5×10-7。
4 地图投影变形指标的回归分析第3.1节至3.3节的计算过程是针对每种地图投影单独进行的,本节将综合考虑多个不同的地图投影,进行回归分析,并计算回归误差。对于ρcg和ρgA,线性回归应具有式(18)给出的形式。
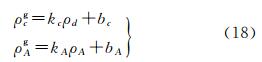 (18)
(18)
针对第3.2节给出的等积投影和第3.3节给出的任意地图投影,采用最小二乘法计算得到的回归系数为kcg=0.423 932 79,bcg=0.757 870 25。针对第3.1节给出的等角投影和第3.3节给出的任意地图投影,采用最小二乘法计算得到的回归系数为kAg=0.995 586 25,bAg=0.185 500 11。
按照上述给定的回归系数及其近似值(kc=0.42,bc=0.76,kA=1,bA=0.18),由ρd和ρA值计算得到ρcg和ρgA值与实际的ρcg和ρgA之间的均方根误差列于表 8中。根据表 8中的结果,ρcg平均误差小于1.10‰,ρgA的平均误差小于1.08‰。由此可知,本文提出的指标与现有微分指标具有较好的线性关系,见式(19)
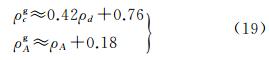 (19)
(19)
| 地图投影 | kc=kgc,bc=bgc | kc=0.42, |
kA=kgA,bA=bgA | kA=1,bA=0.18 |
| 墨卡托投影 | - | - | 0.000 162 4 | 0.000 180 0 |
| 兰伯特等角圆锥 | - | - | 0.000 180 8 | 0.000 180 0 |
| 方位立体投影 | - | - | 0.001 068 1 | 0.001 075 8 |
| 彭纳投影 | 0.000 155 0 | 0.000 153 7 | - | - |
| 兰伯特圆柱投影 | 0.000 181 8 | 0.000 180 0 | - | - |
| 贝尔曼圆柱投影 | 0.000 380 2 | 0.000 397 0 | - | - |
| 高尔-彼得斯投影 | 0.000 270 6 | 0.000 280 7 | - | - |
| 阿尔伯斯投影 | 0.000 160 3 | 0.000 160 4 | - | - |
| 兰伯特等积方位投影 | 0.001 097 6 | 0.001 090 0 | - | - |
| 摩尔维特投影 | 0.000 155 0 | 0.000 159 0 | - | - |
| 正弦曲线投影 | 0.000 109 3 | 0.000 110 0 | - | - |
| Bottomley投影 | 0.000 115 0 | 0.000 113 8 | - | - |
| 汉麦尔-埃托夫投影 | 0.000 112 9 | 0.000 115 1 | - | - |
| 米勒投影 | 0.000 151 3 | 0.000 148 7 | 0.000 165 6 | 0.000 180 0 |
| 透视方位投影 | 0.000 147 3 | 0.000 146 7 | 0.000 182 6 | 0.000 180 0 |
| 卡夫拉依斯基Ⅶ投影 | 0.000 119 7 | 0.000 118 6 | 0.000 179 7 | 0.000 180 0 |
| Wagner Ⅵ投影 | 0.000 119 9 | 0.000 120 0 | 0.000 178 8 | 0.000 180 0 |
5 地图投影变形指标的随机采样方法
上文给出的变形指标计算过程使用完全采样方法,该过程在投影平面上等间隔地划分采样区域并计算变形指标。本节将在两个坐标维度上,使用随机采样方法,评估地图投影的变形。
蒙特卡罗[26-27]是一类随机方法的统称,在模拟运算、近似求解、误差分析等问题中有着广泛的应用。本文给出的随机采样方法首先在单位球面上随机生成近似均匀分布的采样点(记采样点数目为ts),并使用投影正解公式将球面采样点投影到投影平面,然后在投影平面上以采样点为中心建立正方形的投影区域。记正方形的边长为ds,则式(7)和式(8)中的S1=ds2,并将投影区域的4个顶点按照投影反解公式转换到单位球面上,最后根据式(3)、式(4)、式(6)和式(8)计算变形指标。
由于不同地图投影的投影区域不同,使用完全采样方法需要在投影平面针对每种地图投影进行采样,而随机采样方法只需在球面进行采样,能够避免完全采样方法中采样点不统一和采样过程烦琐等问题。
图 8给出了3.3节中3种任意地图投影ρcg指标和ρgA指标的二维分布情况(取ds=2×10-6)。图中椭圆表示对应地图投影大圆变形指标的90%置信区域,3种地图投影的评估范围是纬度小于85°的区域,这与上文内容保持一致,纬度小于85°的区域覆盖了球面上的绝大部分(超过99.6%),只评估小于85°的区域不会对本节评估的结果和结论带来显著的影响。

|
| 图 8 不同采样次数的条件下3种任意地图投影的变形特征 Fig. 8 Distortions characteristic of three arbitrary map projections under different numbers of samples |
对于每种地图投影和给定的采样随机采样点数目ts(从103个到105个),图 8均显示了10次计算过程的90%置信椭圆。图 8(a)由于采样次数(103)较少,10次计算得到置信椭圆的位置存在一定的偏差,随着采样次数的增加,10次计算得到置信椭圆趋于一致,图 8(c)中的10条置信椭圆重叠度最高。
根据上述分析结果,使用随机采样方法能够使用较少的采样点较好地表征地图投影的失真特征,且结果表明使用约105个随机采样点即能够有效分析地图投影的变形情况。
6 结论本文提出了一种基于球面大圆弧的地图投影(大圆)面积变形指标,并在互补比率均值的基础上改进得到了地图投影(大圆)形状变形指标。提出和改进的指标与现有的微分指标一致,也与互补比率均值(即小圆指标)一致,但所提出的指标不依赖于微分计算,也不要求地图投影具有连续可微的投影正解公式,且具有较低的计算复杂度。通过回归分析,本文提出的指标与现有微分指标具有较好的线性关系。最后,本文给出了采用随机采样方法进行地图投影质量评估的计算过程,该过程能够有效地降低采样点的数量,使用约105个随机采样点即能够有效分析地图投影的变形情况。
| [1] |
JENSEN J R, JENSEN R R. Introductory geographic information systems[M]. New York: Pearson Press, 2012.
|
| [2] |
孙达, 蒲英霞. 地图投影[M]. 2版. 南京: 南京大学出版社, 2012. SUN Da, PU Yingxia. Map projections[M]. 2nd ed. Nanjing: Nanjing University Press, 2012. |
| [3] |
万刚, 曹雪峰. 地理空间信息网格的历史演变与思考[J]. 测绘学报, 2016, 45(S1): 15-22. WAN Gang, CAO Xuefeng. The historical evolution and reflection of geospatial information grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 15-22. DOI:10.11947/j.AGCS.2016.F002 |
| [4] |
李志林, 刘启亮, 高培超. 地图信息论:从狭义到广义的发展回顾[J]. 测绘学报, 2016, 45(7): 757-767. LI Zhilin, LIU Qiliang, GAO Peichao. Entropy-based cartographic communication models:evolution from special to general cartographic information theory[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 757-767. DOI:10.11947/j.AGCS.2016.20160235 |
| [5] |
钟业勋, 边少锋, 刘佳奇, 等. 地图投影经纬网构形规律研究[J]. 测绘科学, 2019, 44(2): 12-17. ZHONG Yexun, BIAN Shaofeng, LIU Jiaqi, et al. Research on configuration of meridian and latitude network in map projection[J]. Science of Surveying and Mapping, 2019, 44(2): 12-17. |
| [6] |
马廷刚, 田庆丰, 高晨. 地图投影变换浅析[J]. 测绘与空间地理信息, 2013, 36(10): 266-269. MA Tinggang, TIAN Qingfeng, GAO Chen. Analysis of map projection transformation[J]. Geomatics & Spatial Information Technology, 2013, 36(10): 266-269. |
| [7] |
边少锋, 李厚朴, 李忠美. 地图投影计算机代数分析研究进展[J]. 测绘学报, 2017, 46(10): 1557-1569. BIAN Shaofeng, LI Houpu, LI Zhongmei. Research progress in mathematical analysis of map projection by computer algebra[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1557-1569. DOI:10.11947/j.AGCS.2017.20170396 |
| [8] |
施一民, 朱紫阳, 陈月梅. 减小长度投影变形的一种地图投影新方法[J]. 同济大学学报(自然科学版), 2007, 35(3): 418-421. SHI Yimin, ZHU Ziyang, CHEN Yuemei. A new method of map projection to decrease projection distortion[J]. Journal of Tongji University(Natural Science), 2007, 35(3): 418-421. |
| [9] |
杨晓梅, 杨启和, 赵琦. 一类新的变比例尺地图投影——组合投影研究[J]. 武汉测绘科技大学学报, 1998, 24(2): 162-165. YANG Xiaomei, YANG Qihe, ZHAO Qi. A new kind of variable-scale map projection:research on composite projection[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 24(2): 162-165. |
| [10] |
CANTERS F. Small-scale map projection design[M]. New York: CRC Press, 2002.
|
| [11] |
陈占龙, 周林, 龚希, 等. 小比例尺地图投影设计方法研究[J]. 测绘科学, 2015, 40(11): 13-18. CHEN Zhanlong, ZHOU Lin, GONG Xi, et al. A design method of small-scale map projection[J]. Science of Surveying and Mapping, 2015, 40(11): 13-18. |
| [12] |
JENNY B, ŠAVRIČ B. Enhancing adaptive composite map projections:Wagner transformation between the Lambert azimuthal and the transverse cylindrical equal-area projections[J]. Cartography and Geographic Information Science, 2018, 45(5): 456-463. |
| [13] |
赵虎, 李霖, 龚健雅. 通用地图投影选择研究[J]. 武汉大学学报(信息科学版), 2010, 35(2): 244-247. ZHAO Hu, LI Lin, GONG Jianya. Universal map projection selection[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 244-247. |
| [14] |
徐立, 孙群, 徐明世, 等. 一种基于信息层次的地图投影选择方法[J]. 测绘工程, 2019, 28(2): 41-44, 51. XU Li, SUN Qun, XU Mingshi, et al. A method of map projection selection based on information levels[J]. Engineering of Surveying and Mapping, 2019, 28(2): 41-44, 51. |
| [15] |
周成虎, 欧阳, 马廷. 地理格网模型研究进展[J]. 地理科学进展, 2009, 28(5): 657-662. ZHOU Chenghu, OU Yang, MA Ting. Progresses of geographical grid systems researches[J]. Progress in Geography, 2009, 28(5): 657-662. |
| [16] |
赵学胜, 贲进, 孙文彬, 等. 地球剖分格网研究进展综述[J]. 测绘学报, 2016, 45(S1): 1-14. ZHAO Xuesheng, BEN Jin, SUN Wenbin, et al. Overview of the research progress in the Earth tessellation grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 1-14. DOI:10.11947/j.AGCS.2016.F001 |
| [17] |
胡海, 游涟, 宋丽丽, 等. 地球格网化剖分及其度量问题[J]. 测绘学报, 2016, 45(S1): 56-65. HU Hai, YOU Lian, SONG Lili, et al. Some metric problems on the global grid systems[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 56-65. DOI:10.11947/j.AGCS.2016.F007 |
| [18] |
吴立新, 余接情. 基于球体退化八叉树的全球三维网格与变形特征[J]. 地理与地理信息科学, 2009, 25(1): 1-4. WU Lixin, YU Jieqing. Global 3D-grid based on sphere degenerated octree and its distortion features[J]. Geography and Geo-Information Science, 2009, 25(1): 1-4. |
| [19] |
赵学胜, 苑争一, 赵龙飞, 等. 一种改进的近似等面积QTM剖分模型[J]. 测绘学报, 2016, 45(1): 112-118. ZHAO Xuesheng, YUAN Zhengyi, ZHAO Longfei, et al. An improved QTM subdivision model with approximate equal-area[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 112-118. DOI:10.11947/j.AGCS.2016.20140598 |
| [20] |
袁文, 庄大方, 袁武, 等. 基于等角比例投影的球面三角四叉树剖分模型[J]. 遥感学报, 2009, 13(1): 103-111. YUAN Wen, ZHUANG Dafang, YUAN Wu, et al. Some essential questions in remote sensing science and technology[J]. Journal of Remote Sensing, 2009, 13(1): 103-111. |
| [21] |
张国坤. 关于微分圆投影变成变形椭圆的分析与研究[J]. 测绘科学, 2004, 29(3): 14-15. ZHANG Guokun. The analysis and investigation of the little circle projecting into a deformed ellipse[J]. Science of Surveying and Mapping, 2004, 29(3): 14-15. |
| [22] |
MULCAHY K A, CLARKE K C. Symbolization of map projection distortion:a review[J]. Cartography and Geographic Information Science, 2001, 28(3): 167-182. |
| [23] |
任留成, 叶建栲, 赵琪. 利用算子微分研究投影变形理论[J]. 测绘学报, 1999, 28(1): 77-80. REN Liucheng, YE Jiankao, ZHAO Qi. Researching the theory of projection distortion by using the differential of operators[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 77-80. DOI:10.3321/j.issn:1001-1595.1999.01.015 |
| [24] |
SNYDER J P. Map projections:a working manual[M]. Washington, DC:U.S: Government Printing Office, 1987.
|
| [25] |
YAN Jin, SONG Xiao, GONG Guanghong. Averaged ratio between complementary profiles for evaluating shape distortions of map projections and spherical hierarchical tessellations[J]. Computers & Geosciences, 2016, 87: 41-55. |
| [26] |
王乐洋, 赵英文. 非线性平差精度评定的自适应蒙特卡罗法[J]. 武汉大学学报(信息科学版), 2019, 44(2): 206-213. WANG Leyang, ZHAO Yingwen. Adaptive Monte Carlo method for precision estimation of nonlinear adjustment[J]. Geomatics and Information Science of Wuhan University, 2019, 44(2): 206-213. |
| [27] |
WANG Leyang, ZOU Chuanyi. Accuracy analysis and applications of the sterling interpolation method for nonlinear function error propagation[J]. Measurement, 2019, 146: 55-64. |