2. 钱学森空间技术实验室, 北京 100094
2. Qian Xuesen Laboratory of Space Technology, Beijing 100094, China
激光雷达(light detection and ranging,LiDAR)[1-2]作为一种新兴的地球空间信息观测手段,其发射的激光脉冲能穿透植被直达地面,直接获得被观测对象的三维坐标及强度信息,被广泛地应用于数字地面模型、特征地物提取、三维建模等领域[3-5]。由于原始点云是由不同地形特征(地面、建筑物等)返回的大量离散点组合而成,并无语义信息或拓扑关联,因此在适用于上述应用之前,首先必须将地面和非地面点分离,这个过程称为点云滤波[3]。
在过去的20年里,学者们提出了很多经典的滤波算法[6-7]。基于滤波策略的不同,可以主要分为基于坡度滤波[8-9]、插值法滤波[10-16]、数学形态学滤波[17-19]和聚类分割法滤波[20-21]。文献[22]对8种滤波算法的性能进行了试验比较,其中基于插值法的不规则三角网(triangular irregular network,TIN[23])渐进加密算法[10](progressive TIN densification,PTD)性能最好,对于各种地形均有良好表现,但其在边界和地形复杂区域容易过度侵蚀地面;并且对极低异常值十分敏感,容易将低位地物点与极低异常值误判为地面点。针对以上问题,文献[21]选择法向量和残差作为依据进行点云分割,完善了初始TIN的构建,结合传统PTD方法进行滤波,有效抑制了地面侵蚀问题。文献[24]将数学形态学方法与PTD方法相结合,首先使用形态学中的开运算获得候选种子点,然后利用法向量和残差属性去除其中的非地面噪点,获取最终种子点,最后使用PTD滤波去除植被并保存地形细节。
然而,地形地物往往是尺度多样的,上文所描述的大多数算法仅仅在单一尺度下构建TIN,不能在保留地形细节和去除地物之间达成平衡,于复杂地形下难以获得理想的地面模型。为了增强PTD算法的滤波性能,本文提出了一种基于动态阈值的多尺度滤波方法:使用点云金字塔策略,在PTD滤波的基础之上,通过引入虚拟种子点以及表面拟合区域生长算法,在迭代循环过程中逐渐恢复真实地表。
1 原理与步骤相比于传统算法,本文算法的提升主要集中在3个方面:①使用了数据金字塔策略,以不同尺寸的虚拟格网组织点云,构建点云金字塔,并与三角网迭代滤波相结合,逐层加密,不断逼近真实地面;②扩展虚拟格网,插值虚拟种子点,使TIN完全覆盖点云区域,可有效补充边界区域;③采取“向上”“向下”的区域生长策略,补全受侵蚀地形,完善地形细节。
1.1 滤波流程本文的滤波算法是一个迭代处理过程,经过预处理之后,对整个区域构建点云金字塔,整个迭代顺序是从金字塔最上层(格网尺寸最大)开始,以最上层的种子点构建初始三角网,不断对下一层种子点进行PTD滤波和区域生长,不断获得更高分辨率的地面点,迭代加密三角网,直到最底层(格网尺寸最小)或者满足结束条件。其主要步骤可以分解为:
(1) 数据预处理,仅保留由末次回波生成的点云,并通过半径滤波器去除异常值。
(2) 最大格网尺寸对应金字塔最上层,按照格网尺寸减半的原则,自上而下构建点云金字塔,在每一层的虚拟格网中选取最低点作为种子点,可获得最上层的初始地面种子点以及其他层面的未分类点。
(3) 以当前地面种子点构建TIN,对下层格网未分类点进行PTD滤波处理。
(4) 将PTD滤波得到的非地面点重新设置为未分类点,遍历所有未分类点,以基于动态阈值的区域生长算法进行生长,实时更新地面种子点。
(5) 若生长的点数大于总点数0.1%,返回步骤(4)。
(6) 若未到达点云金字塔底层,则返回步骤(3)。
(7) 滤波结束。
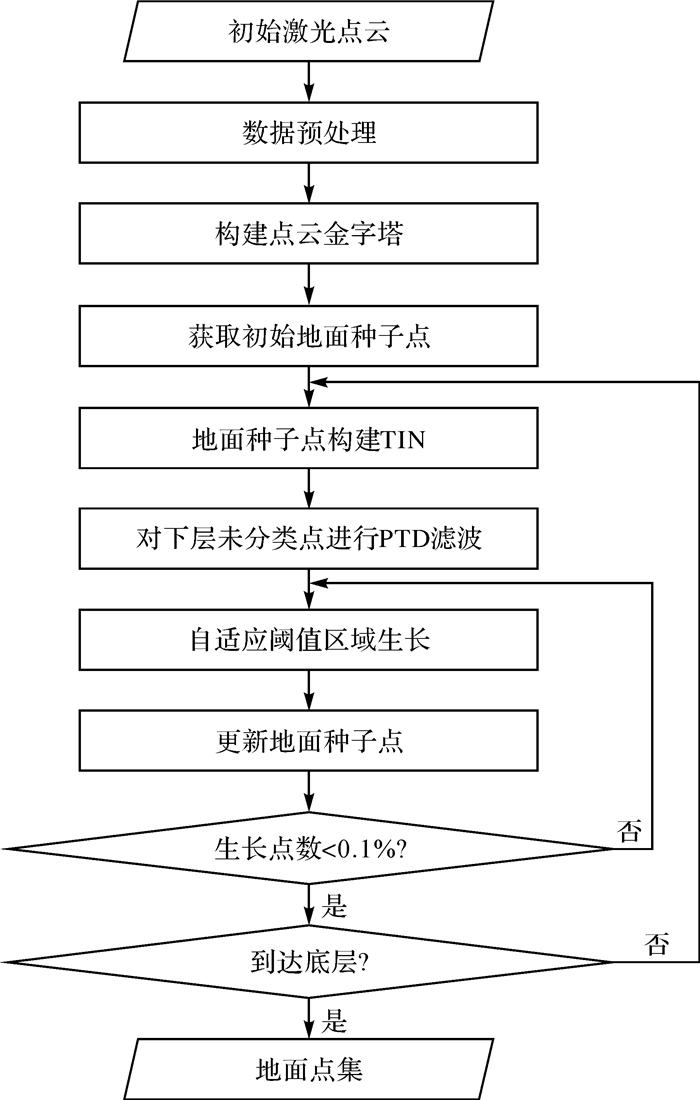
算法流程如图 1所示。
|
| 图 1 算法流程 Fig. 1 Flowchart of the algorithm |
1.2 去除异常值
LiDAR发射的激光脉冲具备一定穿透植被的能力,并且在照射至地物边缘时,依据光斑的照射位置,也可能产生多次回波,显然,只有末次回波才有可能反映地面的真实情况,因此,在进行滤波之前,首先去除非末次回波生成的点云。
由于多路径效应等干扰因素,LiDAR生成的点云数据往往会存在极低异常值,这些异常值通常数量较少,离散分布,且高程显著低于正常激光点。传统PTD中选择最大尺寸格网下的最低种子点构建初始TIN,极低异常值的存在使得初始TIN与真实地面差异巨大,造成局部滤波失败。基于异常值的特性,本文选取半径滤波器去除极低异常值,首先构建kd-tree[25]组织点云,遍历整个点云,搜索每个点在指定范围内的邻近点数,若邻近点数小于给定阈值,则判定为异常值并去除。
1.3 利用虚拟格网构建点云金字塔LiDAR点云数据包含大量拥有独立三维信息的离散点,将点云整合成有序的排列组合对于后续处理非常重要。文献[26]提出了虚拟格网的概念,其基本思想来自于图像处理中像素的概念,具体做法为:在XYZ三维空间中,将所有点云投影到XOY平面上,沿X、Y轴等距划分,将XOY平面分割成众多相同大小的正方形网格,这样点云中每个点对应一个网格,每个网格包含零或数个空间点。基于地面点往往低于非地面点的基本假设,选取格网内最低点作为种子点,以种子点来代表整个网格,形成由种子点构成的“像素”矩阵,其有序紧密的结构很方便进行邻域检索以及计算。为保证参与初次PTD滤波的种子点均为地面点,应保证初始格网尺寸大于点云中最大建筑物尺寸。在每一次迭代过程中,格网尺寸变为原本的1/2,重新构建的虚拟格网获得了更高的分辨率,显示出更加丰富的地形特征。随着格网尺寸不断变小,生成的虚拟格网分辨率也由低到高,组成了点云金字塔。
1.4 PTD滤波获得地面种子点之后,便可以进行PTD滤波,具体过程包括:
(1) 利用地面种子点构建TIN。
(2) 选择一个未分类点,寻找该点所在的三角形。
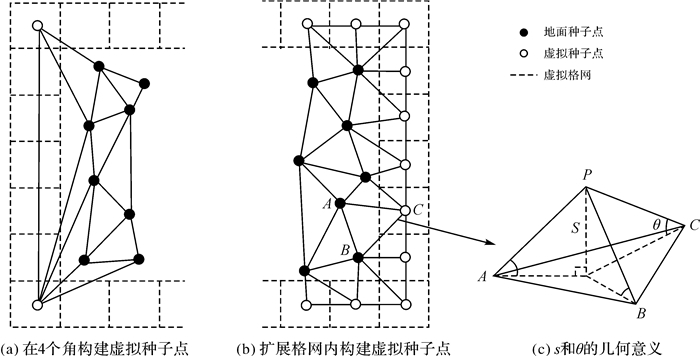
(3) 计算该点到三角形平面的距离s和该点与三角形3个角点的夹角,并选出最大角度θ,具体几何意义可参考图 2(c)。
|
| 图 2 设置虚拟种子点 Fig. 2 Illutration of the process of setting simulated seed points |
(4) 根据人工设置的最大距离阈值sthr和最大角度阈值θthr,若距离s小于sthr且夹角θ小于θthr,即满足式(1),则将该点加入地面点
 (1)
(1)
(5) 重复步骤(2)至步骤(4),直至所有未分类点都判别完毕。
然而在上述过程中会产生如下问题:受最大建筑尺寸影响,初始地面种子点往往十分稀疏,使得初始TIN无法完全覆盖整个点云区域,部分靠近边界的未分类点无法寻找到对应的三角形,从而导致边界区域成片缺失。文献[21]在点云测区的4个角添加模拟角点辅助构建TIN,如图 2(a)所示,这一定程度上解决了问题,但是在边界生成了狭长三角形,在模拟角点高程相差较大的情况下,极易将非地面点误判为地面点,并在迭代过程中不断造成误差累积。
本文针对以上问题对构建TIN的方式作出以下改进:对参与构网的种子点向外扩展延伸,具体做法如图 2(b)所示,大矩形内侧的虚线为原始点云的外边界,从4个边界各向外扩展一层新网格,扩展的虚拟网格与边界内的网格具有相同的尺寸,在每个扩展的网格中心内插一个虚拟种子点。其高程计算如下:搜索虚拟种子点的邻近格网,确定其中的地面种子点;假设地面种子点数为n(n≤3),地面种子点的高程为hi(i=1, 2,…, n),地面种子点与虚拟种子点的距离为di,di之和为d,幂p取2,可由式(2)反距离加权计算虚拟种子点的高程hs
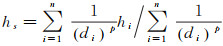 (2)
(2)
PTD算法可以有效地剔除非地面点,但地形凸包、陡坡等复杂地形在滤波过程中受到了过度侵蚀,使得部分地面点被误判为非地面点。如图 4(a)所示,由于P1、P2存在较大高差,造成三角面倾斜,此时地面点P3与三角面的角度明显超过阈值。针对此问题,本文对PTD的分类结果进行二次处理,提取已经获得的地面点,并将非地面点重新判定为未分类点,以基于表面拟合的区域生长算法再次分类。整个生长过程分为向下生长和向上生长两个阶段。
1.5.1 向下生长点云滤波中存在一个基本规律:同一片区域中,一个点的高程越低,那么它是地面点的可能性越大。本文采取点云金字塔组织数据,获取的种子点本身为网格内高程最低点,当网格尺寸较大时,一个网格可以覆盖更多地面,此时种子点中地面点占比极高,假设已知某种子点为未分类点P,若邻近网格中存在至少一个地面点P0,且P0的高程大于P,则基本可以判定P也是地面点,遵循此假设可快速准确地向下生长地形关键点。但在迭代过程中随着网格尺寸逐渐缩小,种子点中非地面点的比例升高,先前的假设在面对一些特殊地形,尤其在斜坡上存在低矮植被时,会出现过度生长的情况,例如samp51(图 3)。在图 3(b)所示生长过程中,未分类点P2(植被点)高程比邻近地面点P1高程低,基于之前的假设,此时P2被误判为地面点,造成二类误差。为抑制此类情况,根据地形的特性,观察图 3(c),在所示9个点中,除P2之外其余点均为地面点,P2高程低于P1、P4、P7,高于其余5个点,可以发现在过度生长的区域,非地面点在一定程度上会被高程更低的地面点包围。基于此判断,本文拓展出向下的生长策略:对未分类点周围的8个格网进行统计,确定其中的地面种子点,比较未分类点与地面种子点的高程,记高程大于未分类点的地面点数为nhigher,高程低于未分类点的地面点数为nlower,若满足式(3)则将未分类点加入地面点集
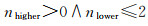 (3)
(3)

|
| 图 3 samp51地形图 Fig. 3 Topographic map of samp51 |
1.5.2 向上生长
PTD滤波的基本假设是当分辨率足够高时,局部地形可近似为一个平面。基于此假设,本文采用平面拟合的方式生长受侵蚀的地面种子点:利用已知的地面点,使用最小二乘法拟合平面,通过动态高差阈值对未分类点进行分类。在点云金字塔的单一层内,点云以虚拟格网形式排列,每个种子点仅有8个邻近点,因此在生长区域边界,未分类点的邻近地面种子点数普遍小于等于3,且分布于未分类点的同一侧。考虑到必须避免参与拟合的地面点排列近似一条直线的情况,本文将拟合的范围定为以未分类点为中心的5×5区块,在区块内已知地面种子点数大于等于6时,可进行平面拟合。
平面的方程可以写成如下形式
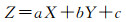 (4)
(4)
式中,(X, Y, Z)为点的三维坐标;a、b、c为平面参数。多点共面时,其矩阵形式可以写作
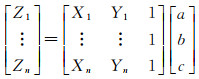 (5)
(5)
上面的乘积形式,即
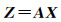 (6)
(6)
式中,Z为地面点高程的列向量;X为平面参数的列向量;A为式(5)对应的系数矩阵。
根据正规方程求解拟合参数,经过转化可得
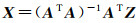 (7)
(7)
最终得到的X即为最小二乘解,代入式(4)即可获得所求平面。
根据笔者拟合出的平面,可以计算出未分类点与平面之间的距离d,通过与最大距离阈值dthr的对比可进行判断:d小于dthr的点为地面点,否则为非地面点。
对于平面拟合而言,大尺度时平面覆盖范围大,平面描述地形的能力较低,且非地面点与地面点可区分程度低,宜采用固定小阈值,本文采用PTD滤波时的最大距离阈值sthr;而随着覆盖范围逐渐减小,地形细节越来越丰富,非地面点与地面点可区分程度升高,此时单一阈值往往难以满足所有分类需求。为了更好地适应不同的地形,本文采取动态阈值设置方法,得到拟合的平面后,计算每个参与拟合的地面种子点到该平面的距离,经过统计可以获得均值dmean以及标准中误差dstd,采用正态分布模型,以2倍的中误差为波动范围计算动态阈值。本文选取网格尺寸l的经验值5 m作为算法阈值,动态阈值dthr计算如下
 (8)
(8)
因此,在整个循环迭代中,首先是大平面获得了生长,随着格网尺寸的减小,小范围拟合面逐渐趋于平坦,如图 4(b),凸包等复杂地形逐渐补全。然而上述方法遇到断裂线时,其表现往往不尽如人意,如图 4(c)所示,地形断裂造成地面的不连续现象,地面点P1、P2产生较大高差,使得拟合面与真实地面不符,断裂线边缘处地面点P3、P4超出阈值被误判为非地面点,因此滤波后往往会在断层处展现出“一刀切”的情况,即在一条直线上,地面点和非地面点分列两侧。针对此问题,本文借鉴梯度滤波的策略,补充以下判断法则:参考图 4(c),如存在至少相邻3个地面点(P1及周围地面点),他们与该未分类点的坡度保持平滑,可认为该分类点是地面点(P3),或者有一个陡峭(P2),但有至少两个坡度平滑的相邻地面点(P3和地面点周围点),也可以认为该点是地面点(P4)。具体计算如下:若d大于dthr,搜索该未分类点的八邻域,确定其中的地面点,计算该未分类点与这些地面点的坡度,并与PTD最大迭代角度θthr进行比较,统计坡度小于θthr的地面点数nflat和坡度大于θthr的地面点数nslope,则满足以下条件的点也被识别为地面点
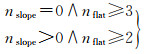 (9)
(9)
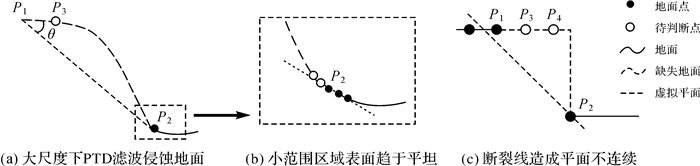
|
| 图 4 地形简图 Fig. 4 Simple demonstration of terrain |
2 试验结果及分析
为了客观评价本文算法的滤波性能,本文采用ISPRS委员会第3小组于2003年提供的基准数据集来进行检验。数据是从7个站点选定的共计15个参考样本,这些样本经过半自动滤波与目视判别修正,已将所有点精准的划分为地面点与非地面点。另外采用文献[22]提出的3个精度指标定量分析算法精度,其中包括Ⅰ类误差(地面点误分为非地面点)、II类误差(非地面点误分为地面点)和总误差(Ⅰ、Ⅱ类误差点数占总点数的比例),Ⅰ类误差反映算法保留地面点的性能,Ⅱ类误差反映算法去除非地面点的性能,总误差则整体反映算法的平衡性和实用性。同时本文还计算了Kappa系数[27],此系数可以对比参考数据与试验数据的一致性,是一种比简单百分比更稳健的测度。以上4个精度指标仅基于交叉矩阵中的4个输入(a、b、c、d)计算,其中a为实际地面点被正确分类为地面点的个数,b为实际地面点被误分类为非地面点的个数,c是实际非地面点被误分类为地面点的个数,d是实际非地面点被正确分类为非地面点的个数。各指标具体计算公式可见表 1。
| 点云总数 | Ⅰ类误差 | Ⅱ类误差 | 总误差 | Po | Pc | Kappa系数 |
| e=a+b+c+d | b/(a+b) | c/(c+d) | (b+c)/e | (a+d)/e | [(a+b)(a+c)+(c+d)(b+d)]/e2 | (Po-Pc)/(1-Pc) |
2.1 定性分析
为了定性评估算法在不同地形条件下的滤波性能,本文选取4个滤波结果(samp11,samp22,samp23,samp51)进行展示,如图 5—图 8所示。所选样本的具体地形特征可见表 2,可以看出滤波后地面与实际地面吻合度较高。从边界信息来看,无论是城区(图 6—图 7)亦或是山区(图 5、图 8),扩充虚拟种子点保证了边界的准确性和完整性,注意图 7左上角边界处的三角形Ⅰ类误差是由点云本身结构导致,由于本文算法选取最低点作为地面种子点,以此构建不规则三角网,因此会将点云边界处高程较高的断层判定为非地面结构,考虑到分割点云区域时可能会切割到房屋,因此本文认为判定为非地面结构是合理的选择。从Ⅱ类误差来看,算法可以有效滤除低矮植被(samp51)、房屋(samp23)、桥梁(samp22)等地物,并且从图 8可以看出,种子点生长算法能在有效生长地形的同时抑制斜坡植被点的生长。从Ⅰ类误差来看,图中并无因极低异常值造成的地面空洞,可验证半径滤波器的有效性,另外城区路面保留齐全,山地陡坡和断层边缘也相对完整。主要误差分布于断裂线附近(图 5与图 7矩形框处),在部分细微地形处也存在小范围Ⅰ类误差,其原因在于本文采取平面拟合的前提假设为点云有足够高的分辨率,而所有的测试集点云分辨率均大于1 m,在部分测试集中甚至达到了2~3 m,点云分辨率不足对于复杂地形的表达是十分不利的,因此当分辨率不足且存在非地面点干扰时,容易使得拟合所需邻近地面点的数目达不到要求,从而导致区域生长停滞不前,造成部分地形缺失。

|
| 图 5 samp11滤波结果 Fig. 5 Filter result of samp11 |

|
| 图 6 samp22滤波结果 Fig. 6 Filter result of samp22 |

|
| 图 7 samp23滤波结果 Fig. 7 Filter result of samp23 |

|
| 图 8 samp51滤波结果 Fig. 8 Filter result of samp51 |
| 样本集 | 地形特征 | 格网间距/m | 角度阈值 | 距离阈值/m | Ⅰ类误差/(%) | Ⅱ类误差/(%) | 总误差/(%) | Kappa/(%) |
| samp11 | 陡坡上的植被和建筑物 | 40 | 0.3 | 1 | 10.89 | 4.69 | 8.25 | 83.36 |
| samp12 | 小型物体(车辆) | 20 | 0.3 | 1.4 | 2.69 | 2.80 | 2.75 | 94.51 |
| samp21 | 狭窄的桥梁 | 20 | 0.25 | 1 | 0.40 | 3.41 | 1.06 | 96.89 |
| samp22 | 大桥(西南)/舷梯(东北) | 40 | 0.4 | 1.4 | 2.21 | 6.02 | 3.40 | 92.06 |
| samp23 | 复杂大型建筑,不连续地形 | 20 | 0.3 | 1.4 | 4.10 | 4.65 | 4.36 | 91.26 |
| samp24 | 坡道 | 25 | 0.25 | 1.4 | 1.82 | 8.41 | 3.63 | 90.82 |
| samp31 | 不连续地形, 极低异常值 | 30 | 0.1 | 1 | 0.69 | 1.16 | 0.90 | 98.19 |
| samp41 | 低点簇(多路径误差) | 30 | 0.3 | 1.4 | 4.07 | 2.84 | 3.46 | 93.11 |
| samp42 | 高低起伏的地物 | 35 | 0.3 | 1.4 | 0.77 | 0.64 | 0.68 | 98.38 |
| samp51 | 斜坡上低矮植被 | 30 | 0.15 | 1 | 1.04 | 4.44 | 1.78 | 94.78 |
| samp52 | 低矮植被、山脊断层 | 20 | 0.6 | 1.4 | 1.57 | 17.95 | 3.29 | 82.15 |
| samp53 | 断层 | 5 | 0.6 | 1.4 | 1.45 | 34.56 | 2.79 | 64.00 |
| samp54 | 低分辨率建筑 | 15 | 0.2 | 1.4 | 2.33 | 2.81 | 2.59 | 94.82 |
| samp61 | 陡峭山脊、沟渠 | 8 | 0.4 | 1.4 | 0.54 | 8.46 | 0.82 | 88.14 |
| samp71 | 大桥 | 40 | 0.3 | 1.4 | 1.04 | 8.25 | 1.85 | 90.78 |
| 平均值 | 2.40 | 3.67 | 2.84 | 93.74 |
2.2 定量分析
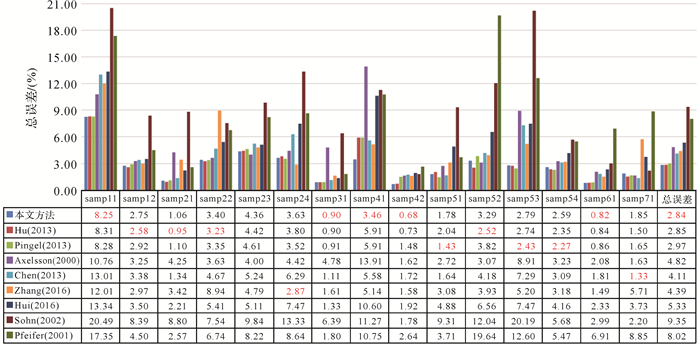
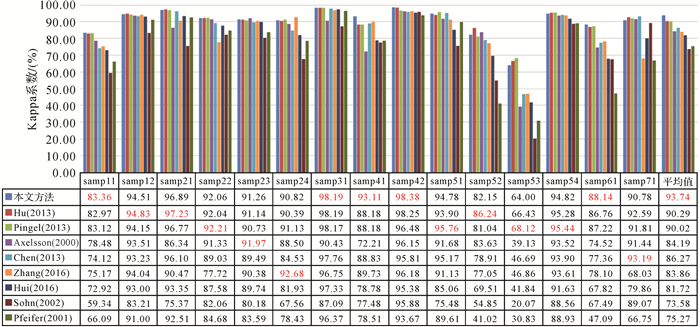
表 2显示了15个测区的地形特征和参数设置情况,同时列出了本文算法获得的各项误差指数以及Kappa系数。另外将本文算法与ISPRS测试中的部分经典算法以及近年来学者们提出的算法进行了对比,其中最低的总误差和最高的Kappa系数用红色加粗表示,具体数据如图 9—图 10所示。
|
| 图 9 不同算法的参考样本误差对比 Fig. 9 Comparison of total error for each reference sample with different algorithms |
|
| 图 10 不同算法的参考样本Kappa系数对比 Fig. 10 Comparison of Kappa coefficient for each reference sample with different algorithms |
从表 2可以看出,在单一样本的试验结果里,本文算法展现出了良好的滤波性能,可以有效地平衡Ⅰ、Ⅱ类误差。从图 9—图 10的数据对比可以看出,本文算法在其中5个样本获得了最好的滤波效果,并获得了所有统计样本下最小的总误差(2.84%)以及最大的Kappa系数(93.74%)。相对于传统PTD算法,本文算法虽然在生长地形时不可避免地增加了部分Ⅱ类误差,却有效降低Ⅰ类误差,使得整体精度获得了较大提升,最终总误差降低幅度41%,Kappa系数提高9.5%。
3 结 语针对传统的PTD滤波过程中过度侵蚀地面、Ⅱ类误差累积的问题,本文采用点云金字塔策略选取和组织地面种子点,在迭代的过程中,采用PTD算法去除非地面点,结合“向上”“向下”的表面拟合区域生长算法补全地形细节,有效地降低了Ⅰ类误差,根据计算拟合平面点的离散程度设置动态高差阈值,可以适应不同地形场景。通过ISPRS给出的15个标准数据集的测试,结果证明本文提出的方法是有效可行的。未来的研究将致力于开发更高效的区域生长算法,针对点云分辨率不足和断裂线部位缺失的问题进行研究,提高算法的性能和稳健性。
| [1] |
WEHR A, LOHR U. Airborne laser scanning-an introduction and overview[J]. ISPRS Journal of Photogram-metry and Remote Sensing, 1999, 54(2-3): 68-82. DOI:10.1016/S0924-2716(99)00011-8 |
| [2] |
张小红. 机载激光雷达测量技术理论与方法[M]. 武汉: 武汉大学出版社, 2007. ZHANG Xiaohong. Theory and method of airborne LiDAR measurement technology[M]. Wuhan: Wuhan University Press, 2007. |
| [3] |
黄先锋, 李卉, 王潇, 等. 机载LiDAR数据滤波方法评述[J]. 测绘学报, 2009, 38(5): 466-469. HUANG Xianfeng, LI Hui, WANG Xiao, et al. Filter algorithms of airborne LiDAR data:review and prospects[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 466-469. DOI:10.3321/j.issn:1001-1595.2009.05.014 |
| [4] |
杨必胜, 梁福逊, 黄荣刚. 三维激光扫描点云数据处理研究进展、挑战与趋势[J]. 测绘学报, 2017, 46(10): 1509-1516. YANG Bisheng, LIANG Fuxun, HUANG Ronggang. Progress, challenges and perspectives of 3D LiDAR point cloud processing[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1509-1516. DOI:10.11947/j.AGCS.2017.20170351 |
| [5] |
李德仁, 王艳军, 邵振峰. 新地理信息时代的信息化测绘[J]. 武汉大学学报(信息科学版), 2012, 3(1): 1-6. LI Deren, WANG Yanjun, SHAO Zhenfeng. Geo-informatization of new geographic information era[J]. Geomatics an Information Science of Wuhan University, 2012, 3(1): 1-6. |
| [6] |
惠振阳, 程朋根, 官云兰, 等. 机载LiDAR点云滤波综述[J]. 激光与光电子学进展, 2018, 55(6): 060001. HUI Zhenyang, CHENG Penggen, GUAN Yunlan, et al. Review on airborne LiDAR point cloud filtering[J]. Laser & Optoelectronics Progress, 2018, 55(6): 060001. |
| [7] |
MENG Xuelian, CURRIT N, ZHAO Kaiguang. Ground filtering algorithms for airborne LiDAR data:a review of critical issues[J]. Remote Sensing, 2010, 2(3): 833-860. DOI:10.3390/rs2030833 |
| [8] |
VOSSELMANN G. Slope-based filtering of laser altimetry data[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(Part B3/2): 935-942. |
| [9] |
SITHOLE G. Filtering of laser altimetry data using a slope adaptive filter[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2001, 34(3/W4): 203-210. |
| [10] |
AXELSSON P. DEM generation from laser scanner data using adaptive TIN models[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2000, 33(Part B4/1): 110-117. |
| [11] |
HU Han, DING Yulin, ZHU Qing, et al. An adaptive surface filter for airborne laser scanning point clouds by means of regularization and bending energy[J]. SPRS Journal of Photogrammetry and Remote Sensing, 2014, 92: 98-111. DOI:10.1016/j.isprsjprs.2014.02.014 |
| [12] |
朱笑笑, 王成, 习晓环, 等. 多级移动曲面拟合的自适应阈值点云滤波方法[J]. 测绘学报, 2018, 47(2): 153-160. ZHU Xiaoxiao, WANG Cheng, XI Xiaohuan, et al. Hierarchical threshold adaptive for point cloud filter algorithm of moving surface fitting[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(2): 153-160. DOI:10.11947/j.AGCS.2018.20170491 |
| [13] |
CHEN Chuanfa, LI Yanyan, LI Wei, et al. A multiresolution hierarchical classification algorithm for filtering airborne LiDAR data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 82: 1-9. DOI:10.1016/j.isprsjprs.2013.05.001 |
| [14] |
ZHANG Wuming, QI Jianbo, WAN Peng, et al. An easy-to-use airborne LiDAR data filtering method based on cloth simulation[J]. Remote Sensing, 2016, 8(6): 501. DOI:10.3390/rs8060501 |
| [15] |
郑辑涛, 张涛. 基于可变半径圆环和B样条拟合的机载LiDAR点云滤波[J]. 测绘学报, 2015, 44(12): 1359-1366. ZHENG Jitao, ZHANG Tao. Filtering of airborne LiDAR point cloud based on variable radius circle and B-spline fitting[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1359-1366. DOI:10.11947/j.AGCS.2015.20140514 |
| [16] |
SOHN G, DOWMAN I J. Terrain surface reconstruction by the use of tetrahedron model with the MDL criterion[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2002, 34(3A): 336-344. |
| [17] |
ZHANG Keqi, CHEN S C, WHITMAN D, et al. A progressive morphological filter for removing nonground measurements from airborne LiDAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 872-882. DOI:10.1109/TGRS.2003.810682 |
| [18] |
HUI Zhenyang, HU Youjian, YEVENYO Y. An improved morphological algorithm for filtering airborne LiDAR point cloud based on multi-level Kriging interpolation[J]. Remote Sensing, 2016, 8(1): 35. DOI:10.3390/rs8010035 |
| [19] |
PINGEL T J, CLARKE K C, MCBRIDE W A. An improved simple morphological filter for the terrain classification of airborne LiDAR data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 77: 21-30. DOI:10.1016/j.isprsjprs.2012.12.002 |
| [20] |
FILIN S. Surface clustering from airborne laser scanning data[J]. International Archives of Photogrammetry and Remote Sensing, 2002, 34(Part 3A): 119-124. |
| [21] |
ZHANG Jixian, LIN Xiangguo. Filtering airborne LiDAR data by embedding smoothness-constrained segmentation in progressive TIN densification[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 81: 44-59. DOI:10.1016/j.isprsjprs.2013.04.001 |
| [22] |
SITHOLE G, VOSSELMAN G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 85-101. DOI:10.1016/j.isprsjprs.2004.05.004 |
| [23] |
LEE D T, SCHACHTER B J. Two algorithms for constructing a delaunay triangulation[J]. International Journal of Computer & Information Sciences, 1980, 9(3): 219-242. |
| [24] |
ZHAO Xiaoqian, GUO Qinghua, SU Yanjun, et al. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 117: 19-91. |
| [25] |
MUJA M, LOWE D G. Fast approximate nearest neighbors with automatic algorithm configura-tion[C]//Proceedings of the 4th International Conference on Computer Vision Theory and Applications. Lisboa, Portugal: [s.n.], 2009. 10.1117/12.928865
|
| [26] |
PFEIFER N, STADLER P, BRIESE C. Derivation of digital terrain models in the SCOP++ environ-ment[C]//Proceedings of OEEPE Workshop on Airborne Laserscanning and Interferometric SAR for Detailed Digital Terrain Models. Stockholm: [s.n.], 2001. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.589.8666&rep=rep1&type=pdf
|
| [27] |
CONGALTON R G. A review of assessing the accuracy of classifications of remotely sensed data[J]. Remote Sensing of Environment, 1991, 37(1): 35-46. DOI:10.1016/0034-4257(91)90048-B |





