河流信息提取对水利资源勘察、水环境监测、水面运输规划、水上目标识别以及防洪防汛工程建设等具有至关重要的实际意义。随着SAR(synthetic aperture radar)成像技术的不断发展和成熟,利用拍摄的SAR图像来获取地物目标信息,已逐渐成为地物目标检测与识别领域的主要手段之一,因此SAR成像被应用到河流检测当中。SAR图像河流提取是上述实际应用的基础环节,因此研究SAR图像河流提取尤为重要。
当下SAR图像河流提取方法大致可归纳为:基于区域的提取方法和基于边缘的提取方法。文献[1]首先依据图像灰度特征分布的匀称性,将1维倒数灰度熵的阈值选取公式扩展到2维,然后在求解2维最佳阈值时,将其化简为求解两个1维最佳阈值,大大减少了公式的计算量,最终利用分解的2维倒数灰度熵法分割出SAR图像中的河流区域。文献[2]提出一种结合空间像素模板和Adaboost的SAR图像河道检测方法。该方法通过过滤式特征选取建立空间像素模板并生成多维特征向量,再采用Adaboost学习算法加权集成多特征,以实现SAR图像中河流的分割。文献[3]利用多特征融合和小波支持向量机(weighted support vector machines, WSVM)来实现SAR图像中河流信息的检测。首先利用均值比描述像素点邻近区域的灰度信息并通过Gabor小波获取其纹理信息,然后综合两类信息并作归一化运算输入到WSVM中,最后利用训练好的WSVM对SAR图像进行分类,提取出其中的河流区域。文献[4]首先采用阈值分割方法划分出SAR图像中初始河流区域及其河岸线,在此基础上充分利用SAR图像的纹理信息来修正河岸线部分,最终获得完整、准确的河流边缘线。文献[5]提出了一种改进的SUSAN算法来提取SAR图像中的河流边界信息。该方法使用了灰度差的自适应阈值,并结合增加边缘像素对比度的方法设置几何阈值,最终实现河流边缘的自动识别与提取。文献[6]首先在小波域利用变换数据在相邻尺度上的空间相关特性,获取图像中河流的初始边缘,在此基础上采用脊线追踪法修补间断的河流边缘,以实现河流边缘的完整提取。上述方法都能实现SAR图像中河流的提取,但在提取准确性或提取效率方面存在不足,方法性能有待进一步提高。
近年来,主动轮廓模型在图像分割领域取得了较大成功[7-16],因此研究人员开始利用主动轮廓提取SAR图像中的河流。文献[17]提出一种基于倒数灰度熵和改进CV模型(reciprocal gray entropy CV, RGECV)的河流提取模型。该模型首先采用基于倒数灰度熵的阈值分割方法对SAR图像进行粗分割,然后将粗分割的结果转换为二次分割的初始条件,最后利用改进CV(Chan-Vese)模型对图像进行二次分割,能快速地提取出图像中的河流,但提取出的河流区域准确性不高。文献[18]提了一种基于交叉熵(cross entropy, CE)的主动轮廓模型来分割SAR河流图像。该方法将CV模型中类内方差形式的外部能量约束项替换为交叉熵形式的外部能量约束项,能更好地衡量曲线内外像素灰度的差异性。因此,利用CE模型提取河流的准确性比CV模型高,但CE模型的适应性不强,往往会出现过提取的问题。文献[19]以CE模型为基础,构建了一种基于对称交叉熵(symmetric cross entropy, SCE)的主动轮廓模型。相较于交叉熵,对称交叉熵能更加稳定、准确地衡量曲线内外像素灰度的差异性,因此SCE模型克服了CE模型适应性不强的问题,且能更加准确地提取SAR图像中的河流。然后SCE模型的提取结果仍然不够理想,提取准确性有待进一步提高。此外,CE模型和SCE模型的提取效率也相对较低。SAR成像时河流区域后向散射系数相对较小,成像较弱,回波信号接近于零,因此河流区在SAR图像中呈现为黑色区域。而图像中干扰区域与其灰度相近,往往会给河流提取效果造成较大干扰。为了克服上述困难,提出了结合L1范数和拉普拉斯能量的主动轮廓模型,以实现SAR图像中河流的准确提取。首先,利用L1范数形式的外部能量约束项替换CV模型中L2范数形式的外部能量约束项,以抑制干扰区域的影响。然后提出了一种新的基于拉普拉斯核函数的外部能量约束项,并将其与L1范数形式的外部能量约束项相结合,利用两种外部能量约束项目描述曲线内外像素灰度差异性,以获取更加准确性的提取结果。此外,为了提高模型的提取效率,引入曲线内外区域像素灰度的绝对中位差替代模型中的常数曲线内外能量权值。针对实际SAR图像进行了河流提取试验,结果表明:提出模型能更精确、更高效地提取出SAR图像中的河流。
1 CV模型简介文献[20]在M-S模型的基础上假设分割图像仅包含两个同质区域,即目标区域和背景区域,并利用二分段光滑函数来拟合分割图像,最后通过最小化分割图像和原始图像的差异程度得到CV模型的能量泛函。其表达式为
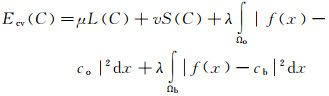 (1)
(1)
式中,x为像素位置信息;C为任意曲线;f(x)为像素灰度;L(C)和S(C)为长度和面积规则项;co和cb分别为目标区域和背景区域内像素灰度的均值;μ、v及λ则是对应能量项的权值。在ECV(C)中,L(C)和S(C)是内部约束项,在模型迭代进程中,维持曲线的光滑性;剩余两项是外部约束项,在模型迭代进程中,驱动曲线逼近目标的边缘。
为了克服拓扑变化的难题,利用水平集函数代替变量来隐含地表示曲线,则式(1)可改写为
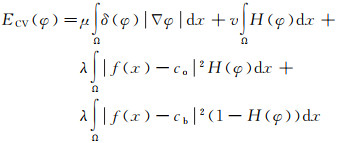 (2)
(2)
式中,φ为水平集函数;δ(φ)和H(φ)分别为Dirac函数、Heaviside函数的正则近似化表示,可通过式(3)和式(4)计算得到
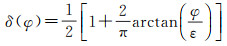 (3)
(3)
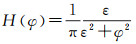 (4)
(4)
式中,ε表示一小正数。
依据变分理论和梯度下降法求解式(2),以获取其迭代方程为
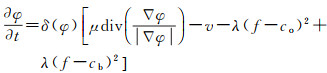 (5)
(5)
观察式(1)可发现,CV模型的外部能量约束项是L2范数形式的,在模型迭代过程中,计算目标区域和背景区域内像素灰度的类内方差信息来驱动曲线演化。当两者的类内方差取得最小值时,图像分割完成。
2 提出模型 2.1 基于L1范数的能量泛函依据上述分析,CV模型是基于L2范数能量的,并遵循类内方差最小准则来分割图像。这导致利用CV模型提取SAR图像中河流区域时,干扰区域往往会被误认为是河流区域。该些干扰区域像素灰度会参加目标区域像素灰度差异性的计算,造成一定的误差。而L2范数是平方的形式,会进一步放大此误差,最终使得CV模型无法准确提取SAR图像中的河流。于是,将CV模型中L2范数形式的外部能量约束项替换为L1范数形式的外部能量约束项,具体表达式为
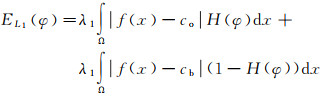 (6)
(6)
式中,和为目标区域和背景区域内像素灰度的均值,可通过式(7)计算
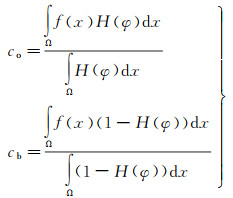 (7)
(7)
基于L1范数的能量泛函可认为是遵循类内绝对差最小准则来实现图像分割的。在模型迭代过程中,计算目标区域和背景区域内像素灰度的类内绝对差信息来指导曲线运动到目标边缘。L1范数是绝对差的形式,被误分割的干扰区域造成的误差不会被放大,因此L1范数形式的外部能量约束项能在一定程度上抑制干扰区域对最终提取结果的影响。
2.2 基于拉普拉斯核函数的能量泛函SAR图像背景的灰度十分复杂,现有主动轮廓模型中的外部能量约束项不能精确地描述目标区域和背景区域内像素灰度的差异程度,导致提取河流区域的准确性不高。于是,基于拉普拉斯核函数,即K(x, y)=e-∣x-y∣/σ,定义了一种新的外部能量约束项。其泛函表达式为
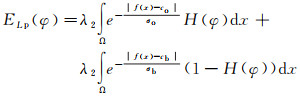 (8)
(8)
式中,σo和σb分别表示目标区域和背景区域内像素灰度的标准差。具体计算表达式为
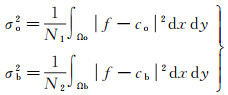 (9)
(9)
式中,N1和N2为目标区域和背景区域内像素的个数。
基于拉普拉斯核函数的能量泛函在模型迭代过程中,计算目标区域和背景区域内像素灰度的拉普拉斯能量引导曲线逼近目标边缘,能较好地描述目标区域和背景区域内像素灰度的差异性,因此该能量泛函能较好地提取SAR图像中的河流区域。
2.3 结合L1范数和拉普拉斯能量的主动轮廓模型SAR图像背景的灰度十分复杂,现有主动轮廓模型大多数只包含一种形式的外部能量约束项,难以稳定、准确地提取SAR图像中河流。为克服这一难题,将基于L1范数的外部能量约束项和基于拉普拉斯核函数的外部能量约束项结合起来,并赋予它们不同的调节系数,于是结合L1范数和拉普拉斯能量(L1Lp)主动轮廓模型的能量泛函表达式为
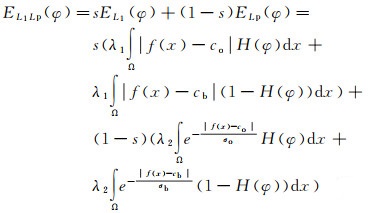 (10)
(10)
式中,s∈[0, 1]为外部能量约束项的调节系数。
在模型迭代过程中,为了保持曲线的光滑和避免演化曲线的初始化,在模型能量泛函中添加长度规则项(EL)和惩罚能量项(EP)[21]。它们可分别通过式(11)和式(12)计算得到
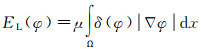 (11)
(11)
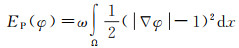 (12)
(12)
式中,μ和ω为相应的能量系数。则结合L1范数和拉普拉斯能量主动轮廓模型的总体迭代方程表达式为
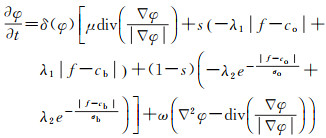 (13)
(13)
结合L1范数和拉普拉斯能量的主动轮廓模型中包含两种形式的外部能量约束项,模型适应性更好,且能更加精确地描述目标区域和背景区域内像素灰度的差异程度。于是,提出模型能实现SAR图像中河流的稳定、准确提取。
3 引入绝对中位差加权的L1Lp主动轮廓模型现有主动轮廓模型中曲线内外区域能量的权值是常数,不会随着曲线的演化而发生改变。然而在模型迭代过程中,曲线的位置和形状是时刻变化的,曲线内外区域能量也随之不断改变。利用常数作为区域能量权值,不能很好地适应能量大小的变化,导致曲线演化较慢、模型的提取效率不高。于是引入曲线内外区域内像素灰度绝对中位差的均值作为曲线内外区域能量的权值,以适应能量大小的变化,则加权L1Lp模型的外部能量约束项表达式为
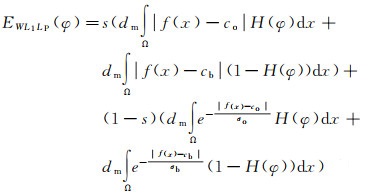 (14)
(14)
式中,dm表示曲线内外区域内像素灰度绝对中位差的均值,可通过式(15)计算得到
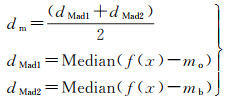 (15)
(15)
式中,dMad1和dMad2分别表示曲线内外区域内像素灰度的绝对中位差;mo和mb分别表示曲线内外区域内像素灰度的中值。
于是引入绝对中位差加权L1Lp-ACM的总体迭代方程为
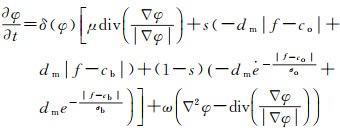 (16)
(16)
由式(15)可知,曲线内外区域内像素灰度绝对中位差的均值与曲线内外区域像素灰度差异程度是正相关的。利用加权L1Lp模型提取目标区域时,在模型迭代初期,曲线内外区域像素灰度差异程度较大,相应的曲线内外区域能量较大,与此同时曲线内外区域内像素灰度绝对中位差的均值也较大,于是模型能充分利用曲线内外区域能量加速曲线运动到目标边缘。在模型迭代末期,曲线内外区域像素灰度差异程度较小,相应的曲线内外区域能量较小,与此同时曲线内外区域内像素灰度绝对中位差的均值也较小,于是曲线逐渐稳定于目标边缘。
相较于现有主动轮廓模型,加权L1Lp模型具有以下优势:
(1) 加权L1Lp模型能获得更准确地提取结果,模型稳定性更强。
现有主动轮廓模型大都只包含一种形式的外部能量约束项,不能很好衡量目标区域和背景区域内像素灰度的差异程度,且受干扰区域影响较大。不同于现有主动轮廓模型,加权L1Lp模型利用两种形式的外部能量约束项来衡量目标区域和背景区域内像素灰度的差异程度。其中,基于L1范数的外部能量约束项能在一定程度上抑制干扰区域的影响,而基于拉普拉斯核函数的外部能量约束项能较精确衡量目标区域和背景区域内像素灰度的差异程度,因此加权L1Lp模型能更准确、稳定地提取出图像中的目标区域。
(2) 加权L1Lp模型能取得更高的提取效率。
现有主动轮廓模型中曲线内外区域能量的权值是常数,不能很好地适应曲线内外区域能量大小的变化,导致模型提取效率较低。加权L1Lp模型引入曲线内外区域内像素灰度绝对中位差的均值以替换模型中常数区域能量权值,能自适应地调节区域能量权值的大小,加速曲线运动到目标的边界并稳定于目标边界。因此,加权L1Lp模型能更高效地提取出图像中的目标区域。
4 试验结果与分析为了说明提取出模型的优越性,选取4幅SAR图像作为试验对象,其分辨率分别为:216×214、199×199、291×290及147×145。利用CV模型、RGECV模型、CE模型、SCE模型及加权L1Lp模型提取上述图像中的河流并对比其提取结果。试验平台为:CPU型号为Intel Core i7-3610QM,主频2.30 GHz,内存6 GB,仿真软件Matlab R2014B,操作系统为Windows 7。图 1—图 4展示了4幅实际SAR图像及其5种模型的河流提取结果。试验模型的相应参数如下[22-25]:在CV模型和RGECV模型中,μ=0.01×255×255,v=0,λ=1,Δt=0.1,ε=1;在CE模型和SCE模型中,μ=0.01×255×255,λ=10,Δt=0.1,ε=1;在加权L1Lp模型中,μ=0.01×255×255,ω=0.5,Δt=0.1,ε=1。另加权L1Lp模型中的外部能量约束项调节系数s需要根据不同图像的灰度特征分别选取,但依据基于L1范数和基于拉普拉斯核函数能量泛函在模型中的作用,将调节系数s的范围限定为0.7~1。

|
| 图 1 SAR图像1及其5种模型的河流提取结果 Fig. 1 SAR image 1 and its river extraction results by five models |

|
| 图 2 SAR图像2及其5种模型的河流提取结果 Fig. 2 SAR image 2 and its river extraction results by five models |

|
| 图 3 SAR图像3及其5种模型的河流提取结果 Fig. 3 SAR image 3 and its river extraction results by five models |

|
| 图 4 SAR图像4及其5种模型的河流提取结果 Fig. 4 SAR image 4 and its river extraction results by five models |
在图 1—图 4中,图(b)表示CV模型的提取结果。CV模型的外部能量约束项是L2范数形式的,在模型迭代过程中,计算曲线内外区域像素灰度的类内方差来驱动曲线运动到目标边缘。当曲线内外区域像素灰度的类内方差达到最小值时,模型迭代停止,图像分割完成。然而灰度值与河流区域相近的干扰区域会被误分为河流区域,导致河流提取效果较差。图(c)表示RGECV模型的提取结果。RGECV首先采用基于倒数灰度熵的图像分割方法对SAR图像进行粗分割,然后利用改进CV模型对图像进行二次分割,以得到最终的河流提取结果。该模型仅在提取效率方面有所提高,提取结果与CV模型的提取结果十分相像。图(d)表示CE模型的提取结果。不同于CV模型,CE模型在迭代过程中计算曲线内外区域像素灰度的交叉熵来衡量曲线内外像素灰度的差异性,准确性相对更高,因此CE模型的河流提取效果要好于CV模型。但该模型适应性不强,在某些情况下,提取效果甚至要差于CV模型(例如图 4(d))。图(e)表示SCE模型的提取结果。该模型将CE模型中交叉熵形式的外部能量约束项替换为对称交叉熵形式的外部能量约束项,能更加稳定、准确地衡量曲线内外像素灰度的差异性,克服了CE模型适应性不强的问题,因此SCE模型能获得较好的河流提取效果。虽然CE模型和SCE模型在河流提取准确性方面有所提高,但其提取结果中仍存在一些干扰区域,提取效果不能令人满意。图(f)表示加权L1Lp模型的提取结果。不同于现有主动轮廓模型,该模型的外部能量约束项由两部分组成,即基于L1范数的外部能量约束项和基于拉普拉斯核函数的外部能量约束项,能在一定程度上抑制干扰区域的影响并更加准确衡量曲线内外区域像素灰度的差异程度。因此,加权L1Lp模型河流提取结果的准确性最高,提取效果最佳。
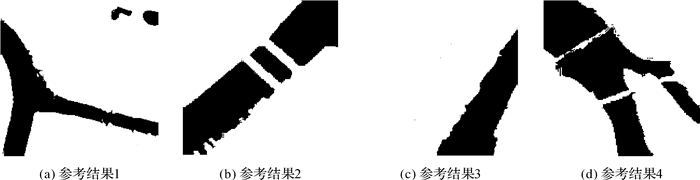
为了更加客观了说明提出模型的有效性,给出了4幅SAR图像的河流提取参考图像,如图 5所示。
|
| 图 5 SAR图像河流提取参考结果 Fig. 5 Reference results of rivers of SAR images |
选择准确率(Ac)和虚警率(FA)来定量评价5种模型的提取结果。准确率和虚警率的计算表示式为
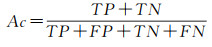 (17)
(17)
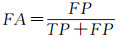 (18)
(18)
式中,TP表示正确提取的河流部分;FP表示错误提取的河流部分;TN表示正确划分的背景部分;FN表示错误划分的背景部分。依据式(17)和式(18)分别计算上述提取结果的准确率和虚警率,列于表 1中。
由表 1的计算结果可知,加权L1Lp模型河流提取结果的准确率最高,都大于95%;虚警率最低,都小于10%。综合准确率和虚警率2个定量评价指标,加权L1Lp模型在河流提取效果方面有较大优势。
为了对比图 5中模型的提取效率,将它们的迭代次数和计算时间列于表 2中。
从表 2的数据可以看出,CV模型的迭代次数和计算时间适中。在模型迭代过程中,其计算曲线内外区域像素灰度的类内方差指导曲线演化,计算复杂度相对不高,因此,CV模型提取河流的效率适中。RGECV模型的迭代次数和计算时间少于CV模型。该模型是二阶段分割模型,计算复杂度稍高于CV模型,但其将CV模型中的Dirac函数更换为边缘强度函数,能加速曲线逼近目标边缘,因此RGECV模型的河流提取效率比CV模型高。不同于CV模型,CE模型通过计算曲线内外区域像素灰度的交叉熵信息来驱动模型迭代,计算复杂度有所提高,于是CE模型的迭代次数和计算时间多于CV模型,河流提取效率相对较低。在CE模型基础上提出的SCE模型将CE模型中交叉熵形式的外部能量约束项替换为对称交叉熵形式的外部能量约束项,计算复杂度进一步提高,导致该模型的迭代次数和计算时间最多,因此SCE模型的河流提取效率最低。上述模型中的曲线内外区域能量的权值是常数,不能很好地适应曲线内外区域能量大小的变化。为了克服这一问题,加权L1Lp模型引入曲线内外区域内像素灰度绝对中位差的均值作为曲线内外区域能量的权值,在模型迭代过程中能自适应地调节区域能量权值的大小,很大程度地提高模型的迭代速率。因此,加权L1Lp模型的迭代次数和计算时间适最少,具有最高的河流提取效率。
5 结 论为了实现SAR图像中河流的准确提取,本文提出了一种结合L1范数和拉普拉斯能量的主动轮廓模型。该模型由两种形式的外部能量约束项组成。其中,基于L1范数的外部能量约束项能在一定程度上抑制干扰区域的影响;而基于拉普拉斯核函数的外部能量约束项能较精确衡量目标区域和背景区域内像素灰度的差异程度。此外,为了提高模型的提取效率,引入曲线内外区域像素灰度绝对中位差的均值作为曲线曲线内外区域能量的权值,以自适应地调节区域能量权值的大小,提高曲线演化速率。试验结果表明:与现有主动轮廓模型相比,提出模型能实现SAR图像中河流的快速、准确提取,在提取准确性和提取效率两方面具有优势。
| [1] |
吴一全, 孟天亮, 吴诗婳, 等. 基于二维倒数灰度熵的河流遥感图像分割[J]. 华中科技大学学报(自然科学版), 2014, 42(12): 70-74, 80. WU Yiquan, MENG Tianliang, WU Shihua, et al. Remote sensing images segmentation of rivers based on two-dimensional reciprocal gray entropy[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(12): 70-74, 80. |
| [2] |
慎利, 唐宏, 王世东, 等. 结合空间像素模板和Adaboost算法的高分辨率遥感影像河流提取[J]. 测绘学报, 2013, 42(3): 344-350. SHEN Li, TANG Hong, WANG Shidong, et al. River extraction from the high-resolution remote sensing image based on spatially correlated pixels template and Adaboost algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 344-350. |
| [3] |
吴一全, 李海杰, 宋昱. 基于多特征和WSVM的SAR图像河流目标检测[J]. 系统工程与电子技术, 2015, 37(6): 1288-1293. WU Yiquan, LI Haijie, SONG Yu. Target detection algorithm for rivers in SAR images based on multi-features and WSVM[J]. Systems Engineering and Electronics, 2015, 37(6): 1288-1293. |
| [4] |
BLAIN C A, LINZELL R, MCKAY P. Simple methodology for deriving continuous shorelines from imagery:application to rivers[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2013, 139(5): 365-382. DOI:10.1061/(ASCE)WW.1943-5460.0000189 |
| [5] |
ZHAO Jianjun, YU Hheng, LI Helin, et al. The edge extraction of yellow river model based on the principle of SUSAN[C]//Proceedings of the 2nd IEEE International Conference on Computing, Control and Industrial Engineering. Wuhan, China: IEEE, 2011: 288-291. 10.1109/CCIENG.2011.6008121
|
| [6] |
SUN Jinping, MAO Shiyi. River detection algorithm in SAR images based on edge extraction and ridge tracing techniques[J]. International Journal of Remote Sensing, 2011, 32(12): 3485-3494. DOI:10.1080/01431161003749477 |
| [7] |
BADURA P, WIECLAWEK W. Calibrating level set approach by granular computing in computed tomography abdominal organs segmentation[J]. Applied Soft Computing, 2016, 49: 887-900. DOI:10.1016/j.asoc.2016.09.028 |
| [8] |
MONDAL A, GHOSH S, GHOSH A. Robust global and local fuzzy energy based active contour for image segmentation[J]. Applied Soft Computing, 2016, 47: 191-215. DOI:10.1016/j.asoc.2016.05.026 |
| [9] |
LI Qiang, DENG Tingquan, XIE Wei. Active contours driven by divergence of gradient vector flow[J]. Signal Processing, 2016, 120: 185-199. DOI:10.1016/j.sigpro.2015.08.020 |
| [10] |
LIU Weiping, SHANG Yanfeng, YANG Xin. Active contour model driven by local histogram fitting energy[J]. Pattern Recognition Letters, 2013, 34(6): 655-662. DOI:10.1016/j.patrec.2013.01.005 |
| [11] |
ZHOU Sanping, WANG Jinjun, ZHANG S, et al. Active contour model based on local and global intensity information for medical image segmentation[J]. Neurocomputing, 2016, 186: 107-118. DOI:10.1016/j.neucom.2015.12.073 |
| [12] |
WANG Hui, HUANG Tingzhu, XU Zongben, et al. An active contour model and its algorithms with local and global Gaussian distribution fitting energies[J]. Information Sciences, 2014, 263: 43-59. DOI:10.1016/j.ins.2013.10.033 |
| [13] |
WANG Hui, HUANG Tingzhu, XU Zhi, et al. A two-stage image segmentation via global and local region active contours[J]. Neurocomputing, 2016, 205: 130-140. DOI:10.1016/j.neucom.2016.03.050 |
| [14] |
ZHOU Yan, SHI Weiren, CHEN Wei, et al. Active contours driven by localizing region and edge-based intensity fitting energy with application to segmentation of the left ventricle in cardiac CT images[J]. Neurocomputing, 2015, 156: 199-210. DOI:10.1016/j.neucom.2014.12.061 |
| [15] |
WU Yue, MA Wenping, GONG Maoguo, et al. Novel fuzzy active contour model with kernel metric for image segmentation[J]. Applied Soft Computing, 2015, 34: 301-311. DOI:10.1016/j.asoc.2015.04.058 |
| [16] |
JIANG Xiaoliang, WANG Qiang, HE Biao, et al. Robust level set image segmentation algorithm using local correntropy-based fuzzy c-means clustering with spatial constraints[J]. Neurocomputing, 2016, 207: 22-35. DOI:10.1016/j.neucom.2016.03.046 |
| [17] |
吴诗婳, 吴一全, 周建江, 等. 利用倒数灰度熵和改进Chan-Vese模型进行SAR河流图像分割[J]. 测绘学报, 2015, 44(11): 1255-1262. WU Shihua, WU Yiquan, ZHOU Jianjiang, et al. SAR river image segmentation based on reciprocal gray entropy and improved Chan-Vese model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1255-1262. DOI:10.11947/j.AGCS.2015.20140519 |
| [18] |
SONG Yu, WU Yiquan, DAI Yimian. A new active contour remote sensing river image segmentation algorithm inspired from the cross entropy[J]. Digital Signal Processing, 2016, 48: 322-332. DOI:10.1016/j.dsp.2015.10.005 |
| [19] |
HAN Bin, WU Yiquan. A novel active contour model based on modified symmetric cross entropy for remote sensing river image segmentation[J]. Pattern Recognition, 2017, 67: 396-409. DOI:10.1016/j.patcog.2017.02.022 |
| [20] |
CHAN T F, VESE L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266-277. DOI:10.1109/83.902291 |
| [21] |
LI Chunming, XU Chenyang, GUI Changfeng, et al. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3243-3254. DOI:10.1109/TIP.2010.2069690 |
| [22] |
HAN Bin, WU Yiquan. Active contours driven by global and local weighted signed pressure force for image segmentation[J]. Pattern Recognition, 2019, 88: 715-728. DOI:10.1016/j.patcog.2018.12.028 |
| [23] |
HAN Bin, WU Yiquan. A hybrid active contour model driven by novel global and local fitting energies for image segmentation[J]. Multimedia Tools and Applications, 2018, 77(21): 29193-29208. DOI:10.1007/s11042-018-6127-x |
| [24] |
HAN Bin, WU Yiquan. River extraction of SAR images via active contours driven by adaptive global fitting energies[J]. International Journal of Remote Sensing, 2018, 39(20): 6995-7013. DOI:10.1080/01431161.2018.1468111 |
| [25] |
RODTOOK A, KIRIMASTHONG K, LOHITVISATE W, et al. Automatic initialization of active contours and level set method in ultrasound images of breast abnormalities[J]. Pattern Recognition, 2018, 79: 172-182. DOI:10.1016/j.patcog.2018.01.032 |



