2. 武汉大学测绘学院, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, Chinat
与只考虑因变量误差影响的加权最小二乘(weighted least squares,WLS)平面线形拟合模型不同,变量误差模型(error-in-variables,EIV)兼顾观测向量(因变量)和系数矩阵(自变量)的误差,平差模型更合理,理论更严密,是当前测绘领域的研究热点之一。
解算EIV模型的流行方法是整体最小二乘法[1](total least squares,TLS),其主要的计算方法有奇异值分解法(singular value decomposition,SVD)和迭代法[2-4]两种。根据是否需要对函数式进行线性化,迭代法可进一步划分为线性化法和非线性化法[5]。目前对TLS的研究主要集中在计算算法开发[5-8]、应用范围扩展[9-15]和解算方法拓展[16-21]等方面。在数学领域,将误差矩阵附有与系数矩阵结构一致性约束的TLS称作约束整体最小二乘(constrained total least squares,CTLS)[22],也常被称作结构TLS(structured total least squares,STLS),也有学者将其称作偏整体最小二乘(partial total least squares,PTLS)[7]。根据已知的先验信息,给TLS附加上参数恒等式约束,可将其扩展为附有等式约束的TLS(equality constrained total least squares,ECTLS)[23]。当约束等式只有固定量时,其被扩展为附有固定等式约束的TLS[24];当约束等式含有随机量时,其被扩展为附有随机等式约束的TLS[25]。它们都属于线性等式约束问题,有关此问题的综合讨论可参阅文献[26]。文献[25, 27]讨论了附有二阶等式约束的TLS平差问题及其解算方法,它属于非线性固定等式约束问题,不含有误差改正数。
正交距离最小二乘和加权整体最小二乘(weighted total least squares,WTLS)在拟合平面线形时都考虑了自变量的误差干扰。但是它们是两种相互独立的方法,前者从几何角度描述拟合准则,后者从代数角度描述拟合准则。几何准则的优点是能保证测量点到拟合对象的正交距离的平方和最小,代数准则的优点是能灵活处理自变量和因变量的随机信息。考虑到基于代数准则的WTLS并不能完全确保其正交距离的平方和为极小值,笔者将几何准则中的正交信息加入其中,建立一种约束方程含有误差改正数的非线性等式约束整体最小二乘平差模型(nonlinear equality constrained total least squares,NECTLS),并研究其解算算法以及在直线拟合中的应用。
1 NECTLS平差法 (1)
(1)
 (2)
(2)
式中,y和ey分别是n×1的观测向量和误差向量;A和EA分别是n×m的系数矩阵和误差矩阵;x和ex=vec(EA)分别是nm×1的观测值向量和误差向量;ξ是m×1的参数向量;符号E和D分别表示期望和方差;σ02表示未知的单位权方差;Qx和Qy分别是nm×nm和n×n的协因数矩阵。在常规模型中,系数矩阵没有常数元素或(和)重复元素,不具有结构特性,同时也不对参数附加额外的等式约束。
当系数矩阵Α含有重复元素(包括随机量和常数)时,ex≠vec(EA),表现出明显的结构特征。为消除其影响,对函数式(1)稍作变换,整理可得
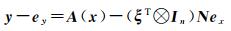 (3)
(3)
式中,A(x)表示A是关于x的矩阵函数;⊗表示克罗内克积;N表示nm×n的转换矩阵[7],根据向量求导法则可推得其计算式[5],即
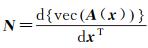 (4)
(4)
为能将几何准则中的正交信息融入WTLS,首先将该正交信息转换为可执行的数学表达式,然后将其作为约束方程加入WTLS,最后综合组成NECTLS平差的函数模型。根据正交几何信息,可以得到如下两个具有等价性的数学表达式,即
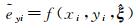 (5)
(5)
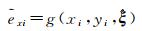 (6)
(6)
式中,带波浪线和带小冒的量分别表示预测值和估计值,误差预测值即是误差改正数;i=1, 2, …, n。
综上所述,NECTLS平差的误差方程、约束方程和平差准则可分别描述为
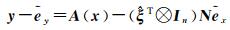 (7)
(7)
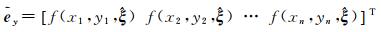 (8)
(8)
或
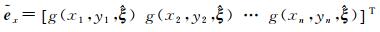 (9)
(9)
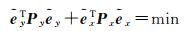 (10)
(10)
式中,Py=Qy-1,Px=Qx-1。
2 NECTLS的解算考虑到约束方程式(8)和式(9)通常具有等价性,笔者在此仅对带有约束方程式(8)的情况进行讨论。
将整体最小二乘平差看成是一个非线性参数估计问题[6, 9],令
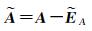 (11)
(11)
 (12)
(12)
则非线性方程式(7)可被线性化为[6]
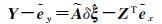
式中,Y=y-Aξ(0),Z=NT(ξ(0)⊗In)。将式(11)和式(12)代入非线性误差方程式(8),对其进行线性化,可得
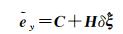 (14)
(14)
式中,
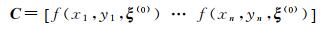 (15)
(15)
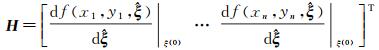 (16)
(16)
它们分别是n×1和n×m的矩阵。值得注意的是,只有当非线性模型接近线性时,即非线性程度较弱时,这种处理才比较合理[28]。
根据线性化后的数学方程和拉格朗日乘数法,可将求解参数最优估值的目标函数定义为
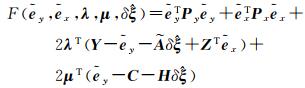 (17)
(17)
式中,λ和μ是n×1的拉格朗日乘积因子。
将目标函数式(17)对各量求偏导,并令它们等于零,则有
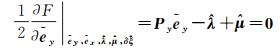 (18)
(18)
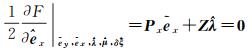 (19)
(19)
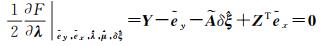 (20)
(20)
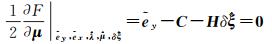 (21)
(21)
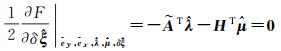 (22)
(22)
由式(18)和式(19)可分别推得预测值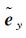
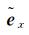
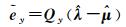 (23)
(23)
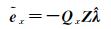 (24)
(24)
它们是关于拉格朗日乘积因子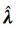
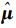
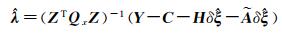 (25)
(25)
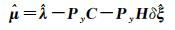 (26)
(26)
将式(25)和式(26)代回式(23)和式(24),可得误差预测值关于ξ(0)和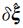
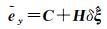 (27)
(27)
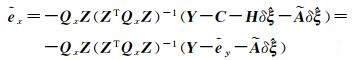 (28)
(28)
将式(25)和式(26)再代回式(22)中,整理后可得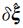
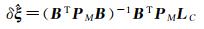 (29)
(29)
式中,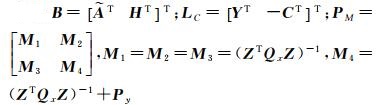
根据式(27)和式(28)计算的观测误差预测值,可求得误差的加权平方和,考虑到误差预测值是关于拉格朗日乘积因子的函数,故也可用式(30)来计算其值,即
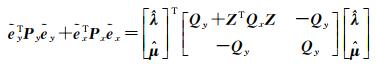 (30)
(30)
将其与多余观测数(n-m)相除,得到验后单位权方差的估计值,其计算公式为
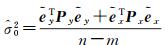 (31)
(31)
根据协因数传播定律,由式(12)、式(29)和式(31)可推得评定参数估计精度的计算式(32)
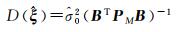 (32)
(32)
虽然约束条件式(8)和式(9)的求解过程类似,但它们求解参数估值的计算公式略有不同。因此,尽管它们可以采用相同的计算流程,但是需要采用与各自相对应的计算公式。本节以式(8)为约束条件推求的计算公式为基础,设计NECTLS的计算算法,具体计算过程如下:
(1)根据已知观测量,给定y,x,Py,Px,N。
(2) 用x组成系数矩阵A,采用WLS估计参数初值:ξ(0)=(ATPyA)-1ATPyy,并令EA(0)=0。
(3) 按线性化公式依次计算下列各值
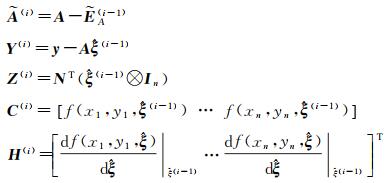
(4) 按下列公式计算参数修正量和误差预测值
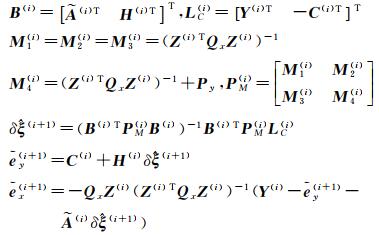
(5) 如果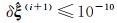
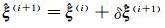
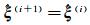
本文以直线参数估计为例,验证笔者提出的方法和算法。设待拟合直线的方程为
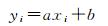 (33)
(33)
式中,a是斜率;b是截距;(xi, yi)是一组观测数据,即测量点。观测值yi组成观测向量y,观测值xi组成系数矩阵A=[x 1];协因数矩阵Qx=[diag(wx1, wx2, …, wxn)-1,Qy=[diag(wy1, yx2, …, wyn)]-1。
要采用NECTLS估计直线参数,需要将测量点与拟合点的连线垂直于拟合直线这一正交几何信息转换成非线性等式约束方程,即
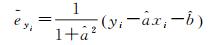 (34)
(34)
或
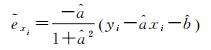 (35)
(35)
对于直线拟合而言,这两种约束具有等价性,参数估计结果完全相同。
对误差约束方程式(34)和式(35)进行线性化,可以分别得到
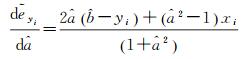 (36)
(36)
 (37)
(37)
和
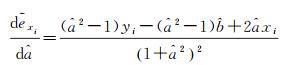 (38)
(38)
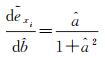 (39)
(39)
将它们分别代入式(15)、式(16)和式(41)、式(42),可求得C、H和K、J的值。在迭代计算时,它们都需要利用前一步的计算结果重新计算。为能从统计上和个例上对本文提出的方法进行检验,设置如下两个试验。
试验1:假设直线的斜率a=0.35,截距b=5.6,给定8个无观测误差的x坐标值(5.88,5.44,4.47,4.62,3.51,3.75,2.86,2.81),以此计算对应的y坐标值,单位为m。分别给x和y坐标,附加上期望为零,方差分别为0.01 m2和0.006 4 m2的随机误差,获得含有随机误差的坐标观测值,模拟1000次, 每次都采用WLS、WTLS(文献[2]的算法)和NECTLS进行解算。
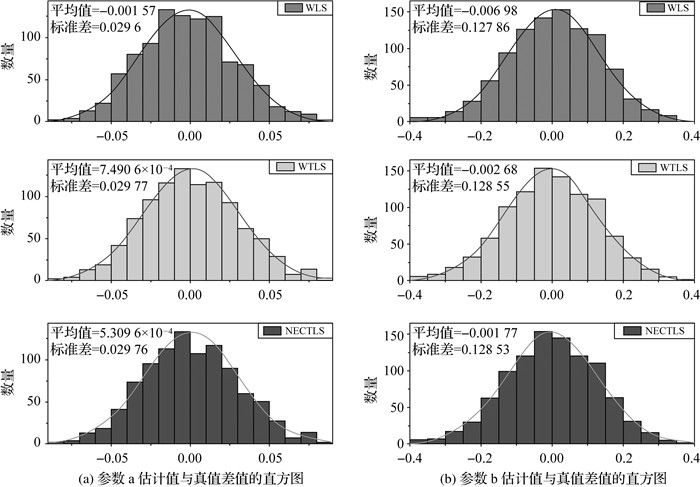
用3种方法估计的参数值减去给定值,分析后发现:①以式(34)或式(35)为约束条件计算的参数估值相同;②就单次模拟计算而言,没有明确规律表明哪一种方法估计的参数值最接近给定值。将这些差值作直方图统计,并拟合出对应的正态分布曲线,如图 1所示。从中可以发现:①WTLS和NECTLS的标准差比WLS的略大,WTLS的比NECTLS略大;②WTLS和NECTLS的平均值比WLS的小,NECTLS的最小。
|
| 图 1 估计参数与真值差值的直方分布 Fig. 1 Histogram of difference between the estimated parameters and the given value |
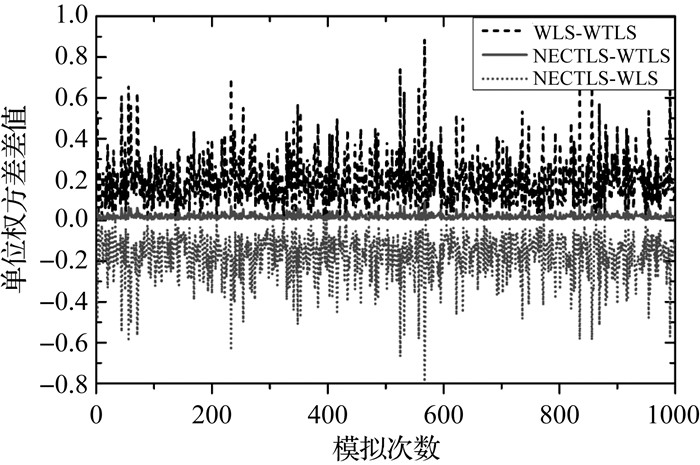
将3种方法每次计算的验后单位权方差相互作差,用WLS减去WTLS(WLS-WTLS),NECTLS减去WLS(NECTLS-WLS),NECTLS减去WTLS(NECTLS-WTLS),结果如图 2所示。
|
| 图 2 验后单位方差之差 Fig. 2 Difference of variance of unit weight |
WLS-WTLS和NECTLS-WTLS的值始终为正值,说明WLS和NECTLS的验后单位权方差始终比WTLS的大;NECTLS-WLS的值始终为负值,说明NECTLS的验后单位权方差始终比WLS的小。因此,3种方法计算的验后单位权方差的大小关系为:WLS>NECTLS>WTLS,3种方法模拟1000次的平均值分别为1.184 07、1.013 75、0.994 19。
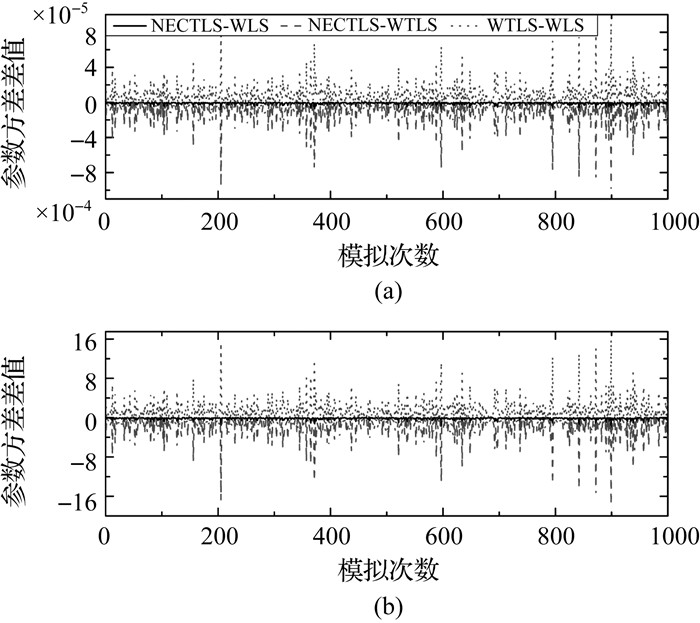
3种方法得到的参数估值的方差也存在明显差异,将它们作差,用NECTLS减去WLS、WTLS的结果,分别用NECTLS-WLS和NECTLS-WTLS表示,WTLS减去WLS的结果用WTLS-WLS表示,结果如图 3所示。
|
| 图 3 参数估值方差之差 Fig. 3 Difference of variance of estimated value |
比较分析可以发现:①尽管NECTLS和WLS的值非常接近,但前者还是略小于后者;②NECTLS-WTLS的值始终为负,说明NECTLS计算的值比WTLS的小;③WTLS-WLS的值始终为正,说明WTLS计算的值比WLS的大。综合而言,NECTLS的值最小。
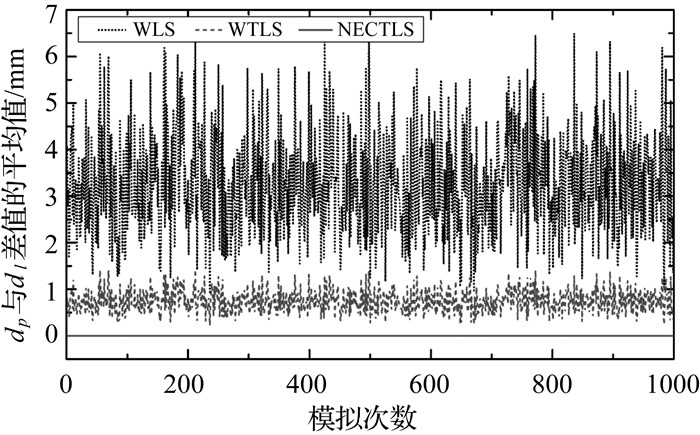
每次模拟计算完成后,计算各测量点到拟合点的距离dp和测量点到拟合直线的距离dl,并计算它们差值的平均值:∑(dp-dl)/8。如图 4所示,NECTLS的差值等于零,表明这两种距离相等;WLS和WTLS的差值大于零,表明这两种距离存在明显差异,且dp大于dl,同时WLS的差异最大。
|
| 图 4 dp减去dl的平均值 Fig. 4 Mean of difference between dp and dl |
在每次模拟计算过程中,根据计算的点到直线的距离dl计算距离的平方和(正交距离平方和),并将不同方法计算的结果做差,用NECTLS减去WLS和WTLS的结果,分别用NECTLS-WLS和NECTLS-WTLS表示,如图 5所示。从图上不难发现,它们的差值始终为负值,说明NECTLS的正交距离平方和最小,与WLS和WTLS相比,NECTLS实现了正交距离平方和最小的参数估计。

|
| 图 5 正交距离平方和差值 Fig. 5 Difference of ∑dl2 between NECTLS and WLS, NECTLS and WTLS |
试验2:采用整体最小二乘研究中常用的直线观测数据进行验证分析,观测数据和相应权值如文献[2]的表 1所示,它们分别取自文献[29]和文献[30]。WLS、WTLS和NECTLS(以式(34)或(35)为约束条件,解算的结果相同)的参数估计结果见表 1。对结果进行比较分析,可以发现:①3种方法估计的模型参数值明显不同;②WTLS计算的验后单位权方差最小;③NECTLS计算的参数估值的方差最小。它们与试验1的统计结果一致。
| 参数 | 方法 | ||
| WLS | WTLS | NECTLS | |
| â | -0.610 8 | -0.480 5 | -0.576 5 |
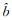 |
6.100 1 | 5.479 9 | 5.867 9 |
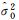 |
4.293 2 | 1.483 3 | 7.133 1 |
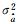 |
0.003 9 | 0.005 0 | 0.000 8 |
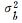 |
0.179 8 | 0.129 1 | 0.015 8 |
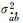 |
-0.026 0 | -0.024 4 | -0.002 7 |
表 2列出了3种方法计算的dp和dl,分析表中数据可以发现:①NECTLS计算的dp和dl相等,WLS和WTLS的不相等;②WLS、WTLS和NECTLS计算的正交距离平方和分别为:0.824 0、0.835 3、0.667 4,NECTLS的值最小。它们与试验1的统计结果一致。
| i | dp | dl | |||||
| WLS | WTLS | NECTLS | WLS | WTLS | NECTLS | ||
| 1 | 0.200 1 | 0.420 0 | 0.027 8 | 0.170 8 | 0.378 6 | 0.027 8 | |
| 2 | 0.150 4 | 0.352 4 | 0.044 1 | 0.128 3 | 0.317 8 | 0.044 1 | |
| 3 | 0.600 6 | 0.214 6 | 0.372 7 | 0.512 6 | 0.193 7 | 0.372 7 | |
| 4 | 0.088 0 | 0.368 6 | 0.200 1 | 0.075 1 | 0.333 0 | 0.200 1 | |
| 5 | 0.584 4 | 0.385 7 | 0.403 2 | 0.498 7 | 0.355 3 | 0.403 2 | |
| 6 | 0.287 5 | 0.318 5 | 0.319 4 | 0.245 3 | 0.301 4 | 0.319 4 | |
| 7 | 0.123 9 | 0.163 6 | 0.060 7 | 0.105 7 | 0.163 3 | 0.060 7 | |
| 8 | 0.425 8 | 0.272 0 | 0.388 8 | 0.363 4 | 0.226 5 | 0.388 8 | |
| 9 | 0.270 2 | 0.084 1 | 0.242 0 | 0.230 6 | 0.039 3 | 0.242 0 | |
| 10 | 0.080 1 | 0.874 7 | 0.088 2 | 0.068 4 | 0.382 1 | 0.088 2 | |
5 结论
本文对约束方程带有误差改正数的非线性等式约束整体最小二乘平差法进行了研究,给出了平差的误差方程和随机模型,利用拉格朗日乘数法推导了估计参数的各种计算公式,并给出了相应的计算算法,最后以直线拟合为例对讨论的方法和给出的计算算法进行了验证分析。根据上述讨论和分析,可以得出以下几点结论:
(1) 本文给出的方法和算法具有可行性。
(2) NECTLS计算的dp和dl相等,WLS和WTLS的不相等。
(3) 与WLS,NECTLS相比,WTLS计算的验后单位权方差最小。
(4) 与WLS和WTLS相比,NECTLS计算的参数估值的方差值最小。
(5) 与WLS和WTLS相比,NECTLS的垂直距离平方和最小。
| [1] |
GOLUB G H, VAN LOAN C F. An analysis of the total least squares problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893. DOI:10.1137/0717073 |
| [2] |
SCHAFFRIN B, WIESER A. On weighted total least-squares adjustment for linear regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. DOI:10.1007/s00190-007-0190-9 |
| [3] |
孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版), 2010, 35(6): 711-714. KONG Jian, YAO Yibin, WU Han. Iterative method for total least-squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 711-714. |
| [4] |
鲁铁定, 周世健. 总体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版), 2010, 35(11): 1351-1354. LU Tieding, ZHOU Shijian. An iterative algorithm for total least squares estimation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1351-1354. |
| [5] |
HU C, CHEN Y, ZHU W D. Generalised total least squares solution based on pseudo-observation method[J]. Survey Review, 2016, 48(348): 157-167. DOI:10.1179/1752270614Y.0000000155 |
| [6] |
SHEN Yunzhong, LI Bofeng, CHEN Yi. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238. DOI:10.1007/s00190-010-0431-1 |
| [7] |
XU Peiliang, LIU Jingnan, SHI Chuang. Total least squares adjustment in partial errors-in-variables models:algorithm and statistical analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675. DOI:10.1007/s00190-012-0552-9 |
| [8] |
FANG Xing. Weighted total least squares:necessary and sufficient conditions, fixed and random parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. DOI:10.1007/s00190-013-0643-2 |
| [9] |
LI Bofeng, SHEN Yunzhong, LOU Lizhi. Noniterative datum transformation revisited with two-dimensional affine model as a case study[J]. Journal of Surveying Engineering, 2013, 139(4): 166-175. DOI:10.1061/(ASCE)SU.1943-5428.0000110 |
| [10] |
LI Bofeng, SHEN Yunzhong, ZHANG Xingfu, et al. Seamless multivariate affine error-in-variables transformation and its application to map rectification[J]. International Journal of Geographical Information Science, 2013, 27(8): 1572-1592. DOI:10.1080/13658816.2012.760202 |
| [11] |
陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722. CHEN Yi, LU Jue. Performing 3D similarity transformation by robust total least squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722. |
| [12] |
FANG Xing. A total least squares solution for geodetic datum transformations[J]. Acta Geodaetica et Geophysica, 2014, 49(2): 189-207. DOI:10.1007/s40328-014-0046-8 |
| [13] |
李忠美, 边少锋, 瞿勇. 多像空间前方交会的抗差总体最小二乘估计[J]. 测绘学报, 2017, 46(5): 593-604. LI Zhongmei, BIAN Shaofeng, QU Yong. Robust total least squares estimation of space intersection appropriate for multi-images[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 593-604. DOI:10.11947/j.AGCS.2017.20160081 |
| [14] |
王乐洋, 李海燕, 温扬茂, 等. 地震同震滑动分布反演的总体最小二乘方法[J]. 测绘学报, 2017, 46(3): 307-315. WANG Leyang, LI Haiyan, WEN Yangmao, et al. Total least squares method inversion for coseismic slip distribution[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 307-315. DOI:10.11947/j.AGCS.2017.20160212 |
| [15] |
FANG Xing. Weighted total least-squares with constraints:a universal formula for geodetic symmetrical transformations[J]. Journal of Geodesy, 2015, 89(5): 459-469. DOI:10.1007/s00190-015-0790-8 |
| [16] |
FANG Xing. On non-combinatorial weighted total least squares with inequality constraints[J]. Journal of Geodesy, 2014, 88(8): 805-816. DOI:10.1007/s00190-014-0723-y |
| [17] |
曾文宪, 方兴, 刘经南. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013-1018. ZENG Wenxian, FANG Xing, LIU Jingnan. Weighted total least squares algorithm with inequality constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1013-1018. DOI:10.13485/j.cnki.11-2089.2014.0173 |
| [18] |
龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888-894, 901. GONG Xunqiang, LI Zhilin. A robust weighted total least squares method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888-894, 901. DOI:10.13485/j.cnki.11-2089.2014.0140 |
| [19] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581. WANG Leyang, YU Dongdong. Virtual observation method to ill-posed total least squares problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581. |
| [20] |
王乐洋, 于冬冬, 吕开云. 复数域总体最小二乘平差[J]. 测绘学报, 2015, 44(8): 866-876. WANG Leyang, YU Dongdong, LÜ Kaiyun, et al. Complex total least squares adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 866-876. DOI:10.11947/j.AGCS.2015.20130701 |
| [21] |
FANG Xing. A structured and constrained total least-squares solution with cross-covariances[J]. Studia Geophysica et Geodaetica, 2014, 58(1): 1-16. DOI:10.1007/s11200-012-0671-z |
| [22] |
LEMMERLING P, DE MOOR B, VAN HUFFEL S. On the equivalence of constrained total least squares and structured total least squares[J]. IEEE Transactions on Signal Processing, 1996, 44(11): 2908-2911. DOI:10.1109/78.542454 |
| [23] |
SCHAFFRIN B, FELUS Y. On total least-squares adjustment with constraints[M]//SANSÒ F. A Window on the Future of Geodesy. Berlin, Heidelberg: Springer, 2005: 417-421.
|
| [24] |
SCHAFFRIN B, FELUS Y A. An algorithmic approach to the total least-squares problem with linear and quadratic constraints[J]. Studia Geophysica et Geodaetica, 2009, 53(1): 1-16. DOI:10.1007/s11200-009-0001-2 |
| [25] |
SCHAFFRIN B. A note on constrained total least-squares estimation[J]. Linear Algebra and its Applications, 2006, 417(1): 245-258. DOI:10.1016/j.laa.2006.03.044 |
| [26] |
王乐洋. 附有等式约束的加权总体最小二乘平差方法[J]. 东华理工大学学报(自然科学版), 2013, 36(2): 245-248. WANG Leyang. Weighted total least squares adjustment with equality constraint[J]. Journal of East China Institute of Technology (Natural Science Edition), 2013, 36(2): 245-248. DOI:10.3969/j.issn.1674-3504.2013.02.023 |
| [27] |
MAHBOUB V, SHARIFI M A. On weighted total least-squares with linear and quadratic constraints[J]. Journal of Geodesy, 2013, 87(3): 279-286. |
| [28] |
刘国林. 非线性最小二乘与测量平差[M]. 北京: 测绘出版社, 2002. LIU Guolin. Nonlinear least squares and measurement adjustment[M]. Beijing: Surveying and Mapping Press, 2002. |
| [29] |
PEARSON K. LⅢ. On lines and planes of closest fit to systems of points in space[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1901, 2(11): 559-572. DOI:10.1080/14786440109462720 |
| [30] |
YORK D. Least-squares fitting of a straight line[J]. Canadian Journal of Physics, 1966, 44(5): 1079-1086. DOI:10.1139/p66-090 |


