精密单点定位(precise point positioning, PPP)的非差模糊度经FCB(fractional cycle biases)产品改正后,可恢复其整周特性,显著缩短PPP的初始化时间[1-3]。目前服务端FCB产品主要采用PPP等3种模型,即消电离层组合PPP(ionospheric-free combined, IF-PPP)[4-6]、无电离层约束的非组合PPP(uncombined and unconstrained, UU-PPP)[7-8]和附加先验电离层约束的非组合PPP(ionospheric-constrained, IC-PPP)[9-11]。由于服务端采用不同PPP模型生成FCB产品时,模糊度参数所吸收的硬件延迟不同,导致不同FCB产品中的硬件延迟不同。通常用户端PPP模型需与服务端PPP模型保持一致,使用户端PPP模糊度固定算法与服务端FCB产品保持自洽,但造成用户端面临不同FCB产品无法使用的问题。同时,多种FCB产品会加重服务端的链路传输压力,不利于用户端实时应用。
非差模糊度的固定关键在于服务端整周模糊度与相位未校准硬件延迟(uncalibrated phase delays, UPD)的正确分离,UPD的小数部分称为FCB。通常用户端模糊度固定算法需与服务端FCB产品保持自洽,目前主要有3种PPP FCB解算模型。对于IF-PPP模型,文献[12]通过星间单差的方式消除接收机端FCB,将星间单差的宽窄巷FCB产品播发给用户端。文献[13]针对服务端测站数量较少的情况,引入双差模糊度作为约束生成窄巷FCB产品。文献[14]通过引入卫星端或接收机端FCB基准,直接估计卫星端FCB产品。相较于传统的消电离层组合PPP,非差非组合PPP模型避免了观测噪声的放大且能够顾及电离层的时变特性。对于UU-PPP模型,文献[15]采用无先验电离层约束的非差非组合PPP模型,基于北斗3个原始频点生成FCB产品。文献[16]基于北斗和伽利略三频的观测数据,采用无电离层约束的非差非组合PPP模型,提出了统一的多频PPP模糊度固定方法。对于IC-PPP模型,文献[17]通过加入先验电离层信息作为约束,基于原始频点L1和L2生成FCB产品。文献[18]证明了3种PPP模型生成的FCB产品中卫星端宽窄巷硬件延迟的一致性,分析了不同FCB产品之间的差异。以上研究主要致力于提高服务端FCB产品的精度和分析产品之间差异,对统一用户端的PPP模糊度固定方法研究较少。
本文提出一种基于3种PPP模型的统一模糊度固定方法。由于模糊度参数与未模型化的电离层延迟存在相关性,顾及目前全球电离层格网模型精度的限制,服务端使用UU-PPP或者IC-PPP模型均无法实时准确分离原始频点模糊度[19]。同时为缓解服务端的链路传输压力,选取IF-PPP模型生成的FCB产品作为服务端播发的唯一FCB产品,用户端可根据需求选择PPP模型进行模糊度固定。证明了服务端FCB产品与所提出IF-PPP、UU-PPP、IC-PPP用户端模糊度固定方法的自洽性。选取全球116个MGEX(multi-GNSS experiment, MGEX)测站作为服务端,采用非差法[20]生成3种FCB产品。选取未参与服务端解算的50个MGEX测站作为用户端,从定位精度、收敛时间和固定率3个方面验证所提出方法的有效性。
1 数学模型GNSS原始的伪距和载波相位观测方程可表示为
 (1)
(1)
式中,Pm,ki、Lm,ki分别表示以米为单位的原始伪距和载波观测量;下标k为测站编号;m表示某一频率;上标i为卫星编号;ρmi为信号发射时刻的站星几何距离;δti为卫星钟差;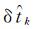
国际GNSS服务(international GNSS service, IGS)提供的钟差产品是基于消电离层组合PPP模型所得到的,因此精密钟差产品中含有消电离层组合的卫星硬件延迟。当使用该产品时,PPP模型的电离层延迟参数会引入卫星端伪距硬件延迟[21]。令DCBP1P2i=d2i-d1i,其中DCB(different code bias, DCB)为差分码偏差,此时电离层延迟可表示为
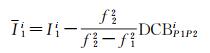 (2)
(2)
式中,f1和f2分别对应L1和L2的载波频率。卫星端DCB可采用CODE(Center for Orbit Determination in Europe)发布的DCB产品直接进行改正,电离层延迟参数均改为Ī1i,此时伪距观测量变为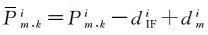
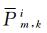
当采用消电离层组合来消除电离层延迟一阶项的影响时,伪距和载波相位观测方程可表示为
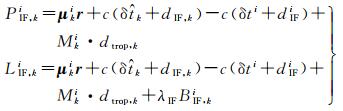 (3)
(3)
式中,下标IF表示消电离层组合;μki=(αi, βi, γi)为站星方向单位向量;r=[δxr δyr δzr]T为3个坐标改正数分量;B表示含有硬件延迟的实数模糊度,表示卫星钟差可采用IGS精密钟差产品直接改正。将载波中硬件延迟归入模糊度参数,此时消电离组合PPP的模糊度参数中硬件延迟为
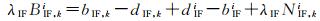 (4)
(4)
由于消电离层组合模糊度失去了整数特性,通常将其分为宽巷和窄巷模糊度分别固定
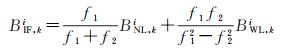 (5)
(5)
式中,宽巷模糊度BWL,ki=B1,ki-B2,ki;窄巷模糊度BNL,ki=B1,ki。宽巷模糊度通常采用MW组合[22]进行历元间平滑得到,将其包含的硬件延迟分为卫星端和接收机端硬件延迟
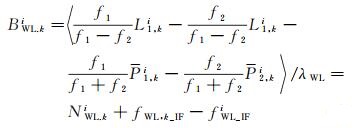 (6)
(6)
式中,〈*〉为逐历元进行平滑;λWL=c/(f1-f2);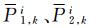
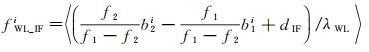 (7)
(7)
考虑到宽巷模糊度波长较长,经宽巷FCB产品改正后可直接取整进行固定。将固定的宽巷模糊度带入消电离层模糊度中,扣除宽巷模糊度即可求得窄巷模糊度实数解
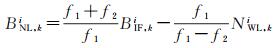 (8)
(8)
由于窄巷模糊度波长较短且模糊度参数之间存在相关性,通常采用LAMADA算法进行模糊度搜索固定。需要注意的是,实际使用中为了消除接收机FCB的影响,用户端使用FCB产品前需对相应模糊度进行星间单差,固定的整周模糊度为星间单差模糊度。
1.2 UU-PPP-AR相对于传统的消电离层组合,非差非组合模型[23]避免了观测噪声的放大。为了直接使用IGS精密钟差产品,将非组合PPP模型中卫星钟差和接收机钟差参数与消电离层组合的伪距硬件延迟进行合并,其余项并入模糊度和电离层
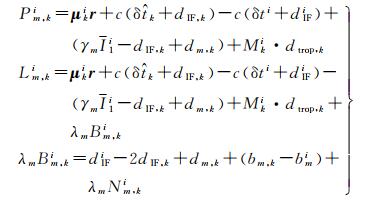 (9)
(9)
式中,Ī1i为经过卫星端DCB改正的电离层延迟参数。对原始频点模糊度重新组成消电离层组合模糊度
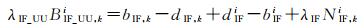 (10)
(10)
与式(4)对比可以看出,UU-PPP模型重构的消电离层模糊度中硬件延迟与消电离层PPP模型解算出的模糊度硬件延迟相同,即
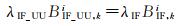 (11)
(11)
考虑到MW组合需要历元间平滑,此处直接对UU-PPP模型解算出的原始频点模糊度作差得宽巷模糊度实数解
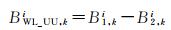 (12)
(12)
同理将硬件延迟分为卫星端和接收机端硬件延迟,其中卫星端宽巷硬件延迟为
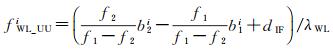 (13)
(13)
与式(7)对比可以看出,IF-PPP模型中通过MW组合得到的宽巷模糊度卫星端FCB与UU-PPP模型中原始频点直接作差得到的宽巷模糊度卫星端FCB相同,即
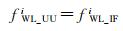 (14)
(14)
直接取整固定宽巷模糊度,由已固定的宽巷模糊度和重构的消电离层模糊度求得窄巷模糊度浮点解,如式(15)所示
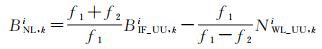 (15)
(15)
式中,NWL_UU, ki表示已固定的宽巷模糊度。可以看出,采用此方法生成的消电离层模糊度和卫星端宽巷模糊度中硬件延迟与IF-PPP模型保持一致,证明了服务端IF FCB产品与所提出UU-PPP用户端模糊度固定方法的自洽性。
1.3 IC-PPP-AR非差非组合PPP模型可顾及先验电离层的时变特性,进一步缩短PPP的初始化时间。加入全球GIM电离层模型进行改正,对接收机DCB进行估计,对电离层参数采用随机游走过程建模并进行估计,初始方差为150 m2,过程噪声为0.04 m2/30 s×Δt。此时观测方程为
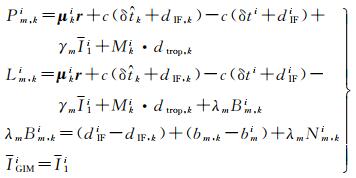 (16)
(16)
式中,ĪGIMi为GIM电离层模型。对原始频点模糊度重新组成消电离层组合模糊度
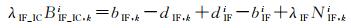 (17)
(17)
与式(4)对比可以看出,IC-PPP模型重构的消电离层模糊度中所包含的硬件延迟与IF模型解算出的模糊度硬件延迟相同,即
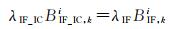 (18)
(18)
由于IC-PPP模型可直接解算原始频点模糊度,同理对其直接作差得到宽巷模糊度实数解
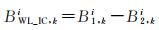 (19)
(19)
同理将硬件延迟分为卫星端和接收机端硬件延迟,其中卫星端宽巷硬件延迟为
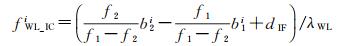 (20)
(20)
与式(7)对比可以看出,IF-PPP模型中通过MW组合得到的宽巷模糊度卫星端FCB与IC-PPP模型中原始频点直接作差得到的宽巷模糊度卫星端FCB相同,即
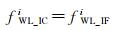 (21)
(21)
同理也可直接固定宽巷模糊度,并与重构的消电离层模糊度求得窄巷模糊度浮点解。可以看出,采用此方法生成的消电离层模糊度和卫星端宽巷模糊度中硬件延迟与服务端IF-PPP模型保持一致,证明了服务端IF FCB产品与所提出IC-PPP用户端模糊度固定方法的自洽性。
因此,相较于传统方法服务端需播发3种FCB产品,本文方法服务端只需发布IF FCB产品,用户端可自由选择PPP模型进行模糊度固定。本文算法流程如图 1所示。对于IF PPP模型用户端,使用MW组合得到宽巷模糊度,经宽巷IF FCB产品改正后直接取整进行固定,利用固定的宽巷模糊度和消电离层模糊度构建窄巷模糊度浮点解,经窄巷IF FCB产品改正后利用LAMADA算法进行搜索固定。对于UU PPP和IC-PPP模型用户端,在原始频点上直接作差即可得到宽巷模糊度浮点解,经宽巷IF FCB产品改正后直接取整固定。基于原始频点重新构建消电离层模糊度,利用固定的宽巷模糊度和构建的消电离组合模糊度生成窄巷模糊度,经窄巷IFFCB产品改正后利用LAMADA算法进行搜索固定。
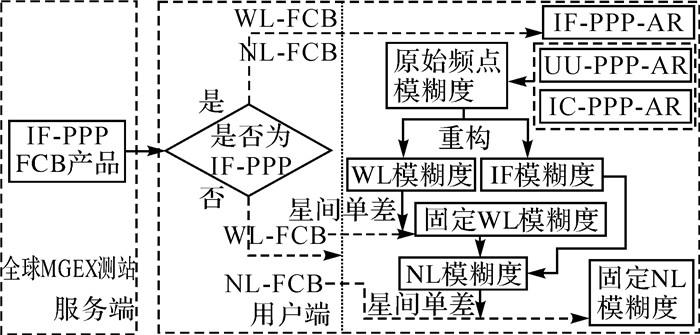
|
| 图 1 本文方法算法流程 Fig. 1 Flowchart of the proposed algorithm |
2 试验与分析
为验证算法的有效性,选取全球116个MGEX测站作为服务端,如图 2中红色五角形所示,采用3种PPP模型,即IF-PPP、UU-PPP、IC-PPP,生成3种FCB产品播发。数据采样间隔为30 s,观测时间为2019年,年积日为81—87 d,参考站的坐标真值为SINEX(solution independent exchange format)周解。选取未参与服务端解算的50个MGEX测站作为用户端,如图 2中黄色三角形所示,采用3种方案进行解算对比:
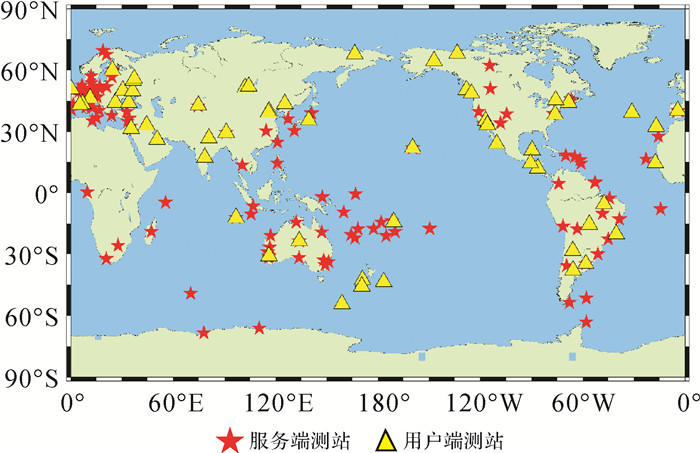
|
| 图 2 选取的全球116个MGEX测站和50个评估测站 Fig. 2 116 global MGEX stations and 50 evaluation stations are selected |
方案1,用户端3种PPP模型均采用浮点解,不进行模糊度固定(float)。
方案2,用户端3种PPP模型采用传统方式进行模糊度固定,即采用相应服务端FCB产品(fixed)。
方案3,用户端3种PPP模型采用本文提出的方法进行模糊度固定(new-fixed)。
服务端采用非差法进行3种FCB产品的解算,其中宽巷FCB产品单天估计一组,窄巷FCB产品每10 min估计一组。将生成的3种FCB产品应用于服务端116个测站,经3种FCB产品改正后的宽巷模糊度残差如图 3所示。可以看出,在使用3种FCB产品改正后,96.3%的IF-PPP宽巷模糊度残差分布在±0.25周之间,97.8%的UU-PPP宽巷模糊度残差分布在±0.25周之间,97.9%的UU-PPP宽巷模糊度残差分布在±0.25周之间,说明生成的3种宽巷FCB产品内符合精度较好。
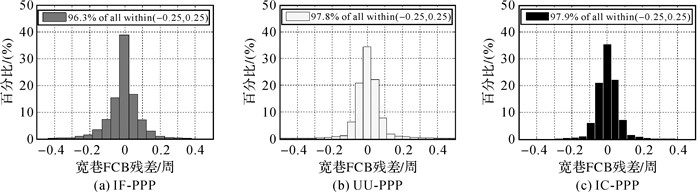
|
| 图 3 3种FCB产品改正后的宽巷模糊度残差 Fig. 3 The residual of wide-lane ambiguity after correction with three kinds of FCB products |
同理将生成的3种FCB产品应用于服务端116个测站,经改正后的窄巷模糊度残差如图 4所示。可以看出,对于服务端116个MGEX测站,97.6%的IF-PPP窄巷模糊度残差分布在±0.25周之间,97.6%的UU-PPP宽巷模糊度残差分布在±0.25周之间,97.5%的UU-PPP宽巷模糊度残差分布在±0.25周之间,说明生成的3种窄巷FCB产品内符合精度较好。
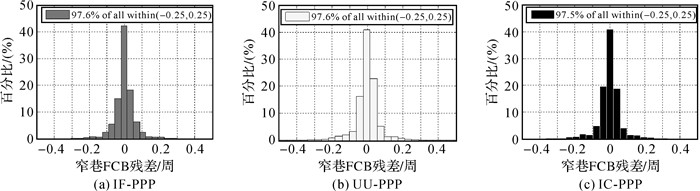
|
| 图 4 3种FCB产品改正后的窄巷模糊度残差 Fig. 4 The residual of narrow-lane ambiguity after correction with three kinds of FCB products |
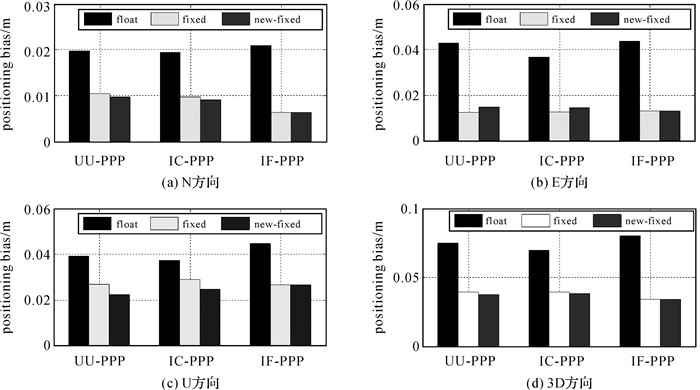
选用全球未参与服务端FCB产品解算的50个测站作为用户端,分别采用3种方案进行静态PPP解算,统计50个测站30 min在N、E、U和3D方向上3种方案的定位精度,如图 5所示。相对于UU-PPP浮点解,传统方案和本文方法定位精度分别提升了47.8%和49.8%,相对于IC-PPP浮点解,传统方案和本文方法定位精度分别提升了43.6%和45.4%。相对于IF-PPP浮点解,传统方案和本文方法定位精度分别提升了57.7%和57.7%。可以看出,相较于传统PPP浮点解,无论是传统方案还是本文方法均能显著提升定位结果的精度。对于采用统一的PPP模糊度固定本文方法,与传统UU-PPP、IC-PPP、IF-PPP模糊度固定方法相比,定位精度均保持一致。
|
| 图 5 统计50个测站3种方案的静态定位精度对比 Fig. 5 Comparison of static positioning accuracy of three methods for 50 stations |
表 1统计了50个测站采用3种方案的静态定位精度对比,30 min内UU-PPP、IC-PPP和IF-PPP浮点解精度分别为7.5、7.0和8.0 cm,而采用传统方案固定模糊度定位精度分别为3.9、3.9和3.4 cm,采用本文方法固定模糊度定位精度分别为3.8、3.8和3.4 cm,说明模糊度固定后可显著提升定位精度,本文方法所采用的统一的PPP模糊度固定方法与3种模型的传统方法定位精度均保持一致。
| 方向 | UU-float | UU-fixed | UU-new | IC-float | IC-fixed | IC-new | IF-float | IF-fixed |
| N | 2.0 | 1.0 | 1.0 | 2.0 | 1.0 | 0.9 | 2.1 | 0.6 |
| E | 4.3 | 1.2 | 1.5 | 3.7 | 1.3 | 1.5 | 4.4 | 1.3 |
| U | 3.9 | 2.7 | 2.3 | 3.7 | 2.9 | 2.5 | 4.5 | 2.6 |
| 3D | 7.5 | 3.9 | 3.8 | 7.0 | 3.9 | 3.8 | 8.0 | 3.4 |
仿动态条件下将测站坐标当作随机游走过程估计,过程噪声方差为10 000 m2。表 2统计了50个测站采用3种方案的仿动态定位精度对比,30 min内UU-PPP、IC-PPP和IF-PPP浮点解精度分别为17.9、15.8和18.1 cm,而采用传统方案固定模糊度定位精度分别为6.4、5.6和5.3 cm,采用本文方法固定模糊度定位精度分别为6.2、3.8和5.3 cm,说明仿动态情况下,本文方法所采用的统一的PPP模糊度固定方法与3种模型的传统方法定位精度均保持一致。
| 方向 | UU-float | UU-fixed | UU-new | IC-float | IC-fixed | IC-new | IF-float | IF-fixed |
| N | 3.2 | 1.4 | 1.5 | 3.3 | 1.2 | 0.9 | 3.4 | 1.2 |
| E | 9.2 | 2.6 | 2.9 | 7.8 | 1.7 | 1.5 | 9.1 | 2.7 |
| U | 11.2 | 3.8 | 3.5 | 9.6 | 3.6 | 2.5 | 11.6 | 3.0 |
| D | 17.9 | 6.4 | 6.2 | 15.8 | 5.6 | 3.8 | 18.1 | 5.3 |
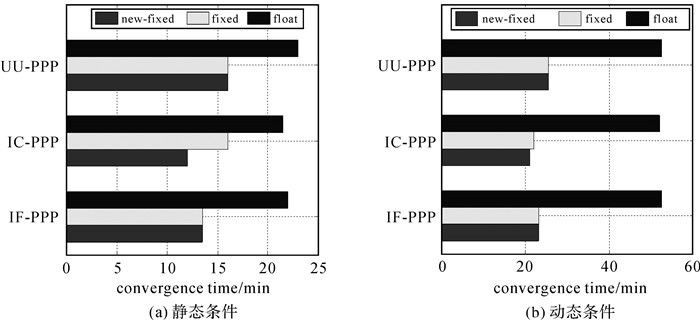
为分析用户端PPP的收敛时间,把PPP在N、E、U 3个方向的定位偏差均小于10 cm且其后5 min均满足该条件作为收敛条件[24]。图 6为50个测站采用3种方案的收敛时间对比。图 6(a)为静态条件下,相对于UU-PPP浮点解,传统方案和本文方法收敛时间分别缩短了38.6%和38.6%。相对于IC-PPP浮点解,传统方案和本文方法收敛时间缩短了25.6%和44.2%。相对于IF-PPP浮点解,传统方案和本文方法收敛时间分别缩短了30.4%和30.4%。图 6(b)为仿动态条件下,相对于UU-PPP浮点解,传统方案和本文方法收敛时间分别缩短了56.2%和56.2%。相对于IC-PPP浮点解,传统方案和本文方法收敛时间分别缩短了57.7%和59.6%。相对于IF-PPP浮点解,传统方案和本文方法收敛时间分别缩短了51.4%和51.4%。可以看出,相较于传统PPP浮点解,无论是传统模糊度固定方案还是本文方法均能显著缩短PPP的收敛时间。本文方法采用统一的PPP模糊度固定方法,与传统UU-PPP、IC-PPP、IF-PPP方法收敛时间均保持一致。
|
|
图 6
统计50个测站3种方案的静态和仿动态收敛时间对比
Fig. 6
Convergence time of three methods for 50 stations in static and dynamic condition |
表 3为50个测站静态和仿动态情况下,传统3种模型的模糊度固定方法与本文方法的模糊度固定率对比。横向对比发现UU-PPP和IC-PPP的固定率均高于IF-PPP,这是因为非组合模型避免了观测噪声的放大便于模糊度的固定[24]。静态条件下,传统方案30 min、1 h和2 h模糊度的平均固定率分别为75.5%、85.0%和88.8%,采用本文方法固定模糊度的平均固定率分别为76.5%、84.8%和87.6%。仿动态条件下采用传统方案30 min、1 h和2 h模糊度的平均固定率分别为68.0%、77.0%和84.8%,采用本文方法固定模糊度的平均固定率分别为77.0%、76.9%和83.8%。说明本文方法所采用的统一的PPP模糊度固定方法与3种模型的传统方案固定率均保持一致性,验证了本文方法的可行性。
| 处理策略 | UU-fixed | UU-new | IC-fixed | IC-new | IF-fixed |
| static—30 min | 78.6 | 80.0 | 78.4 | 80.0 | 69.5 |
| static—1 h | 87.4 | 87.3 | 86.8 | 86.5 | 80.7 |
| static—2 h | 93.5 | 91.3 | 92.1 | 90.9 | 80.7 |
| dynamic—30 min | 69.2 | 71.0 | 72.5 | 72.7 | 62.5 |
| dynamic—1 h | 79.8 | 79.8 | 80.3 | 79.9 | 71.0 |
| dynamic—2 h | 87.6 | 85.7 | 86.7 | 85.7 | 80.0 |
3 结论
试验结果表明:较之传统方法,本文方法解决了用户端面临不同FCB产品的PPP模糊度固定问题,在定位精度提升、缩短收敛时间和固定成功率方面与传统方法均保持一致。相较于PPP浮点解,静态条件下传统方案和本文方法模糊度固定后定位精度分别平均提升49.7%和51.0%,收敛时间分别缩短31.5%和37.7%,1 h固定率分别为85.0%和84.8%;仿动态条件下传统方案和本文方法模糊度固定后定位精度分别平均提升66.6%和65.0%;收敛时间分别缩短55.1%和55.7%,1 h固定率分别为77.0%和76.9%。
| [1] |
GENG Jianghui, TEFERLE F N, SHI C, et al. Ambiguity resolution in precise point positioning with hourly data[J]. GPS Solutions, 2009, 13(4): 263-270. DOI:10.1007/s10291-009-0119-2 |
| [2] |
ZHANG Xiaohong, LI Pan, GUO Fei. Ambiguity resolution in precise point positioning with hourly data for global single receiver[J]. Advances in Space Research, 2013, 51(1): 153-161. |
| [3] |
TU Rui, GE Maorong, ZHANG Hongping, et al. The realization and convergence analysis of combined PPP based on raw observation[J]. Advances in Space Research, 2013, 52(1): 211-221. |
| [4] |
GENG Jianghui. Rapid integer ambiguity resolution in GPS precise point positioning[D]. Nottingham: University of Nottingham, 2011. https://www.researchgate.net/publication/294597208_Rapid_integer_ambiguity_resolution_in_GPS_precise_point_positioning
|
| [5] |
潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210-1218. PAN Zongpeng, CHAI Hongzhou, LIU Jun, et al. GPS partial ambiguity resolution method for zero-difference precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210-1218. DOI:10.11947/j.AGCS.2015.20150056 |
| [6] |
XIAO Guorui, LI Pan, SUI Lifen, et al. Estimating and assessing Galileo satellite fractional cycle bias for PPP ambiguity resolution[J]. GPS Solutions, 2019, 23(1): 3. DOI:10.1007/s10291-018-0793-z |
| [7] |
LI Xingxing, LI Xin, LIU Gege, et al. Triple-frequency PPP ambiguity resolution with multi-constellation GNSS:BDS and Galileo[J]. Journal of Geodesy, 2019, 93(8): 1105-1122. DOI:10.1007/s00190-019-01229-x |
| [8] |
QU Lizhong, DU Mingyi, WANG Jian, et al. Precise point positioning ambiguity resolution by integrating BDS-3E into BDS-2 and GPS[J]. GPS Solutions, 2019, 23(3): 63. DOI:10.1007/s10291-019-0854-y |
| [9] |
GU Shengfeng, LOU Yidong, SHI Chuang, et al. BeiDou phase bias estimation and its application in precise point positioning with triple-frequency observable[J]. Journal of Geodesy, 2015, 89(10): 979-992. DOI:10.1007/s00190-015-0827-z |
| [10] |
臧楠, 李博峰, 沈云中. 3种GPS+BDS组合PPP模型比较与分析[J]. 测绘学报, 2017, 46(12): 1929-1938. ZANG Nan, LI Bofeng, SHEN Yunzhong. Comparison and analysis of three GPS+BDS PPP models[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(12): 1929-1938. DOI:10.11947/j.AGCS.2017.20170111 |
| [11] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099. ZHANG Baocheng. Study on the theoretical methodology and applications of precise point positioning using undifferenced and uncombined GNSS data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099. DOI:10.13485/j.cnki.11-2089.2014.0155 |
| [12] |
GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [13] |
GENG Jianghui, SHI Chuang, GE Maorong, et al. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning[J]. Journal of Geodesy, 2012, 86(8): 579-589. DOI:10.1007/s00190-011-0537-0 |
| [14] |
LI Xingxing, ZHANG Xiaohong. Improving the estimation of uncalibrated fractional phase offsets for PPP ambiguity resolution[J]. The Journal of Navigation, 2012, 65(3): 513-529. DOI:10.1017/S0373463312000112 |
| [15] |
XIAO Guorui, LI Pan, GAO Yang, et al. An unified model for multi-frequency PPP ambiguity resolution and test results with Galileo and BeiDou triple-frequency observations[J]. Remote Sensing, 2019, 11(2): 116. DOI:10.3390/rs11020116 |
| [16] |
LI Pan, ZHANG Xiaohong, GE Maorong, et al. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables[J]. Journal of Geodesy, 2018, 92(12): 1357-1369. DOI:10.1007/s00190-018-1125-3 |
| [17] |
LI Xingxing, GE Maorong, ZHANG Hongping, et al. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning[J]. Journal of Geodesy, 2013, 87(5): 405-416. |
| [18] |
WANG Jin, HUANG Guanwen, YANG Yuanxi, et al. FCB estimation with three different PPP models:equivalence analysis and experiment tests[J]. GPS Solutions, 2019, 23(4): 93. DOI:10.1007/s10291-019-0887-2 |
| [19] |
GU Shengfeng, SHI Chuang, LOU Yidong, et al. Ionospheric effects in uncalibrated phase delay estimation and ambiguity-fixed PPP based on raw observable model[J]. Journal of Geodesy, 2015, 89(5): 447-457. DOI:10.1007/s00190-015-0789-1 |
| [20] |
张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报(信息科学版), 2010, 35(6): 657-660. ZHANG Xiaohong, LI Xingxing. A new method for zero-differenced interger ambiguity resolution and its application to PPP[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 657-660. |
| [21] |
BOCK H, DACH R, YOON Y, et al. GPS clock correction estimation for near real-time orbit determination applications[J]. Aerospace Science and Technology, 2009, 13(7): 415-422. DOI:10.1016/j.ast.2009.08.003 |
| [22] |
WUBBENA G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, Maryland: US Department of Commerce, 1985: 403-412.
|
| [23] |
张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478-483. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise point positioning algorithm based on original dual-frequency GPS code and carrier-phase observations and its application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478-483. |
| [24] |
LI Pan, ZHANG Xiaohong. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning[J]. GPS Solutions, 2014, 18(3): 461-471. DOI:10.1007/s10291-013-0345-5 |



