2. 华中师范大学地理过程分析与模拟湖北省重点实验室, 湖北 武汉 430079;
3. 武汉大学资源与环境科学学院, 湖北 武汉 430079
2. Key Laboratory for Geographical Process Analysis & Simulation of Hubei Province, Central China Normal University, Wuhan 430079, China;
3. School of Resource and Environment Sciences, Wuhan University, Wuhan 430079, Chinat
长期以来,地图制图综合一直是GIS及制图相关领域的研究重点,其中,地理要素空间特征的多尺度表示是自动制图综合的基本组成部分[1-2]。地图多尺度表达是指地图的比例尺在由大到小的变化过程中,在保留地理要素主要形状特征的条件下对其进行化简,实现要素的形状由复杂到粗略的变化[3-5]。从使用者的角度,对地图进行综合及简化可以根据不同的尺度需求调整地图的繁杂程度,以获得与人眼观测能力相匹配的地图;从研究人员的角度,对地理空间要素的化简可以对要素中不同关键等级的形状特征进行提取,进而挖掘隐藏的地理空间过程信息。因此,地图的多尺度表达成为现今地理信息科学的重点研究项目之一。对此,已有不少学者进行了大量的探索与研究。其研究重点大致分为两方面:
(1) 地理要素形状的简化。地理要素的简化可以通过空间域和频率域两种分析方式实现。空间域上的简化方法着眼于曲线实际形状,以去除琐碎的折点或弯曲等方式实现要素化简。Douglas-Peucker算法是在空间域中较为常用的一种简化方法,以设定的垂直距离为阈值,通过删除阈值范围内的冗余点达到目标简化效果[6]。除此之外,Li-OpenShaw算法以及引入了弯曲概念的Wang-Müller算法也是较为常用的简化方法[7-8]。在频域上的化简则着重于曲线的频率特征,通过剔除能量低的曲线高频分量,并利用地理要素频域与空间域的映射实现要素的简化[9-12]。
(2) 简化后地理要素比例尺的度量。文献[13-14]将方根模型进行改进,得到地图比例尺与地理要素简化程度的函数关系,实现了地图的连续尺度表达;文献[15-18]应用多种曲线简化方式,结合插值方法得到地理要素的插值形状与比例尺之间的对应关系,实现了要素渐进的Morphing变换。
理想的地图多尺度表达模型在比例尺上应是无极连续的,即在表达效果上实现要素形状随比例尺连续流畅的变化。然而,受限于人眼的识别能力,对于两个较为相近的地图比例尺所对应的地理要素,人眼并不能敏锐地感知两者之间所有的形状差异。因此在实际应用中,过于连续的地图比例尺是没有必要的。例如在基于矢量瓦片的电子地图渐进式传输过程中,瓦片的大小并不是完全连续可变的,而是通过固定的各层次瓦片大小实现地图的多尺度表达[19]。由此,本文借用原子中的电子跃迁模型,设计了一种离散的、量子化的地图分级层次模型。该模型基于要素信息量的变化将原始地理要素分解为有限个关键尺度,其中在关键比例尺之间属于要素表达的量变,而越过关键比例尺为质变,并以此为基础实现地图的多尺度表达。
根据地图传输理论,地图所传输的是空间信息。在地图综合过程中,地理要素的化简可以被认为是其所含形状信息量的衰减过程。对此,本文使用Fourier变换获取要素的形状描述子,以Shannon信息熵模型计算要素的形状信息量[20],通过信息量的Head-Tail逐级分割探寻要素的关键截止频率[21-26],并借助地图制图中的传统方根模型[27]建立信息量与比例尺之间的映射模型,提出了一种基于量子化关键尺度的地理要素多尺度表达方法。
1 地理要素的频率域信息量 1.1 曲线的傅里叶分析在空间域上,地理要素被描述为坐标串形式,对要素形状的化简常常着眼于局部细节,而在频域中,地理要素则是不同频率曲线波动的叠加,滤波是曲线化简的主要形式。相较于空间域,频域分析更侧重于要素全局的、整体上的形状信息。空间域地理要素上每一个点坐标的微小移动,都会导致频率域上所有频率振幅的改变。因此,在频域上分析地理要素,更能关注其整体的形状特征。
对于闭合的地理要素,将其从空间域转换到频率域一般是通过傅里叶变换的方法实现的。令X(s)、Y(s)分别表示以曲线长度s为自变量的地理要素横纵坐标函数,对其进行傅里叶变换可得
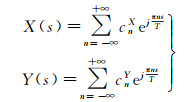 (1)
(1)
式中,j为虚数单位且j2=-1;n为傅里叶展开项数;T为函数的周期;{ejπns/T}n∈Ζ为一组傅里叶正交基;傅里叶系数cnX、cnY分别为
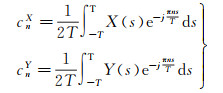 (2)
(2)
将地理要素引入复平面中,可得到其复数域的坐标表达式为P(s)=X(s)+jY(s)。对P(s)进行傅里叶变换,即可得到该地理要素的傅里叶系数cn
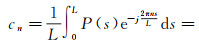
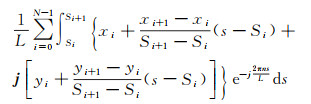 (3)
(3)
式中,xi、yi分别表示地理曲线第i个点的横纵坐标;Si为起始点P0到其余点Pi的曲线长度;L为该地理要素的长度。当傅里叶项数n取到足够大时,由傅里叶系数集ci可以完全还原出曲线的形状。分别取各个频率系数ci的模,即可得到该闭合地理要素的形状特征向量V,并称其为傅里叶描述子[14]
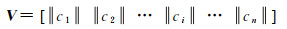 (4)
(4)
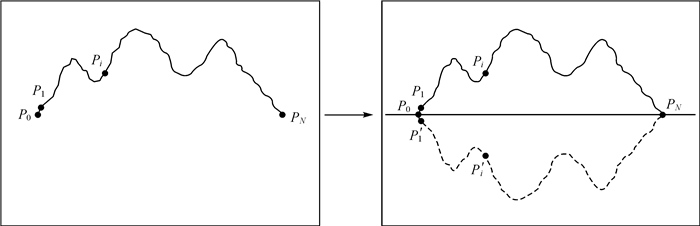
由于闭合地理要素的横纵坐标函数具有周期性,因此可以直接计算其形状特征向量。对于非闭合的地理要素,则需要对其进行镜像对称操作,使其获得周期性,如图 1所示。
|
| 图 1 对非闭合地理要素的镜像操作 Fig. 1 Mirror operation on unclosed geographic features |
随着傅里叶展开次数n的逐渐增大,经过傅里叶展开后的拟合曲线也会逐渐接近于原始曲线。当展开次数n足够大时,拟合曲线形状与原始曲线基本吻合。本文采用描述重合程度的面积重叠率来衡量拟合前后曲线的相似程度,并设定当该比率达到0.995时,傅里叶拟合曲线可以代替原始地理要素[14]。
1.2 地理要素的信息量对于信源H,其香农(Shannon)信息熵表示为[20]
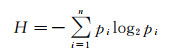 (5)
(5)
式中,pi为信源中的每个信息出现的概率。对于频域上的描述的曲线要素,pi则代表该要素的形状特征向量中每一项所占的比率,由式(6)可得到地理要素中每个频率所包含的信息量
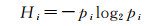 (6)
(6)
式中,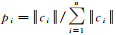
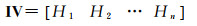 (7)
(7)
当地理要素的傅里叶变换展开至任意频率m时,该要素所包含的频域信息量Im由式(8)计算
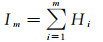 (8)
(8)
当式(8)中m足够大时,Im为地理要素的总信息量。地理要素的总信息量反映了该曲线的形状复杂程度:越复杂的曲线,其包含的频域信息量越大;越简单的曲线,其频域信息量就越少。
2 量子化地图尺度信息层次模型 2.1 量子化地图的关键尺度在电子跃迁理论中,电子在原子中不会绕任意半径的轨道运动,而只能在一组特定半径上的定态轨道上运动。根据玻尔辐射理论,电子只有在吸收或释放一个量子的能量时才会从一个定态轨道跃迁到另一个定态轨道[28]。在自然界中,电磁辐射的能量交换是量子化的,只能以离散的整数形式变化,而不能以绝对连续的形式递增或递减。同样,人对不同尺度地理要素之间形状差异的认知只是在一些关键尺度层次上的跳跃,在相邻两个关键尺度内的形状变化属于量变,受制于人眼的识别能力,人的认知较难体会其差异性。由此,本文借助量子模型,假定地图中要素表达的关键尺度同样也是离散量子化的。由于人的视觉存在延迟性,在比例尺的连续变化过程中,处于关键尺度之间的要素形态变化仍然可以通过视觉内插的方式获取,即量子化的地图虽然只有若干关键尺度的表达,但其在视觉上仍然是连续或接近连续的。因此,对于地图中的地理空间要素,本文尝试借助一种量子化的思想,并结合地图的关键尺度层次来达到地图多尺度表达的目的。
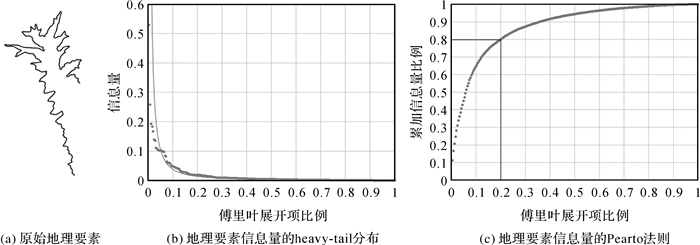
2.2 曲线信息量的Head-Tail分布傅里叶描述子所得到的曲线信息量反映了地理要素整体的复杂程度,但是却不能描述曲线各个频率信息量的比例关系。总体而言,地理要素的傅里叶低频部分反映要素的整体形状,高频部分反映要素的细节特征。从图 2(b)中不难发现地理要素的频域信息量在统计学上符合重尾分布(heavy-tail distribution)的模型;图 2(c)展示了地理要素的逐次累加信息量与傅里叶展开项数之间的关系,即较小部分的头部频率包含了大部分的要素信息量,而较大部分的尾部频率所含的信息量相对较少,符合Pareto法则的特点[29]。
|
| 图 2 地理要素的重尾分布及Pareto法则 Fig. 2 Heavy-tail distribution and Pareto's law of a geographical feature |
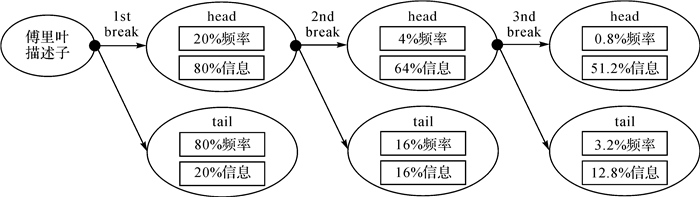
对于图 2中的地理要素,其Pareto法则可以表述为:20%的重要频率占据了80%的形状信息,80%的非重要频率占据了其余20%的形状信息。由此,Pareto法则将该要素的频率分成了两部分:头部的重要频率集以及尾部的非重要频率集。根据该法则就可以以地理要素各个频率所含的信息量为统计量,将不同的频率信号分割成两个部分,即占有绝大部分信息的Head部分和包含小部分信息量的Tail部分。根据Head-Tail数据分布模式,某些符合Heavy-Tail分布的数据集,其头部可以按照一定的比例继续分裂[21-22]。在实际应用中,Head部分仍可按Head-Tail模式继续分割,形成递归模式。如图 2(c),该地理要素的头部部分在一定程度上仍满足Pareto法则,只是在分割比率上会存在一定的差异。对于第i次分裂的地理要素信息向量,若其比例为pi的重要频率集占据了1-pi的形状信息,1-pi的非重要频率集占据了其余比例为pi的形状信息,则可记录其第n次头尾分裂的中断比例为pi,进而可以得到描述该数据集分布状况的分裂比例特征向量Vp=[p0 p1 p2…pi]。以满足“二八定律”的数据集为例,其Head-Tail分布如图 3所示。
|
| 图 3 满足“二八定律”地理要素的Head-Tail分布 Fig. 3 Head-Tail break of geographic features satisfying 80/20 principle |
图 3中,地理要素的初始状态将能够近似表达原始要素的n个傅里叶描述子作为信息总量,因此p0的默认值为1。在接下来的每次分割中,下一层次的头部仅保留上一层次傅里叶展开项数中20%的组成部分,同时包含其80%的信息内容,所以,其分裂比例特征向量Vp=[1.0 0.2 0.2 0.2]。而在一般情况下,在地理要素的信息向量IV中,各个pi的值都各不相等。本文设计了一个近似模型对除p0以外的每个pi值进行估计,如式(9)所示
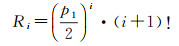 (9)
(9)
式中,Ri为第i次分裂时的头部在总信息量中所占比率的估计值,且pi=Ri/Ri-1(i≥0)。在式(9)中,R0=p0=1,表明信息向量IV是其自身的第0个Head-Tail分布的头部部分;R1=p1,代表信息向量IV的第1次分裂的头部比率;对于其他层次的头部比率,则可以通过p1来计算其近似值。表 1对5条地理要素进行了试验,并将估计值与实际值进行比较,结果表明通过近似比率得到的傅里叶估计头部展开项数与Head-Tail逐次分裂后的真实头部项数基本完全一致。
| 信息向量编号 (IVi) |
要素形状 | 分裂次数 i |
比率估计值 Ri |
实际展开项数 | 估计展开项数 |
| IV1 | 
|
0 | 1 | 1406 | 1406 |
| 1 | 0.165 | 232 | 232 | ||
| 2 | 0.041 | 58 | 57.418 | ||
| 3 | 0.014 | 19 | 18.948 | ||
| 4 | 0.006 | 8 | 7.816 | ||
| IV2 | 
|
0 | 1 | 666 | 666 |
| 1 | 0.171 | 114 | 114 | ||
| 2 | 0.044 | 29 | 29.270 | ||
| 3 | 0.015 | 11 | 10.021 | ||
| 4 | 0.006 | 5 | 4.288 | ||
| IV3 | 
|
0 | 1 | 480 | 480 |
| 1 | 0.190 | 91 | 91 | ||
| 2 | 0.054 | 25 | 25.878 | ||
| 3 | 0.020 | 9 | 9.812 | ||
| 4 | 0.009 | 4 | 4.651 | ||
| IV4 | 
|
0 | 1 | 89 | 89 |
| 1 | 0.146 | 26 | 26 | ||
| 2 | 0.021 | 10 | 11.393 | ||
| 3 | 0.003 | 5 | 6.657 | ||
| IV5 | 
|
0 | 1 | 22 | 22 |
| 1 | 0.364 | 8 | 8 | ||
| 2 | 0.198 | 4 | 4.364 |
将表 1中各层次傅里叶展开项的真实值与模拟值相比,证明了该模型具有较高的准确性,同时也实现了仅用p1一个参数对要素信息向量IV的层次化。该基于Head-Tail分布的层次化方式把地理要素的频率分为若干个重要等级,将包含相近形状信息量的频率划分为同一类别。再根据不同等级所对应的频率范围,即可还原出不同简化程度的地理要素。
2.3 地理要素的信息方根模型文献[27]提出的方根模型是进行地图综合时定量选择地图细节的基本原理,对根据较大比例的原始地图制作较小比例的地图具有重要的价值[27]
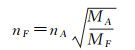 (10)
(10)
式中,nA与nF分别表示在原始地图和简化后地图上显示的地理对象数量;MA与MF表示原地图和简化地图的比例尺分母。根据该模型,如果已知nA、nF和MA,则MF可以通过MF=MA(nA/nF)2计算。从地图信息传输的角度来看,对地图进行化简将丢失源地图的部分信息内容。在对地图的化简过程中,随着地图比例尺分母的逐渐增大,其所包含的信息量也会相应减少。所以,方根模型可以揭示某些地图所含的信息内容与简化后地图之间的定量关系,因为对象的数量可能在某种程度上反映了它们的信息内容。因此,将方根模型与地理要素的频域信息量相结合,就可以得到一种用于量化每个重构曲线对应比例尺的“信息方根模型”,并进一步找出量化后的地理信息与地图比例尺之间的对应关系。其表达式为
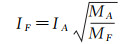 (11)
(11)
式中,IA和IF分别为地理要素在简化前后所包含的频域信息量。由该信息方根模型,结合地理要素的分裂比例特征向量Vp,即可得到与该要素各个分裂层次相对应的“关键尺度”
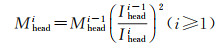 (12)
(12)
式中,Mheadi与Mheadi-1表示地理要素经过头部分割后的第i层次与第i-1层次的地图比例尺分母,Iheadi与Iheadi-1代表这两个分裂层次所对应的要素频域信息量。例如,当i=1时,第1次分裂的地图比例尺分母Mhead1可由原始地理要素的比例尺分母Mhead0以及与二者相对应的频域信息量求得,其他分裂层次依此类推。根据分裂比例特征向量的定义,比例为pi的频率占据了1-pi的形状信息,因此可以得出两个相邻层次的信息量比值Iheadi/Iheadi-1=1-pi。据此,结合式(12),即可得到地理要素的各个层次所对应的地图比例尺分母Mi
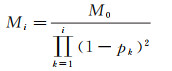 (13)
(13)
式中,M0为第0层次的地理要素,即原始地图的比例尺分母。结合式(9)、式(13),即可实现在仅计算地理要素第1次分裂比例p1的情况下,获取各分裂层次的比例尺分母预测结果
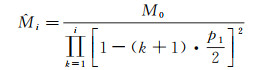 (14)
(14)
以表 1中的IV1为例,其原始地理要素的比例尺为1:5000。原始地理要素全部傅里叶展开项可视为第0层次的Head-Tail分割,因此,可以得到第0层次的地图比例尺分母M0=5000。对于IV1的第1个Head-Tail分割层次,由式(13),可以很容易求得其比例尺分母M1=7 171.408。依此类推,可以计算M2=12 749.17、M3=28 197.38、M4=84 126.06。另外,由式(14)可以通过参数p1计算出它们的估计值,即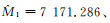
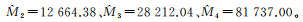
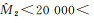
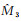
一般情况下,对于一个确定的地理要素,其分割层次是有限度的。因为当该要素分裂到一定层次时,其剩余的头部数据可能不再满足重尾分布或其重尾分布特征不够明显。因此,文献[23]将头部比例的阈值设置为40%,即分裂后头部的傅里叶展开项比例不能大于上一层次头部的40%。一旦分裂后的头部数据比例超过了该阈值限度,则其头部与尾部信息内容之间的差异会过小从而无法区分头部和尾部的重要性。根据此阈值,就可以找到该地理要素可以简化到的最大程度以及与其相对应的最小比例尺。
3 试验与分析 3.1 单独地理要素的分割层次分别选取4条不同复杂程度的闭合地理要素及非闭合地理要素,编号为IV1-IV8。使用Head-Tail分布模式并设置40%的头部阈值对其进行“量子化”层次分割。分割后的各层次结果如表 2所示。

|
表 2中显示了不同层次的地理要素所对应的傅里叶展开项数及相应的拟合形状。由于所有地理要素的分裂比例特征向量中的第1个值Vp(1)都等于1,因此第0层次的拟合形状为满足面积重叠比为0.995的展开次数n所对应的重构曲线,可以认为是原始折线的形状。对于其他的分割层次,地理要素每经过一次Head-Tail分裂,其头部部分的傅里叶展开项就越小,对要素细节的描述就越少,所对应重构曲线的形状就越简单。通过对8条地理要素的试验结果进行比较,可以发现要素各层级的拟合形状具有显著的差异,且层级越高,所含细部特征越少,具有明显的层次性。由此可以说明,该模型可以很好地建立折线的多尺度层次结构。此外,通过设置头部比例的阈值(40%),可以获得要素可以简化到的极限形状,同时也可以避免发生曲线过度简化的情况。
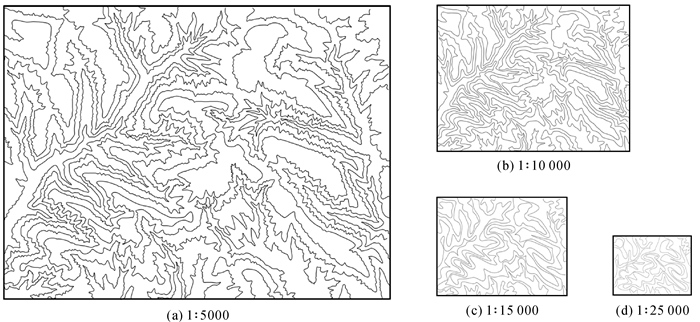
3.2 等高线试验结果分析本文采用山西省某区域的部分等高线作为试验数据,根据原数据的地图比例尺设定不同的目标比例尺,并使用上文中提出的信息方根模型得到等高线各个层次的傅里叶展开项数。最后将地理要素进行重构,并删掉层次差距过大的部分地理要素,最终得到与目标比例尺相对应的要素形状。试验结果如图 4、图 5所示。

|
| 图 4 使用信息方根模型的等高线多尺度表达 Fig. 4 Multi-scale representation of contours using the information radical model |
|
| 图 5 实际尺寸对比下的等高线多尺度表达 Fig. 5 Multi-scale representation of contours under correct size contrast |
图 4和图 5分别显示了等高线在4个不同比例尺下的化简结果。图 4采用了相同大小的显示区域,而图 5则采用了真实大小的显示区域。由图 5可以发现,在比例尺从1:5000至1:25 000的变化过程中,等高线形状的简化程度越来越大,但其主要形状特征仍然保持不变。在不同的设定比例尺下,等高线的形状显示出了较为明显的复杂度差异,在视觉上具有良好的表达效果。此外,由于山脊线与山谷线是等高线数据上的重要形态特征,随着地图的逐渐简化,等高线的细节特征逐渐减少,某些山脊线与山谷线就会随着地图比例尺的减小而逐渐消失。图 6显示了在地图的4个尺度上较为明显的山脊线与山谷线的形态与数量,同时,在得到1:5000原始比例尺山脊线与山谷线数量的基础上,表 3根据式(10)中的传统方根模型,对其他3个比例尺的线条数量进行预测,并与实际数量进行了对比。
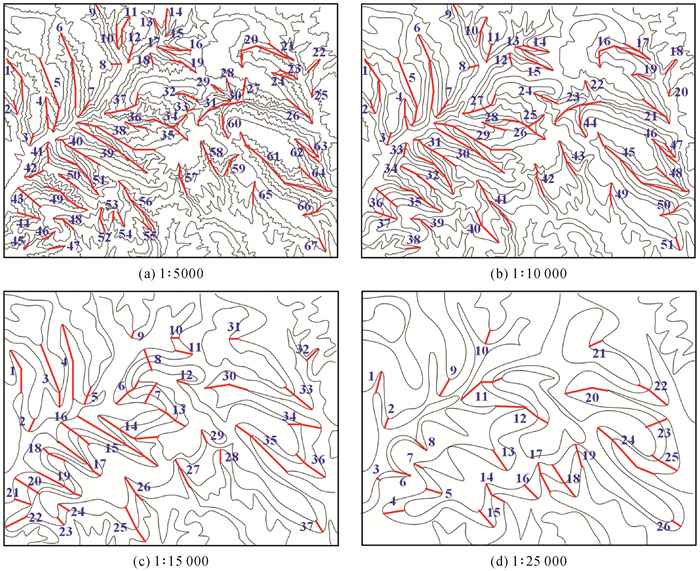
|
| 图 6 不同尺度下的山脊线与山谷线 Fig. 6 Ridge line and valley line at different scales |
| 地图比例尺 | 实际数量 | 预测数量 | 误差率/(%) |
| 1:5000 | 67 | — | — |
| 1:10 000 | 51 | 47.376 | 7.1% |
| 1:15 000 | 37 | 38.682 | 4.5% |
| 1:25 000 | 26 | 29.963 | 15.2% |
由图 6可以看出,随着地图比例尺的逐渐减小,等高线数据间的山脊线与山谷线数量也会随之减少。例如,在较大尺度的地图中,图 6(a)中的线段8、40、67以及图 6(b)中的线段8、38、44在尺度变小的过程中逐渐消失;而当比例尺减小到1:25 000时,简化后的地图仅保留了一些较为关键的山脊线与山谷线形态特征,例如图 6(d)中的线段12、20、24,在4个尺度的地图中均被保留。此外,根据表 3中山脊线与山谷线数量的预测值与实际值对比结果,可以发现地图各个层次比例尺上的山脊线与山谷线数量大致上与传统方根模型的预测结果相符合,且误差率相对较低。这也验证了使用本文方法所得到的地图多尺度表达效果是符合地图综合规律的。
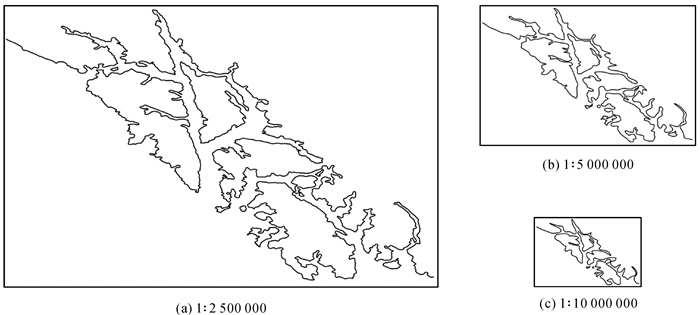
3.3 与经典简化方法的对比分析采用美国某沿海区域的部分海岸线作为试验数据,并设置不同的目标比例尺。试验结果如图 7所示。
|
| 图 7 实际尺寸对比下的海岸线多尺度表达 Fig. 7 Multi-scale representation of coastlines under correct size contrast |
由图 7可以看出,本文模型对于较复杂的海岸线数据,根据设定的目标比例尺所得出的结果同样在视觉上具有较强的层次性。因此,综合图 4—图 7可以得出结论:无论对于小比例尺地图还是大比例尺地图,使用本文模型对地理要素进行多尺度表达均取得较好的效果。为验证本文模型的可行性与优越性,将本文模型与传统的Douglas-Peucker简化算法及Wang-Müller简化算法进行比较,在1:5 000 000与1:10 000 000两个比例尺上,控制原要素与3个简化模型化简后的面积重叠比一致,并得到相对应的要素简化形状。试验对比结果如图 8所示。
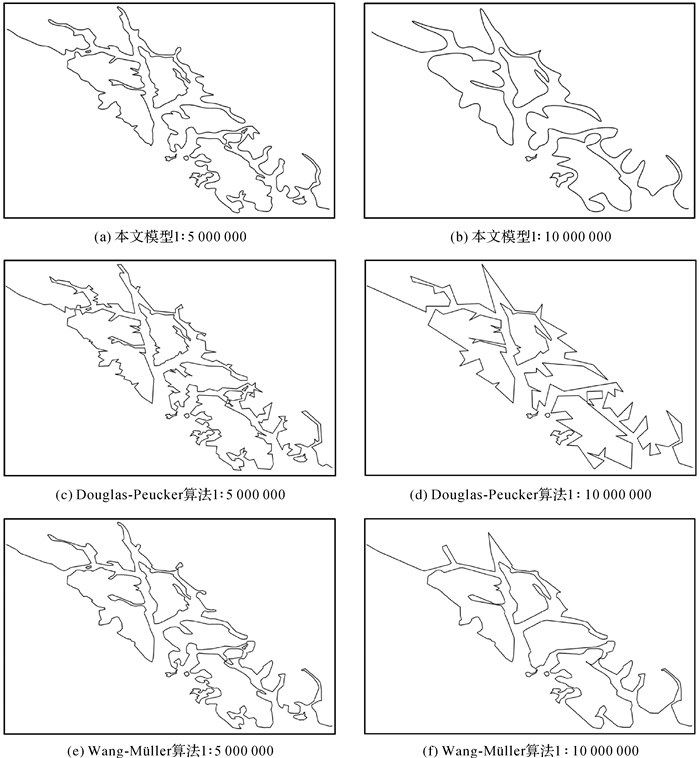
|
| 图 8 本文模型与Douglas-Peucker算法及Wang-Müller算法的对比结果 Fig. 8 Comparison of the proposed model with Douglas-Peucker algorithm and Wang-Müller algorithm |
另外,根据图 8中所得到的要素简化结果,本文根据文献[30]所提出的相似性度量方法,分别选取经过3种方法简化后的3条地理要素,并评估其与原始要素的相似程度。如表 4所示。其中,要素的相似距离越短,代表简化要素与原始要素之间的相似度越高。
| 比例尺 | 要素编号 | 本文算法 | Douglas-Peucker 算法 |
Wang-Müller 算法 |
| 1:5 000 000 | feature 1 | 1.072 | 1.223 | 1.007 |
| feature 2 | 0.632 | 0.662 | 0.679 | |
| feature 3 | 0.746 | 1.617 | 0.921 | |
| 1:10 000 000 | feature 1 | 1.536 | 1.464 | 1.541 |
| feature 2 | 0.642 | 0.717 | 0.677 | |
| feature 3 | 0.948 | 1.238 | 0.984 |
对比图 8(a)、(c)、(e)可以发现当设定的地图比例尺为1:5 000 000时,本文模型所得到的要素形状最为平滑,Wang-Müller算法效果次之,而Douglas-Peucker算法的简化结果则出现了较明显的棱角;同样,对比图 8(b)、(d)、(f),当设定的地图比例尺为1:10 000 000时,本文模型得到的要素形状在删除了细节形状特征的基础上,仍较好地保证了地理要素的平滑性,使化简结果更符合人类的观察特征,其他两种传统简化算法,在该比例尺较小的情况下则出现了不同程度的尖角。此外,通过对比表 4中3种算法所得到的简化结果与原始要素的相似距离可知,采用本文所提出的多尺度表达简化方法在大多数情况下与原始要素的相似程度优于Wang-Müller算法及Douglas-Peucker算法。因此,可以认为本文所采用的量子化地图尺度信息层次模型的多尺度表达效果优于这两种传统的要素简化算法。
4 结论本文以地理要素的傅里叶变换为基础,结合香农信息熵理论计算地理要素的频域信息量,实现了对地理要素所含形状信息的量化。鉴于人的识别特征,以Head-Tail数据分布模式为基础,建立了离散式的量子化地图层次模型,借用传统的方根模型度量信息量与比例尺之间的映射关系,以此建立了一种量子化的地图信息传输模型,并应用于地图的多尺度表达。试验结果表明:对于单个地理要素,使用本文提出的模型对地理要素进行化简所得到的结果具有良好的层次性;对于一片区域的地图数据,根据设定的目标比例尺,使用本文模型所得出的简化形状同样具有良好的表达效果及较好的区分性。然而,对于某些特殊地貌而言,由于其等高线的分布可能过于密集,从而导致本文提出的模型有些情况下会出现曲线自相交和互相交的拓扑冲突,此时需要人工干预。另外,对于信息量与比例尺度量的不确定性问题,也需要在今后的研究中继续探索。
| [1] |
毋河海. 地图信息自动综合基本问题研究[J]. 武汉测绘科技大学学报, 2000, 25(5): 377-386. WU Hehai. Research on fundamental theory and technical approaches of automated map generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 377-386. |
| [2] |
王家耀. 空间数据自动综合研究进展及趋势分析[J]. 测绘科学技术学报, 2008, 25(1): 1-7, 12. WANG Jiayao. The progress and trend of automatic generalization of spatial data[J]. Journal of Geomatics Science and Technology, 2008, 25(1): 1-7, 12. |
| [3] |
贾奋励.电子地图多尺度表达的理论与方法的研究[D].郑州: 信息工程大学, 2002. JIA Fenli. Research on the theories & methods of electronic map's multi-scale representation[D]. Zhengzhou: Information Engineering University, 2002. |
| [4] |
贾奋励.电子地图多尺度表达的研究与实践[D].郑州: 信息工程大学, 2010. JIA Fenli. Research and practice of electric map multi-scale representation[D]. Zhengzhou: Information Engineering University, 2010. |
| [5] |
艾廷华, 成建国. 对空间数据多尺度表达有关问题的思考[J]. 武汉大学学报(信息科学版), 2005, 30(5): 377-382. AI Tinghua, CHENG Jianguo. Key issues of multi-scale representation of spatial data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 377-382. |
| [6] |
DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica:The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112-122. |
| [7] |
LI Zhilin, OPENSHAW S. Algorithms for automated line generalization based on a natural principle of objective generalization[J]. International Journal of Geographical Information Systems, 1992, 6(5): 373-389. |
| [8] |
WANG Zeshen, MVLLER J C. Line generalization based on analysis of shape characteristics[J]. Cartography and Geographic Information Systems, 1998, 25(1): 3-15. |
| [9] |
刘鹏程, 罗静, 艾廷华, 等. 基于线要素综合的形状相似性评价模型[J]. 武汉大学学报(信息科学版), 2012, 37(1): 114-117. LIU Pengcheng, LUO Jing, AI Tinghua, et al. Evaluation model for similarity based on curve generalization[J]. Geomatics and Information Science of Wuhan University, 2012, 37(1): 114-117. |
| [10] |
刘鹏程, 艾廷华, 毕旭. 傅立叶级数支持下的等高线多尺度表达模型[J]. 武汉大学学报(信息科学版), 2013, 38(2): 221-224. LIU Pengcheng, AI Tinghua, BI Xu. Multi-scale representation model for contour based on fourier series[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2): 221-224. |
| [11] |
刘鹏程, 龚冲亚, 陶建斌, 等. 基于图形渐变技术的等高线连续尺度表达模型[J]. 地理科学, 2014, 34(3): 332-337. LIU Pengcheng, GONG Chongya, TAO Jianbin, et al. The continual scale representation model for contour based on morphing technique[J]. Scientia Geographica Sinica, 2014, 34(3): 332-337. |
| [12] |
刘鹏程, 艾廷华, 杨敏. 基于傅里叶级数的等高线网络渐进式传输模型[J]. 测绘学报, 2012, 41(2): 284-290. LIU Pengcheng, AI Tinghua, YANG Min. The internet progressive transmission model for contour based on Fourier series[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 284-290. |
| [13] |
LIU Pengcheng, LI Xingong, LIU Weibo, et al. Fourier-based multi-scale representation and progressive transmission of cartographic curves on the internet[J]. Cartography and Geographic Information Science, 2016, 43(5): 454-468. |
| [14] |
肖天元, 刘鹏程, 艾廷华, 等. 一种基于信息度量的傅里叶展开曲线分形描述方法[J]. 武汉大学学报(信息科学版), 2020, 45(1): 119-125. XIAO Tianyuan, LIU Pengcheng, AI Tinghua, et al. A fractal description method of Fourier expansion curve based on information metrics[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 119-125. |
| [15] |
李精忠, 方文江. 顾及邻域结构的线状要素Morphing方法[J]. 武汉大学学报(信息科学版), 2018, 43(8): 1138-1143. LI Jingzhong, FANG Wenjiang. Morphing polylines by preserving local neighborhood structures[J]. Geomatics and Information Science of Wuhan University, 2018, 43(8): 1138-1143. |
| [16] |
李精忠, 张津铭. 一种基于傅里叶变换的光滑边界面状要素Morphing方法[J]. 武汉大学学报(信息科学版), 2017, 42(8): 1104-1109. LI Jingzhong, ZHANG Jinming. A morphing method for smooth area features based on Fourier transform[J]. Geomatics and Information Science of Wuhan University, 2017, 42(8): 1104-1109. |
| [17] |
方文江, 李精忠. 一种基于形状上下文特征匹配的线状要素Morphing方法[J]. 武汉大学学报(信息科学版), 2017, 42(7): 963-967. FANG Wenjiang, LI Jingzhong. A Morphing of linear feature based on shape context matching[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 963-967. |
| [18] |
谢天, 李精忠, 陈凯. 顾及线状要素综合要求的Morphing算法[J]. 武汉大学学报(信息科学版), 2018, 43(5): 792-797. XIE Tian, LI Jingzhong, CHEN Kai. Morphing algorithm for linear feature considering generalization requirements[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5): 792-797. |
| [19] |
唐雅玲, 马晨燕, 宋佳, 等. 矢量Web网络地图应用研究[J]. 测绘与空间地理信息, 2018, 41(2): 77-80, 83. TANG Yaling, MA Chenyan, SONG Jia, et al. Research on the application of vector web mapping[J]. Geomatics & Spatial Information Technology, 2018, 41(2): 77-80, 83. |
| [20] |
SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(3): 379-423. |
| [21] |
JIANG Bin. Head/Tail breaks for visualization of city structure and dynamics[J]. Cities, 2015, 43: 69-77. |
| [22] |
JIANG Bin. Head/Tail breaks:a new classification scheme for data with a Heavy-Tailed distribution[J]. The Professional Geographer, 2013, 65(3): 482-494. |
| [23] |
JIANG Bin, LIU Xintao, JIA Tao. Scaling of geographic space as a universal rule for map generalization[J]. Annals of the Association of American Geographers, 2013, 103(4): 844-855. |
| [24] |
MA Ding, JIANG Bin. A smooth curve as a fractal under the third definition[J]. Cartographica:The International Journal for Geographic Information and Geovisualization, 2018, 53(3): 203-210. |
| [25] |
JIANG Bin, BRANDT S A. A fractal perspective on scale in geography[J]. ISPRS International Journal of Geo-Information, 2016, 5(6): 95-106. |
| [26] |
JIANG Bin, MA Ding. How complex is a fractal? Head/Tail breaks and fractional hierarchy[J]. Journal of Geovisualization and Spatial Analysis, 2018, 2(1): 6. |
| [27] |
TÖPFER F, PILLEWIZER W. The principles of selection[J]. The Cartographic Journal, 1966, 3(1): 10-16. |
| [28] |
杨福家. 原子物理学[M]. 北京: 高等教育出版社, 1998. YANG Fujia. Atomic physics[M]. Beijing: Higher Education Press, 1998. |
| [29] |
MONGIN P. Spurious unanimity and the Pareto principle[J]. Economics & Philosophy, 2016, 32(3): 511-532. |
| [30] |
ARKIN E M, CHEW L P, HUTTENLOCHER D P, et al. An efficiently computable metric for comparing polygonal shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(3): 209-216. |



