2. 东北大学, 辽宁 沈阳 110819;
3. 武汉大学测绘学院, 湖北 武汉 430079;
4. 中国测绘科学研究院, 北京 100036
2. Northeastern University, Shengyang 110819, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
4. Chinese Academy of Surveying&Mapping, Beiing 100036, China
洋底约占据了固体地球70%的表面积,海底地形(深度)测量是海洋测绘的基本内容之一。传统上海底地形测量基于回声定位原理,利用船舶装载专业测量设备实施[1]。但是,由于船舶航行速度慢且海洋面积巨大,基于现代船测技术手段完成全球海底地形测量预计需要100~200年时间和数十亿美元的资金,且短期内难以实现[2-4]。因此,自20世纪80年代起,学者们开始研究利用卫星测高资料反演海底地形的技术,并于1997年公布了第一个联合卫星测高重力异常和船测水深数据构建的全球海底地形模型[5-7]。国内也有多家研究机构开展了海底地形模型反演的研究工作,并取得了大量成果[8-15]。目前,海底地形反演方法主要可分为频域法[6-7]、空域法(解析法)[16-18]和最小二乘配置法(统计算法)[19-20] 3大类。文献[13, 21]通过算例试验研究了上述反演方法的优劣,综合计算精度、效率,以及对先验模型的依赖程度等,分析认为频域法相对较优,是当前海底地形反演的主流方法。
笔者所在的课题组是国内较早开展卫星测高及其地球科学应用研究的课题组之一,自20世纪90年代以来取得了系列研究成果,并发表了基于卫星测高资料的全球海面高、海洋潮汐、海底地形和重力异常等系列模型产品[22-25],形成了完整的技术能力。目前,利用多源卫星测高资料,课题组构建了新版全球卫星测高重力异常模型[25-27]。本文结合该重力异常模型和全球船测水深数据,构建新一版的全球海底地形模型BAT_WHU2020,并通过与船测水深、国际上公开的SIO V19.1[7](SIO:Scripps Institute of Oceanography,斯克里普斯海洋研究所)、ETOPO1[28]、DTU10[29](DTU:Denmarks Tekniske Universitet,丹麦科技大学)、GEBCO_08[30](General Bathymetric Chart of the Oceans)等海底地形模型,联合船测水深和卫星测高重力垂直梯度异常构建的海底地形模型BAT_VGG[13, 24],以及多波束测深海底地形的比较,分析了BAT_WHU2020模型的精度水平。
1 海底地形反演理论根据挠曲均衡理论[31],在海山h(x)的载荷作用下,洋壳莫霍面(Moho)发生挠曲形变r(x)。因而,产生海面重力异常的主要异常场源是海底地形及其均衡补偿物质。根据文献[32]给出的频域内位场计算级数展开公式(Parker公式),同时顾及海底地形h(x)及其均衡补偿r(x)的影响,则海底地形产生的重力异常为
 (1)
(1)
式中,ΔG(k)为重力异常傅里叶变换;G为万有引力常数;ρm、ρc、ρw分别为地幔、地壳和海水密度;d为平均水深;t为平均洋壳厚度;R(k)、H(k)分别为r(x)、h(x)的傅里叶变换,k=2π/λ,λ为地形波长。在频域内
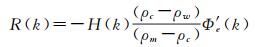 (2)
(2)
式中,Φe′(k)称为挠曲响应函数[33]
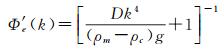 (3)
(3)
式中,D为岩石圈抗挠刚度,D=ETe3/[12(1-υ2)];E为杨氏模量;Te为有效弹性厚度;υ为泊松比;g为重力加速度。
一般情况下,式(1)收敛很快,当仅取该式线性项(n=1),同时顾及式(2)、式(3)时,海底地形产生的重力异常可表达为
 (4)
(4)
即由海底地形至海面重力异常的导纳函数(转换函数)为
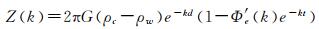 (5)
(5)
它主要由系数2πG(ρc-ρw)、指数衰减函数exp(k)和均衡响应函数φ(k) 3部分构成
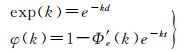 (6)
(6)
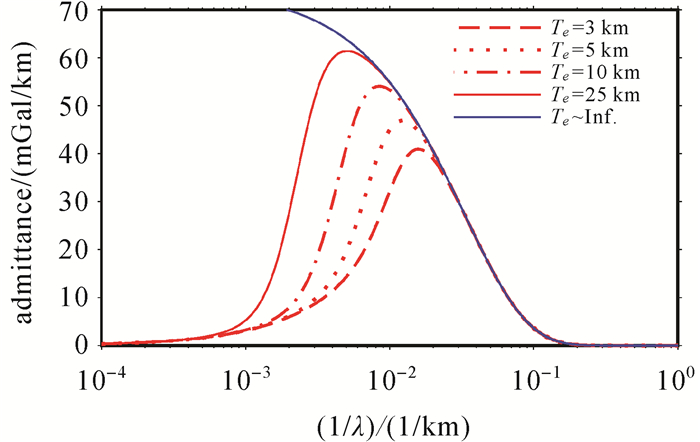
采用表 1中的地壳模型参数,式(6)中指数衰减函数犹如低通滤波器(图 1蓝色实线),而均衡响应函数犹如高通滤波器(图 1),两者组合形成的导纳函数(式(5))形态将如带通滤波器(图 2)。
| 地壳参数 | 公式中的符号 | 参数取值 |
| 海水密度/(kg/m3) | ρw | 1030 |
| 海山密度/(kg/m3) | ρc | 2800 |
| 地幔密度/(kg/m3) | ρm | 3350 |
| 平均洋壳厚度/km | t | 6.5 |
| 平均水深/km | d | 4.5 |
| 有效弹性厚度/km | Te | 3、5、10、25 |
| 杨氏模量/(N/m2) | E | 1011 |
| 泊松比 | υ | 0.25 |

|
| 图 1 均衡响应函数φ(k)与指数衰减函数exp(k) Fig. 1 Isostatic response function φ(k) and exponential decay function φ(k) |
|
| 图 2 挠曲均衡导纳函数Z(k) Fig. 2 Flexural isostatic admittance function Z(k) |
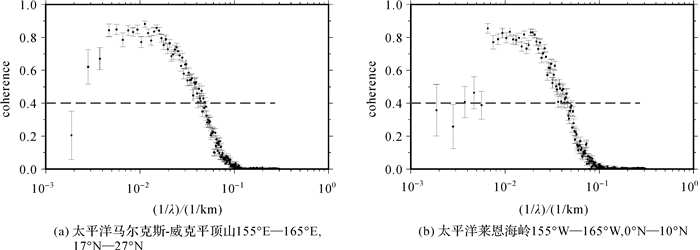
从图 2所示的理论导纳函数看,受均衡补偿和水深延拓效应影响,海面重力异常与海底地形仅在中短波段存在较强的相关性。事实上,在典型海山、海山链等地貌区海底地形与海面重力异常的相干性如图 3所示,仅在中短波段内相干性超过0.4。
|
| 图 3 典型海山区域和海山链的海底地形与重力异常相干性 Fig. 3 The coherence between bathymetry and gravity in the typical seamounts area |
因此,基于挠曲均衡原理,重力异常通常仅用于反演中短波段(10~200 km)的海底地形,而船测水深资料则用于构建长波(> 200 km)海底地形[6-15]。本文基于上述原理,联合船测水深和卫星测高重力异常资料构建了全球海底地形模型BAT_WHU2020。
2 数据来源 2.1 卫星测高重力异常卫星测高技术已成为获取全球海洋重力场最重要的技术手段之一。同时,自20世纪90年代以来,卫星测高重力异常也成为全球海底地形反演的主要数据源。随着ERS、T/P、Jason、CryoSat-2等测高卫星的发射,卫星测高重力异常的空间分辨率和精度逐步提高,并陆续被应用于研制系列海底地形模型[4, 7, 24, 34-35]。
本文采用的1′×1′卫星测高重力异常Grav_Alti_WHU是联合Geosat、ERS-1、ERS-2、Envisat、T/P、Jason-1、CryoSat-2和SARAL/AltiKa等多颗卫星波形资料获取的垂线偏差信息反演的[25],如图 4所示。数据处理过程中改进了波形重跟踪算法,选定了较优的沿轨重采样频率[26-27],在北太平洋海域、墨西哥湾海域与NGDC(National Geophysics Data Center)船测数据之差的均方根约为4 mGal(1 mGal=10-5 m/s),模型精度与SIO V23.1重力异常模型相当,优于DTU10重力异常模型。

|
| 图 4 全球海洋卫星测高重力异常模型Grav_Alti_WHU Fig. 4 Global oceanic gravity grid derived from altimetry data |
2.2 船测水深
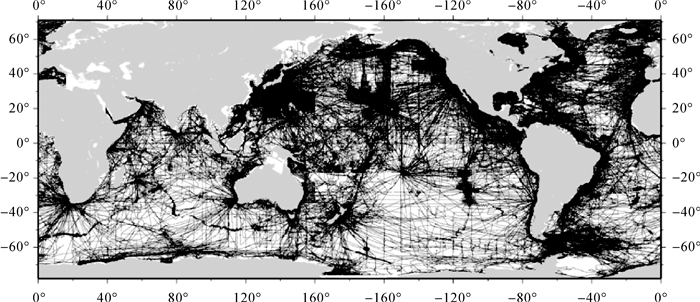
船测水深数据为来自NGDC的数据集,共约44.5百万点,其分布如图 5所示。NGDC数据集已按文献[36]中方法进行过处理和校正,但仍有部分数据存在明显偏差。因此,本文在海底地形模型构建过程中,参考已有海底地形模型[24],逐一计算反演区域内船测水深与模型之差,并剔除水深与模型之差大于3倍标准差的船测值,共剔除约2.7百万点,约占总数据量的6%,余下数据中的80%用于海底地形反演,20%用于最终成果精度检核。
|
| 图 5 来自NGDC的全球船测水深数据分布 Fig. 5 Shipboard depths from NGDC |
3 数据处理
由上文可知,在较短波段内(< 200 km)式(4)中的均衡响应函数部分可以忽略,则由海面重力异常反演海底地形的计算公式为
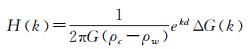 (7)
(7)
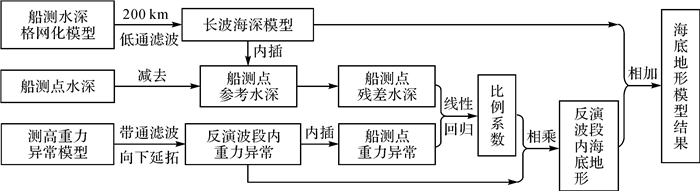
最终海底地形模型将由两部分构成:①由船测水深构建的长波(> 200 km)海深模型;②由重力异常反演的中短波段(约10~200 km)海底地形,数据处理流程如图 6所示。
|
| 图 6 联合船测水深和卫星测高重力异常构建海底地形模型的数据处理流程 Fig. 6 Data processing flow for bathymetry constructing from altimetric gravity anomalies and shipboard depths |
根据图 6所示流程图,联合船测水深和测高重力异常反演水深大于100 m区域的海底地形(陆地及水深浅于100 m区域取SIO V19.1模型值),以2°×2°格网对数据进行分块处理,主要数据处理步骤包括:
(1) 构建长波海深模型hlong(x)。由船测水深格网化后,进行200 km高斯低通滤波处理即可。
(2) 构建反演波段内重力异常δg(x)。采用带通滤波、向下延拓等处理后获得反演波段内重力异常。
(3) 计算反演波段内海底地形与重力异常之比例系数S(x)。内插计算船测点残差水深和反演波段内重力异常,并进行线性回归分析即可获得比例系数。
(4) 计算最终海底地形模型
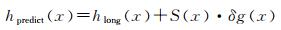 (8)
(8)
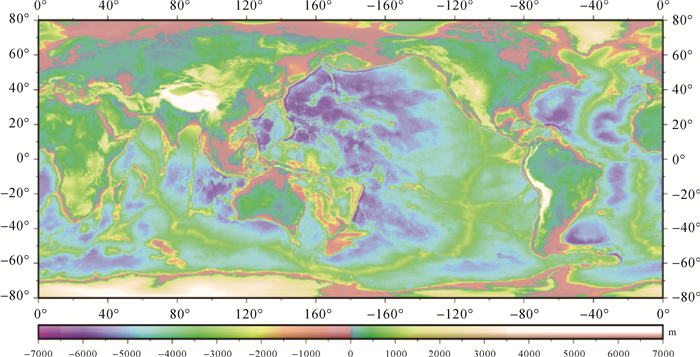
本文利用新构建的全球卫星测高重力异常模型Grav_Alti_WHU(图 4)和船测水深(图 5),根据图 6所示数据处理方法,构建了全球75°S—70°N范围内1′×1′海底地形模型BAT_WHU2020,如图 7所示。模型水平和垂直参考系分别为WGS-84和平均海平面。本节利用未参与计算的船测水深数据对BAT_WHU2020模型在中国海域及邻区,以及全球的精度进行评估,并将其与国际上已有的同等格网分辨率模型(SIO V19.1、ETOPO1、GEBCO_08、DTU10)进行对比分析。SIO V19.1模型由于持续收集了多代卫星测高资料和船测数据[4, 35, 37-38],可以认为其精度水平在上述各模型中最高。ETOPO1模型的大洋地区水深主要是来自SIO的早期模型(2008年)[28]。GEBCO_08模型的最大数据源是历史数字化的等深线数据(主要是500 m等深线数据,部分地区还加入了100、200 m等深线数据)[30]。DTU10是联合GEBCO_08模型和卫星测高重力异常构建的模型,重力异常主要用于反演20~120 km波段的海底地形[29]。
|
| 图 7 全球1′×1′海底地形模型BAT_WHU2020 Fig. 7 The 1′×1′ global bathymetry model BAT_WHU2020 |
4.1 中国海域及邻区模型精度
中国海域及邻区(104°E—160°E,0°N—50°N)海底地形模型反演结果如图 8所示,清晰反映了自中国海域至西太平洋的边缘海、沟-弧-盆等地貌特征。
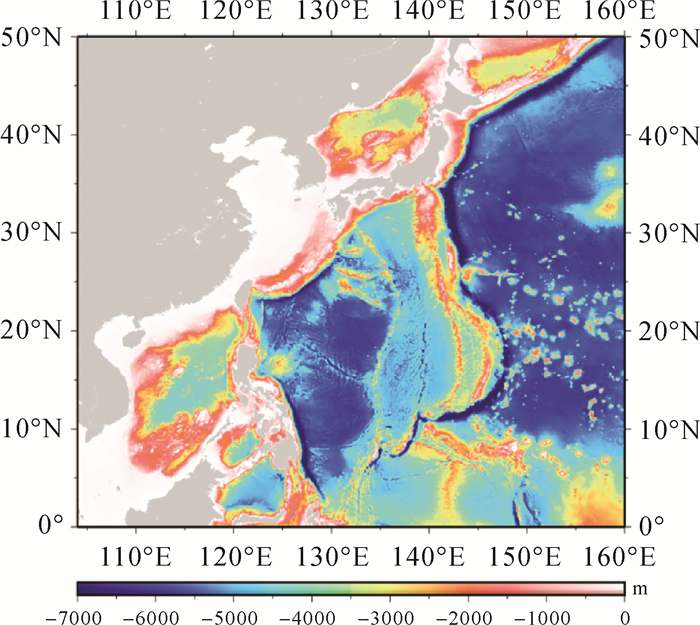
|
| 图 8 中国海域及邻区1′×1′海底地形模型 Fig. 8 The 1′×1′ bathymetry grid in China Sea and its adjacent areas |
以船测水深检核模型精度,中国海域及邻区共有船测检核点约79.7万个,模型值与船测点实测值之差分布见图 9,差值统计见表 2。

|
| 图 9 中国海域及邻区海底地形模型与船测水深之差值的空间分布和频率分布 Fig. 9 The distribution and frequency histogram of differences between bathymetry model and shipboard depths in China Sea and its adjacent areas |
| 模型 | 最小值/m | 最大值/m | 平均值/m | 标准差/m | 相对精度/(%) | 备注 |
| BAT_WHU2020 | -3 270.000 | 2 741.000 | 1.304 | 113.456 | 2.84 | 一次检核 |
| -340.300 | 340.200 | 2.324 | 69.657 | 1.74 | 二次检核,数据保留率97.91% | |
| 本文,利用SIO重力异常反演 | -3 290.000 | 2 742.000 | 1.054 | 112.623 | 2.82 | 一次检核 |
| -337.800 | 337.800 | 2.285 | 69.050 | 1.73 | 二次检核,数据保留率97.77% | |
| 本文,利用DTU重力异常反演 | -3 278.000 | 2 733.000 | 1.420 | 114.809 | 2.87 | 一次检核 |
| -344.400 | 344.300 | 2.509 | 70.529 | 1.76 | 二次检核,数据保留率97.73% | |
| SIO V19.1 | -3 448.000 | 3 103.000 | -9.209 | 111.223 | 2.78 | 一次检核 |
| -333.600 | 333.500 | -6.628 | 64.635 | 1.62 | 二次检核,数据保留率98.22% | |
| DTU10 | -3 389.000 | 2 856.000 | 8.489 | 234.448 | 5.86 | 一次检核 |
| -703.300 | 703.100 | 15.684 | 185.326 | 4.63 | 二次检核,数据保留率98.20% | |
| ETOPO1 | -3 495.000 | 2 945.000 | -5.547 | 183.062 | 4.58 | 一次检核 |
| -549.000 | 549.000 | -0.317 | 128.802 | 3.22 | 二次检核,数据保留率97.54% | |
| GEBCO_08 | -4 886.100 | 4 370.000 | 10.116 | 274.610 | 6.87 | 一次检核 |
| -823.600 | 823.300 | 19.521 | 189.278 | 4.73 | 二次检核,数据保留率98.06% | |
| BAT_VGG | -2 896.000 | 2 757.000 | 8.678 | 142.187 | 3.55 | 一次检核 |
| -426.500 | 426.500 | 7.068 | 101.278 | 2.53 | 二次检核,数据保留率97.76% |
从图 9可看出,本文构建的模型与船测水深一致性良好,两者差值在20 m以内的占比55.91%,100 m以内的占比86.58%,250 m以内的占比达96.06%。
表 2首先给出了基于Grau Alti WHU重力异常模型,以及SIO V23.1重力异常模型和DTU10重力异常模型反演的海底地形模型精度,3种模型一次检核精度可达约110 m,剔除大于3倍标准差的船测点后(数据保留率均超过97%),二次检核精度可达约70 m,说明本文海底地形模型构建过程中采用的数据源和数据处理方法可靠。
表 2同时给出了对国际上发布的SIO V19.1、DTU10、ETOPO1、GEBCO_08等海底地形模型,以及联合船测水深和重力垂直梯度异常构建的海底地形模型BAT_VGG[18]的精度检核统计值,显示SIO V19.1模型具有最高的精度,而本文模型BAT_WHU2020与SIO V19.1精度水平在同一量级,优于DTU10、ETOPO1和GEBCO_08模型,较此前发布的海底地形模型BAT_VGG精度提高了约30%。
本文模型较DTU10、ETOPO1和BAT_VGG模型精度有所提高,主要是因为采用了新的卫星测高重力异常数据,该数据中加入了CryoSat-2、SARAL/AltiKa等较新高精度卫星测高资料,并改善了波形重跟踪等算法[25-27]。与GEBCO_08模型相比,除了数据源不同外,模型构建过程也不一样,GEBCO_08模型主要依据了历史测深等值线数据进行格网化[30],本文则直接利用船测水深和卫星测高重力异常进行融合反演。
4.2 全球模型精度从表 2统计结果和有关文献看[4, 24, 35],SIO发布的系列海底地形模型由于持续加入了新的卫星测高和船测水深资料,其精度代表了当前全球海底地形模型的先进水平。下文主要通过与船测水深和SIO V19.1模型的对比来分析本文模型BAT_WHU2020(图 7)的精度水平。
4.2.1 各类全球海底地形模型与船测水深对比表 3给出了BAT_WHU2020、SIO V19.1、ETOPO1、DTU10、GEBCO_08、BAT_VGG等全球模型与船测水深之差在全球大洋的分区统计,将全球大洋共划分为北太平洋(120°E—280°E,0°N—61°N)、南太平洋(120°E—300°E,-75°N—0°N)、大西洋(-60°E—20°E,-75°N—0°N;-80°E—0°E,0°N—70°N)和印度洋(20°E—120°E,-75°N—26°N) 4个大区进行模型与船测水深之差的统计。从表 3可看出,BAT_WHU2020模型与船测水深相比,剔除大于3倍标准差的船测点后(数据保留率均达到约98%)二次统计标准差为50~65 m,总体精度水平与SIO V15.1模型相当,优于ETOPO1、DTU10、GEBCO_08模型,较此前发布的海底地形模型BAT_VGG精度提高了27%~36%。
| 统计地区 | 模型 | 最小值/m | 最大值/m | 平均值/m | 标准差/m | 相对精度/(%) |
| 北太平洋 | BAT_WHU2020 | -290.400 | 290.400 | 1.874 | 58.111 | 1.35 |
| SIO V19.1 | -284.900 | 284.900 | -5.683 | 55.866 | 1.30 | |
| ETOPO1 | -494.100 | 494.100 | -3.022 | 111.416 | 2.59 | |
| DTU10 | -667.500 | 667.500 | 4.977 | 169.430 | 3.94 | |
| GEBCO_08 | -828.500 | 828.500 | 10.838 | 191.272 | 4.45 | |
| BAT_VGG | -345.900 | 345.900 | 4.642 | 80.233 | 1.87 | |
| 南太平洋 | BAT_WHU2020 | -262.600 | 262.600 | 2.542 | 54.604 | 1.44 |
| SIO V19.1 | -271.900 | 271.900 | -3.565 | 55.576 | 1.46 | |
| ETOPO1 | -517.400 | 517.400 | -2.126 | 126.760 | 3.34 | |
| DTU10 | -751.500 | 751.500 | 1.249 | 186.504 | 4.91 | |
| GEBCO_08 | -944.900 | 944.900 | 4.854 | 216.986 | 5.71 | |
| BAT_VGG | -323.200 | 323.200 | 5.532 | 79.253 | 2.09 | |
| 大西洋 | BAT_WHU2020 | -258.000 | 258.000 | 1.983 | 49.851 | 1.33 |
| SIO V19.1 | -313.800 | 313.800 | -0.555 | 50.942 | 1.36 | |
| ETOPO1 | -484.800 | 484.800 | -0.040 | 104.174 | 2.78 | |
| DTU10 | -576.800 | 576.800 | 14.076 | 150.918 | 4.02 | |
| GEBCO_08 | -680.300 | 680.200 | 13.771 | 158.959 | 4.24 | |
| BAT_VGG | -336.700 | 336.700 | 2.561 | 77.797 | 2.07 | |
| 印度洋 | BAT_WHU2020 | -332.700 | 332.700 | 4.248 | 65.642 | 1.73 |
| SIO V19.1 | -343.300 | 343.100 | -2.023 | 59.811 | 1.57 | |
| ETOPO1 | -505.700 | 505.700 | 0.472 | 118.399 | 3.12 | |
| DTU10 | -520.500 | 520.500 | 12.247 | 139.798 | 3.68 | |
| GEBCO_08 | -548.200 | 548.100 | 15.822 | 137.948 | 3.63 | |
| BAT_VGG | -389.000 | 389.000 | 5.448 | 91.980 | 2.42 |
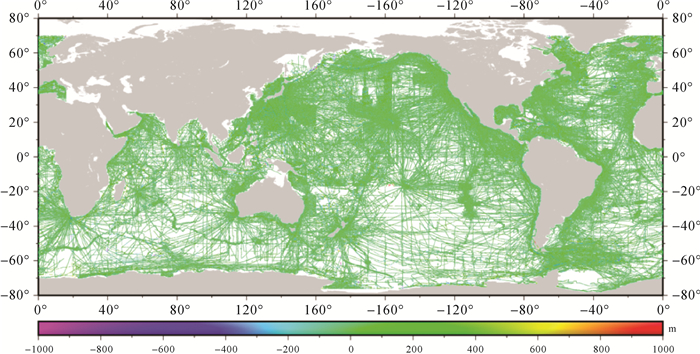
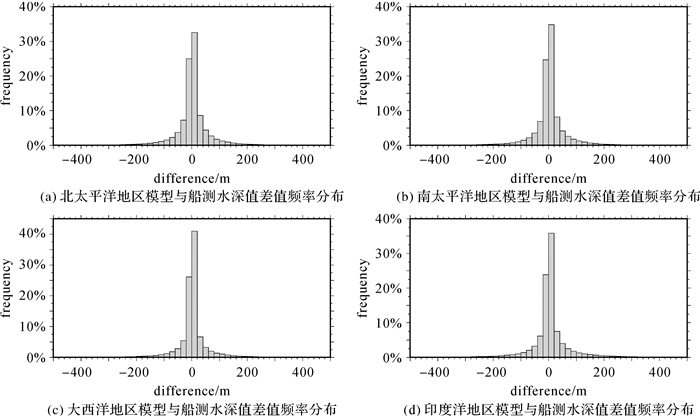
图 10是BAT_WHU2020模型与全球约10.6百万个船测检核点水深之差分布,图 11给出了上述4大区域BAT_WHU2020模型与船测水深之差值的频率分布直方图,两者差值在100 m内的比率达约90%,印度洋略低。
|
| 图 10 BAT_WHU2020海底地形模型与船测水深之差的空间分布 Fig. 10 The differences between BAT_WHU2020 bathymetry model and shipboard depths |
|
| 图 11 BAT_WHU2020与船测水深在全球大洋地区差值频率分布直方图 Fig. 11 The frequency histogram of differences between BAT_WHU2020 and shipboard depths in world oceans |
综上所述,BAT_WHU2020模型与船测水深之差的标准差为50~65 m(二次检核统计结果),差值在100 m以内的比率达约90%,在200 m以内的比率超过95%,说明本文模型与船测水深一致性良好,模型构建方法可靠、数据处理准确、成果精度较高。
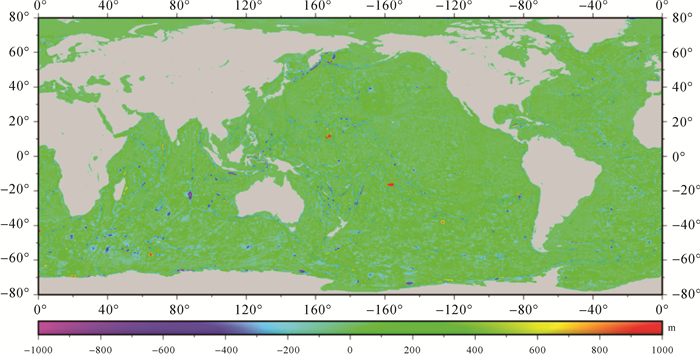
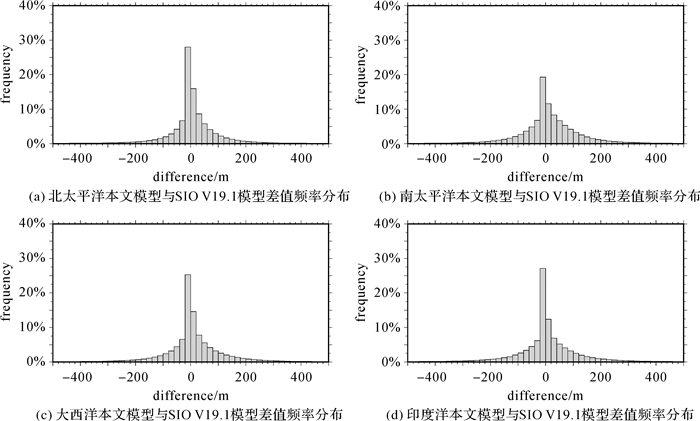
4.2.2 BAT_WHU2020模型与SIO V19.1模型比较BAT_WHU2020模型与SIO V19.1模型之差如图 12所示,在大洋各区域两者差值统计见表 4。从表 4的统计看,两种模型之差值标准差在90~110 m(二次检核统计结果),在北太平洋和大西洋地区符合度优于南太平洋和印度洋。从图 13两种模型差值频率分布直方图看,约90%格网点差值在200 m以内,约95%格网点差值在300 m以内,说明本文构建的BAT_WHU2020模型与SIO V19.1模型一致性良好。
|
| 图 12 BAT_WHU2020模型与SIO V19.1模型之差 Fig. 12 The differences between BAT_WHU2020 and SIO V19.1 |
| 统计地区 | 最小值/m | 最大值/m | 平均值/m | 标准差/m | 备注 |
| 北太平洋 | -3 375.000 | 3 519.000 | 4.635 | 141.273 | 一次检核 |
| -423.000 | 423.000 | 6.612 | 93.023 | 二次检核,数据保留率97.68% | |
| 南太平洋 | -3 435.000 | 3 805.000 | 12.742 | 151.018 | 一次检核 |
| -453.000 | 453.000 | 12.760 | 111.459 | 二次检核,数据保留率97.94% | |
| 大西洋 | -3 259.000 | 3 342.000 | 10.032 | 129.548 | 一次检核 |
| -388.000 | 388.000 | 9.793 | 97.063 | 二次检核,数据保留率97.85% | |
| 印度洋 | -2 580.000 | 2 666.000 | 4.795 | 144.685 | 一次检核 |
| -434.000 | 434.000 | 5.625 | 107.425 | 二次检核,数据保留率97.73% |
|
| 图 13 BAT_WHU2020与SIO V19.1模型在全球大洋地区差值频率分布直方图 Fig. 13 The frequency histogram of differences between BAT_WHU2020 and SIO V19.1 model in world oceans |
5 讨论 5.1 地壳均衡现象对海底地形反演的影响
根据地壳均衡理论,海面重力异常的来源主要包括海底地形及其地壳均衡补偿两部分(式(1)),而由海底地形至重力异常的均衡响应函数犹如高通滤波器(图 1)。海底地形反演过程中的带通滤波(图 6)的长波段截断的主要作用之一即是抑制地壳均衡的影响。
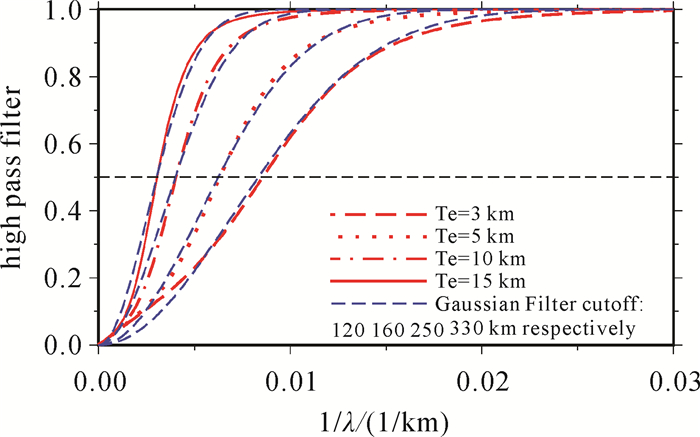
理想状态下可根据不同区域的地壳均衡参数(有效弹性厚度)设计滤波器,根据表 1参数,不同区域地壳均衡对应的高通滤波如图 14所示。岩石圈有效弹性厚度分别为3、5、10、15 km时,对应的高斯滤波器截断波长分别为120、160、250、330 km。
|
| 图 14 不同岩石圈有效弹性厚度时的均衡响应函数及其对应的高斯滤波器截断波长 Fig. 14 Isostatic response functions for different Te and its cutoff wavelength analogy to Gaussian high-pass filters |
文献[6]采用了160 km的截断波长,对应于岩石圈有效弹性厚度为5 km。文献[13, 24]采用了200 km的截断波长,对应于海底岩石圈有效弹性厚度为5~10 km。事实上,全球海底岩石圈有效弹性厚度均值为10 km、标准差为6.7 km,其中10 km以下的区域约占70%[39],说明海底地形反演过程中200 km截断波长的选择是合理的。
海底地形反演时,文献[13]通过在反演式(7)中加入均衡响应函数(式(6))的方式,顾及了均衡效应的影响,结果表明仅在有效弹性厚度较小的区域(165°E—167°E,38°N—40°N;Te=3 km)受到影响,但顾及均衡响应的计算结果精度并未显著提高。文献[24]直接根据CRUST2.0洋壳密度等参数,计算了顾及均衡时海底地形反演结果与不顾及均衡反演时的差别,认为顾及均衡影响不仅会增加计算量,而且计算精度也不一定提高。因此,本文海底地形模型BAT_WHU2020构建的数据处理过程中直接采用了线性项(式(7)),未采用式(6)中的均衡响应函数项。
5.2 Parker公式中高次项对海底地形反演的影响地形起伏计算海面重力异常的级数展开公式(式(1))中还包括高次项(n=2, 3, 4, …, m)的影响。海底地形反演过程中,对高次项的处理策略一般有两种:①正演计算扣除,即利用已有洋壳模型(如CRUST2.0)进行高次项重力效应计算,并在海底地形反演前从重力观测数据中予以扣除[13];②迭代反演计算,即在空域内采用拟牛顿法进行迭代计算[13, 21]或采用Parker-Oldenberg迭代法进行计算[40]。
从正演重力异常看,地形高次项产生的重力异常主要呈现局部特征(短波特征为主)[13],从反演结果看,高次项的影响也主要强化了海底地形的局部变化特征[13, 40],在局部区域可以提高精度,但对大面积海底地形反演精度的影响有限[24]。此外,海底地形反演过程中进行的低通滤波处理一定程度上也会抑制高次项的影响。总之,由于当前地壳结构模型分辨率较低,且顾及高次项的迭代反演对最终成果精度影响有限,因此本文构建全球海底地形模型BAT_WHU2020时直接利用了式(7)的线性近似,未对高次项进行特殊处理。
5.3 BAT_WHU2020模型的空间分辨率目前,DTU10、SIO V19.1、BAT_VGG等基于卫星测高资料反演的海底地形模型一般为1′×1′格网模型,但其真实分辨率与船测数据密度、测高数据分辨率和噪声水平,以及数据处理方法等密切相关。在数据处理过程中,文献[6—7]采用了维纳滤波器进行低通滤波处理,文献[24]则采用了20 km的高斯低通滤波。本文联合卫星测高重力异常和船测水深反演海底地形,采用了文献[6-7]一样的维纳滤波器,因此最终模型成果的分辨率与反演区域的平均水深有关,平均水深分别为1、3、5 km时,对应的分辨率分别为10、15、18 km,如图 15所示,可认为是本文模型的空间分辨率。

|
| 图 15 海底地形反演过程中的低通维纳滤波器 Fig. 15 The Winer low-pass filter for data processing in bathymetry prediction |
国际上虽已有30″甚至15″分辨率的海底地形模型发布[4, 35],但是其模型仅在船测数据丰富的小区域达到了相应分辨率。例如文献[4]联合卫星测高重力异常和超过290百万点船测水深构建的30″分辨率模型,仅约6.5%的格网点有船测水深约束。文献[35]的15″分辨率模型也仅有约10.84%的区域有船测水深数据。
5.4 BAT_WHU2020模型的实际精度评估海底地形反演工作中,一般采用将部分船测水深资料用于反演计算,另一部分用做精度检核的策略,以实现模型构建和精度评估工作。事实上,由于一般采用了在数据库中随机抽取检核点的策略,用于精度检核的船测水深与用于模型构建的船测水深是高度相关的。因此,上述检核方法一般只能检验反演模型与船测水深的“契合”程度,即是一种“内符合”精度,但足以说明模型构建数据处理过程的正确性。
现代多波束测深系统被认为具有最高的观测精度[1],但多波束测深数据在全球海洋覆盖非常稀少,且很多数据因政治、商业等原因而无法获取。笔者从NCEI(National Centers for Environmental Information)、GA(Geoscience Australia)等机构获取了马里亚纳海沟、麦夸里海岭等区域数据,并应用于BAT_WHU2020模型的精度检核。
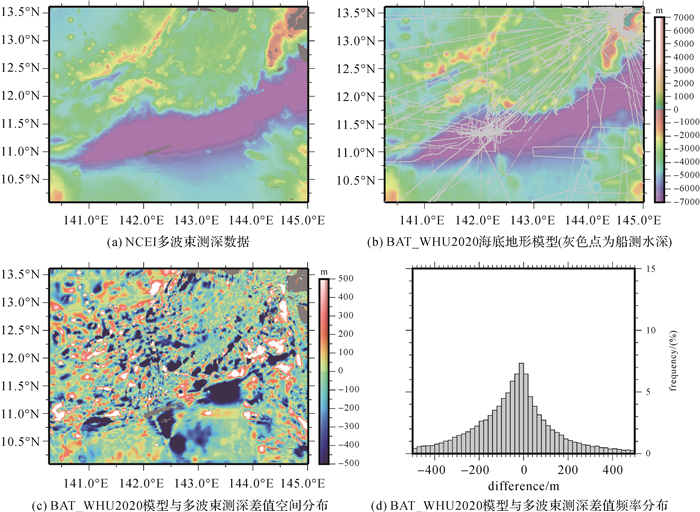
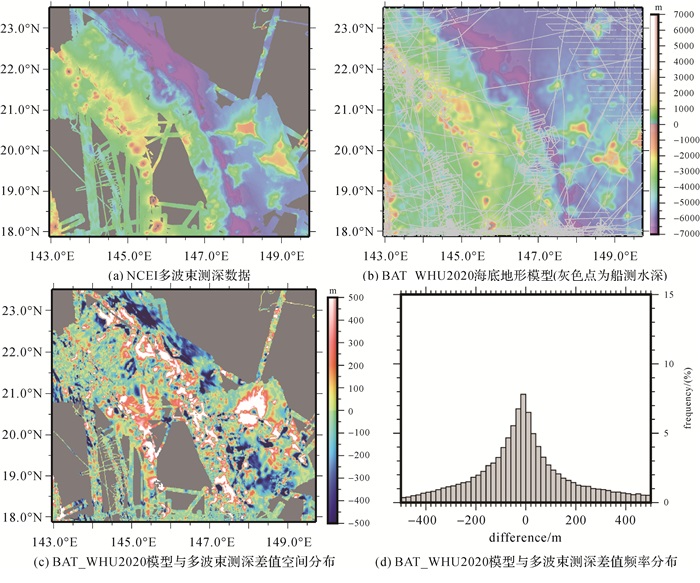
图 16和图 17所示是马里亚纳海沟地区(区域1:140.3°E—145°E,10.1°N—13.6°N;区域2:143°E—149.7°E,17.9°N—23.5°N)BAT_WHU2020模型与来自NCEI的多波束测深格网的比较。从图 16、图 17(a)与(b)对比看,BAT_WHU2020模型较好呈现了区域内海底地形变化的主要特征,但细节刻画详尽程度明显较多波束测深结果低(即空间分辨率低)。从图 16、图 17(c)看,两者的差别主要呈现局部变化特征。从图 16、图 17(d)看,两者差值在300 m以内的比率约80%,标准差分别为232.688、251.6 m,这可以认为是本文反演模型在该区域的精度。将上述标准差与区域平均水深相比,获得两个区域的海底地形模型相对精度分别为5.07%和5.88%。
|
| 图 16 马里亚纳海沟地区(区域1)BAT_WHU2020模型与多波束测深(NCEI)的比较 Fig. 16 The comparison between BAT_WHU2020 model and multibeam bathymetry grid (NCEI) around the Mariana trench (Region 1) |
|
| 图 17 马里亚纳海沟地区(区域2)BAT_WHU2020模型与多波束测深(NCEI)的比较 Fig. 17 The comparison between BAT_WHU2020 model and multibeam bathymetry grid (NCEI) around the Mariana trench (Region 2) |
图 18与图 16、图 17类似,是南太平洋麦夸里海岭地区(155°E—163°E,50°S—60°S)BAT_WHU2020模型与来自GA的多波束测深数据的比较。从图 18看,BAT_WHU2020模型总体反映了该区域的海底地形特征,但空间分辨率较低;模型与多波束测深数据之差标准差为246.444 m,相对精度为6.28%。

|
| 图 18 麦夸里海岭BAT_WHU2020模型与多波束测深的比较 Fig. 18 The comparison between BAT_WHU2020 model and multibeam bathymetry grid (GA) around the Macquarie ridge |
综上所述,在如马里亚纳海沟、麦夸里海岭等区域BAT_WHU2020模型的相对精度为5%~6%。
作为对比,表 5给出了图 16-图 18 3个区域的BAT_WHU2020、SIO V19.1、ETOPO1、DTU10、GEBCO_08模型与多波束测深之差的统计,本文模型在马里亚纳海沟(区域1)优于ETOPO1、DTU10、GEBCO_08模型,在马里亚纳海沟(区域2)略优于DTU10、GEBCO_08模型,在麦夸里海岭地区略优于ETOPO1、GEBCO_08模型。需要注意的是,SIO V19.1模型在所有区域中精度都是最高的,特别是在马里亚纳海沟(区域1)的相对精度为0.83%、马里亚纳海沟(区域2)的相对精度为2.45%,这应该是因为本文的多波束测深数据是构建SIO V19.1模型的源数据之一。上述两个区域的SIO V19.1模型真实精度应低于表 5的统计。
| 统计地区 | 模型 | 最小值/m | 最大值/m | 平均值/m | 标准差/m | 相对精度/(%) |
| 马里亚纳海沟 (区域1) |
BAT_WHU2020 | -871.240 | 871.360 | -50.622 | 232.688 | 5.07 |
| SIO V19.1 | -207.792 | 208.071 | 4.721 | 37.912 | 0.83 | |
| ETOPO1 | -992.440 | 991.920 | -16.896 | 306.377 | 6.68 | |
| DTU10 | -945.780 | 945.580 | -61.974 | 284.034 | 6.19 | |
| GEBCO_08 | -1 162.778 | 1 162.963 | -55.070 | 335.116 | 7.30 | |
| 马里亚纳海沟 (区域2) |
BAT_WHU2020 | -841.111 | 841.000 | 1.256 | 251.600 | 5.88 |
| SIO V19.1 | -403.888 | 403.828 | -6.528 | 104.801 | 2.45 | |
| ETOPO1 | -802.667 | 803.000 | -37.191 | 228.081 | 5.33 | |
| DTU10 | -882.812 | 883.333 | -29.869 | 265.123 | 6.20 | |
| GEBCO_08 | -1 203.665 | 1 202.284 | -35.244 | 332.070 | 7.76 | |
| 麦夸里海岭 | BAT_WHU2020 | -892.566 | 892.948 | -52.790 | 246.444 | 6.28 |
| SIO V19.1 | -865.542 | 865.262 | -2.435 | 239.007 | 6.09 | |
| ETOPO1 | -925.833 | 925.775 | -72.126 | 268.089 | 6.83 | |
| DTU10 | -774.245 | 774.708 | -33.039 | 227.878 | 5.81 | |
| GEBCO_08 | -867.289 | 866.670 | -40.033 | 247.677 | 6.31 |
此外,不同水深处反演精度有所不同,就图 16-图 18这3个区域的总体情况来说,在水深1000 m以浅、1000~2000 m、2000~3000 m、3000~4000 m、4000 m以深,BAT_WHU2020模型与多波束测深之差的标准差分别为227.769、259.136、302.470、248.218、233.735 m,随着水深增加相对精度逐渐提高,由约15.61%提升至约4.77%。
6 结论本文采用新版卫星测高重力异常Grav_Alti_WHU和船测水深数据,构建了新一代全球75°S—70°N范围内1′×1′海底地形模型BAT_WHU2020,并通过与船测水深、现有海底地形模型,以及多波束测深数据的比较,分析了模型精度。主要结论如下:
(1) 以船测水深为参考,在中国海域及邻区BAT_WHU2020模型与船测水深之差的标准差约70 m,与SIO V19.1模型相当,优于DTU10、ETOPO1、GEBCO_08等模型,较此前发布的BAT_VGG模型精度提高了约30%;在全球范围内,BAT_WHU2020模型与船测水深之差的二次检核标准差为50~65 m,差值在200 m以内占比超过95%,与SIO V19.1模型相当,优于DTU10、ETOPO1、GEBCO_08等模型,较BAT_VGG模型精度提高了27%~36%。说明本文模型与船测水深一致性很好,模型构建方法可靠、数据处理正确、成果精度较高。
(2) 以SIO V19.1模型为参考,BAT_WHU2020与SIO V19.1模型之差的二次检核标准差为90~110 m,约90%格网点差值在200 m以内,约95%格网点差值在300 m以内,两者一致性良好。
(3) 以多波束测深数据为参考,在马里亚纳海沟、麦夸里海岭地区,BAT_WHU2020模型与多波束测深模型之差的标准差为230~250 m,相对精度为5%~6%。
(4) 数据处理过程中,为抑制数据噪声对向下延拓等处理的影响,采用了常用的维纳低通滤波器,平均水深分别为1、3、5 km时,对应截断波长分别约10、15、18 km,可认为是本文模型的空间分辨率。
| [1] |
赵建虎, 欧阳永忠, 王爱学. 海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10): 1786-1794. ZHAO Jianhu, OUYANG Yongzhong, WANG Aixue. Status and development tendency for seafloor terrain measurement technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1786-1794. DOI:10.11947/j.AGCS.2017.20170276 |
| [2] |
CARRON M J, VOGT P R, JUNG W Y. A proposed international long-term project to systematically map the world's ocean floors from beach to trench:GOMaP (Global Ocean Mapping Program)[J]. Inter. Hydr. Rev., 2001, 2: 49-50. |
| [3] |
SANDWELL D T, SMITH W H F. Bathymetric estimation[M]//FU L L, CAZENAVE A. Satellite Altimetry and Earth Science. San Diego, CA: Academic Press, 2001: 441-457.
|
| [4] |
BECKER J J, SANDWELL D T, SMITH W H F, et al. Global bathymetry and elevation data at 30 arc seconds resolution:SRTM30_PLUS[J]. Marine Geodesy, 2009, 32(4): 355-371. DOI:10.1080/01490410903297766 |
| [5] |
DIXON T H, NARAGHI M, MCNUTT M K, et al. Bathymetric prediction from SEASAT altimeter data[J]. Journal of Geophysical Research:Oceans, 1983, 88(C3): 1563-1571. DOI:10.1029/JC088iC03p01563 |
| [6] |
SMITH W H F, SANDWELL D T. Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry[J]. Journal of Geophysical Research:Solid Earth, 1994, 99(B11): 21803-21824. DOI:10.1029/94JB00988 |
| [7] |
SMITH W H F, SANDWELL D T. Global sea floor topography from satellite altimetry and ship depth soundings[J]. Science, 1997, 277(5334): 1956-1962. DOI:10.1126/science.277.5334.1956 |
| [8] |
王勇, 许厚泽, 詹金刚. 中国海及其邻近海域高分辨率海底地形[J]. 科学通报, 2001, 46(11): 956-960. WANG Yong, XU Houze, ZHAN Jingang. High resolution bathymetry for China Sea and adjacent waters[J]. Chinese Science Bulletin, 2001, 46(11): 956-960. DOI:10.3321/j.issn:0023-074X.2001.11.018 |
| [9] |
黄谟涛, 翟国君, 欧阳永忠, 等. 利用卫星测高资料反演海底地形研究[J]. 武汉大学学报(信息科学版), 2002, 27(2): 133-137. HUANG Motao, ZHAI Guojun, OUYANG Yongzhong, et al. The recovery of bathymetry from altimeter data[J]. Geomatics and Information Science of Wuhan University, 2002, 27(2): 133-137. |
| [10] |
罗佳, 李建成, 姜卫平. 利用卫星资料研究中国南海海底地形[J]. 武汉大学学报(信息科学版), 2002, 27(3): 256-260. LUO Jia, LI Jiancheng, JIANG Weiping. Bathymetry prediction of South China Sea from satellite data[J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 256-260. |
| [11] |
方剑, 张赤军. 中国海及邻近海域2'×2'海底地形[J]. 武汉大学学报(信息科学版), 2003, 28(S3): 38-40. FANG Jian, ZHANG Chijun. 2'×2' sea floor bathymetry prediction of China Sea and its vicinity[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S3): 38-40. |
| [12] |
吴云孙, 晁定波, 李建成, 等. 利用测高重力梯度异常反演中国南海海底地形[J]. 武汉大学学报(信息科学版), 2009, 34(12): 1423-1425. WU Yunsun, CHAO Dingbo, LI Jiancheng, et al. Recovery of ocean depth model of South China Sea from altimetric gravity gradient anomalies[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12): 1423-1425. |
| [13] |
胡敏章.海底地形反演与地壳均衡研究[D].武汉: 武汉大学, 2013. HU Minzhang. Research on bathymetry prediction and crust isostasy[D]. Wuhan: Wuhan University, 2013. |
| [14] |
欧阳明达, 孙中苗, 翟振和, 等. 采用重力异常的导纳理论推估海底地形[J]. 测绘学报, 2015, 44(10): 1092-1099. OUYANG Mingda, SUN Zhongmiao, ZHAI Zhenhe, et al. Bathymetry prediction based on the admittance theory of gravity anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1092-1099. DOI:10.11947/j.AGCS2.0152.0140427 |
| [15] |
范雕, 李姗姗, 孟书宇, 等. 联合多源重力数据反演菲律宾海域海底地形[J]. 测绘学报, 2018, 47(10): 1307-1315. FAN Diao, LI Shanshan, MENG Shuyu, et al. Recovery of bathymetry over Philippine Sea by combination of multi-source gravity data[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(10): 1307-1315. DOI:10.11947/j.AGCS.2018.20170423 |
| [16] |
CALMANT S. Seamount topography by least-squares inversion of altimetric geoid heights and shipborne profiles of bathymetry and/or gravity anomalies[J]. Geophysical Journal International, 1994, 119(2): 428-452. DOI:10.1111/j.1365-246X.1994.tb00133.x |
| [17] |
RAMILLIEN G, WRIGHT C I. Predicted seafloor topography of the New Zealand region:a nonlinear least squares inversion of satellite altimetry data[J]. Journal of Geophysical Research:Solid Earth, 2000, 105(B7): 16577-16590. DOI:10.1029/2000JB900099 |
| [18] |
CALMANT S BERGE-NGUYEN M, CAZENAVE A. Global seafloor topography from a least-squares inversion of altimetry-based high-resolution mean sea surface and shipboard soundings[J]. Geophysical Journal International, 2002, 151(3): 795-808. DOI:10.1046/j.1365-246X.2002.01802.x |
| [19] |
TSCHERNING C C, KNUDSEN P, FORSBERG R. First experiments with improvement of depth information using gravity anomalies in the mediterranean sea[M]//ARABELOS D, TZIAVOS I N. Mare Nostrum. Thessaloniki: University of Thessaloniki, 1994: 133-148.
|
| [20] |
HWANG C. A bathymetric model for the South China Sea from satellite altimetry and depth data[J]. Marine Geodesy, 1999, 22(1): 37-51. DOI:10.1080/014904199273597 |
| [21] |
胡敏章, 李建成, 邢乐林, 等. 海底地形反演方法比较[J]. 大地测量与地球动力学, 2014, 34(5): 11-16. HU Minzhang, LI Jiancheng, XING Lelin, et al. Comparative analysis of methods for bathymetry prediction[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 11-16. |
| [22] |
金涛勇, 李建成, 姜卫平, 等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报, 2011, 40(6): 723-729. JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The new generation of global mean sea surface height model based on multi-altimetric data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723-729. |
| [23] |
李大炜.多源卫星测高数据确定海洋潮汐模型的研究[D].武汉: 武汉大学, 2013. LI Dawei. Research on ocean tides modeling using satellite altimetry[D]. Wuhan: Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1013210912.htm |
| [24] |
胡敏章, 李建成, 邢乐林. 由垂直重力梯度异常反演全球海底地形模型[J]. 测绘学报, 2014, 43(6): 558-565, 574. HU Minzhang, LI Jiancheng, XING Lelin. Global bathymetry model predicted from vertical gravity gradient anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 558-565, 574. DOI:10.13485/jc.nki1.1-20892.0140.090 |
| [25] |
张胜军. 利用多源卫星测高资料确定海洋重力异常的研究[J]. 测绘学报, 2017, 46(8): 1071. ZHANG Shengjun. Research on determination of marine gravity anomalies from multi-satellite altimeter data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 1071. DOI:10.11947/j.AGCS.2017.20170187 |
| [26] |
ZHANG Shengjun, SANDWELL D T. Retracking of SARAL/AltiKa radar altimetry waveforms for optimal gravity field recovery[J]. Marine Geodesy, 2017, 40(1): 40-56. DOI:10.1080/01490419.2016.1265032 |
| [27] |
ZHANG Shengjun, LI Jiancheng, JIN Taoyong, et al. HY-2A altimeter data initial assessment and corresponding two-pass waveform retracker[J]. Remote Sensing, 2018, 10(4): 507. DOI:10.3390/rs10040507 |
| [28] |
AMANTE C, EAKINS B W. ETOPO11 Arc-minute global relief model: procedures, data sources and analysis[R]. Colorado_National Oceanic and Atmospheric Administration, 2009.
|
| [29] |
ANDERSEN O B, KNUDSEN P. The DNSC08BAT bathymetry developed from satellite altimetry[R]. Presented EGU-2008, Vienna, Austria: EGU, 2008.
|
| [30] |
GOODWILLIE A. User guide to the GEBCO one minute grid[R]. Monaco: International Hydrographic Organization, 2008.
|
| [31] |
WATTS A B. Isostasy and flexure of the lithosphere[M]. London: Cambridge University Press, 2001.
|
| [32] |
PARKER R L. The rapid calculation of potential anomalies[J]. Geophysical Journal of the Royal Astronomical Society, 1973, 31(4): 447-455. DOI:10.1111/j.1365-246X.1973.tb06513.x |
| [33] |
WALCOTT R I. Flexural rigidity, thickness, and viscosity of the lithosphere[J]. Journal of Geophysical Research, 1970, 75(20): 3941-3954. DOI:10.1029/JB075i020p03941 |
| [34] |
HU Minzhang, LI Jiancheng, LI Hui, et al. Predicting global seafloor topography using multi-source data[J]. Marine Geodesy, 2015, 38(2): 176-189. DOI:10.1080/01490419.2014.934415 |
| [35] |
TOZER B, SANDWELL D T, SMITH W H F, et al. Global bathymetry and topography at 15 arc seconds:SRTM15+[J]. Earth and Space Science, 2019, 6(10): 1847-1864. DOI:10.1029/2019EA000658 |
| [36] |
SMITH W H F. On the accuracy of digital bathymetric data[J]. Journal of Geophysical Research:Solid Earth, 1993, 98(B6): 9591-9603. DOI:10.1029/93JB00716 |
| [37] |
SANDWELL D T, SMITH W H F. Global marine gravity from retracked geosat and ERS-1 altimetry:ridge segmentation versus spreading rate[J]. Journal of Geophysical Research:Solid Earth, 2009, 114(B1): B01411. |
| [38] |
SANDWELL D T, MÜLLER R D, SMITH W H F, et al. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure[J]. Science, 346(6205): 65-67. DOI:10.1126/science.1258213 |
| [39] |
胡敏章, 李建成, 徐新禹, 等. 全球1°×1°海洋岩石圈有效弹性厚度模型[J]. 武汉大学学报(信息科学版), 2017, 42(5): 575-582. HU Minzhang, LI Jiancheng, XU Xinyu, et al. A 1°×1° model for lithospheric effective elastic thickness over global seafloor[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 575-582. |
| [40] |
FAN Diao, LI Shanshan, MENG Shuyu, et al. Applying iterative method to solving high-order terms of seafloor topography[J]. Marine Geodesy, 2020, 43(1): 63-85. DOI:10.1080/01490419.2019.1670298 |


