2. 东华理工大学测绘工程学院, 江西 南昌 330013;
3. 武汉大学测绘学院, 湖北 武汉 430079;
4. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. Faculty of Geomatics, East China University of Technology, Nanchang 330013, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
4. GNSS Research Center, Wuhan University, Wuhan 430079, China
载波相位整周模糊度的快速、准确解算是GNSS实时高精度定位的关键。在众多整周模糊度解算方法中,基于整数最小二乘搜索的估计方法成功率最高,而被广泛采用[1-7]。为提高模糊度的搜索效率,文献[5]提出了基于整数变换的LAMBDA降相关算法。随后,许多学者也基于降相关思想开展了相关研究[8-11]。通常认为,模糊度降相关准则是通过降低模糊度分量之间的相关性,实现搜索椭球的压缩,以便提高搜索效率。基于这一准则,降相关系数和条件数常被用作评价降相关性能的指标[8-21]。近来,文献[22-24]通过理论和试验对比发现,条件数和降相关系数并不能准确反映模糊度的降相关性能,模糊度降相关的目的在于通过整数变换,优化条件方差的排序结构,使其尽可能按照降序或升序的方式排序。
尽管降相关性能与排序程度直接相关,但是不同降相关算法排序策略的差异性,致使无法直接判断不同算法性能的优劣[5, 8-10]。为合理评价降相关算法的性能,文献[25-26]通过绘制条件方差的变化趋势图,来直接判读不同算法的性能。但这种方式仅限于单个模糊度方差的比较分析,对降相关性能差异较明显的算法管用;文献[27-30]直接采用搜索时间来衡量不同算法的降相关性能,但是需要经过模糊度搜索环节才能判定算法的优劣,尤其当模糊度精度较高时,不同算法间的搜索时间由于解算耗时量级较小[29],容易受计算机运行误差的影响,不利于算法间性能的合理比较。此外,搜索时间的长短不是模糊度固定的全部性能。
由于评价指标的选取对于正确评价降相关算法的性能至关重要,且便于理解降相关的本质,因此,需要定义合理的评价指标来衡量降相关性能。下文在阐述降相关基本理论基础上,重点从理论上分析排序与模糊度条件方差的数值关系,并定义相应指标,进而通过试验验证定义的指标的合理性。
1 降相关原理假定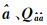
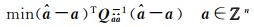 (1)
(1)
式中,a为模糊度整数候选向量。
通常人们采用整数变换来快速获取模糊度整数向量[5, 8-11]。其核心思想是通过采用整数变换矩阵Z对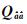
对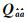
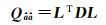 (2)
(2)
式中,L=[li, j],i > j是单位下三角矩阵;D=[di]是对角阵,di为模糊度分量的条件方差。
当li, j > 0.5时,按照下式进行高斯消元
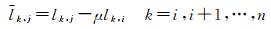 (3)
(3)
式中,μ=[li, j]int表示对li, j取整。
1.2 条件方差排序当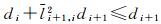
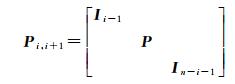 (4)
(4)
式中,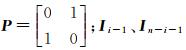
采用Pi, i+1对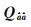
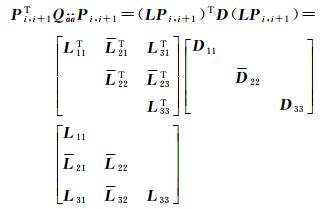 (5)
(5)
式中
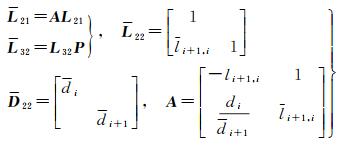 (6)
(6)
式中
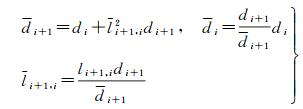 (7)
(7)
不同降相关算法由于采用的整数变换策略不同,导致算法性能各异,需要对其进行有效评价,而当前常用的条件数和降相关系数两个评价指标已不能全面地衡量降相关算法的性能[22-24]。由于评价指标的选取对正确评价降相关算法的性能至关重要,为合理定义评价指标,下文首先分析条件方差的排序结构是影响降相关性能的关键,然后从理论上分析排序后模糊度降相关与条件方差之间的数值关系,最后在此基础上定义合理的评价指标。
不同于文献[22-24]采用的降相关的条件方差的排序分析法,本文将采用二维图形变换的方式对整数高斯消元和条件方差排序的整数变换过程进行分析,剖析二者之间的关系。
给定模糊度方差-协方差矩阵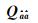
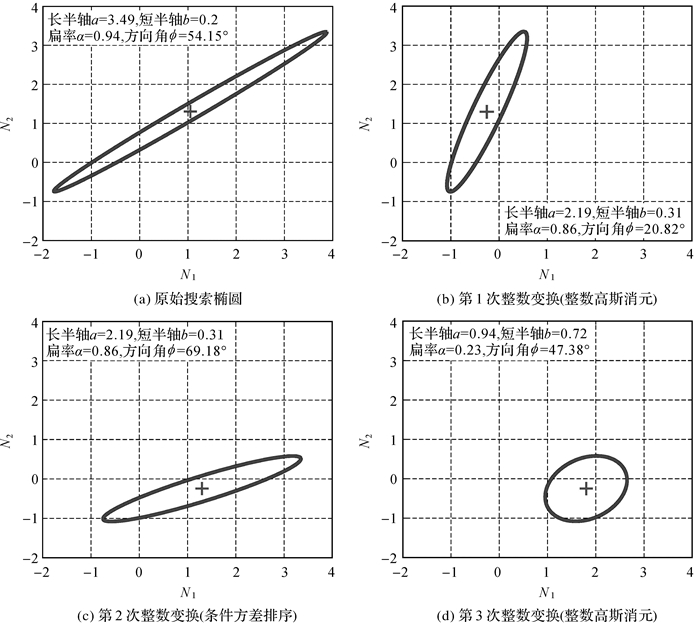
|
| 图 1 整数变换前后椭圆形状变化 Fig. 1 Elliptic shape change before and after integer transformation |
| 转换前 | 第1次 | 第2次 | 第3次 | |||||||
| N2 | N1 | N2 | N1 | N2 | N1 | N2 | N1 | |||
| 3 | * | 3 | * | * | * | * | * | |||
| 2 | 2 | 2 | 2 | * | * | * | * | |||
| 1 | * | 1 | * | 0 | 0 | 0 | 0 | |||
| 0 | * | 0 | * | -1 | * | -1 | * | |||
| 注:搜索节点是指当前模糊度分量满足搜索空间大小的候选点;*表示无搜索节点。 | ||||||||||
尽管降相关是通过整数变换优化条件方差的排列顺序,但是,并不能确保严格依据条件方差的降序排序(针对LTDL分解),即并非完全满足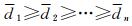
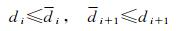 (8)
(8)
具体交换关系见图 2。
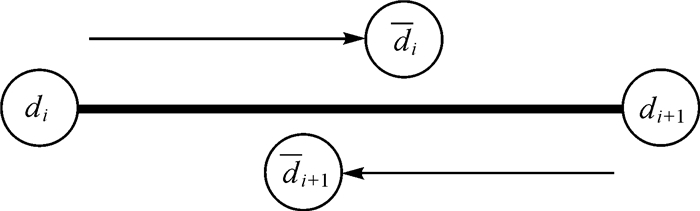
|
| 图 2 相邻条件方差交换 Fig. 2 Diagram of adjacent conditional variance exchange |
根据整数变换不改变矩阵的行列式这一性质,条件方差交换后满足等式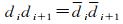
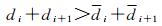 (9)
(9)
不等式(9)证明如下
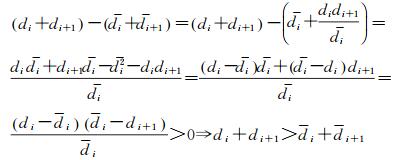 (10)
(10)
由式(8)—式(9)可知,条件方差交换的实质是减少条件方差数值间的差异。降相关性能越强,条件方差交换程度越大,交换的条件方差数值间差异越小,获得的条件方差数值序列累积越小,进而条件方差的整体数值平稳性越好。于是,首先定义“条件方差平稳度”。
定义:条件方差平稳度定义为
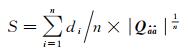 (11)
(11)
式中,S即为“条件方差平稳度”,以此作为衡量模糊度向量排序的合理度。
性质:S满足不等式
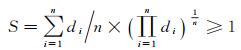 (12)
(12)
当d1=d2=…=dn时,不等式取等号,因此S的取值范围为
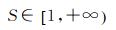 (13)
(13)
上述性质可根据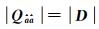
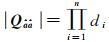
由式(9)—式(12)可以看到,S值取决于条件方差的平稳程度,条件方差数值序列波动越小,解算的S值越小,当条件方差相等时不等式取等号。因此,S值越小,条件方差平稳度越好,此时降相关质量越好,模糊度搜索效率越高;反之亦然。
3 试验数据分析为验证定义的条件方差平稳度是否可以作为衡量模糊度降相关性能的有效评价指标,采用3种排序形式不同的降相关算法来验证降相关性能的差异性,分别为基于自然升序排序的ASCE算法[10]、基于下三角Cholesky(LDLT)分解的LIGT算法[30]和基于最小列旋转的SEQR算法[10]。为保证3种算法降相关性能比较的合理性,3种算法均采用对模糊度协方差矩阵进行LDLT分解的升序排序算法,其中ASCE是对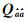
本文采用条件方差变化趋势图[25-26]和搜索耗时[27-30]来定性和定量评价降相关性能,用以判定条件方差平稳度的合理性。其中,搜索算法采用当前最为流行的SE-VB搜索算法[27, 31-33]。
本文的模糊度搜索耗时是在PC机上基于Matlab 2016a软件进行统计的,其软硬件配置为:Intel Core i7-7700 CPU,2.80 GHz主频,8 GB内存,Win10操作系统(64位)。
3.1 仿真试验借鉴文献[27]的模拟方法随机模拟模糊度的方差-协方差阵
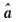
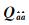
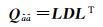 (14)
(14)
式中,L=[li, j],i > j是单位下三角矩阵;D=[di]是对角阵。考虑到实际模糊度前3个条件方差远大于其余模糊度的条件方差[5],条件方差di
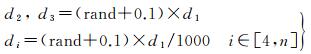 (15)
(15)
式中,rand表示产生在(0, 1)之间均匀分布的随机数。
模糊度浮点解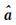
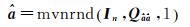 (16)
(16)
式中,mvnrnd (·)表示多元正态分布函数;In为n阶单位阵。
鉴于实际解算的模糊度精度和维数是随历元变化的,为从普遍意义下验证条件方差平稳度评价指标的合理性,本文设计了模糊度不同维数和精度两个角度的仿真试验。
3.1.1 不同维数下仿真试验试验1分别采用20、30、40、50维共4组数据作仿真试验,由于载波相位观测量越多,模糊度维数越大,浮点模糊度精度越高[29, 34],因此4组
表 2给出了原始模糊度(origin)、ASCE、LIGT和SEQR 3种降相关算法的模糊度条件方差平稳度和搜索耗时,图 3为4种模糊度的条件方差变化趋势图。由图表可见,降相关算法获得的条件方差平稳度越小,搜索效率越高,条件方差变化趋势越平稳,整体波动越小。其中,在20维处ASCE的条件方差平稳度小于LIGT、50维处LIGT的条件方差平稳度小于SEQR,此时搜索耗时与条件方差平稳度均呈一一对应关系。
| 维数 | 指标 | origin | ASCE | LIGT | SEQR |
| 20 | 平稳度 | 77.538 | 1.084 6 | 1.124 8 | 1.045 4 |
| 搜索时间/s | 0.897 8 | 0.005 8 | 0.008 9 | 0.004 3 | |
| 30 | 平稳度 | 55.313 | 1.224 3 | 1.163 3 | 1.104 8 |
| 搜索时间/s | 6.429 1 | 0.231 3 | 0.152 1 | 0.067 5 | |
| 40 | 平稳度 | 52.621 | 1.162 1 | 1.117 2 | 1.096 4 |
| 搜索时间/s | 18.824 | 1.302 2 | 0.831 9 | 0.635 4 | |
| 50 | 平稳度 | 60.139 | 1.325 5 | 1.203 6 | 1.207 7 |
| 搜索时间/s | 410.3 | 15.939 | 0.673 9 | 0.885 4 |

|
| 图 3 采用不同降相关算法的模糊度条件方差变化趋势 Fig. 3 The trend of ambiguity conditional variance under different decorrelation algorithms |
3.1.2 不同精度下仿真试验
试验2采用4组维数在10~50维变化的不同精度的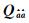
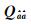

|
| 图 4 不同精度下模糊度条件方差和搜索时间变化趋势 Fig. 4 The trend of ambiguity conditional variance and search time under different precision |
3.2 实测试验
选取两组不同观测环境下的动态车载实测数据(试验基本情况见表 3),并同时统计不同降相关算法的条件数和降相关系数,通过分析比较这两种评价指标,从不同维度对降相关性能评价。其中,通常认为降相关后获得的条件数数值越小、降相关系数数值越大,则降相关算法的降相关性能越强[8-21]。双差模糊度的浮点解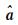
| 数据 | 动态1 | 动态2 |
| 接收机型号 | Septentrio PolaRx5 | 司南M300 |
| 系统和频率 | GPS/BDS三频 | GPS/BDS三频 |
| 观测时间 | 2018-01-23 | 2018-11-28 |
| 历元数 | 3149 | 8226 |
| 采样间隔/s | 5 | 1 |
| 基线长/km | 0.04~4.7 | 0.1~7.5 |
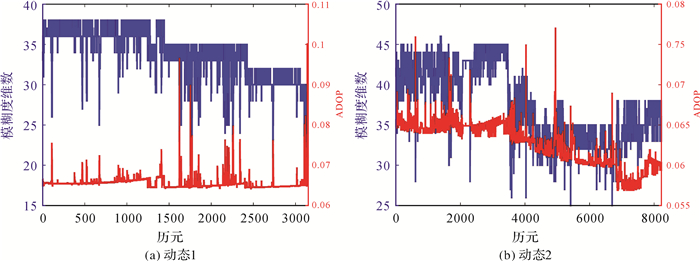
图 5是模糊度维数和ADOP随历元变化的趋势图。由图 5可见,模糊度维数变化范围为25~46,ADOP数值维持在0.10以下。ADOP值取决于两个卫星系统的模糊度维数、站星几何关系和载波相位观测值精度等因素,ADOP并不严格对应模糊度维数。由于ADOP值越小,模糊度精度较高,搜索耗时数量级相对较小[29]。基于此,本文为突出3种算法的时间差异性,模糊度搜索的候选向量个数均设置为20,每组数据搜索5次,并统计每一历元的平均搜索耗时。
|
| 图 5 不同历元下的模糊度维数与ADOP值 Fig. 5 Ambiguity dimensions and the value of ADOP under different epochs |
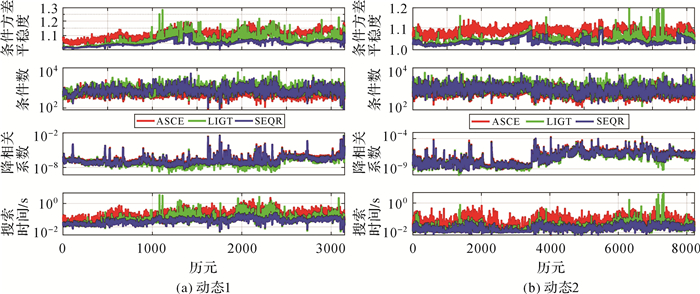
图 6给出了ASCE、LIGT和SEQR 3种算法在不同历元下的解算结果。由图 6可见,在条件方差平稳度方面,SEQR具有最小的条件方差平稳度,LIGT存在部分历元的条件方差平稳度大于ASCE;在搜索耗时方面,考虑到计算机运行误差,LIGT存在个别历元略小于SEQR的现象,整体上3种算法的搜索耗时趋势基本和条件方差平稳度一致。对于条件数和降相关系数两个指标的评价效果,可以通过直接对比ASCE和SEQR两种算法来获得相关结论。根据图 6,ASCE相对于SEQR整体上具有相对较小的条件数,与文献[10]结论一致;ASCE相对于SEQR整体上具有较大的降相关系数(详细比较参见图 7)。
|
| 图 6 不同历元下模糊度评价指标和搜索时间的关系 Fig. 6 The relationship between ambiguity evaluation index and search time under different epochs |
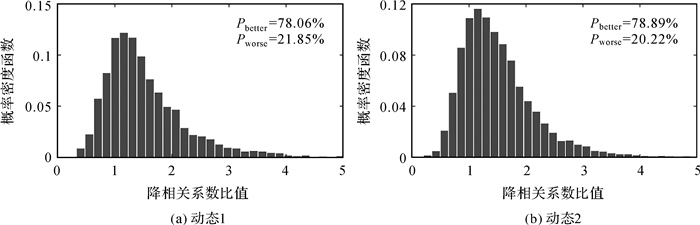
|
| 图 7 降相关系数比值(ASCE/SEQR)的概率密度函数 Fig. 7 Probability density functions of the ratio of decorrelation coefficients for ASCE relative to SEQR |
图 7中,Pbetter表示采用降相关系数统计的ASCE降相关性能优于SEQR的概率;Pworse表示ASCE劣于SEQR的概率。单纯从这两方面比较来看ASCE在降相关性能上优于SEQR。但是,ASCE的搜索效率明显低于SEQR,说明这两种指标在评价降相关质量方面具有一定的片面性,与文献[22-24]结论一致。因此,实际数据结果表明,相对于常用的条件数和降相关系数评价指标,“条件方差平稳度”更能够准确可靠衡量
本文从理论上分析了排序过程对模糊度条件方差的影响,在此基础上,定义了评定降相关性能的“条件方差平稳度”指标。采用模拟和实测数据对其效果进行了验证,可以得到以下两点结论:
(1) 降相关通常采用整数变换,优化条件方差的排序结构,促使条件方差尽量按照升序或降序排序,为此需要对条件方差进行交换。由于两个条件方差交换后将会缩小二者数值间的差异,因此当完成整个降相关过程后,条件方差序列的整体数值差异相对较小,数值序列趋势较平稳。此时降相关性能增强,进而提高搜索效率。
(2) 由于整数变换前后矩阵行列式大小不变,因此变换后的条件方差序列数值之和小于交换前数值之和。根据这一性质,本文定义的条件方差平稳度评价指标更能可靠地反映模糊度条件方差的变化趋势,并能够较直观地衡量模糊度的降相关性能。当获得的平稳度数值越小且趋近于1时,条件方差的趋势变化越平稳,此时降相关性能越好。
理论与实际计算表明,以整数变换优化条件方差的排序结构实现的降相关,可有效缩小条件方差数值间差异,获得一组更平稳的数值序列,进而提高模糊度的搜索效率。
| [1] |
ABIDIN H Z. On the construction of the ambiguity searching space for on-the-fly ambiguity resolution[J]. Navigation, 1993, 40(3): 321-338. DOI:10.1002/j.2161-4296.1993.tb02311.x |
| [2] |
FREI E, BEUTLER G. Rapid static positioning based on the fast ambiguity resolution approach FARA:theory and first results[J]. Manuscripta Geodaetica, 1990, 15(6): 325-356. |
| [3] |
EULER H J, LANDAU H. Fast GPS ambiguity resolution on-the-fly for real-time applications[C]//Proceedings of the 6th International Geodetic Symposium on Satellite Positioning. Ohio: [s.n.], 1992: 650-659.
|
| [4] |
CHEN Dingsheng. Development of a fast ambiguity search filtering (FASF) method for GPS carrier phase ambiguity resolution[D]. Calgary: University of Calgary, 1994. https://www.researchgate.net/publication/242356275_Development_of_a_Fast_Ambiguity_Search_Filtering_FASF_Method_for_GPS_Carrier_Phase_Ambiguity_Resolution
|
| [5] |
TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment:a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. DOI:10.1007/BF00863419 |
| [6] |
TEUNISSEN P J G. An optimality property of the integer least-squares estimator[J]. Journal of Geodesy, 1999, 73(11): 587-593. DOI:10.1007/s001900050269 |
| [7] |
VERHAGEN S, LI Bofeng, TEUNISSEN P J G. Ps-LAMBDA:ambiguity success rate evaluation software for interferometric applications[J]. Computers & Geosciences, 2013, 54: 361-376. |
| [8] |
LIU L T, HSU H T, ZHU Y Z, et al. A new approach to GPS ambiguity decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478-490. DOI:10.1007/PL00004003 |
| [9] |
XU Peiliang. Random simulation and GPS decorrelation[J]. Journal of Geodesy, 2001, 75(7-8): 408-423. DOI:10.1007/s001900100192 |
| [10] |
XU Peiliang. Parallel Cholesky-based reduction for the weighted integer least squares problem[J]. Journal of Geodesy, 2012, 86(1): 35-52. DOI:10.1007/s00190-011-0490-y |
| [11] |
ZHOU Yangmei. A new practical approach to GNSS high-dimensional ambiguity decorrelation[J]. GPS Solutions, 2011, 15(4): 325-331. DOI:10.1007/s10291-010-0192-6 |
| [12] |
TEUNISSEN P J G. A new method for fast carrier phase ambiguity estimation[C]//Proceedings of 1994 IEEE Position, Location and Navigation Symposium-PLANS'94. Las Vegas: IEEE, 1994: 562-573.
|
| [13] |
WANG Jun, FENG Yanming. Orthogonality defect and reduced search-space size for solving integer least-squares problems[J]. GPS Solutions, 2013, 17(2): 261-274. DOI:10.1007/s10291-012-0276-6 |
| [14] |
WU Zemin, LI Houpu, BIAN Shaofeng. Cycled efficient V-BLAST GNSS ambiguity decorrelation and search complexity estimation[J]. GPS Solutions, 2017, 21(4): 1829-1840. DOI:10.1007/s10291-017-0656-z |
| [15] |
DENG Zhongliang, ZHU Di, YIN Lu. N-dimensional LLL reduction algorithm with pivoted reflection[J]. Sensors (Basel), 2018, 18(1): 283. DOI:10.3390/s18010283 |
| [16] |
楼立志. 对GPS模糊度解相关方法的一种改进[J]. 同济大学学报, 2004, 32(2): 237-241. LOU Lizhi. One modified LLL algorithm in GPS decorrelation[J]. Journal of Tongji University, 2004, 32(2): 237-241. DOI:10.3321/j.issn:0253-374X.2004.02.021 |
| [17] |
刘志平, 何秀凤. 改进的GPS模糊度降相关LLL算法[J]. 测绘学报, 2007, 36(3): 286-289. LIU Zhiping, HE Xiufeng. An improved LLL algorithm for GPS ambiguity solution[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 286-289. DOI:10.3321/j.issn:1001-1595.2007.03.008 |
| [18] |
刘志平, 何秀凤, 郭广礼, 等. GNSS模糊度降相关算法及其评价指标研究[J]. 武汉大学学报(信息科学版), 2011, 36(3): 257-261. LIU Zhiping, HE Xiufeng, GUO Guangli, et al. Decorrelation algorithms and its evaluation indexes for GNSS ambiguity solution[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 257-261. |
| [19] |
杨荣华, 花向红, 李昭, 等. GPS模糊度降相关LLL算法的一种改进[J]. 武汉大学学报(信息科学版), 2010, 35(1): 21-24. YANG Ronghua, HUA Xianghong, LI Zhao, et al. An improved LLL algorithm for GPS ambiguity solution[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 21-24. |
| [20] |
刘宁, 熊永良, 冯威, 等. 单频GPS动态定位中整周模糊度的一种快速解算方法[J]. 测绘学报, 2013, 42(2): 211-217. LIU Ning, XIONG Yongliang, FENG Wei, et al. An algorithm for rapid integer ambiguity resolution in single frequency GPS kinematical positioning[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 211-217. |
| [21] |
范龙, 翟国君, 柴洪洲. 模糊度降相关的整数分块正交化算法[J]. 测绘学报, 2014, 43(8): 818-826. FAN Long, ZHAI Guojun, CHAI Hongzhou. Ambiguity decorrelation with integer block orthogonalization algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 818-826. |
| [22] |
BORNO M A, CHANG Xiaowen, XIE X H. On "Decorrelation" in solving integer least-squares problems for ambiguity determination[J]. Survey Review, 2014, 46(334): 37-49. DOI:10.1179/1752270612Y.0000000029 |
| [23] |
JAZAERI S, AMIRI-SIMKOOEI A R, SHARIFI M A. On lattice reduction algorithms for solving weighted integer least squares problems:comparative study[J]. GPS Solutions, 2014, 18(1): 105-114. DOI:10.1007/s10291-013-0314-z |
| [24] |
卢立果, 刘万科, 李江卫. 降相关对模糊度解算中搜索效率的影响分析[J]. 测绘学报, 2015, 44(5): 481-487. LU Liguo, LIU Wanke, LI Jiangwei. Impact of decorrelation on search efficiency of ambiguity resolution[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 481-487. DOI:10.11947/j.AGCS.2015.20140311 |
| [25] |
谢恺, 柴洪洲, 范龙, 等. 一种改进的LLL模糊度降相关算法[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1363-1368. XIE Kai, CHAI Hongzhou, FAN Long, et al. An improved LLL ambiguity decorrelation algorithm[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1363-1368. |
| [26] |
吕浩, 吕志平, 翟树峰, 等. 一种改进的LLL模糊度规约算法[J]. 中国惯性技术学报, 2017, 25(5): 611-617. H ao, LÜ Zhiping, ZHAI Shufeng, et al. Improved LLL ambiguity reduction algorithm[J]. Journal of Chinese Inertial Technology, 2017, 25(5): 611-617. |
| [27] |
CHANG Xiaowen, YANG X, ZHOU T. MLAMBDA:a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565. DOI:10.1007/s00190-005-0004-x |
| [28] |
刘经南, 于兴旺, 张小红. 基于格论的GNSS模糊度解算[J]. 测绘学报, 2012, 41(5): 636-645. LIU Jingnan, YU Xingwang, ZHANG Xiaohong. GNSS ambiguity resolution using the lattice theory[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 636-645. |
| [29] |
刘万科, 卢立果, 单弘煜. 一种快速解算高维模糊度的LLL分块处理算法[J]. 测绘学报, 2016, 45(2): 147-156. LIU Wanke, LU Liguo, SHAN Hongyu. A new block processing algorithm of LLL for fast high-dimension ambiguity resolution[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 147-156. DOI:10.11947/j.AGCS.2016.20150370 |
| [30] |
卢立果, 鲁铁定, 吴汤婷, 等. 下三角Cholesky分解的整数高斯变换算法[J]. 测绘科学, 2017, 42(12): 57-62, 76. LU Liguo, LU Tieding, WU Tangting, et al. Integer Gauss transformation algorithm based on low triangular Cholesky decomposition[J]. Science of Surveying and Mapping, 2017, 42(12): 57-62, 76. |
| [31] |
AGRELL E, ERIKSSON T, VARDY A, et al. Closest point search in lattices[J]. IEEE Transactions on Information Theory, 2002, 48(8): 2201-2214. DOI:10.1109/TIT.2002.800499 |
| [32] |
LI Bofeng, VERHAGEN S, TEUNISSEN P J G. GNSS integer ambiguity estimation and evaluation: LAMBDA and Ps-LAMBDA[C]//Proceeding of 2013 China Satellite Navigation Conference (CSNC). Berlin: Springer, 2013: 291-301.
|
| [33] |
刘万科, 马立烨, 卢立果, 等. 一种改进的SEVB整数模糊度搜索算法[J]. 测绘学报, 2018, 47(1): 17-24. LIU Wanke, MA Liye, LU Liguo, et al. A modified SEVB integer ambiguity search algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 17-24. DOI:10.11947/j.AGCS.2018.20170227 |
| [34] |
卢立果. GNSS整数最小二乘模糊度解算理论与方法研究[D].武汉: 武汉大学, 2017. LU Liguo. Study on theory and method of GNSS integer least squares ambiguity resolution[D]. Wuhan: Wuhan University, 2017. http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201709018.htm |





