2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室, 湖北 武汉 430077
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, Wuhan 430077, China
全球导航卫星系统(GNSS)是一种利用无线信号传播提供导航、定位及授时服务(PNT)无线电导航定位系统[1-3]。由于导航卫星的飞速发展及广泛使用,人们对精度的要求越来越严格,影响导航定位精度的因素较多,其中时间误差的影响不容忽视[4]。1 ns的时间误差相对应的距离误差为3 dm,严重影响当今导航系统的定位精度。为满足当今用户厘米级定位的需求,高精度的时间系统至关重要[5]。IGS发布的钟差产品为事后精密钟差文件,精度较高,但获取时间较长,无法满足实时定位的需求。卫星钟差的预报有助于获取卫星自主导航所需要的先验信息及提高实时动态定位精度[6-7],为提高实时定位精度,卫星钟差数据的精度和时效性亟待解决[4]。
目前关于卫星钟差预报的模型较多,有多项式模型[8]、灰色模型[9]、多项式+周期项模型[10]、ARMA模型[11]、Kalman滤波模型[12]等,还有学者针对单一预报模型的局限性提出了线性组合模型[13-14]等。由于卫星钟易受外界环境的影响,且自身特征比较复杂,卫星钟差呈现非线性特性,线性预报模型往往难以精确地表示卫星钟差变化[15]。针对该问题,许多学者利用适用于非线性处理的神经网络在钟差预报方面进行了大量研究。文献[16]提出EMD-SVM算法进行卫星钟差预测,解决了氢原子钟钟差预测易受非线性和不稳定性影响的问题,预测精度显著提高并不易发散;文献[17]利用径向基函数神经网络进行卫星钟差预报,得到了较高精度的钟差结果;文献[18]提出基于一次差的小波神经网络模型,在6、12和24 h的预测中比IGU-P钟差产品的精度分别提高了约13.53%、31.56%和49.46%,且预测稳定性更高;文献[19]利用ART网络确定ELM网络的隐含层节点数,在长达30 d的预报中,预报精度优于二次多项式模型和灰色模型;文献[20]通过对四阶谐波模型残差的分析得到了钟差数据的额外周期数,并实现了8阶谐波函数建模,预测得到的钟差精度高于IGU产品精度;文献[21]在周期项模型的基础上添加循环项,并利用BP神经网络补偿非线性系统误差,提高了超快速钟差预报的精度;还有学者针对BDS数据建立超快速钟差预报模型,均得到了较好的钟差预报精度[22-24]。
BP神经网络在1986年由文献[25]提出后使用广泛,具有良好的自适应性、抗差性和联想记忆功能,但在使过程中容易陷入局部最优,且收敛速度较慢,影响最终收敛精度。针对卫星钟差的特性和BP神经网络的局限性,利用思维进化算法(MEA)良好的全局搜索能力和较强的收敛性,本文引入思维进化算法来选择BP神经网络所需要的最优权值和阈值,将两者结合建立了基于思维进化算法优化BP神经网络(MEA-BP)的钟差预报模型,计算中对卫星钟差数据作一次差处理,利用一次差后的数据进行建模,预报得到新的一次差值,再将一次差值还原得到预测钟差数据。大量算例表明,按照本文提出的网络结构得到了较高精度、稳定性的MEA-BP钟差预报算法。
1 钟差一次差处理及常规预报模型 1.1 钟差一次差处理同一卫星的钟差数据在前后相邻两个历元的变化量较小,从整体看呈现线性趋势。BP神经网络对于非线性数据有良好的适用性,对原始钟差数据序列不够敏感,对未作处理的数据进行建模预报时严重影响预报精度,故本文先对原始钟差数据作一次差处理,将相位数据转为频率数据,处理后的数据具有很好的非线性特征,适用于神经网络的建模与预报。
设X=x(1), x(2), …, x(n)为一组n维度的卫星钟差序列,其中x(i), i=1, 2, …, n为不同历元的钟差数据,对相邻历元的钟差数据作差,得到新的一次差数据序列为
 (1)
(1)
式中,Δx(i)=x(i+1)-x(i)。
用神经网络对构成的数据序列ΔX进行建模,对之后m历元的卫星钟差进行预报:对该n-1个数据进行建模,预报后m个数据序列ΔX′=Δx(n), Δx(n+1), …, Δx(m+n-1),利用预报的一次差值与建模最后一个钟差数据x(n)恢复待求历元的钟差,即
 (2)
(2)
式中,n≤k≤n+m-1。
1.2 3种预报模型 1.2.1 二次多项式模型(QP模型)[8]卫星钟差预报的二次多项式模型为
 (3)
(3)
式中,i=1, 2, …, n;ti时刻的卫星钟差为xi;t0为卫星钟参考时刻;a0、a1、a2为参考时刻的卫星相位、频偏和频漂;ε为模型随机误差。
利用最小二乘原理即可求得参数估值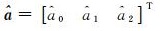
在二次多项式模型的基础上,附加周期项的钟差预报模型为
 (4)
(4)
式中,Ak、fk、φk分别对应周期项的振幅、频率和相位;p为主周期的个数;其余参数同式(3)。
与二次多项式模型计算相似,利用最小二乘原理求得参数估值,代入式(4)中可求得预报历元的钟差值。本文针对卫星钟差数据的特性,将主周期个数设为4,分别为12、6、4和3 h[25]。
1.2.3 灰色模型(GM(1, 1))[9]灰色模型预测钟差的表达式为
 (5)
(5)
式中,k=1, 2, …, n。
参数估值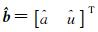
神经网络在非线性时间序列的拟合和预测方面效果显著,其中BP神经网络使用最为广泛。BP神经网络是一种误差反向传播的多层前馈神经网络,包括输入层、隐含层及输出层3部分,学习能力和记忆功能较强,属于自适应的非线性动力学系统[25]。当输出值不是期望值时,该网络会根据误差反向传播调整权值和阈值,进而不断逼近期望输出值。其拓扑结构如图 1所示。

|
| 图 1 BP神经网络拓扑图 Fig. 1 Topologic diagram of BP neural network |
BP神经网络的隐含层可为多层,为减少运算量、提高计算效率,本文将隐含层设为1层。在训练过程中,每层节点的输入层计算为
 (6)
(6)
激活函数常采用sigmoid函数,即
 (7)
(7)
该函数连续可导,可将数据从[-∞, +∞]投影到区间[0, 1]中。
则输入层计算后,对应的输出层计算为
 (8)
(8)
式中,Outn, j为BP神经网络得到的输出值。
BP神经网络通过误差后向传播进行权值更新,更新公式为
 (9)
(9)
式中,t为迭代次数;ε(t)为期望输出与实际输出之差;η为神经网络的学习效率;y(t)为神经元的输出值。
2.2 MEA算法思维进化算法(mind evolutionary algorithm,MEA)由文献[26]于1998年针对遗传算法的局限性提出的一种进化算法。MEA算法保留了遗传算法的“群体”、“个体”、“环境”和“进化”等思想,和遗传算法的“交叉”和“变异”不同的是,提出了“趋同”和“异化”等新的概念。利用MEA算法优化神经网络比使用遗传算法优化有更快的训练速度,大大缩短了神经网络的训练时间,实用性更广[27-28]。首先利用趋同操作对子群体中的个体进行优选,然后成熟的各子群体再通过异化操作进行全局竞争,大大提高了优化的效率。MEA算法的结构如图 2所示。

|
| 图 2 MEA算法结构 Fig. 2 MEA algorithm |
MEA算法是通过迭代进行优化的学习方法,其基本思路与步骤如下:
(1) 在解空间内随机产生一定数量的个体,计算训练个体均方误差的倒数得到各个体的分数,从中选取得分相对较高的若干个体得到优胜个体和临时个体。
(2) 以选出的个体为中心,在各个体周围产生新的个体,分别得到优胜子群体和临时子群体。
(3) 对各个子群体分别进行趋同操作,即在各子群体范围内,个体进行竞争选出优胜者。当胜者不再变化时,表示该子群体已经成熟,将优胜者的得分作为该子群体的得分,并张贴在全局公告板上。
(4) 各子群体完成趋同操作后,在全局范围内对所有子群体进行异化操作,通过比较各子群体间的得分大小,完成优胜子群体和临时子群体的替换、废弃和子群体中个体释放的过程,最后得到全局范围内的最优个体及其得分。
(5) 子群体中释放的个体在解空间中产生新的临时子群体,保持临时子群体总数不发生变化。判断是否满足精度要求,若不满足继续重复步骤(3)和步骤(4)操作,直至迭代结束或最优个体分数不发生变化,输出最优个体。
2.3 MEA优化BP的钟差建模与预报算法BP神经网络是通过反复训练来调整网络中的各权值和阈值,使得输出值逼近期望值。但是初始权值和阈值的选择严重影响BP神经网络的收敛和精度,并且得到的最终结果容易陷入局部最优。针对BP神经网络使用随机参数可能会导致算法结果异常的情况,本文使用MEA算法得到了神经网络中较好的初始化参数,可避免BP神经网络陷入局部最小值,大大提高卫星钟差预测的精度。
设有一组卫星钟差数据为x1, x2, …, xn,使用该n个时刻的数据来进行建模,预报以后时刻的钟差值。通常输出层的个数要和输出数据类型的个数相同,本文输出值为钟差,故将输出节点设为1,利用神经网络建立x1, x2, …, xN与xn+1的映射关系(N为输入节点数),采用滑动窗口的思想,在保证样本数目不变的前提下,不断使用新的预测数据来取代之前的已知数据,实现多历元的卫星钟差预报。利用MEA-BP模型进行卫星钟差预报的具体步骤如下:
(1) 对卫星钟差原始数据进行中位数探测,剔除数据中存在的粗差和钟跳。
(2) 将钟差建模数据分为输入部分和输出部分,使用归一化方法将数据归化到区间[-1, 1],并根据输入值和输出值选择BP神经网络的拓扑结构。
(3) 根据确定好的网络拓扑结构选择编码长度,定义迭代次数、种群大小、优胜子种群个数和临时子种群个数,求得子群体的大小。
(4) 将待优化的权值和阈值根据步骤(3)设置的参数进行编码,并随机产生初始种群。
(5) 根据式(10)和式(11),先计算得到均方误差E,然后对其取倒数得到各种群和个体的得分函数score
 (10)
(10)
 (11)
(11)
式中,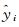
(6) 将当前的得分与历史最优得分比较,通过不断迭代,更新优胜种群及其最优得分。
(7) 判断每次得到的最优个体分数是否发生变化或是否已达到最大迭代次数,若满足精度,输出最优个体,优化过程终止,否则重复步骤(5)和步骤(6)。
(8) 根据步骤(7)获得的最优种群恢复BP神经网络需要的初始权值和阈值,代入神经网络进行训练和预报,对预报值进行反归一化运算,得到最终需要的卫星钟差值。
算法流程如图 3所示。

|
| 图 3 MEA算法优化BP神经网络流程 Fig. 3 BP neural network model optimized by MEA algorithm |
使用n维建模数据完成神经网络训练后,依据神经网络结构,输入节点数为N,输出节点数为1,采用滑动窗口的思想,保证样本数目不变,以此类推,实现多步预报,具体见表 1。
| input | output |
| {xn-N+1, …, xn} | {xn+1} |
| {xn-N+2, …, xn+1} | {xn+2} |
| ⋮ | ⋮ |
| {xn-N+m, …, xn+m-1} | {xn+m} |
得到一次差分序列的预报结果后,通过还原即可得到钟差预测值。
3 算例分析为了验证本文算法的实用性,选用IGS站提供的多天GPS精密钟差产品数据进行试验分析。由于篇幅有限,本文只列出GPS系统week 1919第一天(对应时间为2016年10月16日)的卫星钟差数据,采样间隔为30 s。本文选用5种不同原子钟类型的卫星PRN02、PRN10、PRN24、PRN25和PRN32,原子钟类型分别为:Block Ⅱ R Rb、Block Ⅱ A Cs、Block Ⅱ F Cs、Block Ⅱ F Rb和Block Ⅱ A Rb,使用前12 h的数据进行建模,预报接下来不同时刻的卫星钟差。将预报的钟差值和IGS发布的真实值进行对比,用公式(12)得到数据的均方根误差和误差的极差差值、均值,来评价分析预报结果的准确度
 (12)
(12)
 (13)
(13)
 (14)
(14)
式中,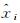
建模采用12 h数据,卫星钟差数据采样间隔为30 s,共1440个数据,所以设置MEA算法种群大小为1440,优胜子种群和临时子种群个数均为5,为使算法充分寻找最优个体,迭代次数设为200。文献[17]在预报不同时长的钟差时使用了不同的输入层和输出层,但实际进行钟差预报时选取较为复杂,并且网络模型的时效性受其结构的影响。本文将输入层设为1,由于隐含层的设置目前还未有可遵循的理论依据,只能依靠经验值进行确定,本文参考Kolmogorov定理[29]选择隐含层单元数
 (15)
(15)
式中,O为隐含层个数;N为输入层个数。
综上所述,本文将输入层节点设为1,输出层节点设为1,经计算得到隐含层节点为3,故最终确定的BP神经网络结构为1-3-1。
3.1 试验1首先验证一次差处理的优势。文献[30]使用一次差法对卫星数据进行处理,比较分析了一次差前后常用模型的预报精度,说明一次差后会造成预报过程中的误差累积,严重影响二次多项式模型的精度;而灰色模型本身就需要对数据进行累加和累减,所以一次差处理对该模型的影响难以给出定性结论。对神经网络而言,数据的非线性特性越明显,理论上预报精度越高。随机选取两颗原子钟不同的卫星进行预报。本文选取2号卫星(Rb)和10号卫星(Cs)举例说明,使用该天前12 h的钟差数据进行训练,预报接下来1 h的钟差,现使用未经优化的BP神经网络模型分别预报20次,对比其RMS值变化情况,如图 4所示。

|
| 图 4 一次差前后BP预报20次RMS的变化 Fig. 4 Variation of RMS using BP to predict clock bias before and after once difference about 20 times |
由图 4可知,对不作一次差处理的数据进行建模预报时,2号卫星和10号卫星预报20次的RMS值变化较大,且精度不高;而经过一次差处理后,两颗卫星的预报精度有了显著提升,并且多次预报的精度相当,有较强的稳定性。表明在同样使用BP神经网络模型进行卫星钟差预报的条件下,不管卫星原子钟是Rb钟还是Cs钟,对原始钟差进行一次差处理后,预报的精度和稳定性均优于一次差处理前。综上所述,一次差处理方法用于BP神经网络,可大幅度提高卫星钟差预报的稳定性和精度,并且适用于本文使用的网络结构。接下来试验将在一次差基础上进行研究分析。
3.2 试验2对比BP模型和MEA-BP模型对卫星钟差的预报性能。选取2号卫星(其他卫星均可)举例说明,为充分对比预报效果,使用该天前12 h的钟差数据分别独立预报10次接下来3、6和12 h的钟差值,两种模型预报的RMS值变化情况如图 5所示。

|
| 图 5 MEA-BP和BP预报10次RMS的变化 Fig. 5 Variation of RMS using MEA-BP and BP to predict SCB about 10 times |
在本试验中,利用MEA-BP和BP模型分别对2号卫星进行不同时段的预测,由图 5可知,MEA-BP和BP模型利用选取的网络结构,多次预报精度并无明显波动,证明了该网络结构的可行性;MEA-BP模型在预报时间增加时,比BP模型有更好的预报性能。在3个时段的钟差预测中,MEA-BP模型的预报精度均优于BP模型,说明通过MEA算法可以改善BP神经网络的初始权值和阈值,避免BP模型陷入局部最优,有效提高预报结果的精度。表明了MEA-BP模型用于钟差预报的可行性,是一种相对稳定的卫星钟差预报算法。
3.3 试验3MEA-BP模型与几种常用模型的预报性能对比。对2号卫星、10号卫星、24号卫星、25号卫星和32号卫星一天中前12 h的数据进行建模,分别预报2 h(240历元)、3 h(360历元)、6 h(720历元)和12 h(1440历元)的钟差。下面给出5颗卫星在以上4个时段的预报中,MEA-BP模型与二次多项式模型、二次多项式+周期项模型和灰色模型的具体精度对比情况,见表 2—表 5。表 1给出了分步预报的情况,12 h的预报误差包含2、3及6 h,故给出预报12 h时5颗卫星均方根误差和误差的极差差值的条形统计图,及MEA-BP模型与3种常用模型的预测误差趋势走向图,如图 6—图 7所示。
| PRN | statistics | QP | SA-QP | GM(1, 1) | MEA-BP |
| PRN02 | range | 1.393 | 1.295 | 1.028 | 0.739 |
| mean | -0.767 | 0.398 | -0.255 | 0.051 | |
| RMS | 0.823 | 0.511 | 0.324 | 0.150 | |
| PRN10 | range | 0.384 | 1.080 | 0.519 | 0.496 |
| mean | 0.680 | -0.363 | -0.448 | -0.217 | |
| RMS | 0.690 | 0.476 | 0.468 | 0.253 | |
| PRN24 | range | 2.182 | 5.086 | 1.581 | 1.700 |
| mean | 1.373 | -2.443 | -0.172 | -0.008 | |
| RMS | 1.460 | 2.891 | 0.409 | 0.358 | |
| PRN25 | range | 0.595 | 0.742 | 0.349 | 0.305 |
| mean | 0.137 | -0.633 | -0.816 | -0.180 | |
| RMS | 0.209 | 0.664 | 0.819 | 0.190 | |
| PRN32 | range | 0.241 | 0.697 | 0.663 | 0.410 |
| mean | -0.351 | -0.772 | -0.980 | -0.205 | |
| RMS | 0.356 | 0.796 | 0.997 | 0.232 |
| PRN | statistics | QP | SA-QP | GM(1, 1) | MEA-BP |
| PRN02 | range | 1.492 | 2.345 | 1.028 | 0.739 |
| mean | -0.969 | 0.766 | -0.351 | -0.030 | |
| RMS | 1.040 | 0.982 | 0.414 | 0.137 | |
| PRN10 | range | 1.020 | 1.370 | 0.519 | 0.496 |
| mean | 0.865 | -0.577 | -0.495 | -0.258 | |
| RMS | 0.916 | 0.700 | 0.513 | 0.287 | |
| PRN24 | range | 3.594 | 8.012 | 2.612 | 2.106 |
| mean | 1.759 | -3.883 | 1.879 | -0.104 | |
| RMS | 1.903 | 4.591 | 0.507 | 0.373 | |
| PRN25 | range | 1.173 | 0.819 | 0.349 | 0.311 |
| mean | 0.344 | -0.747 | -0.804 | -0.161 | |
| RMS | 0.481 | 0.781 | 0.808 | 0.177 | |
| PRN32 | range | 0.241 | 0.697 | 0.934 | 0.503 |
| mean | -0.361 | -0.831 | 1.119 | -0.270 | |
| RMS | 0.365 | 0.850 | 1.147 | 0.299 |
| PRN | statistics | QP | SA-QP | GM(1, 1) | MEA-BP |
| PRN02 | range | 2.686 | 4.557 | 1.260 | 0.948 |
| mean | -1.494 | 1.994 | -0.505 | 0.102 | |
| RMS | 1.624 | 2.422 | 0.558 | 0.179 | |
| PRN10 | range | 3.222 | 2.544 | 0.595 | 0.642 |
| mean | 1.773 | -1.208 | -0.403 | -0.144 | |
| RMS | 2.060 | 1.410 | 0.436 | 0.232 | |
| PRN24 | range | 5.104 | 14.116 | 2.938 | 2.993 |
| mean | 3.057 | -7.184 | 0.750 | 0.075 | |
| RMS | 3.378 | 8.179 | 1.077 | 0.613 | |
| PRN25 | range | 2.880 | 1.319 | 0.441 | 0.469 |
| mean | 1.146 | -1.034 | -0.692 | -0.073 | |
| RMS | 1.464 | 1.091 | 0.704 | 0.161 | |
| PRN32 | range | 1.156 | 1.212 | 1.116 | 0.702 |
| mean | -0.138 | -1.053 | -1.350 | -0.238 | |
| RMS | 0.360 | 1.092 | 1.382 | 0.301 |
| PRN | statistics | QP | SA-QP | GM(1, 1) | MEA-BP |
| PRN02 | range | 5.836 | 8.460 | 1.968 | 1.040 |
| mean | -2.804 | 4.040 | -0.827 | 0.227 | |
| RMS | 3.189 | 4.695 | 0.914 | 0.297 | |
| PRN10 | range | 7.246 | 4.470 | 1.643 | 1.506 |
| mean | 3.599 | -2.269 | -0.754 | -0.441 | |
| RMS | 4.177 | 2.590 | 0.909 | 0.635 | |
| PRN24 | range | 11.744 | 24.434 | 7.261 | 6.293 |
| mean | 4.402 | -14.058 | -1.562 | -0.121 | |
| RMS | 5.196 | 16.024 | 2.503 | 1.553 | |
| PRN25 | range | 6.569 | 1.758 | 1.039 | 0.730 |
| mean | 2.777 | -1.374 | -0.899 | -0.092 | |
| RMS | 3.370 | 1.442 | 0.952 | 0.229 | |
| PRN32 | range | 2.156 | 2.187 | 2.950 | 0.853 |
| mean | 0.432 | -1.564 | -1.995 | -0.167 | |
| RMS | 0.769 | 1.675 | 2.170 | 0.284 |

|
| 图 6 5颗卫星12 h钟差的预报条形统计图 Fig. 6 The prediction bar chart of the 5 satellite clock bias in 12 h |

|
| 图 7 5颗卫星12 h钟差的预报误差对比 Fig. 7 Comparing prediction error of the 5 satellite clock bias in 12 h |
由表 2至表 5的4个时段预报结果可看出,以2号卫星为例,2、3和6 h的预报精度(RMS)相当,均在0.18 ns以内,12 h的预报精度(RMS)相比前3个时段有所增加,但精度也没有超过0.3 ns,说明当预报时间增加时,MEA-BP模型预报误差的变化较小,具有一定的抗干扰能力。通过比较mean值和RMS值可以看出,本文提出的MEA-BP模型在不同时段的钟差预报中,精度均高于3种常用模型,在12 h的预报中更为明显,最小提升24%,最大可提升90%以上。并且在预报时长增加时,除10号卫星和24号卫星的预报精度稍差,其余均控制在0.3 ns以内,说明本文提出方法有较好的稳定性,表中反映稳定性的range值比QP模型、SA-QP模型和GM模型小,说明MEA-BP模型良好的预测性能。其中,24号卫星的预报误差较大,与该卫星这段钟差数据有明显大的波动有关。
从图 7中可知,在预测历元增加时,MEA-BP模型的预报结果比3种常规模型更稳定,误差值更小,并没有发散的情况发生,5颗卫星的12 h预测误差均在0附近波动;在预测时间增加时,总体误差起伏不大,预测的钟差值更贴合IGS发布的真实钟差值,体现出了良好的稳定性。说明在预测历元增加时,经MEA优化后的BP模型并没有陷入局部最优,说明了MEA-BP模型的稳定性及实用性,也在一定程度说明了神经网络结构的可行性,且本文网络结构设置简单,12 h的预测过程平均耗时在30 s以内(与计算机配置有关,本文使用计算机配置为i7处理器,16 GB运行内存),能更好地保证钟差预测的实时性。
4 结论本文首先分析了常规钟差预报模型的不足。由于卫星钟差本身的非线性特性,常用的模型进行钟差预报时,误差会随时间积累,且结果精度不稳定。针对BP神经网络算法在进行卫星钟差预报时存在的问题,本文采用MEA算法,获取较好的初始化权值和阈值等参数,提高了卫星钟差建模的精度,可有效避免BP神经网络陷入局部最优,加快BP算法的计算速度,提出适用于卫星钟差预报的MEA-BP模型。
通过对4种模型的预报精度进行分析,可知MEA-BP模型简单,对钟差进行短期预报有良好的预报精度和稳定性能,在预报时长增加时,精度变化不大,误差曲线起伏不大,比传统的二次多项式模型、二次多项式+周期项模型和灰色模型在2、3、6和12 h预报时,精度最低可分别提升9.09%、18.08%、16.39%和24.35%,最高可分别提升81.77%、86.83%、89%和93.2%。MEA-BP模型和算法具有较强的自适应能力、全局搜索能力和全局收敛性。通过多次“趋同”和“异化”迭代操作,进行全局寻优可得到BP神经网络中初始权值和阈值的全局最优解。相较于传统的BP神经网络模型,MEA-BP算法有更好预测精度和更快的预测效率。相较于传统进化算法(例如遗传算法)优化的神经网络,提高了搜索效率。通过不同子群体及个体的竞争学习,得到的优化值更为精确,提高了神经网络的准确性,从而提高了钟差预报模型的预报精度。该模型在短期内预报中表现较好,实时性较强,可用于卫星钟差的高精度预报。
影响神经网络钟差预报精度的因素有很多,例如粗差、建模数据量、数据采样间隔以及隐含层节点数选取等,本文讨论了部分关键问题,其余内容待进一步研究讨论。
需要说明的是,针对不同的卫星数据,一次差处理后的序列变化并不相同,相应的网络结构还需调整,并且建模数据量的大小也会影响预测精度,这些还需要进一步的研究。
致谢: 特别感谢国际GNSS服务组织MGEX分析中心提供相关的精密卫星钟差产品。
| [1] |
杨元喜, 李晓燕. 微PNT与综合PNT[J]. 测绘学报, 2017, 46(10): 1249-1254. YANG Yuanxi, LI Xiaoyan. Micro-PNT and comprehensive PNT[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1249-1254. DOI:10.11947/j.AGCS.2017.20170249 |
| [2] |
王宇谱. GNSS星载原子钟性能分析与卫星钟差建模预报研究[J]. 测绘学报, 2018, 47(7): 1026. WANG Yupu. Research on modeling and prediction of the satellite clock bias and performance evaluation of GNSS satellite clocks[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 1026. DOI:10.11947/j.AGCS.2018.20170467 |
| [3] |
YANG Yuanxi. Resilient PNT concept frame[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(3): 1-7. |
| [4] |
盛剑锋.高频GNSS准实时钟差估计及其应用[D].武汉: 中国地震局地震研究所, 2019. SHENG Jianfeng. Estimation and applications of the high frequency quasi-real-time GNSS clock[D]. Wuhan: Institute of Seismology, China Earthquake Administration, 2019. |
| [5] |
YANG Yuanxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system:data analysis based on BDS-3 demonstration system[J]. Science China Earth Sciences, 2018, 61(5): 614-624. DOI:10.1007/s11430-017-9186-9 |
| [6] |
HUANG Guanwen, ZHANG Qin, XU Guochang. Real-time clock offset prediction with an improved model[J]. GPS Solutions, 2014, 18(1): 95-104. DOI:10.1007/s10291-013-0313-0 |
| [7] |
YANG H, XU C, GAO Y. Analysis of GPS satellite clock prediction performance with different update intervals and application to real-time PPP[J]. Survey Review, 2019, 51(364): 43-52. DOI:10.1080/00396265.2017.1359473 |
| [8] |
ZHOU Haoyin, NI Kai, ZHOU Qian, et al. An SfM algorithm with good convergence that addresses outliers for realizing mono-SLAM[J]. IEEE Transactions on Industrial Informatics, 2016, 12(2): 515-523. DOI:10.1109/TII.2016.2518481 |
| [9] |
李超, 党亚民, 谷守周. 灰色模型的GLONASS卫星钟差预报[J]. 导航定位学报, 2016, 4(4): 24-29, 35. LI Chao, DANG Yamin, GU Shouzhou. Prediction of GLONASS satellite clock error based on grey model[J]. Journal of Navigation and Positioning, 2016, 4(4): 24-29, 35. |
| [10] |
艾青松, 徐天河, 孙大伟, 等. 顾及周期项误差和起点偏差修正的北斗卫星钟差预报[J]. 测绘学报, 2016, 45(S2): 132-138. AI Qingsong, XU Tianhe, SUN Dawei, et al. The prediction of BeiDou satellite clock bias based on periodic term and starting point deviation correction[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 132-138. DOI:10.11947/j.AGCS.2016.F034 |
| [11] |
XI Chao, CAI Chenglin, LI Simin, et al. Long-term clock bias prediction based on an ARMA model[J]. Chinese Astronomy and Astrophysics, 2014, 38(3): 342-354. DOI:10.1016/j.chinastron.2014.07.010 |
| [12] |
宋会杰, 董绍武, 屈俐俐, 等. 基于Sage窗的自适应Kalman滤波用于钟差预报研究[J]. 仪器仪表学报, 2017, 38(7): 1809-1816. SONG Huijie, DONG Shaowu, QU Lili, et al. Research on clock difference prediction using adaptive Kalman filter based on Sage window[J]. Chinese Journal of Scientific Instrument, 2017, 38(7): 1809-1816. DOI:10.3969/j.issn.0254-3087.2017.07.030 |
| [13] |
WANG Dongxia, GUO Rui, XIAO Shenghong, et al. Atomic clock performance and combined clock error prediction for the new generation of BeiDou navigation satellites[J]. Advances in Space Research, 2019, 63(9): 2889-2898. DOI:10.1016/j.asr.2018.01.020 |
| [14] |
LU Jicang, ZHANG Chao, ZHENG Yong, et al. Fusion-based satellite clock bias prediction considering characteristics and fitted residue[J]. Journal of Navigation, 2018, 71(4): 955-970. DOI:10.1017/S0373463317001035 |
| [15] |
徐超, 李博, 刘军良, 等. 一种改进的高精度频率源钟差仿真方法[J]. 宇航学报, 2017, 38(9): 998-1004. XU Chao, LI Bo, LIU Junliang, et al. A modified method for clock error simulation of high precision frequency source[J]. Journal of Astronautics, 2017, 38(9): 998-1004. |
| [16] |
ZHU Jiangmiao, SUN Panpan, GAO Yuan, et al. Clock differences prediction algorithm based on EMD-SVM[J]. Chinese Journal of Electronics, 2018, 27(1): 128-132. DOI:10.1049/cje.2016.08.039 |
| [17] |
王国成, 柳林涛, 徐爱功, 等. 径向基函数神经网络在GPS卫星钟差预报中的应用[J]. 测绘学报, 2014, 43(8): 803-807, 817. WANG Guocheng, LIU Lintao, XU Aigong, et al. The application of radial basis function neural network in the GPS satellite clock bias prediction[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 803-807, 817. DOI:10.13485/j.cnki.11-2089.2014.0078 |
| [18] |
WANG Yupu, LU Zhiping, QU Yunying, et al. Improving prediction performance of GPS satellite clock bias based on wavelet neural network[J]. GPS Solutions, 2017, 21(2): 523-534. DOI:10.1007/s10291-016-0543-z |
| [19] |
雷雨, 赵丹宁, 蔡宏兵. 利用结构自适应极端学习机预报导航卫星钟差[J]. 武汉大学学报(信息科学版), 2018, 43(5): 664-668, 718. LEI Yu, ZHAO Danning, CAI Hongbing. Prediction of navigation satellite clock offset by adaptive extreme learning machine[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5): 664-668, 718. |
| [20] |
LI Haojun, LIAO Xilin, LI Bofeng, et al. Modeling of the GPS satellite clock error and its performance evaluation in precise point positioning[J]. Advances in Space Research, 2018, 62(4): 845-854. DOI:10.1016/j.asr.2018.05.025 |
| [21] |
HUANG Guanwen, CUI Bobin, ZHANG Qin, et al. An improved predicted model for BDS ultra-rapid satellite clock offsets[J]. Remote Sensing, 2018, 10(2): 60. DOI:10.3390/rs10010060 |
| [22] |
HU Chao, WANG Qianxin, MIN Yanghai, et al. An improved model for BDS satellite ultra-rapid clock offset prediction based on BDS-2 and BDS-3 combined estimation[J]. Acta Geodaetica et Geophysica, 2019, 54(4): 513-543. DOI:10.1007/s40328-019-00270-8 |
| [23] |
WANG Qianxin, HU Chao, ZHANG Kefei. A BDS-2/BDS-3 integrated method for ultra-rapid orbit determination with the aid of precise satellite clock offsets[J]. Remote Sensing, 2019, 11(15): 1758. DOI:10.3390/rs11151758 |
| [24] |
HAN Tao. Fractal behavior of BDS-2 satellite clock offsets and its application to real-time clock offsets prediction[J]. GPS Solutions, 2020, 24: 35. DOI:10.1007/s10291-019-0950-z |
| [25] |
肖恭伟, 欧吉坤, 刘国林, 等. 基于改进的BP神经网络构建区域精密对流层延迟模型[J]. 地球物理学报, 2018, 61(8): 3139-3148. XIAO Gongwei, OU Jikun, LIU Guolin, et al. Construction of a regional precise tropospheric delay model based on improved BP neural network[J]. Chinese Journal of Geophysics, 2018, 61(8): 3139-3148. |
| [26] |
SUN Chengyi, SUN Yan, XIE Keming. Mind-evolution-based machine learning and applications[C]//Proceedings of the 3rd World Congress on Intelligent Control and Automation. Hefei, China: IEEE, 2000: 112-117.
|
| [27] |
WANG Wenxu, TANG Ruichun, LI Cheng, et al. A BP neural network model optimized by mind evolutionary algorithm for predicting the ocean wave heights[J]. Ocean Engineering, 2018, 162: 98-107. DOI:10.1016/j.oceaneng.2018.04.039 |
| [28] |
WANG Zhenhua, MA Gengsheng, GONG Dianyao, et al. Application of mind evolutionary algorithm and artificial neural networks for prediction of profile and flatness in hot strip rolling process[J]. Neural Processing Letters, 2019, 50(3): 2455-2479. DOI:10.1007/s11063-019-10021-z |
| [29] |
王宇谱, 吕志平, 崔阳, 等. 利用遗传小波神经网络预报导航卫星钟差[J]. 武汉大学学报(信息科学版), 2014, 39(7): 809-814. WANG Yupu, LÜ Zhiping, CUI Yang, et al. Predicting navigation satellite clock bias using a genetic wavelet neural network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 809-814. |
| [30] |
王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3): 323-330. WANG Yupu, LÜ Zhiping, CHEN Zhengsheng, et al. Research on the algorithm of wavelet neural network to predict satellite clock bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323-330. |



