2. 地球空间环境与大地测量重点实验室, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China
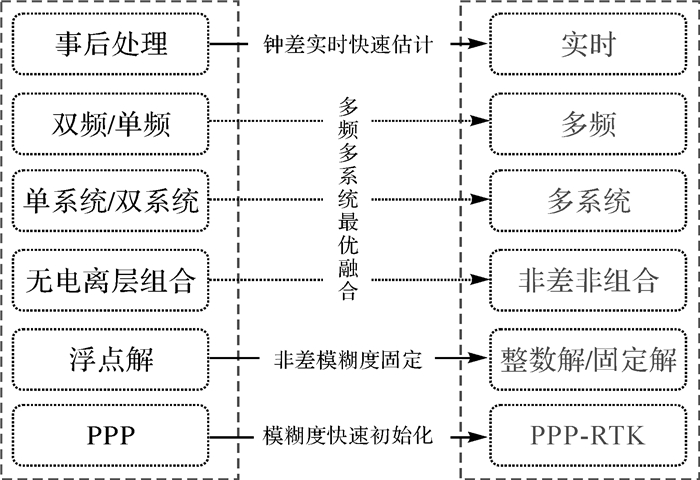
全球卫星导航系统(global navigation satellite system, GNSS)可向全球用户提供高质量的定位、导航和授时(positioning, navigation and timing, PNT)服务,已成为重要的空间信息基础设施,在国民经济建设与军事国防领域发挥着十分重要的作用,其应用仅受限于人们的想象力。卫星导航的定位精度、可靠性和时效性,直接决定了它的科学和工程应用价值。由于受到多种误差的影响,卫星导航系统自身提供的定位精度通常只有5~10 m,无法满足高精度用户的需求。为了实现厘米级甚至毫米级的定位,大地测量学家先后提出了两种精密定位方法,一种是差分定位,另一种是精密单点定位(precise point positioning, PPP)[1-2]。与差分定位相比,PPP因采用非差观测模型,能同时精确估计测站绝对坐标、接收机钟差以及绝对天顶对流层延迟及其水平梯度、倾斜路径电离层延迟等参数,具有显著的优越性。因此,PPP在GNSS精密定位与定轨、精密授时、大气科学、地球动力学等诸多领域具有独特的应用价值。PPP从提出到现在的20余年里,先后历经了从静态到动态、从后处理到实时、从双频到单频再到多频、从GPS单系统到GNSS多系统融合、从浮点解到固定解、从PPP到PPP-RTK等发展过程(图 1),其中,最具标志性的成果就是PPP固定解技术的突破。PPP为建立全球统一无缝的GNSS高精度定位服务模式提供了可能,已成为卫星导航定位领域的前沿热点方向。随着PPP技术的不断发展,国内已有不少商业机构推出了PPP/PPP-RTK服务,譬如:美国NavCom公司的StarFire,海克斯康的VeriPos,诺瓦泰的TerraSTAR,荷兰辉固集团的OminiSTAR,美国天宝的RTX-Fast,合众思壮的中国精度,中海达的全球精度Hi-RTP等,国内还有数家导航企业也正在发展类似的商用系统。
|
| 图 1 PPP主要发展历程 Fig. 1 Development of precise point positioning |
笔者曾于2017年撰写《GNSS精密单点定位技术及应用进展》一文[3],梳理论述了PPP技术及其应用的发展现状和动态。在过去的3年,GPS、Galileo和北斗卫星导航系统都有新的发展和变化:①美国正在实行GPS现代化计划,已有12颗GPS Block ⅡF卫星可以播发L5信号。首颗GPS Block Ⅲ卫星已于2018年12月23日发射成功,新一代的GPS卫星可播发4种民用信号,包括L2C、L5、L1C及传统的民用信号(https://navcen.uscg.gov/?Do=constellationStatus)。②Galileo系统将于2020年底或2021年初建成,截至2020年6月,Galileo星座一共有26颗卫星,其中21颗卫星正常运行,已经基本具备独立提供全球PNT服务能力(https://www.gsc-europa.eu/system-service-status/constellation-information)。③截至2020年6月,我国已发射55颗北斗卫星,北斗三号系统最后一颗组网卫星于2020年6月发射成功,标志我国北斗卫星导航系统即将具有全球PNT服务能力。北斗三号整个星座由30颗卫星组成,其中包括3颗地球静止轨道卫星(GEO),3颗倾斜地球同步轨道(IGSO)和24颗中地球轨道卫星(MEO)组成[4-6]。全球卫星导航系统的建设完成以及区域增强系统的发展,将给导航用户提供更加丰富的观测值、更多频率选择和更优的卫星几何构型,PPP的定位精度、初始化时间、可用性和可靠性将持续改善。此外,低轨星座计划进入蓬勃发展时期,不久的将来,导航用户将能同时接收到GEO、IGSO、MEO、LEO卫星播发的导航信号,低轨卫星几何构型变化更快,有望进一步缩短PPP的初始化时间[7-10]。
鉴于PPP/PPP-RTK广阔的应用前景和当前卫星导航学界对其的高关注度,笔者认为有必要适时梳理总结PPP/PPP-RTK技术在近几年的发展动态,并结合最新的多系统多频观测资料及其精密轨道和钟差产品,对比分析多系统组合PPP特别是北斗二号+北斗三号PPP浮点解和固定解的定位精度、收敛时间、首次固定时间,为PPP/PPP-RTK的进一步发展提供参考。
本文将从两个方面开展论述,首先,笔者将梳理归纳国内外学者最近几年在PPP/PPP-RTK方向所做的代表性工作和取得的主要进展;然后将对比分析当前星座条件下单系统/多系统/北斗二号+北斗三号的PPP浮点解、PPP固定解的定位精度和初始化时间等典型性能指标。需要说明的是:北斗三号系统星座刚建设完成,就目前来说,全球IGS跟踪站现有硬件配置条件能实际观测到的北斗三号卫星较少,IGS各分析中心对北斗三号卫星精密轨道与钟差改正数的支持较晚,且很多MGEX测站能观测到的北斗三号系统信号是B1和B2频点,而现在的精密星历是采用B1和B3频点,因此还无法独立采用北斗三号进行PPP处理。若无特别区分,文中北斗PPP定位结果为北斗二号PPP定位结果。
1 PPP若干热点方向的发展动态纵观近几年PPP技术的发展,关注点主要在高采样率钟差实时快速估计、多频PPP、多系统PPP、PPP增强、PPP-RTK、缩短PPP初始化时间等方面,下面分别展开论述。
1.1 高采样率钟差实时快速估计为了满足实时PPP用户对高采样率精密卫星钟差产品的需求,文献[11]提出了一种高效稳健的快速估钟算法,通过构建非差和历元差分混合钟差解算双线程算子,减少了待估参数的数量,突破了高采样率钟差计算效率的限制,实现了GPS精密卫星钟差的1 s采样率快速更新。文献[12]提出采用全参数模型(FP)和高采样率模型(HR)估计多系统卫星钟差改正数,HR模型中使用FP模型估计得到的最新模糊度及其方差协方差矩阵来降低待估参数的维度,达到钟差快速估计的目的。结果表明,提出的方法能提供1 Hz甚至更高采样率的实时钟差改正数。文献[13]将双频非差模糊度固定方法引入到实时钟差估计中,结果表明,与IGS 30 s最终精密钟差产品相比,模糊度固定的钟差估值在精度上提高了50%~87%,在动态浮点解PPP验证中,使用模糊度固定的钟差产品能提升N方向定位精度至少5%,在E和U方向至少提升10%。文献[14]使用扩展卡尔曼滤波方法同时获取卫星钟差估值以及定位结果,实现实时非差PPP,结果表明在3个IGS测站辅助下,能达到水平2 cm、高程5 cm的定位精度,加入GLONASS观测信息能缩短收敛时间56.9%,提高定位精度31.8%。文献[15]提出了一种在钟差轨道改正数信息短时中断时保持实时PPP在1 dm定位精度的方法。基于IGS RTS产品预测轨道和钟差改正信息,对于几分钟的中断时间,采用二阶多项式和正弦项预测IGS RTS改正数信息;对于更长的中断,使用最近的IGS超快轨道。对于模型需要的参数采用滑动时间窗口进行连续估计,结果表明,在动态和静态测试中,轨道钟差信息中断2 h内仍能保持厘米级定位精度。文献[16]在现有的实时钟差预报模型中,提出使用IGU观测部分钟差的历元差分来估计线性和正弦参数的系数,常系数使用最新的RTS钟差改正数计算,该方法能解决实时解算初期改正数信息中断的问题,减少处理器的内存负担。
笔者认为,以当前星载原子钟的稳定度来讲,1 Hz更新率的精密卫星钟差足够满足PPP/PPP-RTK的厘米级定位需要,现有的计算资源和钟差估计方法已完全能够满足1 Hz实时钟差估计。考虑到计算耗时和钟差播发对通信带宽的负荷等因素,实际应用中采样率未必越高越好。
1.2 PPP模糊度固定方法和UPD产品恢复非差模糊度的整数特性并将其固定成整数是实现PPP固定解的前提。国内外学者先后提出了UPD分离、相位整数钟和钟差去耦等3种实现PPP固定解的方法[17-19]。值得注意的是,由于UPD方法可与各IGS分析中心的精密产品兼容,使用最为广泛。钟差去耦法需要估计两套钟且无公开产品可使用,使用此方法的机构较少。武汉大学测绘学院于2015年起向全球用户免费发布与IGS精密轨道和钟差兼容的GPS卫星端UPD产品,2019年扩展至GPS+Galileo+BDS+QZSS四大系统并备份至Github,用户可通过Github获取对应于各分析中心的UPD产品[20-21];法国CNES基于整数钟方法于2015年公开发布GPS宽巷UPD和整数钟产品,并于2018年年底扩展至GPS+Galileo,用户采用CNES发布的卫星轨道和钟差产品使用整数钟方法可实现PPP模糊度固定[22];2019年武汉大学GNSS中心发布了相位钟差/偏差产品,用户可采用该产品与CODE分析中心的精密轨道产品搭配PRIDE-PPPAR软件使用实现GPS PPP-AR[23]。UPD产品的发布,可以使全球精密定位用户实现PPP固定解。除使用公开发布的UPD产品外,学者们也尝试通过不同方法估计GLONASS/Galileo/BDS卫星端UPD并实现了模糊度固定[24-30]。由于GLONASS采用频分多址的信号体制,不同卫星的观测值之间存在频间偏差的影响,文献[24]利用Trimble NetR8接收机估计了GLONASS卫星的UPD并应用于GLONASS PPP模糊度固定,结果表明相对于GLONASS浮点解的结果,2 h后,GLONASS PPP在E/N/U方向的定位精度由0.66、1.42、1.55 cm分别提高到0.39、0.38、1.39 cm。
PPP模糊度固定理论已经发展较为成熟,3种方法在理论本质以及定位结果上无明显差异。为了保持与IGS当前发布的轨道和钟差产品兼容,笔者认为相位整数钟法和UPD方法将是今后PPP/PPP-RTK模糊度固定的主流方法,实际上各机构发布的UPD产品也已被成功应用于科学研究和工程应用中。
1.3 多系统组合PPP模糊度固定近些年来,随着北斗二号系统的建成、北斗三号完成全球组网以及Galileo系统即将建成,多系统组合PPP方兴未艾。文献[31]建立了GPS和BDS的UPD估计模型并对GPS+BDS双系统PPP固定解的结果进行了初步分析,结果表明:BDS PPP固定解的首次固定时间超过6 h,且固定成功率小于35%,GPS+BDS双系统PPP固定解的首次固定时间在静态模式下缩短到16.9 min,在动态模式下缩短到24.6 min,显著优于GPS单系统PPP固定解的初始化时间。文献[32]使用小网观测数据,将GEO卫星的轨道误差吸收进UPD估值中实现了GPS+BDS模糊度固定,结果表明加上GEO观测数据的模糊度固定率能提升18.2%。文献[27]比较了Galileo卫星与GPS、BDS卫星的UPD估值并实现了GPS+Galileo模糊度固定,结果表明,Galileo的UPD估值稳定性优于GPS和BDS,组合系统的模糊度固定解比浮点解各方向的定位精度均有所提升。文献[33]实现了GPS+GLONASS+BDS三系统模糊度固定,结果表明,10 min观测弧段的动态PPP中,单GPS仅有16.2%的观测数据能实现固定,加上GLONASS之后提升到75.9%,三系统同时参与固定时能提升至90.0%。文献[34]使用非组合模型实现了GPS、GLONASS、BDS和Galileo四系统PPP模糊度固定,将ISB和GLONASS频间码偏差作为待估参数参与估计。结果表明,ISB在天内保持稳定,当卫星钟基准出现变化时,ISB变化较大,四系统静态定位结果能达到毫米级,动态结果达到厘米级。文献[35]通过逐历元估计GPS、BDS、GLONASS和Galileo的UPD,实现了四系统的非差模糊度固定,结果表明,四系统PPP模糊度首次固定时间约为9.21 min,相比于单系统和双系统有明显提升,对于观测时长为10 min的弧段,四系统PPP固定解定位精度比GPS单系统在E、N、U方向分别提升了18.2%、13.9%和84.2%。
笔者看来,多系统组合PPP模糊度固定方面的研究更多侧重于加入更多星座的观测数据对PPP模糊度固定性能带来的增益,就其方法来讲与单系统PPP并无本质差异。当然利用多系统进行PPP模糊度固定时,需要处理好系统间的各种偏差。
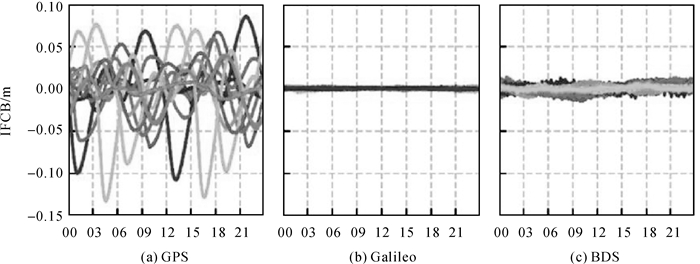
1.4 多频GNSS PPP模型及其模糊度固定多频PPP首先要解决频间钟偏差(inter-frequency clock bias, IFCB)的问题。文献[36]指出,GPS卫星的IFCB大于1 dm,因此目前IGS分析中心基于L1/L2生成的精密钟差产品不能直接被用于L1/L5 PPP中。文献[37]提出了一种能够同时兼容各种三频PPP模型的IFCB估计方法,推导了L1/L5 IF PIFCB、L1/L2/L5 IF PIFCB和L5 UC PIFCB间的数学转换公式,因此用户可根据一组IGS双频无电离层组合卫星钟差、一组PIFCB估值和DCB产品就可实现所有GPS三频PPP模型。为了更系统地认识PIFCB的特性,文献[38]对一整年的GPS单日PIFCB估值时间序列进行谐波分析,建立了由1个线性函数和1个六阶谐波函数组成的GPS PIFCB模型,将该模型应用到GPS实时三频PPP解算中,定位精度改善9%~24%。文献[39]通过研究发现,GPS IFCB的振幅达到1~2 dm,BDS卫星的IFCB振幅为2~3 cm,Galileo卫星的IFCB最小,小于1 cm。图 2代表性地给出了GPS、Galileo和BDS各卫星的IFCB估值。
在多频PPP模型研究方面,文献[40]从函数和随机模型两方面对比了三频PPP定位中两类常用的无电离层组合和一组原始观测值PPP模型,其结果表明在动态观测条件较弱的情况下,加入第三频观测值可有效改善定位性能。文献[41]研究了9种不同的三频GPS线性组合PPP模型,结果表明,三频PPP相对于双频PPP在收敛时间和定位精度方面的改善约10%。文献[42]评估了不同的多频多系统PPP定位模型,结果表明,三频PPP的定位收敛时间略短于双频PPP,当引入外部电离层约束时,GPS+BDS+GLONASS+Galileo+QZSS五系统非组合PPP的收敛时间相比双频组合能缩短19.0%。
在多频PPP模糊度固定方法研究方面,文献[43]基于非差非组合模型估计了BDS三频数据原始频率的UPD并实现多频PPP模糊度固定,结果表明三频固定解相比于双频固定解不仅能改善定位精度,也能在一定程度上缩短收敛时间。文献[44]估计了BDS和Galileo三频UPD,发现超宽巷和宽巷UPD在一月内保持稳定,窄巷UPD在天内保持稳定。BDS+Galileo三频模糊度固定结果表明,动态和静态定位中,固定解比浮点解的定位精度提升了30%~70%,并且三频固定解相对于双频固定解能有效缩短模糊度首次固定时间约14.7%。文献[45]估计了系统间相位偏差和卫星FCB,构建了GPS/BDS/Galileo/QZSS三频观测值的紧组合模型,仅用单历元观测值实现了超宽巷和宽巷模糊度的固定,实现了单历元分米级定位。文献[46]研究了顾及天线相位中心改正的3种不同频率组合的Galileo三频PPP的性能,结果表明在使用Galileo天线相位中心改正数后,E1/E5a/E5b、E1/E5a/E6和E1/E5a/E6 3种组合形式的三频PPP模糊度固定比双频收敛时间分别缩短16.2%、30.3%和17.7%。文献[47]研究了Galileo三频/四频/五频的不同组合模糊度固定,发现E5a/E5b、E5a/E5和E5/E5b超宽巷UPD估值接近0,使用估计得到的UPD产品实现模糊度固定,结果表明,5种类型的三频组合中,E1/E5/E6三频PPP AR的性能最好,平均收敛时间为16.9 min,四频和五频PPP AR的平均收敛时间分别为15.3 min和15.0 min。多频观测值对窄巷模糊度的首次固定时间的缩短不明显,但超宽巷和宽巷模糊度能瞬间固定,首个历元即能达分米级定位精度。文献[39]顾及GPS、Galileo和BDS的IFCB特性,估计了三频原始频率UPD,实现了GPS+Galileo+BDS三频非差非组合模糊度固定,结果表明三频GNSS PPP模糊度固定解相对于双频模糊度固定解能有效提升定位精度,并使收敛时间缩短15.6%。图 3代表性给出了GPS、Galileo和BDS各卫星的超宽巷、宽巷和窄巷UPD估值时间序列图,图 4代表性给出了GPS双频/三频和GPS、Galileo和BDS双频/三频动态PPP固定解定位误差序列图。
综上来看,多频PPP的研究主要围绕不同频率观测值的组合形式、多频PPP模型的性能评估、频率间偏差分析以及多频PPP模糊度固定等问题展开。从目前的研究结果来看,多频观测值的引入对超宽巷和宽巷模糊度的快速固定有显著贡献,使用少数几个历元甚至单历元观测就可以实现分米级精度的PPP定位,但如何缩短窄巷模糊度的固定时间仍没有很好解决。
1.5 缩短PPP初始化时间初始化时间较长一直是制约PPP应用的一个瓶颈。从前文的分析可以看出,多GNSS系统组合、多频观测值的加入都能在一定程度上改善初始化时间[48-49]。从已有的研究结果来看,即使采用四系统,模糊度的首次固定时间仍然需要10~15 min[34-35, 50-51]。除了使用GNSS观测值本身之外,已有诸多学者采用先验大气约束加快PPP初始化时间,结果表明,在外部信息辅助下,可显著缩短PPP初始化时间[52-53]。文献[54]利用高分辨率的数值天气预报模型WRF和近实时GNSS观测数据获得高精度对流层延迟,同时将其约束到实时PPP数据处理中,并与其他两种常用的对流层经验模型UNB 3 m和VMF1-FC约束的实时PPP定位结果进行相比,其定位精度和收敛速度均得到改善。文献[55]在非组合PPP中使用电离层约束和对接收机端DCB的建模分析了缩短收敛时间的效果,结果表明,当使用GIM和区域电离层模型约束时,首个历元的定位精度分别能达到0.4 m和0.2 m,在68%的置信水平下,水平方向收敛到1 dm所用的时间能缩短至7.5 min。文献[56]提出在估计卫星钟差、电离层斜延迟和卫星端FCB之后改正到用户端,使用部分模糊度固定技术同时对GLONASS和GPS的模糊度进行固定,结果表明,仅使用GPS观测值时初始化阶段需要25 min,当双系统模糊度同时固定时,初始化时间缩短到6 min左右。文献[57]提出了估计系统间相位偏差(ISPB)并实现GPS/BDS系统间模糊度固定的方法,相比于传统的系统内固定,多了一个模糊度参数可用于部分模糊度固定的搜索。小时弧段解的动态PPP结果表明,使用系统间模糊度固定时,平均初始化时间能缩短约10%。
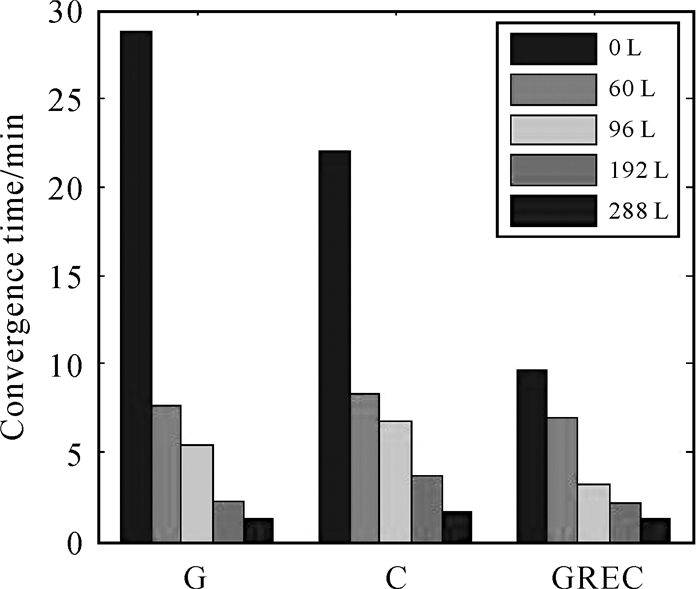
近年来,随着低轨导航增强概念的提出,不少学者通过模拟仿真验证了加入低轨导航卫星后,可以显著改善PPP的收敛时间。文献[8]初步评估了低轨卫星增强PPP,仿真结果表明加入低轨卫星观测之后,PPP收敛时间能缩短到5 min以内;文献[9]基于精细仿真的观测值,评估不同低轨星座增强GNSS PPP双频浮点解性能,结果表明,PPP收敛时间可由单系统的30 min显著缩短至数分钟甚至1 min以内,且收敛速度增强效果主要取决于可见低轨卫星数,通过加入包含60、96、192和288颗星的低轨星座增强Multi-GNSS PPP,中纬度NNOR站上分别可见2.4、3.1、6.3和9.5颗低轨卫星,收敛时间由9.6 min缩短至7.0、3.2、2.1和1.3 min,如图 5所示。但目前对低轨卫星增强PPP的研究仅处于仿真阶段,尚缺乏对于真实数据的定位结果。
综上来看,多频多系统观测值可在一定程度上缩短PPP初始化时间,但仍无法满足实际应用中对于快速初始化的要求;先验大气约束对初始化时间的缩短效果主要取决于大气建模的精度,精度越高越有利于实现快速初始化;低轨卫星观测值加速PPP收敛目前仅处于仿真阶段,在实际应用中,低轨卫星的观测值数量和质量可能无法达到与仿真观测值一样的效果,今后仍需采用实测数据进行验证。
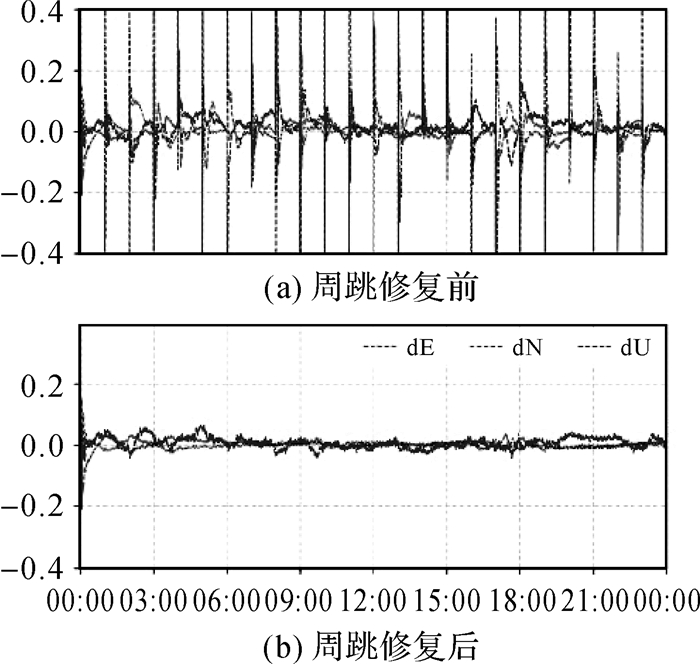
1.6 PPP快速重新初始化由于卫星信号易受遮挡影响,观测数据不可避免会出现中断现象,中断之后各参数重新初始化,通常需要和首次开机初始化一样的时间,严重制约了PPP在实际工程中的应用。因此,有学者针对信号中断后的快速重新初始化技术进行了研究。文献[58]提出利用无几何距离组合观测值实时修复非差周跳,使失锁前后的模糊度参数连接起来,达到快速重新初始化目的。文献[59—60]利用信号中断前后大气延迟信息连接中断观测值,在短时中断时能实现快速重新初始化。文献[61]提出了一种基于卡尔曼滤波的非差周跳估计方法,在非差非组合模型中同时估计周跳和其余待估参数,引入LAMBDA方法和部分模糊度固定概念搜索最佳整数值周跳,结果表明,该方法平均需要1.5~2.5历元实现周跳修复,从而达到快速重新初始化,如图 6所示。除了利用GNSS本身的观测信息之外,文献[62]提出了惯性辅助PPP模糊度固定的方法,利用SINS在短时间内递推的高精度位置信息,改善浮点模糊度的解算精度,加快PPP模糊度固定,该方法将复杂环境下的PPP模糊度固定率,从22.4%提升到80.3%,卫星信号中断10 s内能够实现快速重新初始化和模糊度快速重新固定。
PPP快速重新初始化主要是解决信号短时中断引起的模糊度参数重置造成的定位重新收敛问题。目前的方法主要是转化成周跳的在线实时探测与修复,使模糊度参数能正确传递,但这些方法主要取决于信号中断的时间和大气时变状态,通常要求信号中断前后历元的电离层变化不能太大,当信号长时中断时,这些方法的可靠性和可行性将大大降低。
1.7 精密单点实时动态定位(PPP-RTK)文献[52]首次提出了PPP-RTK的概念。但关于PPP-RTK的概念其实学术界还存在些争议。笔者认为PPP-RTK应该具有3个基本特征:采用PPP定位模型、实时定位、能快速固定模糊度。鉴于此,本文把PPP-RTK单列一节进行讨论。
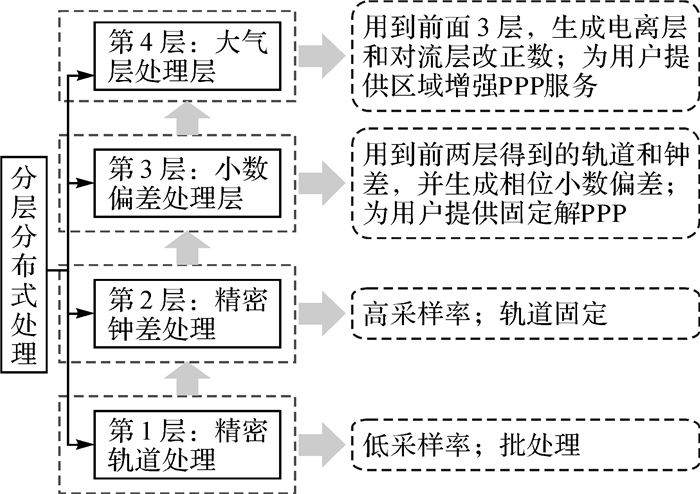
从前面的分析可以看出,如何实现PPP模糊度的快速(或瞬时)固定是PPP-RTK的核心。文献[63]借鉴网络RTK误差处理的思想,提出充分利用已经建立起来的密集基准站网设施,逐站进行精密单点定位整数解,逐站提取精密大气延迟信息,并进行空域和时域建模,将这些增强的改正信息播发给用户使用,解决了非差模糊度的快速固定难题,实现了PPP-RTK定位原型系统。其实现方案如图 7所示。已有或正在发展的一些商业PPP-RTK系统大都采用该方案。
|
| 图 7 PPP-RTK实现方案 Fig. 7 Implementation scheme of PPP-RTK |
文献[64]分别采用法国密集参考网和稀疏参考网数据构建对流层延迟模型,为PPP的对流层参数提供先验约束,试验结果表明,两种模型的实时PPP定位收敛后精度没有显著改善,但是收敛速度得到提高。文献[65]研究了现有3种非差非组合PPP-RTK网络模型,并利用中国陆态网实测数据给出了最适合实时播发卫星相位小数偏差的线性组合,同时评估了PPP-RTK定位性能。文献[66]为了提高区域参考网实时改正数的计算效率,提出了基于多核并行计算技术的相位小数偏差、天顶对流层延迟等各项误差改正数的计算方法,利用香港CORS和美国西南部CORS网数据研究表明,双核、四核、八核、十六核平台并行实现相位小数偏差估计和对流层建模的处理速度可比单核串行处理速提高1.79倍、3.15倍、5.59倍和9.69倍。文献[67]利用CORS网观测数据评估了BDS-2+3/GPS的PPP-RTK定位性能,结果表明,利用区域参数获得的高精度大气模型,可以在1.5和1.6个历元实现单GPS和单BDS-2+3 PPP-RTK定位,其定位精度可收敛至水平毫米级到厘米级、高程厘米级,如图 8所示。
文献[68]研究了多系统PPP-RTK定位性能,利用Curtin大学的PPP-RTK数据处理平台及多系统GNSS观测数据,数据集包含了高质量的大地型接收机和低成本单频接收机,其基准站网包含大网(覆盖澳大利亚)和小网(站间距小于30 km)两种,试验结果表明:利用大网多系统GNSS基准站数据可在15 min实现多系统GNSS PPP-RTK收敛,相比浮点解PPP收敛速度缩短了30 min;基于小网将用户站与基站数据同时解算时,可实现2 min内收敛。文献[69]提出了一种基于B-splines函数的4D电离层层析模型,并用于PPP-RTK用户的电离层延迟改正,可使其初始化时间缩短至20个历元(采样率为30 s)以内。鉴于近年来5G技术的快速发展以及其超低延迟和超大数据传输容量等特点,文献[70]设计了一种新的5G辅助GNSS PPP-RTK系统,该系统可以满足PPP-RTK精密定位中大量高精度大气误差改正数以及其他改正数的快速传输需求,相比已有网络RTK系统,该系统可将卫星钟差、轨道、码偏差、相位偏差以及对流层电离层改正数等播发间隔由5~30 s提高至1 s,其定位精度也可由数厘米提高至1 cm,收敛时间从1 min缩短至2.8 s。
目前,全球PPP-RTK技术仍处于开发和早期应用阶段,在理论方法方面,学术界已提出的多种不同新概念新方法,其理论和结果表现基本等价,但是在工程应用中其差异尚需更多比较分析。PPP-RTK性能优劣与服务端提供的数据量和数据采样率密切相关,如何平衡数据传输量、采样率与带宽的关系是目前仍需要关注的问题。其次,已有全球/区域电离层模型对PPP-RTK性能提升的幅度较为有限,笔者团队初步研究结果表明基于参考网的电离层斜延迟产品能显著提高PPP-RTK性能,但是其播发数据量较大。因此,如何构建高精度的大气模型并确定其播发方式是目前PPP-RTK应用实践需要解决的重要问题之一。最后,在PPP-RTK定位中,大气误差的初始方差确定是影响PPP-RTK快速收敛的关键,现有大气模型/产品提供的精度指标较多是计算过程的内符合精度,而且存在虚高现象,如何准确确定该参数在观测方程中的方差值有待深入研究。
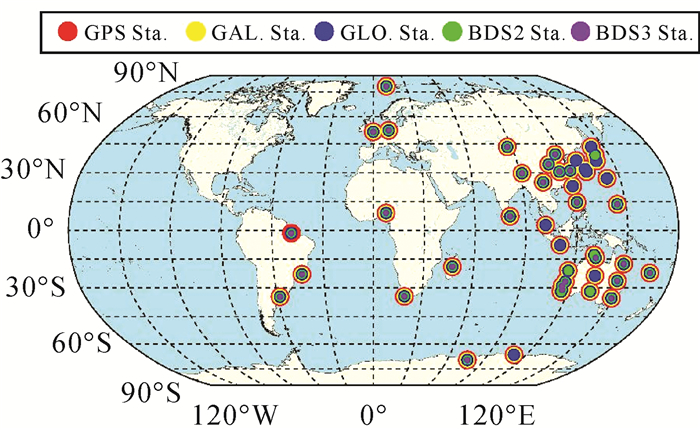
2 北斗/GNSS PPP浮点解及固定解结果与分析本文选取了2020年1月1日至2020年1月7日全球分布(图 9)的53个测站的观测数据进行了单系统和多系统,静态和动态,浮点解和固定解的双频PPP定位,评估当前GNSS单系统和多系统PPP的静态和动态定位性能(静态模拟动态)。由于目前各分析中心生成精密卫星轨道和钟差产品时,对于北斗三号系统使用的频率为B1和B3,而目前仅有较少数MGEX测站支持北斗三号系统的观测,且观测频率多为B1和B2,因此本文选取的测站中包含21个iGMAS测站以更好评估北斗系统的精密单点定位性能。
|
| 图 9 本文用于PPP解算的测站分布 Fig. 9 Distribution of MGEX and iGMAS stations used for PPP solutions |
本文在PPP固定解解算时,采用的相位小数偏差产品为武汉大学测绘学院发布的FCB产品,固定模式为“fix and hold”,ratio值设为3.0,截止高度角为7°。通过本文的数据解算发现,对于北斗三号系统,虽然已经完成了全球组网,但IGS分析中心提供的精密星历最多只支持到C37,因此较多用于定位实验的测站个别时段只有4颗甚至更少的北斗三号可用卫星且可用卫星几何分布不理想,导致某些历元没有定位结果输出,出现重新初始化现象。因此在本文中未给出单北斗三号系统的定位误差图及固定解结果。此外,在本文的数据统计中,对定位性能指标作如下定义:静态解的定位精度为当天收敛到最后一个历元的定位精度,动态解的定位精度为收敛后的各历元定位精度的平均值,参考已知坐标来自SNX周解文件,若周解文件中无参考坐标,则取对应测站7天PPP解算的四系统静态定位结果的平均值;收敛时间为三维方向定位误差小于1 dm并保持至少十个历元所需要的时间;首次固定时间为模糊度首次正确固定且固定解精度优于浮点解精度所需要的时间。
2.1 静态定位在静态PPP浮点解和固定解试验中,本节给出了单个测站的单天解结果,并从定位精度,收敛时间和首次固定时间等方面评估了静态PPP浮点解和固定解性能。图 10代表性地给出了测站MRO1在2020年1月7日GPS、Galileo、GLONASS、BDS-2、BDS-2+3以及以上系统组合的静态PPP浮点解和固定解结果,以及各系统在可解时段的可见卫星数量的单天时间序列图。需要说明的是,因GLONASS采用频分多址技术,笔者当前还没有发布GLONASS的相位小数偏差,因此文中只给出了GLONASS PPP浮点解结果,且在多系统组合模糊度固定时,GLONASS仅作为辅助观测信息,但GLONASS的模糊度没有进行固定。当然,如前文所述,已有学者开展过GLONASS PPP模糊度固定的研究。

|
| 图 10 2020年1月7日MRO1测站静态PPP固定解结果(a)及浮点解结果(b) Fig. 10 Static PPP ambiguity resolution (a) and float solution (b) at station MRO1 on DOY 007, 2020 |
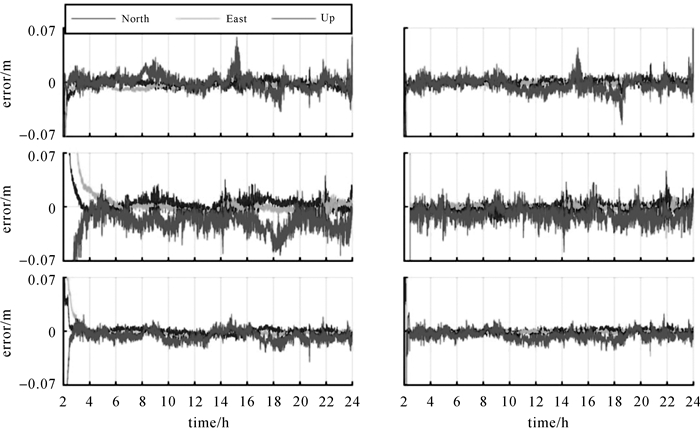
从图 10中可看出,对于当天的MRO1测站,能观测到的GPS、Galileo、BDS2、BDS3和GLONASS的平均卫星数分别为9.0、7.0、10.5、3.2、6.2颗。由于该测站在当天10:00左右仅能观测到3~4颗Galileo卫星,在17:00—18:30 UTC之间观测的GLONASS卫星数也不足以进行PPP解算,因此上述弧段某些历元缺失定位结果。需要说明的是:静态PPP中信号中断之后的历元延用中断前的位置参数,因此当卫星数足以重新进行PPP解算时,位置的先验精度已经很高,所以静态PPP中没有典型的参数重新初始化导致的重新收敛现象。从定位性能来看,各系统固定解结果相对于浮点解在首次固定后各方向定位精度均有明显的提升,GLONASS和BDS的收敛时间略长于GPS和Galileo,多系统组合PPP的收敛速度最快。这是由于虽然BDS可观测卫星数多,但是有5颗为GEO卫星,对收敛的贡献较小,GLONASS卫星在初始历元观测值较少,仅有4~5颗,所以收敛较慢。
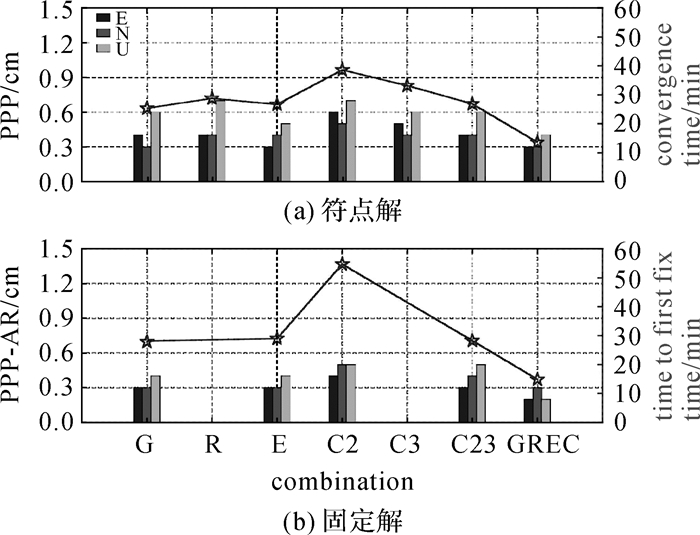
由于单独选取的测站不能同时使所有卫星系统的观测卫星数和观测条件达到最优,所以该测站的结果不能代表各卫星系统所能达到的平均水平。因此,图 11和表 1给出了使用53个测站进行PPP的统计结果,为了表述方便,下文中分别用字母G、R、E、C代替GPS、GLONASS、Galileo和BDS。由于MGEX测站的北斗三号系统卫星观测条件不佳,所以在分析北斗系统的定位性能时,主要采用iGMAS测站的结果。由统计结果可看出,多系统组合PPP浮点解的收敛时间和固定解的首次固定时间相比单系统明显缩短,多系统组合PPP浮点解收敛时间和固定解首次固定解时间分别为:13.6 min和14.9 min。G/R/E/C单系统PPP静态解,收敛后的定位精度基本处于相当水平,GPS和Galileo略优于GLONASS和北斗,多系统组合PPP的定位精度优于单系统PPP定位精度。
|
| 图 11 静态PPP的浮点解(a)与固定解(b)统计精度 Fig. 11 Results of static PPP ambiguity resolution and float solution |
| 浮点解定位误差/cm | 固定解定位误差/cm | 收敛时间 /min |
首次固定时间 /min |
||||||
| 东 | 北 | 高 | 东 | 北 | 高 | ||||
| G | 0.4 | 0.3 | 0.6 | 0.3 | 0.3 | 0.4 | 25.4 | 27.9 | |
| R | 0.4 | 0.4 | 0.7 | — | — | — | 28.8 | — | |
| E | 0.3 | 0.4 | 0.5 | 0.3 | 0.3 | 0.4 | 26.7 | 29.0 | |
| C2 | 0.6 | 0.5 | 0.7 | 0.4 | 0.5 | 0.5 | 38.6 | 54.7 | |
| C3 | 0.5 | 0.4 | 0.6 | — | — | — | 33.2 | — | |
| C23 | 0.4 | 0.4 | 0.6 | 0.3 | 0.4 | 0.5 | 26.9 | 28.3 | |
| GREC | 0.3 | 0.3 | 0.4 | 0.2 | 0.3 | 0.2 | 13.6 | 14.9 | |
2.2 模拟动态定位
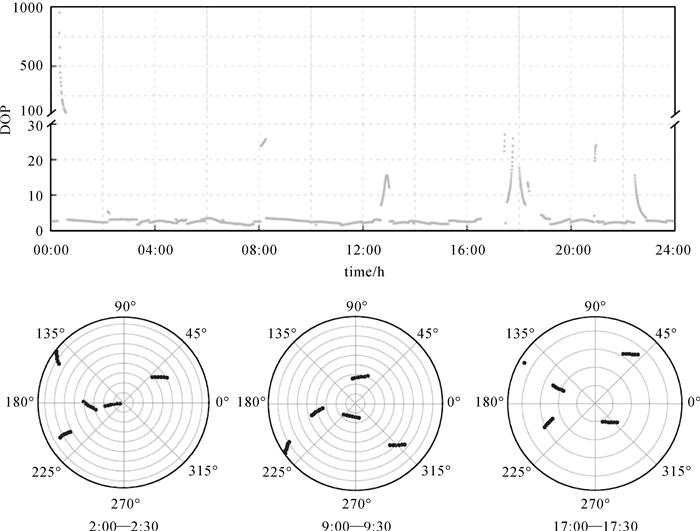
本文使用MGEX和iGMAS测站静态数据模拟动态定位,接收机坐标变化谱密度设置为104 m2/s。需要注意的是,在真实动态环境中,每一个测站的多路径变化以及观测环境都不同,用户需要根据不同观测环境和观测质量调整模糊度固定中不同参数的阈值。图 12代表性地给出了测站MRO1在2020年1月7日GPS、Galileo、GLONASS、BDS-2、BDS-2+3及多系统组合的动态PPP浮点解和固定解结果,以及各系统在可解弧段的可见卫星数量。从图 12中可看出,动态PPP固定解的定位结果比浮点解更稳定,在2.1节指出的卫星数不足的时刻,Galileo和GLONASS在定位解算时各参数重新初始化。四系统组合PPP定位性能仍然明显优于单系统,定位偏差波动减小,定位精度显著提高。当模糊度被正确固定和传递时,PPP的定位精度能得到有效提高。当天GLONASS动态PPP浮点解定位性能较差,图 13给出了GLONASS单天DOP值时间序列图以及3个典型弧段的测站上空卫星弧段天空图,从图 13中可看出,在初始历元及17:00—19:00之间,DOP值较大,说明卫星分布不佳,几何构型不好导致定位结果出现较大偏差。由天空图可看出,在定位偏差较大的弧段,卫星基本分布在测站的单侧或近似处于一条直线,导致解算时可靠度不高,同时也使初始历元的收敛时间偏长。

|
| 图 12 2020年1月7日MRO1测站动态PPP固定解结果(a)及浮点解结果(b) Fig. 12 Kinematic PPP ambiguity resolution (a) and float solution (b) at station MRO1 on DOY 007, 2020 |
|
| 图 13 2020年1月7日MRO1测站观测到GLONASS卫星DOP值及卫星弧段天空 Fig. 13 DOP series and skyplot of GLONASS satellites at station MRO1 on DOY 007, 2020 |
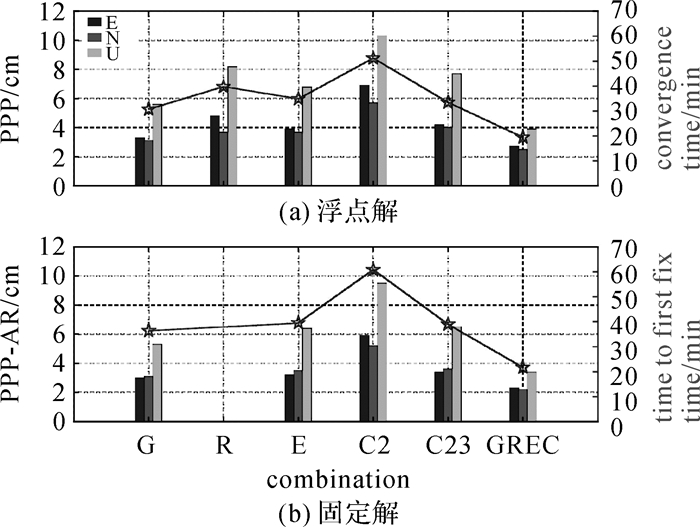
表 2和图 14给出了53个测站一周动态PPP的统计结果。从表 2中可看出,动态PPP的收敛时间和模糊度首次固定时间均要长于相同条件下的静态PPP结果。多系统组合浮点解的定位精度比单GPS浮点解定位精度在水平和高程方向分别提高了18.7%和30.4%。当模糊度被正确固定后,固定解的定位精度明显优于浮点解,多系统组合固定解定位精度比浮点解在东、北、天方向分别提升了14.8%、12.0%和12.8%。多系统组合浮点解的收敛时间和固定解的模糊度首次固定时间均要优于单系统,相比于GPS分别缩短了36.5%和40.4%,具有较明显的提升。对于各单系统而言,GPS的动态PPP定位性能相对最优。
| 浮点解定位误差/cm | 固定解定位误差/cm | 收敛时间 /min |
首次固定时间 /min |
||||||
| 东 | 北 | 高 | 东 | 北 | 高 | ||||
| G | 3.3 | 3.1 | 5.6 | 3.0 | 3.1 | 5.3 | 30.7 | 36.4 | |
| R | 4.8 | 3.7 | 8.2 | — | — | — | 39.8 | — | |
| E | 3.9 | 3.7 | 6.8 | 3.2 | 3.5 | 6.4 | 34.9 | 39.6 | |
| C2 | 6.9 | 5.7 | 10.3 | 5.9 | 5.2 | 9.5 | 51.2 | 60.9 | |
| C23 | 4.2 | 4.0 | 7.7 | 3.4 | 3.6 | 6.5 | 33.5 | 39.0 | |
| GREC | 2.7 | 2.5 | 3.9 | 2.3 | 2.2 | 3.4 | 19.5 | 21.7 | |
|
| 图 14 动态PPP的浮点解(a)与固定解(b)统计精度 Fig. 14 Results of kinematic PPP with ambiguity-fixing solution and float solution |
3 结论与展望
本文首先回顾了PPP的主要发展历程和PPP若干热点研究点的最新进展,然后,利用最新多系统GNSS实测数据,分析和讨论了GPS、GLONASS、Galileo、BDS的PPP定位性能,并重点对我国北斗系统(BDS-2/-3)PPP定位浮点解、固定解的定位精度、收敛时间和首次固定时间进行了分析。
在定位精度方面,四大导航系统的静态PPP无论浮点解还是固定解在收敛后定位精度基本相当,其精度均可达1 cm甚至毫米级,当多系统GNSS融合后,定位精度可得到一定程度提高,但是提高并不明显;而对于动态PPP,多系统融合可以显著提高定位精度,多系统融合动态PPP相比单GPS动态PPP浮点解精度水平和高程方向可分别提高18.7%和30.4%,这是由于动态定位中各时段不同卫星系统的可视卫星数量变化较大,在个别时段会产生较大定位误差,而多系统融合可以有效提高可视卫星的几何分布。相对于多系统组合的PPP浮点解,PPP固定解定位精度可在东、北、天方向分别提升14.8%、12.0%和12.8%。
在收敛/初始化时间方面,GLONASS和BDS的收敛时间略长于GPS和Galileo,多系统GNSS组合的PPP收敛速度最快。其中,北斗二号卫星的静态/动态PPP浮点解收敛时间约为38 min和51 min,固定解的首次固定时间约54 min和60 min,在联合北斗二和三号卫星后,其PPP静态/动态解的收敛时间/首次固定时间可提高至20~40 min。相比单GPS,多系统组合浮点解的收敛时间和固定解的首次固定时间分别缩短了36.5%和40.4%。
值得注意的是,单北斗二号PPP结果由于在不少试验测站上(不在亚太核心服务区)的可用卫星数较少,同时可视卫星中大多数为GEO卫星,其轨道精度较差,使其PPP定位精度相对较差,收敛时间相对较长;单北斗三号卫星虽然总卫星数已接近全星座,可视卫星数也较多,但IGS分析中心提供的精密星历最多只支持到C37,因此较多用于定位实验的测站个别弧段只有四颗甚至更少的北斗三号可用卫星,且可用卫星分布较差,导致某些历元没有定位结果输出,出现重新初始化现象,使得定位结果并不理想。但是,联合北斗二号和北斗三号,对于全球范围内的测站无论是静态还是动态PPP的浮点解/固定解均能达到较高定位精度和较短收敛时间,说明我国北斗卫星导航系统在观测条件相当的情况可以实现与其他导航卫星系统基本相当的PPP定位性能。
纵观已有的文献和最新的试验结果来看,PPP/PPP-RTK的模糊度固定的理论方法已经较为成熟;实时高采样率卫星钟差、UPD产品估计已经较好的解决;多频多系统观测值可在一定程度上缩短PPP初始化时间,但仍无法满足实际应用中对于快速初始化的要求;先验大气约束对初始化时间的缩短主要取决于大气建模的精度,精度越高越有利于实现快速初始化;低轨卫星观测值加速PPP收敛目前仅处于仿真阶段,今后仍需采用实测数据进行验证。
PPP-RTK技术仍处于开发和早期应用阶段,如何平衡数据传输量、采样率与带宽的关系是目前仍需要关注的问题。已有全球/区域电离层模型对PPP-RTK性能提升的幅度较为有限,如何构建高精度的大气模型并确定其播发方式是目前PPP-RTK应用实践需要解决的重要问题之一。大气误差的初始方差确定是影响PPP-RTK快速收敛的关键,现有大气模型/产品提供的精度指标较多是计算过程的内符合精度,而且存在虚高现象,如何准确确定该参数在观测方程中的方差值有待深入研究。PPP的快速初始化仍然是制约PPP技术应用的一大难题,如何在只采用稀疏基站网的条件下,进一步缩短PPP的初始化时间,仍然是PPP发展和推广应用需要持续解决的关键瓶颈。随着低轨导航星座的发展,低轨导航增强PPP-RTK将是今后的重要发展方向,还有不少工作要做。
| [1] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [2] |
KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [3] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407. ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1399-1407. DOI:10.11947/j.AGCS.2017.20170327 |
| [4] |
谭述森. 北斗卫星导航系统的发展与思考[J]. 宇航学报, 2008, 29(2): 391-396. TAN Shusen. Development and thought of compass navigation satellite system[J]. Journal of Astronautics, 2008, 29(2): 391-396. |
| [5] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, contribution and challenges of Compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [6] |
YANG Yuanxi, GAO Weiguang, GUO Shuren, et al. Introduction to BeiDou-3 navigation satellite system[J]. Navigation, 2019, 66(1): 7-18. DOI:10.1002/navi.291 |
| [7] |
KE Mingxing, LV Jing, CHANG Jiang, et al. Integrating GPS and LEO to accelerate convergence time of precise point positioning[C]//Proceedings of 2015 International Conference on Wireless Communications & Signal. Nanjing, China: IEEE, 2015: 1-5. https://ieeexplore.ieee.org/document/7341230
|
| [8] |
GE Haibo, LI Bofeng, GE Maorong, et al. Initial assessment of precise point positioning with LEO enhanced global navigation satellite systems (LeGNSS)[J]. Remote Sensing, 2018, 10(7): 984. DOI:10.3390/rs10070984 |
| [9] |
LI Xingxing, MA Fujian, LI Xin, et al. LEO constellation-augmented multi-GNSS for rapid PPP convergence[J]. Journal of Geodesy, 2019, 93(5): 749-764. DOI:10.1007/s00190-018-1195-2 |
| [10] |
张小红, 马福建. 低轨导航增强GNSS发展综述[J]. 测绘学报, 2019, 48(9): 1073-1087. ZHANG Xiaohong, MA Fujian. Review of the development of LEO navigation-augmented GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1073-1087. DOI:10.11947/j.AGCS.2019.20190176 |
| [11] |
ZHANG Xiaohong, LI Xingxing, GUO Fei. Satellite clock estimation at 1 Hz for realtime kinematic PPP applications[J]. GPS Solutions, 2010, 15(4): 315-324. |
| [12] |
LIU Teng, ZHANG Baocheng, YUAN Yunbin, et al. An efficient undifferenced method for estimating multi-GNSS high-rate clock corrections with data streams in real time[J]. Journal of Geodesy, 2019, 93(9): 1435-1456. DOI:10.1007/s00190-019-01255-9 |
| [13] |
DAI Zhiqiang, DAI Xiaolei, ZHAO Qile, et al. Improving real-time clock estimation with undifferenced ambiguity fixing[J]. GPS Solutions, 2019, 23(2): 44. DOI:10.1007/s10291-019-0837-z |
| [14] |
LIU Zhiqiang, YUE Dongjie, HUANG Zhangyu, et al. Performance of real-time undifferenced precise positioning assisted by remote IGS multi-GNSS stations[J]. GPS Solutions, 2020, 24(2): 58. DOI:10.1007/s10291-020-0972-6 |
| [15] |
EL-MOWAFY A, DEO M, KUBO N. Maintaining real-time precise point positioning during outages of orbit and clock corrections[J]. GPS Solutions, 2017, 21(3): 937-947. DOI:10.1007/s10291-016-0583-4 |
| [16] |
NIE Zhixi, GAO Yang, WANG Zhenjie, et al. An approach to GPS clock prediction for real-time PPP during outages of RTS stream[J]. GPS Solutions, 2018, 22(1): 14. DOI:10.1007/s10291-017-0681-y |
| [17] |
COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing[J]. Navigation, 2010, 57(2): 123-135. DOI:10.1002/j.2161-4296.2010.tb01772.x |
| [18] |
LAURICHESSE D, MERCIER F, BERTHIAS JP, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009, 56(2): 135-149. DOI:10.1002/j.2161-4296.2009.tb01750.x |
| [19] |
GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [20] |
LI Pan, ZHANG Xiaohong, REN Xiaodong, et al. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning[J]. GPS Solutions, 2016, 20(4): 771-782. DOI:10.1007/s10291-015-0483-z |
| [21] |
HU Jiahuan, ZHANG Xiaohong, LI Pan, et al. Multi-GNSS fractional cycle bias products generation for GNSS ambiguity-fixed PPP at Wuhan University[J]. GPS Solutions, 2020, 24(1): 15. DOI:10.1007/s10291-019-0929-9 |
| [22] |
LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS ambiguity resolution at CNES-CLS IGS analysis center[J]. Journal of Geodesy, 2012, 86(11): 991-1003. DOI:10.1007/s00190-012-0559-2 |
| [23] |
GENG Jianghui, CHEN Xingyu, PAN Yuanxin, et al. PRIDE PPP-AR:an open-source software for GPS PPP ambiguity resolution[J]. GPS Solutions, 2019, 23(4): 91. DOI:10.1007/s10291-019-0888-1 |
| [24] |
LIU Yanyan, SONG Weiwei, LOU Yidong, et al. GLONASS phase bias estimation and its PPP ambiguity resolution using homogeneous receivers[J]. GPS Solutions, 2017, 21(2): 427-437. DOI:10.1007/s10291-016-0529-x |
| [25] |
YI Wenting, SONG Weiwei, LOU Yidong, et al. Improved method to estimate undifferenced satellite fractional cycle biases using network observations to support PPP ambiguity resolution[J]. GPS Solutions, 2017, 21(3): 1369-1378. DOI:10.1007/s10291-017-0616-7 |
| [26] |
KAMALI O, COCARD M, SANTERRE R. A sequential network approach for estimating GPS satellite phase biases at the PPP-AR producer-side[J]. GPS Solutions, 2018, 22(3): 59. DOI:10.1007/s10291-018-0724-z |
| [27] |
XIAO Guorui, LI Pan, SUI Lifen, et al. Estimating and assessing Galileo satellite fractional cycle bias for PPP ambiguity resolution[J]. GPS Solutions, 2019, 23(1): 3. DOI:10.1007/s10291-018-0793-z |
| [28] |
XIAO Guorui, SUI Lifen, HECK B, et al. Estimating satellite phase fractional cycle biases based on Kalman filter[J]. GPS Solutions, 2018, 22(3): 82. DOI:10.1007/s10291-018-0749-3 |
| [29] |
YAO Yibin, PENG Wenjie, XU Chaoqian, et al. The realization and evaluation of mixed GPS/BDS PPP ambiguity resolution[J]. Journal of Geodesy, 2019, 93(9): 1283-1295. DOI:10.1007/s00190-019-01245-x |
| [30] |
WANG Jin, HUANG Guanwen, YANG Yuanxi, et al. FCB estimation with three different PPP models:equivalence analysis and experiment tests[J]. GPS Solutions, 2019, 23(4): 93. DOI:10.1007/s10291-019-0887-2 |
| [31] |
LI Pan, ZHANG Xiaohong, GUO Fei. Ambiguity resolved precise point positioning with GPS and BeiDou[J]. Journal of Geodesy, 2017, 91(1): 25-40. DOI:10.1007/s00190-016-0935-4 |
| [32] |
LIU Yanyan, YE Shirong, SONG Weiwei, et al. Integrating GPS and BDS to shorten the initialization time for ambiguity-fixed PPP[J]. GPS Solutions, 2017, 21(2): 333-343. DOI:10.1007/s10291-016-0525-1 |
| [33] |
LIU Yanyan, LOU Yidong, YE Shirong, et al. Assessment of PPP integer ambiguity resolution using GPS, GLONASS and BeiDou (IGSO, MEO) constellations[J]. GPS Solutions, 2017, 21(4): 1647-1659. DOI:10.1007/s10291-017-0641-6 |
| [34] |
LIU Teng, YUAN Yunbin, ZHANG Baocheng, et al. Multi-GNSS precise point positioning (MGPPP) using raw observations[J]. Journal of Geodesy, 2017, 91(3): 253-268. DOI:10.1007/s00190-016-0960-3 |
| [35] |
LI Xingxing, LI Xin, YUAN Yongqiang, et al. Multi-GNSS phase delay estimation and PPP ambiguity resolution:GPS, BDS, GLONASS, Galileo[J]. Journal of Geodesy, 2018, 92(6): 579-608. DOI:10.1007/s00190-017-1081-3 |
| [36] |
MONTENBRUCK O, HUGENTOBLER U, DACH R, et al. Apparent clock variations of the Block ⅡF-1(SVN62) GPS satellite[J]. GPS Solutions, 2012, 16(3): 303-313. DOI:10.1007/s10291-011-0232-x |
| [37] |
PAN Lin, ZHANG Xiaohong, GUO Fei, et al. GPS inter-frequency clock bias estimation for both uncombined and ionospheric-free combined triple-frequency precise point positioning[J]. Journal of Geodesy, 2019, 93(4): 473-487. DOI:10.1007/s00190-018-1176-5 |
| [38] |
PAN Lin, ZHANG Xiaohong, LI Xingxing, et al. GPS inter-frequency clock bias modeling and prediction for real-time precise point positioning[J]. GPS Solutions, 2018, 22(3): 76. DOI:10.1007/s10291-018-0741-y |
| [39] |
LI Pan, JIANG Xinyuan, ZHANG Xiaohong, et al. GPS+Galileo+BeiDou precise point positioning with triple-frequency ambiguity resolution[J]. GPS Solutions, 2020, 24(3): 78. DOI:10.1007/s10291-020-00992-1 |
| [40] |
GUO Fei, ZHANG Xiaohong, WANG Jinling, et al. Modeling and assessment of triple-frequency BDS precise point positioning[J]. Journal of Geodesy, 2016, 90(11): 1223-1235. DOI:10.1007/s00190-016-0920-y |
| [41] |
ELSOBEIEY M. Precise point positioning using triple-Frequency GPS measurements[J]. The Journal of Navigation, 2015, 68(3): 480-492. DOI:10.1017/S0373463314000824 |
| [42] |
SU Ke, JIN Shuanggen, JIAO Guoqiang. Assessment of multi-frequency global navigation satellite system precise point positioning models using GPS, BeiDou, GLONASS, Galileo and QZSS[J]. Measurement Science and Technology, 2020, 31(6): 064008. DOI:10.1088/1361-6501/ab69d5 |
| [43] |
LI Pan, ZHANG Xiaohong, GE Maorong, et al. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables[J]. Journal of Geodesy, 2018, 92(12): 1357-1369. DOI:10.1007/s00190-018-1125-3 |
| [44] |
LI Xingxing, LI Xin, LIU Gege, et al. Triple-frequency PPP ambiguity resolution with multi-constellation GNSS:BDS and Galileo[J]. Journal of Geodesy, 2019, 93(8): 1105-1122. DOI:10.1007/s00190-019-01229-x |
| [45] |
GENG Jianghui, GUO Jiang, MENG Xiaolin, et al. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data[J]. Journal of Geodesy, 2020, 94(1): 6. |
| [46] |
XIN Shaoming, GENG Jianghui, GUO Jiang, et al. On the choice of the third-frequency galileo signals in accelerating PPP ambiguity resolution in case of receiver antenna phase center errors[J]. Remote Sensing, 2020, 12(8): 1315. DOI:10.3390/rs12081315 |
| [47] |
LI Xingxing, LIU Gege, LI Xin, et al. Galileo PPP rapid ambiguity resolution with five-frequency observations[J]. GPS Solutions, 2019, 24(1): 24. |
| [48] |
CAI Changsheng, GAO Yang. Modeling and assessment of combined GPS/GLONASS precise point positioning[J]. GPS Solutions, 2013, 17(2): 223-236. DOI:10.1007/s10291-012-0273-9 |
| [49] |
LI Pan, ZHANG Xiaohong. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning[J]. GPS Solutions, 2014, 18(3): 461-471. DOI:10.1007/s10291-013-0345-5 |
| [50] |
LI Xingxing, GE Maorong, DAI Xiaolei, et al. Accuracy and reliability of multi-GNSS real-time precise positioning:GPS, GLONASS, BeiDou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635. DOI:10.1007/s00190-015-0802-8 |
| [51] |
LI Xingxing, ZHANG Xiaohong, REN Xiaodong, et al. Precise positioning with current multi-constellation Global Navigation Satellite Systems:GPS, GLONASS, Galileo and BeiDou[J]. Scientific Reports, 2015, 5(1): 8328. DOI:10.1038/srep08328 |
| [52] |
WVBBENA G, SCHMITZ M, BAGGE A. PPP-RTK: Precise point positioning Using State-space representation in RTK Networks[C]//Proceedings of the 18th International Technical Meeting (ION GNSS 2005). Long Beach, CA: Long Beach Convention Center, 2005: 13-16.
|
| [53] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D].武汉: 武汉大学, 2013. LI Xingxing. Rapid ambiguity resolution in GNSS precise point positioning[D]. Wuhan: Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm |
| [54] |
WILGAN K, HADAS T, HORDYNIEC P, et al. Real-time precise point positioning augmented with high-resolution numerical weather prediction model[J]. GPS Solutions, 2017, 21(3): 1341-1353. DOI:10.1007/s10291-017-0617-6 |
| [55] |
XIANG Yan, GAO Yang, LI Yihe. Reducing convergence time of precise point positioning with ionospheric constraints and receiver differential code bias modeling[J]. Journal of Geodesy, 2020, 94(1): 8. |
| [56] |
GENG Jianghui, SHI Chuang. Rapid initialization of real-time PPP by resolving undifferenced GPS and GLONASS ambiguities simultaneously[J]. Journal of Geodesy, 2017, 91(4): 361-374. DOI:10.1007/s00190-016-0969-7 |
| [57] |
GENG Jianghui, LI Xiaotao, ZHAO Qile, et al. Inter-system PPP ambiguity resolution between GPS and BeiDou for rapid initialization[J]. Journal of Geodesy, 2019, 93(3): 383-398. DOI:10.1007/s00190-018-1167-6 |
| [58] |
BANVILLE S, LANGLEY R B. Improving real-time kinematic PPP with instantaneous cycle-slip correction[C]//Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009). Savannah, GA: Savannah International Convention Center, 2009: 2470-2478.
|
| [59] |
GENG Jianghui, MENG Xiaolin, DODSON AH, et al. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning[J]. Journal of Geodesy, 2010, 84(12): 705-714. DOI:10.1007/s00190-010-0404-4 |
| [60] |
ZHANG Xiaohong, LI Xingxing. Instantaneous re-initialization in real-time kinematic PPP with cycle slips fixing[J]. GPS Solutions, 2012, 16(3): 315-327. DOI:10.1007/s10291-011-0233-9 |
| [61] |
LI Pan, JIANG Xinyuan, ZHANG Xiaohong, et al. Kalman-filter-based undifferenced cycle slip estimation in real-time precise point positioning[J]. GPS Solutions, 2019, 23(4): 99. DOI:10.1007/s10291-019-0894-3 |
| [62] |
ZHANG Xiaohong, ZHU Feng, ZHANG Yuxi, et al. The improvement in integer ambiguity resolution with INS aiding for kinematic precise point positioning[J]. Journal of Geodesy, 2019, 93(7): 993-1010. DOI:10.1007/s00190-018-1222-3 |
| [63] |
LI Xingxing, ZHANG Xiaohong, GE Maorong. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution[J]. Journal of Geodesy, 2011, 85(3): 151-158. DOI:10.1007/s00190-010-0424-0 |
| [64] |
DE OLIVEIRA PS JR, MOREL L, FUND F, et al. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK[J]. GPS Solutions, 2017, 21(1): 237-250. DOI:10.1007/s10291-016-0518-0 |
| [65] |
ZHANG Baocheng, CHEN Yongchang, YUAN Yunbin. PPP-RTK based on undifferenced and uncombined observations:theoretical and practical aspects[J]. Journal of Geodesy, 2018, 93(7): 1011-1024. |
| [66] |
LI Linyang, LU Zhiping, CHEN Zhengsheng, et al. Parallel computation of regional CORS network corrections based on ionospheric-free PPP[J]. GPS Solutions, 2019, 23(3): 70. DOI:10.1007/s10291-019-0864-9 |
| [67] |
LI Zhao, CHEN Wu, RUAN Rengui, et al. Evaluation of PPP-RTK based on BDS-3/BDS-2/GPS observations:a case study in Europe[J]. GPS Solutions, 2020, 24(2): 38. DOI:10.1007/s10291-019-0948-6 |
| [68] |
NADARAJAH N, KHODABANDEH A, WANG Kan, et al. Multi-GNSS PPP-RTK:from large-to small-scale networks[J]. Sensors, 2018, 18(4): 1078. DOI:10.3390/s18041078 |
| [69] |
OLIVARES-PULIDO G, TERKILDSEN M, ARSOV K, et al. A 4D tomographic ionospheric model to support PPP-RTK[J]. Journal of Geodesy, 2019, 93(9): 1673-1683. DOI:10.1007/s00190-019-01276-4 |
| [70] |
ASARI K, KUBO Y, SUGIMOTO S. Design of GNSS PPP-RTK assistance system and its algorithms for 5G mobile networks[J]. Transactions of the Institute of Systems, Control and Information Engineers, 2020, 33(1): 31-37. DOI:10.5687/iscie.33.31 |