Galileo是由欧盟主持和建设的全球卫星导航系统,旨在提供高精度的导航、定位和授时服务[1]。Galileo于2002年3月开始建设,在2016年12月宣布具备初始服务能力,并计划于2020年全面建成[1]。目前Galileo共有包括4颗在轨试验(in-orbit validation,IOV)卫星和22颗全工作能力(full operational capability,FOC)卫星在内的26颗卫星[2]。稳定可靠的精密轨道产品是Galileo高精度应用的前提。现今,包括欧洲定轨中心(Centre for Orbit Determination in Europe, CODE)、欧空局(European Space Agency, ESA)、德国地学中心(German Research Centre for Geosciences, GFZ)和武汉大学(Wuhan University, WHU)在内的多家MGEX分析中心为Galileo提供精密轨道和钟差产品。上述机构均采用E1/E5a双频无电离层(ionosphere free, IF)组合观测值进行卫星精密定轨[4-6]。
除E1和E5a信号外,Galileo还提供了E5b、E5ab和E6等信号[7]。丰富的卫星频率信号为精密数据处理提供了新的机遇和挑战。非组合(uncombined, UC)模型具有表达形式简单统一且易扩展,观测信息利用充分等优势[8],逐渐成为多频GNSS精密数据处理领域新的研究热门[9]。在精密定位领域,文献[10]提出过一种非组合GPS精密定位方法。文献[11—12]等对非组合精密定位过程中的函数和参数模型进行了深入研究。文献[13]总结了多频GNSS非差非组合精密单点定位模型。文献[14]提出了北斗系统三频非组合和无电离层观测值组合的钟差基准约束准则。文献[15]通过非差非组合模型发展了电离层模型参数化方法。在精密定轨领域,UC模型的相关研究相较于精密定位领域更少。文献[16]基于非组合观测值进行了低轨卫星精密定轨。文献[17—18]曾对非组合精密定轨策略进行了初步的研究。文献[19]在他的研究中论证了双频UC模型和IF模型在GPS卫星精密定轨中的等价性。然而,很少有研究学者使用双频甚至三频信号通过UC模型来进行Galileo卫星精密定轨。本文建立了Galileo三频非组合精密定轨模型,并评估了使用双频和三频的UC和IF模型的Galileo卫星精密定轨结果。
1 Galileo多频定轨模型及策略 1.1 多频非组合定轨模型测站r和卫星s在某一个历元接收到的卫星频率i的伪距观测量和载波相位观测量可以用如下观测方程表示
 (1)
(1)
式中,Pi, rs和Li, rs分别表示以m为单位的伪距观测量和载波观测量;ρrs表示站星几何距离;Mrs表示对流层投影系数;Tr表示天顶对流层湿延迟;I1, rs表示f1的电离层延迟一阶项;γis表示第i频率与fi相关的电离层延迟放大因子,可以表示为fi2/f12;c为光速;dti, r和dtis分别表示接收机和卫星钟差;di, r和dis分别表示接收机和卫星端的伪距硬件延迟;bi, r和bis分别表示接收机和卫星端的相位硬件延迟;λis为第i频率的波长;Ni, rs表示以周为单位的整周模糊度;εi, rs和ξi, rs则是伪距观测量和载波观测量的信号噪声。
诸如天线相位中心偏差(phase center offset, PCO)和天线相位中心变化(phase center variation, PCV)、测站天顶对流层干延迟、相对论效应、潮汐改正(包括固体潮、海潮和极潮)和天线相位缠绕效应等需要的误差可通过对应模型正确改正[20-23]。精密定轨中,对式(1)线性化处理后可表示为
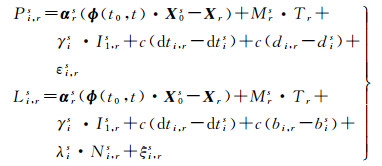 (2)
(2)
式中,αrs=(αx, αy, αz)为站星几何距离的一阶偏导数;t0为初始历元;t为当前历元;ϕ(t0, t)为初始历元到当前历元的状态转移矩阵;X0s为初始历元坐标;Xr为接收机的位置坐标。由于MGEX分析中心产品通常采用IF模型进行估计,在多频数据处理过程中,为了与MGEX分析中心产品保持一致,需要采用IF基准消除方程秩亏。假定以频率i和j的IF组合为基准,此时观测方程式可以表示为[24]
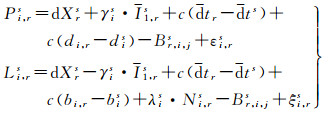 (3)
(3)
式中,dXrs=αrs(ϕ(t0, t)·X0s-Xr)+Mrs·Tr为非频率相关参数;αi, j=fi2/(fi2-fj2)和βi, j=-fj2/(fi2-fj2)为IF组合系数;Br, i, js=c(αi, jdi, r+βi, jdj, r)+c(αi, jdis+βi, jdjs)为引入的硬件延迟改正数;dtr、dts分别为IF组合接收机钟差和卫星钟差。由于钟差基准中所引入的偏差项和卫星及接收机相关,并且伪距和相位观测值中都存在该参数,因此在最小二乘平差准则中,其值能被电离层参数吸收,此时电离层参数可表示为I1, rs=I1, rs+βi, j(di, r-dj, r-dis+djs)。对于频率k,将以频率i和j的无电离层组合基准代入频率k的观测方程,可以得到式(4)
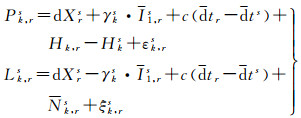 (4)
(4)
式中
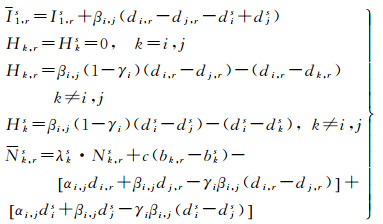 (5)
(5)
从式(5)中可以看到,当以频率i和频率j的双频IF组合为基准时,频率i和频率j的硬件延迟偏差不需要额外估计,其值可以被卫星钟差、接收机钟差及电离层延迟参数吸收。
1.2 双差模糊度固定在精密定轨过程中,非差UC模糊度和IF模糊度因为吸收了卫星硬件延迟和接收机硬件延迟而不具备整周特性。通过恢复模糊度的整周特性可以得到模糊度固定解并显著提高卫星精密定轨精度。考虑到卫星精密定轨需要在一个地面网络下进行,因此可借助双差策略实现模糊度的固定[25]。对于两个卫星和两个测站,通过线性组合可以将4个UC模糊度组成双差模糊度,此时模糊度中包含的卫星端和接收机端偏差项均被消除。对于IF模糊度,常用式(6)固定
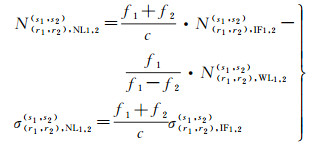 (6)
(6)
式中,NNL为双差窄巷(narrow lane, NL)模糊度;NIF和NWL分别表示双差IF和宽巷(wide line,WL)整数模糊度;σNL和σIF分别为双差NL和双差IF模糊度误差。双差WL模糊度可以借助双差的MW(melbourne-wübbena)组合观测量表示[26-28]。在进行三频IF模糊度固定时,可以先对f1和f2频率的IF模糊度进行双差约束,再对f1和f3频率的IF模糊度进行双差约束,从而固定所有模糊度。此时模糊度的双差约束表达式为
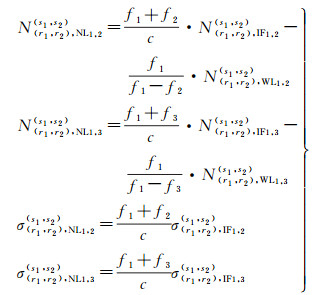 (7)
(7)
UC模糊度与IF模糊度固定策略基本一致,首先借助UC模糊度得到双差WL整数模糊度,然后基于双差WL和双差UC模糊度得到双差NL整数模糊度。双差UC模糊度约束方程如下所示
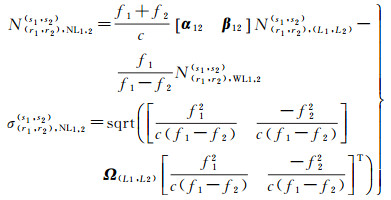 (8)
(8)
式中,N(r1, r2), (L1, L2)(s1, s2)为f1和f2频率的双差UC模糊度;Ω(L1, L2)为f1和f2频率的双差UC模糊度的协方差阵;α12、β12为f1和f2频率的IF组合系数。最后,对于f1和f2频率,其UC模糊度可以表示为
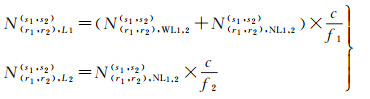 (9)
(9)
在进行三频UC模糊度固定时,可以先对f1和f2频率的UC模糊度进行双差约束,再对f1和f3频率的UC模糊度进行双差约束,从而固定所有模糊度。此时模糊度的双差约束表达式为
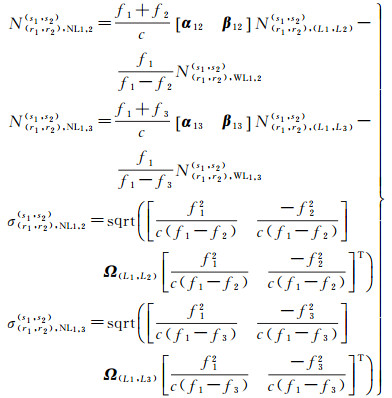 (10)
(10)
3个频率的模糊度可以表示为
 (11)
(11)
本文利用全球分布的150个MGEX测站在2019年年积日080-120共41天的Galileo观测数据来验证Galileo多频UC模型的定轨效果。在选取的这段时间内,Galileo共有24颗可用卫星,所有测站均可接收到Galileo的E1、E5a和E5b的观测数据。具体测站的全球分布情况如图 1所示。
|
| 图 1 MGEX测站分布 Fig. 1 Distribution of MGEX stations |
在数据处理中,共使用6种不同的策略进行Galileo卫星的精密定轨和钟差估计。具体策略可见表 1。除了使用E1/E5b双频观测值进行的定轨策略,其他策略均选取E1/E5a的双频IF钟差作为钟差基准。定轨过程中,观测值的采样率为300 s,定轨弧长为24 h,观测值采用高度角加权,截止高度角为7°。电离层采用斜延迟电离层模型,且仅估计E1频率的电离层延迟。接收机端的E1和E5a观测值的天线相位中心改正由GPS的L1和L2观测值对应的模型改正代替,E5b观测值的天线相位中心改正保持和E5a观测值一致。卫星姿态模型选取名义模型,光压模型为ECOM2模型[29]。观测模型、动力学模型和参数估计等的详细策略见表 2。
| 频率 | 组合方式 | 钟差基准 | 策略标识 |
| E1/E5a | IF | IF E1/E5a | IF-1 |
| E1/E5a | UC | IF E1/E5a | UC-1 |
| E1/E5b | IF | IF E1/E5b | IF-2 |
| E1/E5b | UC | IF E1/E5b | UC-2 |
| E1/E5a/E5b | IF | IF E1/E5a | IF-3 |
| E1/E5a/E5b | UC | IF E1/E5a | UC-3 |
| 模型 | 项目 | 处理策略 |
| 观测模型 | 观测值 | E1/E5a/E5b |
| 定轨采样率 | 300 s | |
| 定轨弧长 | 24 h | |
| 截止高度角 | 7° | |
| 观测值权比 | 高度角加权。高度角E大于30°时为1,否则为2·sin (E) | |
| 天线相位改正 | 卫星端:按照IGS14天线文件改正接收机端:E1、E5a/E5b分别由GPS L1和L2的改正数代替 | |
| 相位缠绕 | 采用模型改正 | |
| 对流层延迟 | 对流层干延迟使用Saastamoinen模型计算,通过GMF投影函数将天顶延迟转换到观测值路径方向;对流层湿延迟采用分段常数估计,间隔为2 h | |
| 动力学模型 | 地球重力场 | EGM2008模型,12×12阶[30] |
| N体引力 | 根据JPL DE405星历计算 | |
| 地球潮汐形变 | 海潮潮汐:FES2004模型[31]固体潮、极潮:IERS conventions 2010[32] | |
| 相对论效应 | 采用IERS conventions 2010的模型改正 | |
| 太阳光压 | ECOM2模型 | |
| 参数估计 | 初始轨道状态 | 卫星位置、速度和ECOM2力模型参数 |
| 测站坐标 | IGS周解的测站坐标 | |
| 接收机钟差 | 作为白噪声逐历元估计,频间码偏差作为常数每天估计一组 | |
| 卫星钟差 | 作为白噪声逐历元估计 | |
| 相位模糊度 | 每个弧段估计一个常数模糊度参数 | |
| ERP参数 | 作为常数估计 |
2 试验结果与分析 2.1 精密产品比较结果
为了评估轨道和钟差的外符合精度,可以将不同策略的定轨和估钟结果与精密产品进行对比。本文选取CODE提供的精密轨道和钟差产品作为外部评估标准。研究表明,CODE提供的Galileo精密轨道产品与ESA、GFZ和WHU提供的精密轨道产品之间比较结果的1DRMS为16.2~28.3 mm,精密钟差产品之间比较结果的STD为0.09~0.24 ns,另外,CODE机构Galileo精密轨道产品的卫星激光测距(satellite laser ranging,SLR)检核残差的STD为30.0~32.0 mm[33]。
轨道方面,将每个定轨弧段解算的轨道与CODE精密轨道产品进行比较得到切向(along-track, A)、法向(cross-track, C)、径向(radial, R)及1D方向的差值序列,并计算得到差值的RMS值。钟差方面,对解算的钟差结果与CODE精密钟差产品进行比较,使用“二次差”的方法,扣除基准偏差,并计算得到每个定轨弧段的STD值[34]。
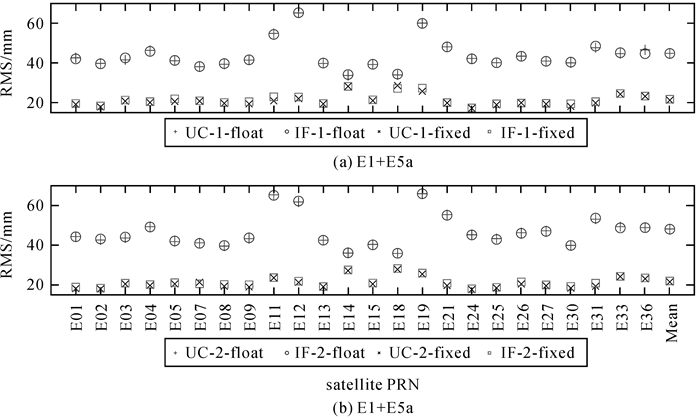
图 2给出了Galileo卫星使用双频观测值时,不同策略下定轨结果与CODE精密轨道产品比较结果的1DRMS平均值。其中UC-1、IF-1、UC-2和IF-2策略浮点解RMS平均值分别为44.6、44.7、48.2 mm和48.1 mm,UC-1与IF-1策略间轨道差异和UC-2与IF-2策略间轨道差异都小于1 mm;固定解RMS平均值分别为21.1、21.6、21.4 mm和22.0 mm,4者差异同样小于1 mm。上述结果表明,在使用相同观测值时,UC策略和IF策略的平均RMS差异在1 mm以内,两者精度相当。
|
| 图 2 双频UC和IF策略定轨结果 Fig. 2 Orbit results of dual-frequency UC and IFmodel |
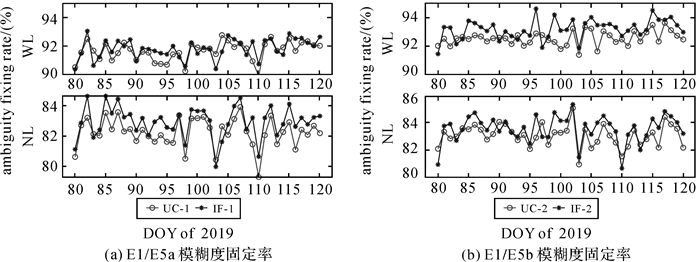
图 3给出了双频情况下UC-1、UC-2、IF-1和IF-2这4种策略WL和NL模糊度的固定率。表 3进一步给出了上述4种策略下,WL和NL模糊度的平均固定率。从上述结果可以发现,UC-1和UC-2策略的WL和NL模糊度固定率均分别略低于IF-1和IF-2策略。其中,UC-1和UC-2策略的WL模糊度固定率分别为91.65%和92.54%,比IF-1和IF-2策略分别低0.17%和0.65%;UC-1和UC-2策略的NL模糊度固定率分别为82.23%和83.09%,也略低于IF-1和IF-2策略的82.93%和83.58%。
|
| 图 3 双频UC和IF策略精密定轨模糊度固定率 Fig. 3 Ambiguity fixed rate of dual-frequency UC and IFmodel |
| 频率 | WL模糊度固定率 | NL模糊度固定率 | |||
| 观测值 | IF | IF | UC | ||
| E1/E5a | 91.82 | 91.65 | 82.93 | 82.23 | |
| E1/E5b | 93.19 | 92.54 | 83.58 | 83.09 | |
图 4给出了双频和三频UC/IF策略定轨结果与CODE精密产品的互差结果。从图 4中可以发现,对于UC-1、UC-2和UC-3这3种策略,UC-2策略的浮点解精度最差,UC-1策略和UC-3策略的浮点解精度相当,3种策略的固定解精度相当。对于IF-1、IF-2和IF-3这3种策略,IF-2策略的浮点解精度最差,IF-1和IF-2策略的浮点解精度一致,3种策略的固定解精度相当。

|
| 图 4 双频和三频UC/IF策略定轨结果与CODE精密产品的互差结果 Fig. 4 RMS values oforbit differences for dual-frequency and triple-frequency UC/IF model compared with CODE precision products |
表 4总结了使用双频和三频观测值的UC和IF策略定轨结果与CODE精密产品的互差结果的平均值。可以发现,使用相同观测值时,UC和IF策略定轨结果的精度差异很小,两者在切向、法向与径向差异均在1 mm以内。使用不同观测值时,UC-2策略浮点解的1DRMS平均值为45.2 mm,比UC-1和UC-2策略分别大了3.1 mm和2.0 mm;IF-2策略浮点解的1DRMS平均值同样为45.2 mm,比IF-1和IF-2策略分别大了3.2 mm和2.1 mm。此外,UC-1、UC-2、UC-3、IF-1、IF-2和IF-3这6种策略固定解的1DRMS平均值分别为20.3、20.3、20.4、20.6、20.6 mm和20.4 mm,相互之间差异小于1 mm,可以认为精度相当。
| 观测值 | UC策略 | IF策略 | ||||||||
| 切向 | 沿向 | 径向 | 1D | 切向 | 沿向 | 径向 | 1D | |||
| 浮点解 | E1/E5a | 48.0 | 46.5 | 29.1 | 42.1 | 47.9 | 46.5 | 29.1 | 42.0 | |
| E1/E5b | 50.6 | 51.8 | 29.9 | 45.2 | 50.6 | 51.8 | 29.9 | 45.2 | ||
| E1/E5a/E5b | 48.7 | 48.6 | 29.6 | 43.2 | 48.4 | 48.6 | 29.6 | 43.1 | ||
| 固定解 | E1/E5a | 22.6 | 19.4 | 18.8 | 20.3 | 23.3 | 19.4 | 18.8 | 20.6 | |
| E1/E5b | 22.3 | 19.9 | 18.5 | 20.3 | 23.0 | 19.9 | 18.5 | 20.6 | ||
| E1/E5a/E5b | 22.6 | 19.9 | 18.4 | 20.4 | 22.6 | 19.9 | 18.4 | 20.4 | ||
图 5给出了双频和三频UC/IF策略下,Galileo卫星固定解定轨和估钟结果与CODE精密产品的互差结果。对于定轨结果,在使用相同观测值时,每颗卫星UC策略和IF策略的定轨精度大致相当。当使用不同观测值时,每颗卫星UC策略和IF策略定轨固定解结果精度基本一致。对于估钟结果,其中IF-1、IF-3、UC-1和UC-3这4种策略所有卫星的钟差STD平均值为0.090 ns、0.089 ns、0.087 ns和0.088 ns,相互间STD值差异小于0.01 ns,可以认为钟差精度基本一致。

|
| 图 5 双频和三频UC/IF策略精密定轨和估钟结果与CODE精密产品的互差结果 Fig. 5 RMS values of clock differences for dual-frequency and triple-frequency UC/IF model compared with CODE precision products |
2.2 轨道边界不连续性
除了和MGEX分析中心提供的精密产品比较外,轨道边界不连续性(orbit boundary discontinuities,OBD)同样可用于评估轨道精度。将24小时定轨结果外推1500 s(采样间隔为300 s时为5个历元),比较外推结果与次日定轨结果的重叠轨道弧段可以得到切向、法向、径向及1D方向的差值序列,并计算得到差值的RMS值。
图 6给出了双频和三频UC/IF策略定轨的OBD结果。从比较结果来看,使用相同观测值时,UC策略和IF策略OBD结果的量级基本一致。使用E1/E5b观测值时,UC策略和IF策略定轨浮点解的OBD结果都略差于使用E1/E5a和E1/E5a/E5b观测值时的结果。表 5进一步给出了双频和三频UC/IF策略定轨的OBD结果的RMS平均值。从表 5中可以发现,在观测值类型相同时,UC策略和IF策略的定轨结果在切向、法向和径向上的OBD结果差异均在2.5 mm以内。UC策略的浮点解中,UC-2策略的精度最差,UC-3策略次之;UC策略的固定解中,UC-2策略的精度最好,UC-3策略次之。对于IF策略,上述结论和UC策略类似。浮点解中,IF-2策略的精度最差,IF-3策略次之;固定解中,IF-2策略的精度最好,IF-3次之。
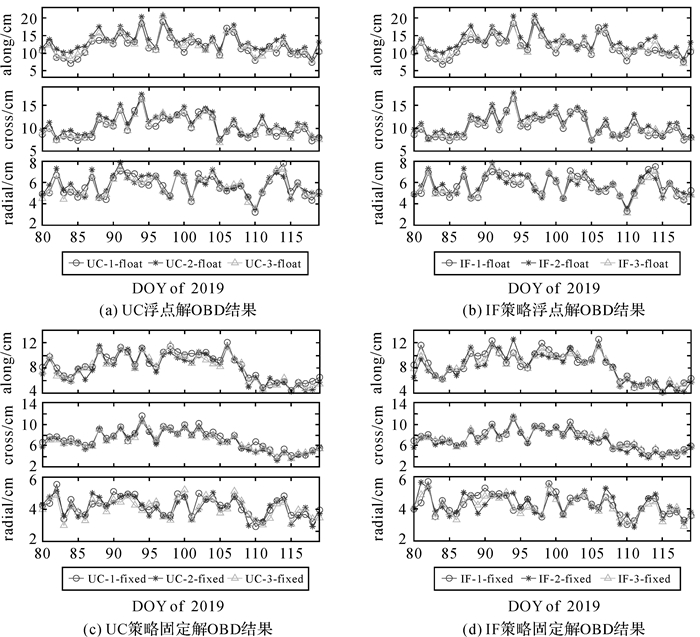
|
| 图 6 双频和三频UC/IF策略精密定轨OBD结果 Fig. 6 RMS values of OBD for dual-frequency and triple-frequency UC/IF model compared with CODE precision products |
| 定轨结果 | 策略 | 切向 | 法向 | 径向 | 1D |
| 浮点解 | UC-1 | 11.73 | 10.20 | 5.63 | 9.55 |
| UC-2 | 13.29 | 10.98 | 5.74 | 10.49 | |
| UC-3 | 12.05 | 10.35 | 5.61 | 9.73 | |
| IF-1 | 11.69 | 10.16 | 5.65 | 9.52 | |
| IF-2 | 13.36 | 10.98 | 5.77 | 10.52 | |
| IF-3 | 12.11 | 10.45 | 5.63 | 9.79 | |
| 固定解 | UC-1 | 8.37 | 7.18 | 4.19 | 6.81 |
| UC-2 | 7.89 | 6.78 | 4.11 | 6.46 | |
| UC-3 | 8.01 | 6.88 | 4.06 | 6.53 | |
| IF-1 | 8.32 | 7.17 | 4.25 | 6.80 | |
| IF-2 | 8.08 | 6.84 | 4.25 | 6.59 | |
| IF-3 | 8.14 | 7.11 | 4.14 | 6.68 |
2.3 SLR检核结果
SLR是一种高精度的绝对距离观测值,因其不包含载波相位模糊度,并具有系统误差小、不受钟差和天线相位中心误差影响的优点,可用于对精密卫星轨道进行检核评估。所有Galileo卫星都配备了用于SLR检核的激光反射器阵列,并由国际激光测距服务(international laser ranging service, ILRS)组织的地面观测网络跟踪[35],因此本文还对不同策略定轨结果进行了SLR检核。
图 7给出了E01、E09、E13、E26卫星在UC-2、IF-2、UC-3和IF-3这4种策略下固定解定轨结果的SLR残差时序图。表 6进一步给出了不同策略下这4颗卫星固定解定轨结果SLR检核结果。需要注意的是,在统计过程中剔除了残差值大于1 m或超过3倍中误差的SLR检核激光点。通过比较可以发现,当观测值类型一致时,UC策略和IF策略定轨结果的SLR残差和STD值都基本相当。总体而言,所有策略的SLR残差平均值的绝对值都小于2 cm,不同策略的SLR残差平均值之间的差异在0.3 cm以内。使用三频观测值时,如果观测值组合策略和双频一致,其SLR残差平均值并没有显著小于双频观测值。以E09为例,其UC-1、UC-2和UC-3策略的SLR残差平均值分别为-2.6 cm、-2.5 cm和-2.6 cm,与IF-1、IF-2和IF-3策略的-2.7 cm、-2.5 cm和-2.5 cm相比,相互间差异都不大于0.2 cm。同样可以比较这几种策略SLR残差STD值,其中UC-1、UC-2和UC-3策略的SLR残差STD值分别为3.0 cm、3.2 cm和2.9 cm,与IF-1、IF-2和IF-3策略的3.0 cm、2.9 cm和3.0 cm相比,相互间差异同样都不大于0.3 cm。
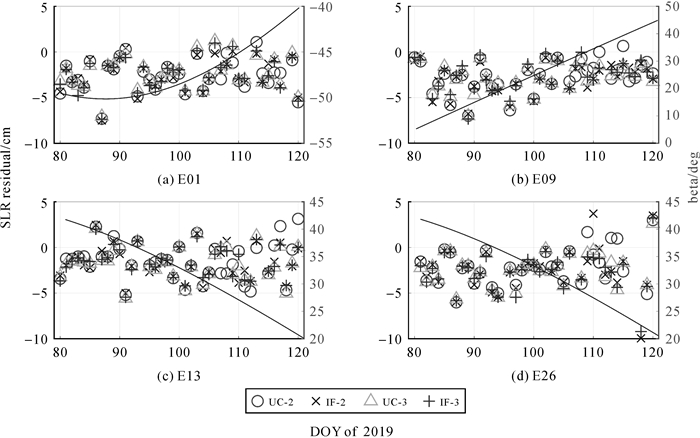
|
| 图 7 双频和三频UC/IF策略定轨固定解SLR残差 Fig. 7 SLR residuals of fixed solutions for dual-frequency and triple-frequency UC/IF model |
| 卫星PRN | Solution | #NP | Offset/cm | STD/cm |
| E01 | UC-1 | 381 | -2.3 | 2.1 |
| UC-2 | 381 | -2.2 | 2.1 | |
| UC-3 | 381 | -2.2 | 2.0 | |
| IF-1 | 381 | -2.3 | 2.1 | |
| IF-3 | 381 | -2.3 | 2.1 | |
| IF-3 | 381 | -2.3 | 2.1 | |
| E09 | UC-1 | 495 | -2.6 | 3.0 |
| UC-2 | 495 | -2.5 | 3.2 | |
| UC-3 | 495 | -2.6 | 2.9 | |
| IF-1 | 495 | -2.7 | 3.0 | |
| IF-2 | 495 | -2.7 | 2.9 | |
| IF-3 | 495 | -2.5 | 3.0 | |
| E13 | UC-1 | 488 | -1.8 | 3.4 |
| UC-2 | 488 | -1.5 | 3.7 | |
| UC-3 | 488 | -1.8 | 3.4 | |
| IF-1 | 488 | -1.8 | 3.4 | |
| IF-2 | 488 | -1.7 | 3.4 | |
| IF-3 | 488 | -1.7 | 3.3 | |
| E26 | UC-1 | 300 | -2.5 | 2.6 |
| UC-2 | 300 | -2.2 | 3.0 | |
| UC-3 | 300 | -2.4 | 2.6 | |
| IF-1 | 300 | -2.5 | 2.5 | |
| IF-2 | 300 | -2.2 | 2.8 | |
| IF-3 | 300 | -2.5 | 2.5 |
3 总结
本文推导了多频UC和IF定轨模型,给出了多频UC定轨模型的双差固定策略。在此基础上,利用全球分布的150个MGEX测站进行了不同策略的Galileo卫星精密定轨。使用与CODE产品比较、OBD和SLR检核这3种方法来评估Galileo定轨产品的精度。通过分析比较结果,得出如下结论:
(1) 在使用E1/E5a与E1/E5b双频观测值的情况下,观测值类型一致时,本文提出的UC策略和传统的IF策略的定轨精度基本相当,两者浮点解轨道精度差异和固定解轨道精度差异都不超过1 mm,浮点解钟差差异和固定解钟差差异都不超过0.01 ns。此外,在双频固定解中,UC-1和UC-2策略的宽巷和窄巷模糊度固定率都分别略低于IF-1和IF-2策略对应的模糊度固定率。
(2) 使用E1/E5a/E5b三频观测值时,浮点解定轨结果相较于双频观测值浮点解定轨结果略有提升。无论是UC策略还是IF策略,其固定解定轨结果的1D RMS和使用E1/E5a和E1/E5b观测值时定轨结果的RMS差异在1 mm以内。双频和三频条件下,UC策略和IF策略固定解的钟差差异在0.01 ns以内。
(3) 在观测值类型一致时,本文提出的UC策略和传统的IF策略的浮点解及固定解OBD结果在切向、法向和径向上的差异小于2.5 mm,不同策略间OBD的1D RMS差异不超过2 mm。
(4) 在观测值类型一致时,UC策略和IF策略的固定解定轨结果的SLR残差和STD值都基本相当。总体而言,所有策略的SLR检核残差小于20 mm,不同策略的SLR检核残差之间的差异不超过3 mm。
(5) Galileo多频非组合精密定轨精度目前仍需进一步改善, 包括E5b信号误差模型精化、UC模糊度双差固定等问题仍需要深入研究和分析。与Galileo类似,北斗三代卫星导航系统(BDS-3)共有B1、B3、B1C、B2a和B2b 5种信号,适用于BDS-3的多频非组合精密定轨模型同样需要进一步研究和评估。
| [1] |
杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505-510. YANG Yuanxi. Concepts of comprehensive PNT and related key technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505-510. DOI:10.11947/j.AGCS.2016.20160127 |
| [2] |
HAYES D, HAHN J. Galileo programme update[C]//Proceedings of 14th Meeting of the International Committee on GNSS. Bangalore, India, 2019.
|
| [3] |
BURY G, SOS'NICA K, ZAJDEL R, et al. Toward the 1-cm Galileo orbits:challenges in modeling of perturbing forces[J]. Journal of Geodesy, 2020, 94(2): 16. |
| [4] |
DACH R, BROCKMANN E, SCHAER S, et al. GNSS processing at CODE:status report[J]. Journal of Geodesy, 2009, 83(3-4): 353-365. DOI:10.1007/s00190-008-0281-2 |
| [5] |
GUO Jing, XU Xiaolong, ZHAO Qile, et al. Precise orbit determination for quad-constellation satellites at Wuhan University:strategy, result validation, and comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159. |
| [6] |
PRANGE L, ORLIAC E, DACH R, et al. CODE's five-system orbit and clock solution-the challenges of multi-GNSS data analysis[J]. Journal of Geodesy, 2017, 91(4): 345-360. DOI:10.1007/s00190-016-0968-8 |
| [7] |
ZHANG Rui, TU Rui, LIU Jinhai, et al. Performance of Galileo:global coverage, precise orbit determination, and precise positioning[J]. Advances in Space Research, 2019, 64(2): 299-313. DOI:10.1016/j.asr.2019.03.042 |
| [8] |
LIU Teng, YUAN Yunbin, ZHANG Baocheng, et al. Multi-GNSS precise point positioning (MGPPP) using raw observations[J]. Journal of Geodesy, 2017, 91(3): 253-268. |
| [9] |
ZHOU Feng, DONG Danan, GE Maorong, et al. Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations[J]. GPS Solutions, 2018, 22(1): 19. DOI:10.1007/s10291-017-0685-7 |
| [10] |
KESHIN M O, LE A Q, VAN DER MAREL H. Single and dual-frequency precise point positioning: approaches and performance[C]//Proceedings of the 3rd ESA Workshop on Satellite Navigation User Equipment Technologies. Noordwijk, The Netherlands: NAVITEC, 2006: 11-13.
|
| [11] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of slant total electron content and satellite-receiver's differential code biases with uncombined precise point positioning technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. |
| [12] |
张宝成, 欧吉坤, 李子申, 等. 利用精密单点定位求解电离层延迟[J]. 地球物理学报, 2011, 54(4): 950-957. ZHANG Baocheng, OU Jikun, LI Zishen, et al. Determination of ionospheric observables with precise point positioning[J]. Chinese Journal of Geophysics, 2011, 54(4): 950-957. |
| [13] |
周锋.多系统GNSS非差非组合精密单点定位相关理论和方法研究[D].上海: 华东师范大学, 2018. ZHOU Feng. Theory and methodology of multi-GNSS undifferenced and uncombined precise point positioning[D]. Shanghai: East China Normal University, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10269-1018710617.htm |
| [14] |
GUO Fei, ZHANG Xiaohong, WANG Jinling, et al. Modeling and assessment of triple-frequency BDS precise point positioning[J]. Journal of Geodesy, 2016, 90(11): 1223-1235. DOI:10.1007/s00190-016-0920-y |
| [15] |
辜声峰.多频GNSS非差非组合精密数据处理理论及其应用[D].武汉: 武汉大学, 2013. GU Shengfeng. Research on the Zero-difference Un-combined data processing model for multi-frequency GNSS and its applications[D]. Wuhan: Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135106.htm |
| [16] |
ZEHENTNER N, MAYER-GVRR T. New approach to estimate time variable gravity fields from high-low satellite tracking data[M]//MARTI U. Gravity, Geoid and Height Systems. Cham: Springer, 2014: 111-116.
|
| [17] |
郭靖.姿态、光压和函数模型对导航卫星精密定轨影响的研究[D].武汉: 武汉大学, 2014. GUO Jing. The impacts of attitude, solar radiation and function model on precise orbit determination for GNSS satellites[D]. Wuhan: Wuhan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm |
| [18] |
陈华.基于原始观测值的GNSS统一快速精密数据处理方法[D].武汉: 武汉大学, 2015. CHEN Hua. An efficient and unified GNSS raw data processing strategy[D]. Wuhan: Wuhan University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015305222.htm |
| [19] |
ZENG Tian, SUI Lifen, RUAN Rengui, et al. Uncombined precise orbit and clock determination of GPS and BDS-3[J]. Satellite Navigation, 2020, 1(1): 19. |
| [20] |
BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF):A new empirical mapping function based on numerical weather model data[J]. Geophysical Research Letters, 2006, 33(7): L07304. |
| [21] |
BOEHM J, HEINKELMANN R, SCHUH H. Short Note:A global model of pressure and temperature for geodetic applications[J]. Journal of Geodesy, 2007, 81(10): 679-683. DOI:10.1007/s00190-007-0135-3 |
| [22] |
SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Géodésique (1946-1975), 1972, 105(1): 279-298. DOI:10.1007/BF02521844 |
| [23] |
WU J, WU S, HAJJ G A, et al. Effects of antenna orientation on GPS carrier phase[J]. Manuscripta Geodaetica, 1993, 18(2): 91-98. |
| [24] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099. ZHANG Baocheng. Study on the theoretical methodology and applications of precise point positioning using undifferenced and uncombined GNSS Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099. DOI:10.13485/j.cnki.11-2089.2014.0155 |
| [25] |
张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报(信息科学版), 2010, 35(6): 657-660. ZHANG Xiaohong, LI Xingxing. A new method for zero-differenced interger ambiguity resolution and its application to PPP[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 657-660. |
| [26] |
BLEWITT G. An automatic editing algorithm for GPS data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. DOI:10.1029/GL017i003p00199 |
| [27] |
HATCH R, JUNG J, ENGE P, et al. Civilian GPS:the benefits of three frequencies[J]. GPS Solutions, 2000, 3(4): 1-9. DOI:10.1007/PL00012810 |
| [28] |
GE Maorong, GENDT G, DICK G, et al. Improving carrier-phase ambiguity resolution in global GPS network solutions[J]. Journal of Geodesy, 2005, 79(1-3): 103-110. DOI:10.1007/s00190-005-0447-0 |
| [29] |
ARNOLD D, MEINDL M, BEUTLER G, et al. CODE's new solar radiation pressure model for GNSS orbit determination[J]. Journal of Geodesy, 2015, 89(8): 775-791. DOI:10.1007/s00190-015-0814-4 |
| [30] |
PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B4): B04406. |
| [31] |
LYARD F, LEFEVRE F, LETELLIER T, et al. Modelling the global ocean tides:modern insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394-415. DOI:10.1007/s10236-006-0086-x |
| [32] |
PETIT G, LUZUM B. IERS conventions 2010[R]. No.36 in IERS Technical Note. Frankfurt am Main, Germany: Verlag des Bundesamts für Kartographie und Geodäsie, 2010.
|
| [33] |
LI Xingxing, ZHU Yiting, ZHENG Kai, et al. Precise orbit and clock products of galileo, BDS and QZSS from MGEX since 2018:comparison and PPP validation[J]. Remote Sensing, 2020, 12(9): 1415. DOI:10.3390/rs12091415 |
| [34] |
GE Maorong, CHEN Junping, DOUŠA J, et al. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime[J]. GPS Solutions, 2012, 16(1): 9-17. DOI:10.1007/s10291-011-0206-z |
| [35] |
PEARLMAN M R, NOLL C E, PAVLIS E C, et al. The ILRS:approaching 20 years and planning for the future[J]. Journal of Geodesy, 2019, 93(11): 2161-2180. DOI:10.1007/s00190-019-01241-1 |


