2. 北京跟踪与通信技术研究所, 北京 100094;
3. 国防科技大学电子科学学院, 湖南 长沙 410073;
4. 北京卫星导航中心, 北京 100094
2. Beijing Institute of Tracking and Telecommunication Technology, Beijing 100094, China;
3. School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China;
4. Beijing Satellite Navigation Center, Beijing 100094, China
随着卫星导航系统空间信号精度逐步改善[1-4],用户段误差对卫星导航系统服务性能提升的瓶颈效应越来越显著[5]。用户段误差是指由用户接收机或者用户环境导致的伪距测量误差。一般认为,用户段误差包括伪距多路径误差和测量随机噪声。本文关注被广泛忽略的伪距偏差,将其作为一种新的误差。需要说明的是,国内外文献均报道了GPS卫星和北斗卫星的伪距波动误差,将其称为伪距偏差[6-8]。上述文献报道的伪距偏差实际上是类似多路径效应的伪距波动。而本文关注的伪距偏差是由卫星导航信号非理想特征导致的伪距测量常数偏差。伪距偏差最早发现于1993年,GPS Block Ⅱ卫星SVN19下行信号出现异常,不同类型接收机伪距测量出现不同偏差,造成用户差分定位精度显著下降[9]。伪距偏差并非仅存在于异常的导航卫星,文献[10—13]的研究表明,即使GPS星座内健康卫星下行信号的伪距测量也存在伪距偏差,是影响星基增强系统服务性能的重要误差。文献[14—15]将不同类型接收机布设成零基线,研究不同系统卫星伪距偏差现象,结果表明GPS、GLONASS、Galileo和北斗卫星不同信号均存在伪距偏差。
Stanford大学星基增强团队对导航信号失真引起的GPS伪距偏差作了深入分析。文献[14]提出了两种分析不同相关间距的方法,一种利用抛物面天线进行数据采集和后处理操作,另一种利用可以配置不同相关间距的硬件接收机实时跟踪信号处理;综合比较了定向天线和全向天线采集信号计算的伪距偏差特性,得出由于定向天线的增益较大,利用大天线采集的信号计算的伪距偏差离散程度较小,而利用全向天线计算的伪距偏差的离散程度较大。通过对同一时刻同一卫星的两种方法的比较,表明两种观测方法得出的伪距偏差具有相似的范围和趋势,不一致性主要反映在观测噪声和多路径影响量级上。分析表明伪距偏差与接收机的相关间隔有关,以0.1码片为参考,相关间距相差越大,信号失真引起的伪距偏差越大,接收机相关间距0.1~1.0码片间平均偏差为0.3 m,0.1~0.2码片的相关间距会导致平均偏差为0.15 m。
信号失真导致的伪距偏差,将进一步影响定位误差。文献[12]比较了伪距偏差对WASS用户双频无电离层组合和单频定位的最差定位误差的影响。对于单频SBAS用户,电离层误差是主要误差,伪距偏差影响相对较小。对于双频或多频的,观测量组合用于消除电离层误差,电离层组合比例因子对伪距偏差具有放大作用,使得伪距偏差成为双频组合观测量的重要误差分量。在单频情况下,最差用户误差为0.35~0.7 m,而双频最差用户误差为1.89~3.86 m。
接收机的前端滤波带宽同样是影响伪距偏差大小的重要因素。为了更有效地避免伪距偏差引起的最大误差的影响,文献[12]提出限制用户接收机相关间距可以避免双频用户定位遭受伪距偏差导致的显著性能降低。单频伪距偏差对最差用户误差的影响从21%~91%降低至4%~8%,双频伪距偏差对误差的影响从44%~264%降低至7%~22%[9]。
GPS系统用户接口控制文件虽未指出伪距偏差现象的存在,但明确了对用户接收机的滤波带宽参数和相关参数的建议。不采用GPS系统用户接口控制文件约定的技术状态的用户接收机(滤波带宽为20.46 MHz,相关器间距为97.75 ns)伪距测量将包含由导航信号非理想导致的测量误差,从而引起用户定位授时误差。
德国DLR团队也对GPS、GLONASS和Galileo导航卫星伪距偏差作了较为详细的分析。文献[14]首先分析了伪距偏差的产生机理。指出导航信号的非理想特性导致不同技术状态的接收机对该信号的伪距测量产生大小和方向不同的伪距偏差。对多种接收机和多系统导航卫星伪距偏差的分析表明,伪距偏差的大小与接收机的相关器间隔和抗多径算法有关。对比发现,GPS L1 C/A伪距偏差大于P1码和P2码,Galileo卫星所有信号伪距偏差均明显小于GPS信号[15]。
北斗系统是我国独立自主建设的全球卫星导航系统,其建设过程分为3步走。2020年7月底,北斗三号完成系统建设,服务区域扩展为全球范围,向全球用户提供导航、定位与授时服务[16-17]。相比于北斗二号卫星,北斗三号卫星空间信号质量、卫星轨道及空间信号精度均有较大提升[18-19]。由于信号体制不同,北斗三号卫星具有与北斗二号卫星显著不同的伪距偏差特征[20]。目前国内外研究集中于对GPS、GLONASS和Galileo卫星伪距偏差测量与标定,但缺乏对北斗卫星下行导航信号伪距偏差的认识。本文根据伪距偏差的特征,提出北斗二号卫星和北斗三号卫星伪距偏差的标定方法,利用基于并置接收机的伪距偏差计算算法完成伪距偏差的精确标定和时空特征提取,并利用实测数据评估了伪距偏差对用户定位精度的影响,将其作为新的误差源。
1 伪距偏差标定方法伪距偏差的计算算法包括并置接收机双差法和基于DCB参数的伪距偏差计算方法。基于这两种方法计算的伪距偏差不受其他误差影响,可如实反映伪距测量的常数偏差。并置接收机双差法可解算出所有频点伪距的偏差,但需将并置接收机部署为短基线或者零基线。基于DCB参数的伪距偏差计算方法可计算得到两个频点伪距偏差互差,不需两台接收机并置设置。需要说明的是,这两种算法计算得到的是两台接收机和两颗卫星的伪距偏差互差,而非绝对的伪距偏差。但是伪距偏差互差对于导航定位精度才有意义。若伪距偏差互差为0,伪距偏差可以被现有导航参数吸收,不会对导航业务处理和导航定位精度产生不利影响。
1.1 并置接收机的伪距偏差计算方法利用并置的两台不同型号接收机计算伪距偏差。并置的两台接收机r1和r2,外接同一时频信号,相距不超过20 m。以B1I频点为例,两台接收机对卫星i的伪距观测方程为
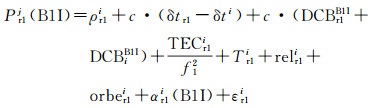 (1)
(1)
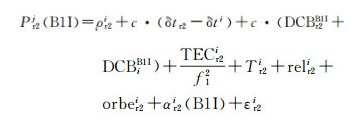 (2)
(2)
式中,以接收机r1与卫星i为例;Pr1i为伪距观测值;ρr1i为利用预报星历计算的星地距离;orber1i为预报星历误差在星地方向上的投影;δtr1为接收机钟差;δti为卫星钟差;c为光速;DCBr1B1I为B1I频点接收机码偏差参数;DCBiB1I为B1I频点卫星码偏差参数;TECr1i为斜路径电子总含量;f1为B1I频点频率;TECr1i为斜路径总电子含量;Tr1i为对流层延迟;relr1i为相对论周期项;αr1i为接收机r1对卫星i的伪距测量偏差;εr1i为伪距多路径误差和噪声。由于r1和r2相距不超过20 m,外接同一时频信号,卫星星历误差、卫星钟差、电离层延迟、对流层延迟和接收机钟差对并置接收机伪距测量的影响是相同的。将r1和r2对卫星i的伪距观测作接收机间差分,得到单差O-C,其数学期望应仅包含r1和r2对卫星i的伪距偏差之差和码偏差参数之差(码偏差在几天弧段内为常数)
 (3)
(3)
由于接收机码偏差参数对所有卫星均相同,选卫星i为基准星,将其他卫星单差O-C均值与卫星i单差O-C均值作差,可得其他卫星相对于卫星i的伪距偏差。
通过上述方法,可完成所有频点伪距偏差的计算。
1.2 基于DCB参数的伪距偏差计算方法对于未布设成并置接收机的监测网络,可通过比较不同接收机解算的DCB参数计算两个频点伪距偏差互差。假设接收机r1对卫星i的B1I频点和B2I频点伪距观测方程为
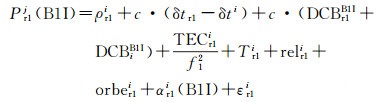 (4)
(4)
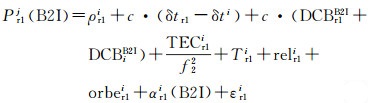 (5)
(5)
式中, f2为B2I频点频率,其余各符号含义与式(1)相同。
将B1I频点伪距与B2频点伪距作差
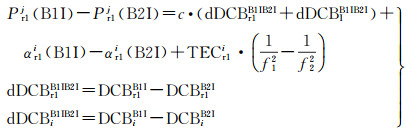 (6)
(6)
被广泛采用的DCB参数和电离层模型参数解算模型将式(6)作为唯一输入观测量[21-22],码偏差参数dDCBr1B1IB2I、dDCBiB1IB2I(两个频点的码偏差参数作差也是一种码偏差参数)和电离层模型系数是待估参数。由式(6)可得,待估码偏差参数与伪距偏差参数是完全相关的,伪距偏差将被完全吸收到卫星和接收机DCB参数的解算结果。
IGS、MGEX、iGMAS为GNSS数据处理科学研究提供了充足的公开数据源[23-25]。可将IGS、MGEX和iGMAS所有接收机按照接收机型号划分为若干子集。利用每个子集的所有接收机观测数据分别解算卫星DCB参数。通过比对每个子集解算的卫星DCB参数,便可得到不同接收机间伪距偏差互差。
并置接收机的伪距偏差计算方法需将两种或者多种不同型号监测接收机布设称为短基线或者零基线,对试验场景要求较苛刻。而基于DCB参数的伪距偏差计算方法不受地理位置限制。并置接收机的伪距偏差计算方法可完成所有频点伪距偏差标定,而基于DCB参数的伪距偏差计算方法仅能计算得到不同频点伪距偏差的差异。
2 北斗卫星伪距偏差标定及特征分析 2.1 伪距偏差标定结果稳定度将两类不同型号的接收机布设成短基线。利用并置接收机伪距相位数据根据短基线双差并置比对法每天弧段计算B1I和B3I频点伪距偏差。数据选择为2020年年积日DOY147—277。计算选择始终对中国区域可视的C01为基准星,完成其他卫星B1I、B3I伪距偏差。
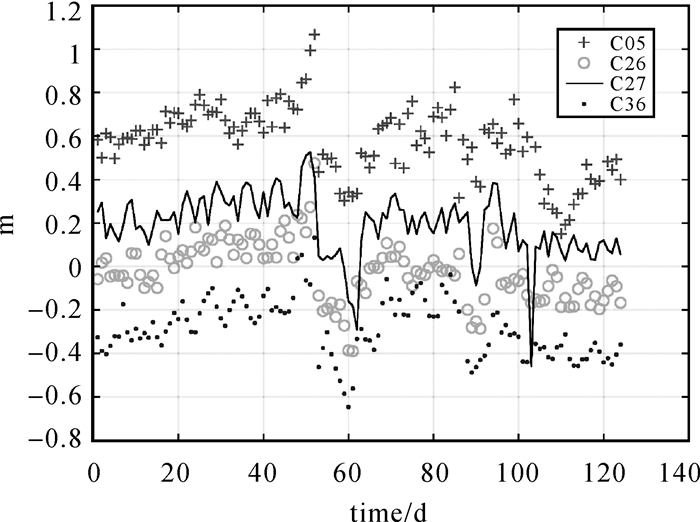
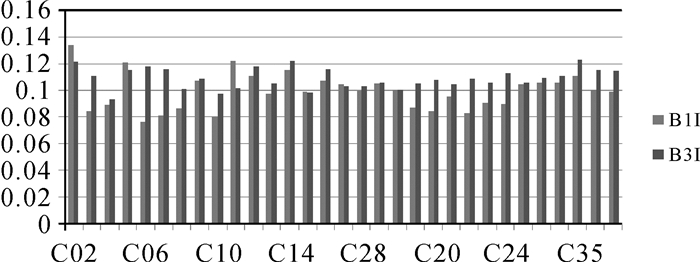
上述弧段观测数据计算的部分卫星B1I伪距偏差序列如图 1所示。所有卫星B1I、B3I伪距偏差标定结果的均值与波动STD情况分别见图 2和图 3。从图 1可以看出,120多天的伪距偏差计算序列比较平稳,虽然波动较大,但未见明显的变化趋势。从图 3可以看出,不同卫星B1I和B3I频点伪距偏差序列波动STD量级大致相当,均约为0.1 m。伪距偏差序列波动STD未呈现与卫星和信号频率明显的关联性。
|
| 图 1 部分卫星B1I频点伪距偏差序列 Fig. 1 Pseudorange deviation sequence of partial satellite B1I frequency points |
|
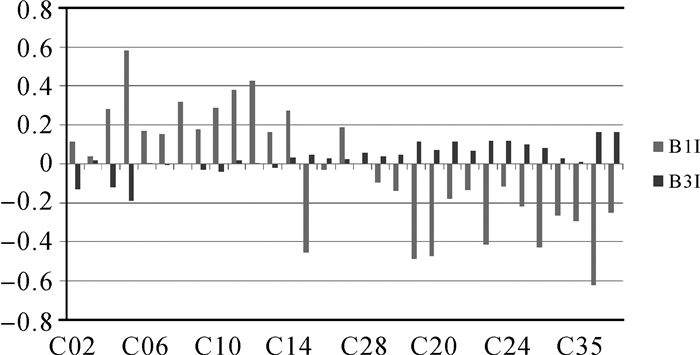
| 图 2 所有卫星B1I、B3I伪距偏差计算序列均值 Fig. 2 Mean values of pseudorange deviations of all satellites B1I and B3I |
|
| 图 3 所有卫星B1I、B3I伪距偏差计算序列波动STD Fig. 3 STD of pseudorange deviation calculation sequence fluctuation of all satellites B1I and B3I |
但是从图 2可以看出,B1I、B3I伪距偏差具有明显的量级差距,且呈现出与卫星和频点的强关联性。不同卫星伪距偏差量级显著不同。以C01为参考星,不同卫星B1I频点伪距偏差量级差别明显,C05卫星的B1I频点伪距偏差可达正向0.5 m,C36卫星的B1I频点伪距偏差可达负向最大值-0.6 m,而部分卫星如C26和C28卫星的B1I频点伪距偏差接近于0。相比之下,卫星B3频点伪距偏差量级差别较小。参考于C01卫星,C05、C36和C37卫星B3I伪距偏差最大,但绝对值小于0.2 m。
虽然北斗卫星B1I伪距偏差计算序列波动STD与B3I伪距偏差计算序列波动STD相当,但B1I频点伪距偏差量级最大为0.6 m,大于B3I频点伪距偏差量级,最大仅为0.2 m。
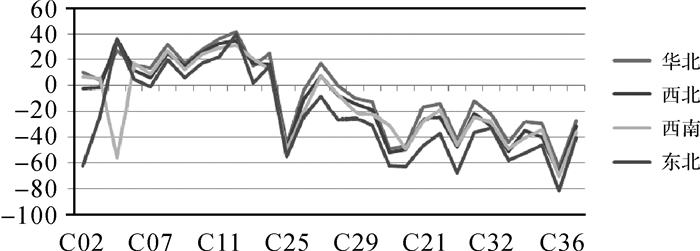
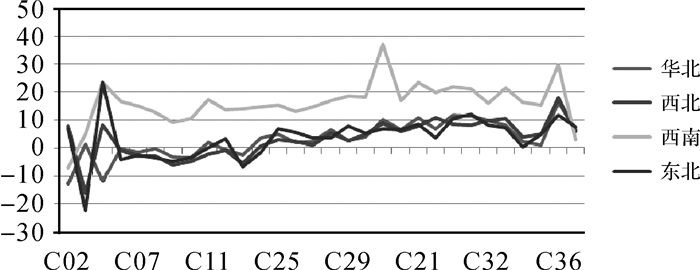
2.2 伪距偏差标定多站一致性分别利用分布于国内东北、西南、西北和华北4个不同站点布设的两种型号接收机,采用短基线双差并置比对法计算北斗卫星B1I和B3I频点伪距偏差,计算结果见图 4和图 5。从图 4可以看出,除西南站对C04卫星伪距偏差计算结果与其他卫星显著不同外,不同位置的短基线双差并置比对法计算的其他卫星B1I频点伪距偏差随卫星号的函数变化趋势相当,最大差异不超过20 cm。从图 5可以看出,西南站对所有卫星B3I频点伪距偏差计算结果与其他各站显著不同,其他各站B3I频点伪距偏差趋势几乎完全相同,最大误差不超过5 cm。结果表明,不同测站标定的伪距偏差具备较高的一致性。
|
| 图 4 不同站对所有卫星B1I伪距偏差计算结果 Fig. 4 Calculation results of pseudorange deviation of all satellites B1I by different stations |
|
| 图 5 不同站对所有卫星B3I伪距偏差计算结果 Fig. 5 Calculation results of pseudorange deviation of all satellites B3I by different stations |
2.3 伪距偏差结果分析
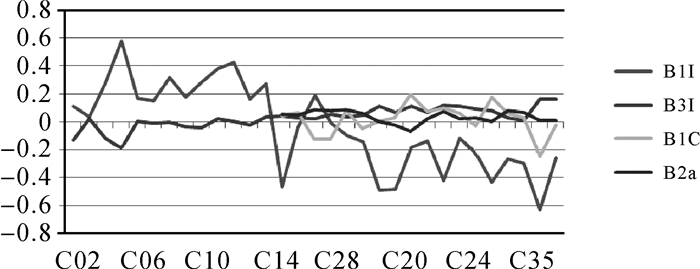
利用短基线双差并置比对法处理相同时段并置接收机观测数据,可得到新体制信号B1C和B2a伪距偏差测量结果。其中新体制信号B1C和B2a伪距偏差测量以C19卫星为参考,B1I和B3I信号伪距偏差测量以C01卫星为参考。将B1C、B2a、B1I和B3I信号伪距偏差随卫星的关系如图 6。从图中可以看出,新体制信号B1C伪距偏差小于0.2 m,明显好于B1频点另一信号分量B1I的伪距偏差。另外,B2a频点伪距偏差最小,约为10 cm,较B3I频点和B1C频点伪距偏差小。
|
| 图 6 北斗卫星不同频点伪距偏差比较 Fig. 6 Comparison of pseudorange deviation between different frequency points of BeiDou satellite |
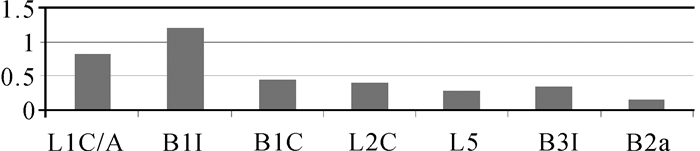
利用相同算法处理接收机对GPS卫星的伪距相位数据,得到GPS卫星L1C/A、L2C和L5C信号分量的伪距偏差。将某个信号的伪距偏差最大值与伪距偏差最小值作差,以衡量信号伪距偏差大小。图 7为GPS卫星信号分量与北斗卫星信号分量伪距偏差最大值与最小值的差。可以看到,北斗卫星B1频点、GPS卫星L1C/A伪距偏差明显均明显大于其他频点。在1.5G频段,北斗卫星B1I频点伪距偏差最大,约为1.2 m,大于GPS卫星L1C/A频点。北斗卫星新体制信号B1C伪距偏差最小,约为0.4 m,较北斗卫星B1I频点伪距偏差明显改善,也明显好于GPS卫星L1C/A频点伪距偏差。
|
| 图 7 北斗卫星与GPS卫星不同频点伪距偏差比较 Fig. 7 Comparison of pseudorange deviation between BeiDou satellite and GPS satellite at different frequency points |
在其他频段,GPS卫星L2C伪距偏差略大于北斗卫星B3I伪距偏差,L5C频点伪距偏差次之,B2a频点伪距偏差最小。这表明,随着北斗系统发展,新体制信号质量得到改善,伪距偏差量级减小。
3 伪距偏差对用户定位精度影响如前所述,伪距偏差是新发现的伪距测量常数偏差。由于卫星发射通道故障或非理想特性均会导致导航信号失真,从而导致接收机测量的伪距产生常数的测量偏差伪距偏差,不同技术状态的接收机对同一导航信号测量产生符号不同、大小不同的常数偏差。若所有卫星导航信号的非理想特性不同,同一接收机对所有卫星的伪距偏差的大小和数值完全相同,该偏差可以完全被接收机钟差或者接收机码偏差参数吸收,从而不对用户导航定位授时精度产生不利影响。若所有用户接收机和监测接收机技术状态完全一致,所有接收机观测到某一卫星的伪距偏差相同,则该偏差可以被卫星钟差或者卫星码偏差参数吸收,从而不对用户导航定位授时精度产生不利影响。但是,不同卫星导航信号的非理想状态并不相同,不同厂家监测接收机和用户接收机技术状态也不一致,伪距偏差无法被卫星钟差或卫星码偏差参数、接收机钟差或者接收机码偏差参数吸收,从而引起导航参数的计算误差,影响导航参数的解算精度,进而引起用户定位精度的恶化。
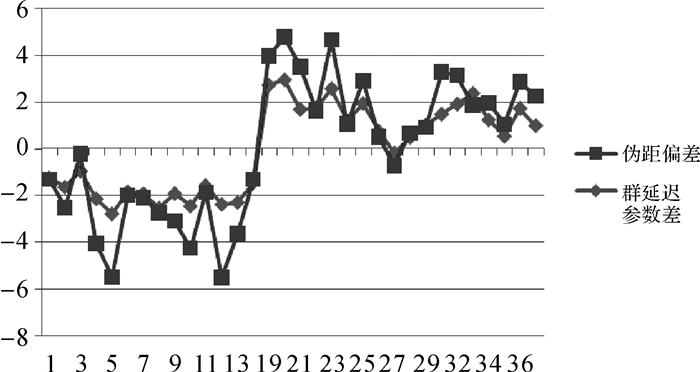
图 8描述为伪距偏差与群延迟参数互差比对情况。对比发现,伪距偏差与群延迟参数互差具备很强的相关性。若用户接收机与基准接收机技术状态存在差别而造成比较大的伪距偏差,用户使用导航电文播发的TGD参数进行定位解算,必将承受比较大的误差。
|
| 图 8 群延迟参数互差与伪距偏差比对 Fig. 8 Comparison between group delay parameter mutual difference and pseudorange deviation ratio |
分别使用IGS提供的群延迟参数和导航电文播发的群延迟参数对IGS站进行定位解算,定位精度如表 1所示。分别使用IGS提供的群延迟参数和导航电文播发的群延迟参数对国内站进行定位解算,定位精度如表 2所示。相比于导航电文的TGD参数, 使用IGS计算的DCB参数可以提升IGS测站的定位精度,但是大幅降低国内接收机的定位精度。同样地,相比于IGS计算的DCB参数, 使用导航电文的TGD参数可以提升国内接收机的定位精度,但是大幅降低IGS测站的定位精度的定位精度。由于伪距偏差存在,并不能找到适用于所有接收机的群延迟参数。
| 群延迟参数来源 | 水平 | 高程 |
| IGS | 1.672 | 2.544 |
| 导航电文 | 2.020 | 2.923 |
| 群延迟参数来源 | 水平 | 高程 |
| IGS | 1.694 | 2.413 |
| 导航电文 | 0.823 | 1.059 |
4 结论
本文提出GNSS精密数据处理和用户导航定位授时解算须顾及新的误差源——伪距测量常数偏差。伪距偏差是由卫星下行导航信号非理想特征引起的不同技术状态接收机对下行信号测量导致的伪距测量常数偏差。该偏差与伪距测量的多路径误差和噪声不同,也无法被现有的与卫星有关或者与接收机有关的导航参数表达,是一种新的误差源。
根据伪距偏差的误差特征,本文提出两种伪距偏差标定方法,即并置接收机双差法和基于DCB参数的伪距偏差计算方法。基于这两种方法计算的伪距偏差不受其他误差影响,可如实反映伪距测量的常数偏差。通过并置接收机双差比对法完成了北斗卫星伪距偏差的计算。结果表明,并置接收机双差比对法得到的伪距偏差离散度约为10 cm。伪距偏差具有不随时间明显变化的特征,不同地理环境布设的伪距偏差具有较好的一致性。对比发现,北斗卫星新体制信号B1C伪距偏差最小,约为0.4 m,较北斗卫星B1I频点伪距偏差明显改善,也明显好于GPS卫星L1C/A频点伪距偏差。北斗卫星B3I伪距偏差略小于GPS卫星L2C伪距偏差,B2a频点伪距偏差也小于L5C频点伪距偏差。
对不同接收机的数据处理表明,伪距偏差与群延迟参数解算高度相关。IGS计算的DCB参数可以提升IGS测站的定位精度,使用导航电文的TGD参数可以提升国内接收机的定位精度。不同技术状态接收机存在的伪距偏差已成为影响用户定位精度的主要误差。大系统需结合用户典型接收方式和不同厂家接收机的参数设置,设计合理的群延迟参数计算数据源,使得导航电文播发的群延迟参数与用户接收机更为自洽。
| [1] |
TEUNISSEN P J G, MONTENBRUCK O. Springer handbook of global navigation satellite systems[M]. Cham: Springer, 2017. DOI:10.1007/978-3-319-42928-1
|
| [2] |
MONTENBRUCK O, STEIGENBERGER P, HAUSCHILD A. Broadcast versus precise ephemerides:a multi-GNSS perspective[J]. GPS Solutions, 2015, 19(2): 321-333. DOI:10.1007/s10291-014-0390-8 |
| [3] |
CHEN Jinping, HU Xiaogong, TANG Chengpan, et al. SIS accuracy and service performance of the BDS-3 basic system[J]. Science China Physics, Mechanics & Astronomy, 2020, 63(6): 269511. |
| [4] |
LI Ran, CAO Yueling, HU Xiaogong, et al. Analysis of the wide area differential correction for BeiDou global satellite navigation system[J]. Research in Astronomy and Astrophysics, 2018, 18(11): 133. DOI:10.1088/1674-4527/18/11/133 |
| [5] |
STEIGENBERGER P, MONTENBRUCK O. Galileo status:orbits, clocks, and positioning[J]. GPS Solutions, 2017, 21(2): 319-331. DOI:10.1007/s10291-016-0566-5 |
| [6] |
WANNINGER L, BEER S. BeiDou satellite-induced code pseudorange variations:diagnosis and therapy[J]. GPS Solutions, 2015, 19(4): 639-648. DOI:10.1007/s10291-014-0423-3 |
| [7] |
BEER S, WANNINGER L. Temporal stability of GPS transmitter group delay variations[J]. Sensors, 2018, 18(6): 1744. DOI:10.3390/s18061744 |
| [8] |
倪少杰, 王耀鼎, 封欣, 等. 北斗卫星伪距信号质量评估及偏差校正[J]. 国防科技大学学报, 2017, 39(4): 87-91. NI Shaojie, WANG Yaoding, FENG Xin, et al. Quality assessment and error correction of BeiDou satellite pseudorange signal[J]. Journal of National University of Defense Technology, 2017, 39(4): 87-91. |
| [9] |
PHELTS R E, AKOS D M, ENGE P. Robust signal quality monitoring and detection of evil waveforms[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation. Anaheim: Institute of Navigation, 2000: 1180-1190.
|
| [10] |
GABRIEL W, PHELTS R E, WALTER T, et al. Characterization of signal deformations for GPS and WAAS satellites[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland: Institute of Navigation, 2010: 3143-3151.
|
| [11] |
WONG G, CHEN Y H, PHELTS R E, et al. Measuring code-phase differences due to inter-satellite hardware differences[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation. Nashville: Institute of Navigation, 2012: 2150-2158. https://www.ion.org/publications/abstract.cfm?articleID=10409
|
| [12] |
WONG G, CHEN Y H, PHELTS R E, et al. Mitigation of nominal signal deformations on dual-frequency WAAS position errors[C]//Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation. Tampa: Institute of Navigation, 2014: 3129-3147. https://www.ion.org/publications/abstract.cfm?articleID=12395
|
| [13] |
WONG G, PHELTS R E, WALTER T, et al. Bounding errors caused by nominal GNSS signal deformations[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation. Portland: Institute of Navigation, 2011: 2657-2664.
|
| [14] |
HAUSCHILD A É, MONTENBRUCK O. The effect of Correlator and front-end design on GNSS pseudorange biases for geodetic receivers[J]. Navigation, 2016, 63(4): 443-453. DOI:10.1002/navi.165 |
| [15] |
HAUSCHILD A, MONTENBRUCK O. A study on the dependency of GNSS pseudorange biases on correlator spacing[J]. GPS Solutions, 2016, 20(2): 159-171. DOI:10.1007/s10291-014-0426-0 |
| [16] |
CHEN Jinping, HU Xiaogong, TANG Chengpan, et al. SIS accuracy and service performance of the BDS-3 basic system[J]. Science China Physics, Mechanics & Astronomy, 2020, 63(6): 269511. |
| [17] |
YANG Yuanxi, GAO Weiguang, GUO Shuren, et al. Introduction to BeiDou-3 navigation satellite system[J]. Navigation, 2019, 66(1): 7-18. |
| [18] |
ZENG Tian, SUI Lifen, JIA Xiaolin, et al. Results and analyses of BDS precise orbit determination with the enhancement of Fengyun-3C[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(3): 68-78. DOI:10.11947/j.JGGS.2019.0307 |
| [19] |
CHEN Qiuli, YANG Hui, CHEN Zhonggui, et al. Solar radiation pressure modeling and application of BDS satellites[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 45-52. DOI:10.11947/j.JGGS.2020.0205 |
| [20] |
郭树人, 蔡洪亮, 孟轶男, 等. 北斗三号导航定位技术体制与服务性能[J]. 测绘学报, 2019, 48(7): 810-821. GUO Shuren, CAI Hongliang, MENG Yinan, et al. BDS-3 RNSS technical characteristics and service performance[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 810-821. DOI:10.11947/j.AGCS.2019.20190091 |
| [21] |
王宁波, 袁运斌, 张宝成, 等. GPS民用广播星历中ISC参数精度分析及其对导航定位的影响[J]. 测绘学报, 2016, 45(8): 919-928. WANG Ningbo, YUAN Yunbin, ZHANG Baocheng, et al. Accuracy evaluation of GPS broadcast inter-signal correction (ISC) parameters and their impacts on GPS standard positioning[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 919-928. DOI:10.11947/j.AGCS.2016.20150554 |
| [22] |
MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps[J]. Navigation, 2014, 61(3): 191-201. DOI:10.1002/navi.64 |
| [23] |
MONTENBRUCK O, STEIGENBERGER P, PRANGE L, et al. The multi-GNSS experiment (MGEX) of the International GNSS Service (IGS)-achievements, prospects and challenges[J]. Advances in Space Research, 2017, 59(7): 1671-1697. DOI:10.1016/j.asr.2017.01.011 |
| [24] |
焦文海, 丁群, 李建文, 等. GNSS开放服务的监测评估[J]. 中国科学:物理学力学天文学, 2011, 41(5): 521-527. JIAO Wenhai, DING Qun, LI Jianwen, et al. Monitoring and assessment of GNSS open services[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2011, 41(5): 521-527. |
| [25] |
DOW J M, NEILAN R E, RIZOS C. The International GNSS Service in a changing landscape of global navigation satellite systems[J]. Journal of Geodesy, 2009, 83(7): 689-689. DOI:10.1007/s00190-009-0315-4 |





