2. 西南石油大学地球科学与技术学院, 四川 成都 610500;
3. 西南交通大学地球科学与环境工程学院, 四川 成都 611756
2. School of Geoscience and Technology, Southwest Petroleum University, Chengdu 610500, China;
3. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China
目前成分分析广泛应用于地球时变重力场的科学研究中。应用最多的是主成分分析(principal component analysis,PCA)。它利用加入二阶统计矩的经验正交函数,从基于像元的观测序列中提取出不相关的主成分(principal component,PC)[1],进而得到各PC对应的空间域长期趋势与时间序列。
鉴于PCA因低阶统计矩导致提取成分仅互不相关,文献[2]最早提出了独立成分分析(independent component analysis,ICA)的基本思想,文献[3]运用信息论严格定义了ICA,且证明了对非高斯源信号的分解具备唯一性。在此基础上,文献[4]提出了基于四阶统计矩(kurtosis, 峭度)的特征矩阵的联合近似对角化(joint approximation diagonalization of eigen-matrices,JADE)算法,实现了在高阶统计矩的条件下各提取成分间相互独立,即得到了独立成分(independent component,IC)。文献[5]通过借鉴信息熵的基本原理指出,衡量数据非高斯性的负熵(negentropy),较峭度更为稳健,并建立了基于负熵的梯度算法和快速不动点算法(即FastICA算法),与此同时,文献[6]也将峭度结合到上述算法中,为各学科的深入研究提供了更多可靠的实现算法。
重力恢复与气候实验(gravity recovery and climate experiment,GRACE)卫星任务是美国国家航空航天局(National Aeronautics and Space Administration,NASA)和德国航空航天中心(DeutschesZentrum für Luft- und Raumfahrt,DLR)联合研发[7],于2002年3月发射,2018年10月终止。GRACE卫星重力任务最主要的特点是通过测定两颗卫星之间的距离及其变化率,测定地球静态及时变重力场。
运用ICA对地球时变重力场进行分析时,文献[8]率先指出,其提取的独立成分有效改善了沿经线方向的条带误差及不切实际的水文滤波;文献[9]认为,ICA可以更好地识别小空间尺度下的分量信号。具体到区域上,文献[10]运用ICA成功将澳大利亚陆地泄漏到周边海洋的噪声分离出来;文献[11]运用ICA提取出的前6个独立成分,能够解释印度84%~99%的水储量变化信息,指出夏季风降水是其变化的主要原因,同时给出了各独立成分间的相位差;文献[12]结合气象指数对云贵高原的研究表明,该区域水储量变化的独立成分受SOI的影响较大,并认为2010年的区域性干旱可能与厄尔尼诺现象有着直接关系。
具体到青藏高原时变重力场的研究中,文献[13]通过ICA分析并结合水隙全球水文模型(water GAP global hydrology model,WGHM)表明,青藏高原西南地区的水资源储量近十年来呈下降趋势,这可能是气候变暖所致,加速了该地区冰川和雪的融化;文献[14]运用ICA成功分离出水储量变化和沿经线方向条带误差,并认为沿30°N方向的两侧,青藏高原的水储量变化截然不同,呈现出“北增南减”的变化趋势。
上述基于ICA的区域时变重力场的分析中,均采用峭度去衡量源信号的非高斯性,文献[15]进一步指出,负熵较峭度在衡量源信号的非高斯性上更为稳健,且FastICA算法的收敛更为稳定。此外,关于青藏高原的研究中,并未以成分作为出发点去探寻水储量变化与其他可能因素之间的联系。因此,本文采用基于负熵的FastICA算法,提取青藏高原区域水储量变化及降水的独立成分,并探讨成分之间的联系。
1 数据 1.1 GRACE数据运用GRACE卫星测定的区域时变重力场进行进一步分析时,通常采用Level-2数据产品。本文采用2002年4月至2015年7月已公布的CSR RL06月重力场数据,其中球谐位系数的C(S)项为60阶(次),C20项系数由SLR的估计结果进行替换[16]。文献[17]通过球谐位系数C和S的变化值ΔClm与ΔSlm,解算出地球等效水高(equivalent water height,EWH)的计算公式,即
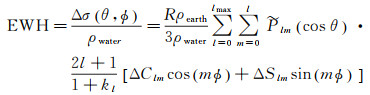 (1)
(1)
式中,R为地球平均半径,通常取6371 km;ρearth为地球的平均密度,值约为5.517×103 kg/m3;ρwater为水的密度,值为1.0×103 kg/m3;θ(ϕ)为地心余纬(经度);Δσ (θ, ϕ)为在像元(θ, ϕ)处的地球质量异常;l(m)为时变地球重力场模型的球谐位系数对应的阶(次);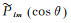
由式(1)可知,空间分辨率由像元(θ, ϕ)的大小决定。为了使得图像细节的呈现上更为清晰,因此本文在对EWH进行计算时均采用0.25°×0.25°的空间分辨率。此外,地心项改正采用文献[18]的计算结果;削弱沿经线方向条带误差的方法沿用了文献[19]的处理方式。文献[13]进一步指出,还需扣除大气、海洋、潮汐、冰川等因素影响,故除模型误差与计算误差之外,以EWH表示的上述模型在陆地区域主要反映了水储量变化及其他客观因素的时空变化情况。此外,为尽可能兼顾时变重力场中有效信号最大化和高阶球谐位系数的噪声影响最小化这一问题,对上述计算得到的EWH进行300 km的高斯滤波。
1.2 TRMM数据热带雨量测量任务(tropical rainfall measurement mission,TRMM)卫星项目是由NASA和日本原国家宇宙开发事业团(National Space Development Agency,NASDA)联合研制[20],该项目旨在从卫星层面监测全球南北纬50°区域范围内的每小时降水情况。本文采用已整理成每月累计的降水量的月度数据产品“3B43”,其空间分辨率和时间尺度与GRACE保持一致。
同时,文献[21]的研究表明,将格网数据球谐展开到一定阶次,并进行高斯滤波,可以在一定程度上减轻误差,从而更好地凸显有效信号。因此,笔者沿用上述有关GRACE数据的阶次项信息,并运用同样的数据处理方式和高斯滤波半径对TRMM数据进行处理。
2 基于负熵的FastICA算法简介ICA是一种基于非高斯源信号并能够实现盲源分离的信号分解方法[22],其得到的各提取成分是统计独立的。FastICA是ICA的一种常见算法,其实质是将n维列向量α作中心化以及白化处理后得到的列向量δ的基础上,通过迭代单位列向量ϑi; j,使得对应的投影ϑi; jTδ的非高斯性趋于稳定,并使之极大化。文献[23]提出,可以采用如下的负熵近似公式来衡量ϑi; jTδ的非高斯性
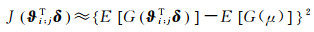 (2)
(2)
由式(2)可知,负熵总是非负的,当且仅当源信号服从高斯分布时,负熵为0[15],源信号负熵越大,非高斯性则越强。μ是与ϑi; jTδ具有相同方差的高斯随机变量所构成的列向量;G(·)为非线性函数,取如下的G(·),使其更好地具备稳健性[24]
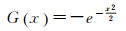 (3)
(3)
在迭代之前,须初始化列向量ϑi; j。文献[15]同时指出,可以将ϑi; j运用到基于负熵的FastICA的迭代公式中
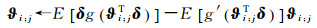 (4)
(4)
式中,g(·)和g′(·)分别为非线性函数G(·)的一阶和二阶导数。
令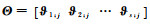
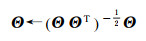 (5)
(5)
重复式(4)和式(5),当上述ϑi; j收敛时,便得到基于二维矩阵Γ提取的IC,其中每个IC所对应的特征值λi是唯一确定的。因此,需借助方差贡献率ηi来确定所需IC,有
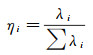 (6)
(6)
将ηi按照从大到小的顺序排列,根据累计ηi的大小确定出所需IC的个数s。
由于经过连续观测的水储量变化是基于时间尺度t(t≥1)和二维空间域m×n的三维矩阵Ψm×n×t,为便于数据处理,需在分析之前降维至二维矩阵Γj×t(j=m×n)。经FastICA算法计算后,再将已提取出的第i个IC重新还原到上述二维空间域中,记为矩阵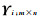
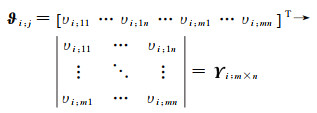 (7)
(7)
该矩阵描述了在二维空间域m×n中第i个IC所对应的年均水储量的变化情况,也即该区域水储量变化的长期趋势。同时,由矩阵Θ可计算出对应的时间序列的集合Ζ,显然矩阵Ζ是s×t维的,有
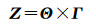 (8)
(8)
令
文献[25]证明了非高斯的区域时变水储量经ICA分解后,空间模态在短期内具有一定的稳定性。
3 青藏高原水储量变化的结果与分析利用FastICA算法对GRACE得到的青藏高原区域水储量变化进行分析前,须先按式(2)计算出负熵。计算结果指出,该区域水储量变化的负熵值为3.353,因此青藏高原的水储量变化是符合非高斯分布的。
上述水储量变化经白化后通过式(4)和式(5)反复迭代,并计算出所有的IC及其特征值,再通过式(6)将各IC对应的方差贡献率由大到小的顺序依次排列,得到水储量变化的前10个IC(记为ICs-GRACE)的方差贡献率见表 1。
| ICs-GRACE | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 方差贡献率/(%) | 69.388 | 12.761 | 9.816 | 2.026 | 1.049 | 0.796 | 0.736 | 0.617 | 0.446 | 0.327 |
由表 1可知,前4个IC的方差贡献率较大,且IC1的方差贡献率远大于其余IC,这意味着这些IC是青藏高原区域水储量变化的主要影响因素;自第5个IC起,方差贡献率偏小且趋于稳定,可不考虑。因此,将累计方差贡献率设定为94%时,能够在很大程度上提取到所需的成分信息,相应可从中提取出前4个方差贡献率较大的IC。青藏高原水储量变化所对应的前4个ICs-GRACE的空间域长期趋势与时间序列如图 1和图 2所示。

|
| 图 1 青藏高原前4个ICs-GRACE所对应的空间域长期趋势 Fig. 1 Long-term trend of spatial domain corresponding to the first 4 ICs-GRACE on the Qinghai-Tibet Plateau |
|
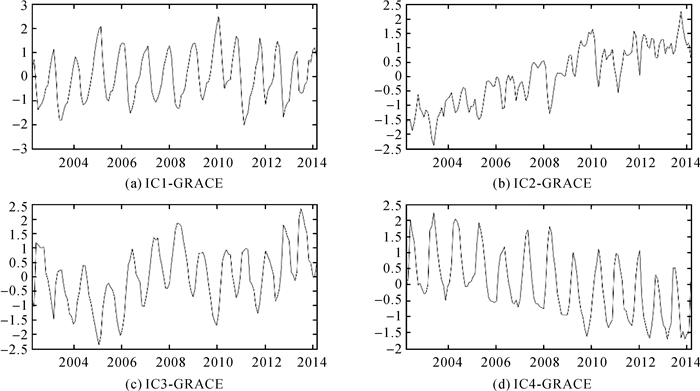
| 图 2 青藏高原前4个ICs-GRACE所对应的时间序列 Fig. 2 Time series corresponding to the first 4 ICs-GRACE on the Qinghai-Tibet Plateau |
图 1中颜色偏红的地区表示该空间域的年均水储量变化对应的EWH增加,而颜色偏蓝则刚好相反,EWH的单位为mm;图 2的时间序列已经过标准化处理,具备明显的年际变化和季节变化;各IC的空间域变化与时间序列的乘积则表示该空间域水储量变化的具体值。为研究区域范围线
总体而言,上述IC所代表的区域特征信号不完全相同,且GRACE监测得到的水储量变化存在明显的季节特征和年际特征。IC1-GRACE的时间序列较为平稳且振幅较强。从特征信号来看,该成分主要表现了青海中东部和西藏西部的EWH变化特征,其中青海中东部的EWH年变化为正向;西藏西部主要受区域外克什米尔地区的特征信号影响,年变化为正向。而西藏中东部的水储量变化趋势较上述两地偏弱且恰好反相,其年变化为负向。
IC2-GRACE的时间序列则出现了逐年递增的新特点,但年周期性和季节特征较差。该成分的特征信号主要反映了帕米尔高原的水储量变化,其年变化为负向;其他特征信号中,西藏中东部和川西高原出现了正向的水储量变化,而青海中西部则刚好相反,其年变化为负向。
IC3-GRACE的方差贡献率较IC2-GRACE接近,且年周期性好于后者。但该成分除青海中部之外,在区域内无明显特征信号,仅在祁连山脉处有区域外较强特征信号向区域内泄漏,其年变化为正向,以及四川盆地的特征信号向本区域内泄漏,其年变化为负向。
IC4-GRACE的时间序列与IC2-GRACE刚好相反,呈现出逐年递减的特点,且年周期性较好。该成分在区域内主要反映了青海地区尤其是阿尔金山脉-昆仑山脉广大区域在内的特征信号。该特征信号的强度较大,其EWH的年变化均呈现正向。
总之,由青藏高原区域水储量变化提取的各IC中,除IC3-GRACE外,均出现了青海与西藏在EWH中变化相反的情形。以方差贡献率最大的IC1-GRACE为例,青海中东部呈现出EWH的年均正向变化,而西藏中东部呈负向变化,这与国内外学者研究的青藏高原中北部与南部重力呈现反向变化的结论一致:文献[26]得到了青藏高原南部即西藏中东部冰川融化所导致的区域质量减少的特征信号,约为-35.0±5.8 Gt/a;文献[27—28]分别计算出青藏高原中北部即青海区域质量增加的特征信号,约为7±7 Gt/a。
4 与TRMM模型的比较 4.1 TRMM模型的分析结果气象学指出,大气具备复杂的非线性混沌特性[29],在大气动力学上(表征为气候序列上)是非平稳的[30],因此降水过程受大气物理的影响,从而具备非高斯性和非平稳性。经计算表明,青藏高原区域TRMM数据的负熵值为5.327,其非高斯性较水储量变化更强。于是本文同样采用FastICA算法对TRMM模型进行分析,并按照方差贡献率从大到小顺序排列出前10个IC(记为ICs-TRMM),如表 2所示。
| ICs-TRMM | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 方差贡献率/(%) | 73.400 | 8.254 | 3.126 | 1.431 | 1.014 | 0.943 | 0.844 | 0.643 | 0.589 | 0.515 |
由表 2可知,青藏高原IC1-TRMM的方差贡献率远大于其他IC,显示出该成分在区域中的主导作用。于是本文参照青藏高原水储量变化的成分提取个数,得到前4个IC-TRMM的累计方差贡献率为86.211%,因而也能够提取出所需信息。上述IC的空间域长期趋势与时间序列如图 3和图 4所示。
|
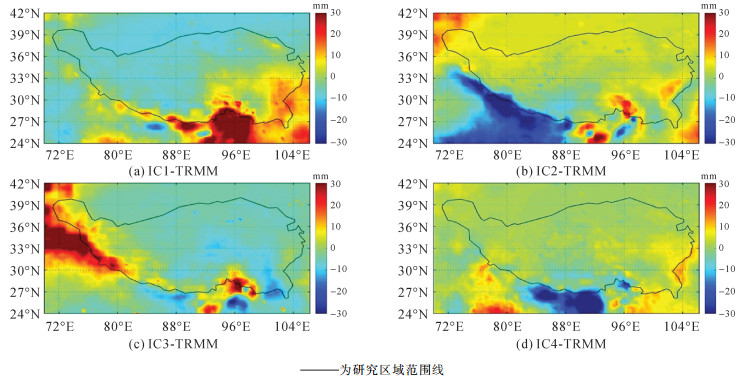
| 图 3 青藏高原前4个ICs-TRMM所对应的空间域长期趋势 Fig. 3 Long-term trend of spatial domain corresponding to the first 4 ICs-TRMMs on the Qinghai-Tibet Plateau |
|
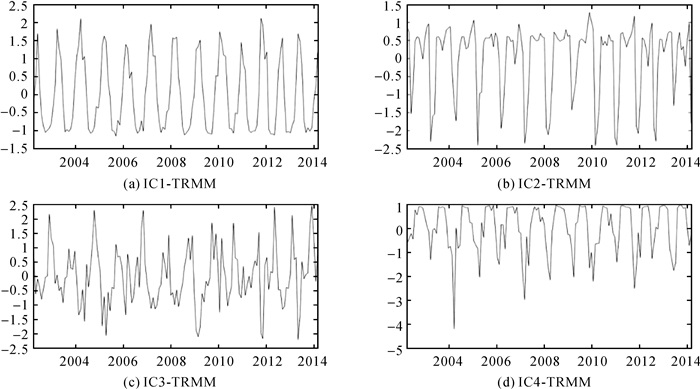
| 图 4 青藏高原前4个ICs-TRMM所对应的时间序列 Fig. 4 Time series corresponding to the first 4 ICs-TRMM on the Qinghai-Tibet Plateau |
除IC3-TRMM的年周期性与季节特征较差之外,其余IC的年周期性均较好,这点与GRACE一致。但TRMM也有其自身特点,由于降水主要受气候的影响,以IC1-TRMM为例,西藏中东部和川西高原的特征信号明显受印度洋季风带来的降水影响,从而导致长期趋势出现增长,而青海大部、西藏西部及帕米尔高原受高原大陆性气候的影响,降水成分并不显著。
4.2 与水储量变化的对比分析由于水储量变化与TRMM模型的时间序列存在着一定的相位差,接下来将运用相空间重构中的坐标延迟重构法对上述时间序列进行相位重建[31],即固定TRMM模型的时间序列的同时,通过月度相位前移的形式,分月份重建水储量变化的时间序列(记为ICs, Δt-GRACE),并计算出相关系数,以此得出青藏高原区域内水储量成分与降水成分之间的时间延迟关系(表 3),并根据两者间空间域特征信号的差异分析出可能的区域水储量变化原因。
| 月份前移量Δt | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| IC1相关系数 | 0.264 | -0.225 | -0.585 | -0.726 | -0.656 | -0.410 | -0.062 | 0.328 | 0.643 | 0.736 | 0.606 | 0.282 |
| IC2相关系数 | 0.198 | 0.326 | 0.186 | -0.060 | -0.169 | -0.134 | -0.067 | -0.058 | -0.090 | -0.097 | -0.040 | 0.058 |
| IC3相关系数 | -0.223 | -0.467 | -0.485 | -0.357 | -0.114 | 0.156 | 0.342 | 0.411 | 0.374 | 0.226 | 0.063 | -0.166 |
| IC4相关系数 | -0.374 | -0.608 | -0.665 | -0.506 | -0.191 | 0.135 | 0.396 | 0.550 | 0.534 | 0.363 | 0.090 | -0.232 |
由表 3可知,ICs-TRMM、ICs-GRACE相对应的时间序列均体现出不同程度的相关性,于是,将上述IC与最相关月份的ICs, Δt-GRACE一并进行对比,如图 5所示。
|
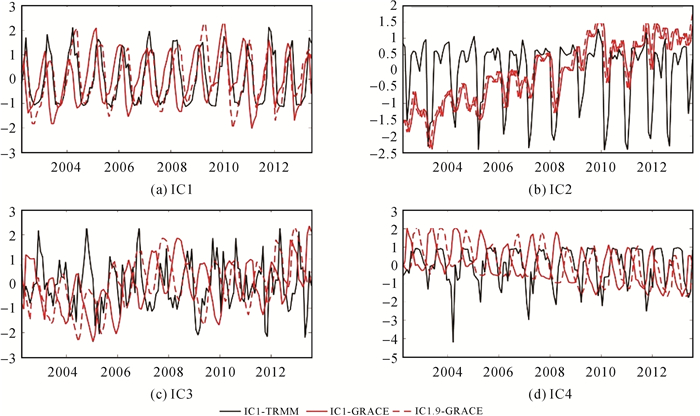
| 图 5 ICs-TRMM、ICs-GRACE与ICs, Δt-GRACE时间序列的结果比较 Fig. 5 Comparison of ICs-TRMM, ICs-GRACE and ICs, Δt-GRACE time series |
由于IC1-GRACE和IC1-TRMM的方差贡献率在各自对应的IC中都是最大的,因此,本文着重讨论上述两个IC1之间的延迟关系。同样由表 3可知,降水成分IC1-TRMM的时间序列时隔7个月出现与水储量成分IC1-GRACE的正相关关系,也即两者的相位差为7个月。事实上,由于所选取TRMM和GRACE的前4个IC的累计方差贡献率分别为86.211%和93.991%,均能代表各自所有的提取信息,本文将上述IC赋以各自的方差贡献率权重,加权得到的相应成分的相位差也为7个月。而文献[32]得出的青海地区降水与水储量变化的相位差为6个月,本文与文献[32]的研究结果基本一致。出现细微差异可能原因有:一是后者采用的降水数据是基于观测站的实测数据,而本文研究中的降水数据是依赖于TRMM卫星的观测数据,数据源的差异,导致结果存在细微差异。二是降水量与降水成分各自所代表的物理意义不同。文献[33]通过季节位移模型表明,上述区域中水储量变化的季节性特征,其主要原因在于夏季风导致的降水影响,证实了IC1-TRMM主要代表的是西藏因季风气候所导致的空间域特征信号。而文献[32]只有实测的站点降水量情况,无法区分出是因何种原因造成的,只能简单地解释为只依赖于季节性冻土的冻融造成的降水与水储量变化反相。三是青藏高原区域水储量成分与降水成分的相位差还存在着小区域内因季节性冻土、冰川等固态水通过升华作用进入大气,再以降水的形式重新反馈到小区域内的可能性[34]。
再从IC1-GRACE和IC1-TRMM的特征信号来看,青海中部水储量成分的长期趋势较降水成分强,其原因可能在于除降水本身带来的水储量变化增量外,在全球变暖的大背景下,冰川与季节性冻土的年消融率增强导致地表径流增强[35],且该区域属于内流区,地表径流带来的水储量变化增量最终转化成湖泊或者地下水的水储量变化增量,从而导致该区域水储量变化的年际特征强于降水。同时注意到西藏中东部水储量变化的年际特征与降水成分相反,其原因可能在于该区域属于外流区,通过地表径流流出该区域的水储量变化超过了以季风降水的形式带来的变化增量,也超过了因季节性冻土和冰川融化所带来的水储量变化增量,从而造成西藏中东部的水储量变化的年际特征呈现出负向。西藏西部的水储量变化情况与青海中部类似。
进一步对比图 1和图 3还可以发现,水储量成分与降水成分的空间域存在着不一致的情况,这说明还可能存在其他的非水文影响因素。文献[36]从大陆动力学角度指出,青藏高原受板块运动影响,存在着多条缝合带,且缝合带附近的重力存在异常,而班公湖-怒江缝合带是该区域内最主要的重力高异常带;文献[37]进一步表明,青藏高原以班公湖-怒江缝合带附近为界,该缝合带以北即青海地区与以南即西藏地区的莫霍面存在着明显的深度错断,指出其原因可能是该缝合带是印度地壳向亚欧板块下地壳挤压时的前沿区域,使得以该缝合带为界的南北区域的板块质量及其重力场出现明显差异。以西藏中东部为例,由于该区域位于班公湖-怒江缝合带以南,因此同时受亚欧板块与印度板块的叠加影响,文献[38—39]指出该区域水储量变化为负的特征信号归因于区域外印度北部的地下水超采以及喜马拉雅山脉的冰川消融,因此除降水外,还可能存在着因板块构造不同所导致的水储量变化差异。
此外,自2013年起,IC1-GRACE的时间序列的年周期性出现了畸变,这其中的原因可能在于此时GRACE卫星轨道高度出现下降,其得到的水储量变化出现失真,从而导致经ICA提取之后,成分所对应的时间序列年周期性失稳。
5 结论近几十年来,由于人类活动加剧了对气候变化的影响,进而导致青藏高原的水储量也出现相应变化。本文采用基于负熵的FastICA算法,由GRACE得到的区域水储量变化与TRMM降水模型的变化中分离出各个相互独立的成分,并提取出相应的时空特征,探究了青藏高原水储量成分与降水成分之间的联系:由时间序列可知,青藏高原的降水成分与水储量成分间均存在不同程度的相位差,其中方差贡献率最大的IC1-TRMM与IC1-GRACE存在着7个月的相位差,显示除冻土在该区域水储量变化的延迟机制起决定性作用之外,还存在着小区域内因局部气候的水交换造成的降水与水储量变化之间的进一步延迟。结合特征信号来看,青海中部受大陆性气候影响,降水无显著增加,但水储量变化的年增幅远强于降水,说明在全球气候变暖的大背景下,由于冰川、季节性冻土等固态水的消融,加上该区域无外流河,是典型的内流区,使得地下水出现了增长,进而导致水储量变化为正。而西藏中东部处在长江、澜沧江、怒江等流域中,属于典型的外流区,虽有季风气候带来的强劲降水,但固态水的加速消融最终转化为区域内的地表径流流向区域外的增量,进而造成该区域的水储量变化呈现出负的特征信号。此外,由于青藏高原内部的板块构造不同,导致西藏中东部的水储量变化因区域外地下水超采泄漏到区域内,从而导致以班公湖-怒江缝合带为界的南北区域的水储量变化也出现明显的差异性。
ICA提取相互独立的信号成分仅需满足各成分间相互独立且符合非高斯分布的先决条件,同时FastICA算法的收敛较梯度算法快,且作为衡量非高斯性的负熵较传统的峭度,其稳健性更好。因此该方法在GRACE卫星反演的水储量变化与气象数据的大尺度范围内的分析中具有很好的应用前景。
致谢: 感谢CSR提供的GRACE RL06时变重力场模型数据和TRMM提供的降水数据。
| [1] |
FOROOTAN E, KUSCHE J. Separation of global time-variable gravity signals into maximally independent components[J]. Journal of Geodesy, 2012, 86(7): 477-497. DOI:10.1007/s00190-011-0532-5 |
| [2] |
HERAULT J, JUTTEN C. Space or time adaptive signal processing by neural network models[C]//Proceedings of American Institute of Physics AIP Conference Melville: AIP Publishing, 1986, 151: 206-211.
|
| [3] |
COMON P. Independent component analysis, a new concept?[J]. Signal Processing, 1994, 36(3): 287-314. DOI:10.1016/0165-1684(94)90029-9 |
| [4] |
CARDOSO J F. Fourth-order cumulant structure forcing: application to blind array processing[C]//Proceedings of the 6th IEEE Signal Processing Workshop on Statistical Signal and Array Processing. Victoria, BC, Canada: IEEE, 1992: 136-139.
|
| [5] |
HYVÄRINEN A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634. DOI:10.1109/72.761722 |
| [6] |
HYVÄRINEN A, OJA E. Independent component analysis:algorithms and applications[J]. Neural Networks, 2000, 13(4-5): 411-430. DOI:10.1016/S0893-6080(00)00026-5 |
| [7] |
宁津生, 王正涛. 测绘学科发展综述[J]. 测绘科学, 2006, 31(1): 9-16. NING Jinsheng, WANG Zhengtao. A summary of the newest progress of Surveying and Mapping[J]. Science of Surveying and Mapping, 2006, 31(1): 9-16. |
| [8] |
FRAPPART F, RAMILLIEN G, MAISONGRANDE P, et al. Denoising satellite gravity signals by independent component analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 421-425. DOI:10.1109/LGRS.2009.2037837 |
| [9] |
MIDDLETON M A, WHITFIELD P H, ALLEN D M, et al. Independent component analysis of local-scale temporal variability in sediment-water interface temperature[J]. Water Resources Research, 2015, 51(12): 9679-9695. DOI:10.1002/2015WR017302 |
| [10] |
FOROOTAN E, AWANGE J L, KUSCHE J, et al. Independent patterns of water mass anomalies over Australia from satellite data and models[J]. Remote Sensing of Environment, 2012, 124: 427-443. DOI:10.1016/j.rse.2012.05.023 |
| [11] |
BANERJEE C, KUMAR D N. Analyzing large-scale hydrologic processes using grace and hydrometeorological datasets[J]. Water Resources Management, 2018, 32(13): 4409-4423. DOI:10.1007/s11269-018-2070-x |
| [12] |
王陈燕, 万祥禹. 中国西南及中南半岛陆地水变化的独立成分分析[J]. 测绘与空间地理信息, 2019, 42(6): 43-46. WANG Chengyan, WAN Xiangyu. Independent component analysis of terrestrial water over southwest China and Indochina Peninsula[J]. Geomatics & Spatial Information Technology, 2019, 42(6): 43-46. |
| [13] |
文汉江, 黄振威, 王友雷, 等. 青藏高原及其周边地区水储量变化的独立成分分析[J]. 测绘学报, 2016, 45(1): 9-15. WEN Hanjiang, HUANG Zhenwei, WANG Youlei, et al. Independent component analysis of water storage changes interpretation over Tibetan plateau and its surrounding areas[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 9-15. DOI:10.11947/j.AGCS.2016.20140447 |
| [14] |
LIU Xin, ZHAO Ning, GUO Jinyun, et al. Equivalent water height changes over Qinghai-Tibet Plateau determined from GRACE with an independent component analysis approach[J]. Arabian Journal of Geosciences, 2020, 13(4): 179. DOI:10.1007/s12517-020-5203-5 |
| [15] |
HYVÄRINEN A, KARHUNEN J, OJA E. Independent component analysis[M]. New York: John Wiley & Sons, 2001: 134-135, 185-192.
|
| [16] |
CHENG Minkang, TAPLEY B D. Variations in the Earth's oblateness during the past 28 years[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B9): B09402. |
| [17] |
WAHR J, MOLENAAR M, BRYAN F. Time variability of the Earth's gravity field:Hydrological and oceanic effects and their possible detection using GRACE[J]. Journal of Geophysical Research, 1998, 103(B12): 30205-30229. DOI:10.1029/98JB02844 |
| [18] |
SWENSON S, CHAMBERS D, WAHR J. Estimating geocenter variations from a combination of GRACE and ocean model output[J]. Journal of Geophysical Research, 2008, 113(B8): B08410. |
| [19] |
SWENSON S, WAHR J. Post-processing removal of correlated errors in GRACE data[J]. Geophysical Research Letters, 2006, 33(8): L08402. |
| [20] |
AWANGE J L, GEBREMICHAEL M, FOROOTAN E, et al. Characterization of Ethiopian mega hydrogeological regimes using GRACE, TRMM and GLDAS Datasets[J]. Advances in Water Resources, 2014, 74: 64-78. DOI:10.1016/j.advwatres.2014.07.012 |
| [21] |
SCANLON B R, LONGUEVERGNE L, LONG D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA[J]. Water Resources Research, 2012, 48(4): W04520. |
| [22] |
BOERGENS E, RANGELOVA E, SIDERIS M G, et al. Assessment of the capabilities of the temporal and spatiotemporal ICA method for geophysical signal separation in GRACE data[J]. Journal of Geophysical Research, 2014, 119(5): 4429-4447. |
| [23] |
HYVÄRINEN A. New approximations of differential entropy for independent component analysis and projection pursuit[C]//JORDAN M I, KEARNS M J, SOLLA S A. Proceedings of Advances in Neural Information. Cambridge: MIT Press, 1998, 151: 273-279.
|
| [24] |
HYVÄRINEN A, OJA E. Independent component analysis:algorithms and applications[J]. Neural Networks, 2000, 13(4-5): 411-430. DOI:10.1016/S0893-6080(00)00026-5 |
| [25] |
FOROOTAN E, KUSCHE J. Separation of deterministic signals using independent component analysis (ICA)[J]. Studia Geophysica Et Geodaetica, 2013, 57(1): 17-26. DOI:10.1007/s11200-012-0718-1 |
| [26] |
YI Shuang, SUN Wenke. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models[J]. Journal of Geophysical Research, 2014, 119(3): 2504-2517. |
| [27] |
JACOB T, WAHR J, PFEFFER W T, et al. Recent contributions of glaciers and ice caps to sea level rise[J]. Nature, 2012, 482(7386): 514-518. DOI:10.1038/nature10847 |
| [28] |
ZHANG Guoqing, YAO Tandong, XIE Hongjie, et al. Increased mass over the Tibetan Plateau:From lakes or glaciers?[J]. Geophysical Research Letters, 2013, 40(10): 2125-2130. DOI:10.1002/grl.50462 |
| [29] |
LORENZ E N. Deterministic nonperiodic flow[J]. Journal of the Atmospheric Sciences, 1963, 20(2): 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [30] |
杨培才, 周秀骥. 气候系统的非平稳行为和预测理论[J]. 气象学报, 2005, 63(5): 556-570. YANG Peicai, ZHOU Xiuji. On nonstationary behaviors and prediction theory of climate systems[J]. Acta Meteorologica Sinica, 2005, 63(5): 556-570. |
| [31] |
PACKARD N H, CRUTCHFIELD J P, FARMER J D, et al. Geometry from a time series[J]. Physical Review Letters, 1980, 45(9): 712-716. DOI:10.1103/PhysRevLett.45.712 |
| [32] |
冯伟.区域陆地水与海平面变化的卫星重力监测研究[D].武汉: 中国科学院大学, 2013: 43-44. FENG Wei. Regional terrestrial water storage and sea level variations inferred from satellite gravimetry[D]. Wuhan: University of Chinese Academy of Sciences, 2013: 43-44. |
| [33] |
ZOU Rong, WANG Qi, FREYMUELLER J T, et al. Seasonal hydrological loading in southern tibet detected by joint analysis of GPS and GRACE[J]. Sensors, 2015, 15(12): 30525-30538. DOI:10.3390/s151229815 |
| [34] |
LI Ying, SU Fengge, CHEN Deliang, et al. Atmospheric water transport to the Endorheic Tibetan Plateau and its effect on the hydrological status in the region[J]. Journal of Geophysical Research:Atmospheres, 2019, 124(23): 12864-12881. DOI:10.1029/2019JD031297 |
| [35] |
王磊, 李秀萍, 周璟, 等. 青藏高原水文模拟的现状及未来[J]. 地球科学进展, 2014, 29(6): 674-682. WANG Lei, LI Xiuping, ZHOU Jing, et al. Hydrological modelling over the Tibetan Plateau:Current status and perspective[J]. Advances in Earth Science, 2014, 29(6): 674-682. |
| [36] |
张燕, 程顺有, 赵炳坤, 等. 青藏高原构造结构特点:新重力异常成果的启示[J]. 地球物理学报, 2013, 56(4): 1369-1380. ZHANG Yan, CHENG Shunyou, ZHAO Bingkun, et al. The feature of tectonics in the Tibet Plateau from new regional gravity signals[J]. China Journal of Geophysics, 2013, 56(4): 1369-1380. |
| [37] |
刘杰, 方剑, 李红蕾, 等. 青藏高原GRACE卫星重力长期变化[J]. 地球物理学报, 2015, 58(10): 3496-3506. LIU Jie, FANG Jian, LI Honglei, et al. Secular variation of gravity anomalies within the Tibetan Plateau derived from GRACE data[J]. Chinese Journal of Geophysics, 2015, 58(10): 3496-3506. |
| [38] |
TIWARI V M, WAHR J, SWENSON S. Dwindling groundwater resources in northern India, from satellite gravity observations[J]. Geophysical Research Letters, 2009, 36(18): L18401. DOI:10.1029/2009GL039401 |
| [39] |
MATSUO K, HEKI K. Time-variable ice loss in Asian high mountains from satellite gravimetry[J]. Earth and Planetary Science Letters, 2010, 290(1-2): 30-36. DOI:10.1016/j.epsl.2009.11.053 |



