2. 中国科学院空天信息创新研究院, 北京 100830;
3. 武汉大学资源与环境科学学院, 湖北 武汉 430079;
4. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. The Aerospace Information Research Institute, Chinese Academic of Sciences, Beijing 100830, China;
3. School of Resources and Environment Science, Wuhan University, Wuhan 430079, China;
4. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
矢量图形之间的形状相似性计算是矢量图形匹配、分类和查询的基础[1],已广泛应用于GIS领域,如基于图形相似性的同名实体匹配[2]、基于模板的居民地化简[3]和基于图形形状的空间查询[4-5]等。建筑物是矢量地图的基础地理要素之一,其形状相似性计算对建筑物图形数据处理具有重要意义。
图形形状相似性计算有赖于对图形形状的定量描述,如基于图形轮廓,可以用傅里叶级数拟合图形轮廓[6-7]、用曲率尺度空间表达图形轮廓的曲率变化[8]、用序列编码图形轮廓的局部特征[1, 9]等;基于图形区域,有基于矩的形状描述方法[10],也可以描述图形的面积、延展度[11]等;基于图形结构,可以用骨架线作为图形的结构化表达[12]。其中,用序列编码图形轮廓的局部特征,能较好地分析图形的轮廓形态;同时,匹配序列中基础元素度量图形间形状相似性较为形象直观,是矢量图形形状相似性计算常采用的方法[1]。用序列编码图形需确定编码的基础元素,并描述基础元素的特征。如基于特征点编码图形,可以描述特征点的角度、相对于邻近点的可变形势、邻近点相对于该点的切线距离函数等[13-15];基于边编码图形,可以描述边的方向、长度等[16];基于弧段编码图形,可以描述弧段的弓高弦长比、弧长弦长比等[17]。但是,建筑物图形通常相对简单,节点较少,基于特征点或边编码的图形相似结果离散程度高、区分度小。另外,建筑物多具有直角表达的形态特征,即几何转折明显且无连续弯曲,不适宜用弧段编码建筑物图形。
DNA序列是生物信息学研究的重要对象,有成熟的计算DNA序列间相似性的方法,如经典的NW算法和SW算法[18]。因此,本文充分考虑建筑物图形多直角表达的形态特征,将建筑物图形编码成类似DNA的序列,利用NW算法和SW算法计算建筑物图形编码序列间相似程度。
1 DNA序列比对的NW算法和SW算法DNA序列比对是生物信息学中基因组测序的关键技术之一,通过匹配DNA序列中碱基获取不同DNA序列间相似程度[18]。其中,NW算法和SW算法是DNA序列比对时常用的两种基于动态规划原理的优化方法:NW算法旨在找到两序列在全局上的最佳匹配,可获取两序列比对的全局最大相似性(GsF);SW算法旨在找到两序列相似性最大的片段,可获取两序列比对的局部最大相似性(LsF)[18]。
首先,DNA序列比对需匹配DNA序列中碱基。依据DNA在自然界的复制规律,DNA中碱基存在匹配(match)、误匹配(mismatch)和空缺(gap)3种匹配关系[18],定义见表 1。例如,给定DNA序列Qm={A, G, C, A, C, T},Qn={A, G, T, A, T},比对序列Qm、Qn可能存在如表 1的匹配关系;其中,匹配对(A, A)、(G, G)、(A, A)、(T, T)为match关系,(C, T)为mismatch关系,(C, -)为gap关系。
| 序列 | 元素 | 匹配关系 | 说明 |
| Qm |  |
 |
match:序列中碱基相互匹配 |
| 匹配 |  |
 |
mismatch:序列中碱基相互不匹配 |
| Qn |  |
 |
gap:序列中碱基在另一序列中不存在匹配 |
然后,不同匹配关系的碱基对对于DNA序列间相似性贡献不一样,可以转化为得分。匹配对关系为match需加分,匹配对关系为mismatch或gap则需罚分,匹配碱基对(xim, xjn)的得分MScore(xsm, xtn)可依据DNA中碱基替换的频率确定[18]。
最后,基于定义的碱基对匹配关系和匹配对得分比对DNA序列Qm和Qn时,NW算法即找到匹配关系fR=Qm→Qn,使QScore=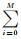
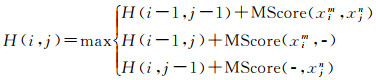 (1)
(1)
式中,xi表示序列Qm第i个位置碱基;xj表示序列Qn第j个位置碱基;“-”表示对应位置为空,即存在gap关系。
SW算法即找到匹配关系fR=Qm→Qn,使QScore=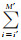
本文建筑物图形形状相似性计算过程为:首先,将建筑物图形编码成类似DNA的序列;其次,定义序列中基础元素的匹配关系与匹配对得分;最后,利用NW算法与SW算法计算相应建筑物图形编码序列间全局相似性(GsF)与局部相似性(LsF)表达对应建筑物图形间形状相似性。
2.1 建筑物图形的序列编码考虑到建筑物图形上节点和边的关联关系,可以将节点与节点关联边构成的转折作为建筑物图形序列编码的基础元素[19]。同时,邻近转折可能会构成特殊的结构,需将邻近的转折联合起来表达。其中,考虑到数据采集、存储误差可能导致的异常节点,如重复点、共线点、尖锐点等需在编码前删除[20]。
假设构成建筑物多边形的有序节点集合为AP={p1, p2, …, pn}, p1≠pn,转折Cm可以表示成点集合{pm-1, pm, pm+1}或边集合{pm-1pm, pmpm+1},pm-1, pm, pm+1∈AP。转折Cm的角度即节点pm处角度(Canglem),为边pm-1pm绕节点pm逆时针旋转至边pmpm+1的角度。依据转折Cm角度的不同,可以利用四方向或八方向编码将建筑物表示成以转折为基础元素的类似DNA的离散编码形式[20]。但是,建筑物作为人造地物,往往呈现出多直角表达的形态特征,如一些建筑物化简方法中会将接近直角一定范围内的转折作为直角处理[19]。因此,利用四方向或八方向对建筑物图形进行编码时,需考虑转折Cm角度是否为直角。本文直角定义如下:若Canglem满足条件|Canglem-90°| < α∨|Canglem-270°| < α,则Canglem为直角;其中,α=15°。依据该定义,对Ordnance Survey开源提供的制图比例尺1∶10 000的街道层次地图中765 961个建筑物图形外轮廓角度特征进行统计分析显示,其中直角占比为96.06%,呈现出明显的多直角表达形态特征(http://freegisdata.rtwilson.com/)。因此,考虑到建筑物图形多直角表达的形态特征,以转折为基础元素的建筑物图形序列编码表见表 2,则图 1(a)所示的建筑物若以转折ABC为起点进行编码,可以表示成以转折为基础元素的有序序列:32552223423,如图 1(e)所示。
| Cangle | [0°, 75°] | [75°, 105°] | [105°, 180°] | [180°, 255°] | [255°, 285°] | [285°, 360°] |
| 编码 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| 图 1 建筑物图形序列编码 Fig. 1 Building sequence coding |
同时,邻近转折可能会构成特殊结构,特别是邻近的直角转折,往往被认为具有较强的视觉含义,常作为建筑物图形数据处理的基础单元[21]。文献[22]将凹部作为建筑物化简的基础结构;文献[23]则依据邻近转折的角度差异将建筑物外轮廓划分为凸部(凹部)和阶梯状结构等。其中,凸部则可以认为是邻近的两个凸角转折构成,如图 1(b)中结构ABCD和结构EFGH;凹部可认为是邻近的两个凹角转折构成,如图 1(c)中结构CDEF;另外,邻近的凸角转折与凹角转折则会组合形成阶梯状结构,如图 1(d)中结构DEFG和结构HIJK。出于不同需要,也可以定义其他特殊结构,如连续的阶梯状结构等,这些结构都可以看成是凸部、凹部和阶梯状结构等的组合[22]。因此,考虑到建筑物图形中邻近转折可能会构成的基础结构,本文将邻近的两个转折联合起来作为基础元素对建筑物图形进行编码,可表示成Sm={Cm, Cm+1}。因此,图 1(a)所示的建筑物若以转折ABC为起点进行编码,可以表示成以邻近转折为基础元素的有序序列:S32S25S55S52S22S22S23S34S42S23(图 1(f))。对前文数据集中建筑物基础结构特征进行统计分析显示,邻近转折均为直角构成的凸部(S22)、凹部(S55)和阶梯状结构(S25和S52)占比分别为89.22%、0.57%和4.77%,是其中的主要基础结构。
2.2 基础元素匹配关系与匹配对得分 2.2.1 基础元素特征描述本文将邻近的两个转折联合起来作为基础元素对建筑物图形进行编码,即Sm={Cm, Cm+1}。其中,构成Sm的转折Cm和Cm+1因角度的凹、凸性会组合形成不同基础结构,如凹部、凸部等(图 1)。另外,需记录基础元素的几何特征,如构成Sm转折的角度、边的长度等。
(1) 类型划分。假设构成Sm的转折Cm和Cm+1角度分别为Canglem与Canglem+1(角度编码见表 2),依据上文分析,基于邻近转折角度的凹、凸性,可以将Sm划分为4种类型(SType,见表 3):凸部(DentS),邻近转折角度均为凸角,如图 1(b)中结构ABCD和结构EFGH;左阶梯结构(LStairS),邻近转折角度为凸角和凹角,如图 1(d)中结构HIJK;右阶梯结构(RStairS),邻近转折角度为凹角和凸角,如图 1(d)中结构DEFG;凹部(SnugS),邻近转折角度均为凹角,如图 1(c)中结构CDEF。
| Smm+1 | Canglem | Canglem+1 | SType |
| 1 | Canglem∈[1, 2, 3] | Canglem+1∈[1, 2, 3] | DentS |
| 2 | Canglem∈[1, 2, 3] | Canglem+1∈[4, 5, 6] | LStairS |
| 3 | Canglem∈[4, 5, 6] | Canglem+1∈[1, 2, 3] | RStairS |
| 4 | Canglem∈[4, 5, 6] | Canglem+1∈[4, 5, 6] | SnugS |
(2) 角度特征。假设构成Sm的转折Cm和Cm+1角度分别为Canglem与Canglem+1,(角度编码见表 2),Sm的角度特征记为Sanglem={Canglem, Canglem+1}。
(3) 长度特征。假设构成Sm的边pm-1pm、pmpm+1和pm+1pm+2长度分别为Lm-1、Lm和Lm+1,Sm的长度特征记为Slengthm={Lm-1, Lm, Lm+1}。
2.2.2 匹配关系与匹配对得分建筑物图形编码基础元素(Sm)存在不同类型(SType),不同类型Sm在视觉上存在明显差异;同一类型Sm在视觉上表现出一定相似性。因此,给定匹配对(S1m, S2n),其匹配关系定义如下。
(1) match:若S1m.SType=S2n.SType,则(S1m, S2n)构成match关系。
(2) mismatch:若S1m.SType≠S2n.SType,则(S1m, S2n)构成mismatch关系。
(3) gap:若(S1m=null)∨(S2n=null)为真,则(S1m, S2n)构成gap关系。
若匹配对(S1m, S2n)为match关系,匹配对得分由基础元素S1m, S2n间相似性确定。其中,若(S1m, S2n)为match关系,则S1m、S2n属于同一类型。因此,基础元素S1m和S2n的相似性由其角度特征和长度特征的相似性确定。假设S1m和S2n的角度特征分别为S1anglem={C1anglem, C1anglem+1}和S2anglen={C2anglen, C2anglen+1}(角度编码见表 2),构成基础元素对应两个转折的角度差值和能表示基础元素间角度特征差异,可以用形如x′i=(max{xi}-xi)/(max{xi}-min{xi})的极值标准化方法表达[11]。其中,构成S1m和S2n对应转折的角度最大差值和为4,最小差值和为0。为避免基础元素角度特征相似性(As)取值为0,取转折角度的最大差值和为5,因此,As的计算见式(2)
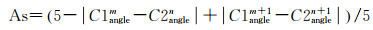 (2)
(2)
假设基础元素S1m和S2n的长度特征分别S1lengthm={L1m-1, L1m, L1m+1}和S2lengthm={L2n-1, L2n, L2n+1},基础元素的长度特征相似性(Ls)由构成基础元素对应3条边的相似性和表示,边的长度相似性可以用边长度的比值表示。因此,基础元素S1m和S2n的Ls定义见式(3)
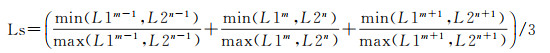 (3)
(3)
基础元素的相似性(Ss)需综合考虑基础元素的As和Ls。其中,角度和长度分别独立描述基础元素的不同侧面,相关性较弱,故Ss可以表示成As和Ls的线性组合[24]
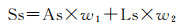 (4)
(4)
式中,w1和w2表示权重,w1+w2=1。
若匹配对(S1m, S2n)为mismatch或gap关系,均需要罚分,表示两图形对应位置在视觉感知上不相似。参考DNA序列匹配针对gap关系的罚分,需考虑gap关系的连续性,即随着gap关系的延续,可能会加强或减弱对应匹配对的相似性[18]。因此,本文针对mismatch或gap关系的罚分见式(5)
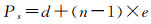 (5)
(5)
式中,d表示开启一个mismatch或gap关系的罚分;n表示延续mismatch或gap关系的个数;e表示延续一个mismatch或gap关系的罚分。
同时,不同基础元素在建筑物图形中重要性不一样,匹配对(S1m, S2n)的得分或罚分需考虑相应基础元素的重要性,如文献[25]认为,人对图形进行视觉感知时,倾向于抓住主要结构而忽略次要细节。因此,重要基础元素构成的匹配对(S1m, S2n)得分或罚分往往相对高,基础元素的重要性可以用其总长度表示。假设存在匹配对(S1m, S2n),构成基础元素S1m和S2n 3条边的总长度分别为sumL1m和sumL2n;若匹配对为gap关系,表示其中一个基础元素不存在,其总长度记为0。假设依据式(4)和式(5)计算出匹配对(S1m,S2n)的得分或罚分为Ss,则匹配对(S1m,S2n)的最终得分或罚分(MScore)计算见式(6)
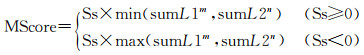 (6)
(6)
假设给定建筑物Pom和Pon,依次选择Pom和Pon中不同节点为起点编码,构成编码集合QSetm={queue1m, queue2m, …, queuepm}和QSetn={queue1n, queue2n, …, queuepn},两两配对集合QSetm和QSetn中序列可获取两建筑物图形编码序列的GsF集合GsSetm={Gs11, Gs12, …, Gsij, …, Gspq}和LsF集合LsSet={Ls11, Ls12, …, Lsij, …, Lspq},则两建筑物的GsF取max{Gs11, Gs12, …, Gsij, …, Gspq},两建筑物的LsF取max{Ls11, Ls12, …, Lsij, …, Lspq}。
建筑物间形状相似性(GLs)需综合考虑两建筑物的GsF与LsF。其中,指标GsF与LsF具有较大的相关性,且LsF≥0,GLs适宜表示成GsF与LsF的乘数组合,见式(7)[24]
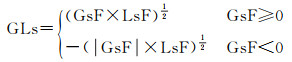 (7)
(7)
选择OSM地图中北京地区建筑物作为源数据制作检验本文方法有效性的形状数据库,源数据见图 2(a),局部区域放大见图 2(b)(下载地址为https://www.openstreetmap.org/)。选择方形(T1)、L形(T2)、T形(T3)、C形(T4)、阶梯形(T5)、十字形(T6)共6种较常见的建筑物图形作为典型建筑物[3],从源数据中选择与对应典型建筑物(T1-T6)形状相似的194个建筑物目标构成形状数据库(图 2(c)),形状数据库的统计结果见表 4。其中,形状数据库中与典型建筑物(T1-T6)形状相似的建筑物是依据多名从事地图学研究的硕士生或博士生的视觉感知试验结果投票选出的,本文形状数据库已开源,下载地址为https://data.mendeley.com/datasets/pfmf4y344h/1。
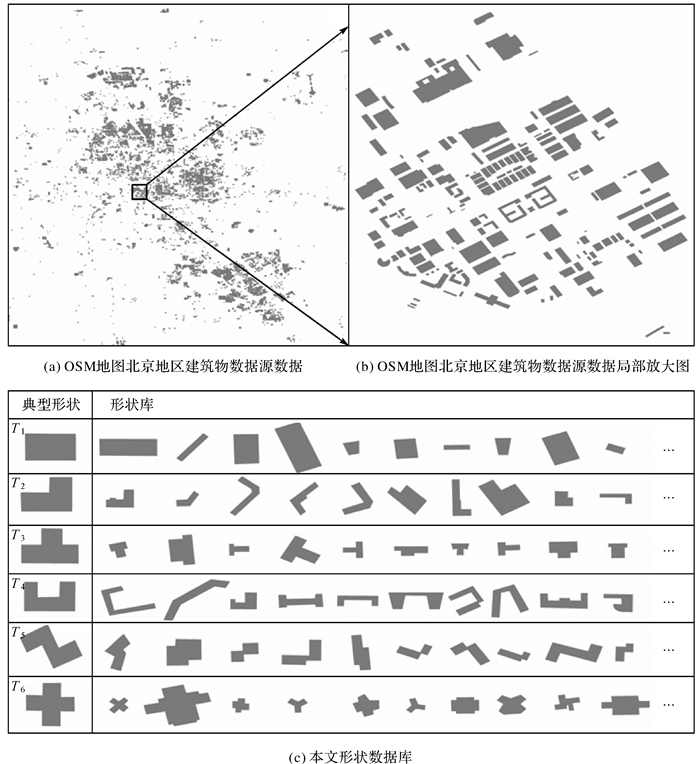
|
| 图 2 形状数据库 Fig. 2 Shape database |
| 典型形状 | 方形(T1) | L形(T2) | T形(T3) | C形(T4) | 阶梯形(T5) | 十字形(T6) | 合计 |
| 数量 | 30 | 52 | 21 | 47 | 29 | 15 | 194 |
在AE10.2基础上利用C#语言二次开发实现本文方法,试验平台为一台CPU为Intel(R) Core(TM) i5-8265U CPU @1.60 GHz、内存为8 GB、操作系统为Windows 10(64位)的计算机。试验参数设置如下:式(5)中取w1=0.8、w2=0.2;式(6)中取d=-0.8,取e=-0.5。
依据形状数据库中建筑物(Bi)与典型建筑物图形(T1-T6)的形状相似性(GLs),确定Bi最相似的典型建筑物(GLs越大表示图形间形状越相似),并与人的视觉认知进行比对,结果统计见表 5。其中,tp表示结果中与人视觉感知一致的建筑物数目,fp表示结果中不被认为是视觉感知相似的建筑物数目,fn表示结果中遗漏的与人视觉感知相似的建筑物数目。由表 5可知,依据GLs正确识别177个,错误识别17个,识别准确率为91.2%。其中,针对不同类型的典型建筑物图形,识别准确率均达到80.8%以上,且对于阶梯形(T5)和十字形(T6)两类典型建筑物,准确率均达到100%。试验结果一定程度上说明,本文方法在基于形状的建筑物图形检索与匹配上具有较好的性能。
| tp | fp | fn | 查全率=tp/(tp+fp)/(%) | 查准率=tp/(tp+fn)/(%) | |
| 方形(T1) | 29 | 1 | 1 | 96.7 | 96.7 |
| L形(T2) | 42 | 10 | 10 | 80.8 | 80.8 |
| T形(T3) | 18 | 3 | 3 | 85.7 | 85.7 |
| C形(T4) | 44 | 3 | 3 | 93.6 | 93.6 |
| 阶梯形(T5) | 29 | 0 | 0 | 100 | 100 |
| 十字形(T6) | 15 | 0 | 0 | 100 | 100 |
| 合计 | 177 | 17 | 17 | 91.2 | 91.2 |
3.2 讨论 3.2.1 方法对比
为验证本文方法的有效性,分别基于转角函数(Ts)[9]和多级弦长函数的傅里叶形状描述子(Fs)[7]计算了建筑物间形状相似性,并与本文方法进行对比,结果见表 6。其中,基于转角函数计算图形间形状相似性对于起始点的选择较为敏感,本文基于转角函数(Ts)计算建筑物间形状相似性时也参考了文献[3]的策略。不同方法的试验耗时为:基于GLs耗时为9.73 s,基于Ts耗时为3.31 s,基于Fs耗时为0.48 s。
| tp | fp | fn | 查全率=tp/(tp+fp)/(%) | 查准率=tp/(tp+fn)/(%) | ||
| 方形(T1) | 基于Ts | 28 | 2 | 2 | 93.3 | 93.3 |
| 基于Fs | 27 | 3 | 3 | 90.0 | 90.0 | |
| L形(T2) | 基于Ts | 28 | 24 | 24 | 53.8 | 53.8 |
| 基于Fs | 8 | 44 | 44 | 15.4 | 15.4 | |
| T形(T3) | 基于Ts | 12 | 9 | 9 | 57.1 | 57.1 |
| 基于Fs | 13 | 8 | 8 | 61.9 | 61.9 | |
| C形(T4) | 基于Ts | 37 | 10 | 10 | 78.7 | 78.7 |
| 基于Fs | 26 | 21 | 21 | 55.3 | 55.3 | |
| 阶梯形(T5) | 基于Ts | 4 | 25 | 25 | 13.8 | 13.8 |
| 基于Fs | 21 | 8 | 8 | 72.4 | 72.4 | |
| 十字形(T6) | 基于Ts | 7 | 8 | 8 | 46.7 | 46.7 |
| 基于Fs | 5 | 10 | 10 | 33.3 | 33.3 | |
| 合计 | 基于Ts | 116 | 78 | 78 | 59.8 | 59.8 |
| 基于Fs | 100 | 94 | 94 | 51.5 | 51.5 |
对比表 5和表 6可知,基于本文方法(GLs)耗时最大,但是其准确率也最高,均明显高于基于Ts的识别准确率(59.8%)和基于Fs的识别准确率(51.5%);基于Fs的耗时最小,但是其识别准确率(51.5%)也最低。同时,基于Ts在识别阶梯形(T5)和十字形(T6)建筑物的准确率为13.8%和46.7%;基于Fs在识别L形(T2)和十字形(T6)建筑物的准确率为15.4%和33.3%;均低于50%,准确率较低。
同时,选择3个典型建筑物图形对比分析3种不同方法,结果见表 7。对于建筑物1,基于GLs和Fs均获得了与视觉认知一致的结果,而基于Ts获得的结果与视觉认知不一致,这是因为Ts相对于GLs没有有效考虑到连续直角构成的特殊结构,这些特殊结构在识别建筑物图形时具有较明显的视觉含义[23]。对于建筑物2,基于GLs获得了与视觉认知一致的结果,而基于Ts和Fs获得的结果均与视觉认知不一致,这是因为Ts相对于GLs在对比局部结构时,没有有效考虑到局部结构比对时可能存在的gap情况。Fs由于是基于图形轮廓从整体上利用傅里叶描述子表达图形形状,当图形间复杂程度接近时Fs相对不敏感,即表 7中建筑物2与各模板相似程度均较大。同时,Fs无法有效顾及建筑物图形多直角表达的形态特征[3]。对于建筑物3,基于Fs获得了与视觉认知一致的结果,而基于Ts和GLs获得的结果均与视觉认知不一致,这是因为基于GLs的识别是以比对连续直角构成的特殊结构组成的序列为基础,若建筑物不具备多直角表达的形态特征,且两建筑物复杂程度差异过大时,GLs往往取值较低,见表 7。因此,GLs相比于Fs更适宜多直角表达的简单图形间的形状相似性计算。其中,前文对Ordnance Survey开源提供的制图比例尺1∶10 000的街道层次地图中765 961个建筑物图形外轮廓角度特征进行统计分析显示,其中直角占比为96.06%,呈现出明显的多直角表达形态特征,因而,建筑物形状相似性计算较适宜使用GLs。而Fs则相对更适宜非多直角表达的复杂图形间的形状相似性计算,如面状湖泊、河流等。
3.2.2 参数敏感性分析
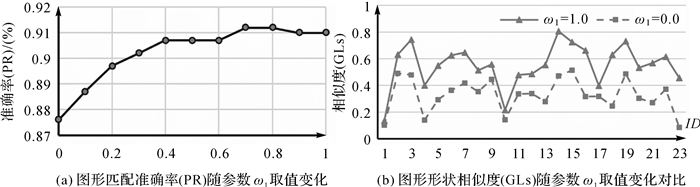
式(5)和式(6)中的参数需要设置,本文依据建筑物图形特征设置了经验阈值。式(5)中,考虑到人对于形状感知时,角度较长度的视觉感知往往更明显[25-26],因此,试验中w1取值大于w2。分析参数w1、w2的影响时,固定式(6)中参数d=-0.8、e=-0.5;分别设置w1=0.0、0.1、…、0.9、1.0,对应设置w2=1.0、0.9、…、0.1、0.0。基于不同参数设置,前文试验中基于GLs的建筑物图形识别准确率(PR)变化见图 3(a)。由图 3(a)可知,当w1取值适当大于w2时,即w1=0.8、w2=0.2或w1=0.7、w2=0.3时,PR最高,为91.2%;当w1取值较大或w1取值小于w2时,PR均有所下降。
|
| 图 3 参数ω1、ωw2影响分析 Fig. 3 Influences analysis for parameters ω1 and ω2 |
同时,统计参数w1、w2取不同值时建筑物图形间形状相似性(GLs)变化。图 3(b)表示参数设置为w1=1.0、w2=0.0和w1=0.0、w2=1.0时,形状数据库中任选的23个建筑物与典型建筑物T3的GLs。由图可知,当w1取值减小时,GLs会减小,这是由于建筑物多直角表达的形态特征所致,即若前文中定义的基础结构构成match关系,则角度特征相似性往往较大,大于对应的长度特征相似性。另外,若w1=0.0、w2=1.0,即只考虑基础结构的长度特征相似性时,GLs均小于0.5,而基于本文的定义,理论上GLs∈[-1, 1],故实际应用中w1取值需适当大于w2。
式(6)中,参考DNA序列匹配时罚分权重的设置,若用于匹配的DNA序列发生碱基对替换的可能性较高,即可能存在较多mismatch或gap关系时,罚分通常设置较高,即对于差异大的序列,可设置较大的罚分[18]。考虑到建筑物图形相对简单,若两图形存在mismatch或gap关系,则该匹配关系就可能在序列中占比较大,因此,试验中设置了较大的d和e。
固定式(5)中参数w1=0.8、w2=0.2,分别取值d=-0.8、e=-0.5和d=-0.4、e=-0.25,分析参数d与e变化对试验结果的影响。图 4(a)表示参数d与e取不同值时,形状数据库中任选的23个建筑物与典型建筑物T3的GLs,由图可知,随着参数d与e取值变大,GLs会变小。图5(b)表示形状数据库中任选的23个建筑物分别与6个典型建筑物(T1-T6)GLs的标准差(STD),由图可知,当参数d与e取值较大时,STD会更大,这意味着此时GLs的区分性更强。
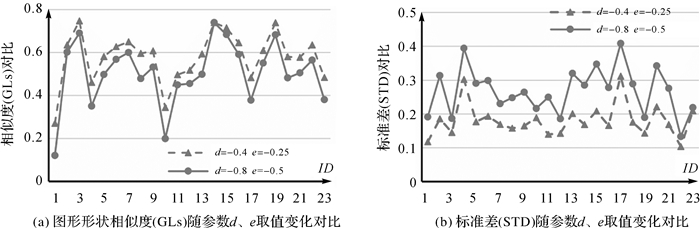
|
| 图 4 参数d、e影响分析 Fig. 4 Influences analysis for parameters d and e |
依据上文分析可知,实际应用时式(5)中w1取值需适当大于w2;式(6)中若用于计算GLs的建筑物图形复杂程度相近时,参数d与e可取较大值,因为此时GLs区分性更好;若用于计算GLs的建筑物图形复杂程度差异大时,参数d与e可取较小值。因此,本文算法针对复杂程度差异不同的建筑物图形分别设置两组参数缺省值:① w1=0.8、w2=0.2,d=-0.8、e=-0.5;② w1=0.8、w2=0.2,d=-0.4、e=-0.35。依据文献[26],建筑物图形的边数比(Er)可作为建筑物图形复杂程度差异的近似度量:若数据集中建筑物间平均边数比aEr>0.6,表示数据集中建筑物间复杂程度相近,取参数组①;否则,取参数组②。另外,本文算法参数均为可选项,实际应用过程中用户也可依据需要进行设置。
4 结论为了计算建筑物图形间形状相似性,本文将建筑物图形编码成序列,应用DNA序列比对的NW算法和SW算法,计算序列间相似性。建筑物图形序列编码时充分顾及了建筑物图形多直角表达的形态特征。试验证明本文方法计算的建筑物图形间形状相似性符合人的视觉空间认知。但是,实际应用中建筑物图形形状复杂多样,未来将结合机器学习方法等动态调整算法参数和基础元素匹配关系,提高算法的智能化程度。
| [1] |
VELTKAMP R C. Shape matching: similarity measures and algorithms[C]//Proceedings of 2001 International Conference on Shape Modeling and Applications. Genova, Italy: IEEE, 2001: 188-197.
|
| [2] |
付仲良, 逯跃锋. 利用弯曲度半径复函数构建综合面实体相似度模型[J]. 测绘学报, 2013, 42(1): 145-151. FU Zhongliang, LU Yuefeng. Establishment of the comprehensive model for similarity of polygon entity by using bending radius complex function[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 145-151. |
| [3] |
晏雄锋, 艾廷华, 杨敏. 居民地要素化简的形状识别与模板匹配方法[J]. 测绘学报, 2016, 45(7): 874-882. YAN Xiongfeng, AI Tinghua, YANG Min. A simplification of residential feature by the shape cognition and template matching method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 874-882. DOI:10.11947/j.AGCS.2016.20150162 |
| [4] |
艾廷华, 帅赟, 李精忠. 基于形状相似性识别的空间查询[J]. 测绘学报, 2009, 38(4): 356-362. AI Tinghua, SHUAI Yun, LI Jingzhong. A spatial query based on shape similarity cognition[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 356-362. DOI:10.3321/j.issn:1001-1595.2009.04.012 |
| [5] |
安晓亚, 刘平芝, 金澄, 等. 手绘地图开域空间方向关系检索法[J]. 测绘学报, 2017, 46(11): 1899-1909. AN Xiaoya, LIU Pingzhi, JIN Cheng, et al. A hand-drawn map retrieval method based on open area spatial direction relation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1899-1909. DOI:10.11947/j.AGCS.2017.20170001 |
| [6] |
AI Tinghua, CHENG Xiaoqiang, LIU Pengcheng, et al. A shape analysis and template matching of building features by the Fourier transform method[J]. Computers, Environment and Urban Systems, 2013, 41: 219-233. DOI:10.1016/j.compenvurbsys.2013.07.002 |
| [7] |
王斌. 一种基于多级弦长函数的傅立叶形状描述子[J]. 计算机学报, 2010, 33(12): 2387-2396. WANG Bin. A Fourier shape descriptor based on multi-level chord length function[J]. Chinese Journal of Computers, 2010, 33(12): 2387-2396. |
| [8] |
ZHANG Dengsheng, LU Guojun. A comparative study of curvature scale space and Fourier descriptors for shape-based image retrieval[J]. Journal of Visual Communication and Image Representation, 2003, 14(1): 39-57. DOI:10.1016/S1047-3203(03)00003-8 |
| [9] |
ARKIN E M, CHEW L P, HUTTENLOCHER D P, et al. An efficiently computable metric for comparing polygonal shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(3): 209-216. DOI:10.1109/34.75509 |
| [10] |
FU Zhongliang, FAN Liang, YU Zhiqiang, et al. A moment-based shape similarity measurement for areal entities in geographical vector data[J]. ISPRS International Journal of Geo-Information, 2018, 7(6): 208. DOI:10.3390/ijgi7060208 |
| [11] |
WEI Zhiwei, GUO Qingsheng, WANG Lin, et al. On the spatial distribution of buildings for map generalization[J]. Cartography and Geographic Information Science, 2018, 45(6): 539-555. DOI:10.1080/15230406.2018.1433068 |
| [12] |
BAI Xiang, JAN LATECKI L. Path similarity skeleton graph matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(7): 1282-1292. DOI:10.1109/TPAMI.2007.70769 |
| [13] |
BELONGIE S, MALIK J, PUZICHA J. Shape matching and object recognition using shape contexts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(4): 509-522. DOI:10.1109/34.993558 |
| [14] |
XU Chunjing, LIU Jianzhuang, TANG Xiaoou. 2D shape matching by contour flexibility[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(1): 180-186. DOI:10.1109/TPAMI.2008.199 |
| [15] |
WANG Junwei, BAI Xiang, YOU Xinge, et al. Shape matching and classification using height functions[J]. Pattern Recognition Letters, 2012, 33(2): 134-143. DOI:10.1016/j.patrec.2011.09.042 |
| [16] |
CHEN Longbin, FERIS R, TURK M. Efficient partial shape matching using Smith-Waterman algorithm[C]//Proceedings of 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. Anchorage, AK: IEEE, 2008.
|
| [17] |
危辉, 李俐瑢. 拱序列的曲线描述与匹配[J]. 中国图象图形学报, 2017, 22(8): 1045-1055. WEI Hui, LI Lirong. Curve description and matching using arch sequence[J]. Journal of Image and Graphics, 2017, 22(8): 1045-1055. |
| [18] |
MOUNT D W. Bioinformatics: sequence and genome analysis[M]. 2nd ed. New York: Cold Spring Harbor Press, 2004.
|
| [19] |
郭庆胜. 以直角方式转折的面状要素图形简化方法[J]. 武汉测绘科技大学学报, 1999, 24(3): 255-258. GUO Qingsheng. The method of graphic simplification of area feature boundary as right angle[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(3): 255-258. |
| [20] |
郭庆胜, 黄远林, 郑春燕, 等. 空间推理与渐进式地图综合[M]. 武汉: 武汉大学出版社, 2007. GUO Qingsheng, HUANG Yuanlin, ZHENG Chunyan, et al. Spatial reasoning and progressive map generalization[M]. Wuhan: Wuhan University Press, 2007. |
| [21] |
许文帅, 龙毅, 周侗, 等. 基于邻近四点法的建筑物多边形化简[J]. 测绘学报, 2013, 42(6): 929-936. XU Wenshuai, LONG Yi, ZHOU Tong, et al. Simplification of building polygon based on adjacent four-point method[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 929-936. |
| [22] |
陈文瀚, 龙毅, 沈婕, 等. 利用约束D-TIN进行建筑物多边形凹部结构识别与渐进式化简[J]. 武汉大学学报(信息科学版), 2011, 36(5): 584-587, 592. CHEN Wenhan, LONG Yi, SHEN Jie, et al. Structure recognition and progressive simplification of the concaves of building polygon based on constrained D-Tin[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5): 584-587, 592. |
| [23] |
SESTER M. Optimization approaches for generalization and data abstraction[J]. International Journal of Geographical Information Science, 2005, 19(8-9): 871-897. DOI:10.1080/13658810500161179 |
| [24] |
苏为华. 多指标综合评价理论与方法问题研究[D]. 厦门: 厦门大学, 2000. SU Weihua. Research on multiple-objective-comprehensive-evaluation[D]. Xiamen: Xiamen University, 2000. |
| [25] |
HU Rongxiang, JIA Wei, ZHAO Yang, et al. Perceptually motivated morphological strategies for shape retrieval[J]. Pattern Recognition, 2012, 45(9): 3222-3230. DOI:10.1016/j.patcog.2012.02.020 |
| [26] |
YAN Haowen, WEIBEL R, YANG Bisheng. A multi-parameter approach to automated building grouping and generalization[J]. Geoinformatica, 2008, 12(1): 73-89. DOI:10.1007/s10707-007-0020-5 |




