2. 湖北第二师范学院计算机学院, 湖北 武汉 430074;
3. 国家地理信息系统工程技术研究中心, 湖北 武汉 430074
2. College of Computer, Hubei University of Education, Wuhan 430074, China;
3. National Engineering Research Center of Geographic Information System, Wuhan 430074, China
空间相似性度量对空间信息的检索、融合与数据挖掘至关重要[1]。广义上的空间相似性指根据特定内容和比例尺对空间的匹配和排序,涉及空间对象几何属性、对象间的空间关系等多种因素[2]。其中,方向关系作为一类重要的空间关系,在空间相似性度量研究中引起广泛关注[3-6],方向关系的相似性度量不仅对矢量空间数据的检索[7-8]、查询[9-10]、匹配[11-12]、质量评估[13]等任务提供重要依据,在遥感影像检索[14-15]任务中也有应用。
现阶段方向关系模型可分为定性模型和定量模型两大类。定性方向关系模型中,经典的三角模型[16]、MBR模型[17]、一维间隔模型[18]等为早期空间推理提供重要支撑,其相关理论为后续定性方向关系模型的发展奠定了基础,并产生了诸多改进模型。文献[19]在以点、线、面为参照目标的空间目标间建立方向关系描述的3层模式结构,实现更细致准确的方向关系描述。文献[20]针对目标对象与参照对象的外接矩形相交或位于其内时的方向关系,提出了一种可表达与参照对象外接矩形内部有关信息的细节方向关系表达模型。以上定性方向关系模型实现不同复杂程度的方向关系表达,对空间方向关系推理具有重要意义,但方向关系间的相似性度量依赖于定量方向关系模型完成,无法通过定性模型实现。定量方向关系模型中,文献[21]通过方向关系矩阵表示对象在不同方向片区的分布,并利用平衡传输方法计算矩阵间距离从而实现方向关系的相似度度量。该模型具有较高的可比性,引起学者们的广泛关注并产生诸多针对性的改进方法。文献[22]将方向关系矩阵拓展至面群间的方向关系表达及相似度计算。文献[23]则提出基于栅格数据的面状目标空间方向矩阵,简化方向关系矩阵元素值和矩阵间距离的计算方法,极大降低了方向关系矩阵相似性度量方法的复杂度,证明了栅格单元作为基本对象计算空间关系相似值的可行性。文献[24]在此基础上提出了基于格网的方向关系矩阵,利用规律格网单元阵列划分对象空间,快速完成对任意尺度对象间的方向关系的表达,解决了多尺度对象间的相似性度量问题。文献[25]采用分解思想,进一步将格网方向关系矩阵应用到多尺度复合对象间的方向关系表达,并优化方向关系矩阵距离计算方法,实现对复杂多尺度对象群间的方向关系相似性度量。
上述方法针对经典方向关系矩阵模型[21]的元素表达方式、距离计算方法、模型应用范围等方面进行了针对性的改进,取得一定成果,但仍存在以下问题:①对同一方向片区内的方向关系变化识别不足;②邻域图的定义与人类实际认知有差异,且计算粒度较粗;③方向关系矩阵距离的计算广泛借鉴运筹学方法,但仅采用初始基作为最终解,其结果并非最优解,一定程度上降低了相似性度量的准确性。
上述基于经典方向关系矩阵[21]改进的模型中,文献[24]提出的格网方向关系矩阵具有表达简单快速,粒度可调且可灵活应用于多尺度对象等优点。为进一步探索对方向关系矩阵模型的高效改进,本文以格网方向关系矩阵[24]为基础,引入对象方向片区质心角度表示对象的位置分布,建立可同时记录目标对象分布比例及分布位置信息的方向关系二元组,实现粒度更高的方向关系表达,区分目标对象分布在同一方向片区内的方向关系;同时结合人类空间认知优化邻域图,建立适用于任意方向间的基准方向距离;并引入EMD(Earth mover's distance)[26]距离计算方向关系矩阵间的最小转化代价,实现对任意方向关系间相似度的精确度量。本文所提方向关系二元组模型亦可基于经典方向关系模型进行改进。
1 方向关系矩阵二元组 1.1 格网方向关系矩阵方向关系矩阵模型利用投影法将参考对象A所在空间划分为{N, S, E, W, NE, SE, SW, NW, O}9个方向片区[21],可通过3×3矩阵记录目标对象B在9个方向片区的分布情况。格网方向关系矩阵[24]引入规律格网单元将空间进一步划分,通过B在各方向片区所占格网单元数目比例,将A、B间的方向关系表示为
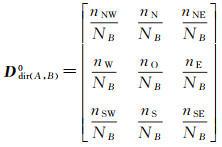 (1)
(1)
矩阵各元素的分子为B在各方向片区所占格网单元数目,分母NB为B所占格网单元总数,其中A、B对象不限尺度,点、线、面对象在各方向片区所占格网单元数目均可被快速计算出[24]。但目前不论是经典方向关系矩阵模型,还是基于其改进的各类模型,均无法区分同一方向片区内的方向关系变化。图 1(a)中,场景2与场景3的方向关系更相似,但图 1(b)根据方向关系矩阵模型划分场景空间后,场景1和场景2中B分布在同一方向片区,两者方向关系矩阵相同,方向关系相似度为1,高于场景2与场景3间的方向关系相似度。这与人类的实际认知有一定偏差,因此方向关系矩阵模型对方向关系的表示及相似性度量仍存在一定缺陷。

|
| 图 1 空间划分前后的场景对比 Fig. 1 Scenes before and after partitioning the space |
1.2 融入质心方位角的方向关系二元组表达
当目标对象在同一方向片区内变化时,可通过对象质心方位角间的差异对方向关系加以区分。目标对象的质心方位角β∈[0, 2π]为参考对象外心的指北方向线,按顺时针方向至该点与目标对象质心连线的水平夹角。与方向关系矩阵类似,本文建立3×3的质心方向矩阵,记录目标对象落在各方向片区内子部分的质心方位角,目标对象B相对参考对象A的质心方向关系矩阵表示为
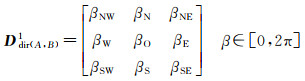 (2)
(2)
当应用格网划分对象空间时,质心方向关系矩阵的各元素可通过目标对象在各方向片区所占格网单元质心方位角的平均值获取,如图 2所示。将参考对象A的外心与目标对象B所占格网单元的质心相连后,可求B所占格网单元的质心方位角为集合αAB={α1, α2, …, αNB},其中分布在NW方向片区的格网单元质心如图 2(c)中实线箭头所指,它们对应的质心方位方位角集合为{α1, α2, …, αnNW}⊆αAB,则B在该片区的质心方位角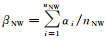
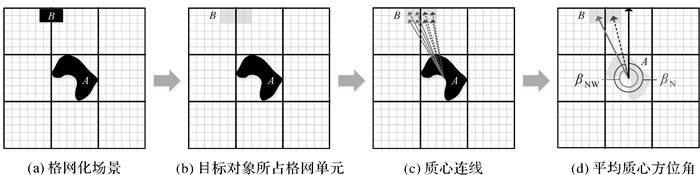
|
| 图 2 基于格网单元求取目标对象在不同方向片区内的质心方位角 Fig. 2 Obtaining centroid azimuth of grids |
在格网方向关系矩阵Ddir(A, B)0的基础上,融入表征目标对象在各方向片区质心分布情况的质心方向关系矩阵Ddir(A, B)1,即为目标对象B相对参考对象A的方向关系二元组
 (3)
(3)
文献[25]结合分解思想将格网方向关系矩阵应用到复合对象间的方向关系表达,同理可将方向关系二元组应用于复合对象。设任意复合参考对象A和复合目标对象B分别由n个和m个子对象组成。计算两者的格网方向关系矩阵时先将A分解为n个子参考对象,则B相对A的格网方向关系矩阵通过B与各子参考对象间的方向关系矩阵加权求和获取,如式(4)所示。其中pi为A中第i(1≤i≤n)个子对象Ai相对A所占的格网单元数目比,Ddir(Ai, B)0为子参考对象Ai与目标对象B间的格网方向关系矩阵。同理,将B分解为m个子目标对象后可将Ddir(Ai, B)0表示为式(5),其中qj为B中第j(1≤j≤m)个子对象Bj相对B所占的格网单元数目比,Ddir(Ai, Bj)0为子目标对象Bj相对子参考对象Ai的格网方向关系矩阵
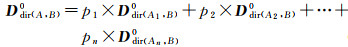 (4)
(4)
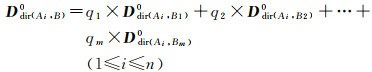 (5)
(5)
结合式(4)、式(5),可得复合对象A与B间的格网方向关系矩阵为
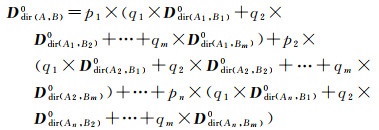 (6)
(6)
利用分解思想计算复合对象间的质心方向关系矩阵时,由于质心方向关系矩阵中各元素值仅与对象在单一方向片区所占格网单元相关,不涉及在其他方向片区所占格网单元,因此质心方向关系矩阵中各元素不共享权重,各元素的权重为该方向片区内子对象与复合对象所占格网单元数目比。在拆分A为m个子参考对象后,B中任意子对象Bj相对Ai的质心方向关系矩阵Ddir(Ai, Bj)1的权重Qij(1≤i≤n, 1≤j≤m)可通过Ddir(Ai, Bj)0与Ddir(Ai, B)0间点除运算得到。Qij为3×3矩阵,其元素值为Bj与B在各方向片区所占的格网单元数目比。通过Qij与Ddir(Ai, Bj)1间的点乘运算即可完成对质心方向关系矩阵所有元素的单独加权,从而子参考对象Ai与复合对象B间的质心方向矩阵可表示为
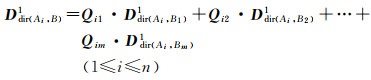 (7)
(7)
同理,在结合多个子参考对象的质心方向关系矩阵时,各子参考对象仅影响其目标对象落入的方向片区元素的权重。记3×3矩阵Pi(1≤i≤n)为Ddir(Ai, B)1的权重,Pi中各元素值为子对象Ai相对复合对象AX所占格网单元数目比,AX为X方向片区有目标对象落入的子参考对象集合。通过Pi与Ddir(Ai, B)1的点乘运算可完成质心方向关系矩阵各元素的单独加权,从而可得最终质心方向距离,如式(8)所示
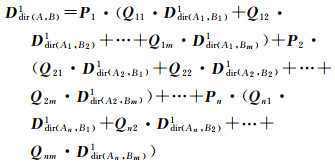 (8)
(8)
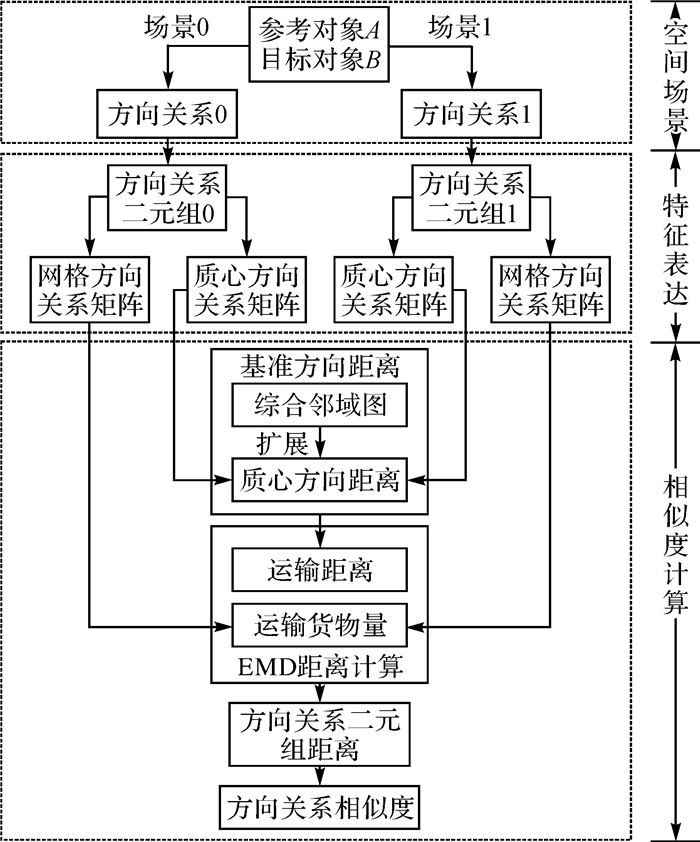
方向关系二元组间的相似性度量同时考虑目标对象在各方向片区内分布比例及质心方位角的变化,整体流程如图 3所示。传统方向关系矩阵模型在计算矩阵距离时所使用的基准方向距离粒度较粗,仅定义了9个方向片区间的距离,未能描述任意方向间的距离,且方向片区间距离定义与人类实际认知存在部分偏差。本文先对传统邻域图进行改进,提出符合人类认知的综合邻域图,并在此基础上将其扩展为适用于任意方向间距离计算的质心方向距离,从而可通过质心方向关系矩阵获取不同对象分布间更精细的基准方向距离,联合格网方向关系矩阵记录的对象分布比例差异,指导EMD距离计算方向关系二元组间的最小转换代价即方向关系二元组间的距离,实现对方向关系相似性的评估。
|
| 图 3 本文方法 Fig. 3 The proposed method |
两个场景的相似度可量化为一个场景转变为另一场景所需的变化数目[4],变化越少相似度越高。方向关系二元组模型通过二元组间的距离量化两个方向关系间的变化量,距离越小方向关系相似度越高。式(9)表示任意场景对(s, t)的方向关系相似度,两场景对应的方向关系二元组间的距离dist(Ddir(s), Ddir(t))越小,它们之间的相似度S(s, t)∈0, 1越大,反之亦然。式中dmax表示不同方向片区间的最大距离,其取值与方向片区间的基准方向距离定义相关
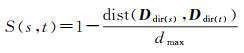 (9)
(9)
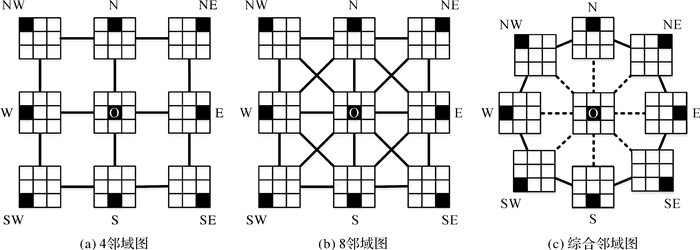
经典方向关系矩阵模型[21]为9个方向片区定义了2种基准方向距离,分别以4邻域图和8邻域图为向导,如图 4(a)、(b)所示。图中连线表示距离1,两方向片区间的距离定义为两者间最短路径经过的连线数目。两类邻域图的差别在于斜对角线方向片区间是否有连线,这使得两者相同方向片区间的距离略有不同,如(SW, NE)的距离在两者中都取得最大值,但在4邻域图中为4,在8邻域图中为2,因此两类邻域图的dmax的值分别为4和2。
|
| 图 4 4邻域图、8邻域图及本文提出的综合邻域图 Fig. 4 Conceptual graphs of 4-neighborhood, 8-neighborhood and comprehensive-neighborhood |
4邻域图和8邻域图为方向关系矩阵的距离计算提供重要依据,但两者仍存在与实际认知不完全相符的问题。人类的方向认知中,相对原始方向偏移角度更小的方向具有更高的方向相似度,偏移角度增大时相似度逐渐降低,当偏移角增至180°时达到人类认知中完全相反的方向,相似度最低。因此当目标对象围绕参考对象旋转180°时方向关系最不相似方向距离最大。4邻域图中斜对角方向如d4(NW, SE)=d4(NE, SW)=4满足最大值,但正方向上相差180°方向片区间距离d4(N, S)=d4(W, E)=2,仅与对象旋转90°后的距离相等;8邻域图满足任意方向与相反方向的距离为其最大值2,如d8(NW, SE)=d8(N, S)=2,但它对方向变化不敏感,仅能区分0, 1, 2 3个程度的方向距离变化,导致有明显差异的方向关系未被区分,如d8(N, NE)=d8(N, E)=1,NE到E的变化被忽视。综上可见两种邻域图的定义并未完全与人类实际认知一致。
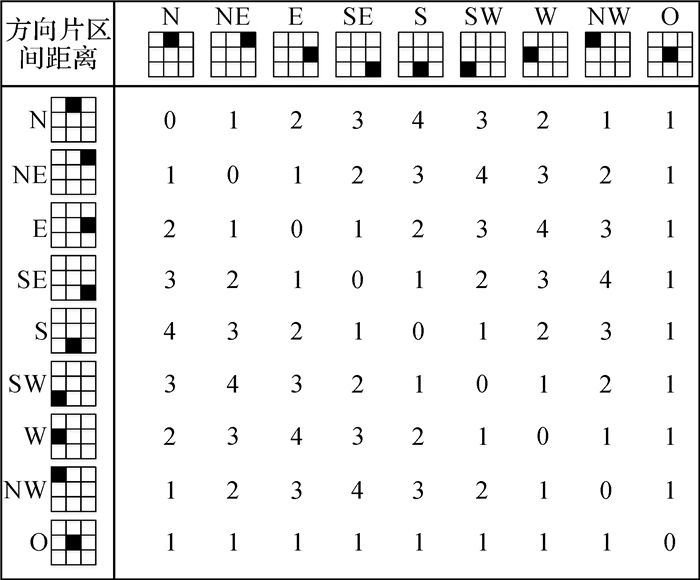
本文结合空间认知提出图 4(c)所示的综合邻域图,实线和虚线均表示距离1,规定方向片区间的最短路径最多经过1条虚线,可得方向片区间的基准距离如图 5所示。中心片区到其他方向片区的距离均为1,其他8个方向片区中任意两者的距离随它们与中心片区外心连线夹角的增大呈现先增大后减小的趋势,夹角为180°时,距离达到最大距离值4,如dc(N, E)=dc(SW, NE)=4;综合邻域图对方向片区间的距离更具区分性,可识别0, 1, 2, 3, 4 5种方向距离变化。相较4邻域图和8邻域图,综合邻域图对方向片区间的距离定义更符合人们对空间方向的实际认知。
|
| 图 5 综合邻域图中方向片区间的距离 Fig. 5 Comprehensive-neighborhood distances between cardinal directions |
2.2 任意方向关系间的基准方向距离定义
邻域图定义了9个方向片区间的基准方向距离,但相同方向片区间的方向距离为0,因此仍无法区分同一方向片区内的变化。此时,目标对象质心方位角间的差异可有效区分两个目标对象间的方向变化。记场景对(s, t)中目标对象的质心方位角为βs和βt,将两者的质心方位角距离θ定义为式(10),其中θ∈[0, 2π]
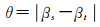 (10)
(10)
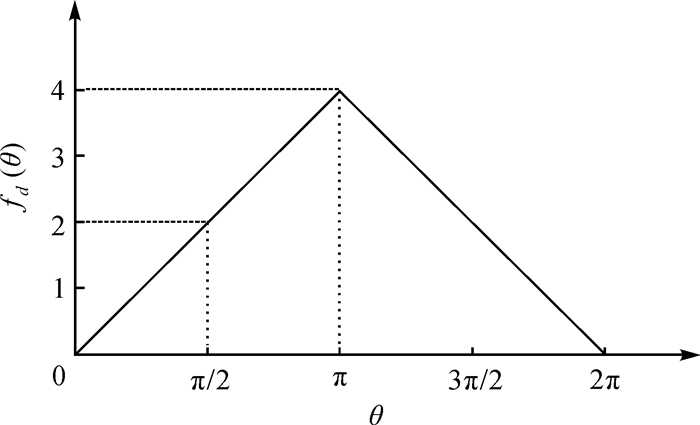
在综合邻域图定义的方向片区间距离的基础上,引入基于θ的质心方向距离fd(θ),如式(11)所示。fd(θ)将θ映射至综合邻域图的值域范围[0, 4]内,从而将基准方向距离由9个方向片区间扩展到任意方向关系间,获取粒度更细的基准方向距离。图 6为fd(θ)相对θ的分布变化,可发现两个目标对象质心方位角间距离θ由0增至180°再至360°时,对应质心方向距离先单调递增再单调递减,并在180°时取得最大值,与人类认知相符。质心方向距离fd(θ)是定义在0, 2π内的连续函数,可反映任意方向间的距离,综合邻域图定义的基准方向距离为该基准方向距离的子集,两者最大方向距离值dmax均为4
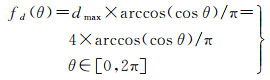 (11)
(11)
|
| 图 6 质心方向距离映射函数 Fig. 6 Mapping function for centroid direction distance |
2.3 方向关系二元组间的EMD距离计算
方向关系二元组间的距离计算是以二元组中的格网方向关系矩阵为实施主体,因此其计算方法与格网方向关系矩阵的距离计算类似。根据矩阵中非零元素数目的情况,格网方向关系矩阵的距离计算可分为如下3种[24]。
(1) 单元素格网方向关系矩阵间的距离。查询邻域图获取。
(2) 单元素与多元素格网方向关系矩阵的距离。将多元素方向关系矩阵拆分为多个单元素子矩阵后,依次计算它们与单元素方向关系矩阵的距离,再以各自的单元素值为权重加权求和获得最终距离。
(3) 多元素方向关系矩阵间的距离。因不能明确元素在矩阵中转移的情况,常借鉴运输问题解决方法如西北角法[27]计算两个矩阵间的最小耗费作为距离。
同理,通过方向关系二元组中的格网方向关系矩阵计算方向关系二元组间的距离,但此时各元素间的距离不再通过邻域图定义的基准距离表示,而是采用质心方向距离fd(θ)表示,通过各元素在二元组中质心方向关系矩阵的对应位置元素值即可求取fd(θ),从而完成更准确的方向关系二元组距离计算。
特别地,在多元素方向关系矩阵间的距离计算中,西北角法由于简单易实施而被广泛采用,但运筹学中认为它并未注意到运输成本的影响,计算结果往往并非最优值[28],这影响了方向关系相似性度量的准确性。文献[26]提出EMD距离表示不同分布间相互转换的最小代价,并被广泛应用于视觉领域和自然语言领域中的特征相似性度量,本文将EMD距离引入方向关系二元组间最小转换代价的计算中。
EMD距离源自运输模型。设有m个供应者P=(p1, wp1), …, (pm, wpm)和n个需求者Q={(q1, wq1), …, (qn, wqn)},其中pi, wpi(1≤i≤m)为第i个供应者及其供应量,qj、wqj(1≤j≤n)为第j个需求者及其需求量。各供应者到各需求者的运输距离及运输量分别通过m×n的运输距离矩阵C=[cij](1≤i≤m, 1≤j≤n)和运输方案矩阵E=[eij](1≤i≤m, 1≤j≤n)表示,可得总运输代价cost(P, Q)为{(q1, wq1), …, (qn, wqn)}
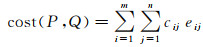 (12)
(12)
式中,运输方案矩阵的元素eij(1≤i≤m, 1≤j≤n)为第i个供应者运往第j个需求者的货物量,且满足如下约束
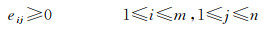 (13)
(13)
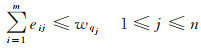 (14)
(14)
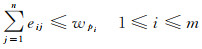 (15)
(15)
当找到一个最优运输方案Eopt=eijopt(1≤i≤m, 1≤j≤n)时,cost(P, Q)取得最小值,即为P与Q间的EMD距离,如式(16)所示
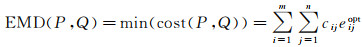 (16)
(16)
采用EMD距离计算任意方向关系二元组Ddir(s)与Ddir(t)间的最小转换代价时,将两者的格网方向关系矩阵Ddir(s)0, Ddir(t)0分别视作供应者集合和需求者集合,Ddir(s)0, Ddir(t)0中非零元素分布的m(1≤m≤9)个方向片区{p1, …, pm}和n(1≤n≤9)个方向片区{q1, …, qn}分别为m个供应者和n个需求者,其元素值{wp1, …, wpm}和{wq1, …, wqn}为各自的供应量与需求量。同时Ddir(s)与Ddir(t)的质心方向关系矩阵Ddir(s)1、Ddir(t)1中相应位置的元素值{βp1, …βpm}、{βq1, …, βqn}分别为各供应者和需求者的质心方位角,则pi(1≤i≤m)到qj(1≤j≤n)的运输距离通过两者的质心方向距离表示,即cij=fd(θij)(1≤i≤m, 1≤j≤n),其中θij=βpi-βqj为两者的质心方位角距离。由此可得方向关系二元组间的EMD距离为
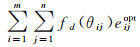 (17)
(17)
结合式(17)和式(9),可得任意两个方向关系二元组间的相似度
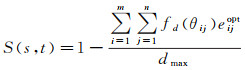 (18)
(18)
式中,dmax为质心方向距离的最大值4。EMD的计算最终转化为对运输问题的求解,可通过运输单纯形法高效计算,这是一种流线型单纯形法,可充分利用约束矩阵的稀疏结构降低运算量。实施过程主要包括:①初始化获取可行解;②最优性检验;③迭代获取新的基可行解,具体过程可参考文献[28],其时间复杂度为O(n2)。现阶段EMD算法在视觉领域发展较为完善,通常利用Russell近似法[29]计算初始基可行解,它相较西北角法更易获取最优解且更易于在计算机上快速完成计算[28]。本文采用经典的C语言EMD算法库[30]完成方向关系二元组距离的计算。
3 试验与讨论以下分析方向关系二元组的表达能力、综合邻域图和质心方向距离的完备性以及EMD距离的可行性进行分析,并探索本文模型在基于方向关系的制图综合结果评估、场景检索等任务中的表现。
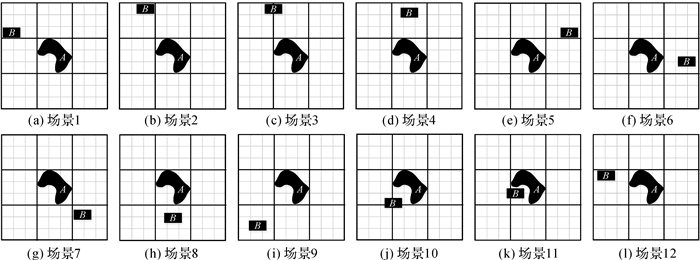
3.1 方向关系二元组模型基本可行性分析 3.1.1 方向关系二元组的表达能力分析图 7为目标对象B以NW片区为起点围绕参考对象A平移,得到的12幅表现不同方向关系的场景。
|
| 图 7 B围绕A平移获取的场景 Fig. 7 The scenes generated by moving object B clockwise with respect to object A |
图 7中场景1和场景2的目标对象落在同一片区内,两者的方向关系二元组如式(19)和式(20)所示。可发现两者的格网方向关系矩阵完全相同,而质心方向关系矩阵同一位置的元素值分别为5.238和5.730,可明显区分两场景的差异,快速得到二元组间距离dist(Ddir(scene 1), Ddir(scene 2))=fd(5.730-5.238)=0.626,对比格网方向关系矩阵间的距离0,更符合人类实际认知。
 (19)
(19)
 (20)
(20)
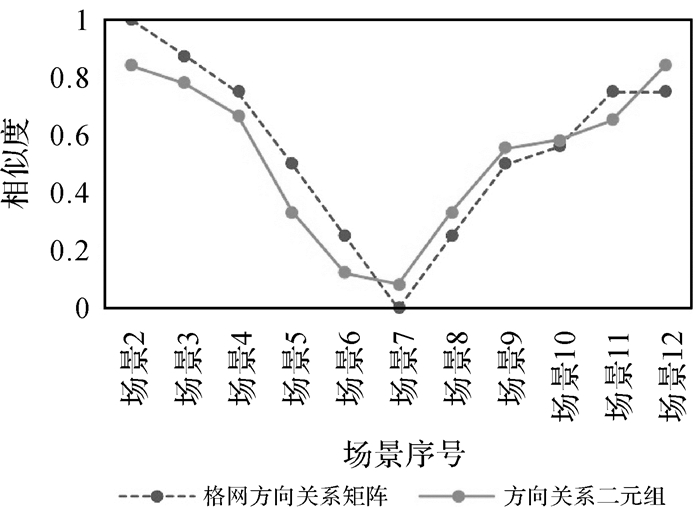
图 8对比了场景1与其他场景在方向关系二元组模型和格网方向关系矩阵模型中的方向关系相似度,两种模型中均采用综合邻域图定义的基准距离。可发现两种相似度结果都呈先降低后上升的形态,整体趋势符合人类对方向关系的认知,但具体到各场景可发现两者区分度的差异。如场景1与场景2在格网方向关系矩阵模型中方向关系相似度Sgrid(scene 1, scene 2)=1,但在方向关系二元组模型中Stuple(scene 1, scene 2)=1-0.626/4=0.844,表明两者的方向关系具有较高的相似度,但并非完全相同。逐个观察图 8中的结果,可发现格网方向关系矩阵仅能体现方向片区间的差异,忽视了具体方向偏移角度间的差异,相比之下方向关系二元组对任意方向关系变化都有较好的识别和区分能力。
|
| 图 8 两种模型下各场景与场景1的方向关系相似性度量结果对比 Fig. 8 Comparison of the cardinal similarity between scene1 and other scenes obtained by two different models |
3.1.2 综合邻域图区分能力分析
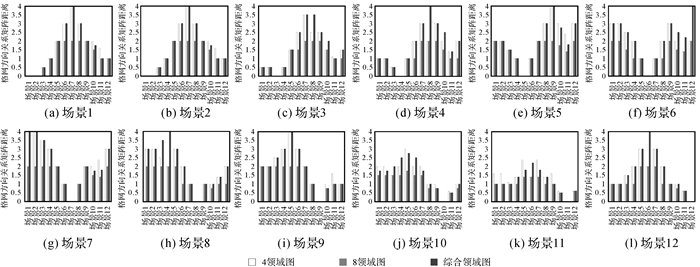
为验证综合邻域图对基准方向距离定义更完备且符合认知,通过格网方向关系矩阵对比图 7中12个场景间在采用4邻域图、8邻域图、综合邻域图这3种基准方向距离定义时的方向距离。
如图 9所示,各分图中距离值均在本场景附近取得较小值,沿着坐标轴往两侧发散时,最初均呈递增趋势,整体上均满足偏移角度越大距离越大,偏移角度越小距离越小的基本规律。对比图中各类邻域图结果对应柱体的值域,可发现表示8邻域图结果的柱体分布范围及变化幅度最小,值域仅在0, 2且走势大多较为平稳,如图 9(i)中场景9与场景1-7这7个场景间的距离均为2,这是不符合实际认知的。4邻域图和综合邻域图对方向变化的识别粒度有很大提升,图中两者值域均为0, 4且走势接近,差异主要体现在相反方向间的距离。如图 9(d)中场景4与场景8在4邻域图中的距离2,小于场景4与场景7间的距离3,即相较场景7,场景8与场景4更相似,这与空间认知中相反方向最不相似的认知相悖,而图中综合邻域图柱体的分布表明它对方向片区间的距离是随着偏移角度变化规律增大或减小的,对不同方向角度变化的距离判断均与人类空间认知一致。相较4邻域图和8邻域图,综合邻域图具有更完备更符合认知的距离定义。
|
| 图 9 4邻域、8邻域和综合邻域图下的格网方向关系矩阵距离分布 Fig. 9 Distances calculated by grid-based relation matrices with 4-neighborhood, 8-neighborhood and comprehensive-neighborhood |
3.1.3 EMD距离最优性分析
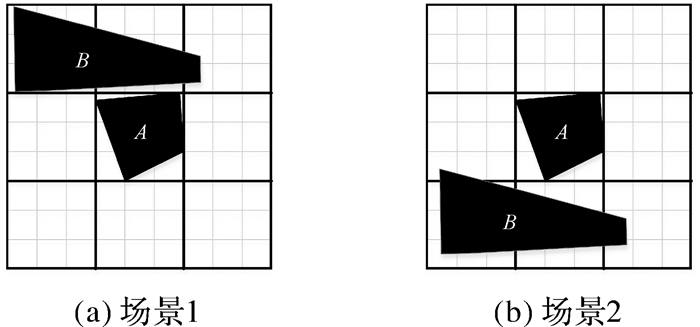
传统方向关系矩阵模型[21, 24]常采用西北角法[27]计算两个矩阵间的最小耗费,西北角法的每次迭代优先计算平衡传输表的西北角即左上角元素,因此其计算结果会因表中行列位置不同而变化,往往并非最优值[28]。以图 10为例,图中两个场景的方向关系二元组均由多元素方向关系矩阵组成。依次通过西北角法和EMD距离计算两个场景在不同基准方向距离下的格网方向关系矩阵距离和方向关系二元组距离,结果见表 1。可发现不论采用何种方向表达模型及基准方向距离定义,两者间的EMD距离均小于或等于西北角法的计算结果。仅采用基于8邻域图的格网方向关系矩阵时两种距离计算方法的结果相同,这也与8邻域图定义的基准距离范围小,不同方向片区间距离值变化不大有关。除此外,EMD距离值均更小,结果更优。
|
| 图 10 目标对象分布在多个方向片区的场景 Fig. 10 Scenes with target objects distributed in several cardinal directions |
3.2 方向关系二元组模型的应用能力分析 3.2.1 基于方向关系的制图综合结果评估
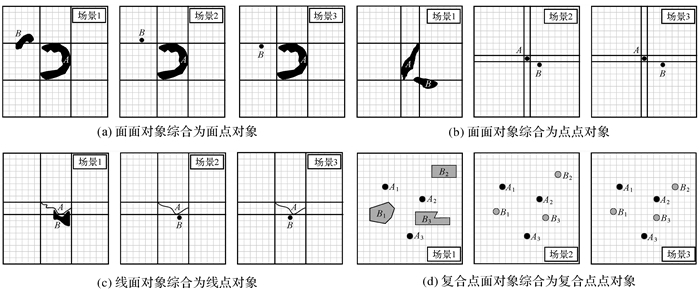
方向关系相似性是多尺度地图空间相似关系的重要部分[2],可作为制图综合结果的评价指标之一[24]。方向关系二元组可表达多尺度对象间的方向关系,并可通过分解思想[25]应用于复合对象。因此可通过方向关系二元组对制图综合前后多尺度对象间及复合对象间方向关系的理性进行评估。如图 11中4个分图分别展示了4个大比例场景的2种制图综合结果,通过本文模型和格网方向关系矩阵模型[24]计算制图综合前后场景的方向关系相似度,结果如表 2所示。对比可发现格网方向关系矩阵仅能判断图 11(a)中这类目标对象明显分布在不同方向片区综合结果的优劣,对图 11(b)、(c)的综合结果无法做出准确评估,而方向关系二元组可判断出4个分图中均为场景2的制图综合结果更合理。特别地,图 11(d)复合对象制图综合案例及相应结果来自文献[25],方向关系二元组模型的判断结果与其一致,即场景2更合理。
|
| 图 11 4个大比例场景的制图综合结果 Fig. 11 Generalization results of four scenes at large-scale |
3.2.2 基于方向关系的空间场景查询
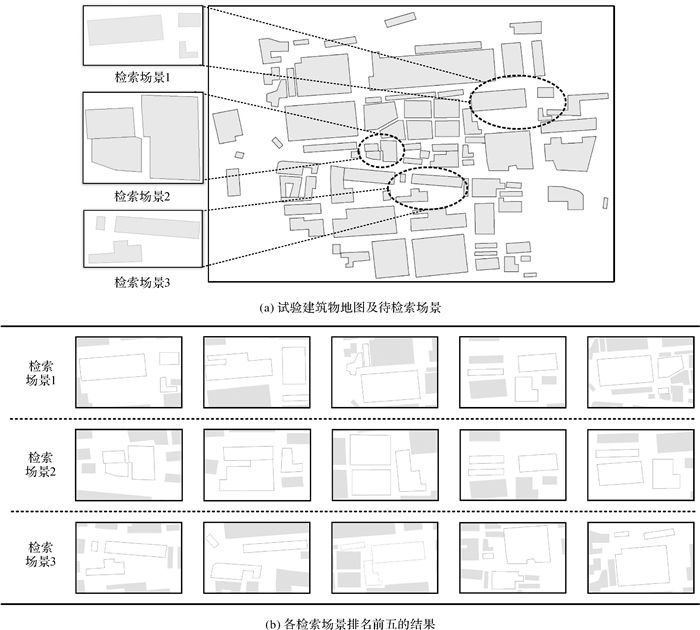
在空间场景的查询与检索任务中,方向关系相似度亦常作为场景相似度的计算因子,一定程度地影响整体场景的相似度评估,可通过方向关系相似度筛选具有类似方向分布的场景。图 12(a)是高德地图采集的上海某区域建筑物地图及3个检索场景。在没有对象几何特征及其他空间关系约束的前提下,为简化对象匹配计算,限定候选场景中对象满足Voronoi相邻且对象数目与检索场景中相同。通过方向关系二元组模型查询出各检索场景最相似的5个场景如图 12(b)所示。观察可发现,每一个检索场景都被检出且为各自结果中相似度最高的,其他结果场景中对象的分布及对象间的方向关系也与检索场景的高度相似,表明方向关系二元组模型可有效实现空间场景对象间的方向关系相似度评估,实现符合人类认知的方向关系检索。
|
| 图 12 基于方向关系的空间场景检索 Fig. 12 Spatial scene retrieval based on direction relation |
4 总结
本文提出一种基于方向关系二元组的方向关系相似性度量方法,从方向关系特征表达、基准方向距离定义、矩阵距离计算3个方面对方向关系矩阵模型进行改进与优化,实现更高效准确的方向关系表达及相似性度量。该方法首先通过方向关系二元组实现细粒度的方向关系表达;然后结合人类认知优化传统邻域图,并在此基础上建立方向距离定义更完备的质心方向距离;最后利用EMD距离,完成对具有任意复杂度的方向关系二元组间距离的优化计算。本文方法可有效识别同一方向片区内的方向变化,更准确地实现任意方向间的相似性的度量,获取更符合人类认知的度量结果。在制图综合结果评估、场景检索等任务中亦有较好的表现,可快速应用于多尺度对象及复合对象间的方向关系表达与相似度计算上,具有广泛的适用性。本文模型建立在格网方向关系矩阵的基础上,同样可通过传统方向关系矩阵实现本文方法以应用到不同任务中。下一步工作将会进一步探讨不同格网密度下或基于不同类型方向关系模型的方向关系二元组的表达能力与适用场景。
| [1] |
LI Bonan, FONSECA F. TDD: a comprehensive model for qualitative spatial similarity assessment[J]. Spatial Cognition & Computation, 2006, 6(1): 31-62. |
| [2] |
闫浩文, 褚衍东. 多尺度地图空间相似关系基本问题研究[J]. 地理与地理信息科学, 2009, 25(4): 42-44, 48. YAN Haowen, CHU Yandong. On the fundamental issues of spatial similarity relations in multi-scale maps[J]. Geography and Geo-Information Science, 2009, 25(4): 42-44, 48. |
| [3] |
NEDAS K A, EGENHOFER M J. Spatial-scene similarity queries[J]. Transactions in GIS, 2008, 12(6): 661-681. DOI:10.1111/j.1467-9671.2008.01127.x |
| [4] |
BRUNS H T, EGENHOFER M J. Similarity of spatial scenes[C]//Proceedings of the 7th International Symposium on Spatial Data Handling. Delft: Taylor & Francis, 1996: 31-42.
|
| [5] |
GOYAL R K, EGENHOFER M J. Similarity of cardinal directions[C]//Proceedings of the 7th International Symposium on Spatial and Temporal Databases. Berlin: Springer, 2001: 36-55.
|
| [6] |
陈占龙, 吕梦楼, 吴亮, 等. 基于特征矩阵和关联图的空间场景相似性度量方法[J]. 武汉大学学报(信息科学版), 2017, 42(7): 956-962. CHEN Zhanlong, LÜ Menglou, WU Liang, et al. Space scene similarity metrics based on feature matrix and associated graph[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 956-962. |
| [7] |
安晓亚, 刘平芝, 金澄, 等. 手绘地图开域空间方向关系检索法[J]. 测绘学报, 2017, 46(11): 1899-1909. AN Xiaoya, LIU Pingzhi, JIN Cheng, et al. A hand-drawn map retrieval method based on open area spatial direction relation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1899-1909. DOI:10.11947/j.AGCS.2017.20170001 |
| [8] |
田泽宇, 门朝光, 汤亚楠. 基于形状及空间关系的场景相似性检索[J]. 电子学报, 2016, 44(8): 1892-1898. TIAN Zeyu, MEN Chaoguang, YANG Yanan. Spatial-scene similarity retrieval based on shape and spatial relation[J]. Acta Electronica Sinica, 2016, 44(8): 1892-1898. DOI:10.3969/j.issn.0372-2112.2016.08.018 |
| [9] |
EGENHOFER M J. Spatial-query-by-sketch[C]//Proceedings of 1996 IEEE Symposium on Visual Languages. Boulder, CO: IEEE, 1996: 60-67.
|
| [10] |
EGENHOFER M J. Query processing in spatial-query-by-sketch[J]. Journal of Visual Languages & Computing, 1997, 8(4): 403-424. |
| [11] |
ZHANG Xiang, AI Tinghua, STOTER J, et al. Data matching of building polygons at multiple map scales improved by contextual information and relaxation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 92: 147-163. DOI:10.1016/j.isprsjprs.2014.03.010 |
| [12] |
陈占龙, 张丁文, 谢忠, 等. 利用多等级相关性反馈进行空间场景匹配[J]. 武汉大学学报(信息科学版), 2018, 43(9): 1422-1428. CHEN Zhanlong, ZHANG Dingwen, XIE Zhong, et al. Spatial scene matching based on multilevel relevance feedback[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1422-1428. |
| [13] |
XU Yongyang, CHEN Zhanlong, XIE Zhong, et al. Quality assessment of building footprint data using a deep autoencoder network[J]. International Journal of Geographical Information Science, 2017, 31(10): 1929-1951. DOI:10.1080/13658816.2017.1341632 |
| [14] |
WANG Min, SONG Tengyi. Remote sensing image retrieval by scene semantic matching[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 2874-2886. DOI:10.1109/TGRS.2012.2217397 |
| [15] |
WANG M, WAN Q M, GU L B, et al. Remote-sensing image retrieval by combining image visual and semantic features[J]. International Journal of Remote Sensing, 2013, 34(12): 4200-4223. DOI:10.1080/01431161.2013.774098 |
| [16] |
HAAR R. Computational models of spatial relations[R]. College Park, MD: University of Maryland, 1976.
|
| [17] |
PAPADIAS D, SELLIS T, THEODORIDIS Y, et al. Topological relations in the world of minimum bounding rectangles: a study with R-trees[J]. ACM SIGMOD Record, 1995, 24(2): 92-103. DOI:10.1145/568271.223798 |
| [18] |
ALLEN J F. Maintaining knowledge about temporal intervals[J]. Communications of the ACM, 1983, 26(11): 832-843. DOI:10.1145/182.358434 |
| [19] |
曹菡, 陈军, 杜道生. 空间目标方向关系的定性扩展描述[J]. 测绘学报, 2001, 30(2): 162-167. CAO Han, CHEN Jun, DU Daosheng. Qualitative extention description for cardinal directions of spatial objects[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 162-167. DOI:10.3321/j.issn:1001-1595.2001.02.011 |
| [20] |
杜世宏, 王桥, 杨一鹏. 一种定性细节方向关系的表达模型[J]. 中国图象图形学报, 2004, 9(12): 1496-1503. DU Shihong, WANG Qiao, YANG Yipeng. A qualitative description model of detailed direction relations[J]. Journal of Image and Graphics, 2004, 9(12): 1496-1503. |
| [21] |
GOYAL R K. Similarity assessment for cardinal directions between extended spatial objects[D]. Orono, ME: The University of Maine, 2000.
|
| [22] |
李靖涵, 巩现勇, 武芳, 等. 一种改进的面目标间方向关系相似性计算模型[J]. 武汉大学学报(信息科学版), 2016, 41(7): 925-931, 951. LI Jinghan, GONG Xianyong, WU Fang, et al. An improved model for calculating the similarity of spatial direction relations between areal objects[J]. Geomatics and Information Science of Wuhan University, 2016, 41(7): 925-931, 951. |
| [23] |
郭庆胜, 丁虹. 基于栅格数据的面状目标空间方向相似性研究[J]. 武汉大学学报(信息科学版), 2004, 29(5): 447-450, 465. GUO Qingsheng, DING Hong. Similarity for spatial directions between areal objects in raster data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(5): 447-450, 465. |
| [24] |
陈占龙, 周林, 龚希, 等. 基于方向关系矩阵的空间方向相似性定量计算方法[J]. 测绘学报, 2015, 44(7): 813-821. CHEN Zhanlong, ZHOU Lin, GONG Xi, et al. A quantitative calculation method of spatial direction similarity based on direction relation matrix[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 813-821. DOI:10.11947/j.AGCS.2015.20140198 |
| [25] |
陈占龙, 龚希, 吴亮, 等. 顾及尺度差异的复合空间对象方向相似度定量计算模型[J]. 测绘学报, 2016, 45(3): 362-371. CHEN Zhanlong, GONG Xi, WU Liang, et al. A quantitative calculation method of composite spatial direction similarity concerning scale differences[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 362-371. DOI:10.11947/j.AGCS.2016.20150099 |
| [26] |
RUBNER Y, TOMASI C, GUIBAS L J. A metric for distributions with applications to image databases[C]//Proceedings of the 6th International Conference on Computer Vision (IEEE Cat. No. 98CH36271). Bombay, India: IEEE, 1998: 59-66.
|
| [27] |
STRAYER J K. Linear programming and its applications[M]. New York: Springer, 1989.
|
| [28] |
HILLIER F S, LIEBERMAN G J, LIBERMAN G. Introduction to mathematical programming[M]. New York: McGraw-Hill Science, 1995.
|
| [29] |
RUSSELL E J. Letters to the editor: extension of Dantzig's algorithm to finding an initial near-optimal basis for the transportation problem[J]. Operations Research, 1969, 17(1): 187-191. DOI:10.1287/opre.17.1.187 |
| [30] |
RUBNER Y. Code for the Earth movers distance (EMD)[EB/OL]. (1999-01-30)[2020-07-29]. http://ai.stanford.edu/~rubner/emd/default.htm.
|



