2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西部矿产资源与地质工程教育部重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geographic Information Engineering, Xi'an 710054, China;
3. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, Xi'an 710054, China
精密单点定位(precise point positioning, PPP)是继RTK、网络RTK技术后出现的又一种GNSS高精度定位技术,具有无须依赖密集参考站网、作业灵活、无作业范围限制的优点[1-4],该技术在智能交通、精密农业、海洋资源勘探等诸多领域有着广阔的应用前景[5]。为了满足广大实时用户的导航定位需求,IGS于2007年6月正式启动了实时计划项目(real-time pilot project,RTPP),并于2013年4月正式提供实时精密产品。对于实时PPP服务,服务端提供的是基于状态空间表述(state space representation,SSR)的改正数,将GNSS定位误差源进行分离,如卫星轨道、钟差改正、卫星信号偏差等,这些误差共同构成了卫星导航定位的状态空间[6]。IGS提供的GPS实时精密产品轨道精度一般优于5 cm,钟差精度优于0.2 ns,通常可满足PPP动态用户厘米级的定位需求[7-11]。
然而在实际应用中,移动端一般通过无线网络接入高精度GNSS服务产品,IGS实时精密产品通常会有数十秒的信息延迟甚至中断[11-13]。另外,由于通信卫星带宽及计算资源的限制,服务端通常会以特定的频率播发SSR轨道和钟差产品。此时,为了获取当前时刻的位置,终端用户必须使用延迟的SSR电文信息进行位置解算。因此,除了精密产品自身的误差,实时PPP还会额外受轨道钟差外推误差的影响。基于单GPS数据,文献[14]通过事后数据模拟延迟及实时数据,分析了SSR轨道和钟差延迟对PPP定位的影响,研究表明:10 s以内的延迟对PPP定位结果的影响相对较小;当延迟超过20 s时,定位精度显著下降。为了提高实时PPP在数据延迟或者中断等异常情况下的定位效果,众多学者对实时精密轨道和钟差短时间预报方法展开了研究[15-18],结果表明钟差预报对短时通信中断下的PPP提升效果甚微,而轨道预报可以在一定程度上提升实时PPP的定位性能。
SSR延迟或中断下的实时定位性能主要取决于轨道钟差外推/预报的精度,随着我国BDS、Galileo等新一代导航卫星的发展[19-20],GNSS精密定位已从GPS单系统发展到多模GNSS融合定位的新阶段。当使用不同系统观测值进行定位时,由于GPS、GLONASS、BDS和Galileo的轨道和卫星钟类型不尽相同,不同系统的轨道钟差外推的精度保持能力可能存在显著差异。为此,有必要详细评估不同系统SSR轨道钟差外推误差及其对实时精密定位的影响,从而优化多模组合时的定位模型,提升其在SSR延迟下的多模GNSS实时定位效果。
本文首先介绍了实时精密产品计算及外推误差评估方法,以及评估SSR外推误差对实时精密单点定位影响的历元间差分模型。然后,基于法国太空研究中心(CNES)的多系统实时精密产品及MGEX实验网观测数据,详细评估GPS、GLONASS、BDS、Galileo 4个系统卫星不同SSR延迟下的轨道、钟差外推误差及其对实时精密定位的影响。本文的评估结果对于提升SSR延迟下的多模GNSS组合实时定位性能及优化轨道钟差改正数的更新频率具有重要意义。
1 实时精密轨道钟差计算及外推误差评估方法 1.1 基于SSR产品的实时轨道及钟差计算方法在实时精密单点定位应用中,用户需要接收服务端提供的实时精密轨道钟差数据流产品,目前使用最为广泛的实时数据流是RTCM标准提供的状态空间表述(SSR)电文[6]。IGS分析中心将实时解算的精密轨道钟差产品按照RTCM-SSR格式进行编码后通过NTRIP协议播发给用户。SSR电文播发的是轨道钟差产品的改正数信息,改正数是基于GNSS卫星的广播星历计算的。因而,在实际应用中,用户需在SSR电文的基础上结合本地接收的广播星历恢复实时精密轨道钟差产品。SSR轨道电文给出的是卫星星固坐标系下的径向、切向和法向坐标改正分量。卫星在t时刻的轨道改正数可以通过式(1)计算[6]
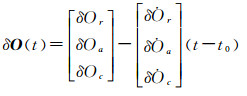 (1)
(1)
式中,δO和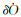
 (2)
(2)
式中,Xb是基于广播星历计算的卫星位置;er、ea、ec是星固系在地心地固坐标系下的单位向量。值得注意的是,在计算精密轨道Xp时广播星历和SSR电文中的IODE/IODC参数需严格匹配。另外,定位应用中所需的卫星坐标参考点是卫星天线相位中心(APC),如果SSR电文中给出的是卫星质心处坐标,需改正天线相位中心偏差。
SSR电文的钟差改正数是基于二次多项式模型给出的,t时刻的卫星钟差改正信息可由式(3)计算[6]
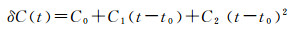 (3)
(3)
式中,Ci是SSR钟差电文多项式的系数,i={0, 1, 2}。与轨道电文参考时刻一样,式(3)中计算钟差的参考时刻等于SSR钟差电文的历元时刻加上钟差更新间隔的一半。将SSR电文计算的钟差信息用于改正广播星历卫星钟差即可恢复精密卫星钟差[6]
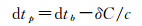 (4)
(4)
式中,dtb是广播星历计算的卫星钟差。
终端精密单点定位的性能与服务端播发的轨道钟差产品精度密切相关。在实时精密单点定位应用中,除了精密轨道钟差产品自身的质量,产品的数据龄期/延迟也会直接影响终端定位的结果。产品的数据龄期/延迟t-t0主要受3个因素的影响:①SSR更新间隔; ②网络延迟; ③SSR数据本身的缺失。
1.2 SSR延迟下精密轨道钟差外推误差的评估方法在实时应用中,SSR延迟会直接影响卫星精密轨道及钟差的计算精度。通常延迟越大,外推精度越低,GNSS定位的性能也会随之降低。本节主要介绍SSR产品延迟下的轨道钟差外推误差评估方法。
对于GNSS定位用户,轨道和钟差信息引入的误差一般叫空间信号测距误差(SISREs)[21]。仅考虑轨道误差时,空间信号测距误差是通过轨道误差在用户观测卫星视线方向的投影计算的,地球上不同位置用户的空间信号测距误差会有所差异,地球上所有用户的平均空间信号测距误差可用式(5)表示[22-23]
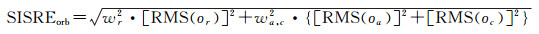 (5)
(5)
式中, οr、οa和οc表示轨道在径向、切向、法向的误差;wr和wa, c表示权重因子,其大小取决于GNSS轨道的高度。表 1给出了4个GNSS系统计算空间信号测距误差所用的权重因子。
| 系统 | wr | wa,c2 |
| GPS | 0.98 | 1/49 |
| GLONASS | 0.98 | 1/45 |
| Galileo | 0.98 | 1/61 |
| BDS(MEO) | 0.98 | 1/54 |
| BDS(GEO, IGSO) | 0.99 | 1/127 |
钟差误差对空间信号测距误差的贡献计算方法为
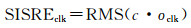 (6)
(6)
式中,οclk表示钟差误差。
当SSR电文出现延迟时,轨道和钟差计算时会引入额外的外推误差,以钟差外推误差为例,其计算公式为
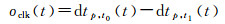 (7)
(7)
式中,t是当前时刻;dtp, t0(t)表示用包含通信延迟的SSR电文外推计算的卫星钟差;t0是延迟电文的参考时刻,产品的数据龄期是t-t0。dtp, t1(t)是t时刻的参考卫星钟差,该钟差是用与当前时刻最近的SSR电文计算得到,该电文参考时刻是t1,其数据龄期t-t1小于钟差更新间隔,当t=t1时,计算的参考钟差不包含外推误差。为了评估不同SSR延迟的轨道钟差外推误差,本文将接收的SSR实时数据流记录成文件便于模拟任意通信延迟。
2 SSR改正数延迟对实时精密定位影响评估方法 2.1 GNSS非差观测方程精密单点定位用户需采用非差观测值,为了消除电离层误差的影响,可采用无电离层组合观测模型
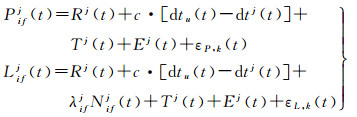 (8)
(8)
式中,P和L分别表示伪距和相位观测值;T表示对流层误差;t表示用户接收机的观测时刻;N为整周模糊度;λ为波长;dtj和dtu分别表示卫星和接收机钟差;εP和εL分别表示伪距和相位观测值噪声;R表示卫星到接收机间的几何距离,可用式(9)表示
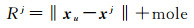 (9)
(9)
式中,xu和xj为用户和接收机的坐标向量;mole表示可用模型改正的误差项,包括对流层干延迟、相对论效应、天线相位中心偏差和变化、天线相位缠绕以及潮汐效应等。卫星坐标xj和钟差dtj是通过精密星历计算的,引入的星历误差用Ej(包含轨道和钟差误差)表示。
2.2 历元间差分模型用于评估SSR延迟对实时精密定位的影响对于实时精密定位,卫星的坐标和钟差通过SSR电文信息计算得到,其包含的误差主要由两部分构成,一部分是服务端提供的精密产品自身误差,另一部分是由SSR延迟引起的外推误差。假设在观测时刻t,用户端接收到最新的SSR电文参考时刻为t0。此时某颗卫星在t时刻的星历误差可用式(10)表示
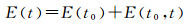 (10)
(10)
式中,E(t0)表示SSR轨道和钟差产品自身的误差,E(t0, t1)表示外推误差。类似地,接收机在t时刻的坐标也可分解为两部分
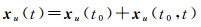 (11)
(11)
式中,xr(t0)表示t0时刻用户端的绝对坐标,xu(t0, t)表示t0到t时刻的位置变化。其中,绝对坐标可利用与SSR电文参考时刻一致的历史观测值基于PPP模型解算,其解算的坐标仅受SSR精密产品自身误差的影响。而位置变化可用历元间差分模型(time-differenced carrier phase, TDCP)解算[24-25],假设从t0到t没有发生周跳,基于式(8),只考虑相位观测值的TDCP观测模型如式(12)所示
 (12)
(12)
此时,式(8)中的模糊度参数已被消除,该模型仅受星历外推误差(包括轨道和钟差)和对流层误差的影响。由于天顶对流层延迟的变化速率一般小于0.01 mm/s[26-27],对流层在几秒或者几分钟内的变化通常可忽略不计。因此,TDCP模型主要受轨道和钟差外推误差的影响,该模型可以较好地评估SSR轨道和钟差延迟对实时精密定位的影响。
将式(12)中的几何项在坐标方向经泰勒级数展开线性化得
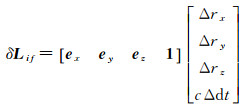 (13)
(13)
式中,Δrx、Δry和Δrz表示t0到t时刻的3个方向坐标分量的变化;ex、ey和ez为对应的系数向量;Δdt是接收机钟差的变化;δLif是历元间差分的相位观测值残差向量,已扣除式(12)中卫星钟差和几何距离的影响。基于式(13)利用加权最小二乘即可解算出用户位置及接收机钟差从t0到t的变化值。式(13)同时适用于单GNSS系统和多系统组合模式,对于多系统组合模式,由于系统间偏差在短时间内的变化可忽略不计,因此只需估计一个接收机钟差参数[28-31]。
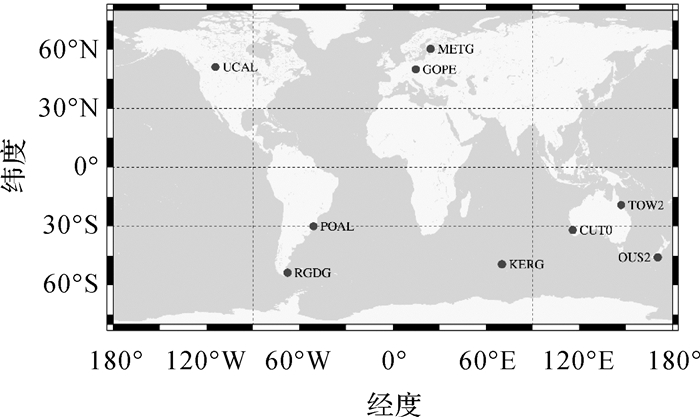
3 试验及结果分析为了评估SSR延迟对实时精密定位的影响,本文收集了2020年5月1日9个MGEX测站的数据进行分析,测站分布如图 1所示,其中RGDG站的采样率为1 s,其他测站的采样率为30 s。所有测站接收机均支持GPS、GLONASS、BDS、Galileo四系统双频信号,其中BDS系统包含BDS-2、BDS-3卫星,所有测站均支持北斗B1I、B3I信号。实时精密轨道钟差采用的是法国太空研究中心(CNES)提供的CLK93数据流,该数据流包含以上4个GNSS系统的精密产品。本文将实时接收的SSR数据流存储为事后文件便于模拟不同的延迟,模拟SSR延迟的区间为1 s~10 min。用于历元间差分计算的当前历元和前一历元在计算卫星位置和钟差时均采用同一参考时刻的SSR电文,其中前一历元的观测时刻和SSR的参考时刻保持一致,当前历元的观测时刻和前一历元的时间差即为模拟的SSR延迟。为了计算简便,本文直接将观测值重采样,使采样间隔与模拟的SSR延迟保持一致。
|
| 图 1 所选的MGEX测站分布 Fig. 1 Distribution of selected MGEX stations |
3.1 SSR延迟对实时精密定位的影响分析
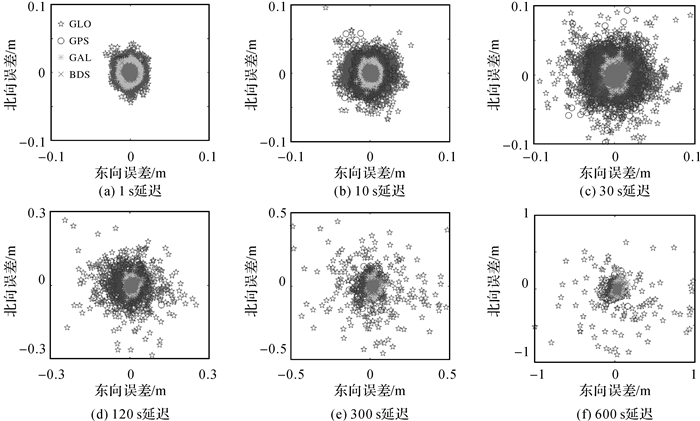
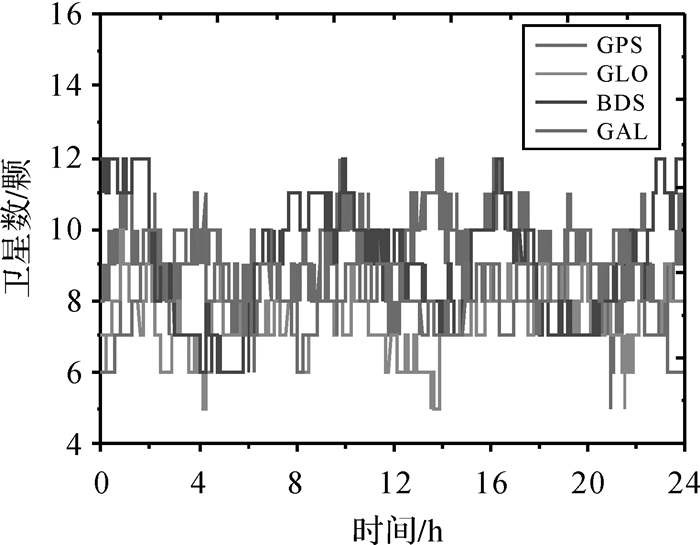
利用历元间差分模型分别对上述GNSS测站的双频数据进行处理。图 2给出了RGDG测站SSR延迟为1、10、30、120、300和600 s时的坐标误差结果。由于静态MGEX站的位置保持不变,解算结果即为坐标误差。由图 2可知,随着SSR延迟时间的增长,历元间差分的误差结果也随之变大,然而不同GNSS系统定位精度下降的幅度存在明显差异。表 2给出了4个系统不同SSR延迟下的RMS统计结果。本文中的BDS均表示BDS-2、BDS-3联合定位的结果。当SSR延迟为1 s时,GPS、BDS、Galileo在水平方向的定位精度均优于0.6 cm,GLONASS定位精度稍差,但其水平方向的定位精度仍优于0.8 cm。当SSR延迟为30 s时,GPS、GLONASS、BDS、Galileo 4个系统水平方向的定位精度分别为2.2、3.3、0.8和0.9 cm,与SSR延迟为1 s相比,GPS、GLONASS系统的定位精度明显下降,而BDS和Galileo的定位误差RMS统计值仍在1 cm以内。当SSR延迟增长到10 min时,GLONASS水平和高程方向的RMS统计值高达77.7和132.6 cm,而BDS、Galileo的水平和高程方向的RMS均在10 cm以内,精度优于GLONASS和GPS。图 3是RGDG站4个系统参与历元间差分解算的卫星数,可以看出对于非亚太区域,BDS参与解算的卫星数可达6颗及以上,且多数时段BDS卫星数多于GLONASS和Galileo系统。
|
| 图 2 不同SSR延迟下4个系统历元间差分定位水平方向误差结果 Fig. 2 Horizontal position error of TDCP solution under different SSR delays for four GNSS systems |
| SSR延迟 | GPS | GLONASS | BDS | Galileo | |||||||
| 水平 | 高程 | 水平 | 高程 | 水平 | 高程 | 水平 | 高程 | ||||
| 1 s | 0.4 | 0.5 | 0.8 | 1.1 | 0.3 | 0.4 | 0.6 | 0.7 | |||
| 10 s | 1.0 | 1.5 | 1.8 | 2.7 | 0.4 | 1.5 | 0.6 | 1.8 | |||
| 30 s | 2.2 | 3.2 | 3.3 | 5.2 | 0.8 | 1.0 | 0.9 | 1.0 | |||
| 2 min | 4.3 | 5.9 | 10.3 | 16.2 | 1.6 | 2.1 | 1.8 | 2.1 | |||
| 5 min | 6.3 | 8.7 | 28.0 | 45.6 | 3.0 | 3.4 | 4.0 | 4.7 | |||
| 10 min | 9.2 | 13.2 | 77.7 | 132.6 | 5.7 | 6.1 | 6.8 | 8.6 | |||
|
| 图 3 GPS、GLONASS、BDS、Galileo四系统参与历元间差分解算的卫星颗数 Fig. 3 The number of satellites involved in TDCP solution for GPS, GLONASS, BDS and Galileo |
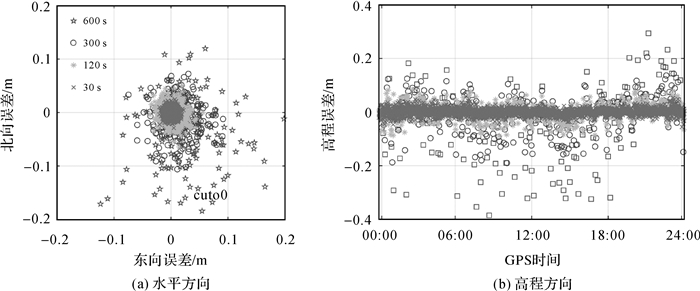
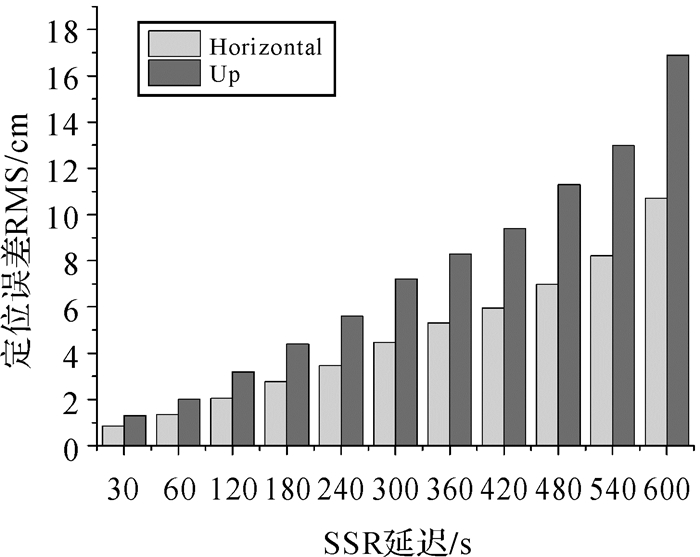
图 4和图 5分别给出了GPS、GLONASS、BDS、Galileo四系统组合定位时不同SSR延迟下的历元间差分定位误差结果。与单系统定位结果类似,随着SSR延迟时间的增长历元间差分定位精度呈下降趋势,当SSR延迟为30 s时,四系统组合定位水平和高程方向的RMS分别为0.8和1.3 cm,SSR延迟为10 min时,其对应的RMS分别为10.7和16.9 cm。将四系统组合的定位结果和单系统的定位结果比较时,可以发现当SSR延迟较小时,其定位精度和单BDS或Galileo的定位结果相当,随着SSR延迟的增大,四系统组合时的定位精度明显低于单BDS或Galileo系统。理论上,历元间差分的定位性能主要取决于卫星几何结构分布及实时精密星历产品精度。对多系统组合定位而言,其几何结构明显优于单系统,因此,其定位精度较低的主要原因是不同系统卫星轨道和钟差外推误差的差异性影响,为了提高SSR延迟情形下的多系统组合定位精度,需对不同系统的轨道和钟差外推误差做进一步评估。
|
| 图 4 SSR延迟为30、120、300和600 s时的四系统组合历元间差分定位误差结果 Fig. 4 Position error of four-system combined TDCP solution under 30, 120, 300, and 600 s SSR delay |
|
| 图 5 四系统组合历元间差分定位随SSR延迟增长的误差统计结果 Fig. 5 RMS statistic results of four-system combined TDCP solution as SSR delay increase |
3.2 GPS、BDS、GLONASS、Galileo系统SSR轨道及钟差产品外推误差分析
根据1.2节中SSR延迟下精密产品外推误差的评估方法,基于记录的CNESSSR数据流,本文处理得到了GPS、GLONASS、BDS、Galileo 4个系统不同SSR延迟下轨道和钟差外推引起的空间信号测距误差统计结果。图 6给出了几颗卫星从1 s~10 min SSR延迟的轨道和钟差外推误差统计结果。可以看出,随着SSR延迟时间的增长,轨道和钟差外推误差均慢慢变大,然而不同卫星的增长速度和趋势不尽相同。就轨道而言,不同卫星的外推误差均与SSR延迟呈线性正相关,不同卫星的外推误差增长速率差异较大,2颗GLONASS卫星(R03、R22)轨道外推10 min引起的空间信号测距误差达20 cm以上。对于钟差外推误差,不同卫星增长趋势差异较大,区别于其他卫星,G12卫星在80 s左右增长速率明显变缓;5颗GNSS卫星(G03、C03、C21、E01、E26)的外推误差明显小于另外3颗卫星(G12、R03、R22)。

|
| 图 6 1~600 s SSR延迟时轨道和钟差外推引起的空间信号测距误差统计结果 Fig. 6 SISREs caused by orbit and clock extrapolating under 1~600 s SSR delay |
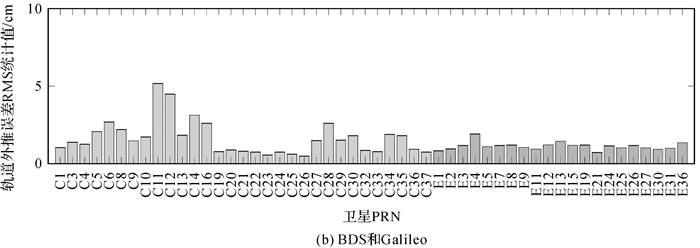
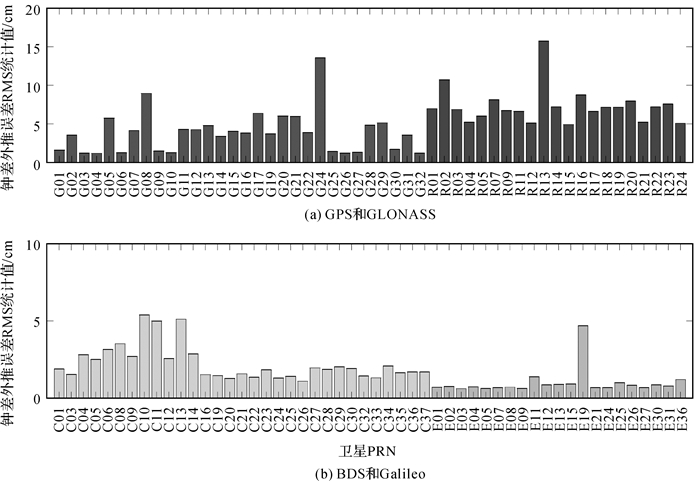
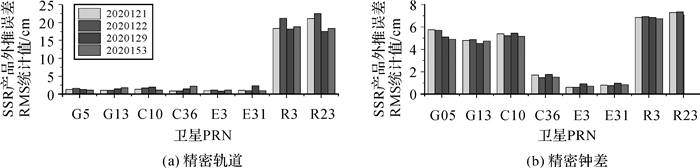
图 7和图 8是SSR延迟为10 min时4个GNSS系统卫星轨道和钟差外推引起的空间信号测距误差统计结果。对于北斗,CNES实时精密产品仅包含卫星号小于37的卫星。GPS、GLONASS、BDS和Galileo卫星在10 min延迟时间的轨道外推误差统计平均值分别是2.5、20.9、1.6和1.2 cm,GLONASS轨道外推误差明显高于其他3个系统。将钟差乘以光速换算为距离后,GPS、GLONASS、BDS和Galileo卫星在10 min延迟时间的钟差外推误差统计平均值分别是3.8、7.3、2.2和1.0 cm,GPS和GLONASS的钟差外推误差明显高于BDS和Galileo。由图 8可知,GPS的G01、G03、G06、G09、G10、G25、G26、G27、G30和G32卫星的钟差外推误差统计值明显小于其他GPS卫星。需要说明的是,这10颗卫星的卫星类型均是Block ⅡF,截至2020年5月1日,GPS共有12颗Block ⅡF卫星,其中上述10颗卫星搭载的是铷钟,而另2颗卫星(G08, G24)搭载的是铯钟(http://www2.unb.ca/gge/Resources/GPSConstellationStatus.txt)。此外,由图 8可以看出,BDS-3卫星的钟差外推误差略小于BDS-2卫星,这可能与BDS-3卫星的原子钟性能提升相关。与此同时,本文处理了另外3 d的精密星历数据,图 9展示了4 d不同星历数据计算的10 min延迟轨道和钟差外推误差统计结果,可以看出,不同天的精密产品外推误差统计结果基本一致。
|
| 图 7 SSR延迟为10 min时轨道外推引起的空间信号测距误差统计结果(2020-05-01) Fig. 7 SISREs caused by orbit extrapolating under 10 min SSR delay on 1 May 2020 |
|
| 图 8 SSR延迟为10 min时钟差外推引起的空间信号测距误差统计结果(2020-05-01) Fig. 8 SISREs caused byclockextrapolating under 10 min SSR delay on 1 May 2020 |
|
| 图 9 4 d不同数据计算的10 min SSR延迟时精密产品外推引起的空间信号误差统计结果 Fig. 9 SISREs caused by orbit and clock extrapolating under 10 minutes SSR delay in four different days |
综合轨道和钟差的外推误差统计结果可知,四系统中GLONASS精密产品外推误差远超过于其他3个系统,Galileo和BDS的精密产品外推精度也明显优于GPS,本节关于精密产品外推误差的评估结果间接印证了3.1节中的定位误差结果,当发生SSR延迟时,BDS和Galileo的实时定位性能要优于GPS和GLONASS。需要说明的是,Galileo精密产品外推误差略小于BDS,而其历元间差分定位精度略差于BDS,主要原因可能是Galileo系统的可用卫星数目少于BDS系统(图 3)。
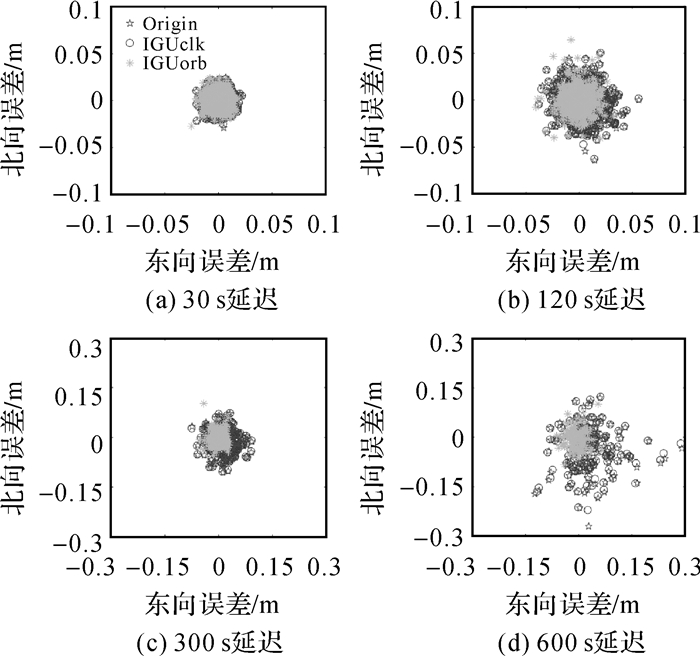
3.3 SSR延迟下的多模GNSS实时精密定位性能提升效果分析由3.1节和3.2节的分析可知,随着SSR延迟时间的增长,实时轨道和钟差的外推精度会逐渐降低,SSR延迟为10 min时,部分卫星的精密产品外推误差分别可达20 cm以上,即便采用四系统组合定位,实时定位水平和高程方向的误差仍达10.7和16.9 cm。为了提高SSR延迟下的实时定位精度,本文首先用长安大学北斗分析中心6 h更新生成的四系统超快速精密轨道和钟差产品分别对上述测站数据采用3种方案进行处理。3种方案的说明见表 3,方案1的轨道和钟差计算均采用延迟的SSR产品外推(与3.1节中的方法一致);方案2中卫星坐标计算采用延迟的SSR轨道产品外推,钟差采用匹配的超快速钟差产品线性内插计算;方案3中钟差计算采用延迟的SSR钟差产品外推,卫星坐标采用匹配的超快速轨道产品进行拉格朗日内插计算。由于超快速精密产品是提前数小时发布的,因此,用户在一定时段内任意观测时刻都能匹配上对应的精密星历产品。图 10和表 4展示了RGDG站SSR延迟下3种轨道/钟差计算方案时的四系统组合历元间差分定位误差结果。相比SSR外推方法(方案1),钟差采用超快速钟差产品时(方案2)的定位精度几乎不变,而轨道采用超快速轨道产品计算时(方案3)的定位精度显著提升,SSR延迟为10 min时,四系统组合定位水平和高程方向的定位精度分别为3.9和5.3 cm,相比方案一,两个方向的定位精度均提升了60%以上。由此说明,服务端轨道长时间的预报精度较高,在SSR延迟较大时,用户端可以采用超快轨道产品替代延迟的SSR产品计算卫星坐标,而卫星钟差特性相对复杂,其长时预报精度难以保障。
| 计算 | 方案1 (Origin) |
方案2 (IGUclk) |
方案3 (IGUorb) |
| 卫星坐标计算 | 延迟的SSR外推 | 延迟的SSR外推 | IGU轨道产品内插 |
| 卫星钟差计算 | 延迟的SSR外推 | IGU钟差产品内插 | 延迟的SSR外推 |
|
| 图 10 发生SSR延迟时采用3种不同轨道钟差计算策略下的四系统组合历元间差分定位误差结果 Fig. 10 Position error of four-system combined TDCP solution using three different orbit and clock calculation strategies under SSR delay situation |
| SSR延迟/s | Orgin | IGUclk | IGUorb | ||||||||
| E | N | U | E | N | U | E | N | U | |||
| 30 | 0.6 | 0.6 | 1.3 | 0.6 | 0.6 | 1.3 | 0.5 | 0.6 | 1.2 | ||
| 120 | 1.4 | 1.6 | 3.2 | 1.4 | 1.5 | 3.2 | 1.0 | 1.2 | 2.3 | ||
| 300 | 2.9 | 3.4 | 7.2 | 2.9 | 3.3 | 7.2 | 1.5 | 2.0 | 3.5 | ||
| 600 | 7.1 | 8.0 | 16.9 | 7.1 | 7.7 | 16.7 | 2.3 | 3.1 | 5.3 | ||
由上面的分析可知,在发生SSR延迟时,利用预报钟差难以提升实时精密定位的精度,不同系统的钟差外推误差差异较大,如GPS、GLONASS、BDS和Galileo 10 min延迟的钟差外推误差的RMS平均值分别是3.8、7.3、2.2和1.0 cm(换算为距离单位后),同一系统不同卫星的钟差外推误差特性也存在显著差异,如GPS 10颗Block ⅡF卫星的钟差外推误差明显小于其他GPS卫星,相比BDS-2卫星,BDS-3卫星的钟差外推误差也整体偏小。因此,在多系统组合实时定位时,除了采用超快速预报轨道产品,可在方案3的基础上根据不同系统不同卫星钟差的外推误差特性进一步优化随机模型(方案4),为BDS/Galileo等钟差外推误差较小的卫星赋予更大的权重,降低GLONASS等钟差外推误差较大的卫星权重,从而提高SSR延迟下的多模GNSS实时定位精度。SSR延迟下优化的随机模型计算方法为
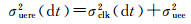 (14)
(14)
传统定位随机模型的先验误差仅包含σuee2,σuee2是接收机端观测值的噪声,一般根据卫星高度角确定;σclk2(dt)是与SSR延迟/数据龄期相关的钟差外推误差。
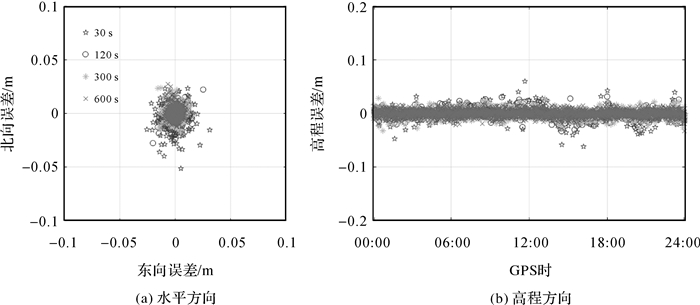
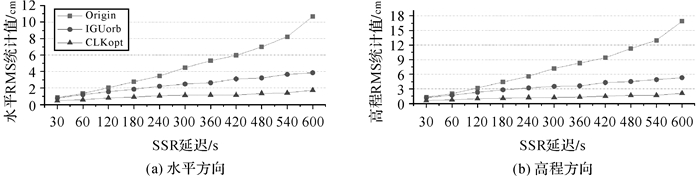
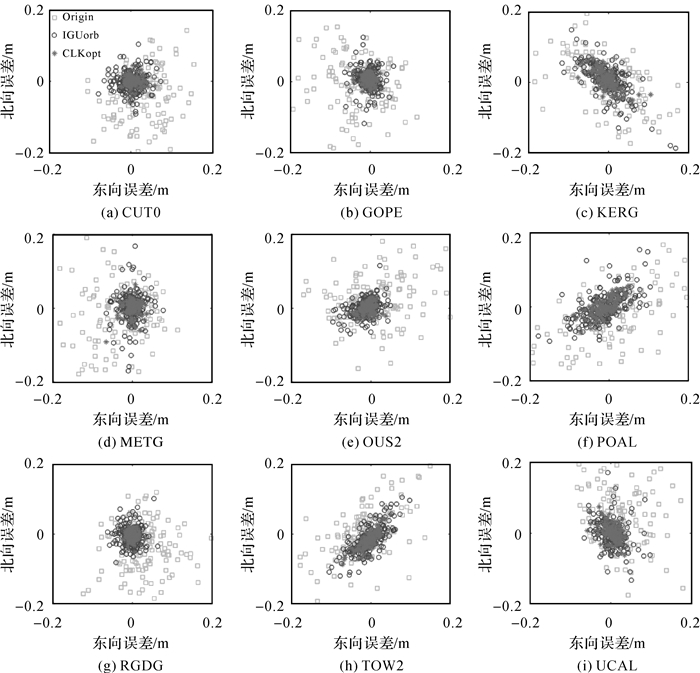
图 11给出了RGDG站在发生SSR延迟时,采用超快速精密轨道并将随机模型优化后(方案4)的四系统组合历元间差分定位误差结果。可以看出,SSR延迟从30 s~10 min变化时,其定位精度未见明显下降,SSR延迟为10 min时,其水平和高程方向的定位精度仍可达1.7和2.1 cm,相比方案1(图 4)的定位结果精度有了显著提升。图 12给出了3种方案随SSR延迟增长的实时定位精度变化情况,其中“CLKopt”表示方案4,从图中可以看出,对于任意的SSR延迟,方案4的定位精度均明显优于方案1和方案3。为了进一步验证方案4的有效性,本文同时处理了上述9个测站的数据。图 13展示了9个测站3种不同方案下的四系统组合定位水平方向的误差分布情况,与RGDG测站的结果一致,在发生SSR延迟时,相比基于传统SSR外推的定位模型(方案1),采用超快速精密轨道进行随机模型优化(方案4)的多系统组合实时定位呈现出较为明显的优势。
|
| 图 11 SSR延迟下顾及卫星钟差外推误差特性的四系统组合历元间差分定位误差结果 Fig. 11 Position error of four-system combined TDCP solution considering clock extrapolating error characteristic under SSR delay situation |
|
| 图 12 SSR延迟增长时3种轨道钟差计算策略下的四系统组合历元间差分误差结果统计 Fig. 12 RMS result of four-system combined TDCP solution using three different orbit and clock calculation strategies as SSR delay increases |
|
| 图 13 SSR延迟为10 min时3种不同方案的四系统组合历元间差分定位误差结果 Fig. 13 Position error of TDCP solution using three different strategies under 10 minutes SSR delay |
4 总结与讨论
针对实时精密单点定位服务产品的延迟/中断问题,本文重点评估了GPS、GLONASS、BDS、Galileo 4个GNSS系统SSR延迟下的轨道、钟差外推误差及其对实时精密定位的影响。本文首先介绍了SSR外推轨道及钟差误差的计算及评估方法;然后给出了发生SSR延迟时基于历元间差分模型的实时精密定位精度评估方法;最后用9个MGEX站的实测数据及CNES提供的实时精密产品进行试验分析并得出以下结论:
(1) 随着SSR延迟时间的增长,GNSS实时定位性能会逐渐下降,然而对于同样的SSR延迟,不同系统的实时定位性能下降幅度存在显著差异,BDS和Galileo在SSR延迟下的定位性能保持能力明显优于GLONASS和GPS。
(2) 与SSR延迟下的定位性能一致,在发生延迟时,SSR外推的钟差及轨道精度均有一定程度的下降,而不同GNSS系统的卫星外推精度保持能力差异较大。在SSR延迟为10 min时,GLONASS卫星轨道及钟差外推引起的空间信号测距误差可达20.9和7.3 cm,而BDS和Galileo的轨道和钟差外推引起的空间信号测距误差保持在2.2 cm以内。另外,同一系统不同卫星的精密卫星外推误差也可能存在明显差异,如GPS的10颗Block IIF卫星SSR延迟下的钟差保持性能优于其他GPS卫星,BDS-3的钟差保持性能也整体优于BDS-2卫星。
(3) 在发生较大SSR延迟时,使用超快速精密轨道可以显著提升多系统组合实时定位的性能,在顾及本文评估的不同系统不同卫星钟差外推误差的差异并优化随机模型后多系统组合定位性能可进一步提升。在SSR延迟时间为10 min时,四系统组合定位水平方向的定位精度从10.7 cm提升到1.7 cm。需要说明的是,SSR卫星轨道钟差产品自身的精度要优于超快速精密轨道钟差产品,在实际应用中,当SSR延迟较小时仍推荐采用SSR产品进行实时精密定位。
本文主要评估精密产品外推误差对实时精密定位的影响,在实际应用中,为了提升SSR延迟下的多GNSS系统实时精密定位性能,需进一步考虑多模GNSS系统精密产品自身的特点。除了优化定位模型,本文评估的相关结论对于优化GNSS实时轨道及钟差改正数的播发频率也具有重要参考价值。
| [1] |
ZUMBERGE J, HEFLIN M, JEFFERSON D, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [2] |
叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002. YE Shirong. Theory and its realization of GPS precise point positioning using un-differenced phase observation[D]. Wuhan: Wuhan University, 2002. |
| [3] |
郭斐. GPS精密单点定位质量控制与分析的相关理论和方法研究[M]. 武汉: 武汉大学出版社, 2016. GUO Fei. Research on theories and methods of GPS precision single point positioning quality control and analysis[M]. Wuhan: Wuhan University Press, 2016. |
| [4] |
施闯, 郑福, 楼益栋. 北斗广域实时精密定位服务系统研究与评估分析[J]. 测绘学报, 2017, 46(10): 1354-1363. SHI Chuang, ZHENG Fu, LOU Yidong. Research and evaluation of BDS real-time wide-area precise positioning service system[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1354-1363. DOI:10.11947/j.AGCS.2017.20170284 |
| [5] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407. ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica Cartographica Sinica, 2017, 46(10): 1399-1407. DOI:10.11947/j.AGCS.2017.20170327 |
| [6] |
China Satellite Navigation Office. BeiDou/Global Navigation Satellite System (GNSS) receiver differential data format(Ⅱ): BD 410003—2015[S]. Beijing: [s. n.], 2016.
|
| [7] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013. LI Xingxing. Rapid ambiguity resolution in GNSS precise point positioning[D]. Wuhan: Wuhan University Press, 2013. |
| [8] |
辜声峰. 多频GNSS非差非组合精密数据处理理论及其应用[D]. 武汉: 武汉大学, 2013. GU Shengfeng. Research on zero-difference uncombined data processing model for multi-GNSS and its application[D]. Wuhan: Wuhan University. 2013. |
| [9] |
ELSOBEIEY M, AL-HARBI S. Performance of real-time precise point positioning using IGS real-time service[J]. GPS Solutions, 2016, 20(3): 565-571. DOI:10.1007/s10291-015-0467-z |
| [10] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018. ZHOU Feng. Theory and methodology of multi-GNSS undifferenced and uncombined precise point positioning[D]. Shanghai: East China Normal University, 2018. |
| [11] |
WANG Z, LI Z, WANG L, WANG X, et al. Assessment of multiple GNSS real-time SSR products from different analysis centers[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 85. DOI:10.3390/ijgi7030085 |
| [12] |
HADAS T, BOSY J. IGS RTS precise orbits and clocks verification and quality degradation over time[J]. GPS Solutions, 2015, 19(1): 93-105. DOI:10.1007/s10291-014-0369-5 |
| [13] |
左翔, 戴志强, 李成钢, 等. SSR轨道和钟差改正数龄期对多系统实时PPP的影响分析[C]//中国卫星导航学术年会. 哈尔滨: [s. n.], 2019. ZUO Xiang, DAI Zhiqiang, LI Chenggang, et al. Impact of SSR orbit and clock corrections age on multi-GNSS real-time PPP[C]//Proceedings of 2019 China Satellite Navigation Conference. Harbin: [s. n.], 2019. |
| [14] |
MARTÍN A, HADAS T. DIMAS A, et al. Influence of real-time products latency on kinematic ppp results[C]//Proceedings of the 5th International Colloquiumon Scientific and Fundamental Aspects of the Galileo Program, Braunschweig, Germany: [s. n.], 2015: 27-29.
|
| [15] |
EL-MOWAFY A, MANOJ D, NOBUAKI K. Maintaining real-time precise point positioning during outages of orbit and clock corrections[J]. GPS Solutions, 2017, 21(3): 937-947. DOI:10.1007/s10291-016-0583-4 |
| [16] |
LV Yifei, DAI Zhiqiang, ZHAO Qile, et al. Improved short- term clock prediction method for real-time positioning[J]. Sensors, 2017, 17(6): 1308. DOI:10.3390/s17061308 |
| [17] |
HUANG Guanwen, CUI Bobin, ZHANG Qin, et al. An improved predicted model for BDS ultra-rapid satellite clock offsets[J]. Remote Sensing, 2018, 10(1): 60. |
| [18] |
PENG Yaquan, LOU Yidong, GONG Xiaopeng, et al. Real- time clock prediction of multi-GNSS satellites and its application in precise point positioning[J]. Advances in Space Research, 2019, 64(7): 1445-1454. DOI:10.1016/j.asr.2019.06.040 |
| [19] |
STEIGENBERGER P, MONTENBRUCK O. Galileo status: orbits, clocks, and positioning[J]. GPS Solutions, 2016, 21(2): 319-331. |
| [20] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测—试验验证数据分析[J]. 中国科学: 地球科学, 2018, 48(5): 584-594. YANG Yuangxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system: data analysis based on BDS-3 demonstration system[J]. Science China Earth Sciences, 2018, 48(5): 584-594. |
| [21] |
MALYS S, LAREZOS M, GOTTSCHALK S, et al. The GPS accuracy improvement initiative[C]//Proceedings of 1997 ION GPS, Kansas, MO, USA: [s. n.], 1997, 375-384.
|
| [22] |
MONTENBRUCK O, STEIGENBERGER P, HAUSCHILD A. Broadcast versus precise ephemerides: a multi-GNSS perspective[J]. GPS Solutions, 2015, 19(2): 321-333. DOI:10.1007/s10291-014-0390-8 |
| [23] |
ROBUSTELLI U, BENASSAI G, PUGLIANO G. Signal in space error and ephemeris validity time evaluation of milena and doresa Galileo satellites[J]. Sensors, 2019, 19(8): 1786. DOI:10.3390/s19081786 |
| [24] |
FREDA P, ANGRISANO A, GAGLIONE S, et al. Time-differenced carrier phases technique for precise GNSS velocity estimation[J]. GPS Solutions, 2015, 19(2): 335-341. DOI:10.1007/s10291-014-0425-1 |
| [25] |
ZHENG K, TANG L. Performance assessment of BDS and GPS/BDS velocity estimation with stand-alone receiver[J]. The Journal of Navigation, 2016, 69(4): 869-882. DOI:10.1017/S0373463315000958 |
| [26] |
LU C, LI X, NILSSON T, NING T, et al. Real-time retrieval of precipitable water vapor from GPS and BeiDou observations[J]. Journal of Geodesy, 2015, 89(9): 843-856. DOI:10.1007/s00190-015-0818-0 |
| [27] |
HADAS T, TEFERLE F N, KAZMIERSKI K, et al. Optimum stochastic modeling for GNSS tropospheric delay estimation in real-time[J]. GPS Solutions, 2017, 21(3): 1069-1081. DOI:10.1007/s10291-016-0595-0 |
| [28] |
QIAN C, LIU H, ZHANG M, et al. A geometry-based cycle slip detection and repair method with time-differenced carrier phase (TDCP) for a single frequency global position system (GPS) + BeiDou navigation satellite system (BDS) receiver[J]. Sensors, 2016, 16(12): 2064. DOI:10.3390/s16122064 |
| [29] |
WANG Jian, HAN Houzeng, LIU Fei, et al. Performance analysis of GNSS/MIMU tight fusion positioning model with complex scene feature constraints[J]. Journal of Geodesy and Geoinformation Science, 2021, 4(2): 1-13. |
| [30] |
ZENG Tian, SUI Lifen, JIA Xiaolin, et al. Results and analyses of BDS precise orbit determination with the enhancement of Fengyun-3C[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(3): 68-78. |
| [31] |
WEI Ziqing, RUAN Rengui, JIA Xiaolin, et al. Satellite positioning and orbit determination system (SPODS): introduction and evaluation[J]. Journal of Geodesy and Geoinformation Science, 2018, 1(1): 25-29. |





