2. 桂林电子科技大学信息与通信学院, 广西 桂林 541004;
3. 广西电网有限公司柳州供电局, 广西 柳州 545005;
4. 广州大学经济与统计学院, 广东 广州 510006
2. College of Information and Communication, GuiLin University of Electronic Technology, Guilin 541004, China;
3. Liuzhou Power Supply Bureau, Guangxi Power Grid Co., Ltd., Liuzhou 545005, China;
4. School of economics and statistics, Guangzhou University, Guangzhou 510006, China
周跳探测与修复是载波相位定位中关键的一步,能否准确探测与修复,直接影响到定位精度。周跳可以是从1到百万的整数[1],大周跳很容易被探测出来,探测最小的1周周跳是精密定位的要求。目前周跳探测的方法有很多,对单频数据而言,简单的方法有高次差法[2]和多项式拟合法[3],这两种方法都能容易地探测出大周跳,但难以探测出小周跳。对于双频数据而言,常用的是TurboEdit[4]方法,它是联合使用MW法和电离层残差法[5]来探测周跳。对于三频数据的周跳探测方法,多数学者采用不同的无电离层组合和MW组合进行求解周跳[6-10],主要是研究如何选取更优的组合系数。
虽然三频组合的数据可以提供更多更优的组合方式[7-10],但是双频数据组合方式有限,在低采样率条件下,要达到高精度探测较为困难。为了更好地推进双频探测周跳的方法,文献[11]提出了在MW基础上向前和向后移动窗口滤波的算法(FBMWA)和电离层残差的二次时间差法(STPIR)。其研究表明FBMWA法比文献[4]提出的用递归的均值滤波器对MW进行滤波效果更好,但需要用到后面历元的数据,不利于实时探测周跳。STPIR法与电离层残差法相比,在电离层变化缓慢时,效果相当;在电离层活跃时,电离层残差法效果较差,而STPIR法依然较好。
另外,文献[12]首先提出了多普勒积分法探测周跳,该方法简单易行,但是多普勒的精度受采样率的约束,即使在1 s采样率时也未必能保证很好地探测出1周周跳。本文提出了一种重构多普勒的方法,重构出的多普勒受采样率的影响小。在低采样率时,重构相应频率的多普勒替代其观测值,代入多普勒积分法进行周跳探测,效果更优。受宽巷组合的启发,本文提出了一种组合双频载波,并重构其多普勒用于积分,进行周跳探测的方法。它只采用相位进行组合,而MW法组合时引入了伪距,伪距噪声较大,所以它比MW法探测精度更优,噪声更低。且它与STPIR法联合求周跳,可以探测出最小的1周周跳以及连续周跳。
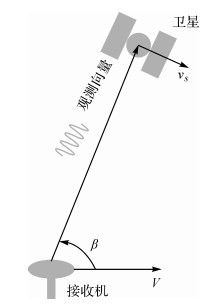
1 重构多普勒积分联合STPIR 1.1 重构多普勒的方法本文利用卫星与接收机间的多普勒形成的原理和模型[13],如图 1所示,提出了一种重构多普勒的方法,仅需要广播星历,适合实时应用。下面阐述重构多普勒的算法模型:由于广播星历计算得到的卫星位置Ps以及卫星速度vs三维向量都是基于地心地固(ECEF)坐标系的,即该坐标系随地球自转而转动,因此不需要考虑地球自转对多普勒的影响。
|
| 图 1 卫星与接收机的多普勒模型 Fig. 1 Doppler model of satellite and receiver |
如图 1所示,向量vs表示接收机的速度,卫星在接收机处的观测向量ρ的方向由接收机指向卫星。设vs=(xv, yv, zv),Ps=(xs, ys, zs),伪距定位方式得到的接收机位置Pu=-(xu, yu, zu)。故ρ=(xρ, yρ, zρ)=(xs-xu, ys-yu, zs-zu)。那么多普勒重构值可由式(1)计算
 (1)
(1)
式中,l是单位观测向量,l=ρ/|ρ|;λ是对应卫星频率的波长;v是接收机速度向量;“·”表示向量点乘。
1.2 重构多普勒积分法分析式(1)可知重构多普勒误差主要来源于中分子计算的部分,若组合出来的波长越长,即式(1)中分母变大,重构误差就会减小。下面以北斗为例,北斗的频率B1=1 561.098 MHz和B2=1 207.14 MHz,对应的相位观测值ϕ1和ϕ2可以表示成如下[14]
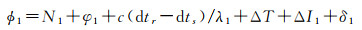 (2)
(2)
 (3)
(3)
在式(2)和式(3)中,c是光速,N1和N2分别表示B1和B2的整周模糊度,单位为周。φ表示相位的小数部分,δ表示其他误差,包括频率相关的接收机和卫星端的非校正硬件延迟、相位延迟,观测噪声、多路径效应及其他未模型化的误差。对于同一台接收机和同一颗卫星而言,接收机钟差dtr、卫星钟差dts,对流层延迟是完全相同的,电离层的误差由于受到频率的影响而不同,而且其他误差δ也具有一定的正相关性。
本文要组合的波长为λWL=c/(B1-B2)=1.024 7 m,下面对双频组合载波相位得到该波长进行推理。设站星距为ρ,用下标1、2、WL分别表示B1、B2、组合频率的波长,那么可列出如下关系
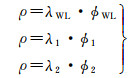 (4)
(4)
因为λ1=c/B1,λ2=c/B2,那么式(4)可改写为
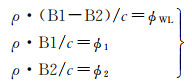 (5)
(5)
所以ϕWL=ϕ1-ϕ2,即组合的载波相位可由式(2)减去式(3)得
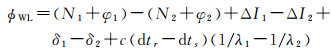 (6)
(6)
设当前历元为ti,后一历元为ti+1,若对式(6)中相邻历元相减,由于式(6)中的卫星钟差和接收机钟差基本相同,可以认为基本消去,那么组合的相位观测量的变化量为
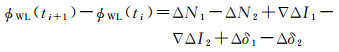 (7)
(7)
在对流层变化平缓时,相邻历元的电离层误差较为接近,因此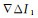
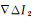
把双频组合的波长代入式(1),重构出的多普勒为fd。按照最初多普勒积分法探测周跳的思路,结合式(6)和式(7),周跳组合可以表示成如下
 (8)
(8)
式中, ΔN1和ΔN2分别表示B1和B2频点上发生的周跳,此时对式(8)右边得到的结果进行四舍五入取整,可以得到ΔN1-ΔN2的整数解。显然当ΔN1=ΔN2时,与无周跳的结果一样,因此需要联合其他方法把这些周跳盲点也探测出来。
1.3 联合探测与修复周跳STPIR法是在电离层残差法上进行时间二次差的方法,当电离层活动较大时,能有效减小电离层误差的影响,探测效果较好[15]。电离层残差可以表示成
 (9)
(9)
电离层残差法是对式(9)进行历元单差,那么
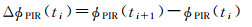 (10)
(10)
式中,ti表示当前历元,ti+1表示下一历元。STPIR法是对式(10)的再次历元间差分,用ti+2表示当前往后第2个历元,则
 (11)
(11)
在式(10)中,若产生周跳,周跳值应为
 (12)
(12)
因此,如果非连续历元,如400历元产生周跳,那么式(12)的再次差分,即STPIR法就会产生图 2中第400 s、401 s中的大小相等、符号相反的周跳探测量,即分别为ΔN1-f1/f2×ΔN2和f1/f2×ΔN2-ΔN1,此时可取前一个值作为周跳检测量。但是,若历元199和历元200发生连续周跳,如图 2中第200 s处(虚线圈出),就会产生重叠,此时前一个历元的周跳探测量仍然取前一个值,即2.305周,而后一个历元的周跳探测量要取后一个值的相反数,即1.987周作为周跳探测量。
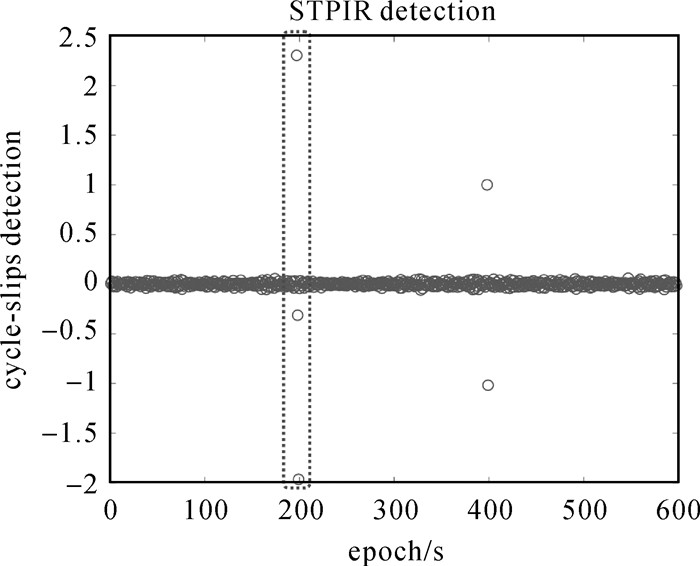
|
| 图 2 STPIR法探测周跳 Fig. 2 STPIR method detect cycle-slip |
结合式(8)和式(12),可以看出上述两种方法都存在探测盲点,对式(8),当ΔN1=ΔN2时探测不出;对式(12),ΔN1≈f1/f2×ΔN2时不敏感,比如(ΔN1, ΔN2)为(9, 7)的周跳。那么就需要联立方程组解算出周跳。设重构多普勒积分法的周跳探测量为a,STPIR法的周跳探测量为b。由于ΔN1和ΔN2都是整数,则ΔN1-ΔN2必然是整数,因此先对a进行四舍五入取整(round),然后联立STPIR法,可得如下方程组
 (13)
(13)
令H=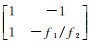
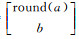
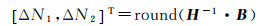 (14)
(14)
周跳的修复方法:若在周跳探测过程中出现了周跳,把对应的相位观测值ϕ1和ϕ2分别减去式(14)得到的跳变值ΔN1和ΔN2即可。
2 重构多普勒误差分析本节首先分析用广播星历对各类卫星重构多普勒的影响,然后对比多普勒观测值和重构多普勒的误差。文献[16]研究了多普勒观测值的精度,研究表明多普勒观测值与卫星高度角有关,高度角越大,误差越小,可以综合认为原始多普勒观测值的精度为2 cm/s。因此,随着采样率的减小,即数据历元间隔的增大,多普勒误差会增大。而分析式(1)可知重构多普勒误差来源于卫星的位置、速度,接收机的位置、速度,以及实际的信号波长。
在式(1)中,当接收机静止时v=0,但接收机运动时,需要知道它的运动速度。为了使该方法在动态中也能进行多普勒估计,推广其适用性,本文用多普勒观测值进行接收机速度的估计。在本文所提出方法中加入了用多普勒观测值计算接收机速度的方法[13, 17],文献研究表明,大约95%定速结果可达0.2 m/s的精度。
本文方法已在北斗和GPS卫星上进行验证,GPS只有MEO卫星,而北斗导航系统由GEO、MEO、IGSO 3种类型的卫星组成[18],所以此处以北斗为例进行说明。3种类型卫星的轨道和速度(相对于地球的速度)都能用广播星历的16参数模型进行计算[19],北斗2号的MEO和IGSO优于2 m[20],而GEO略差,优于5 m[21],并且北斗3号卫星各项性能指标皆优于北斗2号[21-22]。按PDOP为5的保守估计,卫星速度由16参数模型计算的误差应小于4 cm/s,而由18参数模型计算的误差最多只有10-4 m/s量级[23]。目前,伪距单点定位精度可达米级[24],伪距相对定位精度可达亚米级[25]。
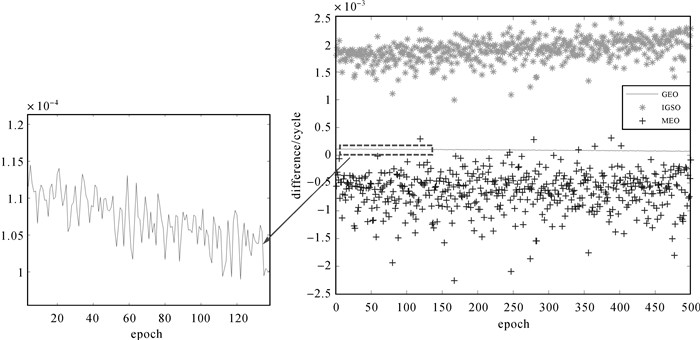
下面用实测静态数据进行验证:首先用精密星历计算得到的卫星位置、速度,用精密单点定位确定接收机位置,并进行多普勒重构。然后用广播星历计算得到卫星的位置、速度,用伪距单点定位计算接收机位置,并进行多普勒重构。最后以精密星历重构的多普勒为基准,以广播星历重构的多普勒结果减去前者。对于广播星历得到的卫星位置,伪距定位得到的接收机位置,都是米级误差,这些误差综合起来可达十几米。但是从图 3重构多普勒对比的结果看,GEO卫星差别最小,是10-4数量级,IGSO和MEO是10-3数量级,这些误差对重构的影响很小。这可以用式(1)中的重构原理进行解释:结合式(1)和表 1,上述米级误差,经过除以107 m数量级的站星距|ρ|,再乘以103 m数量级的卫星速度,这些误差的影响将会降至原来的10-4倍。虽然GEO的轨道精度最差,但是由于它的轨道高度较高,|ρ|较大,且是同步卫星,速度相对于其他卫星很小,从而使得在重构多普勒过程中反而受轨道误差的影响最小。因此用广播星历和伪距单点定位算法得到的卫星位置、速度、接收机位置也能较好地重构多普勒。而经过双频组合后的波长变得很长,重构其多普勒的误差会更小。
|
| 图 3 各类型卫星不同条件下重构多普勒的对比 Fig. 3 Comparison of estimated Doppler for different types of satellites under different conditions |
| 卫星类型 | GEO | MEO | IGSO |
| RMS统计精度/m | 2.05 | 1.53 | 1.14 |
| 轨道高度/m | 35 786×103 | 21 528×103 | 35 786×103 |
| 卫星速度的数量级/(m/s) | 100 | 103 | 103 |
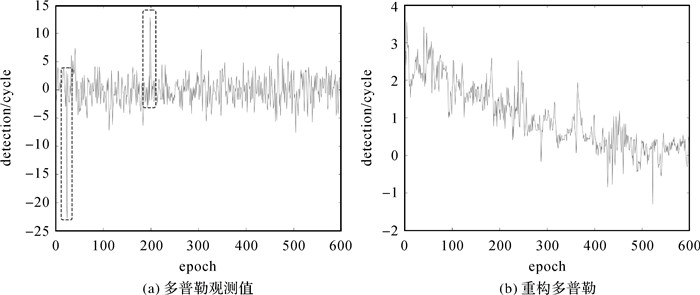
这里再对比北斗B1频点的多普勒观测值和重构值的周跳探测噪声:图 4是采用多普勒积分法对一组无周跳的数据(30 s历元间隔)进行周跳检测的结果,横坐标表示观测历元,纵坐标表示周跳探测的结果。理论上无周跳时,探测结果应该小于1,但明显多普勒观测值的探测误差比较大,特别是在图 4(a)中框出的历元处。对比可知,用重构多普勒进行积分探测周跳的效果要优于用多普勒观测值。
|
| 图 4 两种多普勒积分法对比 Fig. 4 Comparison of two Doppler integral methods |
3 试验与分析
考虑到实际应用场景中,动态采样率较高,静态采样率较低,本文采用1 Hz采样率和30 s采样间隔的实测数据分别进行动态和静态模式下的验证,并且把所提出的重构多普勒积分法跟MW法进行对比。为了展示在不同卫星类型、不同频率组合的试验,其中1 Hz采样率的数据采用GPS的L1和L2频率组合,30 s采样间隔的数据采用B1和B3频率组合。
首先用广播星历计算出卫星位置、卫星速度,接着用伪距定位计算出接收机大概位置。选用的数据无周跳,在表 2的历元中模拟加入周跳(ΔN1, ΔN2)进行验证。由于MW的周跳检测量与重构多普勒积分法都是整数,这里考虑先对其结果先进行四舍五入取整,再求解,如式(12)、式(13)所示。
| 采样率/ (s/次) | 历元 | 周跳模拟 | MW+STPIR | 本文方法 | |||
| 探测结果 | 是否正确 | 探测结果 | 是否正确 | ||||
| 1 | 151 | (1, -1) | (1, -1) | √ | (1, -1) | √ | |
| 253 | (9, 7) | (9, 7) | √ | (9, 7) | √ | ||
| 450 | (1, 1) | (1, 1) | √ | (1, 1) | √ | ||
| 451 | (-1, -2) | (-1, -2) | √ | (-1, -2) | √ | ||
| 76 | (1, 0) | (1, 0) | √ | (1, 0) | √ | ||
| 30 | 175 | (-5, -4) | (-5, -4) | √ | (-5, -4) | √ | |
| 302 | (0, 0) | (4.3) | × | (0, 0) | √ | ||
| 351 | (-2, -2) | (-2, -2) | √ | (-2, -2) | √ | ||
| 375 | (0, 0) | (-5, -4) | × | (0, 0) | √ | ||
| 476 | (0, 1) | (0, 1) | √ | (0, 1) | √ | ||
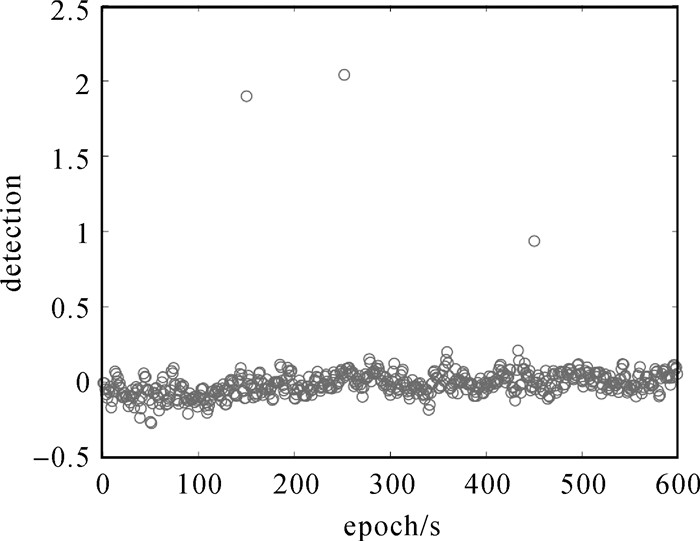
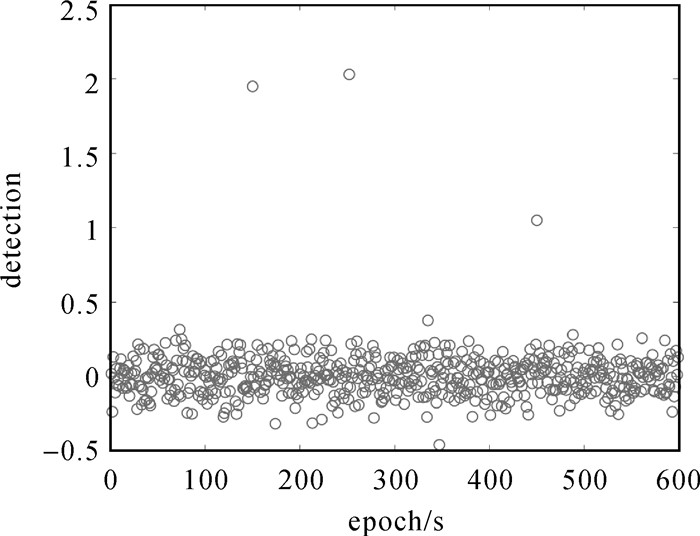
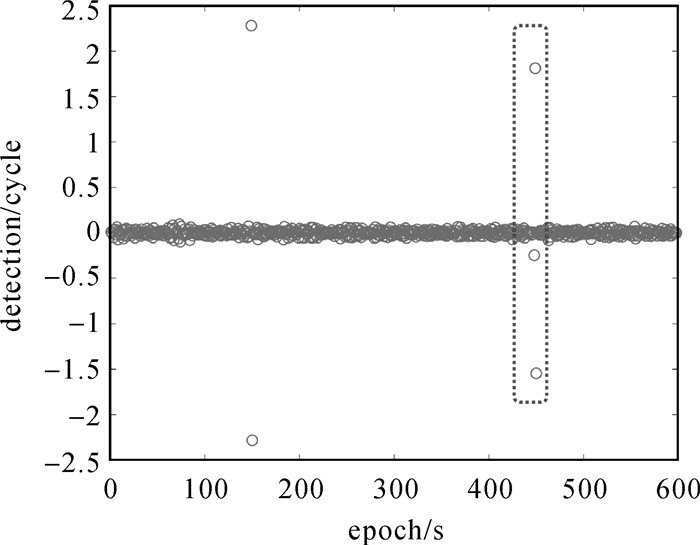
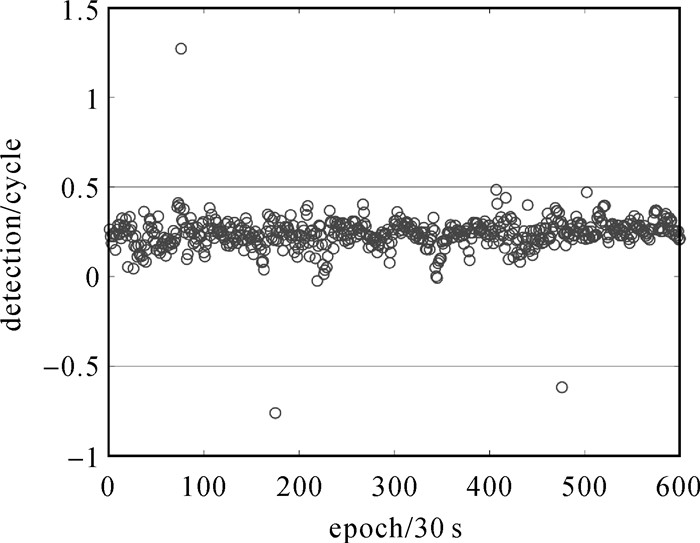
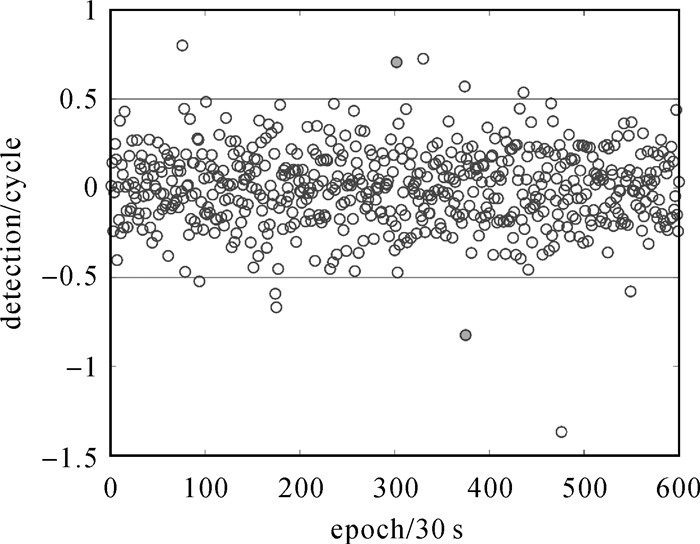
本文试验结果如图 5-图 10所示,可以看出在无周跳时,重构多普勒积分法的探测量比MW法小,即前者探测误差更小。在动态模式中,由于引入接收机速度,也引入相关误差,会对重构多普勒积分法有一定影响,而不会对MW法产生影响。但对比图 5和图 6,显然还是重构多普勒积分法在无周跳时,探测量更接近0,即探测误差更小。虽然在1 s的高采样率情况下,MW能准确探测出ΔN1-ΔN2,即两频率周跳之差。但在30 s低采样率时,结合图 9-图 10以及表 2的探测结果,发现MW有个别历元即使无周跳,其探测量也会大于0.5而导致误判,本文方法在试验过程中未发现探测量大于0.5而导致误判。图 7中框出部分表示相邻历元发生周跳,与图 4中一样会在中间点产生重叠,采用相同处理方法;试验结果表明,可以处理相邻历元出现周跳的情况。图 5、图 6中的第450历元,以及图 9、图 10中的351历元没有出现跳变,正说明了相同周跳出现在两个频率时,恰好是重构多普勒积分法和MW法的共同探测盲点。
|
| 图 5 重构多普勒积分法(1 s) Fig. 5 Reconstruction Doppler integration method(1 s) |
|
| 图 6 MW法(1 s) Fig. 6 MW method(1 s) |
|
| 图 7 STPIR法(1 s) Fig. 7 STPIR method(1 s) |

|
| 图 8 STPIR法(30 s) Fig. 8 STPIR method(30 s) |
|
| 图 9 重构多普勒积分法(30 s) Fig. 9 Reconstruction Doppler integration method(30 s) |
|
| 图 10 MW法(30 s) Fig. 10 MW method(30 s) |
文献[11, 26-27]的研究表明,MW法受观测噪声(伪距噪声较大)和多路径效应的影响,导致其探测噪声较大,都需要对其进行平滑滤波处理才能有好的效果。本文采用的重构多普勒的方法误差主要来源于卫星的位置和速度,以及接收机的位置和速度,目前条件下,仅用广播星历和伪距定位方法得到这些结果对该方法影响不大。
图 9中直线外实心点的历元周跳探测出错。在历元302中,MW法的探测结果是0.707,四舍五入就是1,STPIR法的探测结果是0.024 9。在历元375中,MW法的探测结果是-0.823,四舍五入就是-1,STPIR法的探测结果是0.005 7。其原因是:B1和B3频率上的周跳差值都是1,这是由于MW误判造成的。虽然STPIR法的探测结果都是正确的,但是根据式(12),因为B1/B3=1.230 6,两频率上这种比值的周跳是STPIR法的周跳盲点,而5/4=1.25,4/3=1.333,与B1/B3很接近。所以MW的误判导致用最小二乘法解算得到这些结果。
4 总结本文提出了一种高精度周跳探测与修复的方法,与传统的MW法相比,可更有效地解决周跳探测与修复的问题。结果表明,在低采样率时,重构相应频率的多普勒比多普勒观测值误差更小。为了更有效地提高重构多普勒的周跳检测精度,进而对双频数据进行组合,并重构其多普勒,进行积分以探测周跳。重构多普勒积分法跟MW有共同的探测盲点,而STPIR法也有自身的局限性,用重构多普勒积分法联合STPIR进行周跳探测。用动态1 Hz和静态1/30 Hz采样率的实测数据,加入模拟周跳进行验证,并与无平滑滤波的MW法进行对比。结果表明,重构多普勒积分法探测周跳的误差比MW法小,且在30 s低采样率时也能准确探测出任意整数周跳。
| [1] |
ZANGENEH-NEJAD F, AMIRI-SIMKOOEI A R, SHARIFI M A, et al. Cycle slip detection and repair of undifferenced single-frequency GPS carrier phase observations[J]. GPS Solutions, 2017, 21(4): 1593-1603. DOI:10.1007/s10291-017-0633-6 |
| [2] |
KLEUSBERG A, PEYTON D, WELLS D. Airborne gravimetry and the global positioning system[C]//IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences. Las Vegas, NV: IEEE, 1990.
|
| [3] |
LICHTENEGGER H, HOFMANN-WELLENHOF B. GPS-data preprocessing for cycle-slip detection[M]//BOCK Y, LEPPARD N.Global Positioning System: An Overview. New York: Springer, 1990.
|
| [4] |
BLEWITT G. An automatic editing algorithm for GPS data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. DOI:10.1029/GL017i003p00199 |
| [5] |
GOAD C C. Precise positioning with the GPS[M]//TURNER S. Applied Geodesy. Berlin: Springer, 1987.
|
| [6] |
刘柳, 吕志伟, 于晓东, 等. GNSS三频周跳探测与修复算法[J]. 测绘学报, 2017, 46(4): 453-459. LIU Liu, LÜ Zhiwei, YU Xiaodong, et al. Real-time cycle-slip detection and repair algorithm of GNSS triple-frequency observations[J]. Acta Geodaetica et CartographicaSinica, 2017, 46(4): 453-459. DOI:10.11947/j.AGCS.2017.20160532 |
| [7] |
黄令勇, 翟国君, 欧阳永忠, 等. 削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报, 2015, 44(8): 840-847, 883. HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Triple-frequency TurboEdit cycle-slip processing method of weakening ionospheric activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840-847, 883. DOI:10.11947/j.AGCS.2015.20140380 |
| [8] |
黄令勇, 翟国君, 欧阳永忠, 等. 三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717-725. HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Ionospheric cycle slip processing in triple-frequency GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 717-725. DOI:10.11947/j.AGCS.2015.20140348 |
| [9] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768. HUANG Lingyong, SONG Lijie, WANG Yan, et al. BeiDou triple-frequency geometry-free phase combination for cycle-slip detection and correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768. |
| [10] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722, 729. LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time cycle-slip detection and repair based on code-phase combinations for GNSS triple-frequency un-differenced observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722, 729. |
| [11] |
CAI Changsheng, LIU Zhizhao, XIA Pengfei, et al. Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity[J]. GPS Solutions, 2013, 17(2): 247-260. DOI:10.1007/s10291-012-0275-7 |
| [12] |
LIPP A, GU X. Cycle-slip detection and repair in integrated navigation systems[C]//Proceedings of 1994 IEEE Position, Location and Navigation Symposium-PLANS'94. Las Vegas, NV: IEEE, 1994.
|
| [13] |
谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. XIE Gang. Principles of GPS and reciever design[M]. Beijing: Publishing House of Electronics Industry, 2009. |
| [14] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018. ZHOU Feng. Theory and methodology of multi-GNSS undifferenced and uncombined precise point positioning[D]. Shanghai: East China Normal University, 2018. |
| [15] |
范丽红, 王利, 张明, 等. 基于MW与STPIR组合的周跳探测与修复方法研究[J]. 武汉大学学报(信息科学版), 2015, 40(6): 790-794. FAN Lihong, WANG Li, ZHANG Ming, et al. A combination of MW and second-order time-difference phase ionospheric residual for cycle slip detection and repair[J]. Geomatics and Information Science of Wuhan University, 2015, 40(6): 790-794. |
| [16] |
肖云, 孙中苗, 程广义. 利用GPS多普勒观测值精确确定运动载体的速度[J]. 武汉测绘科技大学学报, 2000, 25(2): 113-118. XIAO Yun, SUN Zhongmiao, CHENG Guangyi. Precise determination of velocity for airborne gravimetry using the GPS Doppler observations[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(2): 113-118. |
| [17] |
KAPLAN E D, HEGARTY C J. GPS principle and application[M]. 2nd ed. Boston, London: Electron Industry Publishing Company, 2008.
|
| [18] |
ZENG Tian, SUI Lifen, JIA Xiaolin, et al. Results and analyses of BDS precise orbit determination with the enhancement of FengYun-3C[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(3): 68-78. |
| [19] |
ZHANG Zhongkai, DU Lan, LIU Li, et al. A 16-parameter GEO broadcast ephemeris[J]. Journal of Geodesy and Geoinformation Science, 2018, 1(1): 46-52. |
| [20] |
张益泽, 陈俊平, 周建华, 等. 北斗广播星历偏差分析及改正[J]. 测绘学报, 2016, 45(S2): 64-71. ZHANG Yize, CHEN Junping, ZHOU Jianhua, et al. Analysis and application of BDS broadcast ephemeris bias[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 64-71. DOI:10.11947/j.AGCS.2016.F027 |
| [21] |
毛亚, 王潜心, 胡超, 等. 北斗在轨卫星广播星历精度分析[J]. 宇航学报, 2018, 39(9): 1012-1020. MAO Ya, WANG Qianxin, HU Chao, et al. Precision analysis of BeiDou satellites broadcast ephemeri[J]. Journal of Astronautics, 2018, 39(9): 1012-1020. |
| [22] |
杨宇飞, 杨元喜, 胡小工, 等. 北斗三号卫星两种定轨模式精度比较分析[J]. 测绘学报, 2019, 48(7): 831-839. YANG Yufei, YANG Yuanxi, HU Xiaogong, et al. Comparison and analysis of two orbit determination methods for BDS-3 satellites[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 831-839. DOI:10.11947/j.AGCS.2019.20180560 |
| [23] |
常志巧, 胡小工, 时鑫, 等. 基于位置观测的北斗广播星历速度精度分析[J]. 空间科学学报, 2018, 38(4): 553-559. CHANG Zhiqiao, HU Xiaogong, SHI Xin, et al. Accuracy analysis of satellites velocity with BDS broadcast ephemeris based on position observations[J]. Chinese Journal of Space Science, 2018, 38(4): 553-559. |
| [24] |
FAN Chunming, GUAN Qinglin, ZHU Zhengping, et al. Fuzzy weighting approach for single point positioning with single-frequency pseudo-range observations[J]. Advances in Space Research, 2019, 63(9): 2982-2994. DOI:10.1016/j.asr.2018.03.027 |
| [25] |
RIFE J. Collaborative vision-integrated pseudorange error removal: team-estimated differential GNSS corrections with no stationary reference receiver[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(1): 15-24. |
| [26] |
蔡成林, 王亮亮, 刘昌盛, 等. 利用改进型TurboEdit算法进行BDS载波相位周跳检测与修复[J]. 武汉大学学报(信息科学版), 2016, 41(12): 1632-1637. CAI Chenglin, WANG Liangliang, LIU Changsheng, et al. The cycle-slip detection and repair of BDS based on improved TurboEdit algorithm[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1632-1637. |
| [27] |
张小红, 曾琪, 何俊, 等. 构建阈值模型改善TurboEdit实时周跳探测[J]. 武汉大学学报(信息科学版), 2017, 42(3): 285-292. ZHANG Xiaohong, ZENG Qi, HE Jun, et al. Improving TurboEdit real-time cycle slip detection by the construction of threshold mode[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 285-292. |



