2. 32021部队, 北京 100000;
3. 北京师范大学, 北京 100036;
4. 中国科学院空天信息创新研究院, 北京 100036
2. Troops 32021, Beijing 100000, China;
3. Beijing Normal University, Beijing 100036, China;
4. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100036, China
星基增强系统(SBAS)通过GEO卫星播发GNSS导航卫星轨道、钟差和格网电离层改正数以及UDRE和GIVE等完好性参数,用以提升区域用户GNSS导航服务精度与可靠性。1992年美国联邦航空管理局(FAA)提出了广域差分(WAAS)构想后,各国开始建设自己的星基增强系统。目前主要的星基增强系统有美国的WAAS、欧盟的EGNOS、日本的MSAS和印度的GAGAN。美国航空无线电技术委员会(Radio Technical Commission for Aeronautics, RTCA)2016年颁布的《全球定位系统/广域增强系统机载设备最低运行性能标准》(DO-229E)[1]详细描述了WAAS报文数据格式与内容。RTCA协议针对GPS L1 C/A频点单频用户进行增强。
北斗二号采用区域网定轨确定卫星轨道,基于星地双向时间同步确定卫星钟差[2-5],利用北斗Klobuchar 8参数广播电离层模型修正电离层延迟以提供基本导航服务,北斗二号SBAS系统播发等效钟差改正数用于修正卫星钟差与轨道径向误差[6-7],并以5°×2.5°空间分辨率播发格网电离层修正参数[8]。北斗三号采用区域网加星间链路定轨确定卫星轨道,利用星地星间双向时间同步确定卫星钟差[9-11],采用北斗BDGIM 9参数广播电离层模型修正电离层延迟以提供基本导航服务[12]。2018年12月27日《北斗卫星导航系统公开服务性能规范》[13]发布,北斗三号全球系统开始提供基本导航服务[14],随着北斗三号全球系统的逐步建成与完善,BDSBAS星基增强系统将成为日后工作重心。BDSBAS需要遵照RTCA协议增强GPS L1 C/A用户,同时需要增强BDS B1C用户。
电离层延迟是影响GNSS单频用户服务精度的主要误差源之一,除各GNSS系统播发的广播电离层参数外,星基增强系统也采用薄壳电离层模型提供更高精度的电离层延迟误差改正[15-16]。电离层延迟可通过双频伪距或精密单点定位提取[17]。WAAS播发电离层格网报文以修正用户电离层延迟[1, 18]。WAAS利用基于梯度变化的克里金插值(KT)算法计算格网点垂直延迟,并基于卡方因子算法实现电离层异常状态的检验及GIVE参数的计算[19-20]。相较于平面拟合算法,基于克里金插值算法处理得到的格网电离层改正精度可提升3%~6%[21]。此后,基于最差用户几何位置的格网点延迟方差估值算法解决了由电离层风暴引起区域电离层梯度剧烈变化导致的服务完好性变差问题[22];基于电离层层析技术的克里金插值后处理算法用以测量美国与巴西上空电子密度总含量[23]。印度GAGAN采用平面拟合算法计算格网点垂直延迟,采用与WAAS一致的算法计算GIVE,并且给出了适合赤道地区电离层活动的先验参考分布[24]。基于印度上空实测数据表明,相较于平面拟合算法,采用克里金插值计算格网点垂直延迟更为稳定[25]。适合中国区域的电离层球壳高度和格网电离层模型在后续研究中得到了详细论证[26-28]。陆态网实测数据表明,中国区域格网电离层采用平面拟合算法估算格网点垂直延迟RMS略低于克里金插值,但存在严重的边际效应[29]。
本文参考WAAS格网电离层计算算法,综合平面拟合与反比距离加权方法实现BDSBAS格网电离层格网点垂直延迟估值的计算。为避免粗差导致平面拟合估计值偏离实际值,根据克里金插值平稳假设,电离层活动正常状态下,利用小范围(5°×5°)内的穿刺点中值估计样本均值,利用样本方差序列中值估计样本方差剔除粗差。考虑到由电离层活动不规则导致的残差分布的非正态性,GIVE的计算考虑了残差分布的峰度系数与偏度系数,最终结合基于历史信息的卡方因子,能够实现99.9%以上的GIVE包络率并有效避免过包络。本文首先介绍了BDSBAS格网电离层容错算法与格网改正数解算算法;接着重点介绍了基于残差分布偏度与峰度系数的GIVE算法;最终用2020年1月BDSBAS监测接收机实测数据验证了算法的有效性并简单评估了格网电离层服务精度。
1 粗差剔除与残差统计采用监测接收机双频相位平滑伪距观测数据提取电离层延迟,不可避免地存在粗差。粗差的存在会导致格网点垂直延迟估值失真,且显著增加平差迭代次数,导致格网电离层解算耗时增加。
对于观测数据中可能存在的粗差,一般可在平差计算格网点电离层延迟时,采用多次迭代的方式剔除。但这种迭代收敛剔除粗差的办法效率较低;此外,粗差的存在会导致平差估值失真,并最终导致最小二乘平差收敛到局部最优解甚至是错误解。针对上述问题,在进行格网电离层解算前,先对双频提取的穿刺点垂直延迟做一次预处理:根据克里金插值平稳假设[20],电离层活动正常状态下,假设电离层梯度在5°×5°小范围内变化不明显,利用小范围(5°×5°)内的穿刺点中值估计样本均值,利用样本方差序列中值估计样本方差δrobust2,剔除偏离样本中值3倍δrobust以上的粗差后进行格网电离层解算,从而得到比较合理的格网点垂直延迟估值的初值,进而采用多次迭代的方式剔除原始数据粗差。
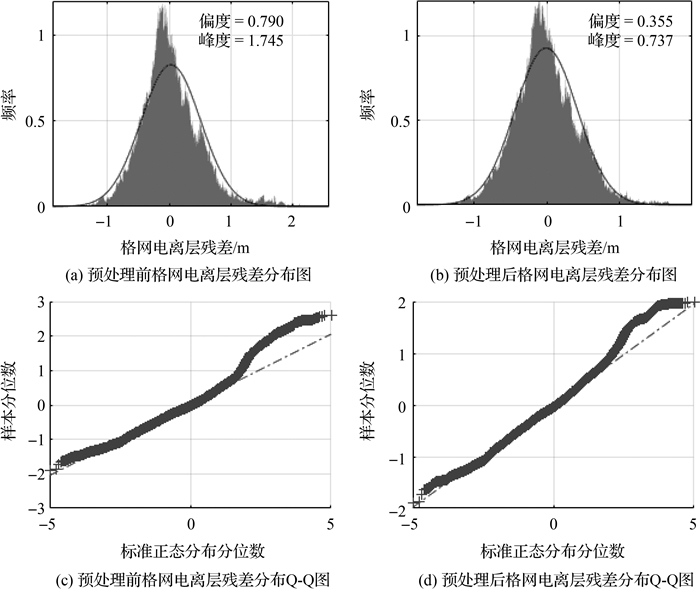
采用上述粗差剔除算法,可显著降低迭代次数并提高格网电离层格网点垂直延迟估值的精度与可靠性。图 1给出了采用中值容错前后的格网电离层残差分布:图 1(a)为未采用中值容错,仅采用多次迭代方式剔除粗差的格网电离层残差频率分布直方图;图 1(b)为采用中值容错后的格网电离层残差频率分布直方图;图 1(c)为对应残差分布的Q-Q图,图中十字点线越靠近参考虚线,则表明样本分布为正态分布的可能性越大;图 1(d)为对应残差分布的Q-Q图。
|
| 图 1 采用中值容错前后的格网电离层残差分布 Fig. 1 Grid ionospheric residual distribution of median fault tolerance |
由图 1可知,采用中值容错剔除粗差后,Q-Q图十字点线更靠近参考虚线,样本分布偏度与峰度值更接近0;格网电离层残差分布会更加靠近正态分布。这说明了粗差剔除合理有效。
2 格网点延迟估计避免电离层梯度变化对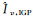
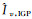
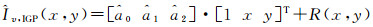 (1)
(1)
式中,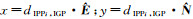

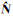
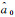
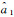
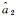
为估计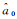
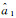
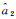
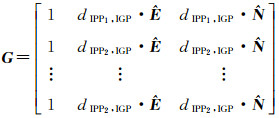 (2)
(2)
同一卫星或者同一监测接收机的观测量间存在相关性,故令协方差矩阵W-1为
 (3)
(3)
式中,δIi, IPPi2为先验的协方差,数值为0.35 m;δdecorr为去相关参数[20];δbias, i, j为先验协方差,取值为
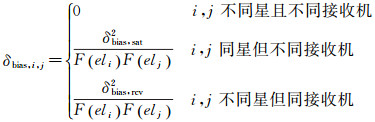 (4)
(4)
式中,δbias, sat2和δbias, rcv2根据监测接收机对观测卫星的观测噪声确定;F(elj)是与卫星仰角有关的函数。
那么,格网点垂直延迟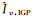
 (5)
(5)
式中,Iv, IPP=[Iv, IPP1 Iv, IPP2 … Iv, IPPn]T为格网点附近的穿刺点(IPP)处电离层垂直延迟。
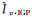
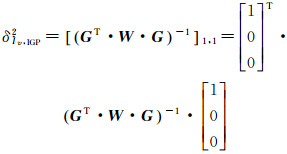 (6)
(6)
采用平面拟合算法计算电离层格网点垂直延迟,可有效避免电离层梯度变化对估值的影响,在服务区内部精度略优于克里金插值,但存在严重的边际效应[29]。为避免边际效应,利用平面拟合残差距离反比加权(IDW)计算格网点垂直延迟改正量,并修正到由平面拟合计算的格网点垂直延迟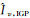
偏度(skewness)[20]反映了残差分布的非对称性,正态分布偏度系数为0。采样于未知分布的样本偏度值绝对值越大,表明该未知分布是正态分布的可能性越小。
偏度(skewness) α的计算方法为
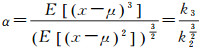 (7)
(7)
式中,μ为未知分布期望,可用样本均值近似;ki为未知分布的i阶矩, 可用样本i阶矩近似,计算公式为
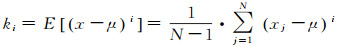 (8)
(8)
式中,xj为采样于未知分布的样本;N为样本总数。
峰度(kurtosis)[30]值β反映了残差分布的拖尾性质,正态分布峰度系数为0。采样于未知分布的样本峰度值绝对值越大,表明该未知分布是正态分布的可能性越小,当峰度(kurtosis)值β小于0时,表示样本分布为厚尾分布。
峰度(kurtosis)β的计算方法为
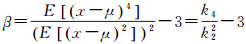 (9)
(9)
采用平面拟合得到格网点垂直延迟后,根据RTCA协议[1]提供的格网电离层用户算法插值计算穿刺点垂直延迟,与双频提取电离层垂直延迟做差得到残差序列,根据残差序列的统计特性确定完好性参数GIVE。
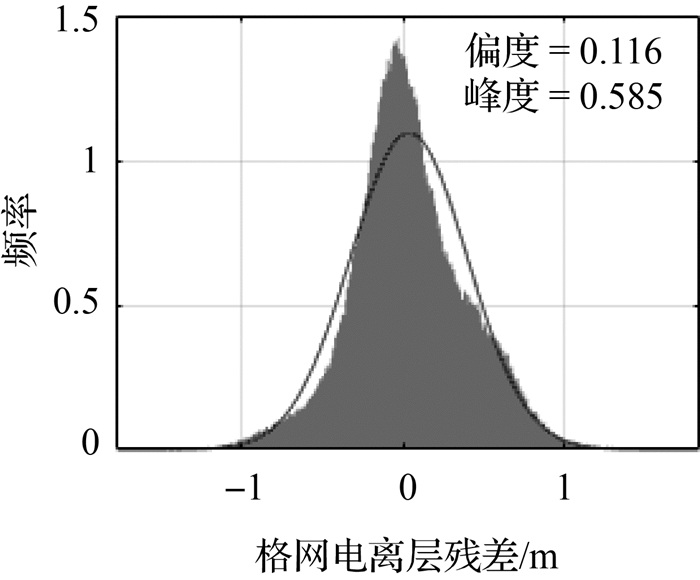
图 2为2019年11月23日—2019年11月25日双频提取与格网计算电离层延迟互差的频率分布直方图,期间未发生电离层暴,计算残差分布偏度值为0.116、峰度值为0.585。
|
| 图 2 未发生电离层暴时电离层格网残差分布的偏度系数与峰度系数s Fig. 2 Skewness coefficient and kurtosis coefficient of the ionospheric grid residual distribution under ideal conditions |
统计2019年10月20日—2020年3月18日的格网电离层残差分布偏度值与峰度值得到表 1。从表中可以看出,99.9%的格网点残差分布偏度值绝对值在2.507以下、峰度值绝对值在9.459以下。当残差分布偏度值与峰度值偏离0时,说明残差分布为正态分布的可能性变小,基于正态分布假设给出的0.999概率置信区间已经不在可靠,需要扩大置信区间。
| 分位数/(%) | 偏度系数|α| | 峰度系数|β| |
| 25.0 | 0.090 | 0.543 |
| 50.0 | 0.189 | 0.772 |
| 75.0 | 0.323 | 0.960 |
| 99.9 | 2.507 | 9.459 |
3.2 边界方差的估计
为反映电离层格网点垂直延迟估值的可靠性,为用户提供最差包络,必须同时考虑残差分布特性与电离层历史信息,WAAS采用卡方因子来实现电离层历史信息的引入。格网点边界方差由式(10)[20]计算
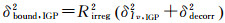 (10)
(10)
式中,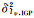
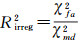 (11)
(11)
卡方检验因子Rirreg2用于电离层异常状态检测,为格网电离层残差分布与描述正常(χfa2)与异常(χmd2)状态的两个由电离层历史信息确定的已知先验分布的卡方统计量的比值确定,其取值在1~6.69[20]。
卡方统计量计算公式为
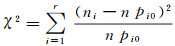 (12)
(12)
式中,pi0为样本落入指定区间的理论概率;ni是落入该区间的样本个数;n是样本总数。卡方统计量χ2服从自由度为r-1的卡方分布。
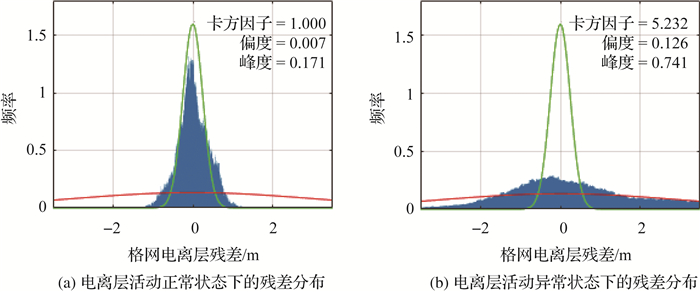
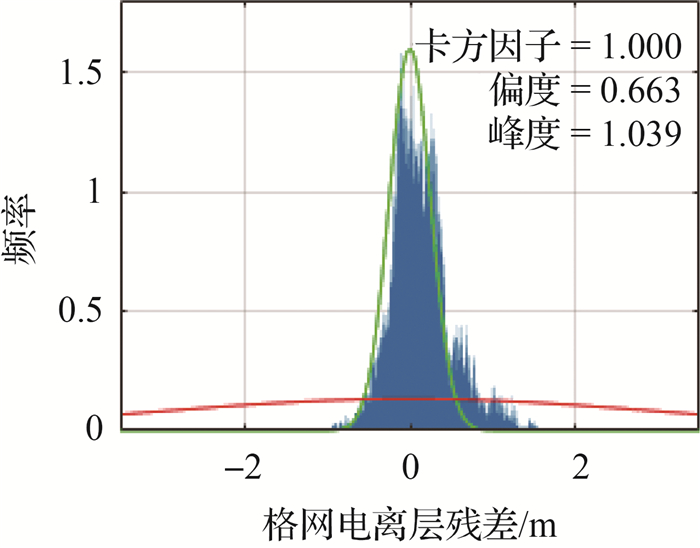
图 3反映了卡方因子Rirreg2对电离层异常天气的响应情况((a)正常状态;(b)异常状态)。图中绿色实线为正常状态参考分布概率密度曲线,红色实线为异常状态参考分布概率密度曲线,蓝色柱形图为频率分布直方图。图 4反映了卡方检验因子Rirreg2对格网电离层残差分布偏离正态分布时的响应情况。从图中可以看出,即使残差分布偏度达到0.6,峰度达到1.0以上时,卡方检验因子仍未及时响应。这是由于当电离层格网残差分布偏离给定的正常状态先验分布、靠近异常状态先验分布时,卡方检验因子Rirreg2才会做出响应,并显著放大格网点边界方差,从而起到电离层异常状态快速响应的作用;但当电离层活动正常,样本残差分布更靠近正常先验分布,由于平面拟合模型表达所导致的残差分布偏离正态分布情况无法被卡方检验因子反映出来,因此在计算格网点边界方差时加入偏度与峰度因子描述残差样本偏离正态分布的程度。
|
| 图 3 卡方检验因子Rirreg2对电离层异常天气的响应情况图 Fig. 3 Response of chi-square test factor Rirreg2 to abnormal space weather in ionosphere |
|
| 图 4 卡方检验因子Rirreg2对格网电离层残差分布偏离正态分布时的响应情况 Fig. 4 Response of chi-square test factor Rirreg2 to grid ionospheric residual distribution deviation from the normal distribution |
去相关参数δdecorr被解释为平面拟合算法模型表达误差,采用去相关参数δdecorr可以有效提高包络率,但可能导致过包络问题。由于地磁赤道穿过中国南部地区,电离层梯度变化更为复杂,当采用与WAAS相同的去相关参数时,服务区南部地区部分格网点包络率低于99.9%,若扩大去相关参数会导致服务区内北部地区部分格网点过包络,BDSBAS格网电离层不宜采用固定的去相关参数δdecorr办法。
考虑到卡方因子无法反映由于平面拟合模型表达所导致的残差分布偏离正态分布情况,计算格网点边界方差时增加与残差分布的偏度和峰度有关的因子Rs_k2
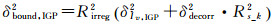 (13)
(13)
式中
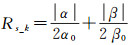 (14)
(14)
式中,α和β为利用格网点附近穿刺点残差计算的样本偏度与峰度系数,根据表 1,α0与β0取其99.9 % 分位数。
加入因子Rs_k2后,基于实测数据动态的调整去相关参数δdecorr,从而使得格网点边界方差δbound, IGP2包含更多的信息:当电离层梯度变化平稳,实测数据满足平面拟合算法模型假设时,动态减小去相关参数;相反的,动态扩大去相关参数。
3.3 GIVE的计算根据式(14)得到格网点边界方差δbound, IGP2,计算δGIVE2
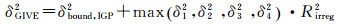 (15)
(15)
式中,δ12、δ22、δ32、δ42为格网点附近4个象限的残差序列方差。
格网点完好性参数GIVE采用式(16)计算
 (16)
(16)
考虑到残差分布可能是非零均值的,计算GIVE时,加入格网电离层残差序列均值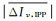
截至2020年3月,中国境内32个BDSBAS监测站数据入站率稳定,监测接收机IFB稳定,能够满足区域格网电离层解算需求。监测站均匀分布在中国境内,每个监测站均配备3台BDS监测接收机、3台GNSS多模监测接收机,可以同时解码获取GPS、GLONASS、Galileo 3系统观测数据与导航电文。目前仅利用北斗三号B1C-B2A、北斗二号B1I-B3I、GPS L1 C/A-L2P双频相位平滑伪距(CNMC)[31]提取电离层延迟参与格网解算。
按照本文所述算法剔除数据粗差后,再根据本文所述算法计算电离层格网点垂直延迟和GIVE,统计格网电离层改正残差RMS、改正百分比和GIVE包络率,以验证算法精度与可靠性。同时为考察BDSBAS格网电离层增强服务精度,利用本文算法计算得到的格网电离层产品,选取服务范围内的4个监测站伪距单点定位,并统计定位精度提升情况。统计结果时间系统均采用北斗时;格网电离层延迟单位为m。
采用2019年12月12日32个监测站双频提取电离层延迟,截止高度角设置为15°,利用三角投影函数[32]计算穿刺点垂直延迟。利用上文所述算法计算格网点垂直延迟,计算GIVE时不考虑去相关参数,统计GIVE一天包络率并绘制图 5。
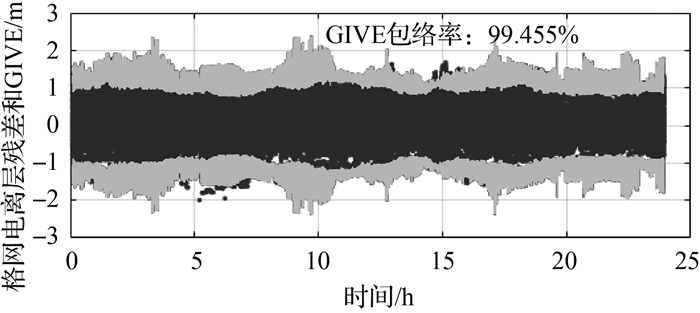
|
| 图 5 2019年12月12日BDSBAS格网电离层未增加Rs_k2因子和去相关参数的GIVE包络情况 Fig. 5 GIVE envelope diagram of the BDSBAS grid ionosphere without Rs_k2 factor and decorrelation parameters on December 12, 2019 |
图 5为不考虑去相关参数并且未增加Rs_k2因子GIVE包络情况;图中实线为GIVE包络线,散点为格网电离层残差序列点。由图 5可知,不考虑去相关参数和残差偏度系数与峰度系数时,GIVE包络率只能达到99%左右。为进一步分析GIVE未能成功包络的残差点,将GIVE未包络的部分单独提取并加以分析得到图 6。
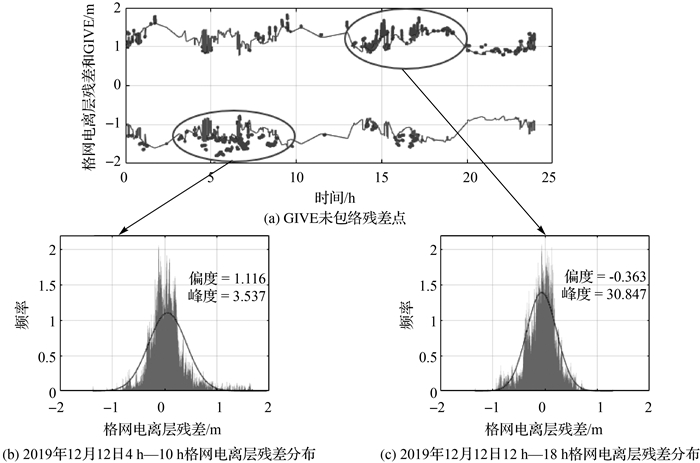
|
| 图 6 2019年12月12日BDSBAS格网电离层GIVE未包络部分残差分布 Fig. 6 Distribution of residuals in the unenveloped part of the ionospheric GIVE on December 12, 2019 |
图 6为GIVE未包络部分残差分布图。由图 6可知,不考虑去相关参数和残差偏度系数与峰度系数时,GIVE包络存在大量的漏警点;将漏警率高的时段单独取出,绘制该时段残差分布图,得到图 6(b)和图 6(c),可以看出,此时段残差分布峰度系数与偏度系数均明显偏离0。
仿照WAAS的做法,固定的去相关参数为0.35 m,计算GIVE并统计一天包络率得到图 7。图 7中实线为GIVE包络线,散点为格网电离层残差序列点。图 7(a)为30°N—55°N范围内的穿刺点包络图,图 7(b)为0°N—30°N范围内的穿刺点包络图。由图 7可以看出,若采用固定的去相关参数,对于中国区域0°N—30°N范围内的穿刺点GIVE过包络现象明显;对于中国区域低纬度地区仍存在不少的漏警点,包络率仅为99.8%左右。若扩大去相关参数,可以进一步减少漏警率并提高GIVE包络率,但难免会引入过包络的问题,使得GIVE估值较实际偏大。
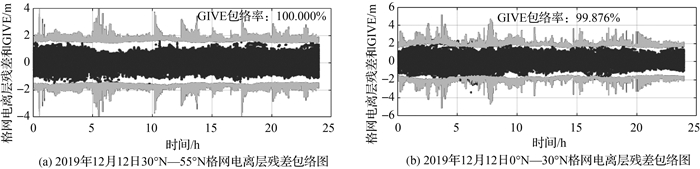
|
| 图 7 2019年12月12日BDSBAS格网电离层采用固定的去相关参数的GIVE包络情况 Fig. 7 GIVE envelope diagram of the BDSBAS ionosphere grid with fixed decorrelation parameters on December 12, 2019 |
按照本文提出的算法,取先验的去相关参数为0.35 m,增加残差分布偏度峰度因子Rs_k2动态调整去相关参数,计算格网点GIVE,统计0°N—55°N所有穿刺点包络率绘制图 8。从图 8可以看出,考虑残差分布偏度系数与峰度系数动态调整去相关参数后,GIVE包络率达到99.9%以上,GIVE漏警率大大降低,同时过包络现象也得到抑制。
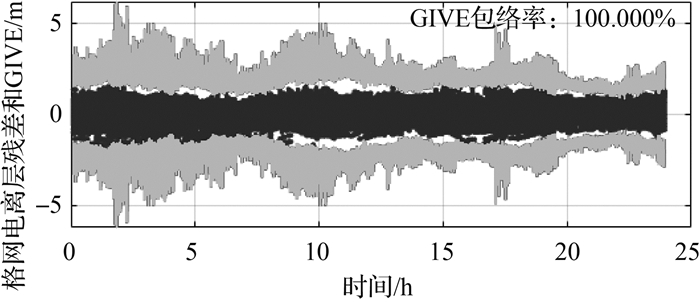
|
| 图 8 2019年12月12日BDSBAS格网电离层增加Rs_k2因子后GIVE包络情况 Fig. 8 GIVE envelope diagram of the BDSBAS ionosphere grid based Rs_k2 on December 12, 2019 |
2020年1月20日发生一次小型电离层暴(http://www.nsmc.org.cn/NSMC),图 9反映了电离层异常天气时的包络性能。图 9(a)采用伯尔尼大学(AIUB)事后处理获取的全球电离层延迟图(GIM)绘制,从图中可以看出当日电离层暴导致了GIM异常双峰现象;图 9(b)为当日境内BDSABS监测站所有穿刺点格网电离层残差频率分布直方图,其偏度值与峰度值靠近公式(14) 给出的阈值;图 9(c)为当天GIVE包络图。从图 9可以看出,残差分布的偏度值峰度值会及时响应电离层暴等异常空间天气,放大GIVE并保证包络率仍在99.9%以上。
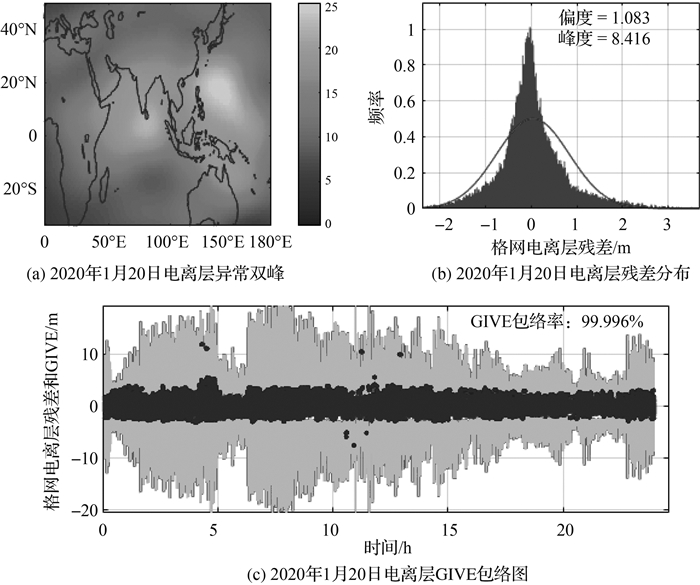
|
| 图 9 2020年1月20日发生电离层暴时GIVE包络情况 Fig. 9 The GIVE envelope diagram during Ionospheric storm on January 20, 2020 |
为进一步评价本文提出的GIVE算法包络性和电离层格网点垂直延迟解算精度,利用2020年1月1日—2020年1月31日连续一个月32个BDSBAS境内监测站实测数据,按照本文算法计算格网点垂直延迟和GIVE,从格网电离层残差RMS(分别与双频实测数据和CODE GIM产品对比)、改正百分比、GIVE包络率3个角度评价BDSBAS格网电离层服务精度。选取华中、华北、华东、华南、西北、东北、西南地区7个格网点,统计2020年1月整月RMS、改正百分比和GIVE包络率得到表 2。
| 格网点经纬度 | RMS | RMS(CODE) | 改正百分比/(%) | 包络率/(%) | 包络率(δdecorr=0.35 m)/(%) |
| 120°E 45°N | 0.433 m/2.666TECU | 0.291 m/1.795TECU | 77.152 | 100.000 | 100.000 |
| 115°E 40°N | 0.451 m/2.779TECU | 0.142 m/0.874TECU | 77.613 | 100.000 | 100.000 |
| 85°E 45°N | 0.365 m/2.249TECU | 0.547 m/3.373TECU | 78.596 | 100.000 | 100.000 |
| 110°E 35°N | 0.504 m/3.103TECU | 0.247 m/1.521TECU | 77.049 | 99.998 | 99.999 |
| 120°E 30°N | 0.620 m/3.822TECU | 0.290 m/1.788TECU | 75.209 | 99.999 | 99.999 |
| 110°E 20°N | 0.578 m/3.560TECU | 0.377 m/2.325TECU | 76.332 | 99.998 | 99.943 |
| 100°E 15°N | 0.482 m/2.967TECU | 0.311 m/1.916TECU | 79.563 | 100.000 | 99.892 |
为简单评估BDSBAS格网电离层服务精度,利用2020年1月1日—2020年1月31日连续一个月32个BDSBAS境内监测站实测数据,按照本文算法计算格网点垂直延迟和GIVE,选取位于华中(Sta1)、华北(Sta2)、华东(Sta3)、华南(Sta4)的4个监测站统计增强定位提升百分比得到表 3。伪距单点定位采用本团队编写的性能监视程序,其双频相位平滑伪距基本导航定位精度在5 m(95%)以内,将事后精密单点定位(PPP)解算坐标作为参考真值考察增强定位提升百分比。
| 监测站编号 | 北/m(95%) | 东/m(95%) | 高/m(95%) | 三维/m(95%) | 提升百分比/(%) | ||||||||
| 基本导航 | 格网增强 | 基本导航 | 格网增强 | 基本导航 | 格网增强 | 基本导航 | 格网增强 | ||||||
| Sta1 | BDS | 1.204 | 0.985 | 1.582 | 1.565 | 3.041 | 2.919 | 3.633 | 3.455 | 5.150 | |||
| GPS | 1.672 | 1.678 | 1.969 | 1.755 | 5.264 | 3.991 | 5.864 | 4.672 | 25.512 | ||||
| Sta2 | BDS | 1.077 | 1.117 | 1.495 | 1.453 | 2.715 | 2.661 | 3.281 | 3.231 | 1.562 | |||
| GPS | 1.644 | 1.683 | 2.005 | 1.847 | 4.796 | 3.191 | 5.452 | 4.053 | 34.520 | ||||
| Sta3 | BDS | 1.299 | 1.217 | 1.624 | 1.587 | 3.161 | 3.146 | 3.784 | 3.728 | 1.501 | |||
| GPS | 1.669 | 1.737 | 1.930 | 1.806 | 5.152 | 3.243 | 5.749 | 4.098 | 40.294 | ||||
| Sta4 | BDS | 1.219 | 1.324 | 1.763 | 1.808 | 3.242 | 3.128 | 3.886 | 3.848 | 1.007 | |||
| GPS | 2.038 | 1.810 | 2.347 | 1.956 | 4.886 | 4.119 | 5.791 | 4.906 | 18.044 | ||||
由表 2和表 3可知,BDSBAS格网电离层改正残差RMS平均在0.4 m左右,大约在2~3 TECU量级;改正百分比均在75%以上,平均在78%左右。利用本文提出的GIVE算法,GIVE包络率均在99.9%以上,由于考虑了残差分布的偏度特性与峰度特性,GIVE包络在降低漏警率的同时抑制了过包络现象。利用BDSBAS监测接收机进行伪距单点定位,在格网电离层增强的状态下,对于BDS BIC频点用户,定位精度增强不明显;对于GPS L1 C/A频点用户,可增强定位精度20%~40%。GPS L1 C/A频点用户增强效果明显,是由于GPS基本导航用户采用了Klobuchar八参数广播电离层模型,该模型改正百分比大约在50%左右;而BDS BIC频点用户采用BDGIM广播电离层模型修正电离层延迟,该模型改正百分比全球平均75%[27],中国境内改正百分比更高,故定位精度提升不明显。考虑到格网电离层电文更新频率比广播电离层模型高,相比于精度提升,电离层异常活动及时预警对于BDS BIC频点用户更为重要。
5 结论本文提出了基于残差分布峰度系数与偏度系数的格网电离层GIVE算法。相比于采用固定的去相关参数计算GIVE,基于残差分布偏度值与峰度值自适应调整去相关参数计算的GIVE可以实现在降低漏警率的同时有效抑制过包络现象。新算法计算的完好性参数GIVE可以做到对服务区内任何纬度范围内的格网点实现99.9%以上的包络率。除此之外,本文同时介绍了BDSBAS容错算法与格网改正数计算算法。基于BDSBAS实测数据的统计表明,格网电离层修正RMS约在2~3 TECU,改正百分比达到75%~79%;修正格网电离层后可提升GPS定位精度20%~40%。
| [1] |
China Satellite Navigation Office. BeiDou navigation satellite system open service performance standard (version 2.0)[S]. [S. l. ]: China Satellite Navigation Office, 2018.
|
| [2] |
RTCA. RTCA/DO-229 Minimum operational performance standards for global positioning system/wide area augmentation system airborne equipment[S]. Washington DC: RTCA, 2016.
|
| [3] |
CAO Yueling, HU Xiaogong, WU Bin, et al. The wide-area difference system for the regional satellite navigation system of Compass[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1307-1315. DOI:10.1007/s11433-012-4746-1 |
| [4] |
CAO Yueling, HU Xiaogong, ZHOU Jianhua, et al. Kinematic wide area differential corrections for BeiDou regional system basing on two-way time synchronization[C]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. Proceedings of 2014 China Satellite Navigation Conference (CSNC). Berlin: Springer, 2014, 305: 277-288.
|
| [5] |
PAN Junyang, HU Xiaogong, ZHOU Shanshi, et al. Time synchronization of new-generation BDS satellites using inter-satellite link measurements[J]. Advances in Space Research, 2018, 61(1): 145-153. DOI:10.1016/j.asr.2017.10.004 |
| [6] |
TANG Chengpan, HU Xiaogong, ZHOU Shanshi, et al. Improvement of orbit determination accuracy for BeiDou navigation satellite system with two-way satellite time frequency transfer[J]. Advances in Space Research, 2016, 58(7): 1390-1400. DOI:10.1016/j.asr.2016.06.007 |
| [7] |
TANG Chengpan, HU Xiaogong, ZHOU Shanshi, et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements[J]. Journal of Geodesy, 2018, 92(10): 1155-1169. DOI:10.1007/s00190-018-1113-7 |
| [8] |
WU Xiaoli, ZHOU Jianhua, WANG Gang, et al. Multipath error detection and correction for GEO/IGSO satellites[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1297-1306. DOI:10.1007/s11433-012-4741-6 |
| [9] |
YANG Yufei, YANG Yuanxi, HU Xiaogong, et al. Inter-satellite link enhanced orbit determination for BeiDou-3[J]. The Journal of Navigation, 2020, 73(1): 115-130. DOI:10.1017/S0373463319000523 |
| [10] |
YANG Yuanxi, GAO Weiguang, GUO Shuren, et al. Introduction to BeiDou-3 navigation satellite system[J]. Navigation, 2019, 66(1): 7-18. DOI:10.1002/navi.291 |
| [11] |
ZHOU Shanshi, HU Xiaogong, LIU Li, et al. Applications of two-way satellite time and frequency transfer in the BeiDou navigation satellite system[J]. Science China Physics, Mechanics & Astronomy, 2016, 59(10): 109511. |
| [12] |
ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit determination and time synchronization for a GEO/IGSO satellite navigation constellation with regional tracking network[J]. Science China Physics, Mechanics & Astronomy, 2011, 54(6): 1089-1097. |
| [13] |
BLANCH J. An ionosphere estimation algorithm for WAAS based on Kriging[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation. Portland: ION, 2002.
|
| [14] |
WALTER T, HANSEN A, BLANCH J, et al. Robust detection of ionospheric irregularities[J]. Navigation, 2001, 48(2): 89-100. DOI:10.1002/j.2161-4296.2001.tb00231.x |
| [15] |
ORU'S R, HERNÁNDEZ-PAJARES M, JUAN J M, et al. Improvement of global ionospheric VTEC maps by using Kriging interpolation technique[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005, 67(16): 1598-1609. DOI:10.1016/j.jastp.2005.07.017 |
| [16] |
PULLEN S, PARK Y S, ENGE P. Impact and mitigation of ionospheric anomalies on ground-based augmentation of GNSS[J]. Radio Science, 2009, 44: RS0A21. |
| [17] |
BLANCH J, WALTER T, ENGE P. A new ionospheric estimation algorithm for SBAS combining Kriging and tomography[C]//Proceeding of 2002 Institute of Navigation National Technical Meeting. San Diego: ION, 2002: 710-724.
|
| [18] |
SARMA A D, VENKATA RATNAM D, KRISHNA REDDY D. Modelling of low-latitude ionosphere using modified planar fit method for GAGAN[J]. IET Radar, Sonar & Navigation, 2009, 3(6): 609-619. |
| [19] |
SHUKLA A K, NAGORI N, DAS S, et al. Statistical comparison of various interpolation algorithms for grid-based single shell ionospheric model over Indian region[J]. Journal of Global Positioning Systems, 2008, 7(1): 72-79. DOI:10.5081/jgps.7.1.72 |
| [20] |
LI Min, YUAN Yunbin, ZHANG Baocheng, et al. Determination of the optimized single-layer ionospheric height for electron content measurements over China[J]. Journal of Geodesy, 2018, 92(2): 169-183. DOI:10.1007/s00190-017-1054-6 |
| [21] |
黄玲, 章红平, 徐培亮, 等. 中国区域VTEC模型Kriging算法研究[J]. 武汉大学学报(信息科学版), 2016, 41(6): 729-737. HUANG Ling, ZHANG Hongping, XU Peiliang, et al. VTEC modeling with Kriging algorithm over China area[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 729-737. |
| [22] |
HUANG Z, YUAN Haiqing. Analysis and improvement of ionospheric thin shell model used in SBAS for China region[J]. Advances in Space Research, 2013, 51(11): 2035-2042. DOI:10.1016/j.asr.2012.12.018 |
| [23] |
CRESSIE N. Statistics for spatial data[M]. Revised ed. Hoboken, NJ: John Wiley & Sons Inc, 1994.
|
| [24] |
WU Xiaoli, ZHOU Jianhua, WANG Gang, et al. Multipath error detection and correction for GEO/IGSO satellites[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1297-1306. DOI:10.1007/s11433-012-4741-6 |
| [25] |
KOMJATHY A, LANGLEY R B. The effect of shell height on high precision ionospheric modeling using GPS[C]//Proceedings of 1996 the IGS Workshop International GPS Service for Geodynamics (IGS). Spring, MD: [s. n. ], 1996.
|
| [26] |
SCHAER S. Mapping and predicting the earth's ionosphere using the global positioning system[D]. Berne: University of Bern, 1999.
|
| [27] |
YUAN Yunbin, WANG Ningbo, LI Zishen, et al. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results[J]. Navigation, 2019, 66(1): 55-69. DOI:10.1002/navi.292 |
| [28] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, contribution and challenges of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [29] |
范国清, 王威, 郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报, 2010, 39(1): 16-21. FAN Guoqing, WANG Wei, XI Xiaoning. Modeling of ionosphere VTEC using generalized regression neural network[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 16-21. |
| [30] |
袁运斌, 欧吉坤. WAAS系统下单频GPS用户电离层延迟改正新方法[J]. 测绘学报, 2000, 29(S1): 96-102. YUAN Yunbin, OU Jikun. A new method on ionospheric delay correction for single frequency GPS users in WAAS[J]. Acta Geodaetica Et Cartographica Sinica, 2000, 29(S1): 96-102. |
| [31] |
阮仁桂, 吴显兵, 冯来平, 等. 同时估计电离层延迟的单频精密单点定位方法[J]. 测绘学报, 2012, 41(4): 490-495. YUAN Rengui, WU Xianbing, FENG Laiping, et al. Single-frequency precise point positioning with simultaneous ionospheric delay estimation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 490-495. |
| [32] |
袁运斌, 霍星亮, 张宝成. 近年来我国GNSS电离层延迟精确建模及修正研究进展[J]. 测绘学报, 2017, 46(10): 1364-1378. YUAN Yunbin, HUO Xingliang, ZHANG Baocheng. Research progress of precise models and correction for GNSS ionospheric delay in china over recent years[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1364-1378. DOI:10.11947/j.AGCS.2017.20170349 |




