GNSS导航信号差分码偏差(differential code bias, DCB)是指由于硬件延迟导致同一时刻不同频率或同一频率上不同测码信号之间的时延差异,包括卫星端差分码偏差和接收机端差分码偏差[1]。差分码偏差是影响电离层总电子含量(total electron content, TEC)监测和建模的主要误差源[2-4],忽略卫星和接收机DCB会导致TEC计算误差达到数十个纳秒[4-5]。差分码偏差也直接影响利用伪距进行导航定位与授时的精度,其误差可达数米[6-8]。因此,在电离层延迟估计与建模、导航定位与授时等应用中必须准确分离卫星和接收机DCB。自1998年以来,国际GNSS服务组织(International GNSS Service, IGS)启动了电离层工作组,将GPS卫星DCB作为其电离层模型的副产品。从2003年起,IGS分析中心开始提供GLONASS卫星的DCB[9]。文献[10-12]基于GPS观测数据对GPS卫星和接收机的DCB参数进行了一系列的研究,解算结果与IGS发布的结果差异为亚纳秒级。近年来,随着我国北斗卫星导航系统的发展,文献[3]提出采用“两步法”,利用区域电离层模型通过较少的跟踪站即可精确估计北斗二号卫星的DCB。在此基础上,文献[13]在MGEX框架(multi-GNSS experiment, MGEX)下实现了多模GNSS的差分码偏差估计,取得了与欧洲定轨中心(Centre for Orbit Determination in Europe, CODE)、德国宇航中心(Deutsches Zentrum für Luft- und Raumfahrt, DLR)等机构相当的精度。
2020年6月23日,随着最后一颗北斗三号组网卫星成功送入预定轨道,北斗三号全球导航卫星系统星座部署全面完成。相较于北斗二号卫星,北斗三号卫星提供的频率资源和调制方式更加丰富。它不仅继承了北斗二号卫星的频率,还增加了两个互操作频点B1C和B2a,且同一频率具有多个支路,其频点与伪距通道信息见表 1[14-19]。北斗三号更多的可用卫星和更加丰富的频率资源为导航定位带来了新的发展机遇。与此同时,多频率多通道信号也衍生出一系列新的偏差亟需解决,而差分码偏差就是其中之一。早在北斗三号系统建设之初,已有学者对北斗三号卫星的DCB估计方法及其特性进行了研究[2, 15, 20-21]。但受限于当时可用的北斗三号卫星数量较少,且地面接收设备观测值类型的限制,绝大多数研究只聚焦于B1Ⅰ、B2Ⅰ和B3Ⅰ 3个频点的少数几类DCB。截至目前,全球可持续稳定提供DCB产品的机构中国科学院(Chinese Academy of Science, CAS)和DLR分别只提供8种、6种北斗卫星DCB,具体的DCB类型见表 2。尽管通过线性组合方式可重构计算部分其他类型的DCB,但仍无法涵盖所有类型的DCB。当前,随着北斗三号系统的全面组网和地面接收机的更新和升级,使得北斗三号多频多通道的DCB研究成为可能。因此,本文针对北斗三号多频多通道的差分码偏差估计研究,对于提升北斗导航定位与授时服务性能具有重要的现实意义。
| 信号 | 频率/MHz | 伪距 | |
| BDS-2 | BDS-3 | ||
| B1Ⅰ | 1561.098 | C2Ⅰ C2Q C2X | |
| B3Ⅰ | 1268.52 | C6Ⅰ C6Q C6X | |
| B2Ⅰ | 1207.140 | C7Ⅰ | - |
| C7Q | - | ||
| C7X | - | ||
| B1C | 1575.42 | - | C1D |
| - | C1P | ||
| - | C1X | ||
| B2a | 1176.45 | - | C5D |
| - | C5P | ||
| - | C5X | ||
| B2b | 1207.140 | - | C7D |
| - | C7P | ||
| - | C7Z | ||
| B2(B2a+ B2b) |
- | C8D | |
| 1191.795 | - | C8P | |
| - | C8X | ||
| 机构 | CAS | DLR |
| DCB类型 | C1P-C5P C1P-C6Ⅰ C1X-C5X C1X-C6Ⅰ C1X-C7Z C1X-C8X C2Ⅰ-C7Ⅰ C2Ⅰ-C6Ⅰ |
C1X-C2Ⅰ C2Ⅰ-C5X C2Ⅰ-C8X C2Ⅰ-C6Ⅰ C2Ⅰ-C7Ⅰ C2Ⅰ-C7Z |
1 差分码偏差估计方法 1.1 DCB估计数学模型
忽略伪距观测噪声和多路径误差,任意两种类型的码观测值的观测方程可以表示为[15]
 (1)
(1)
式中,P表示码观测值;上标s和下标r分别表示卫星端和接收机端;Li和Lj分别表示频率i和频率j;x和y分别表示码观测值为x类型和y类型;ρrs表示卫星与测站间的几何距离;IsLi和IsLj分别表示Li和Lj频率上的电离层延迟;Trs表示对流层延迟;br, Li, x和bsLi, x分别表示卫星端和接收机端PLi, xs码观测值的硬件延迟;br, Lj, y和bLj, ys分别表示卫星端和接收机端PLj, ys码观测值的硬件延迟。将式(1)中两种码观测值的观测方程作差,形成无几何距离(geometry-free, GF)组合观测量
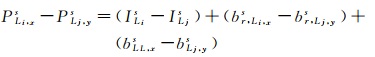 (2)
(2)
由于电离层延迟与频率有关,当i=j时,即两种码观测值在同一频率上,电离层延迟相同,IsLi-IsLj=0。当i≠j时,即两种码观测值在不同频率上,电离层延迟无法消除。此时DCB估计方法主要有两种[13]。一种方法是在电离层建模时,同步估计频间DCB参数。另一种方法是采用经验或已知的电离层模型修正电离层延迟,然后再估计频间DCB参数。CAS和DLR分别采用第一种和第二种估计方法。对于全球电离层TEC模型,第一种方法计算量大且只能估计参与计算的信号间DCB;对于区域电离层TEC模型,卫星DCB解算受区域模型的精度影响较大。由于北斗观测站数量和分布的限制,仅使用北斗观测数据难以确定精确的电离层模型[22]。因此本文采用第二种方法,利用已有的高精度电离层格网产品(global ionosphere maps, GIM)改正电离层延迟,进而估计频间DCB。
通常认为一天内的DCB为常数,将式(2)中无几何组合观测量在一天内取平均,削弱观测噪声和多路径误差,得到综合的DCB观测值
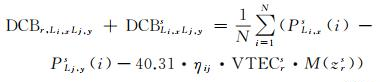 (3)
(3)
式中,DCBr, Li, xLj, y和DCBsLi, xLj, y分别为待估的接收机端和卫星端DCB参数;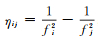
由于卫星端和接收机端DCB参数线性相关,所形成的法方程秩亏。通常将该类型所有卫星端DCB之和约束为0,即添加“零基准”约束,其约束方程可以表示为
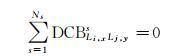 (4)
(4)
式中,Ns为该类型DCB所包含的卫星总数。约束方程的不同会导致DCB估计结果的不同,而不同机构采用的约束方程可能不一致,同一机构不同时间受观测卫星数量变化影响其基准也会产生变化。因此,不同机构或不同时间之间的DCB要进行基准统一才能进行比较[23-26]。
1.2 DCB估值基准统一假设A基准有m颗卫星,B基准有A的m颗卫星中的n颗卫星(n < m)。A基准下,对m颗卫星施加“零基准”,其约束方程可以表示为
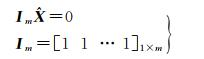 (5)
(5)
式中,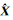
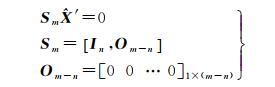 (6)
(6)
式中,Sm为B基准下约束方程系数向量,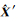
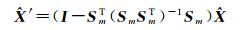 (7)
(7)
式中,I为m阶单位矩阵。如果n > m,则采用相同的方式,把B基准下的DCB参数调整到A基准下。如果要分析一段时间跨度内DCB的稳定性,由于会存在某些天某些卫星值缺失的情况,选取所有天都有效的卫星施加零基准约束,再将每天的基准统一到此零基准,只有这样,才能对一段时间内的DCB进行稳定性分析。
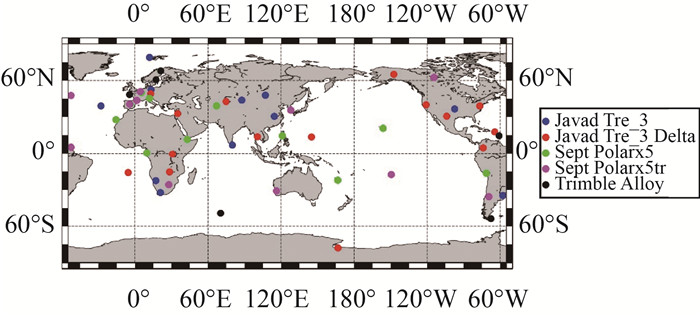
2 试验数据与处理策略 2.1 试验数据获取当前,大部分支持北斗的测站均能接收到C2Ⅰ、C6Ⅰ、C7Ⅰ这3种码观测值,三者之间的DCB容易估计。为了确保其余各类DCB的可估性,首先需要搜集尽可能多的北斗多频多通道码观测值。其次,为了客观评价本文DCB估值与参考值之间的一致性和稳定性,还需要选取与DLR、CAS尽可能相同的测站数及分布。表 3为利用2020年4月1日至2020年4月30日(对应DOY 92-DOY 121)一个月内所有IGS站网数据,统计得到的可估DCB类型及可用测站数。将这些测站取并集,综合考虑测站的空间分布与观测质量,得到本文试验所用的58个测站,如图 1所示,图中不同颜色代表不同类型的接收机,这与DLR和CAS所选的测站基本一致。
| DCB类型 | 测站数 | DCB类型 | 测站数 | |
| C1P-C2Ⅰ | 25 | C2Ⅰ-C5X | 34 | |
| C1P-C5P | 25 | C5X-C6Ⅰ | 34 | |
| C1P-C6Ⅰ | 25 | C5X-C7Z | 27 | |
| C1X-C2Ⅰ | 28 | C5X-C8X | 23 | |
| C1X-C5X | 28 | C2Ⅰ-C8X | 23 | |
| C1X-C6Ⅰ | 28 | C6Ⅰ-C8X | 23 | |
| C1X-C7Z | 21 | C7Z-C8X | 22 | |
| C1X-C8X | 17 | C2Ⅰ-C7Z | 28 | |
| C2Ⅰ-C5P | 25 | C6Ⅰ-C7Z | 27 | |
| C5P-C6Ⅰ | 25 |
|
| 图 1 测站分布 Fig. 1 Distribution of stations |
本文使用CODE发布的GIM产品改正电离层延迟。CODE采用基于球谐函数的全球电离层TEC建模方法计算GIM,其内符合精度约为2.4TECU[27-28]。
2.2 数据处理策略图 2给出了DCB估计的数据处理流程。其中,质量控制部分主要包括设置卫星截止高度角为20°、剔除波动大(标准差大于1)和观测数量少(时长小于50min)的GF组合时间序列;最小二乘中单位权中误差σ0=0.1,依据标准差给综合DCB观测值定权。

|
| 图 2 DCB估计 Fig. 2 DCB estimation |
由表 3可知,可估的北斗三号DCB类型共有19种,各类码组合的可用测站数为17~34个。为了与北斗二号进行比较,同时还估计了C2Ⅰ-C6Ⅰ、C2Ⅰ-C7Ⅰ、C6Ⅰ-C7Ⅰ这3种DCB类型,总共估计得到了22种类型的DCB。其中C2Ⅰ-C7Ⅰ、C6Ⅰ-C7Ⅰ类型的DCB只存在于北斗二号卫星,C2Ⅰ-C6Ⅰ类型的DCB同时存在于北斗二号和北斗三号卫星,其余类型的DCB则只存在于北斗三号卫星。
为了评估北斗三号多频多通道DCB估计的精度和可靠性,从内符合精度、外符合精度、估值稳定性等方面进行分析。需要注意的是,在比较分析之前需要采用1.2节中的方法消除由不同机构的基准差异、同一机构不同时间卫星数量变化引起的基准不一致。
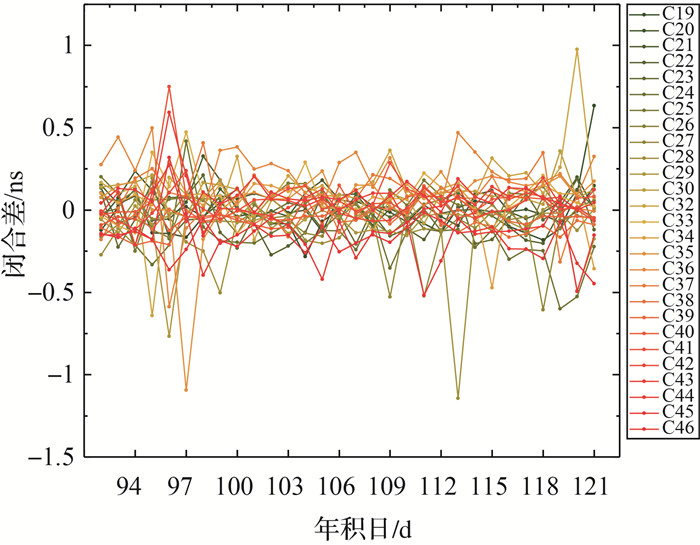
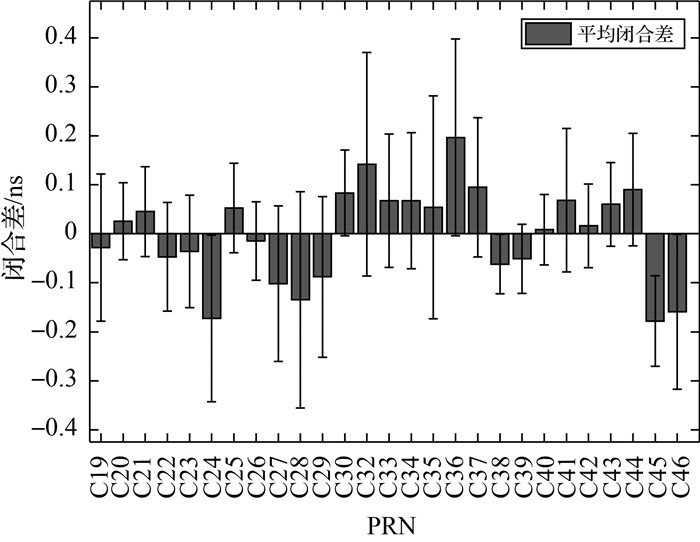
3 试验结果与分析 3.1 内符合精度分析闭合差是反映内符合精度的重要指标,给定任意3个码观测值,可构造3个DCB,但是,理论上只有两个独立的DCB,即3个DCB之间的闭合差为零[29-30]。由于各类DCB是基于不同观测值独立解算的,且平差计算时受观测噪声和模型误差影响,导致其闭合差通常并不等于零。闭合差的大小反映了DCB估值与模型的吻合程度,闭合差越小,内符合精度越高。以北斗三号卫星3个新频点之间形成的3类DCB(C1X-C5X、C1X-C8X、C5X-C8X)为例,图 3给出了北斗三号各卫星的每日的DCB闭合差(DCBC1X-C5X+DCBC5X-C8X+DCBC8X-C1X)时间序列。由图 3可知,各卫星每日的DCB闭合差在零值附近波动,无显著系统性偏差,且绝大多数闭合差分布在0.3ns以内。少数卫星如C28、C32、C35卫星分别在DOY 113、DOY 120、DOY 97的闭合差达到1ns,这可能与当天可用的观测数量和数据质量有关。统计北斗三号各卫星DCB月平均闭合差及其标准差,如图 4所示。从图 4中可以看出,北斗三号卫星DCB估值的内符合精度较好,平均闭合差都在0.2ns以内,且大部分优于0.1ns,其中C40卫星平均闭合差最小为0.008ns,C36卫星的平均闭合差最大为0.2ns。各卫星闭合差的标准差都在0.4ns以内,且大部分优于0.2ns,这表明C1X-C5X、C1X-C8X、C5X-C8X 3个DCB估值之间具有较好的一致性,内部符合精度较高。其他类型的DCB闭合差具有类似的统计特性,限于篇幅,不单独罗列。
|
| 图 3 北斗三号各卫星DCB日闭合差时间序列(C1X-C5X、C1X-C8X、C5X-C8X) Fig. 3 Time series of BDS-3 satellite DCB daily closure errors (C1X-C5X、C1X-C8X、C5X-C8X) |
|
| 图 4 北斗三号各卫星DCB月平均闭合差及标准差(C1X-C5X、C1X-C8X、C5X-C8X) Fig. 4 Monthly mean closure errors and STDs of BDS-3 satellite DCBs (C1X-C5X、C1X-C8X、C5X-C8X) |
3.2 外符合精度分析
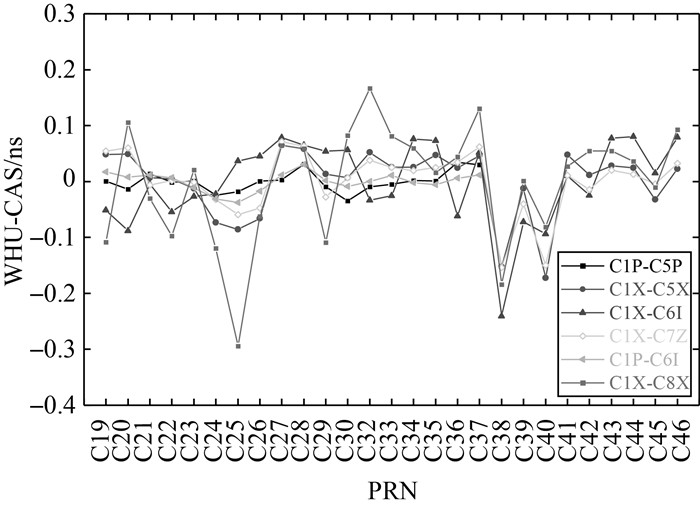
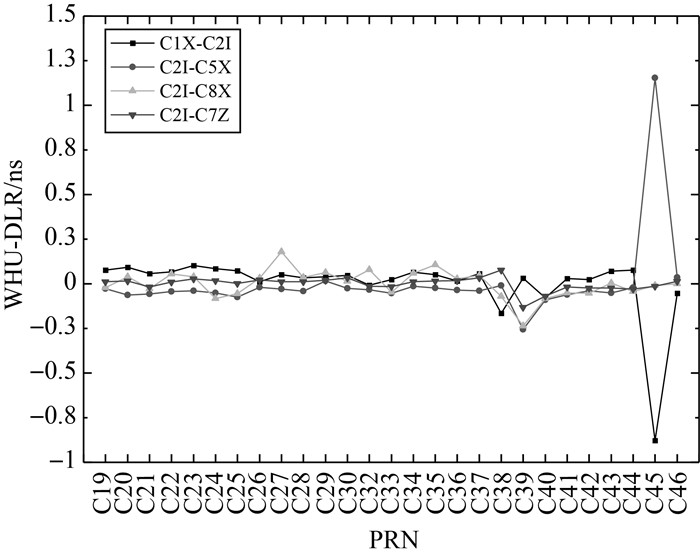
为了验证北斗三号卫星DCB估计结果的外符合精度,将本文的估计结果(下文简称为WHU)与CAS和DLR机构的DCB产品进行比较。除C2Ⅰ-C6Ⅰ之外,CAS和DLR的DCB产品中分别有6种、4种北斗三号卫星DCB类型,将其依次与WHU求差,得到北斗三号各卫星DCB估值的外符合精度,如图 5、图 6所示。从图 5中可以看出WHU和CAS的平均偏差基本都在0.1ns以内,这说明WHU与CAS的DCB产品之间一致性较好。其中C25卫星C1X-C8X类型DCB平均偏差较大,达到0.3ns,这与C1X-C8X类型DCB的数据质量有关,见表 3,用于估计C1X-C8X类DCB的测站数量仅为17,明显少于其他DCB类型。从图 6中可以看出,除C45卫星之外,WHU与DLR之间DCB的平均偏差基本在0.2ns以内,说明二者之间也具有较好的一致性。至于C45卫星,DLR和WHU之间C1X-C2Ⅰ、C2Ⅰ-C5X两种类型的DCB差值分别为-0.88、1.15ns。这与该卫星的数据、质量和这两类DCB的稳定性有关,分析DLR和WHU的DCB估值方差-协方差矩阵发现,所有卫星C1X-C2Ⅰ的月平均标准差分别为0.054、0.051ns,而C45卫星的标准差分别为0.308、0.155ns;类似的,C45卫星C2Ⅰ-C5X的月平均标准差分别为0.135、0.213ns,显著大于其他卫星。
|
| 图 5 WHU与CAS估计的6种北斗三号卫星DCB之间的平均偏差 Fig. 5 The 6 types of BDS-3 satellite DCB mean differences of WHU and CAS |
|
| 图 6 WHU与DLR估计的4种北斗三号卫星DCB之间的平均偏差 Fig. 6 The 4 types of BDS-3 satellite DCB mean differencesbetween WHU and DLR |
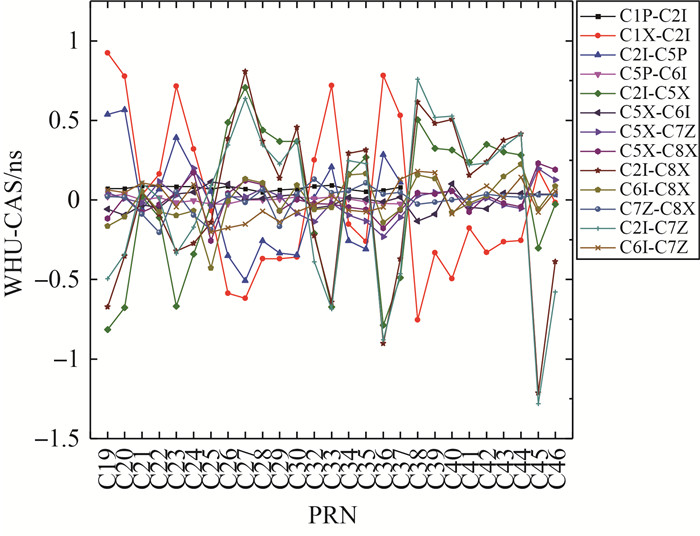
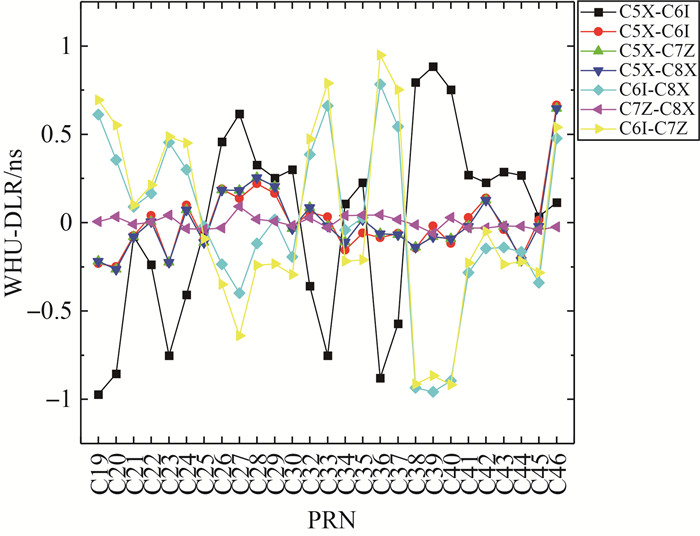
尽管CAS和DLR只提供少数几种DCB产品类型,但是根据DCB之间的线性关系,可利用已有的DCB类型经过转换得到一些新的DCB类型,比如DCBC1X-C8X=DCBC1X-C5X+DCBC5X-C8X。因此,还可将WHU的DCB估值与CAS和DLR的部分DCB转换值进行间接比较,如图 7、图 8所示。从图 7和图 8中可以看出,相比于图 4和图 5中DCB估值的直接比较法,由于受误差传播的影响,间接法获得的各机构之间的DCB差值明显更大,一致性较差,其差值分布在1ns之内,这也说明了直接估计多频多通道DCB的必要性。
|
| 图 7 WHU与CAS的13种北斗三号卫星DCB(转换值)之间的平均偏差 Fig. 7 The 13 types of BDS-3 satellite DCB (transform values) mean differences between WHU and CAS |
|
| 图 8 WHU与DLR的7种北斗三号卫星DCB(转换值)之间的平均偏差 Fig. 8 The 7 types of BDS-3 satellite DCB (transform values) mean differences between WHU and DLR |
3.3 估值稳定性分析
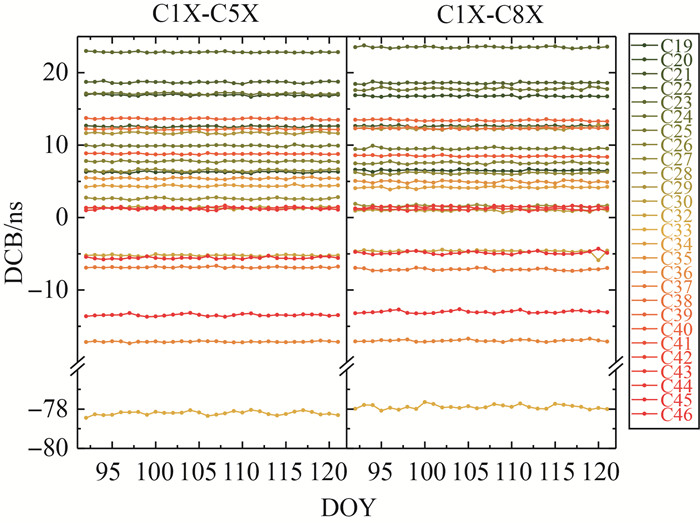
为分析北斗三号卫星DCB估值的稳定性,首先选取3个新增频点上的码观测值C1X、C5X和C8X构成的DCB类型C1X-C5X、C1X-C8X为例,将2020年4月内各卫星对应的DCB每日估值的时间序列绘于图 9。可以看出,大多数卫星的DCB估值分布在±20ns,少数卫星的DCB数值较大,其中C33卫星的DCB估值达到-78.2ns左右,在导航定位与授时中若不考虑,将带来严重的系统偏差。在一个月的时间内,各卫星的DCB估值变化较小,表明它们具有较好的天稳定度。
|
| 图 9 BDS-3各卫星C1X-C5X和C1X-C8X DCB时间序列 Fig. 9 Time series of BDS-3 satellites C1X-C5X and C1X-C8X DCB |
进一步分析各类DCB的稳定性,表 4给出WHU、CAS和DLR直接估计或通过线性转换得到的DCB值的月平均标准差(STD)。其中,黑体表示线性转换值。由表 4可知, WHU的DCB估值稳定性普遍优于CAS和DLR,反映本文估计的DCB稳定性良好。DLR的平均STD虽优于CAS,但其产品提供的DCB类型较少,且涵盖的码观测值类型也较少,导致某些DCB类型无法通过线性转换得到。利用CAS的DCB产品,虽然可通过线性转换恢复所有DCB类型,但因受误差传递和累积的影响,转换得到的DCB稳定性明显较差,进一步说明了直接估计多频多通道DCB的必要性。
| DCB类型 | WHU | CAS | DLR |
| C1P-C2Ⅰ | 0.026 | 0.069 | - |
| C1P-C5P | 0.073 | 0.103 | - |
| C1P-C6Ⅰ | 0.063 | 0.081 | - |
| C1X-C2Ⅰ | 0.037 | 0.093 | 0.054 |
| C1X-C5X | 0.096 | 0.107 | - |
| C1X-C6Ⅰ | 0.076 | 0.090 | - |
| C1X-C7Z | 0.084 | 0.100 | - |
| C1X-C8X | 0.103 | 0.196 | - |
| C2Ⅰ-C5P | 0.080 | 0.077 | - |
| C5P-C6Ⅰ | 0.037 | 0.048 | - |
| C2Ⅰ-C5X | 0.089 | 0.122 | 0.101 |
| C5X-C6Ⅰ | 0.051 | 0.100 | 0.089 |
| C5X-C7Z | 0.038 | 0.078 | 0.071 |
| C5X-C8X | 0.093 | 0.162 | 0.073 |
| C2Ⅰ-C8X | 0.093 | 0.205 | 0.095 |
| C6Ⅰ-C8X | 0.128 | 0.197 | 0.108 |
| C7Z-C8X | 0.103 | 0.165 | 0.046 |
| C2Ⅰ-C7Ⅰ | 0.103 | 0.082 | 0.103 |
| C2Ⅰ-C6Ⅰ | 0.079 | 0.084 | 0.106 |
| C6Ⅰ-C7Ⅰ | 0.055 | 0.057 | 0.068 |
| C2Ⅰ-C7Z | 0.082 | 0.118 | 0.090 |
| C6Ⅰ-C7Z | 0.068 | 0.101 | 0.104 |
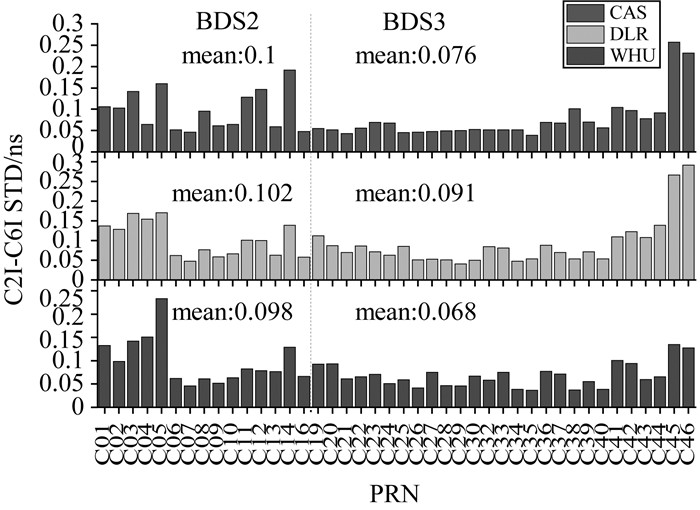
此外,本文还对比分析了北斗三号卫星与北斗二号卫星DCB估值的稳定性。以北斗二号和北斗三号共有的C2Ⅰ-C6Ⅰ类型DCB为例,图 10给出了WHU、CAS和DLR对应的DCB估值月平均标准差。统计结果表明,WHU北斗二号、三号卫星DCB的平均STD分别为0.098、0.068ns;CAS分别为0.1、0.076ns;DLR分别为0.102、0.091ns。总体而言,北斗三号卫星的DCB估值的稳定性略优于北斗二号。北斗二号卫星中C01-C05(GEO卫星)的稳定度较差,北斗三号卫星中C45、C46卫星稳定度较差,这与前面的分析一致。
|
| 图 10 北斗卫星DCB STD对比 Fig. 10 DCB STD comparison of BDS satellites |
4 结论与展望
本文利用最新的北斗实测数据,研究了北斗三号卫星多频多通道差分码偏差估计方法,准确分离了所有可估的DCB类型,并从内符合精度、外符合精度、稳定性3个方面进行了分析,得出以下结论:
(1) 当前,北斗三号卫星在6个频点上提供18种码观测值。本文基于IGS跟踪站实测数据,估计得到了22种不同类型的DCB。而目前能持续稳定提供DCB产品的机构CAS和DLR只提供少数几种类型的北斗DCB。
(2) 北斗三号卫星DCB估值的内符合精度较好,平均闭合差在0.2ns以内,且大部分优于0.1ns,估值之间具有较好的一致性。以CAS和DLR提供的DCB估值为参考,本文DCB估值的平均偏差为0.1~0.2ns,具有较高的外符合精度。
(3) 尽管利用CAS和DLR提供的DCB产品可以通过线性组合方式,转换得到一些其他类型的DCB,但是,由于受到误差传递与积累的影响,转换得到的DCB精度和可靠性不如直接估计的DCB。
(4) 北斗三号卫星DCB估值具有较好的长期稳定性,一个月内的平均标准差约为0.1ns。相比于北斗二号卫星,北斗三号卫星的DCB稳定性相对更优。
需要说明的是,当前可用于估计北斗三号卫星各类DCB的测站数量仍然有限,仅有17~34个站,北斗多频多通道的DCB估计仍有较大的提升空间。
| [1] |
姚宜斌, 刘磊, 孔建, 等. GIM和不同约束条件相结合的BDS差分码偏差估计[J]. 测绘学报, 2017, 46(2): 135-143. YAO Yibin, LIU Lei, KONG Jian, et al. Estimation of BDS DCB combining GIM and different zero-mean constraints[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 135-143. DOI:10.11947/j.AGCS.2017.20160375 |
| [2] |
WANG Qisheng, JIN Shuanggen, YUAN Liangliang, et al. Estimation and analysis of BDS-3 differential code biases from MGEX observations[J]. Remote Sensing, 2020, 12(1): 68. |
| [3] |
LI Zishen, YUAN Yunbin, LI Hui, et al. Two-step method for the determination of the differential code biases of COMPASS satellites[J]. Journal of Geodesy, 2012, 86(11): 1059-1076. DOI:10.1007/s00190-012-0565-4 |
| [4] |
LI Min, YUAN Yunbin, WANG Ningbo, et al. Estimation and analysis of Galileo differential code biases[J]. Journal of Geodesy, 2017, 91(3): 279-293. DOI:10.1007/s00190-016-0962-1 |
| [5] |
WILSON B D, MANNUCCI A J. Instrumental biases in ionospheric measurements derived from GPS data[C]//Proceedings of the 6th International Technical Meeting of the Satellite Division of The Institute of Navigation. Salt Lake City, UT: Salt Palace Convention Center, 1993: 1343-1351.
|
| [6] |
曾添, 隋立芬, 鲍亚东, 等. BDS卫星端差分码偏差对定位的影响及改正模型研究[J]. 大地测量与地球动力学, 2017, 37(1): 53-57. ZENG Tian, SUI Lifen, BAO Yadong, et al. The impact of satellite differential code bias on BDS positioning and correction model research[J]. Journal of Geodesy and Geodynamics, 2017, 37(1): 53-57. |
| [7] |
王宁波, 袁运斌, 张宝成, 等. GPS民用广播星历中ISC参数精度分析及其对导航定位的影响[J]. 测绘学报, 2016, 45(8): 919-928. WANG Ningbo, YUAN Yunbin, ZHANG Baocheng, et al. Accuracy evaluation of GPS broadcast inter-signal correction (ISC) parameters and their impacts on GPS standard positioning[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 919-928. DOI:10.11947/j.AGCS.2016.20150554 |
| [8] |
WILSON B, YINGER C, FEESS W, et al. New and improved-the broadcast interfrequency biases[EB/OL].[1999-01-06]. http://hdl.handle.net/2014/18173.
|
| [9] |
SCHAER S. Biases relevant to GPS and GLONASS data processing[C]//Proceedings of 2014 IGS Workshop. Pasadena, California: [s.n.], 2014.
|
| [10] |
袁运斌, 欧吉坤. GPS观测数据中的仪器偏差对确定电离层延迟的影响及处理方法[J]. 测绘学报, 1999, 28(2): 110-114. YUAN Yunbin, OU Jikun. The effects of instrumental bias in GPS observations on determining ionospheric delays and the methods of its calibration[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 110-114. DOI:10.3321/j.issn:1001-1595.1999.02.001 |
| [11] |
JIN Rui, JIN Shuanggen, FENG Guiping. M_DCB:Matlab code for estimating GNSS satellite and receiver differential code biases[J]. GPS Solutions, 2012, 16(4): 541-548. DOI:10.1007/s10291-012-0279-3 |
| [12] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of slant total electron content and satellite-receiver's differential code biases with uncombined precise point positioning technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. |
| [13] |
WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Determination of differential code biases with multi-GNSS observations[J]. Journal of Geodesy, 2016, 90(3): 209-228. DOI:10.1007/s00190-015-0867-4 |
| [14] |
IGS RINEX WG. RINEX-the receiver independent exchange format, Version 3.05[EB/OL].[2020-12-01]. https://files.igs.org/pub/data/format/rinex305.pdf.
|
| [15] |
LI Xingxing, XIE Weiliang, HUANG Jiaxin, et al. Estimation and analysis of differential code biases for BDS3/BDS2 using iGMAS and MGEX observations[J]. Journal of Geodesy, 2019, 93(3): 419-435. DOI:10.1007/s00190-018-1170-y |
| [16] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1Ⅰ (3.0版)[EB/OL].[2019-02-27]. http://www.beidou.gov.cn. China Satellite Navigation Office. BeiDou navigation satellite system signal in space interface control document open service signal B1Ⅰ (Version 3.0)[EB/OL].[2019-02-27]. http://www.beidou.gov.cn. |
| [17] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B3Ⅰ(1.0版)[EB/OL].[2018-02-09]. http://www.beidou.gov.cn. China Satellite Navigation Office. BeiDou navigation satellite system signal in space interface control document open service signal B3Ⅰ (Version 1.0)[EB/OL].[2018-02-29]. http://www.beidou.gov.cn. |
| [18] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1C(1.0版)[EB/OL].[2017-12-27]. http://www.beidou.gov.cn. China Satellite Navigation Office. BeiDou navigation satellite system signal in space interface control document open service signal B1C (Version 1.0)[EB/OL].[2017-02-27]. http://www.beidou.gov.cn. |
| [19] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B2a(1.0版)[EB/OL].[2017-12-27]. http://www.beidou.gov.cn. China Satellite Navigation Office. BeiDou navigation satellite system signal in space interface control document open service signal B2a (Version 1.0)[EB/OL].[2017-12-27]. http://www.beidou.gov.cn. |
| [20] |
ZHU Yongxing, TAN Shusen, FENG Laiping, et al. Estimation of the DCB for the BDS-3 new signals based on BDGIM constraints[J]. Advances in Space Research, 2020, 66(6): 1405-1414. DOI:10.1016/j.asr.2020.05.019 |
| [21] |
GU Shengfeng, WANG Yintong, ZHAO Qile, et al. BDS-3 differential code bias estimation with undifferenced uncombined model based on triple-frequency observation[J]. Journal of Geodesy, 2020, 94(4): 45. DOI:10.1007/s00190-020-01364-w |
| [22] |
张强, 赵齐乐, 章红平, 等. 利用北斗观测实验网解算北斗卫星差分码偏差[J]. 武汉大学学报(信息科学版), 2016, 41(12): 1649-1655. ZHANG Qiang, ZHAO Qile, ZHANG Hongping, et al. BDS differential code bias estimation using BeiDou experimental tracking stations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1649-1655. |
| [23] |
SANZ J, MIGUEL JUAN J, ROVIRA-GARCIA A, et al. GPS differential code biases determination:methodology and analysis[J]. GPS Solutions, 2017, 21(4): 1549-1561. DOI:10.1007/s10291-017-0634-5 |
| [24] |
解为良.多系统GNSS高精度电离层建模和差分码偏差估计[D].武汉: 武汉大学, 2018. XIE Weiliang. Precise ionospheric modeling and differential code bias estimation from Multi-GNSS observation[D]. Wuhan: Wuhan University, 2018. |
| [25] |
任晓东.多系统GNSS电离层TEC高精度建模及差分码偏差精确估计[D].武汉: 武汉大学, 2017. REN Xiaodong. Theory and methodology of ionospheric TEC modelling and differential code biases estimation with multi-GNSS[D]. Wuhan: Wuhan University, 2017. |
| [26] |
WANG Ningbo, LI Zishen, MONTENBRUCK O, et al. Quality assessment of GPS, Galileo and BeiDou-2/3 satellite broadcast group delays[J]. Advances in Space Research, 2019, 64(9): 1764-1779. DOI:10.1016/j.asr.2019.07.029 |
| [27] |
李子申, 王宁波, 李敏, 等. 国际GNSS服务组织全球电离层TEC格网精度评估与分析[J]. 地球物理学报, 2017, 60(10): 3718-3729. LI Zishen, WANG Ningbo, LI Min, et al. Evaluation and analysis of the global ionospheric TEC map in the frame of international GNSS services[J]. Chinese Journal of Geophysics, 2017, 60(10): 3718-3729. |
| [28] |
ZHANG Xiaohong, REN Xiaodong, WU Fengbo, et al. Short-term prediction of ionospheric TEC based on ARIMA model[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 9-16. DOI:10.11947/j.JGGS.2019.0102 |
| [29] |
MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps[J]. Navigation-Journal of the Institute of Navigation, 2014, 61(3): 191-201. |
| [30] |
GUO Fei, ZHANG Xiaohong, WANG Jinling. Timing group delay and differential code bias corrections for BeiDou positioning[J]. Journal of Geodesy, 2015, 89(5): 427-445. DOI:10.1007/s00190-015-0788-2 |



