2. 西安卫星测控中心, 陕西 西安 710043
2. Xi'an Satellite Control Center, Xi'an 710043, China
北斗导航卫星系统(BeiDou Navigation Satellite System, BDS)是我国自主建设、独立运行的全球导航卫星系统。按照“三步走”发展战略,北斗二号系统(BDS-2)已于2012年宣布对亚太地区提供定位、授时和短报文服务,北斗三号全球导航卫星系统(BDS-3)于2020年7月31日正式建成开通并提供全球服务[1-3]。与国际上其他全球导航卫星系统纷纷采用单一轨道卫星部署星座不同,我国的北斗导航卫星系统首次采取了异构的GEO+IGSO+MEO混合星座方案。目前,在轨提供基本服务的卫星共45颗,包括北斗二号5颗GEO卫星,7颗IGSO卫星和3颗MEO卫星以及北斗三号3颗GEO卫星,3颗IGSO卫星和24颗MEO卫星。
北斗卫星精密轨道确定历来是学者研究的热点问题。文献[4-7]研究了BDS单系统精密定轨方法,初步分析了BDS卫星轨道和钟差精度。文献[8-11]对多GNSS融合定轨展开研究,采用GPS/BDS“两步法”联合定轨,轨道径向精度优于10cm。文献[12]比较了多系统融合定轨和单系统定轨的异同,并对两种方法下北斗不同星座卫星定轨精度进行了分析。文献[13-14]利用MGEX (multi-GNSS experiment)站和中国区域基准站的BDS和GPS观测数据,进行了北斗精密定轨,分析了中国区域的国家级基准站对BDS定轨的贡献。文献[15-16]进行了BDS-3和BDS-2联合精密定轨,并分析了地面站分布、模糊度固定、卫星姿态模式等因素对轨道精度的影响。文献[17-18]对北斗GEO和IGSO卫星零偏姿态模式下的精密定轨和卫星轨道机动后的快速恢复进行了研究。文献[19-20]分析了光压模型优化和低轨卫星增强对北斗卫星定轨精度的改进效果。文献[21-24]基于北斗三号卫星搭载的高精度星间链路载荷,分析了星间链路测量噪声和测距精度,开展了联合星间观测和星间链路观测点卫星定轨试验,证明加入星间链路数据能够显著改善轨道精度。
北斗系统首创的混合星座设计,在成功实现先区域、后全球服务发展思路的同时,也为北斗卫星精密定轨带来了一些新的挑战。由于采用异构星座,不同星座卫星姿态控制模式、地面观测几何构型、动力学模型不尽相同,定轨精度也有较大差异。特别是GEO卫星,其相对地面站的观测几乎静止不动,观测方程不随时间变化,在定轨解算过程中轨道参数和其他误差参数交联,难以分离求解,导致北斗GEO卫星定轨精度远低于IGSO/MEO卫星,出现同一导航系统内不同星座的卫星具有不同量级的轨道精度的现象。
在传统的导航卫星精密定轨方案中,无论是单系统定轨还是多系统融合定轨,都习惯将同一导航系统作为一个整体,采用相同的先验信息和约束条件对导航系统内所有卫星同时进行定轨计算。然而,由于北斗采用混合星座,GEO卫星精密轨道精度比IGSO/MEO卫星低一个量级,如果将所有卫星同时进行轨道解算,尤其是在双差观测模型下,轨道和伪距观测精度低一个量级的GEO卫星势必对IGOS/MEO卫星轨道解算带来不利影响。同时,由于GEO卫星的“静地”特性,难以对其形成有效约束,导致GEO卫星定轨精度较低。本文提出一种基于双差观测模型的混合星座分层约束下的精密定轨方法,在传统的GPS/BDS“两步法”基础上,将北斗卫星分为非GEO(IGSO/MEO)和GEO两部分,引入不同约束条件进行分步解算,以达到提高定轨精度的目的。
1 精密定轨方法 1.1 参数约束模型线性化的观测方程可以表示为
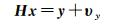 (1)
(1)
式中,x表示待估参数改进量;y表示实际观测值和由参考轨道计算的理论观测值之差;H表示模型观测量对参考矢量的偏导数Jacobi矩阵;υy为残差矢量。线性最小二乘问题法方程和一般解分别为
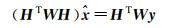 (2)
(2)
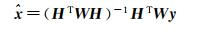 (3)
(3)
在一个理论模型中,一种类型的观测数据并不一定会对所有的参数敏感,在这种情况下,法方程是奇异的。需要在最小二乘求解中引入附加的信息或约束来使法方程非奇异,附加信息可以表示为
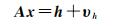 (4)
(4)
式中,h表示引入的约束信息;H表示约束信息对参考矢量的偏导数Jacobi矩阵;υh为残差矢量。可以认为式(4)的约束是增加的伪观测量,或者作为假想观测量。重新考虑观测方程如下
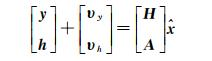 (5)
(5)
加入约束信息后的法方程变为
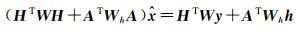 (6)
(6)
式(6)显示,可以在原始的法方程中叠加ATWhA和ATWhh两项作为参数的初始信息。
参数约束的实现方式可以分为以下几种[25]:①绝对约束,任何参数都可以通过使用形如xi=0的虚拟数据将参数改进约束为零,进而将参数约束到它的初值,这个虚拟观测量的权重Wi可以参考该参数的先验精度信息设置。②相对约束,也可以使用形如xi-xj=0的虚拟观测量来实现两个参数相对于彼此的约束。③零均值约束,将一组参数估计改进量的均值约束为0,即∑xi=0。④参数固定,参数如果被固定,将不会作为未知量出现在法方程系统中,而是作为已知量固定到其初始值。
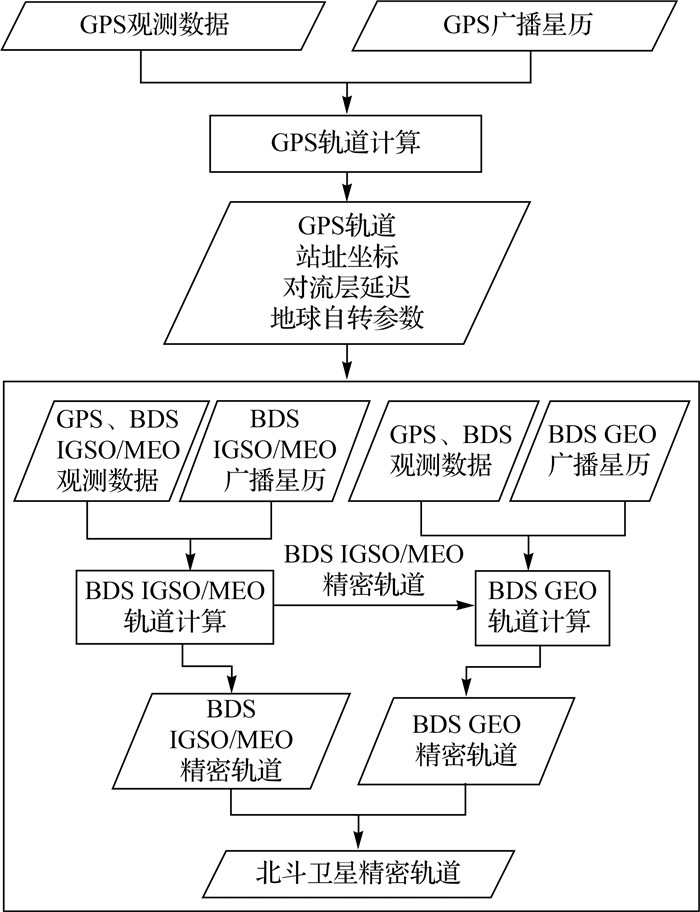
1.2 分层约束的定轨方案本文解算流程如图 1所示,主要思想是:利用GPS解算结果对北斗IGSO/MEO精密定轨形成有效约束,又避免全系统卫星在同一平差模型中处理时GEO卫星轨道精度低带来的不利影响;利用GPS和北斗IGSO/MEO解算结果,单独对北斗GEO卫星进行强约束下的轨道解算,最终达到同时改进GEO和非GEO卫星定轨精度的效果。具体解算流程如下:
|
| 图 1 北斗混合星座分层约束下的分步解算流程 Fig. 1 BeiDou mixed constellation step-by-step solution under layered constraints |
第1步,利用IGS(International GNSS Service)、MGEX和iGMAS(International GNSS Monitoring & Assessment System)跟踪网的GPS卫星观测数据,精确确定GPS卫星轨道以及多模接收机在IGS框架下的测站坐标、对流层延迟和地球自转参数等公共参数。
第2步,将MGEX和iGMAS的GPS和北斗IGSO/MEO数据联合处理,形成双系统三星座观测值混合双差,引入并固定第1步解算得到的GPS卫星轨道以及其他公共参数,解算北斗IGSO/MEO卫星轨道。
第3步,将MGEX和iGMAS的GPS和北斗GEO/IGSO/MEO数据联合处理,形成双系统四星座观测值混合双差,引入并固定第2步解算得到的北斗IGSO/MEO卫星轨道和第1步解算得到的GPS卫星轨道以及其他公共参数,解算北斗GEO卫星轨道。
数据处理及参数约束策略见表 1。
| 类型 | 参数 | GPS | BDS IGSO/MEO | BDS GEO |
| 观测量 | 处理数据 | GPS双差消电离层载波相位数据 | GPS、BDS IGSO/MEO混合双差消电离层载波相位数据 | GPS、BDS混合双差消电离层载波相位数据和BDS双差消电离层伪距数据 |
| 数据弧长/h | 72 | 72 | 72 | |
| 高度截止角/(°) | 10 | 10 | 10 | |
| 采样间隔/s | 300 | 300 | 300 | |
| 高度角相关权函数 | sin(E) | sin(E) | sin(E) | |
| 数据权重比 | 所有GPS卫星等权 | GPS/BDS:1/1 | 伪距/相位:1/100IGSO/MEO/GEO:1/1/1 | |
| 模糊度 | 固定 | 固定 | 非GEO卫星固定 | |
| 模型 | 光压模型 | ECOM光压模型 | ECOM光压模型 | ECOM光压模型 |
| 卫星天线相位中心 | PCO & PCV(IGS14) | PCO(中国卫星导航系统管理办公室2019年12月30日发布) | PCO(中国卫星导航系统管理办公室2019年12月30日发布) | |
| 接收机天线相位中心 | PCO & PCV(IGS14) | PCO (IGS14,若不存在采用GPS值) | PCO (IGS14,若不存在采用GPS值) | |
| 相位缠绕 | 模型改正 | 模型改正 | 模型改正 | |
| 二阶电离层影响改正 | IERS2010 | IERS2010 | IERS2010 | |
| 对流层先验模型 | 气象参数:GPT 天顶延迟:Saastamoinen 映射函数:GMF 梯度模型:未采用 |
气象参数:GPT 天顶延迟:Saastamoinen 映射函数:GMF 梯度模型:未采用 |
气象参数:GPT 天顶延迟:Saastamoinen 映射函数:GMF 梯度模型:未采用 |
|
| 参数约束 | 卫星/接收机钟差 | 双差消除 | 双差消除 | 双差消除 |
| 站坐标参数 | 待估参数:所有测站的坐标约束:先验值为IGS14,核心站整体无旋转约束 | 待估参数:无约束:固定为GPS解算结果 | 待估参数:无约束:固定为GPS解算结果 | |
| 卫星轨道参数 | 待估参数:GPS卫星初始位置速度;光压模型9参数;迹向每12h一组伪随机脉冲 先验约束:光压D、Y方向周期项为1×10-12m/s2迹向伪随机脉冲为1×10-6m/s2 |
待估参数:BDS IGSO/MEO卫星初始位置速度;光压模型5参数;动偏姿态模式时迹向每12h一组伪随机脉冲,零偏姿态模式时径向、迹向和法向每6h一组伪随机脉冲 先验约束:伪随机脉冲径向和迹向为1×10-6m/s2,法向为1×10-9m/s2 |
待估参数:BDS GEO卫星初始位置速度;光压模型9参数;径向、迹向和法向每6h一组伪随机脉冲 先验约束:光压D、Y方向周期项为1×10-12m/s2伪随机脉冲径向和迹向为1×10-6m/s2,法向为1×10-9m/s2 |
|
| 对流层参数 | 待估参数:分段线性测站天顶延迟每2h解1组,N-S和E-W梯度每24h解1组约束:相邻段松相关性 | 待估参数:无 约束:固定为GPS解算结果 |
待估参数:无 约束:固定为GPS解算结果 |
|
| 地球自转参数 | 待估参数:X极移、Y极移、X极移速率、Y极移速率、LOD、UT1,每天解1组约束:UT1紧约束到IERS | 待估参数:无 约束:固定为GPS解算结果 |
待估参数:无 约束:固定为GPS解算结果 |
2 算例分析
利用全球分布的约15个IGS测站、60个MGEX测站和15个iGMAS测站2020年DOY 121-DOY 130共10天的多模观测数据,采用本文方法(记为方案1)进行精密定轨试验。为便于比较分析,验证轨道精度改进效果,引入传统的GPS/BDS融合“两步法”定轨[26]作为对比方案(记为方案2),分别采用重叠弧段对比、SLR检核和静态PPP等手段验证轨道精度。需要说明的是,试验所采用的IGS测站数据仅用于第1步解算GPS轨道和公共参数,采用的MGEX和iGMAS测站均可接收GPS/BDS多模观测数据。另外,由于北斗三号3颗GEO卫星及C38至C46等9颗IGSO/MEO卫星入网运行时间相对较晚,目前能够接收其信号的测站相对较少,故未将这些卫星纳入定轨试验。
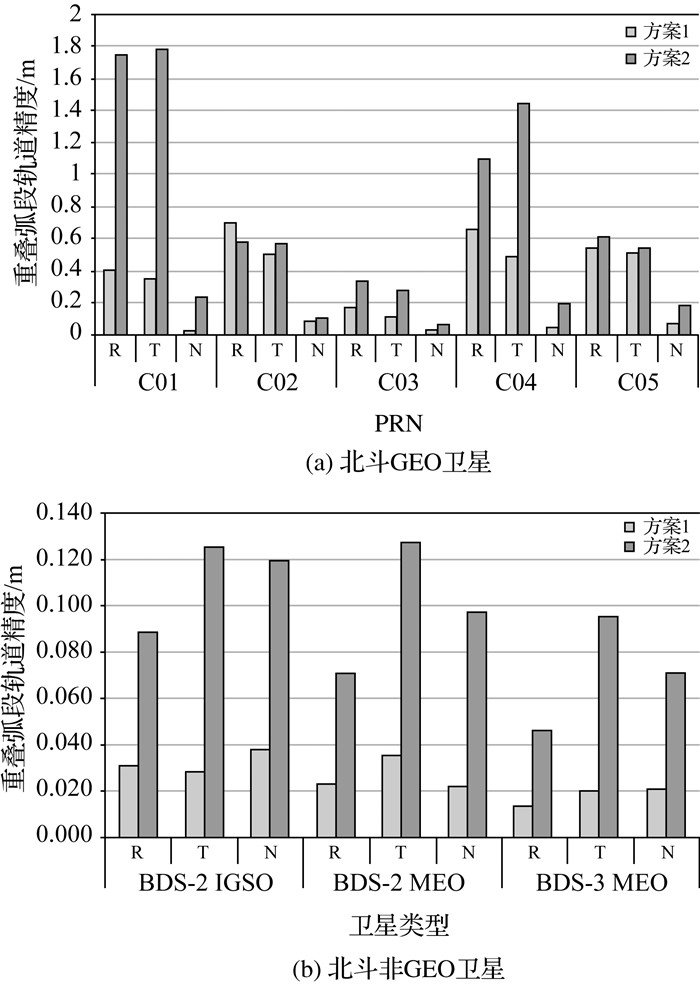
将两种方案得到的轨道分别进行重叠弧段比较(3d弧段,重叠2d),表 2给出了两种方案下各卫星在径向(R)、切向(T)、法向(N)和三维位置(P)重叠弧段轨道的均方根误差(RMS),为便于比较分析,图 2给出了其图示形式。统计结果表明,相对于方案2,采用方案1解算的北斗GEO和非GEO卫星三维重叠弧段轨道精度分别由1.501、0.152m提高至0.688、0.042m,分别提升了54.2%和72.4%。北斗GEO卫星和非GEO卫星在R、T、N方向上精度分别提升47.1%、60.1%、63.3%和66.8%、76.8%、70.1%。可以看出,本文提出的定轨方案对北斗全星座定轨精度改进作用明显,且R、T、N方向上精度均有所提高。
|
| 图 2 北斗卫星重叠弧段轨道精度对比 Fig. 2 Comparison of BeiDou satellites overlapping orbit precision |
| 星座 | PRN | R | T | N | P(3D) | |||||||
| S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | |||||
| GEO | C01 | 0.412 | 1.749 | 0.356 | 1.785 | 0.036 | 0.242 | 0.545 | 2.511 | |||
| C02 | 0.702 | 0.584 | 0.511 | 0.566 | 0.093 | 0.116 | 0.873 | 0.822 | ||||
| C03 | 0.175 | 0.338 | 0.123 | 0.280 | 0.039 | 0.074 | 0.217 | 0.446 | ||||
| C04 | 0.661 | 1.105 | 0.497 | 1.450 | 0.051 | 0.204 | 0.829 | 1.834 | ||||
| C05 | 0.550 | 0.618 | 0.516 | 0.550 | 0.083 | 0.190 | 0.759 | 0.849 | ||||
| mean | 0.535 | 1.012 | 0.428 | 1.095 | 0.065 | 0.176 | 0.688 | 1.501 | ||||
| BDS2-IGSO | C06 | 0.020 | 0.077 | 0.025 | 0.110 | 0.045 | 0.073 | 0.055 | 0.152 | |||
| C07 | 0.040 | 0.085 | 0.030 | 0.118 | 0.034 | 0.089 | 0.061 | 0.170 | ||||
| C08 | 0.039 | 0.151 | 0.031 | 0.189 | 0.055 | 0.219 | 0.074 | 0.326 | ||||
| C09 | 0.042 | 0.051 | 0.038 | 0.093 | 0.037 | 0.076 | 0.068 | 0.131 | ||||
| C10 | 0.021 | 0.068 | 0.022 | 0.128 | 0.028 | 0.090 | 0.042 | 0.170 | ||||
| C13 | 0.029 | 0.078 | 0.033 | 0.100 | 0.028 | 0.148 | 0.052 | 0.195 | ||||
| C16 | 0.018 | 0.078 | 0.022 | 0.111 | 0.034 | 0.058 | 0.045 | 0.147 | ||||
| mean | 0.032 | 0.089 | 0.029 | 0.125 | 0.038 | 0.120 | 0.058 | 0.194 | ||||
| BDS2-MEO | C11 | 0.022 | 0.071 | 0.036 | 0.136 | 0.017 | 0.094 | 0.046 | 0.180 | |||
| C12 | 0.027 | 0.086 | 0.038 | 0.133 | 0.026 | 0.105 | 0.053 | 0.190 | ||||
| C14 | 0.021 | 0.052 | 0.032 | 0.113 | 0.023 | 0.094 | 0.044 | 0.155 | ||||
| mean | 0.023 | 0.071 | 0.035 | 0.128 | 0.022 | 0.098 | 0.048 | 0.176 | ||||
| BDS3-MEO | C19 | 0.017 | 0.045 | 0.024 | 0.100 | 0.027 | 0.065 | 0.040 | 0.127 | |||
| C20 | 0.011 | 0.038 | 0.017 | 0.090 | 0.020 | 0.048 | 0.028 | 0.109 | ||||
| C21 | 0.010 | 0.073 | 0.017 | 0.108 | 0.026 | 0.076 | 0.033 | 0.151 | ||||
| C22 | 0.010 | 0.098 | 0.017 | 0.227 | 0.025 | 0.178 | 0.032 | 0.304 | ||||
| C23 | 0.017 | 0.043 | 0.023 | 0.078 | 0.017 | 0.054 | 0.034 | 0.104 | ||||
| C24 | 0.019 | 0.040 | 0.021 | 0.057 | 0.022 | 0.072 | 0.036 | 0.100 | ||||
| C25 | 0.016 | 0.033 | 0.022 | 0.079 | 0.017 | 0.030 | 0.032 | 0.090 | ||||
| C26 | 0.013 | 0.049 | 0.020 | 0.061 | 0.021 | 0.064 | 0.031 | 0.101 | ||||
| C27 | 0.009 | 0.041 | 0.015 | 0.094 | 0.015 | 0.052 | 0.024 | 0.115 | ||||
| C28 | 0.009 | 0.031 | 0.013 | 0.077 | 0.015 | 0.037 | 0.022 | 0.091 | ||||
| C29 | 0.017 | 0.049 | 0.027 | 0.106 | 0.019 | 0.058 | 0.037 | 0.130 | ||||
| C30 | 0.015 | 0.037 | 0.023 | 0.087 | 0.017 | 0.045 | 0.032 | 0.105 | ||||
| C32 | 0.011 | 0.040 | 0.015 | 0.088 | 0.018 | 0.051 | 0.026 | 0.109 | ||||
| C33 | 0.011 | 0.035 | 0.019 | 0.079 | 0.019 | 0.099 | 0.029 | 0.131 | ||||
| C34 | 0.015 | 0.030 | 0.022 | 0.054 | 0.020 | 0.063 | 0.034 | 0.088 | ||||
| C35 | 0.009 | 0.036 | 0.017 | 0.069 | 0.023 | 0.063 | 0.030 | 0.100 | ||||
| C36 | 0.017 | 0.040 | 0.025 | 0.080 | 0.028 | 0.056 | 0.041 | 0.106 | ||||
| C37 | 0.015 | 0.024 | 0.026 | 0.041 | 0.023 | 0.038 | 0.038 | 0.061 | ||||
| mean | 0.014 | 0.046 | 0.021 | 0.095 | 0.021 | 0.071 | 0.033 | 0.128 | ||||
对于上述结果,初步分析如下:
(1) 本文采用双差观测模型,在方案2第2步解算北斗卫星轨道过程中进行星间组差时会出现部分非GEO与GEO卫星之间的组差数据,由于GEO卫星“静地”特性,其轨道精度比非GEO卫星低一个量级,在统一平差过程中势必对非GEO卫星产生不利影响。而方案1由于在解算非GEO卫星轨道时没有GEO卫星数据参与,系统内只会在非GEO卫星内部进行组差,避免了上述问题。
(2) GEO卫星“静地”特性也使得其载波相位模糊度很难固定,对于非GEO卫星,其与GEO卫星组差后模糊度固定难度亦增加,导致整体模糊度固定率较低(方案1非GEO模糊度固定率比方案2高10%左右),这也是方案1非GEO卫星轨道精度提升的原因。
(3) 对于GEO卫星,方案1在第3步单独对其解算时,一方面,GPS和BDS非GEO卫星轨道均已精确确定,GEO卫星与它们组差解算时,受到的观测约束更强,有利于其精度提高;另一方面,在组基线时只需考虑GEO卫星,采用针对GEO卫星的“OBS-MAX”策略,即按照共同GEO观测数据最多的原则来组基线,在一定程度上增加了参与GEO轨道解算数据的数量,同样有利于GEO卫星轨道精度的改善。
不同于重叠弧段主要反映轨道内符合精度,激光测距(satellite laser ranging, SLR)检核是一种独立检核卫星轨道外符合精度的手段。利用参与国际激光联测(ILRS)的部分北斗卫星的激光测距数据对两种方案下的轨道进行检核,检核残差统计见表 3。可以看出,方案1与方案2相比,除C30卫星外,其余卫星激光检核残差均有不同程度减小,SLR检核精度整体提升了44.3%。
| PRN | NPTs | mean | STD | RMS | |||||
| S1 | S2 | S1 | S2 | S1 | S2 | ||||
| C01 | 32 | -413.7 | -337.4 | 529.4 | 1189.2 | 665.3 | 1218.1 | ||
| C08 | 57 | -87.7 | -75.3 | 59.3 | 111.1 | 105.6 | 133.4 | ||
| C10 | 12 | 34.3 | 35.2 | 56.8 | 112.9 | 64.3 | 113.7 | ||
| C11 | 77 | 0.2 | -19.9 | 29.8 | 54.8 | 29.6 | 58.0 | ||
| C20 | 97 | 43.7 | 51.9 | 26.6 | 42.1 | 51.1 | 66.7 | ||
| C21 | 122 | 36.6 | 56.2 | 21.6 | 66.8 | 42.5 | 87.0 | ||
| C29 | 74 | -31.3 | -32.0 | 40.6 | 55.4 | 51.1 | 63.6 | ||
| C30 | 83 | -25.3 | -11.0 | 32.3 | 39.2 | 40.9 | 40.5 | ||
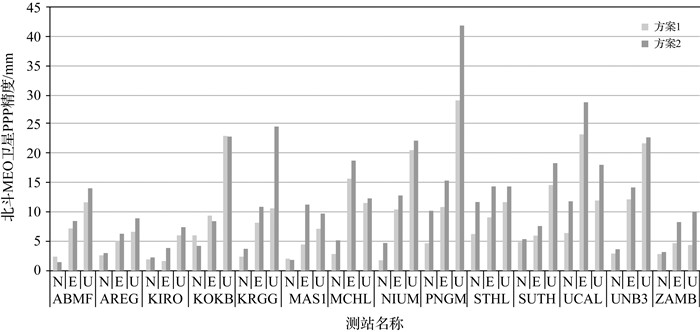
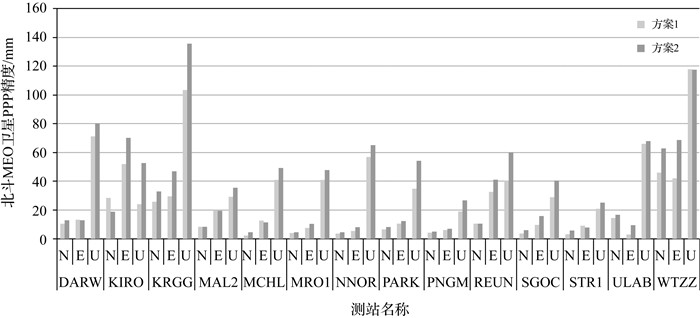
为进一步综合验证本文所提方案解算的北斗轨道精度,选取部分MGEX测站进行了静态精密单点定位(precise point positioning, PPP)试验,分别采用方案1和方案2解算的北斗轨道和钟差组合,完成测站坐标静态PPP解算,将解算的结果与IGS最终坐标产品比较。为方便分析不同星座轨道精度,试验分以下两组进行:第1组,利用北斗MEO卫星对全球分布的14个测站进行静态PPP解算。第2组,利用北斗二号GEO/IGSO卫星对亚太地区14个测站进行静态PPP解算。图 3和图 4分别给出了两组试验解算的测站坐标在N、E、U方向上的精度对比。统计结果表明,利用方案1解算的北斗卫星轨道,北斗MEO卫星PPP精度在水平和高程方向上分别达到11.3和21.7mm,北斗GEO/IGSO卫星PPP精度在水平和高程方向上分别达到40.6和115.1mm,在方案2条件下PPP精度分别提高24.2%、22.1%和26.1%、15.8%。
|
| 图 3 北斗MEO卫星PPP精度对比 Fig. 3 Comparison of BeiDou MEO satellites PPP precision |
|
| 图 4 北斗GEO/IGSO卫星PPP精度对比 Fig. 4 Comparison of BeiDou GEO/IGSO satellites PPP precision |
3 结论
本文针对北斗系统混合星座特点,研究了一种区分星座、分层约束、分步解算的北斗卫星精密定轨方法。利用实测数据进行了精密定轨试验,采用重叠弧段轨道、激光测距检核和测站坐标静态PPP等手段对轨道精度进行了验证,并与传统方法进行了对比。试验结果表明,本文提出的方法能够显著改善北斗卫星的定轨精度。北斗GEO卫星在R、T、N方向上重叠弧段轨道精度分别达到0.535、0.428、0.065m,北斗非GEO卫星在R、T、N方向上重叠弧段轨道精度分别达到0.021、0.025、0.027m,三维重叠弧段精度综合提高54.9%。唯一参与国际激光联测的GEO卫星C01激光检核残差RMS由1218.1mm减小到665.3mm,其余非GEO卫星激光检核残差RMS由78.5mm减小到54.6mm。北斗不同星座精密单点定位精度在水平和高程方向上均有所提升。
致谢: 特别感谢iGMAS和IGS组织为本文提供观测数据。
| [1] |
YANG Yuanxi, MAO Yue, SUN Bijiao. Basic performance and future developments of BeiDou global navigation satellite system[J]. Satellite Navigation, 2020, 1: 1. DOI:10.1186/s43020-019-0006-0 |
| [2] |
中华人民共和国国务院新闻办公室.中国北斗卫星导航系统: 白皮书[EB/OL]. 2016-06-16. http://www.gov.cn/zhengce/2016-06/16/content_5082748.htm. The State Council Information Office of the People's Republic of China. China's BeiDou Navigation Satellite System[EB/OL]. 2016-06-16. http://www.gov.cn/zhengce/2016-06/16/content_5082748.htm. |
| [3] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, contribution and challenges of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [4] |
ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit determination and time synchronization for a GEO/IGSO satellite navigation constellation with regional tracking network[J]. Science China:Physics, Mechanics & Astronomy, 2011, 54(6): 1089-1097. |
| [5] |
GE Maorong, ZHANG Hongping, JIA Xiaolin, et al. What is achievable with the current compass constellation[J]. GPS World, 2012, 23(11): 29-35. |
| [6] |
ZHU Jun, WANG Jiasong, ZENG Guang, et al. Precise orbit determination of BeiDou regional navigation satellite system via double-difference observations[C]//Proceedings of 2013 China Satellite Navigation Conference (CSNC). Berlin, Heidelberg: Springer, 2013, 245: 77-88.
|
| [7] |
刘伟平, 郝金明, 邓科, 等. 北斗卫星单系统精密定轨方法对比分析[J]. 天文学报, 2016, 57(5): 534-543. LIU Weiping, HAO Jinming, DENG Ke, et al. Comparison and analysis of BeiDou satellite single-system precise orbit determination[J]. Acta Astronomica Sinica, 2016, 57(5): 534-543. |
| [8] |
STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and clock analysis of COMPASS GEO and IGSO satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525. DOI:10.1007/s00190-013-0625-4 |
| [9] |
ZHAO Qile, GUO Jing, LI Min, et al. Initial results of precise orbit and clock determination for COMPASS navigation satellite system[J]. Journal of Geodesy, 2013, 87(5): 475-486. DOI:10.1007/s00190-013-0622-7 |
| [10] |
施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854-861. SHI Chuang, ZHAO Qile, LI Min, et al. Precise orbit determination of BeiDou satellites with precise positioning[J]. Science China:Earth Sciences, 2012, 42(6): 854-861. |
| [11] |
刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132-1138. LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS joint precise orbit determination of BeiDou navigation satellite system[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132-1138. |
| [12] |
LOU Yidong, LIU Yang, SHI Chuang, et al. Precise orbit determination of BeiDou constellation:method comparison[J]. GPS Solutions, 2016, 20(2): 259-268. DOI:10.1007/s10291-014-0436-y |
| [13] |
陈明, 郭际明, 武军郦, 等. 北斗精密定轨精度评估及站点分布影响分析[J]. 测绘学报, 2018, 47(S0): 93-100. CHEN Ming, GUO Jiming, WU Junli, et al. Accuracy assessment of BDS precision orbit determination and the influence analysis of site distribution[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S0): 93-100. DOI:10.11947/j.AGCS.2018.20180278 |
| [14] |
CHEN Ming, LIU Yang, GUO Jiming, et al. Precise orbit determination of BeiDou satellites with contributions from Chinese national continuous operating reference stations[J]. Remote Sensing, 2017, 9(8): 810. DOI:10.3390/rs9080810 |
| [15] |
LI Xingxing, YUAN Yongqiang, ZHU Yiting, et al. Precise orbit determination for BDS3 experimental satellites using iGMAS and MGEX tracking networks[J]. Journal of Geodesy, 2019, 93(1): 103-117. DOI:10.1007/s00190-018-1144-0 |
| [16] |
TAN Bingfeng, YUAN Yunbin, WEN Mingyue, et al. Initial results of the precise orbit determination for the new-generation BeiDou satellites (BeiDou-3) based on the iGMAS network[J]. ISPRS International Journal of Geo-Information, 2016, 5(11): 196. DOI:10.3390/ijgi5110196 |
| [17] |
郭睿, 周建华, 胡小工, 等. 北斗IGSO卫星姿态零偏航状态下精密定轨[J]. 测绘学报, 2018, 47(S0): 18-27. GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. Precise orbit determination for the BDS IGSO satellites under the yaw-steering mode[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S0): 18-27. DOI:10.11947/j.AGCS.2018.20180286 |
| [18] |
GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. Precise orbit determination and rapid orbit recovery supported by time synchronization[J]. Advances in Space Research, 2015, 55(12): 2889-2898. DOI:10.1016/j.asr.2015.03.001 |
| [19] |
CHEN Qiuli, YANG Hui, CHEN Zhonggui, et al. Solar radiation pressure modeling and application of BDS satellites[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 45-52. |
| [20] |
ZENG Tian, SUI Lifen, JIA Xiaolin, et al. Results and analyses of BDS precise orbit determination with the enhancement of Fengyun-3C[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(3): 68-78. |
| [21] |
REN Xia, YANG Yuanxi, ZHU Jun, et al. Orbit determination of the next-generation BeiDou satellites with intersatellite link measurements and a priori orbit constraints[J]. Advances in Space Research, 2017, 60(10): 2155-2165. |
| [22] |
YANG Daoning, YANG Jun, LI Gang, et al. Globalization highlight:orbit determination using BeiDou inter-satellite ranging measurements[J]. GPS Solutions, 2017, 21(3): 1395-1404. |
| [23] |
TANG Chengpan, HU Xiaogong, ZHOU Shanshi, et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements[J]. Journal of Geodesy, 2018, 92(10): 1155-1169. DOI:10.1007/s00190-018-1113-7 |
| [24] |
杨宇飞, 杨元喜, 胡小工, 等. 北斗三号卫星两种定轨模式精度比较分析[J]. 测绘学报, 2019, 48(7): 831-839. YANG Yufei, YANG Yuanxi, HU Xiaogong, et al. Comparison and analysis of two orbit determination methods for BDS-3 satellites[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 831-839. DOI:10.11947/j.AGCS.2019.20180560 |
| [25] |
DACH R, LUTZ S, WALSER P, et al. Bernese GNSS Software, Version 5.2[M]. Bern: Astronomical Institute, University of Bern, 2015.
|
| [26] |
房亚男, 辛景民, 曾光, 等. 模糊度固定的北斗卫星多系统融合精密轨道确定[J]. 测绘学报, 2018, 47(3): 341-347. FANG Yanan, XIN Jingmin, ZENG Guang, et al. BeiDou satellites multi-GNSS precise orbit determination with ambiguity fixed[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 341-347. DOI:10.11947/j.AGCS.2018.20170378 |



