2. 西安测绘研究所, 陕西 西安 710054;
3. 信息工程大学, 河南 郑州 450001;
4. 中山大学物理与天文学院天琴中心, 广东 珠海 519082
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. Information Engineering University, Zhengzhou 450001, China;
4. TianQin Research Center for Gravitational Physics and School of Physics and Astronomy, Sun Yat-sen University (Zhuhai Campus), Zhuhai 519082, China
分布式干涉合成孔径雷达(interferometric synthtic aperture radar, InSAR)卫星系统在对地观测领域中发挥着重要的作用,可实现地面目标三维定位、地表形变和动目标检测等任务,是获得高精度全球数字高程模型的重要手段[1]。低轨卫星编队的高精度轨道和星间基线确定对分布式InSAR卫星系统任务的顺利实施至关重要,尤其是星间基线的确定精度直接影响系统的测高精度[2]。以德国的TanDEM-X任务为例,该任务由TerraSAR-X和TanDEM-X两颗卫星组成,是经过在轨验证并成功应用的分布式InSAR卫星系统典型代表。为了满足该系统2 m相对高程测量精度要求,其星间基线确定精度需达到每轴1~2 mm[3]。目前,基于星载GNSS数据的分布式InSAR编队卫星绝对和相对轨道确定是获得高精度轨道和基线产品的主要手段。基于该方法确定的TanDEM-X任务单星绝对轨道精度达到5 cm[4],双星相对轨道精度每轴可以达到1 mm左右[5-6]。天绘二号编队是我国第一代分布式InSAR编队卫星系统,由A星和B星两颗卫星组成,卫星运行在高度约512 km的太阳同步轨道上,正常工作模式下双星编队距离约几百米[7]。两颗卫星均搭载了双频GNSS接收机用于精密定轨,研究基于GNSS数据的绝对和相对定轨技术对其科学任务的实现与应用具有重要的意义。
基于星载GNSS数据的低轨卫星精密定轨方法主要有运动学法、动力学法和缩减动力学法。运动学方法不依赖卫星运动的先验信息,单纯采用GNSS观测数据实现卫星精密定轨,然而该方法过度依赖GNSS观测数据质量,受限于观测几何、数据间断等情况,轨道可靠性不高[8]。动力学方法采用卫星运动的力学模型对卫星位置进行约束,能够提供连续的卫星轨道位置和预报结果[9-10],但该方法精度受到大气阻力、太阳光压等摄动力建模误差的制约。缩减动力学定轨方法是目前低轨卫星编队单星绝对定轨和双星相对定轨的主流方法[11]。该方法是在轨道动力学模型的约束下,通过引入经验加速度或伪随机脉冲等随机参数,使得卫星轨道解与GNSS观测数据之间达到最优匹配,能够提供连续光滑的高精度轨道产品。对于编队飞行的低轨卫星,通常采用载波相位差分GNSS技术,消除或削弱公共误差项的影响,并通过固定双差相位整周模糊度,实现高精度的相对轨道确定。目前,在单星绝对定轨方面,基于双频GNSS数据的缩减动力学单星定轨精度可达到厘米级,GRACE、GOCE和SWARM等任务卫星定轨精度达到2~3 cm[12-14]。在双星相对定轨方面,利用缩减动力学定轨方法,GRACE、TanDEM-X和SWARM编队任务的基线确定精度达到毫米级甚至亚毫米级[15-17]。其中,星载GNSS观测数据质量是影响卫星精密定轨精度的关键因素之一,尤其是在相对定轨中,基于Melbourne-Wübbena(M-W)线性组合的双差宽巷整周模糊度固定依赖于伪码数据质量[18],双星共视GNSS卫星情况也直接影响相对定轨精度[19]。
分布式InSAR编队卫星为保持编队构型,需要进行频繁的轨道机动[6],机动条件下的绝对和相对定轨是需要解决的关键问题之一。文献[6]指出,AIUB、GFZ和DLR机构在缩减动力学定轨框架下分别使用Bernese、EPOS和GHOST软件进行TanDEM-X任务卫星绝对和相对定轨。不同机构采用的定轨软件在机动处理策略上存在差异,Bernese与EPOS软件采用速度脉冲处理机动,缺点是难以进行长时间机动的精确建模,GHOST软件采用常值加速度模型处理机动,然而由于软件算法的限制,只能在绝对定轨部分进行机动建模,无法进行相对定轨部分的机动建模处理。文献[20]通过对机动力进行常值加速度建模以及机动附近积分方法的改进,消除了轨道机动对GRACE编队绝对和相对定轨的影响,机动条件下的GRACE双星基线KBR检核精度达到0.7 mm。文献[21]进一步对GRACE、TanDEM-X和PRISMA编队卫星的机动力进行常值加速度建模,结果表明该方法可有效消除轨道机动对相对定轨的影响。
基于以上分析,本文收集了天绘二号编队A星和B星2019年9月7日至14日的双频GPS数据,分析了接收机跟踪性能、伪码和相位噪声水平。进一步基于星载双频GPS数据进行编队卫星绝对和相对轨道确定,利用机动常值加速度建模方法消除轨道机动对绝对和相对定轨的影响,通过GPS相位定轨残差、重叠弧段互比对、卫星激光测距(satellite laser ranging, SLR)数据检核以及与外部产品互比对等手段,对绝对和相对定轨结果进行分析和评估。
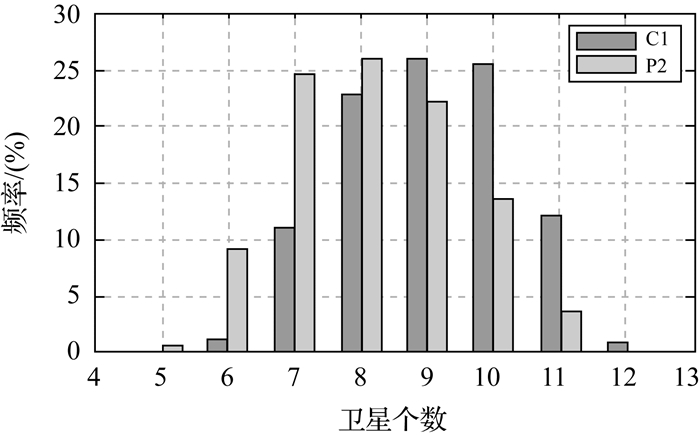
1 星载GPS观测数据质量分析A星和B星搭载的国产GNSS接收机分别有12个通道跟踪GPS卫星数据,可获取GPS C1码与P2码和L1相位与L2相位观测值。图 1给出了A星在年积日(day of year, DOY)253的C1码和P2码可视GPS卫星个数的历元比例。可见,接收机的最大可视GPS卫星个数为12颗,C1码和P2码平均可视卫星数分别为9.0颗和8.2颗。试验期间,B星与A星在数据跟踪方面情况基本相同。
|
| 图 1 A星C1码和P2码的可视GPS卫星个数的历元比例 Fig. 1 Frequency of the number of visible GPS satellites for C1 and P2 of satellite A |
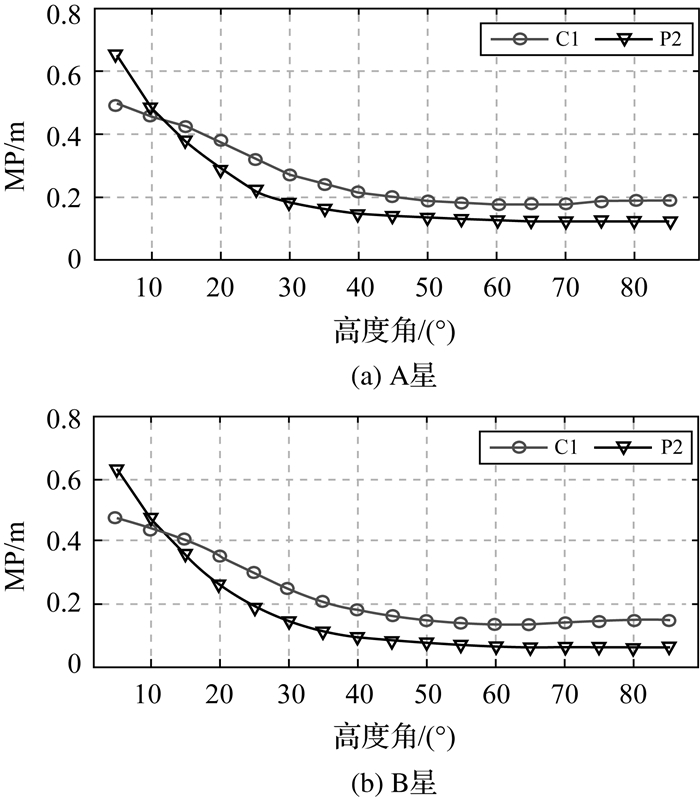
伪码多路径(multipath, MP)组合可有效消除几何距离、钟差和电离层延迟的影响,常用来提取伪码观测噪声,评估伪码观测数据的质量[22]。图 2绘制了A星和B星C1码和P2码多路径误差大小随高度角变化曲线。可见,多路径误差随高度角变大而逐渐减小。A卫星C1码和P2码的多路径误差RMS分别为0.30 m和0.25 m,而B卫星C1码和P2码的多路径误差RMS分别为0.27 m和0.22 m。与国内天宫二号[23]、HY-2A[24]相比,A星和B星C1码与同频点天宫二号0.3 m的多路径误差RMS类似,明显小于HY-2A 0.9 m的多路径误差RMS,A星和B星P2码略小于同频点的天宫二号0.3 m与HY-2A 0.3 m的多路径误差RMS。
|
| 图 2 A星和B星多路径误差大小随高度角变化关系 Fig. 2 Function of multipath error with elevation angle for satellite A and satellite B |
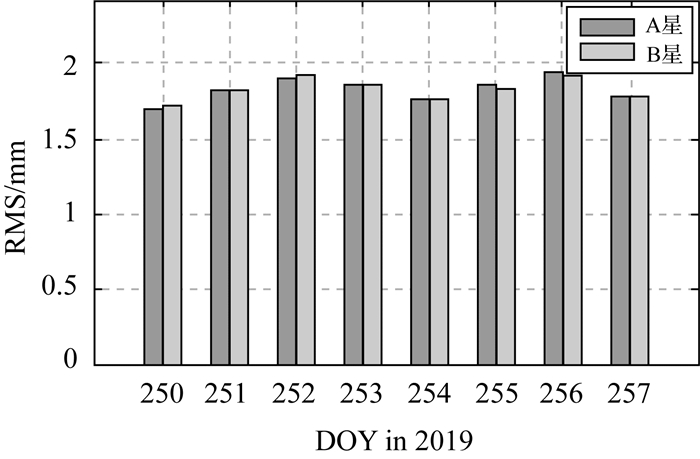
采用相位观测量的无几何距离组合(L1-L2)提取电离层延迟与相位噪声,然后通过三阶滑动多项式拟合电离层延迟,将余下的残差作为相位随机噪声,可以反映相位L1-L2组合的内符合精度[23]。图 3统计了每天A星和B星L1-L2组合多项式拟合残差RMS值,其平均值分别为1.82 mm和1.83 mm,略小于天宫二号平均2.3 mm的拟合残差RMS值[23]。
|
| 图 3 A星和B星相位L1-L2组合多项式拟合残差RMS Fig. 3 RMS of polynomial fitting residuals using phase L1-L2 combination for satellite A and satellite B |
2 定轨原理与数据处理策略 2.1 定轨基本原理
本文基于星载双频GPS数据对天绘二号编队卫星进行绝对和相对轨道确定。其中,单星绝对定轨采用伪码和相位观测值的消电离层(ionosphere-free, IF)组合作为基本观测模型,可表示为[21]
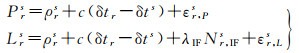 (1)
(1)
式中,s为GPS卫星编号;r为低轨卫星接收机编号;P和L分别为IF组合的伪码和相位观测值;ρ为接收机天线相位中心到GPS卫星天线相位中心之间的几何距离;c为光速;δtr和δts分别为接收机端和GPS卫星端钟差;λIF为IF组合载波波长;NIF为IF组合模糊度;εP和εL分别为伪码和相位观测噪声。
利用缩减动力学定轨方法对低轨卫星进行精密轨道确定,待估参数包括轨道动力学参数、相位模糊度和接收机钟差参数。记卫星r的轨道动力学参数为
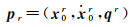
式中,x0r和ẋ0r分别表示初始位置和速度矢量;qr表示摄动加速度模型中的待估参数矢量,通过对动力学参数pr的积分计算可获得任意时刻卫星轨道状态。将基本观测方程式(1)进行线性化,通过逐历元叠加的方式构建法方程,采用最小二乘方法对动力学参数pr、模糊度参数和钟差参数进行估计[23]。
对于双星相对定轨,需要对两颗近距离低轨卫星的GPS观测数据进行差分处理,消除GPS卫星钟差、接收机钟差等影响,采用伪码和相位观测值的双差IF组合作为基本观测模型,可表示为[18]
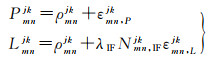 (2)
(2)
式中,j和k代表GPS卫星编号;m和n为低轨卫星接收机编号。双差模糊度具有整数特性,采用宽窄巷策略固定双差整周模糊度[18]。
同样采用缩减动力学定轨方法确定编队卫星相对轨道参数,通常使A星单独定轨结果保持固定,将编队卫星相对状态参数的求解转化为B星各项参数的求解,进而得到B星相对轨道,通过B星与A星的位置作差获取两颗星之间的相对位置。
2.2 数据处理策略本文采用国防科技大学自主研制的定轨软件NUDTTK进行编队卫星绝对和相对轨道确定,采用缩减动力学定轨结合最小二乘批处理方法确定定轨参数,具体数据处理策略见表 1。
| 模型项 | 描述 |
| 观测数据及其误差修正 | 非差伪码、相位消电离层组合(绝对定轨) 双差伪码、相位消电离层组合(相对定轨) 采样间隔10 s GPS卫星天线相位中心模型,igs14.atx 相位缠绕模型改正[25] 相对论模型改正[26] C1码偏差改正,CODE DCB产品[27] |
| GPS轨道钟差 | CODE最终轨道和30 s钟差产品 |
| 观测权值 | 高度角θ加权:大于30°时权值为1;小于30°时权值为2sin θ |
| 模糊度参数 | 非差模糊度浮点解(绝对定轨) 双差模糊度固定解(相对定轨) |
| 地球重力场 | GGM05S 120×120 |
| 固体潮、极潮 | IERS 2003[28] |
| 海潮模型 | FES2004 |
| 第三体引力 | 太阳、月球和行星引力,DE405 |
| 相对论摄动 | 仅Schwarzschild项 |
| 大气阻力摄动 | 大气密度Jacchia 71[29],每6 h估计1个大气阻力系数 |
| 太阳光压摄动 | Cannon-ball模型,整个弧段估计一个太阳光压系数 |
| 机动力 | 常值加速度[20] |
| 经验力加速度 | 切向(T)和法向(N)线性样条加速度模型,每15 min估计一组参数 径向(R)常值加速度模型,全弧段常数 |
| 地球旋转参数 | IERS Standard Rapid产品 |
| 参数估计 | 批处理最小二乘 |
试验期间,A星每天机动3次,每次机动持续时间约为1~5 s,而B星不进行机动。为消除轨道机动对定轨的影响,采用常值加速度模型来描述卫星的轨道机动控制,可表示为[20]
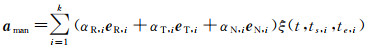 (3)
(3)
式中,aman为机动力摄动加速度矢量;k表示机动区间总个数;αi为机动加速度待估参数;eR、eT、eN表示R、T和N方向的单位矢量;ts, i、te, i表示第i个区间的起始和结束时间;ξ表示子区间[ts, i, te, i]上的示性函数。由于机动持续时间相比于轨道周期而言较短,通常量级较大且作用区间不固定,导致运动方程存在明显的不连续,在机动处理时,需要对轨道数值积分方法进行调整。本文在处理机动条件下的轨道积分问题时,使用了一种单步法与多步法结合的数值积分方法,即在非机动时采用高阶Adams-Cowell积分器,进一步根据机动起始时间信息,仅在机动附近采用8阶Runge-Kutta单步法对运动方程和变分方程进行积分,具体方法参考文献[20]。
西安测绘研究所同样采用自主研制的基线处理软件确定天绘二号编队卫星相对轨道[7],在数据处理策略上与本文有明显差异:一方面,其采用速度脉冲模型吸收未模型化的力学模型误差;另一方面,增加机动速度脉冲参数对机动进行处理,具体策略参考文献[30-31]。由于采用不同的基线处理软件和简化动力学策略,保证了各自的基线产品具有一定的独立性,通过互比对可以反映出天绘二号编队基线确定精度。
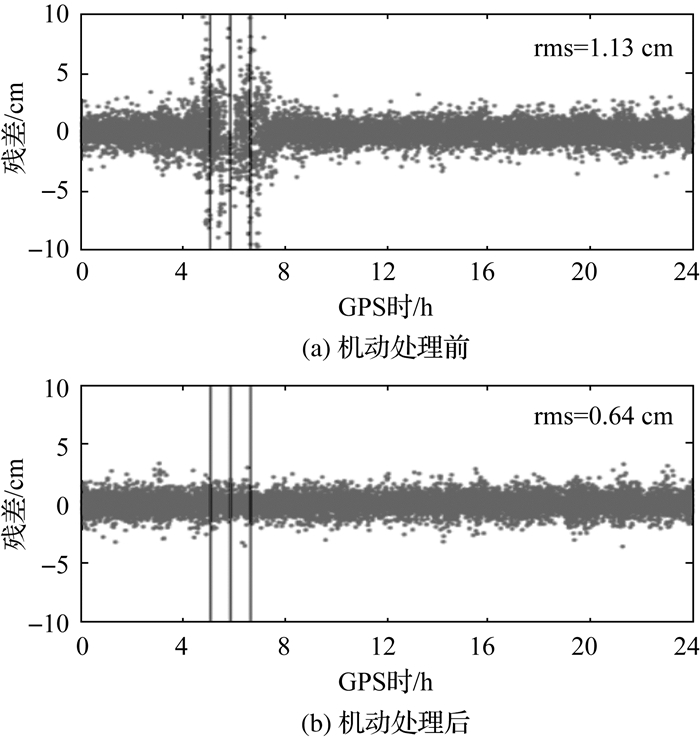
3 绝对和相对定轨精度分析 3.1 机动处理效果分析首先,通过相位定轨残差来反映机动期间的定轨质量。图 4给出2019年9月7日A星机动处理前后相位定轨残差情况。其中,竖线表示机动时刻,机动期间定轨残差超过10 cm未在图中显示,其最大残差达30 cm左右。可见,在机动期间未添加额外的机动加速度补偿时,相位定轨残差将急剧增大。随着观测时间的增加,相位定轨残差逐渐减小,但需要一段时间才能恢复到正常水平。而当进行机动加速度参数补偿后,相位定轨残差都在正常水平。
|
| 图 4 A星机动处理前后相位定轨残差情况 Fig. 4 Orbit post-fit phase residuals for satellite A with and without estimating maneuvers |
进一步,统计了每天单星定轨残差和双星相对定轨残差,结果见表 2。由于B星无机动,其每天单星定轨残差RMS值都约为0.64 cm,未在表 2中给出。同时,A星机动处理后的相位观测值定轨残差RMS都在0.7 cm以内,反映出本文使用的观测模型和动力学模型与实际情况吻合程度较好。双星相对定轨在单星绝对定轨结果的基础上进行,轨道机动同样影响双星相对定轨,使机动附近相对定轨残差明显变大。进行机动处理后,双星相对定轨残差RMS均值从0.98 cm减小到0.41 cm,机动处理同样消除了相对定轨中残差波动现象。
| DOY | A星绝对定轨 | 双星相对定轨 | |||
| 处理前 | 处理后 | 处理前 | 处理后 | ||
| 250 | 1.13 | 0.64 | 1.14 | 0.40 | |
| 251 | 1.06 | 0.65 | 1.00 | 0.41 | |
| 252 | 1.03 | 0.64 | 0.93 | 0.41 | |
| 253 | 1.04 | 0.65 | 0.85 | 0.40 | |
| 254 | 1.14 | 0.64 | 0.84 | 0.40 | |
| 255 | 1.19 | 0.64 | 0.92 | 0.40 | |
| 256 | 1.13 | 0.65 | 1.05 | 0.42 | |
| 257 | 1.20 | 0.65 | 1.07 | 0.41 | |
| mean | 1.11 | 0.65 | 0.98 | 0.41 | |
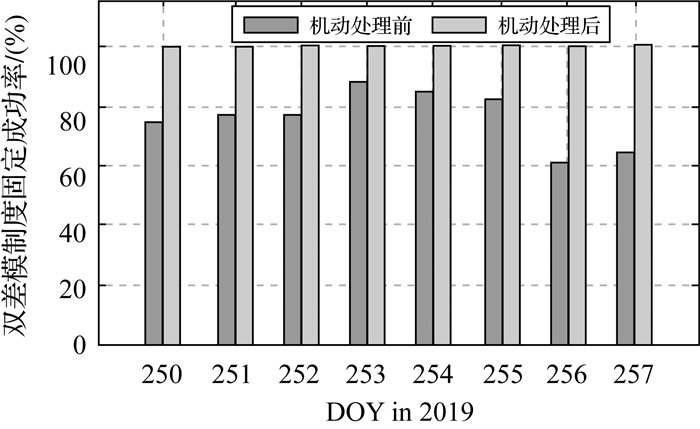
此外,双差宽巷模糊度的固定仅依赖于观测数据的M-W组合,与轨道力学模型无关。由于天绘二号编队卫星伪码和相位观测数据质量达到较高水平,且双星星间距离较近,双差宽巷模糊度固定成功率达到100%。而双差窄巷模糊度的固定成功率与轨道力学模型的表示精度有关,如果机动力在定轨过程中处理不当,则会严重影响双差窄巷模糊度的固定成功率,进而影响相对定轨精度。机动处理前后的双差窄巷模糊度固定成功率如图 5所示。机动处理后,双差窄巷模糊度平均固定成功率由76%提高到100%。
|
| 图 5 机动处理前后相对定轨双差窄巷模糊度固定成功率 Fig. 5 Fixing rate of narrow-lane ambiguity in relative orbit determination with and without estimating maneuvers |
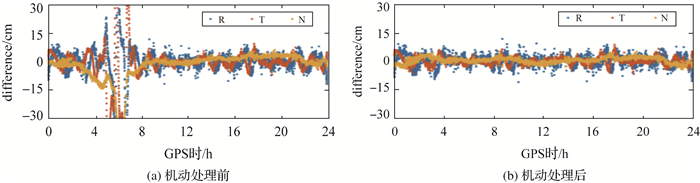
由于运动学定轨方法与轨道力学模型无关,因此通过与运动学轨道互比对进一步检核机动处理效果。图 6给出了2019年9月7日,机动处理前后的A星缩减动力学轨道与运动学轨道在R、T和N方向的比对结果,机动期间互比对差值超过30 cm未在图中显示。可见,经机动处理后,机动期间缩减动力学与运动学互比对差值明显恢复正常水平。
|
| 图 6 A星机动处理前后单星缩减动力学轨道与运动学轨道互比对 Fig. 6 Differences between reduced-dynamic and kinematic orbits for satellite A with and without estimating maneuvers |
3.2 绝对定轨精度分析
在机动处理条件下,对单星绝对定轨精度进行检核和分析。检核方法包括6 h重叠弧段互比对、与运动学轨道互比对以及SLR数据检核,统计结果见表 3。其中,本文定轨弧段长度设为30 h,即从前一天21:00至后一天03:00,相邻弧段之间有6 h重叠,可通过比较重叠弧段检核轨道的内部一致性。见表 3,单星轨道在单个方向重叠精度都优于0.8 cm,三维方向优于1.2 cm,表明基于双频GPS数据的单星定轨结果具有良好的内部一致性。
| satellite | 重叠轨道差值RMS | 与运动学互比对RMS | SLR检核残差 | |||||||||
| R | T | N | 3D | R | T | N | 3D | mean | RMS | |||
| A | 0.45 | 0.62 | 0.69 | 1.05 | 2.89 | 2.23 | 1.42 | 3.92 | 1.77 | 2.76 | ||
| B | 0.49 | 0.59 | 0.82 | 1.15 | 2.92 | 2.21 | 1.51 | 3.97 | 0.12 | 2.33 | ||
进一步通过运动学轨道与缩减动力学轨道互比对评估定轨精度。A星和B星的两种轨道互比对差值平均3D RMS分别为3.92 cm和3.97 cm,轨道互比对在径向的RMS明显大于其他方向,原因是径向GPS卫星观测几何较差,观测数据偏少,造成径向运动学定轨精度较低[14]。
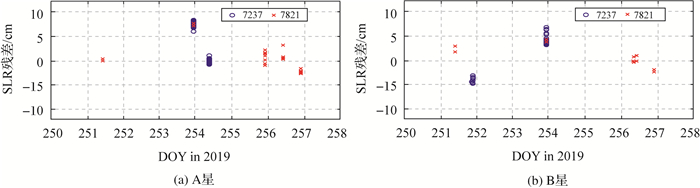
由于SLR观测数据精度优于1 cm,对安装了SLR反射器的低轨卫星而言,可作为一种独立的测量手段检核卫星轨道的定轨精度[32]。选取长春(ID: 7237)和上海(ID: 7821)2个SLR测站数据对定轨结果进行检核,两颗卫星的SLR检核残差如图 7所示。其中,用于A星和B星轨道检核的SLR弧段个数分别为7条和6条。可见,B星的SLR检核精度略优于A星,两颗卫星轨道SLR检核残差RMS都优于3 cm,表明单星绝对轨道具有良好的外部检核精度。
|
| 图 7 A星和B星轨道的SLR检核残差 Fig. 7 SLR validation residuals for satellite A and satellite B |
3.3 相对定轨精度分析
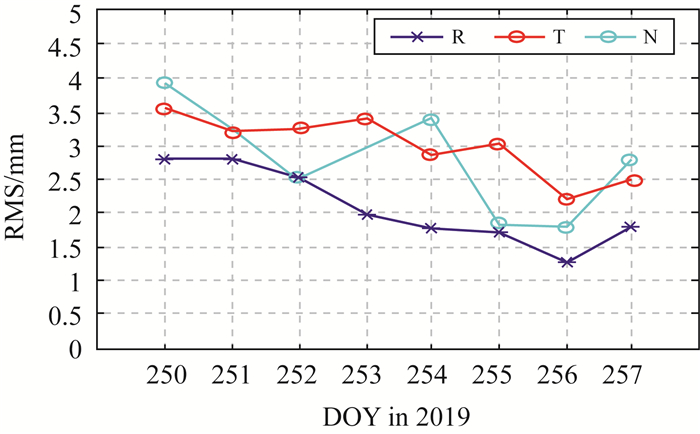
在机动处理条件下,对双星相对定轨精度进行检核和分析。通过直接对两颗卫星单星精密轨道产品作差,获得差分的精密轨道产品(记为dPOD),进一步将本文精密相对轨道确定产品(记为PROD)与dPOD进行互比对,可对相对轨道产品进行初步检查和评估。图 8绘制了每天dPOD与PROD基线在R、T和N方向互比对差值RMS。结果表明,每天互比对差值RMS在T方向都大于R方向,在R、T和N方向的平均RMS值分别为2.08 mm、2.99 mm和2.79 mm,互比对结果与其他卫星编队任务如TanDEM-X[5]、SWARM[17]的结果相一致。
|
| 图 8 dPOD和PROD互比对差值RMS Fig. 8 RMS of differences between dPOD and PROD |
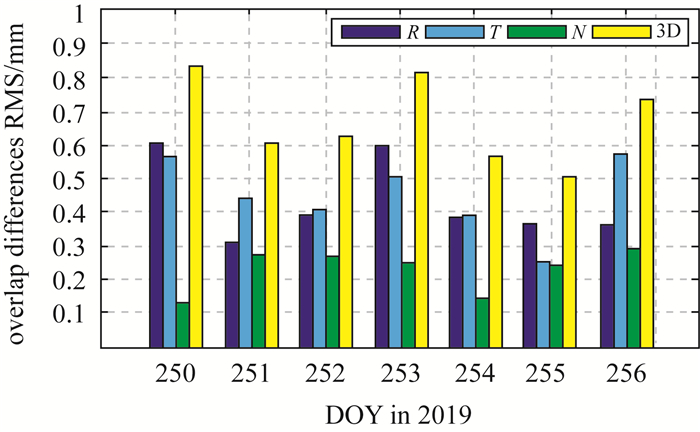
图 9给出了6 h重叠弧段基线差值在R、T、N以及3D方向的RMS统计结果。可见,每天重叠弧段基线精度都优于1 mm,在R、T、N以及3D方向平均RMS分别为0.43 mm、0.44 mm、0.23 mm以及0.66 mm,表明本文确定的相对轨道产品具有良好的内部一致性。
|
| 图 9 6 h重叠弧段基线差值RMS Fig. 9 RMS of 6 h overlapping baseline differences |
图 10给出了2019年9月7日,本文基线产品与西安测绘研究所基线产品在R、T和N方向的互比对偏差情况。为排除轨道机动的影响,进出机动前后1 h的基线产品(图 10中虚线之间部分)不进行互比对。表 4给出试验期间本文基线产品与西安测绘研究所基线产品互比对差值RMS统计结果。可见,每天不同机构基线产品互比对差值3D RMS都在2 mm以内,平均RMS在一维方向为1 mm左右,表明双星相对轨道产品具有很好的外部检核精度,与TanDEM-X任务的相对定轨精度水平相当[6]。

|
| 图 10 不同机构的基线产品在R、T和N方向的互比对差值 Fig. 10 Differences between different baseline products in R, T and N directions |
| DOY | R | T | N | 3D |
| 250 | 0.66 | 0.86 | 0.56 | 1.22 |
| 251 | 0.70 | 0.99 | 0.52 | 1.32 |
| 252 | 0.67 | 1.03 | 0.42 | 1.30 |
| 253 | 0.98 | 1.63 | 0.59 | 1.99 |
| 254 | 0.70 | 0.92 | 0.56 | 1.28 |
| 255 | 0.64 | 0.88 | 0.42 | 1.17 |
| 256 | 0.68 | 1.14 | 0.47 | 1.40 |
| 257 | 0.83 | 1.42 | 0.52 | 1.72 |
| mean | 0.73 | 1.11 | 0.51 | 1.43 |
4 总结
本文针对分布式InSAR编队卫星绝对和相对轨道确定问题进行研究,以天绘二号编队为例,分析了其星载GPS数据质量,并基于缩减动力学定轨方法,分别采用GPS非差和双差观测值实现了绝对和相对定轨,重点对定轨结果内符合与外符合精度进行评估。GPS数据质量结果表明,A星和B星对GPS数据的跟踪能力基本相同,伪码和相位观测数据质量达到较高水平。通过对机动力的常值加速度建模,可有效消除轨道机动对该编队卫星绝对和相对定轨的影响。机动处理后,A星绝对定轨残差RMS由1.11 cm减少到0.65 cm,相对定轨双差模糊度固定成功率由76%提高到100%。在单星精密定轨方面,A星和B星6 h重叠弧段轨道差值3D RMS分别为1.05 cm和1.15 cm,SLR检核残差RMS分别为2.76 cm和2.33 cm,缩减动力学轨道与运动学轨道互比对偏差3D RMS分别3.92 cm和3.97 cm,表明绝对定轨的内外符合精度都达到厘米级。
在双星相对定轨方面,6 h重叠弧段基线差值3D RMS值为0.66 mm,本文基线产品与外部基线产品互比对差值3D RMS为1.43 mm,表明相对定轨的内外符合精度都达到毫米级。本文基于星载GNSS数据可得到天绘二号编队卫星高精度的绝对和相对轨道产品,研究结果对其科学任务的实现与应用具有重要参考价值。
| [1] |
TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping applications using automatic SAR imaging[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 27-37. DOI:10.11947/j.JGGS.2019.0204 |
| [2] |
KRIEGER G, HAJNSEK I, PAPATHANASSIOU K P, et al. Interferometric synthetic aperture radar (SAR) missions employing formation flying[J]. Proceedings of the IEEE, 2010, 98(5): 816-843. DOI:10.1109/JPROC.2009.2038948 |
| [3] |
ANTONY J W, GONZALEZ J H, SCHWERDT M, et al. Results of the TanDEM-X baseline calibration[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1495-1501. DOI:10.1109/JSTARS.2013.2258328 |
| [4] |
YOON Y T, EINEDER M, YAGUE-MARTINEZ N, et al. TerraSAR-X precise trajectory estimation and quality assessment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(6): 1859-1868. DOI:10.1109/TGRS.2008.2006983 |
| [5] |
MONTENBRUCK O, WERMUTH M, KAHLE R. GPS based relative navigation for the TanDEM-X mission-First flight results[J]. Navigation, 2011, 58(4): 293-304. DOI:10.1002/j.2161-4296.2011.tb02587.x |
| [6] |
JÄGGI A, MONTENBRUCK O, MOON Y, et al. Inter-agency comparison of TanDEM-X baseline solutions[J]. Advances in Space Research, 2012, 50(2): 260-271. DOI:10.1016/j.asr.2012.03.027 |
| [7] |
楼良盛, 刘志铭, 张昊, 等. 天绘二号卫星工程设计与实现[J]. 测绘学报, 2020, 49(10): 1252-1264. LOU Liangsheng, LIU Zhiming, ZHANG Hao, et al. TH-2 satellite engineering design and implementation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10): 1252-1264. DOI:10.11947/j.AGCS.2020.20200175 |
| [8] |
MONTENBRUCK O. Kinematic GPS positioning of LEO satellites using ionosphere-free single frequency measurements kinematische GPS positionierung von LEO satelliten mittels ionosphärenfreier einfrequenz-messungen[J]. Aerospace Science and Technology, 2003, 7(5): 396-405. DOI:10.1016/S1270-9638(03)00034-8 |
| [9] |
MONTENBRUCK O, VAN HELLEPUTTE T, KROES R, et al. Reduced dynamic orbit determination using GPS code and carrier measurements reduziert-dynamische bahnbestimmung mit GPS Code- und phasenmessungen[J]. Aerospace Science and Technology, 2005, 9(3): 261-271. DOI:10.1016/j.ast.2005.01.003 |
| [10] |
张兵兵, 聂琳娟, 吴汤婷, 等. SWARM卫星简化动力学厘米级精密定轨[J]. 测绘学报, 2016, 45(11): 1278-1284. ZHANG Bingbing, NIE Linjuan, WU Tangting, et al. Centimeter precise orbit determination for SWARM satellite via reduced-dynamic method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1278-1284. DOI:10.11947/j.AGCS.2016.20160284 |
| [11] |
WU S C, YUNCK T P, THORNTON C L. Reduced-dynamic technique for precise orbit determination of low earth satellites[J]. Journal of Guidance, Control and Dynamics, 1991, 14(1): 24-30. DOI:10.2514/3.20600 |
| [12] |
KROES R, MONTENBRUCK O, BERTIGER W, et al. Precise GRACE baseline determination using GPS[J]. GPS Solutions, 2005, 9(1): 21-31. DOI:10.1007/s10291-004-0123-5 |
| [13] |
BOCK H, JÄGGI A, BEUTLER G, et al. GOCE: precise orbit determination for the entire mission[J]. Journal of Geodesy, 2014, 88(11): 1047-1060. DOI:10.1007/s00190-014-0742-8 |
| [14] |
VAN DEN IJSSEL J, ENCARNAÇÃO J, DOORNBOS E, et al. Precise science orbits for the Swarm satellite constellation[J]. Advances in Space Research, 2015, 56(6): 1042-1055. DOI:10.1016/j.asr.2015.06.002 |
| [15] |
JÄGGI A, HUGENTOBLER U, BOCK H, et al. Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data[J]. Advances in Space Research, 2007, 39(10): 1612-1619. DOI:10.1016/j.asr.2007.03.012 |
| [16] |
ALLENDE-ALBA G, MONTENBRUCK O. Robust and precise baseline determination of distributed spacecraft in LEO[J]. Advances in Space Research, 2016, 57(1): 46-63. DOI:10.1016/j.asr.2015.09.034 |
| [17] |
ALLENDE-ALBA G, MONTENBRUCK O, JÄGGI A, et al. Reduced-dynamic and kinematic baseline determination for the Swarm mission[J]. GPS Solutions, 2017, 21(3): 1275-1284. DOI:10.1007/s10291-017-0611-z |
| [18] |
GU Defeng, JU Bing, LIU Junhong, et al. Enhanced GPS-based GRACE baseline determination by using a new strategy for ambiguity resolution and relative phase center variation corrections[J]. Acta Astronautica, 2017, 138: 176-184. DOI:10.1016/j.actaastro.2017.05.022 |
| [19] |
KROES R. Precise relative positioning of formation flying spacecraft using GPS[D]. Delft: Delft University of Technology, 2006.
|
| [20] |
JU Bing, GU Defeng, HERRING T A, et al. Precise orbit and baseline determination for maneuvering low earth orbiters[J]. GPS Solutions, 2017, 21(1): 53-64. DOI:10.1007/s10291-015-0505-x |
| [21] |
ALLENDE-ALBA G, MONTENBRUCK O, ARDAENS J S, et al. Estimating maneuvers for precise relative orbit determination using GPS[J]. Advances in Space Research, 2017, 59(1): 45-62. DOI:10.1016/j.asr.2016.08.039 |
| [22] |
MONTENBRUCK O, KROES R. In-flight performance analysis of the CHAMP BlackJack GPS receiver[J]. GPS Solutions, 2003, 7(2): 74-86. DOI:10.1007/s10291-003-0055-5 |
| [23] |
SHAO Kai, GU Defeng, JU Bing, et al. Analysis of Tiangong-2 orbit determination and prediction using onboard dual-frequency GNSS data[J]. GPS Solutions, 2020, 24(11): 1-13. |
| [24] |
GUO Jing, ZHAO Qile, GUO Xiang, et al. Quality assessment of onboard GPS receiver and its combination with DORIS and SLR for Haiyang 2A precise orbit determination[J]. Science China Earth Sciences, 2015, 58(1): 138-150. DOI:10.1007/s11430-014-4943-z |
| [25] |
WU J T, WU S C, HAJJ G A, et al. Effects of antenna orientation on GPS carrier phase[C]//Proceedings of the AAS/AIAA Astrodynamics Conference. San Diego, CA: AIAA, 1992: 1647-1660.
|
| [26] |
GU Defeng, YI Dongyun. Reduced dynamic orbit determination using differenced phase in adjacent epochs for spaceborne dual-frequency GPS[J]. Chinese Journal of Aeronautics, 2011, 24(6): 789-796. DOI:10.1016/S1000-9361(11)60093-9 |
| [27] |
DACH R, BROCKMANN E, SCHAER S, et al. GNSS processing at CODE: status report[J]. Journal of Geodesy, 2009, 83(3): 353-365. |
| [28] |
MCCARTHY D D, PETIT G. IERS conventions 2003[R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2004.
|
| [29] |
JACCHIA L G. Revised static models of the thermosphere and exosphere with empirical temperature profiles[R]. Cambridge: Smithsonian Institution, 1971.
|
| [30] |
秦显平. 星载GPS低轨卫星定轨理论及方法研究[D]. 郑州: 信息工程大学, 2009. QIN Xianping. Research on precision orbit determination theory and method of low earth orbiter based on GPS technique[D]. Zengzhou: Information Engineering University, 2009. |
| [31] |
易彬, 秦显平, 谷德峰, 等. 多机构比对融合的分布式InSAR编队星间基线确定[J]. 航空学报, 2018, 39(1): 238-247. YI Bin, QIN Xianping, GU Defeng, et al. Baseline determination for distributed InSAR satellite system using inter-agency comparison and fusion[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 238-247. |
| [32] |
PEARLMAN M R, DEGNAN J J, BOSWORTH J M. The international laser ranging service[J]. Advances in Space Research, 2015, 30(2): 135-143. |



