在大地测量数据处理领域,严格的线性模型并不多见[1-3],而非线性特征一般更接近客观事物的性质,已渗透于现代空间测量技术的各个领域,如地球重力场[4]、摄影测量与遥感、海洋测绘等领域,所涉及的函数模型普遍是非线性模型。传统的获取非线性模型的参数估值与精度信息的方法是最小二乘(least squares,LS)法,其函数模型为高斯-马尔可夫(Gauss Markov,GM)模型,为线性模型[5-8]。随着测量手段的多样化和智能化,对平差结果的精度要求也越高,若采用传统线性化的理论方法处理具有较高精度的观测数据,可能会产生大于观测误差的模型误差,进而导致平差结果的精度损失与特征转变。因此,线性近似方法可能无法满足部分高精度的要求,对非线性平差参数估计与精度评定方法的研究成为测绘领域所研究的热点问题之一[9-11],也是提升成果质量的重要需求。
已有能够解决非线性模型中未知量最佳估值获取问题的方法主要有线性化法、迭代解法及搜索算法3种[12-13]。线性化法是用线性模型的求解理论与方法近似求解,其弊端在于当模型的非线性程度较强时,将严重影响结果质量。迭代解法包含牛顿迭代法、高斯-牛顿法、信赖域法、拟牛顿法等,此类方法的局限性在于对迭代初值较为敏感,对较差的初值可能会出现迭代不收敛现象[9, 13-14]。搜索算法包含粒子群算法、模拟退火法、遗传算法等,该类方法无法获取参数的解析表达式,通常以牺牲计算耗时来代替求导计算[15-17]。
已有能够获取参数估值二阶精度信息的非线性精度评定方法主要有近似函数法和近似非线性函数的概率密度分布两种方法。近似函数法利用泰勒公式对非线性模型展开并截取至二次项,根据误差传播定律获取参数估值的方差-协方差阵。文献[18]推导了非线性函数协方差传播的一般公式和含有二次项的协方差传播公式。文献[19]将高阶泰勒级数展开式方法用于GIS误差传播中,丰富了近似函数法在非线性精度评定的理论研究。文献[20]将总体最小二乘(total least squares,TLS)视为一般的非线性模型,通过泰勒级数展开,导出了参数估值二阶精度的协方差阵计算公式和改正数的偏差计算公式。近似函数法具有固定的方差阵解析表达式,但无法避免求导计算。当遇到未知参数向量与观测值向量之间存在复杂非线性关系或观测数据量较大的多维非线性函数时,求导计算复杂且获取困难。
近些年,通过采样来代替求导计算的近似非线性函数概率密度分布的精度评定方法流行起来,包括蒙特卡罗(Monte Carlo,MC)法[21-23]、Jackknife方法[24]等。蒙特卡罗法通过重复模拟随机样本来近似非线性函数的概率密度分布,进而输出待统计量的精度信息。文献[22]采用蒙特卡罗法计算近似单位权方差的偏差,并将偏差改正后的单位权方差估值用于求解参数估值的均方误差。针对蒙特卡罗法模拟次数的选择具有主观性且无法对精度进行直接控制的问题,文献[23]将自适应蒙特卡罗法用于非线性模型精度评定,采用对偶变量的思想,给出了获取参数估值偏差的对偶自适应蒙特卡罗法的计算流程。当代计算机技术的发展使得蒙特卡罗方法的实现成为了可能,但该方法的模拟次数通常需要设置在105次以上,它往往以增加计算耗时来获得精度信息,并且随着采样次数的变化其精度统计信息并不唯一[25-26]。Jackknife采样方法按顺序逐次减小特定数目的观测值来生成一系列Jackknife样本,从而获取方差信息。文献[24]将Jackknife方法用于TLS精度评定,给出了获取参数估值精度信息的详细采样步骤,进一步扩展了非线性精度评定的近似函数概率分布法理论。但Jackknife方法需要保证足够的观测数据才能获得合理的精度信息,并且随着d值的增大,其计算量也会迅速增加[26]。
Bootstrap方法[27-29]称自助法,是与Jackknife方法紧密相关的一种统计推断方法,均用于估计或修正统计估计值的偏差或方差信息。与Jackknife方法一样,Bootstrap方法通过检查样本数据内的变化,而不是通过参数假设来估计一个统计量的变异性,但Jackknife方法并没有Bootstrap方法那么普及[30]。文献[27]首次提出了通过重复采样得到的自助世界的经验分布来逼近总体真实分布的思想,并给出了其基本采样策略和相关理论证明。由于Bootstrap方法通过重采样代替求导计算,只需选择采样次数并结合有放回抽样策略获取自助样本,最后解算每个样本便可求得未知统计量的均值和协方差阵,因此历年来有较多学者将该方法用于偏差分析和方差计算[31-34]。目前,Bootstrap方法的研究主要集中于该方法在统计学上的性质,将该方法用于解决大地测量领域非线性模型精度评定的问题有待研究;考虑到Bootstrap方法的原始采样策略为等概率采样,对于不等概率的采样方式的适用性还有待验证。
针对以上问题,本文从获取更为合理的精度信息出发,针对现有非线性精度评定方法的不足,将Bootstrap方法用于获取非线性模型参数估值的精度信息;顾及Bootstrap方法原始的等概率采样方式,提出加权采样策略的改进方法,以至获取更加合理的方差估值;最后通过算例验证本文非线性模型精度评定的Bootstrap方法的有效性及本文改进方法的正确性和优势。
1 非线性精度评定及其二阶近似方差-协方差将非线性平差函数模型定义为
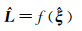 (1)
(1)
式中,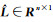
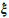
参照文献[35]的推导思路,可得参数估值的二阶近似方差-协方差阵为[35]
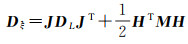 (2)
(2)
式中,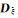
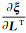
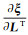
其中,J、H可以具体表示为
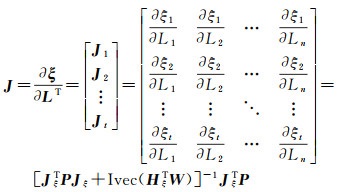 (3)
(3)
式中,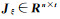
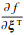
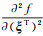
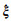
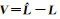
 (4)
(4)
式中,
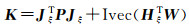 (5)
(5)
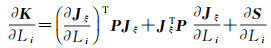 (6)
(6)
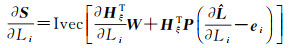 (7)
(7)
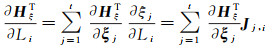 (8)
(8)
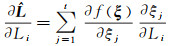 (9)
(9)
式中,ei=[0 0…1…0 0]T∈Rn×1,第i处为1,其余为零。
由式(2)可以看出,在非线性模型精度评定中,若采用近似函数法获取非线性模型参数估值的二阶近似协方差信息,其泰勒级数展开过程需要计算非线性模型的Jacobian矩阵和Hessian矩阵,且当遇到数据量较大的多维非线性函数或非线性程度强的模型时,偏导数的计算十分困难。因此,为避免复杂的求导计算并获取更加合理的精度信息,本文将Bootstrap采样方法及其加权采样的改进方法引入非线性模型精度评定中,试图有效解决近似函数法难以对非线性函数求导的问题。
2 非线性模型精度评定的Bootstrap方法非线性平差模型的参数估计与精度评定问题可以理解为,利用从总体中抽取的固定原始观测样本对非线性模型中的未知统计量及其精度信息进行统计推断。Bootstrap方法是将原始样本作为总体,利用有放回随机抽样法从总体分布函数中得到一系列独立样本(称为自助样本),并通过计算每个自助样本来获取未知统计量抽样分布的经验估计[27, 30],最后利用这个估计的抽样分布来做总体推断。该方法的优势性主要表现在它不需要对未知模型及分布做任何假设,也无须推导估计量的精确表达式,只需通过检验样本内统计量的变化便能够估计未知参数的整个抽样分布。
假设给定样本集(x1, x2, …, xn)来自于独立同分布的样本,总体的分布函数为F(X, ξ),其中X为随机项(例如,固定的观测数据样本X1或非线性模型中的观测误差项X2,假设X的样本容量为n,xi是X的样本值),ξ为未知参数,其估值表示为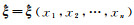
Bootstrap方法首先将原始样本集定义为一个总体,然后将1/n的概率分别设置在随机项中每个元素xi上,并通过一个随机数生成过程来抽取一个包含某些特定随机项的自助样本;通过某种估计方法获取未知参数估计值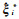
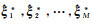
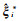
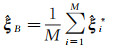 (10)
(10)
式中,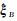
顾及非线性优化算法解算得到的参数估值不再是无偏估计量,而Bootstrap方法经有放回抽样获取的大量自助样本能够减小参数估值的偏差,在一定程度上能够有效改善参数估值的质量[32]。因此,本文将式(10)的结果作为未知参数的自助估计。
在获取参数均值后,将Bootstrap重采样获取的统计量(
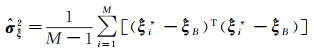 (11)
(11)
式中,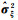
Bootstrap方法的重采样要点是采样这个过程的随机项。因此,根据重采样对象的不同,Bootstrap方法又可分为:重采样观测值的Bootstrap方法和重采样残差的Bootstrap方法[30]。Bootstrap方法通过重采样随机项获取自助样本的方式代替复杂的或难以实现的求导计算,可以用于求取非线性平差参数估值的方差或协方差阵。因此,本文将这两种采样策略引入非线性模型的精度评定问题中,给出了获取参数方差的具体步骤。
2.1 重采样观测值的Bootstrap方法重采样观测值的Bootstrap方法,通过对观测值的有放回随机抽样将原始观测数据采样成多个自助样本,原始样本集中的每个样本点被采样到的概率相同,每个自助样本的样本容量与原始样本相同。对于不等精度的观测数据,需要保证自助样本中的观测值与其权值相对应,因此在重采样获得观测值自助样本的过程中需要对观测值的权Pi进行重采样,两者采样方式一致,具体表现为以随机数序列元素为自助样本元素的下标,对观测值及其权值进行赋值,进而获取自助样本及对应权阵。根据以上分析,总结得到重采样观测值的Bootstrap方法用于非线性精度评定的完整计算流程:
(1) 假设观测值N=(x1, x2, …, xn)为随机项样本X1,其权阵为P=diag(P1, P2, …, Pn),将1/n的概率分别设置在(x1, x2, …, xn)各样本值上。
(2) 产生满足均匀分布的n个随机数(i1, i2, …, in),其中1≤ij≤n, j=1, 2, 3, …, n。
(3) 对N和P中的元素进行重采样,生成自助样本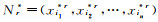
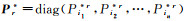
(4) 将Nr*和Pr*代入参数求解算法(例如高斯牛顿迭代法),得到未知参数的估值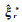
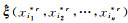
(5) 循环步骤(2)-步骤(4)M次,得到M组参数估计值。
(6) 利用式(10)获取参数均值,利用式(11)获取参数估值的方差。
重采样观测值的Bootstrap方法的采样过程将原始观测值采样成了多个自助样本,尽管每个自助样本的样本容量与原始样本相同,但并不是改变观测值的先后排列顺序,有放回随机抽样过程使得每个自助样本中可能存在重复的原始数据点,而另外一些样本点没有出现。因此,每个自助样本将随机地异于原始样本,导致每个自助样本获得的参数估值存在细微差异。
2.2 重采样残差的Bootstrap方法文献[27]在提出Bootstrap方法的同时,对抽取独立同分布样本点的采样方式进行了延伸和拓展,结合多元回归分析给出了一种对残差进行抽样的采样策略。具体做法是,首先使用所有样本点建立模型并获取残差,然后对残差进行采样并根据模型的方程重构观测向量,最后计算参数并重复该步骤。因此,当模型的自变量为固定常数,因变量为自变量和一个随机误差项的函数时,基于模型的误差结构,可将因变量的残差设置为采样过程的随机项。
重采样残差的Bootstrap方法与重采样观测值的Bootstrap方法相比,主要的区别在于重采样对象不同。采用重采样残差的Bootstrap方法解决精度评定问题的计算步骤为:
(1) 输入独立观测值向量L及其权阵P,计算参数估值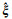
(2) 将参数估值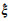
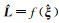
(3) 计算观测误差向量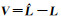
(4) 产生满足均匀分布的随机数(i1, i2, …, in),对V进行有放回随机采样,得到样本大小仍为n的样本Vr*。
(5) 获取观测值的自助样本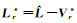
(6) 根据自助样本Lr*及权阵P,计算参数估值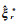
(7) 重复步骤(4)-步骤(6)M次,共得到M组参数估值。
(8) 通过式(10)获取未知参数的自助估计值,利用式(11)计算参数估值的方差。
重采样观测值与重采样残差的样本数据均来源于原始固定样本,并未根据更多的观测信息进行计算。因此,这两种采样方法均是利用相同的观测数据最终得到未知参数估值及方差信息,仅是采样过程中的随机项不同,其采样过程均不会产生额外的模型误差,也不会改变模型态性;并且循环有放回随机采样过程获得的大量自助样本能够减小迭代方法求解非线性参数估值的偏差,从而提高参数估值的精确度。
3 改进的Bootstrap方法Bootstrap方法在重采样随机项元素构建自助样本过程中,每个元素被采样到的概率相同且均为1/n。可以看出,Bootstrap方法在采样时将样本数据视为等精度观测,在构建自助样本过程中忽略了数据的权值信息,使得精度不等的观测数据出现在自助样本中的概率却相同,因此可能无法较好地逼近总体分布函数,在一定程度上有损理论严密性。
为使得Bootstrap方法能够更加充分利用总体包含在样本中的先验信息和数据性质,使得自助样本的经验分布更加逼近总体分布函数,若利用观测值的分布信息来构建经验分布函数,通常需要借助分布假设,并且所得分布函数将严重依赖于所作的假设。当观测样本的分布假设与实际观测样本的分布存在较大偏差时,所得样本经验分布函数并不能很好地逼近总体分布函数,导致统计推断结果与实际存在一定的偏差[36]。顾及观测值的权的获取方式较观测值的分布信息获取方式更为简便,并且利用观测权来构建经验分布函数可以有效避免对观测样本分布的假设。因此,权作为比较观测值之间精度高低的一种先验信息,可用于调整随机项的抽样概率,以至获取更加逼近总体分布函数的样本经验分布函数。因此,本文将原始观测样本的权值纳入重采样获取自助样本的过程。在该过程中,权值被用于构建一个自助样本获取准则,通过对随机项元素进行采样可能性的重新分配,使得每个元素被抽样到的概率与其对应的观测精度相匹配。
首先,对原始样本所有元素的权值进行归一化预处理,使得归一化权值之和为1
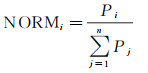 (12)
(12)
式中,NORMi表示第i个观测元素的归一化权值;Pi是原始观测样本中第i个元素的权;n为原始样本的样本容量。
将NORMi作为随机项中各元素xi的采样概率,其概率值的大小取决于各元素所对应的权值与所有观测权之和的比值大小。因此,可构建Bootstrap采样过程中随机变量的分布律函数
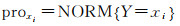 (13)
(13)
式中,xi为随机项X中的样本值;Y为随机项X中的随机变量,其可能的取值为xi(i=1, 2, …, n);proxi表示事件{Y=xi}的概率。
根据分布律函数,可构建一个经验分布函数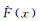
 (14)
(14)
在获取经验分布函数后,可返回一组满足分布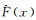
与Bootstrap方法相比,改进后的Bootstrap方法主要的区别在于,通过对原始样本元素的权值进行归一化处理,可将随机项样本元素xi的抽样概率1/n调整为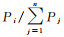
由于Bootstrap法在采样过程中随机项的选择不同,Bootstrap法可区分为重采样观测值的Bootstrap方法和重采样残差的Bootstrap方法,将以上加权采样策略应用到该两种方法中,分别给出将改进方法用于非线性模型精度评定中的详细计算步骤。
3.1 改进的重采样观测值的Bootstrap方法该方法首先对观测数据的权值进行归一化处理,计算每个样本元素被采样到自助样本的概率值;构建采样过程中的随机变量的分布律函数;产生满足该分布律函数的随机数,通过赋值获取自助样本并计算参数;然后将生成自助样本到获取参数的整个过程循环M次;最后对未知统计量的均值和方差进行统计推断。每个自助样本的样本容量与原始样本相同,但原始样本中的每个元素被采样到的概率受其权值影响而不同,这取决于该样本点的权值大小。根据以上分析,总结得到改进的重采样观测值的Bootstrap方法的计算流程:
(1) 假设观测值样本N=(x1, x2, …, xn)为采样过程中的随机项X1,其权阵为P=diag(P1, P2, …, Pn)。
(2) 利用式(12)对权阵进行归一化处理,使得归一化后的权值之和为1。
(3) 将随机项样本元素xi的抽样概率分别设置为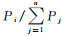
(4) 通过式(13)、式(14)构建随机变量的经验分布函数。
(5) 产生满足该分布函数的n个随机数(i1, i2, …, in),其中1≤ij≤n, j=1, 2, 3, …, n。
(6) 根据随机数对原始样本N中的观测值进行采样,获取自助样本
(7) 获取自助样本的权阵Pr*=diag(P*ri1, P*ri2, …, P*rin),保持自助样本的权值与样本元素相对应,其中1≤r≤M。
(8) 将Nr*和Pr*代入非线性算法,得到未知参数的估值向量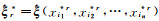
(9) 重复步骤(5)-步骤(8)M次,得到M组参数估计值。
(10) 由于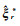
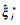
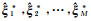
(11) 分别通过式(10)、式(11)获取参数的均值和方差。
重采样观测值的Bootstrap方法及其改进方法均是将相同的原始观测数据重采样成了多个自助样本,且获取的自助样本个数及每个自助样本的样本容量均相同,但改进方法由于采用了加权采样的策略,将等概率重采样转变为不等概率采样方式,使得权值大的原始样本元素出现在自助样本中的概率增大,从而使得自助样本能够更加贴合原始样本。
3.2 改进的重采样残差的Bootstrap方法与重采样残差的Bootstrap方法一致,改进的重采样残差的Bootstrap方法仍将因变量的残差作为采样过程中的随机项,主要区别在于改进方法在采样前对权值进行了归一化预处理,通过获取随机项中随机变量的分布函数,使得对残差项的等概率采样转化为加权采样。改进的重采样残差的Bootstrap精度评定方法的计算步骤总结为:
(1) 从总体中获取固定的观测向量L及其权阵P,作为拟合该模型的原始样本。
(2) 利用非线性参数估计方法获取未知参数的估计值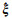
(3) 将参数估值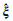

(4) 计算观测误差向量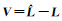
(5) 对权阵P的对角元素Pi进行归一化处理。
(6) 将随机项样本元素Vi的抽样概率分别设置为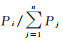
(7) 通过式(13)、式(14)构建随机变量的经验分布律函数。
(8) 产生满足该分布律的随机数(i1, i2, …, in),其中1≤ij≤n, j=1, 2, 3, …, n。
(9) 对Vi进行有放回抽样,获取残差样本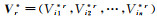
(10) 将观测值的平差值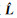
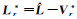
(11) 将自助观测向量样本Lr*及权阵P代入非线性算法获取参数估值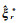
(12) 循环步骤(8)-步骤(11)M次,得到M组参数估值。
(13) 参数估值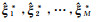
(14) 分别通过式(10)、式(11)获取未知参数的自助估计值及方差。
重采样残差方法和改进的重采样残差方法在自助样本获取过程中,均未对原始观测样本进行采样,因此均利用了原始样本中的所有观测值,但对随机项的有放回抽样使得每个自助样本包含的元素不同,进而使得每个自助样本得到的估值存在差异。
根据以上4种精度评定流程可以发现,不管是采样观测值,还是采样残差,抑或是改进方法,重复M次的Bootstrap采样过程仅由有放回抽样的随机性和满足的抽样分布所决定,即第i次的自助样本获取过程并不会影响第j次的重采样,这使得自助样本的获取过程是独立的。此外,由于自助样本中的所有元素均来源于原始样本,未利用其他的观测值进行计算,并且由于受自助法自身有放回抽样性质以及抽样随机性影响,使得自助样本之间可能包含重复的随机项元素,导致自助样本存在一定的相关性。第i组参数估值仅仅由第i个自助样本决定,因此每个自助样本的解算过程是独立的;但由于自助样本i与自助样本j可能包含相同元素,使得M组参数估值存在一定的相关性,使得各自助样本的参数估值在自助均值左右浮动并且较为接近。但在采用矩法估计计算自助方差时,并不能简单忽略M组参数估值的分布规律或者将其视为相同,这是因为自助重采样的目的便是要得到一个较好的抽样分布估计来对模型中的未知统计量进行统计推断。
经试验,通过实施Bootstrap采样得到的M个自助样本中,任意2个自助样本之间包含的重合观测个数满足一个典型的正态分布,其均值约等于原始样本容量n的2/5,这使得自助样本之间存在一定的相关性。根据Bootstrap的统计理论,对于样本容量为n的原始观测样本,总共存在C2n-1n种可能的自助样本类型[37],并且随着原始样本容量的增加,自助样本类型总数也会急剧增大,M次采样得到的M个自助样本出现强相关情形的概率也将急剧减小。在测量平差领域的普遍情况下,自助重采样过程中总是包含较多种类的自助样本,并不会出现M个自助样本之间强相关的情况。因此,采用矩估计所得参数自助方差并不会过小或者导致自助法结果高估参数估值精度。此外,在实际实施Bootstrap采样时,尽管Bootstrap的有放回随机采样机制可能会使得自助样本之间的重合观测个数满足均值为2n/5的正态分布,但基于此规律下,Bootstrap方法能够得到合理的自助抽样分布,进而输出精确的自助均值及自助方差。
4 案例研究与分析经试验,Bootstrap采样方法适用于线性平差模型的参数估计与精度评定问题,通过有放回随机抽样能够在一定程度上提升参数质量,并且获取合理的参数估值精度信息,表明在线性模型精度评定问题中,Bootstrap方法具有可靠性和优势性。与最小二乘法相比,尽管实施Bootstrap采样会增加精度评定过程计算耗时,但自助法具有操作简单、易于编码实现的优点,并且其结果存在一定程度上的质量提升,不失为一种较好的精度评定方法。在非线性模型精度评定问题中,本文第一节已证明已有的基于泰勒级数展开的近似函数法,在精度评定过程中需要计算非线性函数的一阶或二阶偏导数,当遇到高维且非线性程度较强的模型时,求导过程复杂难以获取。而自助法用于解决非线性模型精度评定问题最大的优势在于,获取参数精度信息过程中能够避免导数计算,该方法是通过对原始样本的重采样过程来代替复杂的Jacobian矩阵或Hessian矩阵计算过程,最后利用抽样分布估计对未知参数进行统计推断。因此,为充分体现Bootstrap方法在测量平差精度评定问题中的优势性,本文考虑的是非线性模型情形。
为评估Bootstrap方法和本文改进方法在获取非线性模型参数估值精度信息方面的性能,以及探讨在大地测量领域中的应用,本文共设计了4个算例:两个非线性强度不同的非线性回归模型、边角网平差模型、火山形变Mogi模型。通过算例1和算例2来验证Bootstrap方法在非线性模型精度评定中的可行性及本文改进方法的正确性;通过算例3和算例4来展示Bootstrap方法在大地测量非线性精度评定中的应用价值,并验证本文改进方法在参数方差获取方面的优势。对比试验中,Monte Carlo方法的模拟次数取值为105。Bootstrap方法重采样次数的选择取决于统计量的具体研究问题并且依赖于需要做的检验[38]。文献[38-41]指出,当重采样次数为50~200时,Bootstrap方法能够得到较为合理的未知参数方差或中误差;当采样次数超过200时,方差近似值的改进很小。经试验,通过增加Bootstrap重采样次数在一定程度上能够提升精度评定结果质量,但随着采样次数的增加,中误差结果趋于较为稳定的值。这与已有文献的结论较为一致。因此,本文依据已有研究的经验取值并顾及非线性平差精度评定问题,在保证较高的计算精度条件下,同时考虑较高的精度评定效率,将Bootstrap方法的采样次数设置为103。案例研究中出现的字符及对应含义列于表 1。
| 缩写 | 含义 |
| LS | 最小二乘法(least squares method) |
| GN | 高斯牛顿解法(Gauss-newton algorithm) |
| AF | 近似函数法(approximate function method) |
| FO | 一阶近似函数法(first order approximate function method) |
| SO | 二阶近似函数法(second order approximate function method) |
| JK | 刀切法(Jackknife resampling method) |
| BO | 重采样观测值的自助法(Bootstrap method based on the resampling observations) |
| MBO | 改进的重采样观测值的自助法(modified Bootstrap method based on the resampling observations) |
| BR | 重采样残差的自助法(Bootstrap method based on the resampling residuals) |
| MBR | 改进的重采样残差的自助法(modified Bootstrap method based on the resampling residuals) |
| MC | 蒙特卡罗方法(Monte Carlo method) |
4.1 Bootstrap方法及本文改进方法的可行性及正确性验证分析
针对非线性回归模型的非线性强度不同,设计两个仿真试验,通过Bootstrap方法及加权采样方法在参数估计中的应用,以及与AF法、JK法、MC法在参数标准差估计中的性能评估对比,以清楚地揭示本文精度评定方法的可行性和有效性。
4.1.1 算例1算例1采用的非线性回归模型函数形式如下
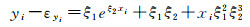 (15)
(15)
式中,xi为n维自变量向量的元素;yi为对应因变量值;εyi为因变量yi的随机误差;ξ1、ξ2为回归参数。
自变量xi在0与10之间随机取60个观测点(i=1, 2, …, 60);参数的真值设置为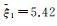
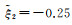
为进一步探讨AF法、JK法、MC法、Bootstrap方法及本文加权采样方法在更复杂非线性情况下的方差估计性能和计算特性,采用比算例1非线性程度更强的回归函数,其函数形式定义如下
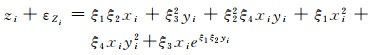 (16)
(16)
式中,xi、yi分别为横坐标x和纵坐标y的自变量;zi为n维自变量向量中的元素;εzi为zi的随机误差,ξ1、ξ2、ξ3、ξ4为回归参数。
自变量xi、yi分别在[0, 10]和[0, 4]之间随机取60个观测点,并将参数的真值分别设置为
在获取模拟观测数据后,分别采用LS法、GN法、BO法、MBO法、BR法及MBR法解算并获取参数均值,其结果及差值二范数列于表 2;再分别采用BO法、MBO法、BR法及MBR法对随机项进行采样,并通过高斯-牛顿解法解算自助样本,获取回归系数的标准差及协方差信息,最后与FO法、SO法、JK法及MC法的结果进行对比,各方法的结果列于表 3。
| 算例 | 参数 | 真值 | LS法 | GN法 | BO法 | MBO法 | BR法 | MBR法 |
| 算例1 | 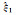 |
5.420 00 | 5.759 46 | 5.295 82 | 5.307 22 | 5.328 76 | 5.302 62 | 5.311 09 |
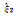 |
-0.250 00 | -0.276 88 | -0.253 35 | -0.253 34 | -0.252 94 | -0.253 47 | -0.253 14 | |
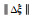 |
- | 0.340 52 | 0.124 23 | 0.112 83 | 0.091 29 | 0.117 43 | 0.108 96 | |
| 算例2 | 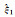 |
0.210 00 | 0.214 62 | 0.211 46 | 0.211 16 | 0.210 97 | 0.211 42 | 0.211 58 |
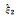 |
0.950 00 | 0.848 37 | 0.939 93 | 0.951 25 | 0.951 58 | 0.950 25 | 0.949 34 | |
 |
1.530 00 | 1.544 03 | 1.524 03 | 1.523 05 | 1.523 97 | 1.523 38 | 1.524 20 | |
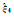 |
0.780 00 | 0.796 16 | 0.779 47 | 0.779 43 | 0.779 30 | 0.779 48 | 0.779 57 | |
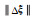 |
- | 0.103 95 | 0.011 80 | 0.007 18 | 0.006 34 | 0.006 78 | 0.006 06 |
| 算例 | 标准差或协方差 | FO法 | SO法 | JK法 | MC法 | BO法 | MBO法 | BR法 | MBR法 |
| 算例1 | 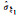 |
0.066 84 | 0.066 84 | 0.094 05 | 0.068 65 | 0.073 65 | 0.066 55 | 0.081 01 | 0.070 67 |
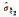 |
0.001 78 | 0.001 79 | 0.002 20 | 0.001 73 | 0.001 97 | 0.001 79 | 0.002 19 | 0.001 93 | |
 |
0.000 11 | 0.000 11 | 0.000 14 | 0.000 11 | 0.000 14 | 0.000 11 | 0.000 17 | 0.000 13 | |
| 算例2 | 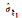 |
0.001 99 | 0.002 00 | 0.002 81 | 0.001 97 | 0.002 17 | 0.002 14 | 0.002 45 | 0.002 19 |
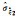 |
0.009 37 | 0.009 38 | 0.012 87 | 0.009 49 | 0.010 39 | 0.009 77 | 0.011 74 | 0.010 59 | |
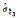 |
0.005 33 | 0.005 33 | 0.007 37 | 0.005 37 | 0.005 53 | 0.004 97 | 0.006 76 | 0.006 01 | |
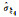
|
0.001 61 | 0.001 61 | 0.002 05 | 0.001 64 | 0.001 78 | 0.001 65 | 0.002 02 | 0.001 94 | |
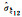
|
-0.000 01 | -0.000 01 | -0.000 02 | -0.00002 | -0.000 02 | -0.000 02 | -0.000 02 | -0.000 02 | |
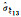
|
0.000 01 | 0.000 01 | 0.000 06 | 0.000 05 | 0.000 06 | 0.000 06 | 0.000 07 | 0.000 06 | |
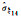
|
0.000 02 | 0.000 02 | 0.000 03 | 0.000 02 | 0.000 03 | 0.000 04 | 0.000 03 | 0.000 03 | |
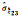
|
-0.000 35 | -0.000 35 | -0.000 43 | -0.000 37 | -0.000 42 | -0.000 34 | -0.000 58 | -0.000 47 | |
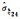
|
-0.000 13 | -0.000 13 | -0.000 18 | -0.000 13 | -0.000 16 | -0.000 14 | -0.000 20 | -0.000 17 | |
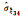
|
0.000 05 | 0.000 05 | 0.000 06 | 0.000 05 | 0.000 57 | 0.000 04 | 0.000 08 | 0.000 07 |
由表 2的参数估值及范数结果可以看出,在非线性强度不同的两个仿真设置中,LS法的结果均为最差,表明LS法在将非线性模型线性近似的过程中,引入了较大的模型误差,从而严重影响估计值的质量。而相比于LS法,GN法得到的参数估值较优,说明GN法能够削弱非线性回归模型线性近似所带来的模型误差的影响,其循环迭代过程可以不断修正参数估值,在一定程度上能够有效改善传统LS法在对非线性模型线性化过程中所引起的精度损失,使其参数估值比传统的线性近似方法更接近参数真值。BO法和BR法得到的参数估值与真值的范数均比LS法和GN法的结果更小,表明BO法和BR法通过实施Bootstrap并采用GN法解算自助样本,在削弱线性化带来的影响的基础上,能够在一定程度上减小参数估值的偏差,获取更为精确的参数估值。与BO法相比,MBO法得到的参数估值与真值的范数更小,表明采用了加权采样的重采样观测值方法在参数的精确度方面得到了较明显的改善;而相比于BR法,MBR法也能够提升参数估值的精确度。这表明MBO法及MBR法在获取较高精度的参数估值方面比BO法和BR法更加有效。试验结果表明,本文的加权采样策略在非线性回归模型的参数估计方面是可行且有效的,改进方法通过重采样获得的自助样本能够充分利用原始样本的先验信息,从而使得MBO法和MBR法获得的估值较BO法和BR法更接近参数真值。
由表 3可知,在两个不同的仿真设置下,二阶近似函数法获取的参数估值标准差在数值上略大于一阶近似函数法得到的标准差结果,且更接近于蒙特卡罗方法获取的参数标准差。这是因为二阶近似函数法顾及了非线性平差模型的二阶项,说明由一阶近似函数法得到的结果可能高估了非线性平差模型参数估值的精度。但由于二阶近似函数法也仅仅包含至二阶项,忽略了高阶项,因此也说明了蒙特卡罗方法获取的精度信息更加合理。并且试验证明,当原始样本量增大时,二阶近似函数法所涉及的Hessian矩阵维数也将增大,也说明了无须求导计算的Bootstrap方法更加适用较大量的观测数据。相比于蒙特卡罗方法的结果,Jackknife法获得的标准差偏离较大,是因为Jackknife法易受原始样本容量大小的影响且其重采样过程获取的Jackknife样本较少,与文献[24]中的结论一致。这表明Jackknife法往往会低估非线性模型参数估值的精度,因此该方法无法反映非线性模型参数估值的真实精度。
利用基于Bootstrap的方法对该非线性函数进行精度评定所获得的标准差与近似函数法的结果在符号和量级上相同、在数值上相近,表明该4种方法均能够对非线性平差模型进行有效的精度评定。从计算结果上看,BO法和BR法获取的参数的标准差小于Jackknife法的结果且更接近于蒙特卡罗方法的计算精度,表明BO法和BR法较Jackknife法更加精确。相比于BO法,MBO法获取的参数估值标准差在数值上更小,且与蒙特卡罗方法的结果更为接近;MBR法计算得到的参数标准差比BR法的结果更小并且同样更靠近于蒙特卡罗方法获取的标准差,说明MBO法和MBR法能够获取更为合理的参数标准差。结合表 2中的参数估值结果,说明本文加权采样的获取自助样本方式不仅适用于重采样观测值,也适用于重采样残差情形。试验结果表明,将Bootstrap方法用于解决非线性参数估计与精度评定问题是可行且有效的,本文加权采样方法获取的更为精确的参数估值和精度信息,也证明了本文改进方法更具可靠性和优势。
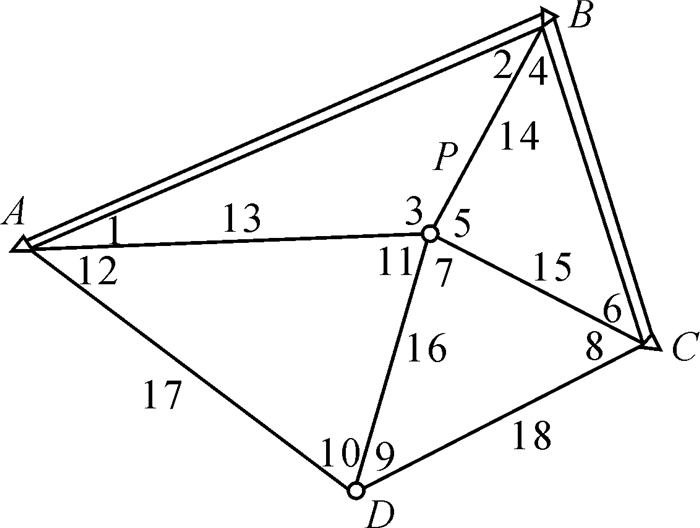
4.2 算例3:Bootstrap方法及本文改进方法在边角网平差模型中的应用将文献[42]中的例3-2-1进行改化,独立不等精度观测如图 1所示,边角网有12个角度和6条边长,其中A、B、C为已知点,P、D为待定点。起算数据和观测值分别列于表 4和表 5。
|
| 图 1 边角网 Fig. 1 The sketch of triangulateration network |
| 点号 | 坐标 | 坐标方位角 | 边长 | ||||
| Xi | Yi | (°) | (′) | (″) | |||
| A | 92.162 | 31.420 | 66 162 |
34 12 |
1.2 51.5 |
172.158 102.503 |
|
| B | 160.625 | 189.379 | |||||
| C | 63.022 | 220.689 | |||||
| 编号 | 观测角 | 权值 | 编号 | 观测角 | 权值 | 编号 | 观测边/m | 权值 | ||||
| (°) | (′) | (″) | (°) | (′) | (″) | |||||||
| 1 | 21 | 4 | 58.6 | 6.114 6 | 7 | 78 | 31 | 16.3 | 6.673 9 | 13 | 123.618 | 5.261 8 |
| 2 | 38 | 3 | 8.7 | 1.664 9 | 8 | 54 | 33 | 8.4 | 4.999 4 | 14 | 72.146 | 6.597 3 |
| 3 | 120 | 52 | 2.0 | 5.365 4 | 9 | 46 | 55 | 31.2 | 1.961 6 | 15 | 74.117 | 4.049 3 |
| 4 | 46 | 18 | 4.5 | 8.140 0 | 10 | 69 | 33 | 21.2 | 6.058 9 | 16 | 82.665 | 8.571 1 |
| 5 | 88 | 57 | 54.3 | 3.566 8 | 11 | 71 | 38 | 35.3 | 6.360 3 | 17 | 125.212 | 5.700 9 |
| 6 | 44 | 43 | 42.1 | 4.823 0 | 12 | 38 | 47 | 56.8 | 6.548 5 | 18 | 99.443 | 7.962 3 |
在获取角度和边长观测数据后,首先采用余切公式计算得到待定点坐标估值作为迭代初值,再分别采用BO法、MBO法、BR法及MBR法对随机项采样并通过高斯-牛顿迭代获取未知点坐标,其参数结果及差值二范数列于表 6。通过算例1和算例2的结果可知,Jackknife法的结果不足以反映参数估值的真实精度;而一阶近似方法的结果可能会高估参数估值的精度;并且根据边长观测方程及测角观测方程可以看出,边角网平差模型中的未知点坐标与观测值向量之间存在复杂的非线性关系,若采用泰勒级数展开并截取至二次项的方法获取未知参数的方差信息,需要进行多次计算偏导,其求导过程十分复杂且较难获得。针对以上问题,因此算例3不再使用一阶近似函数法、二阶近似函数法及Jackknife方法求解参数估值的精度信息,仅通过基于Bootstrap的4种方法与MC法进行对比,来验证本文方法的正确性和优势。待定点坐标标准差及协方差结果列于表 7。
| 参数 | 真值 | BO法 | MBO法 | BR法 | MBR法 |
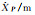
|
97.230 | 97.230 | 97.230 | 97.229 | 97.229 |
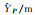
|
154.934 | 154.934 | 154.934 | 154.931 | 154.933 |
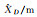
|
17.768 | 17.755 | 17.758 | 17.751 | 17.751 |
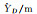
|
132.138 | 132.132 | 132.129 | 132.126 | 132.131 |
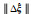
|
- | 0.0143 2 | 0.0134 5 | 0.0210 5 | 0.0184 4 |
| 标准差或协方差 | BO法 | MBO法 | BR法 | MBR法 | MC法 |
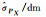
|
0.070 07 | 0.044 94 | 0.017 47 | 0.013 57 | 0.030 34 |
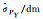
|
0.079 51 | 0.061 76 | 0.019 36 | 0.014 27 | 0.030 60 |
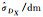
|
1.888 47 | 1.150 17 | 2.158 91 | 1.338 20 | 1.799 37 |
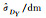
|
0.913 18 | 0.433 66 | 0.685 74 | 0.464 44 | 0.919 41 |
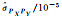
|
5.387 56 | 1.770 98 | 0.087 35 | 0.050 78 | 0.102 24 |
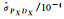
|
4.769 55 | -0.144 64 | -1.002 81 | -0.183 25 | -4.618 82 |
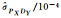
|
2.188 36 | -0.045 27 | -0.343 96 | -0.055 39 | -1.414 62 |
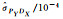
|
4.701 98 | -1.645 76 | -0.487 62 | -0.135 76 | -4.879 25 |
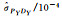
|
2.313 23 | -0.314 63 | -0.069 82 | -8.708 37 | -1.700 63 |
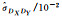
|
1.326 28 | 0.393 71 | 1.455 91 | 0.610 22 | 2.549 81 |
对比表 6中BO法、MBO法、BR法及MBR法的结果可以看出,4种方法所得坐标估值均与坐标真值较为接近,再次验证了Bootstrap方法及本文改进方法的正确性。同时,通过对比估值与真值的范数可知,MBO法所得估值较BO法的结果更接近于真值;与BR法的结果相比,MBR法所得结果的范数有较为明显的改善。这表明MBO法及MBR法在获取更高精度的边角网坐标估值方面比BO法和BR法更加有效。本算例的参数估值结果证明了Bootstrap方法在边角网平差模型中依然适用,也再次证明了本文改进方法的有效性及加权采样的必要性。
由表 7可知,在边角网平差模型中,BO法、BR法、MBO法及MBR法计算得到的待定点坐标估值标准差在符号和量级上均与MC法的结果保持一致,同样验证了该4种方法在非线性平差精度评定问题中的正确性和有效性。由于边角观测方程的复杂非线性关系,使得二阶近似函数法获取参数中误差较为困难,从侧面体现了通过执行Bootstrap采样来避免复杂求导运算仍能获取合理精度信息的优势,也说明了在面对高维复杂非线性模型的精度评定问题时,基于Bootstrap的方法具有更强的适用性。相比于BO法及BR法计算得到的标准差结果,MBO法和MBR法的结果在数值上更小,这表明通过充分利用观测值先验信息的加权采样方法能够在一定程度上提升参数精度的可靠性,也说明为更加合理反映参数估值的精度信息,采用加权采样的抽样方式更加有效。
4.3 算例4:Bootstrap方法以及本文改进方法在火山形变Mogi模型反演中的应用为进一步验证Bootstrap方法及本文改进方法在大地测量非线性精度评定中的广泛适用性和应用价值,算例4采用文献[43]首次提出的Mogi模型。该模型是一种研究由火山爆炸源所引起的地表形变位移及重力变化的地球物理模型,它能够有效地用于模拟和解释大量的火山区地表形变。应用火山区的地表形变观测数据来反演岩浆压力源参数,对火山的危险性评价有着重大的实际意义。地表位移又可分为垂直位移和水平位移,本文采用垂直位移单一反演的Mogi模型。
假设地面直角坐标系为(x, y, z),岩浆压力源的中心坐标表示为(x0, y0, D),因此岩浆房膨胀所引起的地表垂直位移与等效压力源参数之间的表达式可以表示为[44]
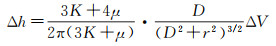 (17)
(17)
式中,Δh表示地表垂直位移;K表示为体积弹性模量;μ表示剪切模量;D表示为源的中心深度;r表示地表径向距离且当r=0时垂直位移取到最大值;ΔV为岩浆房体增量。
当地壳为泊松介质时,取泊松比v=0.25且顾及岩浆房体积的膨胀为半径为R的等效球体,因此体积弹性模量K与剪切模量μ存在以下关系式
 (18)
(18)
将式(18)代入式(17),地表垂直位移可以化简为
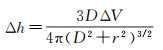 (19)
(19)
假设地表存在n个观测点,则第i个监测点到岩浆压力源的地表径向距离为
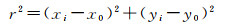 (20)
(20)
式中,(x0, y0)为岩浆压力源的中心在平面上的投影坐标。
将式(20)代入式(19),地表垂直位移可表示为一个多维非线性函数
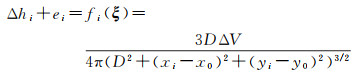 (21)
(21)
式中,i=1, 2, …, n;ei为第i个监测点的垂直位移Δhi的随机误差;f(·)表示未知参数向量ξ与观测值之间的非线性映射关系;ξ=[ΔV D x0 y0]T为待求的未知参数。
利用泰勒级数对式(21)在参数初值ξ0处展开并舍去二次及以上项,得到垂直位移反演压力源参数的平差模型
 (22)
(22)
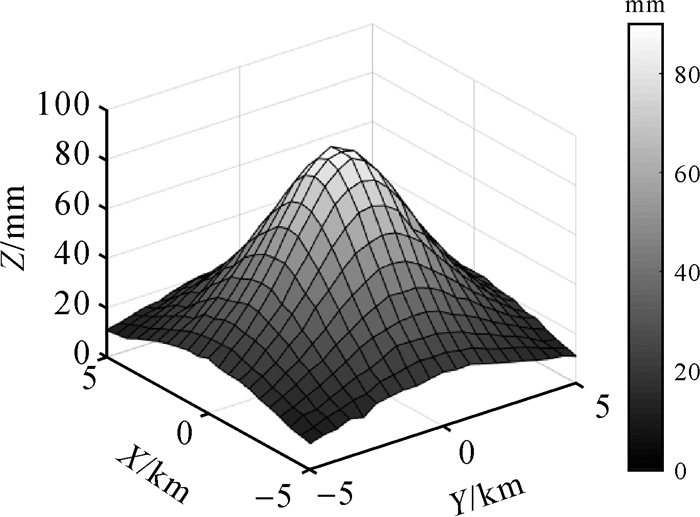
通过仿真获取某一火山区域的垂直位移观测资料:观测点的取值范围为[x, y]∈[-5, 5] km×[-5, 5] km,相邻垂直形变监测点的间隔为0.5 km,每个观测点的权值在[0, 25]之间随机取值。压力源参数真值设置为:体积增量ΔV=6000×103 m3、源的中心深度D=4 km、膨胀源的中心坐标x0=0 km、y0=0 km;将地面监测点坐标及压力源参数真值代入Mogi模型,正演得到地表垂直位移;最后对垂直位移模拟位移值施加均值为0、单位权方差为2 mm的随机误差,得到的垂直位移如图 2所示。
|
| 图 2 由火山Mogi模型正演得到的地表垂直形变 Fig. 2 The vertical displacement of forward the volcano Mogi model |
由于垂直位移反演压力源参数的平差模型是由泰勒级数对式(17)进行线性化处理后获得,针对反演过程中可能出现的病态奇异情形[45],算例4采用岭估计法进行参数求解,分别采用BO法、MBO法、BR法和MBR法进行垂直位移单一反演,具体表现为在获取自助样本后,通过岭估计方法来解决法矩阵求逆不稳定的问题并获取岩浆压力源参数[46-47]。4种方法反演得到的参数估值结果及差值二范数列于表 8。
| 岩浆压力源参数 | 真值 | BO法 | MBO法 | BR法 | MBR法 |
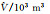
|
6000 | 6 002.118 30 | 6 001.255 84 | 5 996.318 31 | 6 001.490 63 |
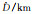
|
4 | 4.003 47 | 4.001 96 | 4.000 99 | 4.003 22 |
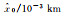
|
0 | 0.912 63 | 0.738 61 | 0.994 50 | 1.031 58 |

|
0 | -0.267 62 | -1.592 40 | -0.323 25 | -0.360 23 |
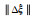
|
- | 2.118 26 | 1.255 81 | 3.681 70 | 1.490 63 |
由表 8中的参数估值可以看出,本文提出的4种方法获取的估值与真值的差异主要表现在岩浆房体积增量和岩浆压力源的中心深度。MBO法所得结果优于BO法,其参数估值与真值之间的范数减小了40.7%;与BR法相比,MBR法的范数减小了58.5%。结果表明,本文方法均能得到合理的参数估值,而采用了加权采样的MBO法和MBR法在提升估值质量方面更具优势。试验结果说明,将Bootstrap方法用于法矩阵病态性严重的火山形变Mogi模型参数反演是可行且有效的,也说明了本文的加权采样策略同样适用于大地测量领域病态模型的参数估计问题。
由式(17)-式(22)可以看出,火山Mogi模型中的未知参数向量ξ与地表垂直位移观测值向量Δh之间存在复杂的高维非线性关系,若采用对非线性模型泰勒级数展开的近似函数方法获取未知参数的方差信息,需要进行多次计算偏导,使得精度评定过程十分复杂。因此,算例4仅采用本文提出的4种方法及MC法进行精度评定,各方法获取的压力源参数标准差结果列于表 9。
| 标准差或协方差 | BO法 | MBO法 | BR法 | MBR法 | MC法 |
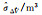
|
6.863 94 | 6.539 41 | 9.062 90 | 7.261 09 | 6.491 36 |
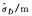
|
3.706 99 | 3.441 61 | 4.741 25 | 3.745 37 | 3.423 85 |
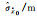
|
2.296 18 | 2.245 26 | 3.140 24 | 2.415 15 | 2.228 09 |
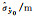
|
2.208 14 | 2.175 82 | 3.035 99 | 2.492 92 | 2.154 91 |
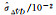
|
2.290 29 | 1.939 05 | 3.863 27 | 2.461 00 | 1.990 70 |
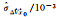
|
-0.948 43 | -1.010 21 | -0.843 83 | -0.268 34 | -0.999 03 |
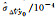
|
-0.247 98 | -8.123 95 | -0.157 88 | -0.673 58 | -1.686 62 |
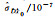
|
-4.087 26 | -4.778 37 | -4.236 31 | -0.802 00 | -0.821 53 |
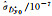
|
-1.450 07 | -5.068 10 | -9.196 30 | -2.395 99 | -2.561 41 |
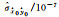
|
3.363 28 | 3.094 14 | 1.061 78 | 1.128 33 | 0.991 36 |
由表 9可知,BO法、BR法、MBO法及MBR法计算得到的参数估值标准差与MC法的结果在符号和量级上均保持一致,说明了本文Bootstrap方法精度评定的可行性和有效性。从估值的近似标准差结果来看,相比于BO法所获得的参数标准差,MBO法计算得到的标准差比BO法的计算结果在数值上更小,且比BO法的结果更加接近于MC法所获得的精度,说明MBO法能够获取比BO法更为合理的精度信息;与BR法的计算结果相比,MBR法的标准差有较为明显的减小且更为靠近MC法的计算精度,结果同样说明了MBR法计算得到的标准差比BR法更为精确。试验结果表明,将Bootstrap方法用于获取病态非线性平差模型的参数估值及精度信息依然是可靠且有效的,本文改进方法在集结Bootstrap方法的所有优点外,通过加权采样的抽样方式还能够更加充分地利用权值信息,从而能够获得更加精确的估值与精度信息值。
5 结论为获得统计意义上更为合理的精度信息,若采用泰勒展开的近似函数法,则无法避免地需要计算非线性函数的Jacobian矩阵和Hessian矩阵;若采用蒙特卡罗方法,则通常需要105以上次的模拟计算。因此,提出无需求导计算且计算效率相对较高的非线性精度评定方法显得尤为重要。本文在阐述非线性模型精度评定原理及Bootstrap方法重采样原理的基础上,给出了非线性模型精度评定重采样观测值Bootstrap方法及重采样残差的Bootstrap方法,并分别给出了具体的采样步骤,试图通过这两种方法在避免求导计算的情形下依然能获取合理的精度评定结果。针对Bootstrap方法的重采样过程是对模型随机项的等概率采样,本文通过对原始样本的权重信息进行归一化处理并获取随机变量的经验分布函数,将传统自助法的等概率采样转化为加权采样,尝试能够更加充分利用总体包含在原始样本中的先验信息和数据性质,以至于自助样本的经验分布更加逼近总体分布,进而获取更为精确的参数方差估值。
对本文案例研究中的各方法进行对比分析可知,非线性模型精度评定的Bootstrap方法能够获取比近似函数法、Jackknife方法更为合理的参数标准差,这说明将Bootstrap方法用于解决非线性模型的精度评定问题是可行且有效的;同时,采用了本文给出的改进算法能够得到比直接实施Bootstrap更加精确的精度信息,说明了本文加权采样方法的可靠性与优势性。因此,建议在获取非线性模型参数估值的方差-协方差时,采用本文的加权采样方法。
本文方法适用于观测值相互独立的情况,Bootstrap方法在相关观测数据的非线性精度评定问题,以及该方法的进一步应用是接下来需要研究的内容。随着Bootstrap方法引入非线性模型精度评定中,拓展该方法在大地测量领域中的应用,也将是非线性平差理论研究的一个重要补充。
| [1] |
杨元喜, 张丽萍. 中国大地测量数据处理60年重要进展第一部分: 函数模型和随机模型进展[J]. 地理空间信息, 2009, 7(6): 1-5. YANG Yuanxi, ZHANG Liping. Progress of geodetic data processing for 60 years in china part 1: progress of functional and stochastic model[J]. Geospatial Information, 2009, 7(6): 1-5. DOI:10.3969/j.issn.1672-4623.2009.06.001 |
| [2] |
杨元喜, 张丽萍. 中国大地测量数据处理60年重要进展第二部分: 大地测量参数估计理论与方法的主要进展[J]. 地理空间信息, 2010, 8(1): 1-6. YANG Yuanxi, ZHANG Liping. Progress of geodetic data processing for 60 years in china part 2: progress of parameter estimation theory and methodology[J]. Geospatial Information, 2010, 8(1): 1-6. DOI:10.3969/j.issn.1672-4623.2010.01.001 |
| [3] |
彭军还. 非线性M估计研究及其应用[D]. 武汉: 武汉大学, 2003. PENG Junhuan. Research on non-linear M-estimates and its application[D]. Wuhan: Wuhan University, 2003. |
| [4] |
沈云中. 动力学法的卫星重力反演算法特点与改进设想[J]. 测绘学报, 2017, 46(10): 1308-1315. SHEN Yunzhong. Algorithm characteristics of dynamic approach-based satellite gravimetry and its improvement proposals[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1308-1315. DOI:10.11947/j.AGCS.2017.20170380 |
| [5] |
彭军还, 李淑慧, 师芸, 等. 不等式约束M估计的均方误差矩阵和解的改善条件[J]. 测绘学报, 2010, 39(2): 129-134. PENG Junhuan, LI Shuhui, SHI Yun, et al. The mean squares error matrix of inequality constrained M-estimate and the conditions for improving solutions[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 129-134. |
| [6] |
李斐, 郝卫峰, 王文睿, 等. 非线性病态问题解算的扰动分析[J]. 测绘学报, 2011, 40(1): 5-9. LI Fei, HAO Weifeng, WANG Wenrui, et al. The perturbation analysis of nonlinear ill-conditioned solution[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 5-9. |
| [7] |
薛树强, 杨元喜, 党亚民. 测距定位方程非线性平差的封闭牛顿迭代公式[J]. 测绘学报, 2014, 43(8): 771-777. XUE Shuqiang, YANG Yuanxi, DANG Yamin. A closed-form of Newton iterative formula for nonlinear adjustment of distance equations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 771-777. |
| [8] |
ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Complex least squares adjustment to improve tree height inversion problem in PolInSAR[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 1-8. DOI:10.11947/j.JGGS.2019.0101 |
| [9] |
曲国庆, 孙振, 苏晓庆, 等. 非线性参数估计的自适应松弛正则化算法[J]. 武汉大学学报(信息科学版), 2019, 44(10): 1491-1497. QU Guoqing, SUN Zhen, SU Xiaoqing, et al. Adaptive relaxation regularization algorithm for nonlinear parameter estimation[J]. Geomatics and Information Science of Wuhan University, 2019, 44(10): 1491-1497. |
| [10] |
薛树强. 大地测量观测优化理论与方法研究[D]. 西安: 长安大学, 2018. XUE Shuqiang. Research on geodetic observation optimization theory and methods[D]. Xi'an: Chang'an University, 2018. |
| [11] |
牟忠凯, 隋立芬, 张清华, 等. 顾及线性化模型误差补偿的卡尔曼滤波算法[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1073-1076. MOU Zhongkai, SUI Lifen, ZHANG Qinghua, et al. An improved EKF algorithm considering model errors of linearization[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1073-1076. |
| [12] |
NOCEDAL J, WRIGHT S J. Numerical optimization[M]. New York: Springer Press, 2006.
|
| [13] |
王新洲. 非线性模型参数估计理论与应用[M]. 武汉: 武汉大学出版社, 2002. WANG Xinzhou. Theories and applications of nonlinear model parameter estimation[M]. Wuhan: Wuhan University Press, 2002. |
| [14] |
曾小牛, 刘代志, 牛超, 等. 改进高斯-牛顿法的位场向下延拓[J]. 测绘学报, 2014, 43(1): 37-44. ZENG Xiaoniu, LIU Daizhi, NIU Chao, et al. A modified Gauss-Newton method for downward continuation of potential field[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 37-44. DOI:10.13485/j.cnki.11-2089.2014.0006 |
| [15] |
马昌凤. 最优化方法及其MATLAB程序设计[M]. 北京: 科学出版社, 2010. MA Changfeng. Optimization method and the MATLAB programming[M]. Beijing: Science Press, 2010. |
| [16] |
冯万鹏, 李振洪. InSAR资料约束下震源参数的PSO混合算法反演策略[J]. 地球物理学进展, 2010, 25(4): 1189-1196. FENG Wanpeng, LI Zhenhong. A novel hybrid PSO/simplex algorithm for determining earthquake source parameters using InSAR data[J]. Progress in Geophysics, 2010, 25(4): 1189-1196. DOI:10.3969/j.issn.1004-2903.2010.04.007 |
| [17] |
万永革, 刘瑞丰, 李鸿吉. 用遗传算法反演京津唐张地区的三维地壳结构和震源位置[J]. 地震学报, 1997, 19(6): 623-633. WAN Yongge, LIU Ruifeng, LI Hongji. Inversion of 3D crustal structure and source location in Jing-Jin-Tang-Zhang area by genetic algorithm[J]. Acta Seismologica Sinica, 1997, 19(6): 623-633. |
| [18] |
徐培亮. 非线性函数的协方差传播公式[J]. 武汉测绘科技大学学报, 1986(2): 92-99. XU Peiliang. Variance-covariance propagation for a nonlinear function[J]. Journal of Wuhan University of Surveying and Mapping, 1986(2): 92-99. |
| [19] |
XUE Jie, LEUNG Y, MA Jianghong. High-order Taylor series expansion methods for error propagation in geographic information systems[J]. Journal of Geographical Systems, 2015, 17(2): 187-206. DOI:10.1007/s10109-014-0207-x |
| [20] |
WANG Leyang, ZHAO Yingwen. Second-order approximation function method for precision estimation of total least squares[J]. Journal of Surveying Engineering, 2019, 145(1): 04018011. DOI:10.1061/(ASCE)SU.1943-5428.0000266 |
| [21] |
ALKHATIB H, SCHUH W D. Integration of the Monte Carlo covariance estimation strategy into tailored solution procedures for large-scale least squares problems[J]. Journal of Geodesy, 2007, 81(1): 53-66. DOI:10.1007/s00190-006-0034-z |
| [22] |
SHEN Yunzhong, LI Bofeng, CHEN Yi. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238. DOI:10.1007/s00190-010-0431-1 |
| [23] |
王乐洋, 赵英文. 非线性平差精度评定的自适应蒙特卡罗法[J]. 武汉大学学报(信息科学版), 2019, 44(2): 206-213, 220. WANG Leyang, ZHAO Yingwen. Adaptive Monte Carlo method for precision estimation of nonlinear adjustment[J]. Geomatics and Information Science of Wuhan University, 2019, 44(2): 206-213, 220. |
| [24] |
WANG Leyang, YU Fengbin. Jackknife resample method for precision estimation of weighted total least squares[J]. Communications in Statistics-Simulation and Computa-tion, 2021, 50(5): 1272-1289. DOI:10.1080/03610918.2019.1580727 |
| [25] |
WANG Leyang, DING Rui. Inversion and precision estimation of earthquake fault parameters based on scaled unscented transformation and hybrid PSO/Simplex algorithm with GPS measurement data[J]. Measurement, 2020, 153: 107422. DOI:10.1016/j.measurement.2019.107422 |
| [26] |
WANG Leyang, ZOU Chuanyi. Accuracy analysis and applications of the Sterling interpolation method for nonlinear function error propagation[J]. Measurement, 2019, 146: 55-64. DOI:10.1016/j.measurement.2019.06.017 |
| [27] |
EFRON B. Bootstrap methods: another look at the jackknife[J]. The Annals of Statistics, 1979, 7(1): 1-26. |
| [28] |
JOHNSON R W. An introduction to the Bootstrap[J]. Teaching Statistics, 2001, 23(2): 49-54. DOI:10.1111/1467-9639.00050 |
| [29] |
CHEN Xiaohui. Gaussian and Bootstrap approximations for high-dimensional u-statistics and their applications[J]. The Annals of Statistics, 2018, 46(2): 642-678. |
| [30] |
SAHINLER S, TOPUZ D. Bootstrap and Jackknife resampling algorithms for estimation of regression parameters[J]. Journal of Applied Quantitative Methods, 2007, 2(2): 188-199. |
| [31] |
MARTÍNEZ-CAMBLOR P, CORRAL N. A general Bootstrap algorithm for hypothesis testing[J]. Journal of Statistical Planning and Inference, 2012, 142(2): 589-600. DOI:10.1016/j.jspi.2011.09.003 |
| [32] |
KITAGAWA G, KONISHI S. Bias and variance reduction techniques for Bootstrap information criteria[J]. Annals of the Institute of Statistical Mathematics, 2010, 62(1): 209-234. DOI:10.1007/s10463-009-0237-1 |
| [33] |
PAN L, POLITIS D N. Bootstrap prediction intervals for linear, nonlinear and nonparametric autoregressions[J]. Journal of Statistical Planning and Inference, 2016, 177: 1-27. DOI:10.1016/j.jspi.2014.10.003 |
| [34] |
O'HAGAN A, MURPHY T B, SCRUCCA L, et al. Investigation of parameter uncertainty in clustering using a Gaussian mixture model via Jackknife, Bootstrap and weighted likelihood Bootstrap[J]. Computational Statistics, 2019, 34(4): 1779-1813. DOI:10.1007/s00180-019-00897-9 |
| [35] |
李桂苓, 李瑞华, 陶华学. 非线性最小二乘平差参数精度的评定[J]. 石油大学学报(自然科学版), 2001, 25(1): 102-106. LI Guiling, LI Ruihua, TAO Huaxue. Accuracy of parameters adjusted by variance-covariance propagation of nonlinear least squares for different types of observed values[J]. Journal of the University of Petroleum, China, 2001, 25(1): 102-106. DOI:10.3321/j.issn:1000-5870.2001.01.026 |
| [36] |
DICICCIO T J, ROMANO J P. A review of Bootstrap confidence intervals[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1989, 51(3): 470. DOI:10.1111/j.2517-6161.1989.tb01442.x |
| [37] |
ANGRISANO A, MARATEA A, GAGLIONE S. A resampling strategy based on Bootstrap to reduce the effect of large blunders in GPS absolute positioning[J]. Journal of Geodesy, 2018, 92(1): 81-92. DOI:10.1007/s00190-017-1046-6 |
| [38] |
EFRON B. Nonparametric standard errors and confidence intervals[J]. Canadian Journal of Statistics, 1981, 9(2): 139-158. DOI:10.2307/3314608 |
| [39] |
EFRON B, TIBSHIRANI R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy[J]. Statistical Science, 1986, 1(1): 54-75. |
| [40] |
STINE R. An introduction to Bootstrap methods: examples and ideas[J]. Sociological Methods & Research, 1989, 18(2-3): 243-291. |
| [41] |
LÉGER C, POLITIS D N, ROMANO O P. Bootstrap technology and applications[J]. Technometrics, 1992, 34(4): 378-398. DOI:10.1080/00401706.1992.10484950 |
| [42] |
崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差(新版)[M]. 武汉: 武汉大学出版社, 2005. CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized surveying adjustment (new edition)[M]. Wuhan: Wuhan University Publishing House, 2005. |
| [43] |
MOGI K. Relations between the eruptions of various volcanoes and the deformations of the ground surface around them[J]. Bulletin of the Earthquake Research Institute, University of Tokyo, 1958, 36: 99-134. |
| [44] |
YAMAKAWA N. On the strain produced in a semi-infinite elastic solid by an interior source of stress[J]. Journal of the Seismological Society of Japan, 1955, 8: 84-98. |
| [45] |
王乐洋, 余航. 火山Mogi模型反演的总体最小二乘联合平差方法[J]. 武汉大学学报(信息科学版), 2018, 43(9): 1333-1341. WANG Leyang, YU Hang. Application of total least squares joint adjustment to volcano inversion of Mogi model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1333-1341. |
| [46] |
GU Yongwei, GUI Qingming, ZHANG Xuan, et al. Iterative solution of regularization to ill-conditioned problems in geodesy and geophysics[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 59-65. DOI:10.11947/j.JGGS.2019.0107 |
| [47] |
SHEN Yunzhong, XU Peiliang, LI Bofeng. Bias-corrected regularized solution to inverse ill-posed models[J]. Journal of Geodesy, 2012, 86(8): 597-608. DOI:10.1007/s00190-012-0542-y |




