合成孔径雷达(synthetic aperture radar, SAR)卫星使用微波波段进行对地观测,可提供广泛的业务化对地观测能力,在植被、农作物、海冰、湿地等资源监测监管方面,油膜等污染物监测方面,洪水火山等自然灾害方面,海洋、湖水、冰体等水资源监测方面,舰船监测方面均发挥着极为重要的作用,且取得了较为成功的业务化应用成果[1]。相比于前述各类以后向散射系数为主的应用来说,以精确的几何和相位测量为核心的地形测绘业务化应用受到了极大限制。SAR卫星的地形测绘能力是指卫星在常规模式下可完成的平面和高程的确定性测量能力。在进行业务化运行之前,卫星需完成精确的在轨测试,消除系统误差[2]。业务化运行过程中,一般不再进行额外的几何参数估计和修正,这对星上参数的稳定性、精确性提出了较高的要求。在极高精度的测绘应用过程中,地面系统还需要对各环境变量进行逐一修正,例如大气误差、绝对相位误差、地球动力学误差等。本文探讨的业务化地形测绘能力,主要包含平面定位能力和高程测量能力两类,其中平面定位能力是每颗SAR卫星均具备的基础能力。高程测量能力则不同,虽然大部分SAR卫星均可使用雷达干涉(interferometric SAR, InSAR)或立体测量手段完成部分地区的高程测量,但可业务化应用的卫星并不多,迄今为止国外民用SAR领域仅有航天飞机雷达地形测绘任务(shuttle radar topography mission, SRTM)以及TanDEM-X两个业务化高程测量任务。国内SAR领域的机载地形测绘任务较多,例如以X波段为主的1∶50 000西部测图任务[3],以及以Ka波段为主的1∶5000贵州测图示范任务等[4],均属于比较优秀的业务化应用案例。但是我国星载地形测绘任务较少,在2019年4月30日发射的天绘二号卫星,是我国迄今为止唯一的星载InSAR地形测绘任务的卫星,它提供的产品可满足1∶50 000比例尺地形图测绘精度指标[5]。
1 业务化地形测绘标准规范在进行地图绘制、基础设施规划或地理信息框架建设过程中,会使用到地物的平面信息、高程信息、水文信息或其他特征信息,这些信息可来自于传统测量手段,例如水准仪以及经纬仪等,也可来自于航空设备,包括测绘飞艇及无人机等,大规模的大洲或全球级测绘则必须使用卫星手段。无论使用何种手段,所有的产品都应该是基于产品性能去定义的,而不是基于某种特定角度去表达,或是基于某种特定处理手段去表达,这样才能确保产品的一致性,易于进行产品的扩展和维护。
现阶段星载地形测绘的精度已经进入了大比例尺时代,我国的业务化地形测绘能力最高的高分七号卫星已经可以进行1∶10 000比例尺地形图测绘,以及1∶5000比例尺地形图补测和修测。按照测绘的行业标准要求,各比例尺对应的指标见表 1[6],如不做特殊说明,均以一级指标为准。国标中未对数字高程模型(digital elevation model, DEM)的平面定位精度予以规定,然而对应的数字正射模型(digital orthophoto map, DOM)产品规范中指出,平地与丘陵地区的平面位置中误差不大于图上0.5 mm,山地和高山地的平面位置中误差不大于图上0.75 mm[7]。在没有新的标准规范要求的情况下,应用过程中将以对应指标为准。
| 比例尺 | DOM分辨率 | DEM格网尺寸 | 高程中误差 | |||||
| 一级 | 二级 | 三级 | ||||||
| 1∶5000 | 0.5 | 2.5 | 平地 | 0.5 | 平地 | 0.7 | 平地 | 1.0 |
| 丘陵地 | 1.2 | 丘陵地 | 1.7 | 丘陵地 | 2.5 | |||
| 山地 | 2.5 | 山地 | 3.3 | 山地 | 5.0 | |||
| 高山地 | 4.0 | 高山地 | 6.0 | 高山地 | 8.0 | |||
| 1∶10 000 | 1 | 5 | 平地 | 0.5 | 平地 | 0.7 | 平地 | 1.0 |
| 丘陵地 | 1.2 | 丘陵地 | 1.7 | 丘陵地 | 2.5 | |||
| 山地 | 2.5 | 山地 | 3.3 | 山地 | 5.0 | |||
| 高山地 | 5.0 | 高山地 | 6.7 | 高山地 | 10.0 | |||
| 1∶25 000 | 2.5 | 10 | 平地 | 1.5 | 平地 | 2.0 | 平地 | 3.0 |
| 丘陵地 | 2.5 | 丘陵地 | 3.5 | 丘陵地 | 5.0 | |||
| 山地 | 4.0 | 山地 | 5.5 | 山地 | 8.0 | |||
| 高山地 | 7.0 | 高山地 | 9.5 | 高山地 | 14.0 | |||
| 1∶50 000 | 5 | 25 | 平地 | 3.0 | 平地 | 4.0 | 平地 | 6.0 |
| 丘陵地 | 5.0 | 丘陵地 | 7.0 | 丘陵地 | 10.0 | |||
| 山地 | 8.0 | 山地 | 11.0 | 山地 | 16.0 | |||
| 高山地 | 14.0 | 高山地 | 19.0 | 高山地 | 28.0 | |||
国际标准与我国国标的定义有所不同,见表 2,特别是以SRTM为代表的SAR卫星地形测绘任务,其标准在通用性的前提下,进行了适应性约束。SRTM遵循美国国家地理空间情报局(National Geospatial-Intelligence Agency, NGA)发布的数字地形高程图标准(digital terrain elevation data, DTED)[8]。DTED-2规定,在84世界大地测量系(world geodetic system 1984, WGS-84)中,绝对定位的90%圆误差(90% circular error, CE90)不大于23 m,在平均海平面下,绝对高程的90%线性误差(90% linear error, LE90)不大于18 m。不同于我国国标的是,DTED-2同时规定了相对高程精度,即在平均海平面下,0~20%坡度(不含20%)的中低等起伏地形LE90不大于12 m,大于20%坡度的高起伏地形LE90不大于15 m,地形起伏定义为在1°格网内的主导地形。在此基础上,SRTM给出了其产品标准,即绝对高程LE90为16 m,相对高程LE90为10 m,绝对水平CE90为20 m。SAR测绘卫星的另一个全球性任务为TanDEM-X,TanDEM-X是由两颗性能指标几乎完全相同的TerraSAR-X卫星构成,TanDEM-X的设计指标更高,设计过程中遵循高分辨率地形信息标准(high resolution terrain information, HRTI)。HRTI-3规定,在WGS-84坐标系下,绝对平面定位CE90为10 m,绝对高程LE90为10 m,0~20%坡度(不含20%)的中低等起伏地形相对高程LE90不大于2 m,大于等于20%坡度的高起伏地形相对高程LE90不大于4 m[9]。
| 指标 | DTED-2 | HRTI-3 | |
| 相对高程精度 | 坡度<20% | 12 | 2 |
| LE90 | 坡度≥20% | 15 | 4 |
| 绝对高程精度LE90 | 18 | 10 | |
| 相对平面精度CE90 | 15 | 3 | |
| 绝对平面精度CE90 | 23 | 10 | |
| 格网尺寸 | 30 | 12 | |
从DTED-2、HRTI-3及我国国标定义可以看出。三者的精度评判标准有所差异,中误差代表了63%~68%的数据分布情况,与1σ代表的67%相似,而LE90以及CE90代表的是90%的数据分布情况。一般来说,LE90对应的误差约为均方根误差的1.6倍,而CE90对应的误差约为均方根误差的2.1倍。中误差统计过程中易受粗差影响,LE90以及CE90的抗差性则较好,在使用过程中,LE90以及CE90更为合理。SRTM遵循的DTED-2标准中,DEM产品的空间分辨率为30 m,其产品并不能满足我国1∶50 000比例尺的25 m格网尺寸要求。TanDEM-X的标准产品遵循HRTI-3指标,然而实际的绝对高程精度已经与相对高程精度一致,达到了4 m以内,转换为中误差约为2.5 m,其精度较高,但其格网尺寸不满足我国1∶25 000比例尺的10 m格网尺寸要求。而事实上,TanDEM-X还提供其他分辨率和精度的产品,例如4 m@6 m(精度@格网尺寸)、1 m@25 m、0.5 m@50 m等[10],这些产品并非业务化产品,而是依据商业需求进行定制生产的,它可满足不同精度与不同分辨率的产品需求。
我国的测绘产品除满足精度之外,还需满足其他质检标准。在进行DEM产品生产过程中,达不到高程精度要求的区域,需划分为DEM高程推测区,数据中断时需赋予高程值-9999[11]。此外,由于SAR采用侧视成像,因此阴影和叠掩会带来低质量区和无效区,这在产品质检过程中,会影像产品质量分级[12]。在实际生产过程中,为了降低阴影和叠掩的影响,提高测绘产品质量,一般会进行升降轨数据融合,而在DEM产品生产过程中,为了确保产品精度,除升降轨数据融合之外,还需要针对沙漠、森林、高山地等特殊地形地表区进行3次或4次覆盖[13]。本文将集中探讨干涉几何精度,对多次观测等策略性的质量提升方案不再做深入探讨。
2 平面定位模型与误差 2.1 平面定位模型由于SAR卫星成像过程中存在着与光学类似的映射关系,因此早期采用与光学类似的定位方程,例如G.Konecny共线方程使用二次方程描述地面点到像点之间的关系
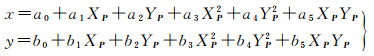 (1)
(1)
式中,(XP, YP, ZP)是地面点对应的坐标矢量P;(x, y)是距离向和方位向像素坐标。为了确定方程的多项式系数,需要至少5个地面控制点,控制点数量足够多且质量较好的情况下,定位方程在平面地区的解算精度可达到1个像素[14],以此为基础也产生了区域网平差的概念,用于消除多景影像拼接过程中的拼接缝。共线方程能够描述的仅有简单的拉伸、平移、旋转等畸变,无法描述地表高程起伏较大情况下的阴影、叠掩等现象,且定位精度有限,因此其后又从光学概念中衍生了针对SAR影像的有理函数或有理多项式(rational function model, RFM;rational polynomial coeffici-ents, RPC)模型,这种起源于20世纪80年代的方法在IKONOS之后取得了极大关注,在光学影像中应用广泛。在SAR影像中,也可使用类似的表达方式,即
 (2)
(2)
式中,NumL(P, L, H)、NumS(P, L, H)、DenL(P, L, H)、DenS(P, L, H)均为P、L、H的三次多项式,各包含有20个未知系数,即共80个未知系数。P、L、H、x′、y′为地面点经纬度坐标和像素坐标的正则化函数。RFM/RPC参数求解过程中需要用到严格成像模型,对严格成像模型格网化之后,使用最小二乘获得RPC拟合参数。使用RFM/RPC拟合斜距-多普勒(range-Doppler, R-D)模型,拟合的精度可达到1%像素,拟合InSAR相高转换模型的精度可达1‰波长[15],在Radarsat以及GF-3的业务化应用中,均包含了此类模型。虽然这种模型精度较高,但是RFM/RPC模型在拟合之后,就隐藏了SAR成像过程中的几何参数,在基线参数求解、地面无控定位等过程中限制较大。合理的SAR定位模型需结合自身的几何特性进行精密的坐标转换,例如文献[16]综合考虑了距离方程和零多普勒方程,提出了机载成像过程中的Leberl模型,然而这种模型无法表达星载成像过程中的非零多普勒状态。因此现阶段多使用R-D模型进行SAR相关的几何分析。R-D模型表达为
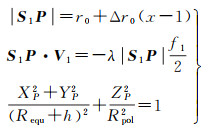 (3)
(3)
式中,S1P是从主影像相位中心到地面点的向量;r0是主影像近地点斜距;Δr0是斜距分辨率;V1是主影像速度矢量;λ是雷达波长;f1是主影像多普勒中心频率;Requ是地球平均赤道半径;Rpol是地球极半径;·表示对向量取模;式(3)中至上而下的3个方程分别是斜距方程、多普勒方程和椭球方程,前两个方程对应雷达成像的两个基本特性,即侧视成像、合成孔径成像,这3个模型是雷达成像的严密几何模型。定位误差的来源以及定位精度的提升,均需以R-D模型为基础进行分析。
R-D模型应用极为广泛,在影像的聚焦成像、影像定位、基线估计、相高转换及地理编码过程中均会用到。它依赖精确的卫星定轨信息、测速信息,这两项参数通常使用星上提供的GPS数据进行插值获得。插值过程中需使用时间的多项式,其阶数不高于6阶,更高阶的拟合不会带来精度的提升[17]。在GPS信息足够准确的前提下,卫星方位向成像时间的误差,将是方位向定位的主要误差。
然而,在实际处理过程中,为了得到DOM,在完成上述的坐标定位之外,还需进行整景影像的辐射校正、地理编码、区域性辐射校正、影像镶嵌,这些过程以平面定位为根本,且不会对平面定位精度有过多干扰。本文不再进行数据处理相关的探讨。
2.2 平面误差及检校方法从R-D模型可以看出,SAR卫星定位过程中主要依靠卫星位置、速度、多普勒、斜距参数、地表高程以及椭球参数等,在上述参数精确测量的前提下,SAR的定位精度将会极高。值得说明的是,在评估卫星的定位能力时,一般不以地面不精确输入参数为误差源,例如地表高程参数误差、椭球参数误差、刺点误差等。SAR的高精度定位特性也使得SAR测地学的概念应运而生[18]。SAR测地学依赖于毫米至厘米级的轨道信息、精确的成像时间参数以及1‰像素的定位精度,现阶段这种精度已经在TerraSAR-X的全球控制点产品中得到了业务化应用。
SAR影像是一个二维平面,其定位精度依赖于方位向和距离向精度。其中方位向精度表达为地面特征点的成像时刻与方位向计时器之间的差异,即
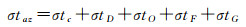 (4)
(4)
式中,右侧5项分别为卫星平台与载荷时钟对准误差、卫星动力学误差、卫星轨道误差、地面特征点误差及地球动力学误差带来的方位向时间延迟。地面接收信号的时刻与卫星平台记录的时刻之间存在时间差异,在现阶段定轨误差达到厘米级的情况下,这种误差是方位向定位的主要误差源。由于这部分误差在长时间内保持为一个常数,因此是重要的检校参数之一。卫星动力学误差是从卫星发出信号到卫星接收信号过程中卫星的持续运动,这种运动可达数十米,而地面接收到信号的瞬间是在收发信号的中间时刻,这种误差可采用停-走模型表达。卫星轨道误差需要控制在极小的范围内,现在普遍可达到5 cm,TerraSAR-X的科学轨道产品的定轨精度则已经达到了4.2 cm,测速精度也达到了3 mm/s[19]。天绘二号的A星和B星的定轨中误差分别达到了2.7 cm和2.6 cm,测速精度分别优于0.17 mm/s和0.19 mm/s[5]。地面特征点是用来确定目标点精确的像素坐标的,用以获取精确的方位向成像时间,拟合成像时刻的卫星位置和速度,对于一般散射体来说,没有明显的反射中心,位置确定精度较差,但是对于永久散射体(persistent scatterer, PS)及角反射器(corner reflector, CR)来说,其像素的定位精度可提升至1/1000像素,对应的方位向定位精度将能达到厘米级[20]。这也意味着,使用CR能够最大程度抑制刺点误差,完成方位向平台与载荷时钟对准误差的解算。地球动力学的影响较为复杂,其中地球自转的影响可通过国际地球自转服务条例进行修正。地球固体潮来源于太阳和月球引力带来的地球表面变化,这种变化量在径向可达40 cm,在水平方向为厘米级。地球极点的变化带来的旋转轴变化,会引发对应的极潮,其径向方向的影响约25 mm,水平方向则为7 mm。由于海水运动引发的地球形变在近海岸带区域的影响较大,径向形变可达到数厘米,而在内陆地区的形变有可能会小于1 cm。但是内陆地区的大气负载带来的地球形变范围高达15~20 mm,其径向波动范围的常规值也在4 mm,水平向为0.5 mm。水文负载的影响可通过GNSS获取,其最大值为2 cm,一般在数毫米。
距离向精度依赖于斜距测量精度,斜距误差一般表达为时间延迟误差στr,στr具体包含如下分量
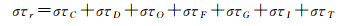 (5)
(5)
式中,右侧7项分别为由卫星计时器延迟、卫星动力学误差、卫星轨道误差、地面特征点误差、地球动力学误差、电离层误差、对流层误差带来的距离向时间延迟。其中卫星计时器的延迟是卫星由信号发出到信号接收过程中,计时器的延迟与真实时间之间的差异,这部分误差在较长时间内保持稳定,因此是重要的检校参数之一。卫星动力学误差、卫星轨道误差、地面特征点误差、地球动力学误差与方位向的误差来源一致。大气延迟的可采用现有模型进行修正[21]。大气延迟一般包含电离层的电荷影响以及对流层的水汽影响,其中电离层延迟依赖于大气中的电荷数,一般为5~10总电子数单位(total electron content unit, TEC, TECU),极端情况下也可能达到100。假设在常规的5TECU下,L、C、X波段的天顶角方向电离层延迟分别是1.29 m、0.064 2 m、0.021 6 m,波长越短,影响越小。此外,现阶段卫星高度一般为数百公里,电离层的F层可高达数千千米,低轨卫星精确建模过程中需考虑这种差异,例如卫星飞行高度在500 km时,其电离层延迟约为总延迟的75%[20]。此外,电荷数的变化较为频繁,需使用较高时间分辨率的TEC参数进行建模,不同时相的TEC参数在X波段中差异不大,但是在C波段和L波段中不可忽视。对流层的影响分为干分量和湿分量,干分量是由于大气的影响带来的,在海平面的累积延迟可达到2.3 m,而湿分量主要取决于水汽含量,其延迟量最多可达40 cm,对流层的这两类影响与频率无关。在以上的各类影响中,经过地面修正之后,固体潮以及对流层水汽影响带来的斜距误差最大,可达厘米级[22]。
卫星检校必须使用精确的CR装备,消除地面刺点误差,精确获取方位向成像时间以及斜距参数。CR装备设计过程中,主要考虑雷达截面积(radar cross section, RCS),RCS增大,将会带来更大的后向散射强度,提高定位精度。提高RCS一方面需要采用对微波信号反射较好的金属材料,另一方面需设计为直角三面CR,并增加CR边长。CR的参数要经过严格控制以及内业标校,例如直角三面CR,如果三面夹角从90°变为88°,那么信号强度将会降低100倍。CR的边长也并非越长越好,在信杂比高于30 dB的前提下,确保接收信号不达到饱和即可。另外,CR的反射相位中心的测量精度也需要达到毫米级,以减少检校误差。为了确保CR一直朝向信号入射方向,最佳方案是设定远程控制方案,卫星过境时对CR的俯仰角和朝向角进行微调,并随时测定反射相位中心坐标。检校过程中对两方向的误差进行独立修正,以减小方位向和距离向的误差叠加。具体的检校方法如图 1所示。

|
| 图 1 平面定位参数误差检校方法 Fig. 1 The planar location parameter calibration method |
2.3 业务化平面定位能力
表 3中给出了国际常用卫星的业务化成像模式下可满足的DOM基本比例尺。虽然SAR卫星定位能力参差不齐,但是可以看出,国外SAR卫星的业务化定位能力正在逐步提升,国外第1颗SAR卫星Seasat的平面定位精度为25 m[23-24],综合考虑其分辨率,可满足1∶250 000比例尺DOM产品生产要求。Radarsat-1、SRTM及Envisat虽然仅能满足1∶500 000比例尺DOM产品生产要求,但是其定位精度已经有了较大提升。Radarsat-1要求检校后的平面定位精度小于40 m,其标准成像模式的实际值优于17 m[25]。SRTM遵循的精度指标为DETD-2,平面定位精度要求20 m,实际定位精度优于13 m[26]。Envisat的精细成像模式(image mode precision, IMP)、单视复数成像模式(image mode single-look-complex, IMS)、交替极化精细成像模式(alternating polarization precision image, APP)、交替极化单视复数成像模式(alternating polarization single-look-complex, APS)多模式下的定位精度的统计结果为14 m[27]。Radarsat-2的分辨率和精度均优于Radarsat-1,其标准成像模式下,距离向定位精度优于5 m,方位向定位精度优于2 m[28],Ultra-Fine模式下多入射角影像进行定位时,可将精度提升为1 m[29],已经完全满足1∶250 000比例尺DOM产品生产要求。欧洲遥感卫星(European Remote-Sensing Satellite, ERS)及ALOS-PALSAR可支持1∶100 000比例尺DOM产品生产。ERS在Imaging模式下,检校之前的北向和东向定位精度为40~50 m[30],检校处理之后,平面定位精度可达到10 m[31]。ALOS-PALSAR的精细波束单极化模式(fine beam single-pol, FBS)、精细波束双极化模式(fine beam dual-pol, FBD)、直接下传模式(direct downlink mode, DDM)、极化模式(polarimetry mode, POL)的平面定位精度是9.3 m,ScanSAR的平面定位精度是70 m[32]。随着卫星定量化要求越来越高,卫星的分辨率和定位精度都得到了极大提升,已经逐步进入了1∶50 000比例尺DOM产品生产能力范畴,例如TerraSAR-X的Stripmap模式平面定位精度2 m,实际方位向定位精度优于0.3 m,距离向定位精度优于0.5 m,在CR的支持下,多角度数据平面定位精度2~3 cm[20]。第2代COSMO-SkyMed(COSMO-SkyMed second generation, CSG)的快速分发模式的平面定位精度为25 m,标准模式下,Stripmap精度为3.75 m,Spotlight精度为12 m,科研模式下,Spotlight精度达到1.25 m,这种模式下的数据仅供非政府组织使用[33]。Sentinel-1常规模式下的平面定位精度为2.3 m,经过与TerraSAR-X类似的处理之后,距离向可达6 cm,方位向可达14 cm[34],然而由于此模式下,分辨率较差,因此仅能满足我国1∶500 000比例尺的DOM产品生产要求。我国高分三号精细条带Ⅱ、精细条带Ⅰ、扫描模式下的定位精度分别优于62 m、47 m、26 m,检校之后精度均可优于13 m[21]。天绘二号的平面定位精度未做直接说明,但是其精度与TerraSAR-X相当[5]。SAR影像可用于DOM产品的生产,测绘行业标准中要求DOM的地面分辨率为图上0.1 mm,对应1∶50 000、1∶100 000、1∶250 000及1∶500 000等基本比例尺的地面分辨率分别为5 m、10 m、25 m和50 m。
| 卫星 | 发射时间 | 业务化成像模式 | 分辨率/m(方位向×距离向) | 定位精度/m | 满足的基本比例尺 |
| Seasat | 1978 | Stripmap Scanning | 25×25 | 25.0 | 1∶250 000 |
| ERS | 1991 | imaging mode | 25×5 | 10.0 | 1∶100 000 |
| Radarsat-1 | 1995 | standard | 25×28 | 17.0 | 1∶500 000 |
| SRTM | 2000 | ScanSAR | 30×30 | 13.0 | 1∶500 000 |
| Envisat | 2002 | Img及AP | 28×28/29×30 | 9.0 | 1∶500 000 |
| ALOS-PALSAR | 2006 | FBD | 14~88×14~88 | 10.0 | 1∶100 000 |
| TerraSAR-X | 2007 | Stripmap | 3×3 | 2.0 | 1∶50 000 |
| Radarsat-2 | 2007 | Standard | 25×28 | 6.0 | 1∶250 000 |
| COSMO-SkyMed | 2007 | Stripmap | 3×3 | 4.0 | 1∶50 000 |
| Sentinel-1 | 2014 | interferometric wide swath mode | 5×20 | 2.0 | 1∶250 000 |
| 高分三号 | 2016 | 精细条带Ⅱ | 10×10 | 13.0 | 1∶100 000 |
| 天绘二号 | 2019 | 条带模式 | 3×3 | — | 1∶50 000 |
3 高程测量模型与误差 3.1 高程测量模型
在以SRTM和TanDEM-X为代表的全球性高程模型的业务化生产过程中,使用的是InSAR技术,即对相位进行处理,得到高精度的地面点三维坐标。然而SAR与光学之间的高相似性,也使得SAR具有立体量测功能,其模型与光学有诸多相似之处[17],且得益于SAR的高精度定位能力,针对PS点或其他明显点目标,三维定位能力可达到4 cm,然而这种方式无法针对大规模面目标得到具有统一精度的高程数据,在业务化地形测绘过程中存在一定的限制。PolInSAR可采用卫星的极化和干涉信息,获取地表的高精度树高信息[35]。除此之外,干涉数据还可使用立体干涉测量[36]的方法精确解算干涉过程中的整周未知数,对于无控高程测量来说具有极为重要的意义,然而由于其功能单一,故此处不对其进行深入阐述。
InSAR干涉测量的高精度的高程信息依赖高精度的基线和相位信息,在相位转到高程的过程中,一般使用VPQ坐标系进行视线向向量的求解和转换,V为速度方向的单位矢量,速度矢量和基线矢量构成一个平面,这个平面的垂线(右手法则)为Q,P向量与VQ向量遵守右手法则。在主星位置已知的情况下,地面点的坐标表达为
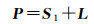 (6)
(6)
式中,L为雷达视线向向量。视向量在VPQ中的三分量的基向量可表达为如下公式
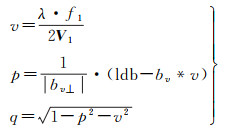 (7)
(7)
式中,b为基线长度;bv为基线在V方向的分量;bv⊥为基线在P方向的分量。ldb表达式如下
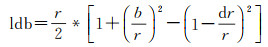 (8)
(8)
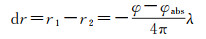 (9)
(9)
式中,φ为解缠相位;φabs为绝对相位偏置,可通过立体干涉测量方法获得,也可使用地面控制点进行粗略估计[37]。
解算得到雷达视线方向的向量之后,即可获取地面点的三维坐标,从而解算地面点的高程。从上述解算过程中发现,相高转换过程中需要首先获取的是地面点三维坐标,随后才获取的地面点高程。对于地形测绘来说,可跳过相高转换的过程,直接将相位信息一步转换为非规则格网的DSM。
相比于光学立体摄影测量的影像匹配技术,干涉测量模型的优点在于,每个高相干像素点均可得到有效的高程信息,数据的有效性极高。同时,模型的计算过程简单,可实现性较强,从而确保了其业务化运行的稳定性和可靠性。干涉测量的前提,是卫星具备较好的无控定位能力,从而确保解算过程中无须考虑平面定位参数带来的相关误差,因此一般也在干涉处理之前,要求卫星能够达到的无控定位能力满足对应的比例尺要求。然而,在实际数据处理过程中,为了完成像素坐标到地面点坐标的精确转换,得到DEM,一般需要进行影像的配准、去平、滤波、相位解缠、地理编码、升降轨融合、区域网平差、人工编辑等过程,这些过程的参数配置、误差传播与误差吸收,均会影响最终的DEM产品质量[38]。然而各类处理过程的误差已经不是SAR影像能否干涉、干涉精度高低的决定性因素。本文不再进行数据处理相关的探讨。
3.2 高程误差及检校方法InSAR业务化测绘过程中,主要的误差来源于基线误差以及相位误差,这也是多数SAR卫星无法实现业务化应用的关键。下面将按照主次程度逐一剖析高程误差的来源以及检校技术的发展现状。
空间相干性是能否形成干涉的关键因素。干涉的前提条件,是主从影像的频率有一定的重叠率,重叠率越高,相干性越大。空间内垂直基线的存在,使得主从影像之间的频率差异增加,这种差异一旦超过了距离向带宽,就会带来彻底的失相干,此时的基线即被称为极限基线,表达为
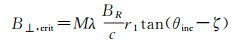 (10)
(10)
式中,M为干涉模式,单发双收模式下为2,单发单收模式下为1;θinc为本地入射角;ζ为本地坡度角;BR为距离向带宽,它是距离向分辨率μr的函数,即
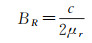 (11)
(11)
这同样也意味着距离向分辨率越低,极限基线越短,同样条件下,失相干的概率越大。这也是很多低分辨率影像,例如ScanSAR模式下的数据难以形成干涉的主要原因之一。提高空间相干性,需要卫星针对重复轨道管道半径进行设计和控制,确保严格回归过程中,卫星对预期位置的偏移控制在一定范围之内。
时间相干性是卫星进行业务化测绘的第2项重要考虑内容。时间相干性并不能完全表达为时间基线的函数,它描述了在严格回归过程中地面的随机波动情况。当地面的随机波动超过半个波长,就会带来完全的失相干。不同地物对时间基线的敏感性差异极大,流动水体在超过1 s的时间间隔时,随机波动就足以造成完全的时间失相干,而PS点则会在数年内保持稳定。为了确保业务化运作,需要保证各类地物的时间相干性差异一致,这就要在增加波长的同时,降低回归周期。因此在仅考虑相干性高低的条件下,可采用长波段进行单发双收的干涉模式设计,将时间基线降低为0。实际的业务化运作过程中,常采用L、C、X波段,并保持一定的空间基线长度,以平衡测量敏感性与相干性之间的关系。
总体相干性除了包含上述两项之外,还包括信噪比相干性、体散射相干性、模糊相干性、量化相干性、多普勒相干性、处理相干性等。这6类相干性多与载荷、地物和应用系统相关,从Seasat可进行干涉这一点可以推断,载荷已经不成为影响干涉成功与否的核心因素,对于高分三号来说,信噪比相干性高达0.98,这也说明其载荷设计指标处于较为优秀的水平。地物带来的体散射相干性损失,与地面成像和处理带来的损失,在合理的参数配置前提下,可控制在0.8以上。相干性损失会使得干涉相位误差σφ增大,带来的精度损失是随机的,即
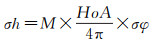 (12)
(12)
从式(12)可看出,相干性降低带来的是相对高程精度的损失,而这种损失是无法通过后期的检校进行修正的。
相位误差除上述误差项之外,还包括φabs的精确求解问题。这一问题在全球无控测量过程中极为重要,它一方面为评价卫星的直接测量精度提供了解决方案,另一方面也为误差的深入剖析和消除提供了必要手段。严格来说,绝对相位偏置为非整数,包含了相位解缠过程中参考点的整周未知数,以及参考点的相位误差,前者可通过立体干涉测量的方式获得,此处不再赘述。而后者无法在检校过程中消除,需通过后处理予以消除[38]。
在影像可较好的干涉的前提下,测绘精度除受到前述平面误差和相位误差的影响之外,最大的误差源就是基线的测量误差。对于重轨干涉来说,基线的直接估计精度取决于定轨精度,在轨道误差服从独立同分布的前提下,基线误差是轨道误差的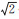
高程模型的检校过程中,主要处理两类参数,即绝对相位及基线相关参数。每景影像的绝对相位均不相同,需要采用立体干涉[36]或双频干涉[5]算法进行求解。因此严格来说,检校目标仅有基线参数一类。SRTM的基线参数包括基线长度和基线倾角,然而在11 d的数据采集任务中,SRTM的有效基线一直变化,业务化运作过程中,无法进行基线参数的准确检校。此外,基线倾角误差与绝对相位误差的耦合性较高,无法完成精确检校,这也导致后续的处理过程中必须引入大洲级的区域网平差完成误差的进一步消除。TanDEM-X的检校对象是垂直基线和平行基线,检校过程中采用了距离较远的两个检校场,为了准确区分两类参数,需要使用近端波位和远端波位陆续成像,分析距离向高程误差梯度,完成平行基线误差估计,随后估计垂直基线误差。图 2是以TanDEM-X为代表的双星绕飞业务化地形测绘过程中的干涉测量检校方法[38]。

|
| 图 2 以TanDEM-X为代表的双星绕飞业务化地形测绘高程测量参数误差检校方法 Fig. 2 The height parameter calibration method used for bi-static satellite formation such as TanDEM-X |
3.3 业务化高程测量能力
虽然卫星的平面定位能力是普遍存在的,在业务化运行过程中,完成平面误差的检校之后,任何SAR影像的定位水平都会得到极大提升,然而SAR卫星高程测量的业务化却有比较大的硬件障碍。SAR卫星业务化高程测量过程中,除了确保平面定位精度之外,还需要克服时间去相干问题、基线保持及测量问题。因此,在时间去相干不严重、干涉对的基线足够短的情况下,在处理过程中引入基线精估计,也是可以完成高程测量的,例如经过处理的Seasat数据可获取50 m格网,5 m高程精度的DSM数据[42]。ERS首先进行了业务化干涉的尝试,采用了双星串飞的TanDEM模式,克服时间失相干的影响,进行地表的高程测量,其高程精度多分布在15~25 m,但在有较大地形起伏的情况下,精度会弱化至25~50 m[43]。Radarsat-1在设计过程中完全未考虑干涉应用,也并未采取任何精密定轨措施,其定轨精度只能达到10 m量级,回归管道半径也高达5 km,InSAR应用较为困难[44-45]。Radarsat-2卫星加装了精密定轨设备,定轨精度可控制在10 m以内,但较低的定轨精度为干涉和定量化应用带来了一定的困难。其回归管道半径依然为5000 m,干涉应用并不理想。然而,即使在这种情况下,经过地面点的修正,使用Radarsat-2的雷达立体模式获取的地表高程精度依然可达到3.3 m[46]。InSAR的业务化地形测绘应用在SRTM中达到了第1个巅峰,SRTM为全球-56°S~60°N范围内的陆地提供了30 m分辨率的10 m高程精度的数字表面模型(digital surface model, DSM)数据[26],其分辨率和高程精度接近但不能完全符合我国1∶50 000比例尺DEM指标要求,可满足我国1∶100 000比例尺DEM指标要求。Envisat-ASAR的主要任务是进行对地观测,由于未针对回归轨道半径进行约束,加之回归周期较长,因此其干涉能力一般,但是依然可以使用多角度数据获取6 m高程精度的结果[47]。值得说明的是,Envisat-ASAR与ERS在同一轨道,其时间间隔仅有28 min,两者虽然频率相差31 MHz,但是在平地区域可通过2 km的垂直基线完成频率补偿,从而形成交叉干涉,可有效减少时间失相干的影响,其最高干涉精度可达到4.8 m[48]。ALOS-1搭载了3个传感器,其中全色立体测图遥感设备(panchromatic remote-sensing instrument for stereo mapping, PRISM)是光学传感器,它获取了全球6.6 m精度的DSM数据,PALSAR并非全球业务化DSM产品生产的载荷,然而部分条件下的精度可达到4.6 m[49]。ALOS-2虽然将回归轨道半径缩短为500 m,时间基线缩短为14天,但InSAR地形测绘能力并不突出,与现有非测绘SAR卫星相同,其误差波动范围极大,较差情况下误差可达数千米[50],但是在HoA同时满足敏感度和相位解缠精度要求的前提下,进行基线以及绝对相位等参数修正后,也能达到27 m左右的精度[51]。TanDEM-X是继SRTM之后的第2个InSAR全球测图项目,其产品的高程精度已经远超过HRTI-3要求的10 m,达到了3.49 m,如果不考虑茂密植被区以及冰雪覆盖区,那么其精度将达到0.88 m[52],其格网尺寸及高程精度接近但不满足我国1∶25 000比例尺指标要求,可满足我国1∶50 000比例尺指标要求。此外,如果使用雷达立体的方式进行三维坐标量测,那么TerraSAR-X在PS点的三维定位精度将高达4 cm,高程测量精度为2~4 cm。COSMO-SkyMed使用了4颗卫星构成星座,这将单星的严格回归时间压缩至4 d,使得时间失相干有所降低,使用InSAR技术获得的DSM高程精度可达3.9 m[53],其立体测量精度也可达7.3 m[54]。Sentinel-1严格控制了回归轨道,其回归管道半径为50 m,再加上较短的时间基线,卫星可实现高精度的干涉,确保相位测量精度。然而卫星的重轨干涉特性决定了基线精度仅能达到定轨精度的2倍,无法用于业务化干涉。但是使用外部高程数据进行校正之后,高程精度依然可达到1.26 m[55]。我国第1颗民用C波段全极化SAR卫星高分三号是一颗海洋星,并未针对干涉任务进行特殊设计,这导致了卫星的回归轨道管道半径漂移极大,空间相干性难以保障,其回归周期29 d,时间相干性也较差,但是在这种情况下,经过精确的地面修正,依然可获取极高精度的DEM,最优情况下,高程精度甚至能达到0.57 m[56]。天绘二号的测试结果表明,在其有效基线为550 m左右,覆盖范围为南北纬60°之间时,高程精度满足1∶50 000比例尺要求[5]。
在此需要进行特别说明的是,表 4中提供的高程精度,是在相干性足够好,以及地面修正精度足够高的情况下才可达到。例如笔者获取的高分三号DSM,其对应的相干性高达0.96,这在数百对干涉对中极为少见。使用这种科研特例进行业务化应用将存在较大的风险。业务化应用过程中,需使用单发双收的模式,例如双星或多星绕飞干涉,双天线干涉等,消除时间失相干,控制空间失相干,并确保干涉参数的精度。
| 卫星 | 单星回归周期/天 | 业务化模式极限基线/m | 定轨精度/m | 可查到的高程精度/m | 满足的基本比例尺 | 主要业务化高程测量限制 |
| Seasat | 17 | 1700 | 1.4 | 5.0 | — | 时空失相干 |
| ERS | 35 | 9222 | 0.15 | 15.0 | — | 空间失相干干涉参数精度 |
| Radarsat-1 | 24 | 609 | 10 | 12.0 | — | 时空失相干 |
| SRTM | — | — | 1 | 10.0 | 1∶100 000 | 可业务化 |
| Envisat | 35 | 307 | 0.1 | 6.0 | — | 时空失相干 |
| ALOS-PALSAR | 46 | 8470 | 0.15 | 4.6 | — | 时空失相干 |
| TanDEM-X | 11 | 3633 | 0.02 | 0.9 | 1∶50 000 | 可业务化 |
| Radarsat-2 | 24 | 618 | 10 | 3.3 | — | 时空失相干 |
| COSMO-SkyMed | 16 | 2066 | 0.2 | 3.9 | — | 时空失相干 |
| Sentinel-1 | 12 | 1376 | 0.03 | 1.3 | — | 干涉参数精度 |
| ALOS-PALSAR2 | 14 | 7687 | 0.05 | 27 | — | 时间失相干干涉参数精度 |
| 高分三号 | 29 | 1613 | 0.05 | 0.6 | — | 时空失相干 |
| 天绘二号 | 19 | 550 | 0.03 | — | 1∶50 000 | 可业务化 |
4 结论与展望
本文对现阶段常用的SAR卫星的业务化测绘能力进行了综述分析。国际常用的SAR卫星中,以TerraSAR-X、COSMO-SkyMed及天绘二号为代表的高分辨率成像卫星,其几何定位能力已经可以满足我国1∶50 000比例尺DOM产品的业务化生产需求。以TerraSAR-X为代表的高精度地形测绘卫星,已经可以业务化生产平面精度为2~3 cm精度的控制点库数据,这为我国的平面定位能力的提升指明了方向。在高程测量中,可业务化运行的航空航天任务包括SRTM、TanDEM-X与天绘二号,其中SRTM标准产品可满足我国1∶100 000比例尺DEM精度及格网尺寸要求,TanDEM-X标准产品、天绘二号产品可满足我国1∶50 000比例尺DEM精度及格网尺寸要求。
除上述精度指标之外,本文还对定位和测高过程中的误差进行了分析,并给出了平面和高程相关参数的检校方法,从参数设计和指标提升来看,卫星的业务化地形测绘任务,是卫星-地面-应用的一体化设计结果。例如,在百米级的地面定位过程中,卫星上的很多误差无须考虑,应用系统也不需要进行过多的复杂设计。而在米级定位的过程中,要求卫星的直接无控定位精度需要从百米级提高到十米级,地面也需要开展定期的检校实验,修正卫星设备的系统性误差。在厘米级乃至毫米级定位过程中,连SAR卫星中央电子设备的传输路径误差都需要考虑在内。卫星采样时钟的频率也是不可忽略的误差源之一,在采样时间间隔中,卫星的方位向运动距离是不可精确测量的,卫星在700 km高度飞行时,10 μs的采样时钟误差将带来7 cm的方位向误差,这种星上参数地面无法进行修改或补偿。甚至地球表面与卫星飞行高度之间的重力势能带来的亚毫米级乃至微米级的定位误差都需要谨慎考虑。卫星的信号发射和接收过程中,成像像素数与实际脉冲发射和接收之间的脉冲数目之间也会有一定的差异,在TerraSAR-X中,这种差异在10-6量级,如果使用多景影像进行立体测量,确保多角度观测的情况下斜距误差小于1 cm,那么影像之间的采样频率差异必须小于4.8 Hz。同时,地面应用系统需要完成高精度保相成像、运动补偿、地球动力学误差补偿等,才可以完成高达厘米级的定位。至于极高精度的地形测绘任务,地面应用系统需要承担的任务则更加重要,包括业务化的数据处理、初始DSM数据到最终DSM数据的区域网平差,用于消除检校过程中无法吸收的各类残差,并完成DSM到DEM的编辑过程。
SAR卫星在国际上的诸多应用,使得我国的SAR卫星后起直追,快速发展。现阶段除了环境-1C以及高分三号之外,我国还将在2021年前后发射多颗民用SAR卫星。其中L波段差分干涉SAR卫星将作为我国第一颗民用的业务化干涉应用SAR卫星,完成地表的形变监测和高程测量任务。随着我国天地一体化卫星设计能力的提升,我国SAR卫星将逐渐从对地的定性观测向定量观测转变,从单一的振幅信息收集深入到干涉数据解算,充分发挥SAR影像相位观测的优势,使用不同波长的测绘“量尺”完成地表的分米级高程测量、厘米级定位测量、毫米级形变测量,使得我国的SAR卫星能够像光学卫星一样,在国际星载地形测绘中占据一席之地。
| [1] |
WINOKUR R S. Operational use of civil space-based synthetic aperture radar(SAR) [R]. Pasadena, California: JPL Publication, 1996.
|
| [2] |
TANG Xinming, LI Tao, GAO Xiaoming Gao, et al. Research on key technologies of precise InSAR surveying and mapping applications using automatic SAR imaging[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 27-37. |
| [3] |
黄国满. 机载多波段多极化干涉SAR测图系统——CASMSAR[J]. 测绘科学, 2014, 39(8): 111-115. HUANG Guoman. An airborne interferometric SAR mapping system with multi-band and multi-polarization: CASMSAR[J]. Science of Surveying and Mapping, 2014, 39(8): 111-115. |
| [4] |
刘哲延, 姚秀光, 刘东烈. 机载毫米波InSAR系统在贵州山区1∶5000专题测绘产品生产中的应用[C]. 第七届高分辨率对地观测学术年会. 长沙: 高分辨率对地观测学术联盟, 2020. LIU Zheyan, YAO Xiuguang, LIU Donglie. The application of airborne millimeter-wave InSAR system for producing thematic surveying and mapping achievements in scale of 1∶5000 in mountainous area of Guizhou[C]. The 7th China High Resolution Earth Observation Conference. Changsha, China: Academic Consortium for High Resolution Earth Observation, 2020. |
| [5] |
楼良盛, 刘志铭, 张昊, 等. 天绘二号卫星工程设计与实现[J]. 测绘学报, 2020, 49(10): 1252-1264. LOU Liangsheng, LIU Zhiming, ZHANG Hao, et al. TH-2 satellite engineering design and implementation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10): 1252-1264. DOI:10.11947/j.AGCS.2020.20200175 |
| [6] |
国家测绘局. 中华人民共和国测绘行业标准: 基础地理信息数字成果1∶5000 1∶10 000 1∶25 000 1∶50 000 1∶100 000数字高程模型CH/T 9009.2—2010[S]. 北京: 测绘出版社, 2010. National Bureau of Surveying and Mapping. Surveying and Mapping Industry Standard for the People's Republic of China: Digital Products of Fundamental Geographic Informa-tion 1∶5000 1∶10 000 1∶25 000 1∶50 000 1∶100 000 Digital Elevation Models CH/T 9009.2—2010[S]. Beijing: Surveying and Mapping Publishing House, 2010. |
| [7] |
国家测绘局. 中华人民共和国测绘行业标准: 基础地理信息数字成果1∶5000 1∶10 000 1∶25 000 1∶50 000 1∶100 000数字正射影像图CH/T 9009.3—2010[S]. 北京: 测绘出版社, 2010. National Bureau of Surveying and Mapping. Surveying and Mapping Industry Standard for the People's Republic of China: Digital Products of Fundamental Geographic Information 1∶5000 1∶10 000 1∶25 000 1∶50 000 1∶100 000 Digital Orthophoto Maps CH/T 9009.3—2010[S]. Beijing: Surveying and Mapping Publishing House, 2010. |
| [8] |
Department of Defense. Performance specification digital terrain elevation data (DTED) MIL-PRF-89020B[S]. Reston, VA: National Imagery and Mapping Agency, 2000.
|
| [9] |
KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X: a satellite formation for high-resolution SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3317-3341. DOI:10.1109/TGRS.2007.900693 |
| [10] |
GAO Xiaoming, LIU Yaolin, LI Tao, et al. High precision DEM generation algorithm based on InSAR multi-look iteration[J]. Remote Sensing, 2017, 9(7): 741. DOI:10.3390/rs9070741 |
| [11] |
李志林, 朱庆, 谢潇. 数字高程模型[M]. 北京: 科学出版社, 2017. Li Zhilin, Zhu Qing, Xie Xiao. Digital Elevation Model[M]. Beijing: Science Press, 2017. |
| [12] |
中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会. 中华人民共和国推荐性国家标准: 数字测绘成果质量检查与验收GB/T 18316—2008[S]. 北京: 中国标准出版社, 2008. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of China. Recommends national standard of the People's Republic of China: Specifications for Inspection and Acceptance of Quality of Digital Surveying and Mapping Achievements GB/T 18316—2008[S]. Beijing: China Standards Press, 2008. |
| [13] |
RIZZOLI P, BRÄUTIGAM B, KRAUS T, et al. Relative height error analysis of TanDEM-X elevation data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 30-38. DOI:10.1016/j.isprsjprs.2012.06.004 |
| [14] |
KONECNY G, SCHUHR W. Reliability of radar image data[C]//ISPRS 88 Kyoto-Congress. Kyoto, Japan: ISPRS, 1988.
|
| [15] |
费文波, 张过, 唐新明, 等. 基于有理多项式模型的星载InSAR影像制作数字高程模型的研究[J]. 测绘学报, 2014, 43(1): 83-88. FEI Wenbo, ZHANG Guo, TANG Xinming, et al. Research of DEM generation by spaceborne InSAR images based RFM model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 83-88. |
| [16] |
FRANZ W, LEBER L. Radargrammetric image processing[M]. Boston, London: Artech House, 1989.
|
| [17] |
GISINGER C, BALSS U, PAIL R, et al. Precise three-dimensional stereo localization of corner reflectors and persistent scatterers with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 1782-1802. DOI:10.1109/TGRS.2014.2348859 |
| [18] |
EINEDER M, GISINGER C, BALSS U, et al. SAR imaging geodesy-recent results for TerraSAR-X and for Sentinel-1[C]//ESA Fringe Workshop. Helsinki, Finland: ESA, 2017.
|
| [19] |
HONG S, CHOI Y, PARK I, et al. Comparison of orbit-based and time-offset-based geometric correction models for SAR satellite imagery based on error simulation[J]. Sensors, 2017, 17(12): 170. DOI:10.3390/s17010170 |
| [20] |
MONTAZERI S, GISINGER C, EINEDER M, et al. Automatic detection and positioning of ground control points using TerraSAR-X multiaspect acquisitions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(5): 2613-2632. DOI:10.1109/TGRS.2017.2769078 |
| [21] |
丁刘建, 陶秋香, 李涛, 等. 高分三号SAR影像广域范围联合几何检校技术[J]. 测绘学报, 2020, 49(5): 598-610. DING Liujian, TAO Qiuxiang, LI Tao, et al. A joint geometric calibration technique for GF-3 SAR image in wide area[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(5): 598-610. |
| [22] |
EINEDER M, MINET C, STEIGENBERGER P, et al. Imaging geodesy: toward centimeter-level ranging accuracy with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 661-671. DOI:10.1109/TGRS.2010.2060264 |
| [23] |
TOUTIN T, CARBONNEAU Y. MOS and Seasat image geometric corrections[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(3): 603-609. DOI:10.1109/36.142938 |
| [24] |
EVANS D L, ALPERS W, CAZENAVE A, et al. Seasat: a 25-year legacy of success[J]. Remote Sensing of Environment, 2005, 94(3): 384-404. DOI:10.1016/j.rse.2004.09.011 |
| [25] |
COTE S, SRIVASTAVA S, MUIR S, et al. Radarsat-1 and -2 government calibration activities[C]//2009 IEEE International Geoscience and Remote Sensing Symposium. Cape Town, South Africa: IEEE, 2009.
|
| [26] |
FARR T G, ROSEN P A, CARO E, et al. The shuttle radar topography mission[J]. Reviews of Geophysics, 2007, 45(2): 361-393. |
| [27] |
LIU Yongxue, HU Chuanmin, DONG Yanzhu, et al. Geometric accuracy of remote sensing images over oceans: the use of global offshore platforms[J]. Remote Sensing of Environment, 2019, 222: 244-266. DOI:10.1016/j.rse.2019.01.002 |
| [28] |
WILLIAMS D, WANG Yiman, FITZGERALD G, et al. Radarsat-2: image quality and calibration update[C]//European Conference on Synthetic Aperture Radar. Hamburg, Germany: VDE, 2016.
|
| [29] |
TOUTIN T, CHENIER R. 3-D radargrammetric modeling of Radarsat-2 ultrafine mode: preliminary results of the geometric calibration[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 611-615. DOI:10.1109/LGRS.2009.2024391 |
| [30] |
JOHNSEN H, LAUKNES L, GUNERIUSSEN T. Geocoding of fast-delivery ERS-l SAR image mode product using DEM data[J]. International Journal of Remote Sensing, 1995, 16(11): 1957-1968. DOI:10.1080/01431169508954532 |
| [31] |
MOHR J J, MADSEN S N. Geometric calibration of ERS satellite SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(4): 842-850. DOI:10.1109/36.917909 |
| [32] |
SHIMADA M, ISOGUCHI O, TADONO T, et al. PALSAR CalVal summary(Jaxa-PI193)[C]//IGARSS2008. Boston, USA: IGARSS, 2007.
|
| [33] |
COVELLO F, BATTAZZA F, COLETTA A, et al. COSMO-SkyMed an existing opportunity for observing the earth[J]. Journal of Geodynamics, 2010, 49(3-4): 171-180. DOI:10.1016/j.jog.2010.01.001 |
| [34] |
SCHMIDT K, REIMANN J, RAMON N T, et al. Geometric accuracy of sentinel-1A and 1B derived from SAR raw data with GPS surveyed corner reflector positions[J]. Remote Sensing, 2018, 10(4): 523. DOI:10.3390/rs10040523 |
| [35] |
ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Complex least squares adjustment to improve tree height inversion problem in PolInSAR[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 1-8. |
| [36] |
BAMLER R. Interferometric stereo radargrammetry: absolute height determination from ERS-Envisat interferograms[C]//Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium. Honolulu, HI, USA: IEEE, 2000.
|
| [37] |
范军, 李涛, 左小清, 等. 利用参数独立分解的星载SAR干涉测量检校方法[J]. 测绘学报, 2019, 48(6): 737-746. FAN Jun, LI Tao, ZUO Xiaoqing, et al. Interferometric calibration method for spaceborne SAR based on independent parameter decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(6): 737-746. |
| [38] |
唐新明, 李涛, 高小明, 等. 雷达卫星自动成图的精密干涉测量关键技术[J]. 测绘学报, 2018, 47(6): 730-740. TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping application using automatic SAR imaging[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(6): 730-740. |
| [39] |
MONTENBRUCK O, WERMUTH M, KAHLE R. GPS based relative navigation for the TanDEM-X mission: first flight results[J]. Navigation, 2011, 58(4): 293-304. DOI:10.1002/j.2161-4296.2011.tb02587.x |
| [40] |
GONZÁLEZ J H, WALTER ANTONY J M, BACHMANN M, et al. Bistatic system and baseline calibration in TanDEM-X to ensure the global digital elevation model quality[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 3-11. DOI:10.1016/j.isprsjprs.2012.05.008 |
| [41] |
梁斌, 朱海龙, 张涛, 等. 星敏感器技术研究现状及发展趋势[J]. 中国光学, 2016, 9(1): 16-29. LIANG Bin, ZHU Hailong, ZHANG Tao, et al. Research status and development tendency of star tracker technique[J]. Chinese Optics, 2016, 9(1): 16-29. |
| [42] |
GOLDSTEIN R M, ZEBKER H A, WERNER C L. Satellite radar interferometry: two-dimensional phase unwrapping[J]. Radio Science, 1988, 23(4): 713-720. DOI:10.1029/RS023i004p00713 |
| [43] |
SCHTTLER B, EINEDER M, KNPFLE W, et al. Operational interferometric ERS TanDEM data processing[C]. Proceedings of the CEOS SAR Workshop. Toulouse, France: DLR, 1999.
|
| [44] |
BÄHR H. Orbital effects in spaceborne synthetic aperture radar interferometry[M]. [S. l. ]Scientific Publishing. 2013.
|
| [45] |
SEYMOUR M, CUMMING I. Updating DEMs using Radarsat-1 data[J]. Canadian Journal of Remote Sensing, 2004, 30(6): 927-942. DOI:10.5589/m04-046 |
| [46] |
TOUTIN T, OMARI K. DTM generation with Radarsat-2 data without GCP[C]. International Archives of Photogrammetry and Remote Sensing. Hannover, Germany: ISPRS, 2011.
|
| [47] |
李新武, 郭华东, 李震. Envisat/ASAR多角度干涉雷达数据山区DEM生成及精度分析[J]. 遥感学报, 2009, 13(2): 276-281. LI Xinwu, GUO Huadong, LI Zhen. DEM generation and accuracy analysis on rugged terrain using Envisat/ASAR multi-angle InSAR data[J]. Journal of Remote Sensing, 2009, 13(2): 276-281. |
| [48] |
WEGMVLLER U, SANTORO M, WERNER C, et al. DEM generation using ERS-Envisat interferometry[J]. Journal of Applied Geophysics, 2009, 69(1): 51-58. DOI:10.1016/j.jappgeo.2009.04.002 |
| [49] |
SHAWKY M, MOUSSA A, HASSAN Q K, et al. Pixel-based geometric assessment of channel networks/orders derived from global spaceborne digital elevation models[J]. Remote Sensing, 2019, 11(3): 235. |
| [50] |
ROSA R A S, OLIVEIRA C G, RODRIGUES T G, et al. Repeat pass interferometry using ALOS-2 PALSAR-2 data (study case in Brazil)[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2020, 107-113. |
| [51] |
姜德才. 重轨卫星InSAR技术在多云雨山区DEM生成及更新中的应用研究[D]. 北京: 中国测绘科学研究院, 2017. JIANG Decai. Repeat-pass spaceborne SAR interferometry for DEM generation in cloudy-rainy mountainous area[D]. Beijing: Chinese Academy of Surveying and Mapping, 2017. |
| [52] |
RIZZOLI P, MARTONE M, GONZALEZ C, et al. Generation and performance assessment of the global TanDEM-X digital elevation model[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 132: 119-139. |
| [53] |
LOMBARDI N, LORUSSO R, FASANO L, et al. Interferometric COSMO-SkyMed spotlight DEM generation[C]//2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Beijing, China: IEEE, 2016.
|
| [54] |
AGRAWAL R, DAS A, RAJAWAT A S. Accuracy assessment of digital elevation model generated by SAR stereoscopic technique using COSMO-SkyMed data[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(10): 1739-1747. |
| [55] |
GHANNADI M A, ENAYATI H, KHESALI E. Interferometric Sentinel-1 DEM generation: a case study in Tehran, Iran[C]. ISPRS Internatinal Joint Conference. Tehran, Iran: ISPRS, 2017.
|
| [56] |
LI Tao, TANG Xinming, CHEN Qianfu, et al. Research on the interferograms selection principles using Gaofen-3 for DSM production[C]//2019 Asia-Pacific Conference on Synthetic Aperture Radar. Xiamen, China: [s. n. ], 2019.
|



