干涉合成孔径雷达(interferometric synthetic aperture radar, InSAR)技术具有高空间分辨率,高精度等优点,已被广泛地应用于地形测量[1-3]和地表形变监测领域[4-9]。然而,传统差分InSAR(differential InSAR, DInSAR)技术仅可以获得真实地表形变沿视线向(line of sight, LOS)的一维形变投影,在地质灾害解译过程中具有极大的局限性[10-11]。为了克服这一缺点,文献[12-14]分别提出了像素偏移量跟踪(pixel offset-tracking, POT)、多孔径雷达(multi-aperture InSAR,MAI)技术和哨兵数据方位向子带重叠区域干涉(burst overlap InSAR,BOI)技术来获取地表真实形变沿雷达卫星方位向(azimuth, AZI)的投影形变。结合升降轨DInSAR和MAI/POT技术,利用加权最小二乘(weighted least square, WLS)即可解算地震、火山、冰川、滑坡等导致的真实三维地表形变场[5, 15-24]。此外,全球导航卫星系统(global navigation satellite system,GNSS)观测数据与InSAR数据在空间分辨率和测量精度方面优势互补,二者融合也可实现高精度、高空间分辨率三维地表形变场的获取[25-29]。
然而,上述研究均基于单个点进行三维形变解算,并未考虑临近点三维形变之间的力学关系。文献[30]基于弹性理论提出了一种SISTEM(simultaneous and integrated strain tensor estima-tion from geodetic and satellite deformation measure- ments)方法,首次将应力应变模型(strain model, SM)引入InSAR与GNSS数据相结合的地表三维形变求解当中。但是,现实情况往往很难获取大范围的GNSS观测,文献[31]对SISTEM方法进行了扩展,仅需InSAR观测值即可进行高精度三维形变解算。为了方便起见,本文将DInSAR、MAI、POT和BOI等技术获取的形变观测数据统称为InSAR观测值。然而,在解算真实三维地表形变时,必须要融合不同方向的多源异质观测数据,因此精确确定不同数据之间的权重比例具有重要意义[6, 32]。为了实现此目的,科研人员研究利用一个固定的滑动窗口求解窗口内数据的标准差作为先验信息进行定权[17],这种定权方式是基于数据各态历经性的假设,即假设观测数据在某一数值上下一定范围内是随机分布的,但是对于地震等导致的大梯度形变而言,往往难以满足。也有相关学者在假设远场区域不包含形变信号的前提下,将远场一定区域数据的均方根值作为该类观测值整个区域的先验方差[33-34]。这种方法忽略了InSAR观测噪声在空间上的差异性,因此也会影响三维地表形变的求解精度。文献[25]在求解时序数据的平均形变速率时引入了方差分量估计(variance component estimation, VCE)进行定权,验证了VCE在多源InSAR观测数据定权方面的优越性。但是,对于瞬时形变场的求解,由于缺少多余观测,应用VCE进行定权受到了极大限制。
基于此,文献[35]提出了一种基于地表应力应变模型和方差分量估计的InSAR三维地表形变监测方法(SM-VCE)。该方法基于一定窗口范围内不同像素点三维形变之间的力学关系(SM)建立函数模型,显著增加了冗余观测个数,进而可利用VCE实现不同类InSAR观测值之间的精确定权。研究表明,基于窗口的SM-VCE方法比传统单点解算的加权最小二乘方法得到的三维地表形变精度更高[36]。在原始SM-VCE方法中,求解不同目标点的三维形变时,窗口大小是固定不变的,并且窗口内的InSAR观测值被认为是等精度的。对于同震形变场而言,在地震破裂带附近往往难以获得有效的InSAR观测值,使得固定窗口大小的SM-VCE方法难以获取完整的三维同震地表形变。即使在断层附近有InSAR观测值的情况下,窗口内往往会包含断层两侧的异质InSAR观测值,使得原始SM-VCE方法难以得到可靠的近场三维形变。而近场地表形变结果对于约束断层浅部滑动又是十分重要的[23, 37-38]。因此,有必要重建地震破裂带附近三维地表形变场。同时,InSAR观测值极易受到失相干等噪声影响,窗口内同一类观测值中不同像素点的形变测量值精度往往各不相同,因此,忽略窗口内InSAR观测值精度差异的做法将会降低三维地表形变精度。
鉴于此,本文在SM-VCE方法的框架下,提出一种顾及断层破裂带及自适应变化窗口的观测值选取策略,进而基于邻近的InSAR有效观测值即可重建地震破裂带附近的三维地表形变场,同时,引入迭代加权最小二乘(iterative weighted least squares,IWLS)方法[39]实现窗口内同一类InSAR观测值的内部自适应定权。本文首先利用模拟试验验证了本文中窗口优化SM-VCE方法的可靠性和优势,进而基于升降轨哨兵1号卫星数据,获取了2019年7.1级Ridgecrest地震的高精度三维地表形变场。
1 SM-VCE方法文献[35]较为系统地介绍了SM-VCE方法,本文在此基础上,提出了顾及断裂线和自适应变化窗口的观测值选取策略和基于IWLS方法实现窗口内同一类观测值内部的自适应定权方法,旨在基于SM-VCE方法的框架,获取精度更高、更为完整的三维同震地表形变场。
1.1 基于SM建立观测方程当发生火山喷发,地震等板块活动时,地表可认为是均匀应变场[30, 40]。假设地表存在邻近两点P0和Pk,对应的三维坐标和三维形变分别为x0=[xe0 xn0 xu0]T,d0=[de0 dn0 du0]T,xk=[xek xnk xuk]T,dk=[dek dnk duk]T,那么根据SM可得
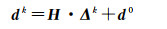 (1)
(1)
式中,Δk=xk-x0=[Δxek Δxnk Δxuk]T;H代表形变梯度矩阵,可表示为
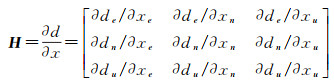 (2)
(2)
文献[30]将矩阵H表示为一个对称矩阵和一个非对称矩阵之和
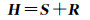 (3)
(3)
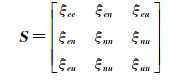 (4)
(4)
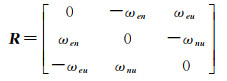 (5)
(5)
式中,ξ和ω代表地表应力应变模型中的应变参数和旋转参数。在原始SM-VCE方法中,H用式(3)表示,进而可将式(1)写成
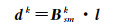 (6)
(6)
式中,l=[de(0) dn(0) du(0) ξee ξen ξeu ξnn ξnu ξuu ω en ωeu ωnu]T代表点P0处的未知参数向量;Bsmk代表地表应力应变模型系数矩阵
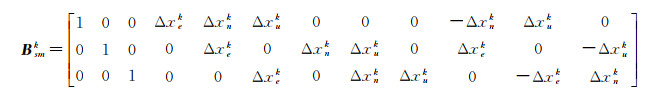 (7)
(7)
进一步,假设研究区域共有J类InSAR观测,在Pk处的第j(j=1, 2, …, J)类观测所对应的观测数据为Ljk,所对应的卫星方位角和入射角分别为αjk和θjk,则根据SAR卫星成像几何可得
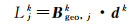 (8)
(8)
式中
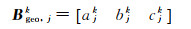 (9)
(9)
当Ljk为InSAR视线向形变观测值时
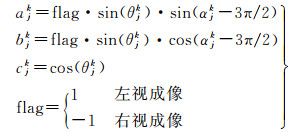
当Ljk为InSAR方位向形变观测值时
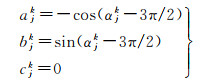
综合式(6)、式(8),可得
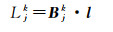 (10)
(10)
式中
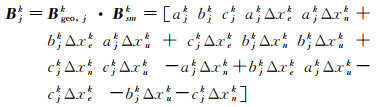
若假设点P0周围有Kj个第j类InSAR观测值,则最终可得
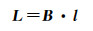 (11)
(11)
式中
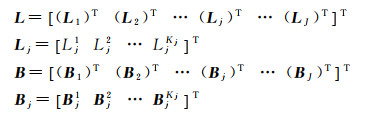
此时,建立了综合考虑InSAR观测值与三维形变之间的几何关系,以及地表邻近点三维形变之间的力学关系的InSAR三维形变估计函数模型。
1.2 利用VCE实现不同类观测值之间的精确定权令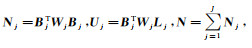
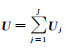
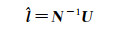 (12)
(12)
式中,Wj代表第j类InSAR观测的初始权矩阵,一般取值为单位矩阵。进而根据方差分量估计算法[41]可得各类InSAR观测值的单位权中误差向量为
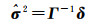 (13)
(13)
式中,
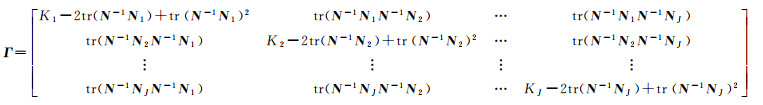
为J×J大小的矩阵,第j个对角线元素为Kj-2tr(N-1Nj)+tr(N-1Nj)2,第j1行、第j2列的非对角线元素为tr(N-1Nj1N-1Nj2),1≤j1≤J, 1≤j2≤J且j1≠j2。式中,tr(■)代表求迹函数。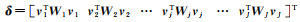
根据方差分量估计算法可知,当各类观测值单位权中误差近似相等时,即
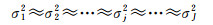 (14)
(14)
此时的观测值权重矩阵为最优权阵。由于初始权重矩阵Wj未考虑不同类别InSAR观测数据之间的精度差异,因此,式(13)得到的 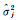
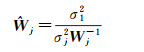 (15)
(15)
利用更新后观测值权重矩阵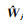
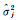
当上述迭代过程结束时,可根据各个单位权中误差及其相应权阵计算各类观测值对应的方差矩阵为
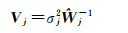 (16)
(16)
同时,通过式(12)即可得到三维地表形变的最优估值。
在观测值方差已知的前提下,根据误差传播定律可以计算得到三维形变的方差。在使用误差传播定律时,应尽可能地保证观测值之间相互独立。因此,在计算三维地表形变的方差时,本文将观测方程式(11)简化为
 (17)
(17)
即仅考虑了观测值与三维地表形变之间的几何关系。此时,三维地表形变的方差矩阵为
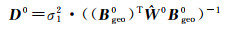 (18)
(18)
式中,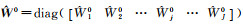
针对不同像元重复利用本章介绍的算法,直至所有像素点的三维形变解算完成。
1.3 顾及断裂线和自适应变化窗口的观测值选取策略在利用SM-VCE方法进行三维地表形变求解时,其中的关键一步是选取一定大小窗口范围内的像素点建立观测方程。原始SM-VCE方法选取固定大小窗口(如15×15像素)内的所有点来建立观测方程[35]。这种选取方法在地表形变未发生跳变或者原始形变观测值相干性较高时可以得到较高精度的三维形变[36]。然而,地震导致的地表形变在震中区域往往会发生跳变,且精度较高相位观测值(如DInSAR获取的形变观测值)会发生失相干现象。鉴于此,本文提出顾及断裂线和自适应变化窗口的观测值选取策略,旨在获取可靠的近场三维地表形变结果。
根据光学影像或者POT获取的形变数据人工勾勒出地震发生后导致的主要断裂线,基于该断裂线即可排除窗口内与中心点不在断层同一侧的像素点。在设置初始窗口大小为S×S像素的情况下,当解算震中某像素点的三维形变时,S×S像素大小的窗口内的失相干像素将会被掩膜,以保证解算结果的精度和可靠性。但是,在这种情况下,精度较高的相位观测值的像素点个数可能少于某一阈值Kthr,进而无法得到可靠的三维形变结果。本文提出的窗口大小自适应变化的观测值选取策略将会在Kj < Kthr时,自动增加窗口大小S×S,直至Kj≥Kthr。值得注意的是,当窗口过大时,窗口内不同点的三维形变将不满足地表应力应变模型,因此窗口大小S应小于某一阈值Sthr。也就是说,当失相干区域过大时,通过本文提及的选点准则将无法完全恢复失相干区域的三维形变结果。
结合已有的地表应力应变模型在火山[35]、地震[31, 40]方面的研究发现,参与SM建模的像素点个数大于200之后,即可得到较为稳健的未知参数平差值。基于此,本文设置窗口大小的初值S=15像素,像素点个数阈值Kthr=200。为了确定Sthr的取值大小,本文基于InSAR观测值进行变异函数拟合[40, 42]
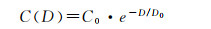 (19)
(19)
式中,C(D)表示距离为D的像素之间的协方差;C0代表区域内的方差;D0即为相关距离。事实上,当两点间距离大于D0时,根据相关距离及像素空间分辨率即可确定不同InSAR观测值对应的阈值Sthr, j。最终的阈值Sthr为
 (20)
(20)
式中,min(■)代表取最小值。本文取一系列Sthr, j的最小值作为最终阈值Sthr的取值,从而保证每一类观测中距离为Sthr的两点对应的观测值都是相关的。在本文中,利用式(19)、式(20)对真实数据进行拟合,计算得到Sthr=63像素。
1.4 基于迭代加权最小二乘的窗口内同一类观测值自适应定权方法在上述SM-VCE方法中,权重矩阵Wj(或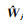
由于点P0和Pk距离较近,则两点处的InSAR成像几何差异可忽略不计。基于式(1)、式(2)和式(8),在式(1)等号左右两侧乘以Bgeok,则可得
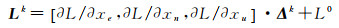 (21)
(21)
为了简单起见,这里省略了下标j。顾及周围的K个点,则可得
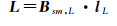 (22)
(22)
式中
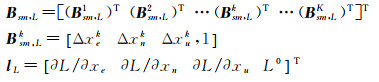
式(22)的建立是为了提供不同空间点上InSAR观测值之间的相互约束关系,进而为IWLS定权提供了可能。在假定W为单位阵的基础上,基于加权最小二乘准则[43-44]即可得到未知参数lL的初始解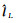
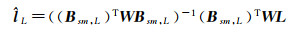 (23)
(23)
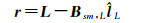 (24)
(24)
进而,可基于观测值残差r得到更新后的权重矩阵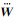
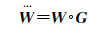 (25)
(25)
式中,∘代表哈达玛运算;G为对角矩阵,其对角线元素可认为是降权因子。G的第k个对角线元素gk可基于以下权函数确定
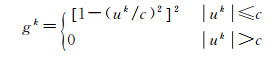 (26)
(26)
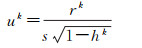 (27)
(27)
式中,uk代表标准化残差;rk代表r中的第k个元素;s为绝对值r的中位值;hk为方阵Bsm, L((Bsm, L)TBsm, L) -1(Bsm, L)T的第k个对角线元素;c是一个校准常数,在95%的置信度下可取值为4.685[39]。利用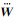
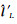
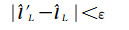 (28)
(28)
式中,ε的取值与观测值精度相关。例如,当L为DInSAR观测值时,ε=1 mm。基于IWLS得到的是窗口内同一类观测值中不同点的相对权重,进而可将此权重矩阵(即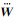
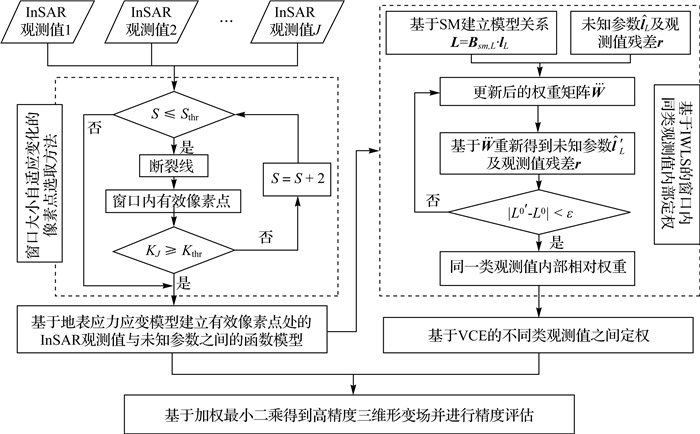
|
| 注:虚线框内是本文的主要方法创新点。 图 1 SM-VCE方法的流程 Fig. 1 The flowchart ofthe SM-VCE method |
2 模拟试验
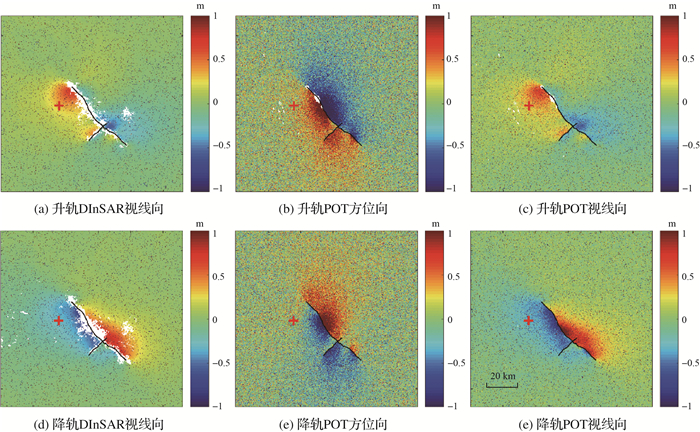
本文利用2019年Ridgecrest地震的已有的断层几何和滑动分布数据[45]正演了三维地表形变场,整个形变场的大小为890×1120像素,像素分辨率约为100 m×100 m。根据真实数据的卫星成像几何参数(表 1)计算得到InSAR视线向与方位向的形变信息。在此基础上,加入不同量级的高斯噪声(升轨DInSAR视线向、升轨POT方位向、升轨POT视线向、降轨DInSAR视线向、降轨POT方位向、降轨POT视线向的高斯噪声均方差分别为5、300、100、5、300和100 mm),同时在不同的观测值上随机挑选了5%的像素点加入了粗差。需要说明的是,模拟试验中粗差的模拟方法为:将整个影像上随机选取一定比例p=5%的像素作为粗差点,粗差点上的数值为整个形变场中最大形变值的±m倍,其中m的取值与预设的M值有关,不同粗差点处m的取值不一定相同,但所有粗差点处m的取值服从[M-5, M+5]区间内的均匀分布,并且不同粗差点处m取值的正负也是随机的。在此次模拟试验中M=5。另外,为了更加符合真实数据中的InSAR噪声源,本文在升降轨InSAR视线向的模拟数据中加入了模拟的大气噪声,其中大气噪声是利用代尔夫特理工大学开发的Matlab工具包中的分形函数fracsurf进行模拟的,分形维度为2.2,大气噪声的范围为[-2.8 cm, 2.8 cm],在C波段哨兵数据的干涉图上约为2个条纹。通过以上步骤即可得到用于模拟实验的InSAR观测数据(图 2)。
| 轨道方向 | 主辅影像获取日期 | 垂直基线/m | 入射角/(°) | 方位角/(°) |
| 升轨 | 2019-07-04—2019-07-10 | -130 | 41.69 | -13.11 |
| 降轨 | 2019-07-04—2019-07-16 | 30 | 41.60 | 193.11 |
随后,分别利用原始SM-VCE方法和本文的SM-VCE方法计算了模拟数据的三维形变,如图 3(d)-(f)和(j)-(l)所示。整体而言,两种方法得到的三维形变与模拟数据图 3(a)-(c)较为一致。图 3(g)-(i)和图 3(m)-(o)分别给出了两种方法得到的三维形变残差图。可以看出,在断层破裂区域,原始SM-VCE方法仅能利用精度较低的POT方法进行三维形变解算,且未区分窗口内断层两侧的异质点,使得该区域的三维形变结果过于平滑、残差值较大。本文的SM-VCE方法则通过窗口大小自适应变化使得高精度的InSAR形变观测值也可以参与解算,同时通过顾及断裂线位置剔除了窗口内的异质点,最终得到的断层破裂区域的三维形变结果残差更小、精度更高。通过两种方法在断层破裂区域的对比,说明了本文提出的顾及断裂线和自适应变化窗口的观测值选取策略的优越性。

|
| 注:黑色折线为断裂线。 图 3 模拟试验中不同方法得到的三维形变场 Fig. 3 The 3D deformation obtained by different methods in the simulation |
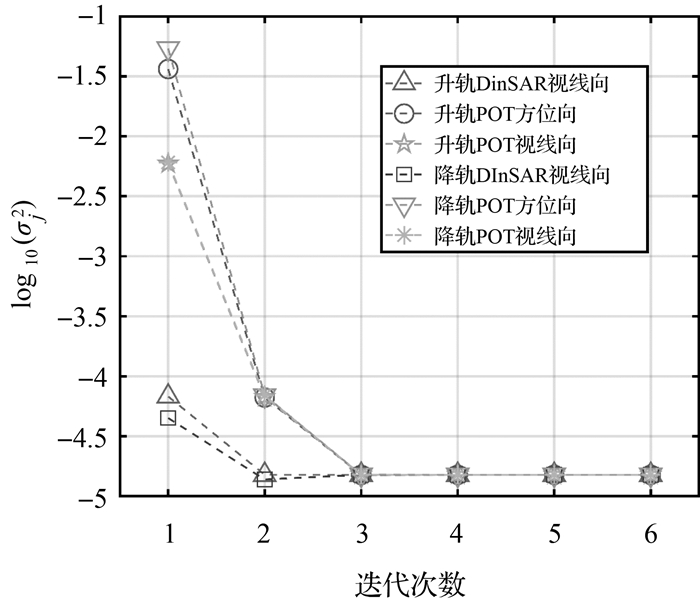
在远场区域,由于IWLS可在VCE定权之前通过对窗口内不同精度的观测值分配不同的权重,在一定程度上降低了误差较大的观测值对三维形变求解的影响。对比图 3中本文SM-VCE方法和原始SM-VCE方法的残差可以发现,本文SM-VCE方法通过IWLS进行观测值内部定权可以显著抑制粗差观测值对三维地表形变结果的影响。需要说明的是,因为升降轨DInSAR观测值添加了大气噪声,且SM-VCE方法对空间高频噪声抑制效果较好,因此,在图 3(m)、(o)中本文SM-VCE方法得到东西向和垂直向形变残差具有较为明显的大气信号。为了更加直观地展示IWLS在窗口内的定权效果,图 4给出了行列号(454, 357)处(即图 2中的红色加号)15×15窗口内6类观测值数据及IWLS的定权结果,可以看出,IWLS方法可以有效识别出观测值粗差并将其权重设置为0,即认为相应的粗差观测值不参与未知参数的求解,同时对噪声较大的观测值进行了降权处理,即认为降低了相应噪声较大观测值对未知参数求解的影响。在本文的SM-VCE方法中,IWLS对每一类观测值内部定权之后,仍需要利用VCE方法实现不同类观测值之间的相对定权。图 5为行列号(454, 357)处(即图 2中的红色加号)VCE定权过程中方差分量σj2的收敛示意图。可以看出,在此次模拟试验中3次迭代之后方差分量估计即可收敛。然而,在真实数据处理中,观测值包含了十分复杂的噪声源信号,在极个别情况下,VCE会出现不收敛或者负方差的情况。因此,在真实试验中,本文设置的迭代次数阈值为10。同时,当出现负方差时,会事先利用远场区域计算一个观测值的先验方差,进而对出现负方差的观测值进行人为的经验定权。为了更加定量地说明IWLS方法的效果,本文将断裂线两侧10像素缓冲区内的残差值进行了掩膜,用剩下的数据计算了均方根误差(表 2)。可以看出,在模拟试验中,IWLS方法可较为显著地提高三维形变精度。

|
| 注:观测值的权重是无量纲。 图 4 行列号(454, 357)处15×15窗口内(a)—(f)6类观测值数据及(g)—(l)IWLS得到的每一类观测值内部的相对权重 Fig. 4 (a)—(f) The six kinds of measurements and (g)—(l) the corresponding weights from the IWLS method in the 15×15 window of the pixel (454, 357) |
|
| 注:σj的单位为m。 图 5 行列号(454, 357)处方差分量估计迭代过程中的单位权中误差σj2收敛 Fig. 5 Convergence of the variance component estimation at the pixel (454, 357) |
| 方法 | 东西向 | 南北向 | 垂直向 |
| 原始SM-VCE | 6.5 | 17.8 | 6.6 |
| 本文SM-VCE | 1.0 | 2.5 | 1.0 |
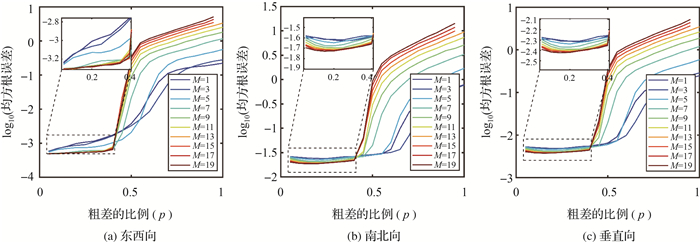
此外,鉴于IWLS主要是为了抑制粗差观测值对三维形变结果的影响,本文进一步利用模拟试验研究了不同粗差量级(即不同的M取值)和不同粗差个数(即不同的p取值)情况下,利用本文的IWLS方法获取三维形变结果的精度(图 6)。为了避免大气噪声的影响,此处的模拟试验中未添加大气噪声。不难发现,随着观测值中粗差比例的增加,得到的三维形变精度在不断下降。当粗差比例小于等于40%时,不同粗差量级的模拟试验均可得到较为可靠的形变结果。而且,当粗差比例小于等于40%时,粗差量级越大得到的三维形变结果精度越高。这是因为粗差量级越大,IWLS方法识别出粗差的正确率就会越高。但是,当粗差观测值比例过大时(例如大于40%),本文提及的IWLS方法也无法十分有效地抑制粗差观测值对三维形变结果的影响。此外,南北向和垂直向形变结果均方根误差呈现先减小后增大的趋势(拐点出现在粗差比例约为20%时)。这是因为南北向形变主要是由POT方位向观测值计算而来,并且在计算三维形变时,垂直向形变结果受南北向形变影响较大[46],而POT方位向观测值本身的方差就比较大,当粗差比例较小时,IWLS方法对粗差的敏感度并不高,随着粗差比例的增大,使得观测值噪声的分布更加非高斯性,进而IWLS可以更为准确地识别出粗差、提高结果精度。而当粗差比例过大时,形变结果的精度会不断降低。为了验证上述观点,本文将模拟试验中DInSAR和POT观测值中的高斯噪声方差均设置为5 mm,得到的南北向和垂直向均方根误差变化曲线和东西向变化曲线较为一致,未发现局部极小值的现象。
|
| 注:均方根误差的单位是m。 图 6 不同粗差量级(即不同的M取值)和不同粗差比例(即不同的p取值)情况下,利用本文SM-VCE方法获取的模拟试验三维形变结果的精度对比 Fig. 6 The root mean squares errors of the three-dimensional deformations estimated by the enhanced SM-VCE method in this paper with the simulated experiments under different magnitude and different proportion of the gross error |
需要说明的是,SM-VCE方法在获取三维同震地表形变时的优势主要有两点:①基于地表应力应变模型构建了邻近点三维形变之间的模型关系,有效抑制了空间高频噪声,使得引入力学模型的InSAR三维地表形变估计函数模型更加符合实际情况;②顾及地表应力应变模型建立的InSAR三维地表形变估计函数模型显著增加了多余观测个数,使得利用方差分量估计进行验后迭代定权成为可能,相比于传统的先验定权方法,方差分量估计算法可以显著提高多源观测数据的定权精度,进而可以获得更加精确、可靠的三维地表形变场。相对于传统仅利用观测值与三维形变之间几何关系进行求解的方法[17]而言,SM-VCE方法通过顾及形变在空间上的关联关系以及观测值之间的准确定权,可以得到更为精确的三维地表形变结果。
另外,基于地表应力应变模型构建形变在空间上的关联关系在一定程度上可以认为是一个滤波过程,进而会导致SM-VCE方法对一些空间上的局部高频形变信号不敏感。但是,地表应力应变模型作为一个力学模型,用于三维形变求解时,肯定比纯数学的滤波效果更好。此外,传统逐像素求解的WLS方法,由于缺少多余观测数据,难以利用VCE算法进行验后精确定权,对于SM-VCE方法而言,正是因为顾及地表应力应变模型建立的函数模型具有较多的多余观测数据,才能够利用方差分量估计算法进行观测值精确定权。
同时,SM-VCE方法中的窗口大小是一个必不可少的参数。理想情况下,窗口范围内的形变应满足地表应力应变模型,即形变梯度应为一个常数。因此,窗口的范围应远小于感兴趣的形变场尺度。对于高空间分辨率影像,或者大尺度形变场而言,本文中所述的15×15像素,甚至63×63像素均可以得到可靠的三维地表形变。对于本文提出的顾及断裂线和自适应变化窗口的观测值选取策略,当面对浅部发生的中小型地震时,由于断裂带小范围产生的复杂形变特征造成窗口内的观测值呈现异质性,此时应减小窗口阈值Sthr以保证近场三维地表形变结果的可靠性。
在观测值噪声服从理想的高斯分布时,方差分量估计可以较为准确地得到各类观测值的验后权重。但是,真实的形变观测值往往会包含各种复杂的误差源信号(例如大气噪声、地形残差、轨道误差等),在个别情况下,多源误差信号整体上表现为严重的非高斯性,进而使得方差分量估计难以收敛,甚至出现负方差,因此,需要针对个别情况进行人为干预的先验定权,或者引入更为稳健的算法来抑制相关误差源的影响。
3 2019年Ridgecrest地震的InSAR三维地表形变场 3.1 研究区域及所用数据2019年7月6日(UTC), 美国加州Ridgecrest地区(震中35.770°N,117.599°W)发生了M7.1级地震,震源深度约为8.0 km。Ridgecrest地震的发震断层位于东加利福尼亚剪切带上(east California shear zone,ECSZ)。该区域是圣安德烈亚斯断层(San Andreas fault,SAF)南段以东的一个地震活跃区域,与莫哈韦沙漠大致重合,具有多个与SAF平行的右旋走滑断层。因此,对加州地震展开地表形变监测可为研究该地震,ECSZ及SAF的构造运动提供基础资料。
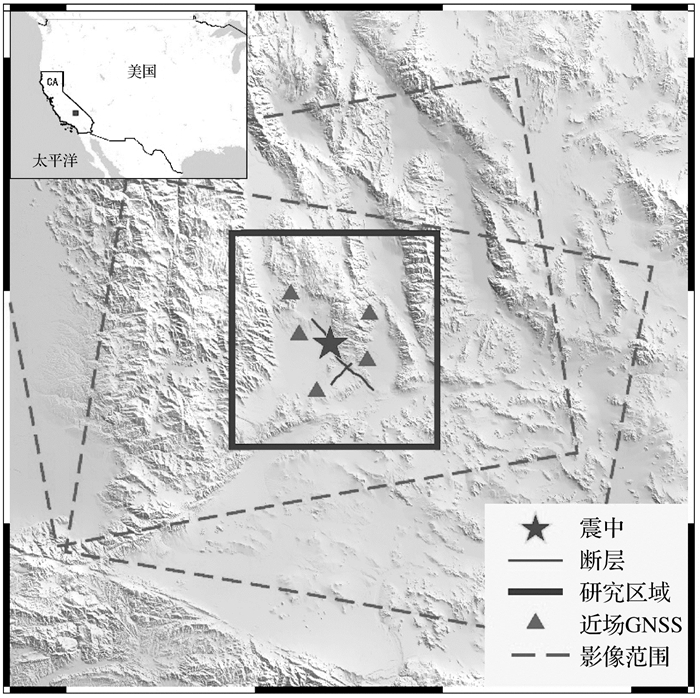
针对2019年Ridgecrest地震,本次研究使用了升降轨哨兵1号卫星SAR数据(如表 1和图 7)。基于瑞士的GAMMA软件,分别利用DInSAR和POT技术进行了数据处理。其中,SRTM(shuttle radar topography mission) 30 m分辨率的DEM数据被用于去除地形相位及地形起伏引起的配准误差。为了抑制失相干噪声、提高计算效率,采用了32×8的多视因子(距离向×方位向)。在DInSAR处理过程中,利用基于最小二乘的滤波方法对多视后的干涉图进行滤波处理[47],基于最小费用流方法对滤波后的干涉图进行解缠[48]。在POT的数据处理过程中,哨兵数据的匹配窗口为128×128像素,过采样因子为2。
|
| 图 7 研究区域与数据覆盖情况 Fig. 7 Shaded relief map of the study area |
图 8为本文获取的6个InSAR形变观测数据。可以看出,Ridgecrest地震震中的形变可达米级。由于震中地表破坏较为严重,DInSAR获取的形变观测结果在断裂带附近失相干现象较为严重。相反,POT技术可以较好地抵制失相干现象,获得了较为完整的地表形变场。但是,由于POT技术是根据强度匹配获取地表形变,该技术往往比DInSAR技术获取的形变精度低。因此,尽管融合升降轨POT数据即可获得较为完整的三维形变,本文仍有必要通过窗口大小自适应变化的观测值选取策略来使得更高精度的DInSAR形变观测数据参与断裂带附近的三维形变解算。此外,图 8(b)、(c)、(e)和(f)显示,基于POT获取的地表形变观测数据噪声较大。图 8(b)、(c)和(e)中的形变场左侧还出现了明显的条带信号,通过对比光学影像发现,条带信号与光学影像中的公路较为相似,并且公路走向与卫星飞行方向越相近,POT方位向观测值中的条带信号越强,进而推测此条带信号是因为公路对电磁波反射信号过强,导致影像匹配时公路上的强反射信号沿公路走向较为相似,进而引起了配准错误。本文则基于IWLS方法,通过测量平差数据处理过程中的权重因子来抑制相关噪声(包括图 8(b)、(c)和(e)中的条带信号)对SM-VCE方法解算三维形变的影响。

|
| 注:正值代表地面朝向卫星运动,或沿卫星飞行方向运动, 紫色曲线代表断层线。 图 8 不同数据不同方法获取的Ridgecrest地震InSAR形变观测值 Fig. 8 The InSAR measurements of the Ridgecrest earthquake |
3.2 InSAR三维地表形变场
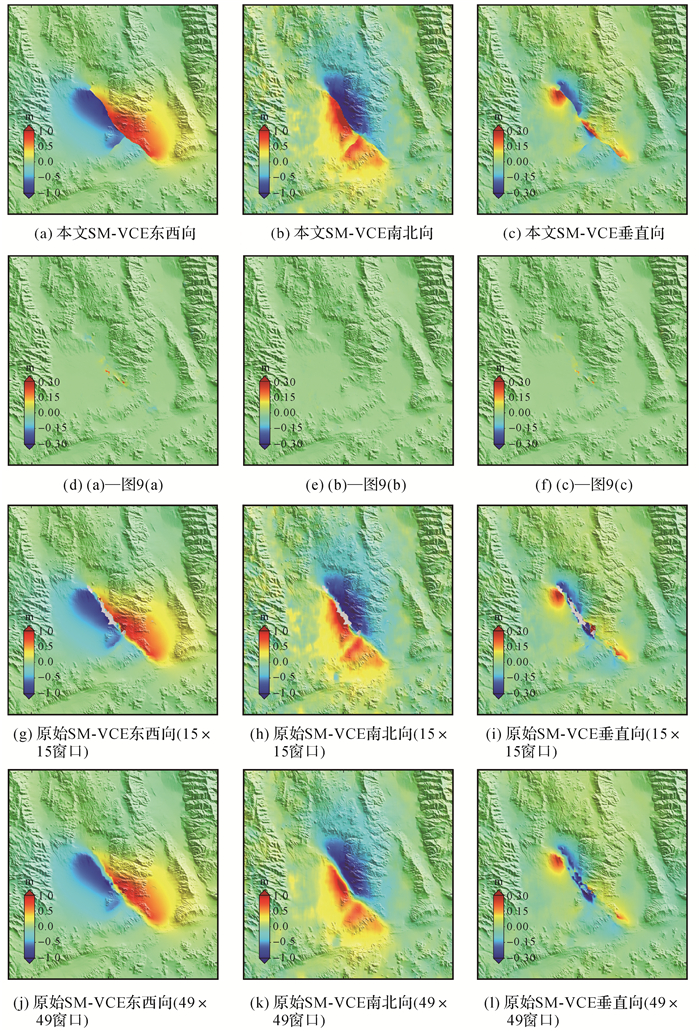
与模拟试验类似,本文分别利用原始SM-VCE方法和本文SM-VCE方法获取了该地震的三维地表形变场(图 9)。可以看出,不同方法得到的三维地表形变具有高度一致性。其中,水平向和垂直向的最大形变分别约为2.1 m和0.38 m。然而,由于原始SM-VCE方法在断层附近无法兼顾高精度的相位观测数据,且未区分窗口内断层两侧的异质点,图 9(d)-(f)中,由该方法得到的三维地表形变在断层附近的三维形变场过于平滑,严重偏离真实情况。从图 9(g)-(i),本文SM-VCE方法和原始SM-VCE方法得到的三维形变场差异图中可以看出,两种方法得到的三维形变在大部分区域是基本相同的,在断裂带附近差异最大,说明了本文SM-VCE方法获取可靠断裂带附近三维形变的优越性。同时,在远离断裂带区域(如图 9(h)中主断裂带的西南侧),本文SM-VCE方法可以较好地抑制一些局部误差信号对三维地表形变结果的影响,说明了IWLS在抑制粗差观测值方面的优势。
此外,为了更加突出窗口自适应选点方法的优越性,本文仅基于DInSAR获取的视线向和POT获取的方位向4个形变观测值,利用本文的SM-VCE方法获取了该地震的三维地表形变结果,如图 10(a)-(c)所示。与图 9(a)-(c)基于6个观测值的结果对比发现,二者的差异几乎可以忽略,如图 10(d)-(f),尤其在断层破裂带区域,在DInSAR完全失相干的情况下,本文的SM-VCE方法也可得到较为可靠的三维地表形变结果。然而,在DInSAR失相干区域,原始SM-VCE方法在15×15像素固定窗口内仅有两个观测值(即升降轨获取的POT方位向的形变观测值),导致最终的三维地表形变场图 10(g)-(i)在DInSAR失相干区域必定会缺失,并且在断裂带附近,由于15×15像素固定窗口内的像素点个数较少,三维形变结果会出现较多的跳变信号。尽管在窗口大小为49×49像素情况下,原始SM-VCE方法可以得到完整的三维形变场,如图 10(j)-(l),但是在断裂带附近,由于窗口内包含了较多的异质点,原始SM-VCE方法得到的三维形变结果会出现较多的错误形变信号,进一步说明了本文方法在获取高精度、完整三维同震形变场的优势。
需要说明的是,本文所提出的自适应选点方法主要是针对位于发震断层处的地震破裂带区域。一般情况下,结合历史资料、实地调研及大地测量等数据可以较为准确地获取发震断层断裂线数据,进而利用本文的自适应选点方法可以获取可靠的近场三维同震形变场。实际地震中,部分非发震断层在受到应力挤压、拉张等作用下,也可能表现出形变场不连续的现象。与发震断层处不同的是,InSAR技术在这些区域往往可以获取完整的地表形变场,进而基于断裂线的人工识别即可得到可靠的三维地表形变场。对于Ridgecrest地震而言,真实地表破裂较多[49],在本文中为了简单起见,仅使用了两个主要的发震断层破裂线计算三维同震形变场来说明本文方法的优越性。
此外,本文利用Nevada Geodetic Laboratory(http://geodesy.unr.edu/)免费公开的5个近场GNSS站点数据(站点分布如图 7所示)对两种方法得到的三维地表形变进行了精度评估。原始SM-VCE方法在东西向、南北向和垂直向形变精度分别为7.8、6.5和2.6 cm,而本文SM-VCE方法则分别为7.9、5.6和2.6 cm。可以发现,本文方法相比于原始方法仅在南北向分量有一定的改善效果。与模拟试验对比发现,真实观测数据中的粗差量级和个数相对较小,仅在POT方位向形变观测值中具有较为明显的粗差观测值信号,因此,在与GNSS对比中,本文SM-VCE仅在南北向分量改进较为明显。此外,InSAR数据和GNSS数据的时空分辨率均不相同,GNSS数据本身就包含误差,因此,利用GNSS进行InSAR精度评估并不完全可靠[16]。
4 总结融合多源InSAR形变观测数据是实现InSAR三维同震地表形变监测的基本途径,其中三维同震地表形变求解过程中建立的函数模型与随机模型对三维形变结果的精度影响至关重要。本文详细介绍了一种基于地表应力应变模型(SM)和方差分量估计(VCE)的InSAR三维地表形变监测方法(SM-VCE)。该方法通过顾及一定窗口范围内不同像素点三维形变之间的力学关系(即SM)建立函数模型,进而利用VCE算法实现多源InSAR形变观测数据随机模型的准确确定。相比于传统的单点求解方法,SM-VCE方法可得到更为准确的三维地表形变结果。
为了使得该方法可以得到更为精确的、完整的三维同震地表形变场,本文进一步提出了顾及断裂线位置和窗口大小自适应变化的观测值选取策略和一种基于迭代加权最小二乘的窗口内同一类观测值相对定权方法。其中,观测值选取策略是为了解决断裂带附近InSAR形变观测数据易缺失且不连续导致的SM-VCE方法精度较低和形变结果缺失问题,而同一类观测值内部相对定权方法是通过迭代加权最小二乘方法抑制窗口内的异常形变观测值,进而提高三维形变的解算精度。
模拟试验和基于升降轨哨兵数据2019年Ridgecrest地震三维形变的研究表明,本文提及的方法可得到更为精确的三维同震形变结果,尤其在断层破裂带附近,窗口优化的SM-VCE方法可在数据缺失的情况下,利用邻近的有效InSAR形变观测值恢复得到可靠的三维地表形变场。同时,本文通过模拟试验验证了观测值中不同的粗差比例对三维形变结果的影响。结果表明,当粗差比例小于等于40%时,窗口优化的SM-VCE方法通过迭代加权最小二乘可显著抑制粗差观测值对结果的影响。
本文介绍的SM-VCE方法也可联合星载、地基InSAR面观测数据和GNSS、水准等传统大地测量点观测数据实现多种地质灾害(例如火山喷发、滑坡等)的三维地表形变准确测量。同时,在独立观测数据较少的情况下,例如只有升降轨的DInSAR观测数据,也可利用SM-VCE方法实现二维地表形变测量,或者,通过引入可靠的先验信息约束(例如坡度约束、地下开采沉陷模型约束)实现三维地表形变测量。此外,本文介绍的窗口大小自适应变化的准则是窗口内的有效观测值个数,只是从数值解算的稳定性方面进行考虑,未来可发展基于数据本身或者局部实际地表形变梯度的窗口大小自适应确定方法,以提高三维地表形变的精度及可靠性。
| [1] |
LI Gang, LIN Hui, YE Qinghua, et al. Acceleration of glacier mass loss after 2013 at the Mt. Qomolangma[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(4): 60-69. DOI:10.11947/j.JGGS.2020.0406 |
| [2] |
TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping applications using automatic SAR imaging[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 27-37. DOI:10.11947/j.JGGS.2019.0204 |
| [3] |
ZISK S H. Lunar topography: first radar-interferometer measurements of the alphonsus-ptolemaeus-arzachel region[J]. Science, 1972, 178(4064): 977-980. DOI:10.1126/science.178.4064.977 |
| [4] |
GABRIEL A K, GOLDSTEIN R M, ZEBKER H A. Mapping small elevation changes over large areas: differential radar interferometry[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B7): 9183-9191. DOI:10.1029/JB094iB07p09183 |
| [5] |
FIALKO Y, SANDWELL D, SIMONS M, et al. Three-dimensional deformation caused by the Bam, Iran, earthquake and the origin of shallow slip deficit[J]. Nature, 2005, 435(7040): 295-299. DOI:10.1038/nature03425 |
| [6] |
HU Jun, LI Zhiwei, DING Xiaoli, et al. Resolving three-dimensional surface displacements from InSAR measurements: a review[J]. Earth-Science Reviews, 2014, 133: 1-17. DOI:10.1016/j.earscirev.2014.02.005 |
| [7] |
李珊珊, 李志伟, 胡俊, 等. SBAS-InSAR技术监测青藏高原季节性冻土形变[J]. 地球物理学报, 2013, 56(5): 1476-1486. LI Shanshan, LI Zhiwei, HU Jun, et al. Investigation of the seasonal oscillation of the permafrost over Qinghai-Tibet plateau with SBAS-InSAR algorithm[J]. Chinese Journal of Geophysics, 2013, 56(5): 1476-1486. |
| [8] |
单新建, 宋小刚, 韩宇飞, 等. 汶川Ms 8.0地震前InSAR垂直形变场变化特征研究[J]. 地球物理学报, 2009, 52(11): 2739-2745. SHAN Xinjian, SONG Xiaogang, HAN Yufei, et al. The characteristics of surface vertical deformation before the Wenchuan Ms8.0 earthquake from InSAR[J]. Chinese Journal of Geophysics, 2009, 52(11): 2739-2745. |
| [9] |
WANG Leyang, ZHAO Xiong. Determination of smoothing factor for the inversion of co-seismic slip distribution[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 25-35. DOI:10.11947/j.JGGS.2020.0103 |
| [10] |
WRIGHT T J, PARSONS B E, LU Zhong. Toward mapping surface deformation in three dimensions using InSAR[J]. Geophysical Research Letters, 2004, 31(1): 169-178. DOI:10.1029/2003GL018827 |
| [11] |
秦晓琼, 杨梦诗, 王寒梅, 等. 高分辨率PS-InSAR在轨道交通形变特征探测中的应用[J]. 测绘学报, 2016, 45(6): 713-721. QIN Xiaoqiong, YANG Mengshi, WANG Hanmei, et al. Application of high-resolution PS-InSAR in deformation characteristics probe of urban rail transit[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 713-721. DOI:10.11947/j.AGCS.2016.20150440 |
| [12] |
MICHEL R, AVOUAC J P, TABOURY J. Measuring ground displacements from SAR amplitude images: application to the Landers earthquake[J]. Geophysical Research Letters, 1999, 26(7): 875-878. DOI:10.1029/1999GL900138 |
| [13] |
BECHOR N B D, ZEBKER H A. Measuring two-dimensional movements using a single InSAR pair[J]. Geophysical Research Letters, 2006, 33(16): L16311. DOI:10.1029/2006GL026883 |
| [14] |
GRANDIN R, KLEIN E, MÉTOIS M, et al. Three-dimensional displacement field of the 2015 Mw 8.3 Illapel earthquake (Chile) from across- and along-track Sentinel-1 TOPS interferometry[J]. Geophysical Research Letters, 2016, 43(6): 2552-2561. DOI:10.1002/2016GL067954 |
| [15] |
FUNNING G J, PARSONS B, WRIGHT T J, et al. Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B9). DOI:10.1029/2004JB003338 |
| [16] |
HU Jun, LI Zhiwei, ZHU Jianjun, et al. 3D coseismic displacement of 2010 Darfield, New Zealand earthquake estimated from multi-aperture InSAR and D-InSAR measurements[J]. Journal of Geodesy, 2012, 86(11): 1029-1041. DOI:10.1007/s00190-012-0563-6 |
| [17] |
JUNG H S, LU Z, WON J S, et al. Mapping three-dimensional surface deformation by combining multiple-aperture interferometry and conventional interferometry: application to the June 2007 eruption of Kilauea volcano, Hawaii[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(1): 34-38. DOI:10.1109/LGRS.2010.2051793 |
| [18] |
LI Jia, LI Zhiwei, WU Lixin, et al. Deriving a time series of 3D glacier motion to investigate interactions of a large mountain glacial system with its glacial lake: use of synthetic aperture radar pixel offset-small baseline subset technique[J]. Journal of Hydrology, 2018, 559: 596-608. DOI:10.1016/j.jhydrol.2018.02.067 |
| [19] |
FIALKO Y, SIMONS M, AGNEW D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw7.1 Hector mine earthquake, California, from space geodetic observations[J]. Geophysical Research Letters, 2001, 28(16): 3063-3066. DOI:10.1029/2001GL013174 |
| [20] |
王志伟. 基于多源InSAR数据的三维地表形变解算方法研究[J]. 测绘学报, 2019, 48(9): 1206. WANG Zhiwei. Research on resolving of three-dimensional displacement from multi-source InSAR data[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1206. DOI:10.11947/j.AGCS.2019.20180490 |
| [21] |
朱建军, 杨泽发, 李志伟. InSAR矿区地表三维形变监测与预计研究进展[J]. 测绘学报, 2019, 48(2): 135-144. ZHU Jianjun, YANG Zefa, LI Zhiwei. Recent progress in retrieving and predicting mining-induced 3D displacements using InSAR[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(2): 135-144. DOI:10.11947/j.AGCS.2019.20180188 |
| [22] |
JIANG Houjun, FENG Guangcai, WANG Teng, et al. Toward full exploitation of coherent and incoherent information in Sentinel-1 TOPS data for retrieving surface displacement: application to the 2016 Kumamoto (Japan) earthquake[J]. Geophysical Research Letters, 2017, 44: 1758-1767. DOI:10.1002/2016GL072253 |
| [23] |
HE Ping, WEN Yangmao, XU Caijun, et al. Complete three-dimensional near-field surface displacements from imaging geodesy techniques applied to the 2016 Kumamoto earthquake[J]. Remote Sensing of Environment, 2019, 232: UNPS 111321. DOI:10.1016/j.rse.2019.111321 |
| [24] |
HE Ping, WEN Yangmao, XU Caijun, et al. High-quality three-dimensional displacement fields from new-generation SAR imagery: application to the 2017 Ezgeleh, Iran, earthquake[J]. Journal of Geodesy, 2019, 93(4): 573-591. DOI:10.1007/s00190-018-1183-6 |
| [25] |
HU Jun, LI Zhiwei, SUN Qian, et al. Three-dimensional surface displacements from InSAR and GPS measurements with variance component estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 754-758. DOI:10.1109/LGRS.2011.2181154 |
| [26] |
LUO Haipeng, CHEN Ting. Three-dimensional surface displace-ment field associated with the 25 April 2015 Gorkha, Nepal, earthquake: solution from integrated InSAR and GPS measurements with an extended SISTEM approach[J]. Remote Sensing, 2016, 8(7): rs8070559. DOI:10.3390/rs8070559 |
| [27] |
GUDMUNDSSON S, SIGMUNDSSON F, CARSTENSEN J M. Three-dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10): 2250. DOI:10.1029/2001jb000283 |
| [28] |
王霞迎, 张菊清, 张勤, 等. 升降轨InSAR和GPS数据集成反演西安形变场[J]. 测绘学报, 2016, 45(7): 810-817. WANG Xiaying, ZHANG Juqing, ZHANG Qin, et al. Inferring multi-dimensional deformation filed in Xi'an by combining insar of ascending and descending orbits with GPS data[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 810-817. DOI:10.11947/j.AGCS.2016.20150485 |
| [29] |
罗海滨, 何秀凤, 刘焱雄. 利用DInSAR和GPS综合方法估计地表 3维形变速率[J]. 测绘学报, 2008, 37(2): 168-171. LUO Haibin, HE Xiufeng, LIU Yanxiong. Estimation of three-dimensional surface motion velocities using integration of DInSAR and GPS[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 168-171. DOI:10.3321/j.issn:1001-1595.2008.02.007 |
| [30] |
GUGLIELMINO F, NUNNARI G, PUGLISI G, et al. Simultaneous and integrated strain tensor estimation from geodetic and satellite deformation measurements to obtain three-dimensional displacement maps[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 1815-1826. DOI:10.1109/TGRS.2010.2103078 |
| [31] |
WANG Xiaowen, LIU Guoxiang, YU Bing, et al. An integrated method based on DInSAR, MAI and displacement gradient tensor for mapping the 3D coseismic deformation field related to the 2011 Tarlay earthquake (Myanmar)[J]. Remote Sensing of Environment, 2015, 170: 388-404. DOI:10.1016/j.rse.2015.09.024 |
| [32] |
朱建军, 李志伟, 胡俊. InSAR变形监测方法与研究进展[J]. 测绘学报, 2017, 46(10): 1717-1733. ZHU Jianjun, LI Zhiwei, HU Jun. Research progress and methods of InSAR for deformation monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1717-1733. DOI:10.11947/j.AGCS.2017.20170350 |
| [33] |
WANG Teng, WEI Shengji, SHI Xuhua, et al. The 2016 Kaikōura earthquake: simultaneous rupture of the subduction interface and overlying faults[J]. Earth and Planetary Science Letters, 2018, 482: 44-51. DOI:10.1016/j.epsl.2017.10.056 |
| [34] |
XU Wenbin, FENG Guangcai, MENG Lingsen, et al. Tran-spressional rupture cascade of the 2016 Mw 7.8 Kaikoura earthquake, New Zealand[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(3): 2396-2409. DOI:10.1002/2017JB015168 |
| [35] |
LIU Jihong, HU Jun, LI Zhiwei, et al. A method for measuring 3-D surface deformations with InSAR based on strain model and variance component estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 239-250. DOI:10.1109/TGRS.2017.2745576 |
| [36] |
LIU Jihong, HU Jun, XU Wenbin, et al. Complete three-dimensional coseismic deformation field of the 2016 central Tottori earthquake by integrating left- and right-looking InSAR observations with the improved SM-VCE method[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(11): 12099-12115. DOI:10.1029/2018JB017159 |
| [37] |
WANG Teng, JÓNSSON S. Improved SAR amplitude image offset measurements for deriving three-dimensional coseismic displacements[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(7): 3271-3278. DOI:10.1109/JSTARS.2014.2387865 |
| [38] |
SCOTT C P, ARROWSMITH R, NISSEN E, et al. The M7 2016 Kumamoto, Japan, earthquake: 3-D deformation along the fault and within the damage zone constrained from differential LiDAR topography[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(7): 6138-6155. DOI:10.1029/2018JB015581 |
| [39] |
LIANG Hongyu, ZHANG Lei, DING Xiaoli, et al. Suppression of coherence matrix bias for phase linking and ambiguity detection in MT InSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 59(2): 1263-1274. DOI:10.1109/TGRS.2020.3000991 |
| [40] |
甘洁, 胡俊, 李志伟, 等. 基于InSAR和地应变特征获取2015年Mw7.2级Murghab地震同震三维地表形变场[J]. 中国科学: 地球科学, 2018, 48(10): 1335-1351. GAN Jie, HU Jun, LI Zhiwei, et al. Mapping three-dimensional co-seismic surface deformations associated with the 2015 Mw7.2 Murghab earthquake based on InSAR and characteristics of crustal strain[J]. SCIENCE CHINA Earth Science, 2018, 48(10): 1335-1351. |
| [41] |
胡圣武, 肖本林. 现代测量数据处理理论与应用[M]. 北京: 测绘出版社, 2016. HU Shengwu, XIAO Benlin. Modern theory and application of surveying data processing[M]. Beijing: Surveying and Mapping Press, 2016. |
| [42] |
SUDHAUS H, JONSSON S. Improved source modelling through combined use of InSAR and GPS under consideration of correlated data errors: application to the June 2000 Kleifarvatn earthquake, Iceland[J]. Geophysical Journal International, 2009, 176(2): 389-404. DOI:10.1111/j.1365-246X.2008.03989.x |
| [43] |
张亚彬, 王利, 范丽红, 等. 组合粗差探测的MHSS ARAIM算法[J]. 测绘学报, 2019, 48(1): 9-17. ZHANG Yabin, WANG Li, FAN Lihong, et al. MHSS ARAIM algorithm combined with gross error detection[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(1): 9-17. DOI:10.11947/j.AGCS.2019.20170367 |
| [44] |
ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Complex least squares adjustment to improve tree height inversion problem in PolInSAR[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 1-8. DOI:10.11947/j.JGGS.2019.0101 |
| [45] |
XU Xiaohua, SANDWELL D T, WARD L A, et al. Surface deformation associated with fractures near the 2019 Ridgecrest earthquake sequence[J]. Science, 2020, 370(6516): 605-608. DOI:10.1126/SCIENCE.ABD1690 |
| [46] |
MONTAZERI Sina, XIAO Xiangzhu, EINEDER Michael, et al. Three-dimensional deformation monitoring of urban infrastructure by tomographic SAR using multitrack TerraSAR-X data stacks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 6868-6878. DOI:10.1109/TGRS.2016.2585741 |
| [47] |
LI Zhiwei, DING Xiaoli, HUANG C, et al. Improved filtering parameter determination for the Goldstein radar interferogram filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(6): 621-634. DOI:10.1016/j.isprsjprs.2008.03.001 |
| [48] |
CHEN C W, ZEBKER H A. Phase unwrapping for large SAR interferograms: statistical segmentation and generalized network models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1709-1719. DOI:10.1109/TGRS.2002.802453 |
| [49] |
XU X, SANDWELL D T, WARD L A, et al. Surface deformation associated with fractures near the 2019 Ridgecrest earthquake sequence[J]. Science, 2020, 370(6516): 605-608. DOI:10.1126/SCIENCE.ABD1690 |