全球离散网格系统(discrete global grid system, DGGS)是一种面向全球的新型多分辨率数据融合与地学模拟解决方案[1-3],它借助特定方法对地球空间进行均匀递归剖分,构建多分辨率的无缝不重叠网格结构,在数据操作中使用格元编码代替传统的地理空间坐标[4]。空间填充曲线以分形几何、代数等数学理论为支撑,刻画被遍历空间中各点在曲线上对应位置之间的关系及其随阶数的变化,具备构建抽象、严格、一般性的数学模型的理论潜力[5]。空间填充曲线编码较好地顾及了格元邻近关系表达的需求,在执行邻域操作时效率较高[6]。
研究人员经过广泛研究对比后发现,在众多空间填充曲线中,Hilbert曲线具有最好的空间聚簇性[7-8],即多维空间中位置相邻或相近的空间目标映射到Hilbert曲线上后能够保持最佳的邻近关系,可有效提高多维数据在磁盘等一维物理存储中的访问效率[9],已被广泛应用于网格单元编码研究领域[10]。文献[11]提出剖分影像金字塔模型及建塔策略,利用网格单元编码的唯一性和Hilbert曲线空间连续性对影像块进行索引与组织。文献[12]采用Hilbert曲线构建菱形网格单元编码模型,并配合提出Hilbert码与地理坐标的相互转换算法。文献[13]结合其八叉树结构,设计立体网格单元Hilbert编码方法,并针对多分辨率数据组织要求,提出紧致Hilbert索引[14]。文献[15]将地球圈层空间网格的研究范围扩展至地月空间,按照类似方法构建了地月圈层网格[16],分析给出了圈层网格Hilbert码与“行-列-高”码的转换方法,邻近圈层单元查找模型以及圈层单元拓扑模型[17]。文献[18]通过层次嵌套细分构建了规则的多分辨率时空网格,并基于Hilbert曲线提出一种时空数据索引方法。文献[19]面向时空数据设计了四维Hilbert码索引,并提出一种查询窗口与Hilbert码段的转换方式。文献[20]针对时空轨迹数据设计了一种时空网格系统,提出基于Hilbert曲线的时空数据索引进行轨迹数据管理。
格元Hilbert码的计算效率是影响全球离散网格系统中数据组织效率的关键之一,包括笛卡儿坐标(或地理坐标)至Hilbert码的转换计算以及邻近格元Hilbert码的计算等。笛卡儿坐标至Hilbert码转换计算的经典方法是由文献[21]针对二维空间构造提出的。该算法是基于Morton码的二进制位迭代法,算法复杂度为O(n2)。文献[22]对n维m阶Hilbert曲线的空间变换进行研究,提出基于空间坐标变换、自底向上的迭代生成算法,算法复杂度为O(nm)。文献[23]提出状态转移矩阵描述二维Hilbert的层级演进关系,将坐标变换转换为C++中的数组运算,减少了嵌套循环中迭代次数。文献[24]研究了三维Hilbert曲线的层级演进关系,给出了三维Hilbert曲线的初始地址表与层级演进表,但是其给出的地址表形式为若干个二进制数的简单集合,无法直接应用于编码运算。
邻近格元索引是空间聚类、查询等基本空间操作的基础[25]。计算得到邻近格元Hilbert码是实现邻近格元索引的前提。典型的邻近格元Hilbert码计算基于Morton码与Hilbert码之间的空间变换关系实现[26-27],分析其步骤可发现其存在两个缺点:①需要逐层级拆解,将Hilbert码转换为Morton码,耗费较长时间,单次拆解复杂度为O(n),n为Hilbert曲线维度。②当中心格元层级为m时,需要进行2次步长为m的循环,总时间复杂度为O(2nm),随着格元层级的增高,效率随之降低。文献[28]总结了二维Hilbert曲线的层级演进关系,通过记录中心格元在各层级中的相对位置,实现邻近格元Hilbert码计算,对比Morton码转换算法在效率上有较大提升,但是空间维度变化会带来空间填充顺序与演进关系的差异,导致二维Hilbert码算法无法直接应用至更高维度曲线中。
Hilbert曲线具有自相似性[5],其体现为曲线在不同层级间的形状特征是相似的,高阶曲线由多条低阶曲线做空间变换后相连构成。研究高低阶Hilbert曲线之间的层级演进关系将会为Hilbert码的计算效率带来显著提升,并为之后的空间分析带来新的模型与方法[15, 24, 29]。本文首先设计八叉树网格的Hilbert编码结构,然后构建Hilbert曲线层级演进模型,最后以层级演进模型为基础,分别解决笛卡儿坐标至Hilbert码转换计算、邻近格元Hilbert码计算问题。
1 格元Hilbert码设计Hilbert空间填充曲线与网格单元(简称格元)之间的连续映射关系在数学角度上可描述为一种线段T至n维数据空间Rn上的连续映射函数,即线段T中的每一等份t与n维数据空间Rn中的每一格元Q之间的存在一一映射关系,格元Q的大小由线段的等分次数m确定。在Hilbert空间填充曲线的构造过程中,m-1阶曲线(低阶)至m阶曲线(高阶)的一次演进时,将各个维度等分为2m等份,那么n维数据空间Rn则被剖分为2mn个m层级格元Q,这些m层级格元Q与线段T的2mn等分的t之间一一对应,由同一个m-1格元剖分得到的2n个m层级格元的集合被称作Hilbert细胞[30]。
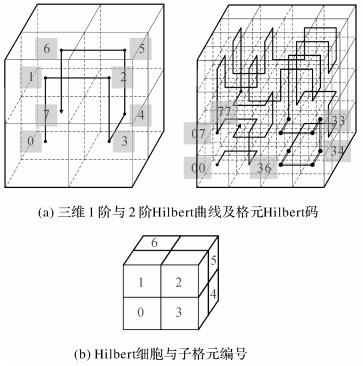
八叉树网格与三维Hilbert曲线相对应,如图 1(a)所示。约定若一条Hilbert曲线可以填充一个2m×2m×2m的三维空间R3,则称该条三维Hilbert曲线为一个三维m阶Hilbert曲线,记作Hm3。一个三维Hilbert细胞由23个同一格元剖分得到的子格元组成,记作C3,不同子格元按照方向位置分别编号为0、1、2、3、4、5、6、7,如图 1(b)所示。
|
| 图 1 Hilbert码与Hilbert细胞 Fig. 1 Hilbert code and Hilbert cell |
通过记录1至m阶曲线演进过程中,格元在每一个细胞中的填充顺序,可为格元设置唯一对应的Hilbert码,其编码形式如图 1(a)所示。将m层级格元的Hilbert码记作hm,格元在各层级细胞中的填充顺序记作i1, i2, …, im,Hilbert码hm满足式(1)
 (1)
(1)
式中,符号⊕表示左移一位后相加。Hilbert码hm存在以下特性:①m层级格元的Hilbert码hm共有m位;②子格元Hilbert码与父格元Hilbert码只相差最后一位,子格元Hilbert码等于父格元Hilbert码左移一位后相加上子格元的填充顺序。
2 Hilbert曲线层级演进模型 2.1 Hilbert曲线状态向量将Hilbert曲线在细胞中的第k种填充顺序记作Ck3,其填充的第i个子格元记作Ck3(i)。所有填充顺序的推导过程如下:
(1) 确定填充起点Ck3(0)。三维Hilbert曲线在细胞中的填充顺序具有以下性质[5]:①Ck3(0) 与Ck3(7)之间的曼哈顿距离为1,即填充起点与终点存在公共面。②若k≠k′,则Ck3(0)与Ck′3(0)之间的曼哈顿距离为偶数,即不同填充顺序的填充起点之间存在公共边。
将8个子格元分为两个集合,集合A={0, 2, 4, 6}与集合B={1, 3, 5, 7}。根据上述性质①可知,若填充起点Ck3(0)位于集合A内,则其终点必定位于集合B中;相反,若填充起点Ck3(0)位于集合B内,则其终点必定位于集合A中。将填充起点与终点互换的填充顺序看作一种填充顺序,可仅考虑填充起点位于集合A内的填充顺序,即Ck3(0)∈{0, 2, 4, 6},共存在4种取值。
(2) 确定填充终点Ck3(7)。由上述性质①可知,填充终点Ck3(7)可由填充起点Ck3(0)直接计算得到,即计算与Ck3(0)曼哈顿距离为1的子格元。在三维空间中,曼哈顿距离为1表现为在笛卡儿坐标系中3个轴上的坐标值有且仅有1位相差为1,可以确定Ck3(7)存在3种取值。
(3) 确定其余格元填充顺序。Hilbert曲线在8个子格元间无重复遍历填充,相邻格元间的曼哈顿距离为1。按照文献[31]所给出的Hilbert曲线L系统表示方法,Hilbert曲线的填充规律为{+Xa+Xb-Xa+Xc+Xa-Xb-Xa},其含义为先沿Xa方向填充1个格元,其次再沿Xb方向填充1个格元,然后再向Xa反方向填充1个格元……排除指向终点方向,Xa只有两种可能方向取值;待Xa确定后,Xb仅剩下唯一的取值情况。所以在确定细胞填充起点Ck3(0)与终点Ck3(7)后,其余格元顺序存在2×1=2种情况。
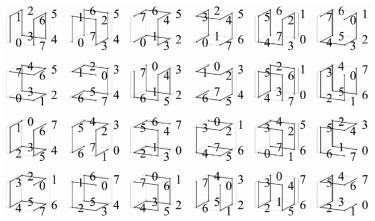
综合上述步骤,填充顺序存在4×3×2=24种情况,如图 2所示左至右,上至下分别为C13, C23, …, C243。
|
| 图 2 24种填充顺序 Fig. 2 24 filling sequences |
为描述24种不同的填充顺序,引入三维Hilbert曲线细胞的状态向量s:按照子格元〈0, 1, 2, …, 7〉的顺序,记录在填充顺序Ck3中,各个子格元对应的填充顺序i。将24种填充顺序对应的状态向量合成状态矩阵S,状态矩阵S的第u行(从0开始取值)对应状态向量su+1,对应细胞的填充顺序Cu+13,见式(2)
 (2)
(2)
Hilbert曲线构造方法为:高阶Hilbert曲线Hm3由低阶曲线Hm-13做坐标变换G [i](i∈{0, 1, …, 7})后得到的Hm-13[i]替换H13中的每一个顶点构成。坐标变换包含交换“↔”与求反“′”两种,各个位置上的坐标变换G [i]组合成为基因列表G={G[0], G[1], …,G[7]},不同的一阶曲线H13对应不同的基因列表[30]。文献[30]给出了以填充顺序为C23的一阶曲线对应基因列表见表 1。
| 坐标变换 | G[0] | G[1] | G[2] | G[3] |
| 交换 | Z↔Y | X↔Y | - | Z↔Y |
| 求反 | - | - | - | Z′, Y′ |
| 坐标变换 | G[4] | G[5] | G[6] | G[7] |
| 交换 | Z↔Y | - | X↔Y | Z↔Y |
| 求反 | - | - | X′, Y′ | Z′, Y′ |
| 注:“-”表示无变换。 | ||||
以基因列表为基础,可对状态向量在层级间的映射关系进行如下推导。
由曲线构造过程可得,一个状态向量为sk的细胞(对应一个m层级格元),其各个子格元(m+1层级格元)的状态向量满足以下层级映射公式
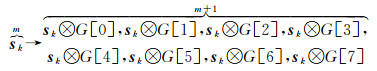 (3)
(3)
式中,表达式sk⊗G[i]表示对状态向量sk的细胞做坐标变换G[i]后重新记录状态向量。
将填充顺序C23的基因列表代入式(3)中,可得一个状态向量为s2的细胞,其各个子格元的状态向量满足以下层级映射公式(图 3)
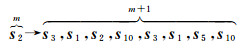 (4)
(4)
|
| 图 3 状态向量s2的层级映射 Fig. 3 state vector s2's level mapping diagram |
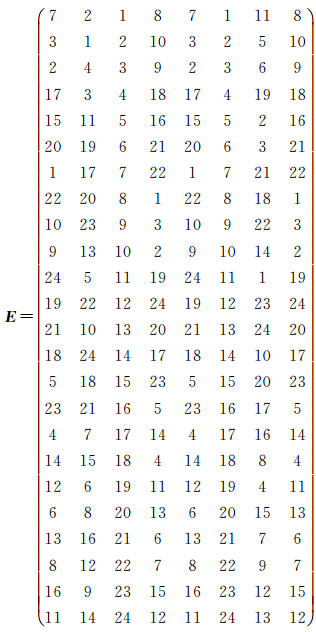
以式(4)为基础,通过以下步骤递推可得其余状态向量的层级映射:①计算状态向量s2与状态向量sk(k≠2)之间的坐标变换G(k, 2);②将式(4)左右两边各做坐标变换G(k, 2),得状态向量sk满足以下映射关系
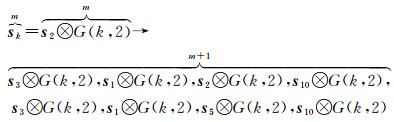 (5)
(5)
计算所有状态向量的层级映射关系后,引入演进矩阵E记录24种低阶状态向量与高阶状态向量间的映射关系,见式(6)
 (6)
(6)
状态演进矩阵E的第u行对应映射关系为
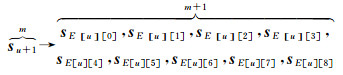 (7)
(7)
状态矩阵S与演进矩阵E是本文进行三维Hilbert曲线编码层级演进模型描述的重要工具:状态矩阵S记录了三维Hilbert曲线的填充顺序,演进矩阵E记录了三维Hilbert曲线填充顺序在高低阶曲线之间的变化趋势,两个矩阵相互配合实现三维Hilbert曲线层级演进模型的形式化描述。
在文献[22, 30]中,基因列表只表示了Hilbert曲线某一种填充顺序在层级间的层级演进关系,因而在运算使用中需要临时通过多维度迭代计算,才能得出下一层级格元的填充顺序。本文中,首先,求取了三维Hilbert曲线所有情况的填充顺序,然后,推导所有填充顺序的层级演进关系,运算使用中可直接从层级演进关系模型中提取得到当前填充顺序与下一层级填充顺序,因此便于设计更加简洁直观的算法。
3 基于层级演进模型的格元Hilbert码计算Hilbert曲线层级演进模型对曲线的填充顺序以及其在层级间的变化关系进行描述,在此基础上可以进行Hilbert曲线构造过程的复现,并设计实现格元Hilbert码计算方法。
3.1 笛卡儿坐标至Hilbert码计算全球离散网格采用网格单元编码代替传统的二维、三维笛卡儿坐标参与运算。然而现有的多数地理空间数据仍然采用笛卡儿坐标给出,为保证现有数据能够融入全球离散网格系统中,需要设计相应的格元笛卡儿坐标至Hilbert码计算的方法。
笛卡儿坐标至Hilbert码的计算实质是对格元剖分和曲线演进的复现,即记录格元在各次曲线演进过程中所处的细胞填充顺序,故曲线演进过程复现的效率不同将导致计算效率存在差异。本文借助Hilbert曲线层级演进模型复现曲线演进过程,避免了各维度迭代步骤,具有直观简洁的特点。
对于给定坐标的格元P(x, y, z),假设曲线阶数为m,由Hilbert曲线的构造方法可知,Hm3由8个Hm-13[i]连接构成,那么格元P(x, y, z)必定位于某个Hm-13[i]中。曲线在填充至Hm-13[i]前,一共经过i个m-1阶的曲线。因此,计算格元P(x, y, z)的m阶Hilbert码hm的关键是:确定在各层级演进产生的细胞中,格元P(x, y, z)所处的填充顺序i。
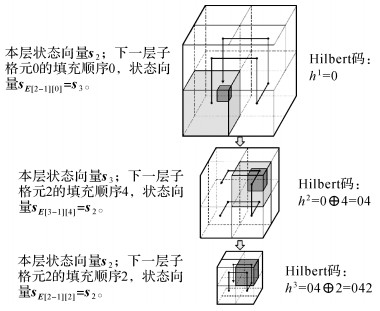
以状态矩阵S与演进矩阵E为工具,本文的格元剖分和曲线演进复现思路如下:从1层级格元和1阶Hilbert曲线为起点,逐层级、阶级向高层级、阶级剖分演进,其中在各次剖分和演进过程中,先使用状态矩阵S判断当前格元的填充顺序,后使用演进矩阵E更新下一层级细胞的状态向量。图 4给出了计算示意图,图中深色格元坐标P(3, 0, 3),采用状态矩阵S与演进矩阵E进行三次复现后,得到Hilbert码h3=042。计算过程的具体步骤如图 5所示。
|
| 图 4 笛卡儿坐标至Hilbert码计算 Fig. 4 Cartesian coordinate to Hilbert code calculation |

|
| 图 5 笛卡儿坐标至Hilbert码计算流程 Fig. 5 calculation process from Cartesian coordinates to Hilbert code |
文献[22]实现笛卡儿坐标至Hilbert码的转换计算过程中,单次运算共需要对n个维度上的坐标进行迭代变换,复杂度为O(n),算法共需要进行m次循环运算,其总时间复杂度为O(nm)。本文使用Hilbert曲线层级演进模型复现曲线构造过程,不存在迭代变换步骤,单次运算只需使用状态矩阵S查询填充顺序、演进矩阵E查询下一层级状态向量,查询复杂度为O(1),全程需进行m次循环,总时间复杂度为O(m),相比于文献[22]迭代算法复杂度更小。
3.2 邻近格元Hilbert码计算邻近格元索引是空间聚类、邻近分析等空间操作的基础。本文以Hilbert曲线层级演进模型为基础,设计邻近格元Hilbert码计算方法,实现邻近格元索引。
在Hilbert码包含父格元与子格元的层级关系,子格元Hilbert码与父格元Hilbert码只相差最后一位,子格元Hilbert码等于父格元Hilbert码左移一位后相加上子格元的填充顺序。因此,通过Hilbert码位运算可实现父子单元的查询,位运算分为左移与右移两种形式:①右移运算。hm≫1,即m级格元Hilbert码右移1位得到其m-1级父格元的Hilbert码。②左移运算。hm≪1,即m级格元Hilbert码左移1位得到其m+1级子格元中第一个填充的子格元Hilbert码,若需计算第i个填充子格元的Hilbert码,则左移1位后将最后一位替换为i。
若通过右移运算可寻找到公共父格元,则可采用左移运算得到邻近格元。进行位运算的同时,需要对Hilbert曲线采取相应的退化与演进操作,以确定格元的填充顺序i以及父子格元的状态向量。
使用本文提出的状态矩阵S与演进矩阵E来描述Hilbert曲线的退化与演进。将层级为m,Hilbert码为h的格元记作vhm,退化时计算父格元状态向量,演进时计算子格元状态向量。
(1) 子格元状态向量计算。将格元vhm填充顺序为i的子格元记作C(v, i)。若已知格元vhm的状态向量为sk,其填充顺序为i的子格元的状态向量s(C(v, i))计算方式为
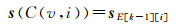 (8)
(8)
(2) 父格元状态向量计算。若已知C(v, i)的状态向量为sk,其父格元vhm的状态向量计算方式为
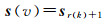 (9)
(9)
式中,r(k)表示演进矩阵E第i列中值为k的元素所在行数。获得父格元状态向量后,先依据填充顺序判断当前格元所处的子格元编号,后判断指定邻近方向DirN上邻近格元与中心格元是否同属于一个父格元(判断依据见表 2)。若同属于一个父格元,则查询得到公共父格元,下一步开始演进过程。
| 邻近方向 | 中心格元编号 | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 上 | 1 | 0* | 3* | 2 | 5 | 4* | 7* | 6 |
| 下 | 1* | 0 | 3 | 2* | 5* | 4 | 7 | 6* |
| 左 | 3* | 2* | 1 | 0 | 7 | 6 | 5* | 4* |
| 右 | 3 | 2 | 1* | 0* | 7* | 6* | 5 | 4 |
| 内 | 7 | 6 | 5 | 4 | 3* | 2* | 1* | 0* |
| 外 | 7* | 6* | 5* | 4* | 3 | 2 | 1 | 0 |
| *表示该子格元与当前中心子格元不属于同一个父格元。 | ||||||||
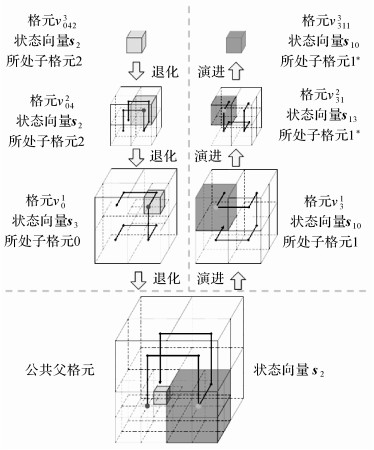
图 6为计算格元v0423在邻近方向R上,邻近格元Hilbert码的过程,先通过3次退化查询得到公共父格元,后进行3次演进得到邻近格元v3113。邻近格元Hilbert码计算具体流程如图 7所示。
|
| 图 6 邻近格元Hilbert码计算 Fig. 6 Hilbert code calculation of neighbor grid elements |

|
| 图 7 邻近格元Hilbert码计算流程 Fig. 7 Calculation flow of Hilbert codes with neighbor grid elements |
在文献[26]的转换算法中,为了生成邻近格元Hilbert码,需要通过2m次复杂度为O(n)的拆解转换步骤,其时间复杂度为O(2nm),因此随着格元层级m的增高,其计算效率将会逐渐降低。在本文计算方法中,采用Hilbert曲线层级演进模型实现了Hilbert曲线的退化与演进,无需将Hilbert码转换为其他类型的码或坐标,算法的时间复杂度为O(2k),k为中心格元与公共父格元之间的层级差。本文方法单次计算复杂度为O(1),相较文献[26]转换算法更低,且循环次数与格元层级无关,故计算效率更高。
4 试验与分析为测试上述以Hilbert曲线层级演进模型为基础的算法效率,本文采用Visual C++ 2015开发工具分别实现了笛卡儿坐标至Hilbert码的迭代计算方法[22]与本文计算方法,以及Morton码转换邻近格元Hilbert码计算方法[26]与本文邻近格元Hilbert码计算方法。全部程序编译为Release版本,并在计算机(CPU Intel Core i7-7700K双核4.2 GHz,内存64 GB,硬盘7200 r/min)上进行测试。
4.1 笛卡儿坐标至Hilbert码计算效率测试为测试本文基于Hilbert曲线层级演进模型的笛卡儿坐标至Hilbert码计算效率,设计试验进行测试:首先,在不同计算次数、相同阶数情况下,测试本文算法完成计算所需时间,并与迭代算法进行对比。然后,在不同阶数、相同计算次数情况下,测试本文算法完成计算所需时间,并与迭代算法进行对比。测试具体数值设置如下。
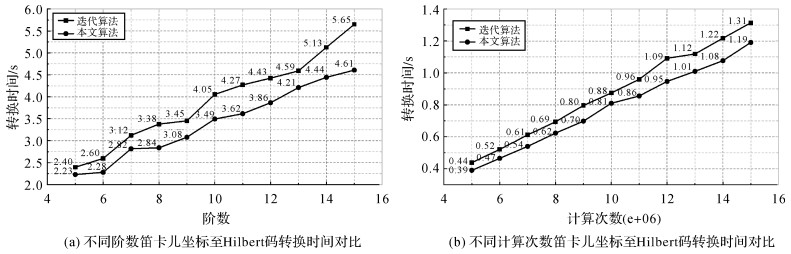
(1) 随机生成5×106个格元P(x, y, z),使用本文计算方法和迭代计算方法生成格元对应的5-15阶Hilbert码,记录两种算法计算耗时,结果如图 8(a)所示。
|
| 图 8 测试结果 Fig. 8 Test results |
(2) 随机生成{1×105,2×105,…, 20×105}个格元P(x, y, z),使用两种计算方法生成格元对应的10阶Hilbert码,记录两种算法计算耗时,结果如图 8(b)所示。
由测试结果可知:
(1) 图 8(a)中,在计算不同阶数Hilbert码时,本文方法所需的转换时间随转换阶数的增加而呈上升趋势,在阶数15时,进行1次转换所需的平均时间约为0.8 μs;对比迭代方法,在不同阶数时,本文方法的计算耗时更少,效率更高,如表 3所示在各组试验中,本文算法效率提升7%至23%。
| 阶数 | 计算耗时/s | 提升百分比 | |
| 迭代算法 | 本文算法 | ||
| 5 | 2.395 | 2.229 | 7% |
| 6 | 2.595 | 2.28 | 14% |
| 7 | 3.123 | 2.816 | 11% |
| 8 | 3.378 | 2.839 | 19% |
| 9 | 3.452 | 3.078 | 12% |
| 10 | 4.054 | 3.493 | 16% |
| 11 | 4.271 | 3.615 | 18% |
| 12 | 4.425 | 3.864 | 15% |
| 13 | 4.591 | 4.21 | 9% |
| 14 | 5.126 | 4.443 | 15% |
| 15 | 5.651 | 4.608 | 23% |
(2) 图 8(b)中,在计算不同次数的Hilbert码时,本文方法所需的转换时间随转换次数的增加而呈上升趋势,进行1次转换所需的平均时间约为0.7 μs;对比迭代方法,本文方法的计算耗时更少,效率更高,见表 4。在各组试验中,本文算法效率提升8%至15%。
| 计算次数/(e+06) | 计算耗时/s | 提升百分比 | |
| 迭代算法 | 本文算法 | ||
| 5 | 0.438 | 0.39 | 12% |
| 6 | 0.521 | 0.465 | 12% |
| 7 | 0.612 | 0.54 | 13% |
| 8 | 0.694 | 0.623 | 11% |
| 9 | 0.796 | 0.698 | 14% |
| 10 | 0.875 | 0.81 | 8% |
| 11 | 0.96 | 0.856 | 12% |
| 12 | 1.092 | 0.947 | 15% |
| 13 | 1.119 | 1.01 | 11% |
| 14 | 1.218 | 1.077 | 13% |
| 15 | 1.314 | 1.191 | 10% |
分析差异产生原因,本文方法以Hilbert码的层级演进模型为基础,采用状态矩阵S与演进矩阵E复现Hilbert曲线演进过程,避免了多维度迭代的步骤,算法过程更加直接简洁,因而获得更高的效率。本文方法能够以微妙级时间为代价完成1次笛卡儿坐标至Hilbert码的转换,对比于迭代算法,计算耗时更少,效率更高。
4.2 邻近格元Hilbert码计算效率测试为测试本文基于Hilbert曲线层级演进模型的邻近格元Hilbert,码计算效率,设计试验进行测试:首先,在相同层级、不同格元个数情况下,测试本文邻近格元Hilbert码计算方法完成计算所需时间,并与迭代算法进行对比。随后,在相同格元个数、不同格元层级情况下,测试本文邻近格元Hilbert码计算方法完成计算所需时间,并与迭代算法进行对比。测试试验具体数值设置如下。
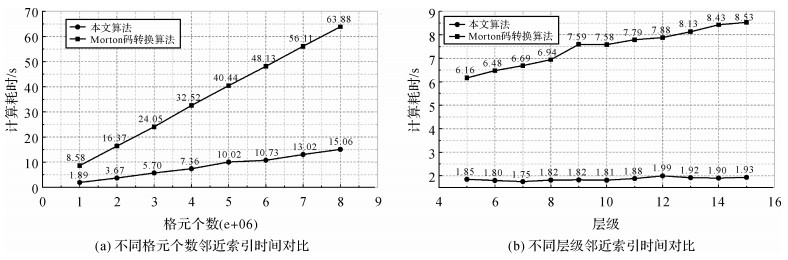
(1) 在层级15情况下,随机选取当前层级的{1×106, 2×106, …, 8×106}个格元,使用Morton码转换邻近格元Hilbert码计算方法与本文邻近格元Hilbert码计算方法进行某一随机方向上邻近格元Hilbert码计算,记录两种算法计算耗时,结果如图 9(a)所示。
|
| 图 9 测试结果 Fig. 9 Test results |
(2) 在层级5—15下,随机选取当前层级中的1×106个格元,并分别采用两种计算方法进行某一随机方向上邻近格元Hilbert码计算,记录两种算法计算耗时,结果如图 9(b)所示。
由测试结果可知:
(1) 图 9(a)中,相同格元层级情况下,两种方法对应曲线随着格元个数的增加均匀上升,表明两种方法的计算所需时间均与格元个数呈正相关;对比同一格元数下,两种方法所需的计算时间,本文方法的计算时间均要少于转换方法,各组测试中本文算法效率提高4.0至4.5倍,见表 5。
| 格元数/×106 | 计算总时间 | 提升倍数 | |
| 本文算法/s | 转换算法/s | ||
| 1 | 1.891 | 8.578 | 4.536 |
| 2 | 3.669 | 16.373 | 4.462 |
| 3 | 5.698 | 24.05 | 4.220 |
| 4 | 7.357 | 32.522 | 4.420 |
| 5 | 10.018 | 40.438 | 4.036 |
| 6 | 10.73 | 48.131 | 4.485 |
| 7 | 13.022 | 56.109 | 4.308 |
| 8 | 15.06 | 63.876 | 4.241 |
(2) 图 9(b)中,相同格元个数情况下,转换方法对应曲线随层级增加呈现较为均匀的增长趋势,说明其计算效率随层级的增加而线性降低;本文方法对应曲线较为平缓,随着层级的增加存在较为微小的波动,但计算耗时整体处于2 s以内,表明本文方法效率受层级影响较小。对比图 9(b)中同一层级下,两种方法所需的计算时间,本文方法所需时间均小于转换方法。本文算法效率提升倍数随层级增加有扩大趋势,在层级15情况下,效率提升了4.4倍,见表 6。
| 层级 | 计算总时间 | 提升倍数 | |
| 本文算法/s | 转换算法/s | ||
| 5 | 1.848 | 6.164 | 3.335 |
| 6 | 1.799 | 6.476 | 3.599 |
| 7 | 1.751 | 6.688 | 3.819 |
| 8 | 1.817 | 6.942 | 3.820 |
| 9 | 1.823 | 7.592 | 4.164 |
| 10 | 1.813 | 7.584 | 4.183 |
| 11 | 1.88 | 7.792 | 4.144 |
| 12 | 1.994 | 7.883 | 3.953 |
| 13 | 1.917 | 8.132 | 4.242 |
| 14 | 1.899 | 8.428 | 4.438 |
| 15 | 1.931 | 8.531 | 4.417 |
分析差异产生原因,转换方法需要将Hilbert码通过层级拆解转换为Morton码后,才能实现邻近格元Hilbert码计算,其时间复杂度与层级呈线性相关;本文计算方法则是通过层级演进模型复现了填充顺序在层级间的变化关系,只需寻找公共父格元即可实现邻近格元Hilbert码计算,因而效率更高,且算法时间复杂度只与中心格元与公共父格元的层级差相关,计算效率不随中心格元的层级发生显著改变。综上所述,在邻近格元Hilbert码计算效率上,本文方法的效率优于转换方法。
5 总结与展望高效、简便的网格单元编码运算及索引是全球离散网格系统的核心问题。作为网格编码研究的重要工具,Hilbert曲线网格编码实现了坐标等效降维表达,但是如何直接计算Hilbert曲线不同层级之间的变换、如何将格元多维空间结构与关系转换到一维Hilbert码的相关运算上仍然需要深入研究。本文对八叉树网格Hilbert曲线层级演进关系进行建模,采用状态矩阵S与演进矩阵E复现三维Hilbert曲线的演进过程。以层级演进模型为理论基础,设计笛卡儿坐标至Hilbert码计算方法以及邻近格元Hilbert码计算方法,避免现有算法中烦琐的迭代步骤,提高了Hilbert码层级属性的利用率,计算效率较高。下一步还需要研究如何在全球离散网格系统上运用Hilbert曲线层级演进模型这样的工具,包括:从局部欧氏空间到全球流形的变化带来方向、距离等度量不同,不同的全球离散网格系统在剖分方法上的不一致带来空间填充曲线具体实现等问题。
| [1] |
SAHR K, WHITE D, KIMERLING A J. Geodesic discrete global grid systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134. DOI:10.1559/152304003100011090 |
| [2] |
DUTTON G. Part 4: Mathematical, algorithmic and data structure issues: geodesic modelling of planetary relief[J]. Cartographica: The International Journal for Geographic Information & Geovisualization, 1984, 21(2-3): 188-207. |
| [3] |
万刚, 曹雪峰. 地理空间信息网格的历史演变与思考[J]. 测绘学报, 2016, 45(S1): 15-22. WAN Gang, CAO Xuefeng. The historical evolution and reflection of geospatial information grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 15-22. DOI:10.11947/j.AGCS.2016.F002 |
| [4] |
GOODCHILD M F, SHIREN Y. A hierarchical spatial data structure for global geographic information systems[R]. Santa Barbara: University of California, 1989.
|
| [5] |
SAGAN H. Space-filling curves[M]. New York: Springer- Verlag, 1994.
|
| [6] |
KUMAR A. Mean-variance analysis of the performance of spatial ordering methods[J]. International Journal of Geographical Information Science, 1998, 12(3): 269-289. DOI:10.1080/136588198241897 |
| [7] |
RONG Y, FALOUTSOS C. Analysis of the clustering property of Peano curves[M]. City of College Park: University of Maryland Press, 1991.
|
| [8] |
MOON B, JAGADISH H V, FALOUTSOS C, et al. Analysis of the clustering properties of the Hilbert space-filling curve[J]. IEEE Transactions on Knowledge and Data Engineering, 2001, 13(1): 124-141. DOI:10.1109/69.908985 |
| [9] |
SAMET H. Foundations of multidimensional and metric data structures[M]. Boston: Elsevier, 2006.
|
| [10] |
赵学胜, 贲进, 孙文彬, 等. 地球剖分格网研究进展综述[J]. 测绘学报, 2016, 45(S1): 1-14. ZHAO Xuesheng, BEN Jin, SUN Wenbin, et al. Overview of the research progress in the earth tessellation grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 1-14. DOI:10.11947/j.AGCS.2016.F001 |
| [11] |
程承旗, 张恩东, 万元嵬, 等. 遥感影像剖分金字塔研究[J]. 地理与地理信息科学, 2010, 26(1): 19-23. CHENG Chengqi, ZHANG Endong, WAN Yuanwei, et al. Research on remote sensing image subdivision pyramid[J]. Geography and Geo-Information Science, 2010, 26(1): 19-23. |
| [12] |
林冰仙, 许德朋, 盛业华, 等. 正二十面体球面菱形离散格网的编码模型及其映射方法[J]. 测绘学报, 2016, 45(S1): 23-31. LIN Bingxian, XU Depeng, SHENG Yehua, et al. Coding model and mapping method of spherical diamond discrete grids based on icosahedron[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 23-31. DOI:10.11947/j.AGCS.2016.F003 |
| [13] |
曹雪峰. 地球圈层空间网格理论与算法研究[D]. 郑州: 信息工程大学, 2012. CAO Xuefeng. Research on earth sphere shell space grid theory and algorithms[D]. Zhengzhou: Information Engineering University, 2012. |
| [14] |
曹雪峰, 万刚, 张宗佩. 紧致的Hilbert曲线Gray码索引算法[J]. 测绘学报, 2016, 45(S1): 90-98. CAO Xuefeng, WAN Gang, ZHANG Zongpei. Compact Hilbert curve index algorithm based on Gray code[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 90-98. DOI:10.11947/j.AGCS.2016.F010 |
| [15] |
张宗佩. 地月圈层立体网格理论与应用研究[D]. 郑州: 信息工程大学, 2015. ZHANG Zongpei. Research on earth-lunar sphere shell space grid theory and application[D]. Zhengzhou: Information Engineering University, 2015. |
| [16] |
张宗佩, 万刚, 曹雪峰, 等. 地月圈层空间立体网格技术及其编码转换方法[J]. 测绘通报, 2015(6): 20-23, 27. ZHANG Zongpei, WAN Gang, CAO Xuefeng, et al. Earth-lunar shell space solid grid technology and coding-conversion[J]. Bulletin of Surveying and Mapping, 2015(6): 20-23, 27. DOI:10.13474/j.cnki.11-2246.2015.0169 |
| [17] |
张宗佩, 万刚, 曹雪峰, 等. 月球圈层空间立体网格技术研究[J]. 测绘科学技术学报, 2015(1): 101-105, 110. ZHANG Zongpei, WAN Gang, CAO Xuefeng, et al. Lunar shell space solid grid technology[J]. Journal of Geomatics Science and Technology, 2015(1): 101-105, 110. DOI:10.3969/j.issn.1673-6338.2015.01.021 |
| [18] |
吴宇豪, 曹雪峰. 虚拟战场环境时空数据的Hilbert码索引方法[J]. 武汉大学学报(信息科学版), 2020, 45(9): 1403-1411. WU Yuhao, CAO Xuefeng. Hilbert code index method for spatiotemporal data of virtual battlefield environment[J]. Geomatics and Information Science of Wuhan University, 2020, 45(9): 1403-1411. |
| [19] |
GUAN Xuefeng, VAN OOSTEROM P, CHENG Bo. A parallel N-dimensional space-filling curve library and its application in massive point cloud management[J]. ISPRS International Journal of Geo-Information, 2018, 7(8): 327. DOI:10.3390/ijgi7080327 |
| [20] |
WU Yuhao, CAO Xuefeng, AN Zipeng. A spatiotemporal trajectory data index based on the Hilbert curve code[C]//Proceedings of the First China Digital Earth Conference 18-20 November 2019, Beijing, China: IOP Conference Series: Earth and Environmental Science, 2020.
|
| [21] |
LIU Xian, SCHRACK G. Encoding and decoding the Hilbert order[J]. Software: Practice and Experience, 1996, 26(12): 1335-1346. DOI:10.1002/(SICI)1097-024X(199612)26:12<1335::AID-SPE60>3.0.CO;2-A |
| [22] |
LI Chenyang, FENG Yucai. Algorithm for analyzing N-dimensional Hilbert curve[C]//Proceedings of International Conference on Web-Age Information Management. Hangzhou, China: Springer, 2005: 657-662.
|
| [23] |
李绍俊, 钟耳顺, 王少华, 等. 基于状态转移矩阵的Hilbert码快速生成算法[J]. 地球信息科学学报, 2014, 16(6): 846-851. LI Shaojun, ZHONG Ershun, WANG Shaohua, et al. An algorithm for Hilbert ordering code based on state-transition matrix[J]. Journal of Geo-Information Science, 2014, 16(6): 846-851. |
| [24] |
曹雪峰, 万刚, 张宗佩. Hilbert曲线层级演进关系[J]. 测绘学报, 2016, 45(S1): 77-84. CAO Xuefeng, WAN Gang, ZHANG Zongpei. Hilbert curve hierarchical evolution relationship[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 77-84. DOI:10.11947/j.AGCS.2016.F009 |
| [25] |
CHOI M G, JU E, CHANG J W, et al. Linkless Octree using multi-level perfect hashing[J]. Computer Graphics Forum, 2009, 28(7): 1773-1780. DOI:10.1111/j.1467-8659.2009.01554.x |
| [26] |
CHEN H L, CHANG Y I. Neighbor-finding based on space- filling curves[J]. Information Systems, 2005, 30(3): 205-226. DOI:10.1016/j.is.2003.12.002 |
| [27] |
徐红波, 郝忠孝. 基于空间填充曲线网格划分的最近邻查询算法[J]. 计算机科学, 2010, 37(1): 184-188. XU Hongbo, HAO Zhongxiao. Nearest-neighbor query algorithm based on grid partition of space-filling curve[J]. Computer Science, 2010, 37(1): 184-188. DOI:10.3969/j.issn.1002-137X.2010.01.043 |
| [28] |
CHEN H L, CHANG Y I. All-nearest-neighbors finding based on the Hilbert curve[J]. Expert Systems with Applications, 2011, 38(6): 7462-7475. DOI:10.1016/j.eswa.2010.12.077 |
| [29] |
WU Yuhao, CAO Xuefeng, SUN Wanzhong. MI-HCS: monotonically increasing Hilbert code segments for 3D geospatial query window[J]. IEEE Access, 2020, 8: 47580-47595. DOI:10.1109/ACCESS.2020.2979250 |
| [30] |
李晨阳, 段雄文, 冯玉才. N维Hilbert曲线生成算法[J]. 中国图象图形学报, 2006, 11(8): 1068-1075. LI Chenyang, DUAN Xiongwen, FENG Yucai. Algorithm for generating N-dimensional Hilbert curve[J]. Journal of Image and Graphics, 2006, 11(8): 1068-1075. DOI:10.3969/j.issn.1006-8961.2006.08.003 |
| [31] |
巴恩斯利M F. 分形图形学[M]. 和风, 译. 北京: 海洋出版社, 1995. BARNSLEY M F. The science of fractal images[M]. HE Feng, trans. Beijing: China Ocean Press, 1995. |



