观测值频间偏差(inter-frequency bias, IFB)一直是影响GLONASS导航定位性能的重要因素。IFB主要是源于同一频段(L1/L2)上不同GLONASS卫星的观测信号硬件延迟差异[1]。在基于双差模型的基线解算中,观测值站间单差能够消除卫星端IFB,而接收机端IFB受测站固件设备影响,难以直接消除。按观测值类型,IFB可划分为频间相位偏差(inter-frequency phase bias, IFPB)和频间码偏差(inter-frequency code bias, IFCB)[2]。文献[3-4]指出IFPB的本质是伪距观测值和载波观测值的硬件延迟之差,并将IFPB划分为数字信号处理引起的延迟和硬件本身引起的延迟两部分,且数字信号处理引起的延迟占主要部分,因此,IFPB与信号频率和接收机类型有很强的相关性。基于IFPB与信号频率的线性关系,许多学者采用估计IFPB变化率、构建纯载波观测值组合等方式,实现了毫米级的IFPB改正,消除IFPB对高精度定位的影响[5-9]。IFPB相关参数已经引入接收机独立交换格式RINEX3.03文件和差分GNSS数据传输协议RTCM10403.X中,在导航定位服务中取得了良好的应用[10]。
IFCB主要因接收设备的前端带宽和相关器设计导致的芯片畸变产生,且每个信号通道的畸变量存在差异[11]。与能够高精度模型化的IFPB相比,IFCB的变化规律较为复杂[12]。文献[13]采用精密单点定位模型估计了来自5家厂商的133台接收机的非差消电离层组合IFCB,验证了接收机或天线的品牌、系列和固件版本都会对IFCB的量级产生影响。文献[14-15]提出了组合观测值的IFCB的估计策略,指出虽然IFCB与频率存在相关性,但难以构建通用的高精度线性模型,且个别测站的IFCB存在明显差异。综合多位学者的研究成果,IFCB的主要特性可归纳为:①L1和L2上IFCB的量级不同,都具有一定的长期稳定性;②同质基线的IFCB量级相差很小,但也有一些特例存在;③异质基线的双差IFCB可达数米;④不同接收设备的IFCB与通道号的线性关系不一致,导致IFCB无法采用统一模型改正。本文将GNSS信号接收设备(接收机类型、固件版本、天线类型)完全相同的测站构成的基线称为同质基线,其他基线统称为异质基线。
由于IFCB难以基于经验模型改正,在异质基线或精密单点定位解算中,通常将每颗卫星的IFCB或其与频率号相关的变化率作为一个静态参数估计。文献[13-15]将基于历史观测值估计HMW或消电离层组合的IFCB用于GLONASS伪距组合观测值实时改正。文献[16]直接将各颗卫星IFCB作为一个静态参数估计,进行载波观测值变换合成超窄巷模糊度,实现长基线GLONASS模糊度固定,但该算法受限于观测值噪声,仅能用于事后解算。文献[17]在RTK定位模型中,将IFCB与频率号相关的变化率作为静态参数进行估计,但从其结果来看,IFCB变化率参数估计策略显然是不符合IFCB特性的。文献[18]提出了一种用于精密单点定位消电离层组合的IFCB实时改正方法,能够明显改善GLONASS PPP定位的收敛速度和浮点解精度。德国地学研究中心(German Research Centre for Geosciences, GFZ)已经开始发布与接收机类型相关的消电离层组合IFCB[19]。但是,上述研究都是针对观测值组合的IFCB,且难以直接用于GLONASS实时非组合模糊度固定。尤其是异质基线的中长距离RTK定位解算,伪距观测值的IFCB可导致模糊度参数估计偏差,进而模糊度固定困难。
本文针对异质基线GLONASS双差IFCB难以消除的问题,基于HMW组合和消电离层组合观测值,提出一种非组合站间IFCB估计方法,对两个频段伪距观测值的站间IFCB进行研究,并将该算法用于GPS/GLONASS组合RTK定位解算。需要指出的是,本文主要对GLONASS IFCB特性进行研究,IFPB直接采用相关学者发布的先验值进行改正[5],见表 1。
| 接收机品牌 | IFPB变化率/cm |
| Trimble | -0.7 |
| Javad, JPS, TPS | 0.0 |
| Leica, Novatel | 2.3 |
| Septentrio | 4.9 |
1 数学模型 1.1 GLONASS站间IFCB估计方法
GLONASS双差观测值可模型化为[5]
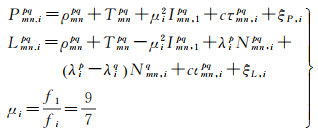 (1)
(1)
式中,P和L分别代表伪距和载波相位观测值,单位为m;ρ表示卫星到测站的几何距离;p和q为GLONASS卫星PRN,pq表示星间单差,q为参考星;m和n为基线测站编号,mn表示站间单差;T为对流层延迟;Imn, 1pq为第一频点上的双差电离层延迟;f1和f2为观测值频率;τ为IFCB,ι为IFPB,单位为s;λ为载波波长;N为整周模糊度;ξ为多路径和观测噪声;c为光速。GLONASS两个单差模糊度转化为一个双差和一个单差模糊度。由于GLONASS频分多址信号不同卫星的同一频段载波波长相差很小,在毫米级,即λip-λiq量级很小,单差模糊度可以直接取近似值引入观测量。
双差HMW(Hatch-Melbourne-Wübbena)组合可分解为一个双差伪距窄巷组合(narrow-lane, NL)和一个双差宽巷载波组合(wide-lane, WL),顾及GLONASS IFB的影响,HMW组合可模型化为[15, 20]
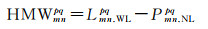 (2)
(2)
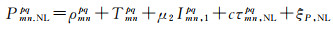 (3)
(3)
 (4)
(4)
式中
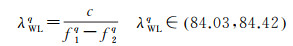 (5)
(5)
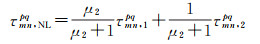 (6)
(6)
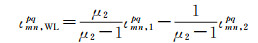 (7)
(7)
综合式(2)-式(7)可获双差IFCB的窄巷组合,如式(8)所示
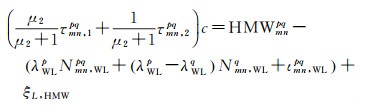 (8)
(8)
式中,单差宽巷模糊度可以通过伪距观测值和载波观测值做差直接获得。文献[21]中给出了GLONASS宽巷模糊度实时固定方法,IFPB采用先验值修正,于是式(8)等号右侧部分可以实时获取。
GLONASS双差伪距观测值消电离层组合可表示为
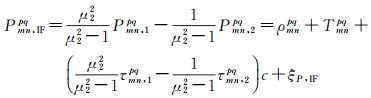 (9)
(9)
式中,IF表示消电离层组合;等号右侧部分,GNSS RTK定位精度一般能够快速收敛到分米甚至厘米级,获得分米级以上精度的双差星地几何距离ρmnpq;采用GTP2w模型估计,可以获得厘米级精度的对流层干延迟[22-23];IFPB可基于先验信息改正。因此,式(9)右侧部分也能够实时获取。
将对流层湿延迟模型化为天顶对流层湿延迟和VMF1映射函数,可得式(10)
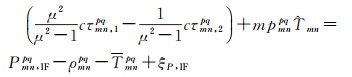 (10)
(10)
式中,Tmnpq为对流层模型计算量;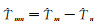
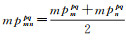
基于式(8)和式(10),可得一个GLONASS卫星非组合双差IFCB解算方程
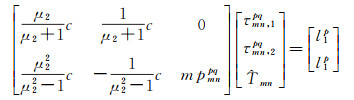 (11)
(11)
通过矩阵转换,可将双差IFCB参数变换为站间单差IFCB,如式(12)所示
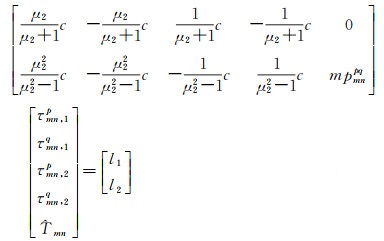 (12)
(12)
为消除方程秩亏,将参考卫星各频段(P1、P2)站间IFCB为0,测站间天顶方向对流层湿延迟等于0,3个条件作为虚拟观测值引入模型,可得非组合站间IFCB的估计模型
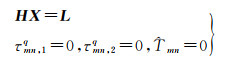 (13)
(13)
常规GNSS的RTK函数模型[9]为
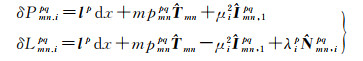 (14)
(14)
式中,δPmn.ipq和δLmn.ipq表示双差伪距和载波非组合观测值残差;lp为卫星到流动站的方向余弦向量;mp为对流层延迟映射函数;dx、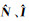
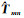
综合式(1)和式(14)可知,若RTK函数模型未顾及GLONASS站间IFCB,站间IFCB与电离层参数具有相关性,式(14)中电离层和模糊度参数的含义为
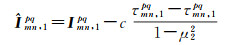 (15)
(15)
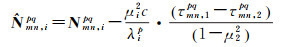 (16)
(16)
对于忽略大气延迟参数的短基线RTK,站间IFCB也会影响流动站坐标改正参数的估值,导致模糊度参数收敛速度减缓。
基于上文的GLONASS站间IFCB估计方法,本文提出一种实时修正GLONASS站间IFCB的RTK定位解算模型,如式(17)所示。利用文献[21]的中长距离基线解算模型,进行GPS/GLONASS组合RTK定位,获得GLONASS宽巷整周模糊度和流动站近似坐标,实时估计GLONASS站间IFCB。并将宽巷模糊度作为RTK定位解算的未知参数,构建RTK定位模型,实现站间IFCB改正和RTK定位同步进行
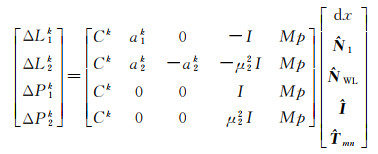 (17)
(17)
式中,k为历元编号;[ΔL1k ΔL2k ΔP1k ΔP2k]T为当前历元的双频观测值残差向量;C为卫星到流动站的方向余弦向量;a1k和a2k为对角矩阵diag(λ11 λ12 … λ1α)和diag(λ21 λ22 … λ2α),α为可见卫星数;I为α×α单位矩阵,Mp为卫星的天顶对流层湿延迟映射函数向量;dx、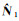
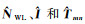
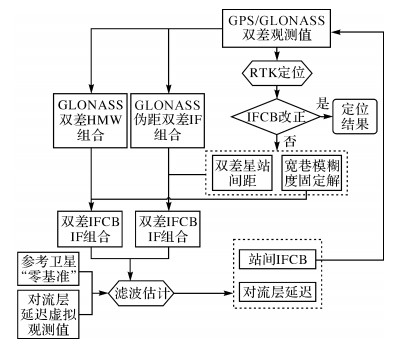
图 1给出了站间IFCB实时改正的RTK定位解算流程,可划分为以下4个步骤:
|
| 图 1 站间IFCB实时改正的RTK定位解算 Fig. 1 Real time inter-station IFCB correction algorithm in RTK |
(1) 采用式(17)进行RTK定位解算,如果已经改正IFCB,直接输出定位结果,结束当前历元解算。
(2) 若未改正IFCB,则输出双差星站间距和宽巷模糊度固定解,分别与GLONASS伪距双差消电离层组合和HMW组合一起,基于式(8)和式(10),获得双差IFCB窄巷组合和消电离层组合观测量。
(3) 基于双差站间IFCB宽巷组合和消电离层组合,引入参考星“零基准”和站间天顶对流层延迟虚拟观测值,构建式(13)模型,滤波估计站间IFCB,实时改正GLONASS双差伪距观测值。
(4) 站间IFCB改正后,重新开始步骤(1)的解算,输出RTK定位结果。
本文在基线长度小于20 km的RTK定位中忽略大气延迟的影响,中长距离的RTK定位将大气延迟作为参数进行估计。对流层延迟先利用经验模型改正干分量、湿分量作为未知参数估计。将各颗卫星L1的双差电离层延迟作为未知参数估计且历元间不相关。
2 试验与分析 2.1 试验说明试验数据源为欧洲区域参考框架连续GNSS观测网络(EUREF permanent GNSS network, EPN)24个基准站的观测数据(http://www.epncb.oma.be/index.php)[24],构建12条基线进行RTK定位解算,见表 2。12条基线中BS10为同质基线,其他基线为异质基线。基线长度分布在0~130 km,BS01-BS03基线长度小于5 km;BS04-BS12基线长度在20 km以上。
| 基线名 | 基准站 | 接收机 | 天线 | 流动站 | 接收机 | 天线 | 基线长/km |
| BS1 | GOPE | TRIMBLE ALLOY 5.44 | TPSCR.G3 TPSH | GOP6 | SEPT POLARX5 5.3.2 | SEPCHOKE_B3E6 SPKE | 0.004 |
| BS2 | MAR6 | SEPT POLARX5 5.3.0 | AOAD/M_T OSOD | MAR7 | TRIMBLE ALLOY 5.43 | LEIAR25.R3 LEIT | 0.011 |
| BS3 | MET3 | JAVAD TRE_3 DELTA 3.7.7 | JAVRINGANT_DM SCIS | METG | TRIMBLE NETR9 5.43 | TRM59800.00 SCIS | 2.8 |
| BS4 | PASA | LEICA GR30 4.31/7.403 | LEIAR20 LEIM | SCOA | LEICA GR25 4.31 | TRM55971.00 NONE | 22.1 |
| BS5 | PADO | SEPT POLARX5 5.3.2 | SEPCHOKE_B3E6 SPKE | VEN1 | LEICA GR30 4.20 | LEIAR20 NONE | 35.0 |
| BS6 | BCLN | LEICA GR10 3.11.1639/6.524 | LEIAR25.R4 LEIT | BELL | LEICA GR50 4.31/7.403 | LEIAR25.R4 NONE | 55.0 |
| BS7 | DENT | SEPT POLARX4 2.9.6 | TRM59800.00 NONE | VLIS | LEICA GR50 4.31/7.403 | LEIAR25.R4 LEIT | 58.4 |
| BS8 | HEL2 | LEICA GR50 4.31.101/7.403 | LEIAR25.R4 LEIT | RANT | JAVAD TRE_3 DELTA 3.7.9 | LEIAR25.R4 LEIT | 74.5 |
| BS9 | TERS | SEPT POLARX4 2.9.6 | LEIAR25.R4 LEIT | BORJ | JAVAD TRE_3 DELTA 3.7.9 | LEIAR25.R4 LEIT | 99.1 |
| BS10 | CRAK | LEICA GR30 4.31/7.403 | LEIAR25.R4 EIT | CTAB | LEICA GR30 4.31/7.403 | LEIAR25.R4 LEIT | 103.3 |
| BS11 | TOIL | LEICA GR25 4.31/6.713 | LEIAR25.R4 LEIT | VIR2 | JAVAD TRE_3 DELTA 3.7.7 | JAVRINGANT_DM SCIS | 126.0 |
| BS12 | LEON | LEICA GR25 3.11.1639 | LEIAR25 NONE | VALA | LEICA GR30 4.31/7.403 | LEIAR25.R3 NONE | 127.6 |
本文进行了站间IFCB估计及特性分析、实时改正站间IFCB的RTK定位两个试验,其具体试验设置如下:
(1) 站间IFCB估计及特性分析试验。基于2020年DOY 100-DOY 119,20 d,采样间隔30 s,GPS/GLONASS观测数据估计站间IFCB并对其特性进行分析。采用参数可变的序贯最小二乘平差算法估计站间IFCB和测站间天顶对流层湿延迟参数。站间IFCB作为不随时间变化的恒定参数,天顶对流层湿延迟的过程噪声采用随机游走模型表示。顾及GLONASS伪距IFCB的影响,试验设定GLOANSS伪距的先验噪声为0.5 m,GPS伪距先验噪声为0.3 m,GPS和GLONASS载波相位的先验噪声为0.003 m;观测值高度角定权策略为P=1, el>30°; P=sin(el), el≤30°[14, 25]。卫星高度角阈值为7°。由于各颗卫星的站间IFCB估值是基于一定基准的相对值,如果以双差解算的参考星为基准,解算过程中参考星的变换会导致站间IFCB的数值变化。为便于统计分析,站间IFCB单天解估计选取所有可见卫星各频段的站间IFCB之和等于0为基准,以确保整个解算过程的基准统一。
(2) 实时改正站间IFCB的RTK定位试验。利用2020年DOY 119的24 h,采样间隔1 s,GPS/GLONASS观测数据验证本文GLONASS站间IFCB实时改正算法对RTK定位解算的影响。观测值噪声、高度角定权和阈值、对流层延迟估计、站间IFCB估计等策略与试验(1)相同。以参考星的站间IFCB为0作为基准。RTK模糊度解算采用分步固定的部分模糊度固定策略。首先,采用取整算法固定宽巷模糊度,取整阈值为0.25周,浮点解理论成功率大于99.9%。其次,基于宽巷模糊度固定解更新解算方程,采用LAMBDA算法搜索窄巷模糊度,并进行ratio检验[26],ratio阈值设为2.5。如果模糊度搜索未通过ratio检验,则删除搜索区域中高度角最低卫星的模糊度,重新搜索,直到通过ratio检验。RTK定位过程中,当前历元仅继承上一历元的浮点解,滤波解算后,重新进行模糊度搜索固定,以避免继承上一个历元错误的固定解。
为验证实时站间IFCB算法可行性,本文采用单GPS、未改正站间IFCB的GPS/GLONASS组合,以及实时改正站间IFCB的GPS/GLONASS组合3种RTK定位模式,分别以G、GRuc-IFCB和GR rtc-IFCB表示。RTK定位解算每小时初始化一次,统计其收敛时间、首次固定时间、模糊度固定率和定位偏差等指标。
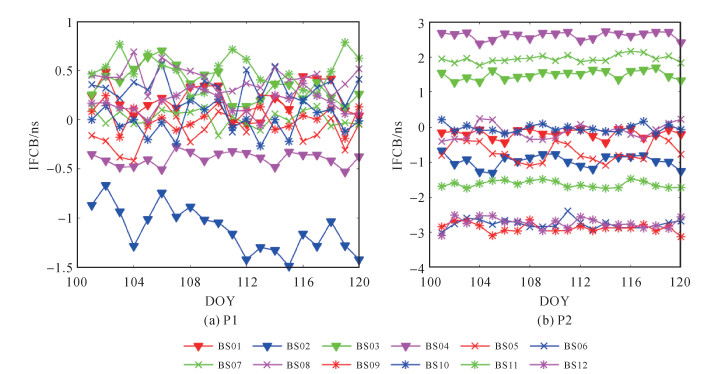
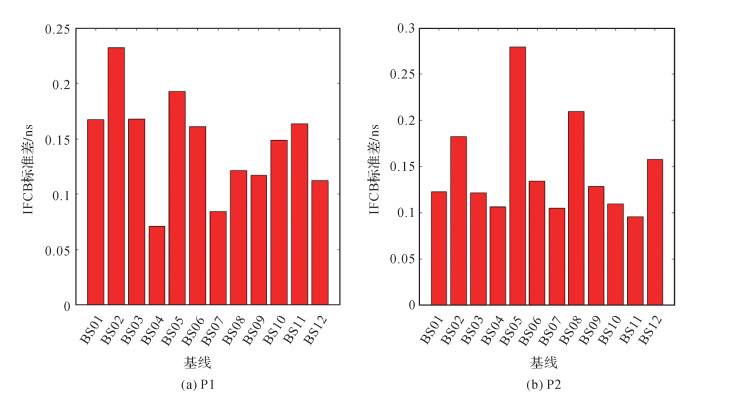
2.2 站间IFCB估计结果和特性分析图 2给出了GLONASSR01卫星两个频段伪距(P1和P2)的站间IFCB单天解时间序列。各条基线站间IFCB存在明显差异,一些基线的站间IFCB接近3 ns,如基线BS06、BS09、BS12的P2站间IFCB。同一条基线P1和P2站间IFCB的量级存在很大差异,如基线BS04 P1站间IFCB约-0.4 ns,而P2站间IFCB达到2.6 ns。同质基线BS10的站间IFCB估值明显比异质基线小,其P1和P2上站间IFCB估值均小于0.3 ns。站间IFCB单天解估值具有一定的稳定性,如图 3所示,所有基线的GLONASSR01卫星单天解的标准差均小于0.3 ns。受多路径等未模型化误差的影响,基线BS02 P1和基线BS05 P2的站间IFCB标准差较大,分别约0.24 ns和0.28 ns。
|
| 图 2 GLONASS R01卫星站间IFCB单天解估值的时间序列 Fig. 2 Daily estimate values of GLONASS R01 inter-station IFCB |
|
| 图 3 GLONASS R01卫星站间IFCB单天解估值的标准差 Fig. 3 Standard deviation of daily GLONASS R01 inter-station IFCB |
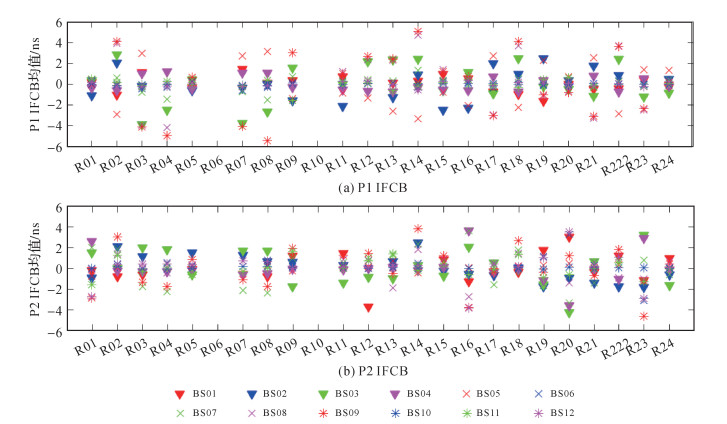
图 4中给出了所有基线各颗GLONASS卫星的站间IFCB单天解估值均值。图 4中信息能够证明基于图 2和图 3获取的结论具有普适性。以卫星R14为例,基线BS09 P1站间IFCB的量级接近6 ns;基线BS09和BS05的P1站间IFCB之差约10 ns。基线BS01 R12卫星P1站间IFCB小于-0.3 ns,而其P2站间IFCB接近-4 ns。同质基线所有卫星的站间IFCB估值分布在[-0.6, 0.6] ns区间内。
|
| 图 4 各颗GLONASS卫星站间IFCB单天解平均值 Fig. 4 The averages of GLONASS inter-station IFCB daily estimate values |
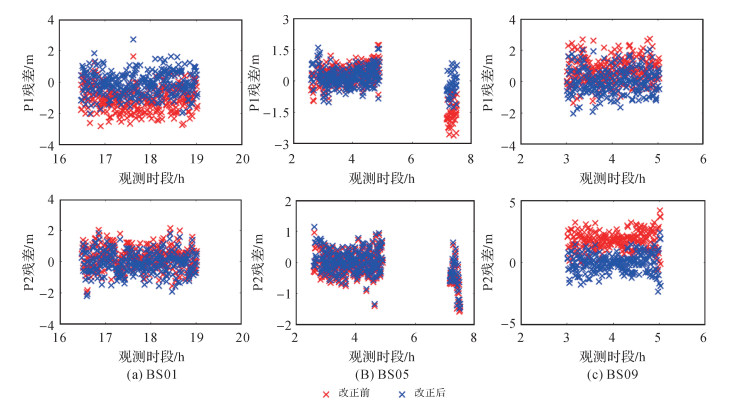
图 5给出了R09卫星改正站间IFCB前后的伪距观测值残差。由图 5可知,BS01 P1、BS05 P1、BS09 P1、BS09 P2都存在明显的系统性偏差。例如,BS09 P2的残差分布在区间[0, 5] m之间,均值在2.3 m左右。由于参考卫星的变换,BS05 P1残差在两个观测时段的系统偏差项不同。改正站间IFCB以后,所有卫星的伪距残差分布区间明显向0平移,BS05伪距残差在两个观测时段的分布区间差异也被消除。
|
| 图 5 卫星R09改正站间IFCB前后的伪距观测值残差 Fig. 5 Residual errors of R09 pseudorange observations before and after IFCB correction |
2.3 站间IFCB改正对RTK定位的影响
站间IFCB导致异质基线双差伪距观测值的系统性偏差,影响RTK定位结果。由于IFCB与接收机类型、固件版本和天线类型相关的复杂特性,甚至同质基线也可能存在系统性偏差。因此,需要采用与接收设备无关的实时校正算法,实现伪距观测值系统性偏差的消除。
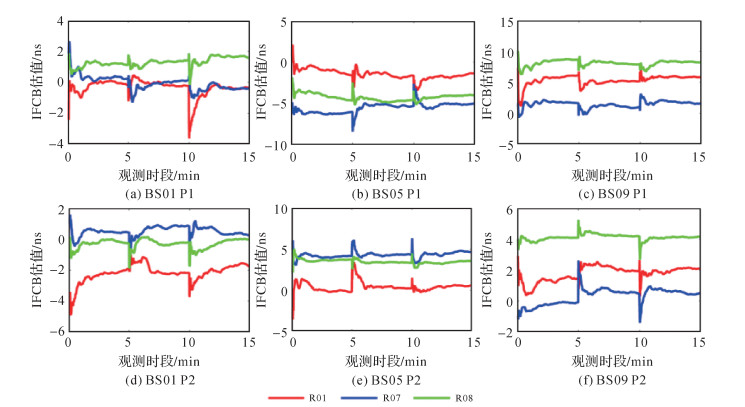
图 6给出了短基线BS01、中距离基线BS05和长距离基线BS09的R01、R07和R08 3颗GLONASS卫星站间IFCB实时估值的时间序列。试验数据观测时段2020年DOY 119 UTC 06∶00-06∶30,采样间隔为1 s,每5 min进行一次站间IFCB重新初始化解算。由图 6可知,站间IFCB估值通过约30 s序贯最小二乘平差迭代即可获得分米级的精度,1 min内完成收敛。因此,将迭代1 min的站间IFCB估值用于修正GLONASS伪距观测值具有可行性。
|
| 图 6 基线BS09GLONASS卫星站间IFCB实时估值时间序列 Fig. 6 Time series of GLONASS inter-station IFCB estimates on baseline BS09 |
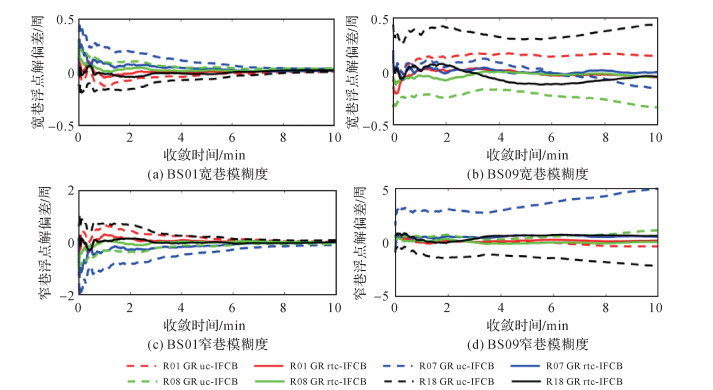
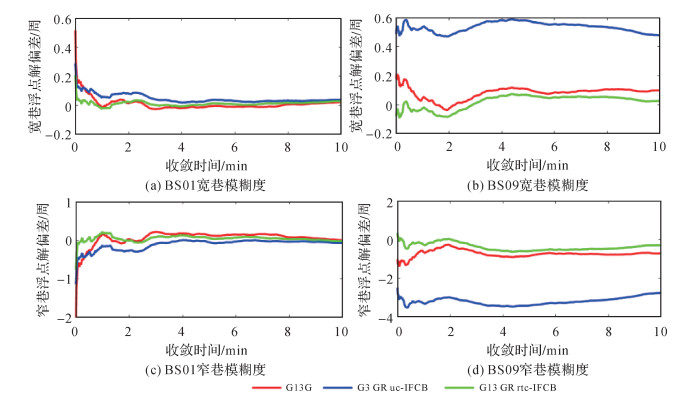
采用G、GR uc-IFCB和GR rtc-IFCB 3种模式分别进行RTK定位解算。图 7和图 8给出了基线BS01和BS09的GLONSS和GPS卫星模糊度浮点解偏差。短基线RTK场景下,忽略了双差大气延迟的影响,GLONASS站间IFCB在解算过程中主要归入残差向量,需要通过更长时间的滤波,才可以获得准确的模糊度浮点解。因此,短基线BS01,未改正站间IFCB时,GLONASS卫星需要约6 min时间才能获得稳定的高精度模糊度参数浮点解,站间IFCB实时改正算法可将收敛时间缩短到3 min以内;如图 8左侧图所示,改正站间IFCB可以明显加快GPS卫星模糊度浮点解收敛。在中长基线RTK场景下,需估计电离层和对流层延迟参数,由于电离层参数与站间IFCB的强相关性,导致电离层参数估值产生偏差,进而影响模糊度浮点解。修正GLONASS伪距观测值对中长基线RTK定位至关重要,可有效消除估计参数偏差,改善模糊度准确度,提高模糊度固定率和RTK定位性能。
|
| 图 7 GLONSS卫星宽巷和窄巷模糊度浮点解偏差 Fig. 7 The bias of GLONASS satellite wide-lane and narrow-lane ambiguity float solutions |
|
| 图 8 GPS卫星G13宽巷和窄巷模糊度浮点解偏差 Fig. 8 The bias of GPS satellite G13 wide-lane and narrow-lane ambiguity float solutions |
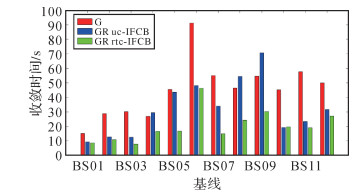
图 9统计了所有基线不同模型RTK解算模式下的收敛时间。本文将RTK定位水平方向偏差稳定在小于0.1 m作为判定收敛完成的阈值[14, 27]。基线BS04、BS08和BS09受站间IFCB的影响,GPS/GLONASS组合RTK定位收敛速度较单GPS RTK定位变慢。站间IFCB实时改正后,GPS/GLONASS组合RTK收敛速度明显加快,大部分基线的收敛时间减小到单GPS RTK的60%以下,解决了因引入GLONASS卫星导致异质基线收敛速度降低的问题。站间IFCB改正算法对同质基线BS10 GPS/GLONASS组合RTK定位收敛时间的影响很小。基线BS06因流动站数据质量较差,定位收敛速度较慢,单GPS RTK需要约90 s完成收敛。
|
| 图 9 不同模式RTK解算的收敛时间 Fig. 9 Convergence time of RTK positioning solutions |
采用式(18)和式(19)统计模糊度固定成功率Psuc和正确率Pcor
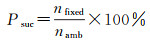 (18)
(18)
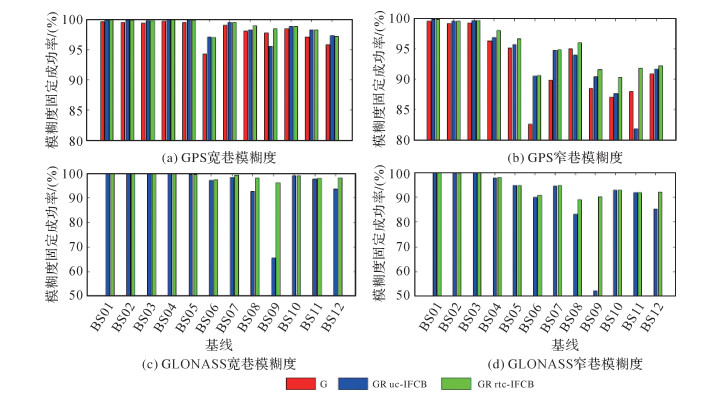
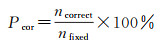 (19)
(19)
式中,namb为解算中模糊度参数的总数;nfixed为固定的模糊度参数个数;ncorrect为正确固定的模糊度参数个数。
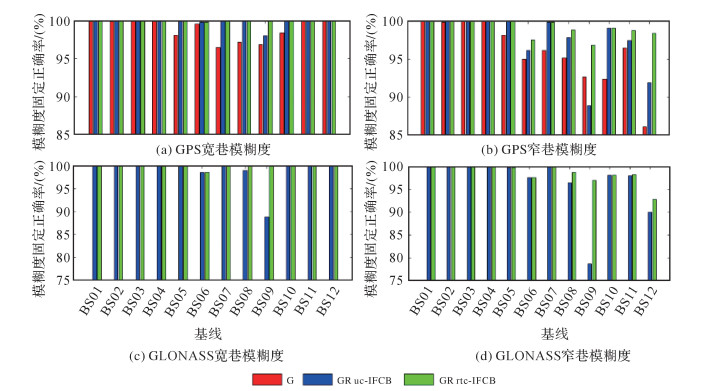
站间IFCB改正能够显著提高中长距离基线的GPS和GLONASS卫星模糊度固定成功率和正确率,如图 10和图 11所示。站间IFCB导致基线BS09的GLONASS卫星窄巷模糊度固定成功率低至52%,改正后提高到约90%,模糊度固定正确率也从85%提高到96%。短基线(BS01-BS04),双差大气延迟量级较小,可忽略,模糊度固定容易,改正站间IFCB对模糊度固定的影响不大。但是,当站间IFCB量级很大时,改正站间IFCB对提高模糊度固定效率十分必要。
|
| 图 10 RTK定位解算模糊度参数固定成功率 Fig. 10 The successful fixing rates of ambiguity parameters in RTK solution |
|
| 图 11 RTK定位解算模糊度参数固定正确率 Fig. 11 The correct fixing rates of ambiguity parameters in RTK solution |
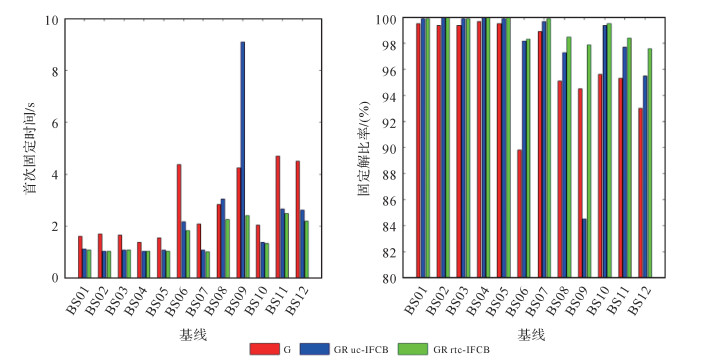
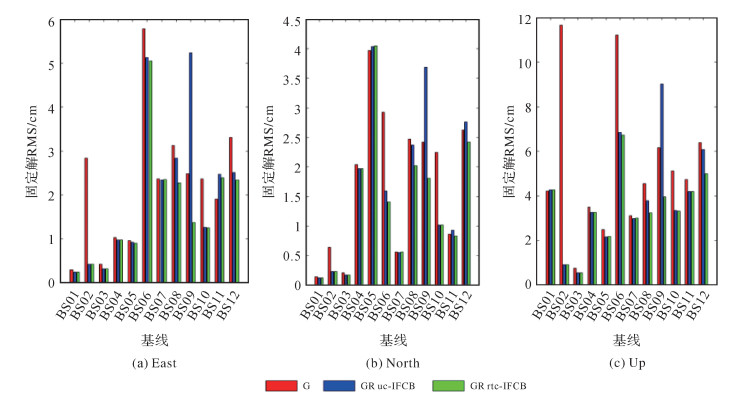
采用分步部分模糊度固定策略获得RTK固定解,统计其首次固定时间、固定解比率和固定解偏差RMS,如图 12和图 13所示。以EPN网站发布的坐标值作为参考站和流动站坐标的真值。与上文试验结果类似,站间IFCB改正算法能够明显改善中长距离基线GPS/GLONASS组合RTK定位性能。相比单GPS,站间IFCB导致基线BS09的GPS/GLONASS组合RTK首次固定时间变长且固定解比率降低。进行站间IFCB改正后,首次固定时间统计值从9.2 s提高到2.1 s,固定解比率从84.5%提高到97.9%。由于短基线RTK能够实时获得固定解,站间IFCB改正对定位结果的影响不明显。改正站间IFCB后,模糊度固定率提高,RTK固定解的定位偏差也有不同程度的改善。如基线BS12东北天方向的定位偏差RMS分别从2.5、2.8、6.1 cm提高到2.3、2.4、5.0 cm,其中高程方向改善率达18%。
|
| 图 12 RTK定位首次获取固定解时间和固定解比率 Fig. 12 Time to first fixed and rates of RTK fixed solutions |
|
| 图 13 RTK定位固定解ENU方向的RMS Fig. 13 Positioning bias RMS of RTK fixed solutions on E/N/U direction |
3 结论
本文提出了一种不依赖测站设备信息的站间IFCB实时估计方法,对GLONASS卫星各频段站间IFCB进行了特性分析,并将站间IFCB实时改正算法应用于GPS/GLONASS组合RTK定位,获得了以下结论:
(1) 站间IFCB单天解具有一定的稳定性,20 d内单天解估值的标准差小于0.3 ns,同一条基线不同频段站间IFCB的量级存在很大差异,可达几个纳秒。站间IFCB会导致异质基线RTK解算模糊度固定失败,甚至个别基线GPS/GLONASS组合定位的性能比单GPS差。
(2) 将站间IFCB实时估计算法用于GPS/GLONASS组合RTK定位,能够显著改善GPS/GLONASS组合RTK定位性能。对于受站间IFCB影响严重的基线,算法能够将GLONASS卫星窄巷模糊度固定成功率从52%提高到90%以上,东北天方向的定位偏差RMS分别从2.5、2.8、6.1 cm提高到2.3、2.4、5.0 cm。
| [1] |
WANNINGER L, WALLSTAB-FREITAG S. Combined processing of GPS, GLONASS, and SBAS Code phase and carrier phase measurements[C]//Proceedings of 2011 International Technical Meeting of the Satellite Division of the Institute of Navigation. [S. l.]: Fort Worth Press, 2007: 866-875.
|
| [2] |
REUSSNER N, WANNINGER L. GLONASS inter-frequency biases and their effects on RTK and PPP carrier-phase ambiguity resolution[C]//Proceedings of Inter-national Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, Oregon, USA: [s. n.], 2011, 10(1): 712-716.
|
| [3] |
SLEEWAGEN J, SIMSKY A, WILDE W, et al. Demystifying GLONASS inter-frequency carrier phase biases[J]. Inside GNSS, 2012, 7(3): 57-61. |
| [4] |
GENG J, ZHAO Q, SHI C, et al. A review on the inter-frequency biases of GLONASS carrier-phase data[J]. Journal of Geodesy, 91(3): 329-340. DOI:10.1007/s00190-016-0967-9 |
| [5] |
WANNINGER L. Carrier-phase inter-frequency biases of GLONASS receivers[J]. Journal of Geodesy, 2012, 86(2): 139-148. DOI:10.1007/s00190-011-0502-y |
| [6] |
BANVILLE S, COLLINS P, LAHAYE F. GLONASS ambiguity resolution of mixed receiver types without external calibration[J]. GPS Solutions, 2013, 17(3): 275-282. DOI:10.1007/s10291-013-0319-7 |
| [7] |
GENG J, BOCK Y. GLONASS fractional-cycle bias estimation across inhomogeneous receivers for PPP ambiguity resolution[J]. Journal of Geodesy, 2015, 90(4): 379-396. DOI:10.1007/s00190-015-0879-0 |
| [8] |
JIANG W, AN X, CHEN H, et al. A new method for GLONASS inter-frequency bias estimation based on long baselines[J]. GPS Solutions, 2017, 21(4): 1765-1779. DOI:10.1007/s10291-017-0652-3 |
| [9] |
TIAN Y, GE M, FRANK N, et al. Improvements on the particle-filter-based GLONASS phase inter-frequency bias estimation approach[J]. GPS Solutions, 2018, 22(5): 1771-1780. DOI:10.1007/s10291-018-0735-9 |
| [10] |
隋心, 徐爱功, 郝雨时, 等. 实时GLONASSS相位频间偏差粒子群优化估计方法[J]. 测绘学报, 2018, 47(5): 584-591. SUI Xin, XU Aigong, HAO Yushi, et al. Real-time estimation method for GLONASS phase inter-frequency bias based on particle swarm optimization[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5): 584-591. DOI:10.11947/j.AGCS.2018.20170391 |
| [11] |
HAUSCHILD A, MONTENBRUCK O. A study on the dependency of GNSS pseudorange biases on correlator spacing[J]. GPS Solutions, 2014, 18(2): 159-171. DOI:10.1007/s10291-014-0426-0 |
| [12] |
YAMADA H, TAKASU T, KUBO N, et al. Evaluation and calibration of receiver inter-channel biases for RTK-GPS/GLONASS[C]//Proceedings of ION GNSS 2010, Portland, Oregon, USA: [s. n.], 2010: 1580-1587.
|
| [13] |
SHI C, YI W, SONG W, et al. GLONASS pseudorange inter-channel biases and their effects on combined GPS/GLONASS precise point positioning[J]. GPS Solutions, 2013, 17(4): 439-451. DOI:10.1007/s10291-013-0332-x |
| [14] |
刘志强, 王解先, 段兵兵. 单站多参数GLONASS码频间偏差估计及其对组合精密单点定位的影响[J]. 测绘学报, 2015, 44(2): 150-159. LIU Zhiqiang, WANG Jiexian, DUAN Bingbing. Estimation of GLONASS code inter- frequency biases with multiple parameters based on a single station and its impaction on combined precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 150-159. DOI:10.11947/j.AGCS.2015.20130800 |
| [15] |
徐龙威, 刘晖, 舒宝, 等. GLONASS频间码偏差特性分析及其在宽巷模糊度固定中的应用[J]. 测绘学报, 2018, 47(4): 465-472. XU Longwei, LIU Hui, SHU Bao, et al. Characteristics of GLONASS inter-frequency code bias and its application on wide-lane ambiguity resolution[J]. Acta Geodaeticaet Cartographica Sinica, 2018, 47(4): 465-472. DOI:10.11947/j.AGCS.2018.20170430 |
| [16] |
LIU Y, GE M, SHI C, et al. Improving integer ambiguity resolution for GLONASS precise orbit determination[J]. Journal of Geodesy, 2016, 90(8): 715-726. DOI:10.1007/s00190-016-0904-y |
| [17] |
AL-SHAERY A, ZHANG S, RIZOS C. An enhanced calibration method of GLONASS inter-channel bias for GNSS RTK[J]. GPS Solutions, 2013, 17(2): 165-173. DOI:10.1007/s10291-012-0269-5 |
| [18] |
CHEN L, LI M, HU Z, et al. Method for real-time self-calibrating GLONASS code inter-frequency bias and improvements on single point positioning[J]. GPS Solutions, 2018, 22(4). DOI:10.1007/s10291-018-0774-2 |
| [19] |
MONTENBRUCK O, STEIGENBERGER P, PRANGE L, et al. The multi-GNSS experiment (MGEX) of the international GNSS service (IGS)-achievements, prospects and challenges[J]. Advances in Space Research, 2017, 59(7): 1671-1697. DOI:10.1016/j.asr.2017.01.011 |
| [20] |
ZHANG X, HE X, LIU W. Characteristics of systematic errors in the BDS Hatch-Melbourne-Wübbena combination and its influence on wide-lane ambiguity resolution[J]. GPS Solutions, 2017, 21(1): 265-277. DOI:10.1007/s10291-016-0520-6 |
| [21] |
XU L, LIU H, SHU B, et al. GLONASS real-time wide-lane ambiguity resolution with an enhanced geometry-based model for medium-range baselines[J]. Advances in Space Research, 2018, 62(9): 2467-2479. DOI:10.1016/j.asr.2018.07.027 |
| [22] |
BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J]. GPS Solutions, 2014, 18(3): 433-441. DOI:10.1007/s10291-014-0403-7 |
| [23] |
FAN H. A two-step estimation method of troposphere delay with consideration of mapping function errors[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 76-84. DOI:10.11947/j.JGGS.2020.0108 |
| [24] |
BRUYNINX C, LEGRAND J, FABIAN A, et al. GNSS metadata and data validation in the EUREF permanent network[J]. GPS Solutions, 2019, 23(4): 106. DOI:10.1007/s10291-019-0880-9 |
| [25] |
李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min. Research on multi-GNSS precise orbit determination theory and application[D]. Wuhan: Wuhan University, 2011. |
| [26] |
TEUNISSEN P.J.G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995(70): 65-82. |
| [27] |
LI X, LV H, MA F, et al. GNSS RTK positioning augmented with large LEO constellation[J]. Remote Sensing, 2019, 11(3): 228. DOI:10.3390/rs11030228 |


