2. 山东科技大学测绘与空间信息学院, 山东 青岛 266590
2. College of Geodesy and Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
非线性最小二乘法作为基本的非线性优化方法,广泛应用于非线性函数模型的参数估计中[1-6]。然而,根据实际问题的来源,许多非线性函数模型具有特殊结构,若函数模型中待求参数一部分变量是线性的,一部分变量是非线性的,并且函数模型为非线性函数的线性组合形式,数学上称为可分离非线性最小二乘(separable nonlinear least squares,SNLS)问题[7-9]。测绘领域中存在许多这种模型结构的参数估计问题,如激光雷达(light detection and ranging,LiDAR)全波形回波信号高斯函数分解模型中,高斯特征参数的求解[10-11];空间直角坐标转换模型中,旋转参数、平移参数和尺度参数的求解[12-13];神经网络预测模型中,激活函数的中心位置、宽度和权值参数的求解[14]等。
传统求解可分离非线性最小二乘问题的方法是将所有的待求参数(非线性和线性)均看作非线性参数,然后进行泰勒级数展开,利用非线性迭代法或直接搜索法寻找问题的最优解[15-16]。文献[17]将LiDAR波形数据根据高斯分量的重要性进行筛选,然后利用非线性Levenberg-Marquardt(LM)优化算法求解各波形分量非线性参数(波峰位置、波形宽度)和线性参数(振幅)的最优值。文献[18]对机载激光测深波形分解中LM与Expectation Maximization(EM)参数优化方法进行了比较,就波形拟合效果而言,模拟数据分析和实测数据试验均说明LM方法通常可得到比EM方法更接近原始波形的拟合结果,有利于进一步的波形分析,但受波形数据质量的影响较大。文献[19]针对三维坐标转换模型参数求解中先验精度未知和观测数据质量不佳的问题,以坐标转换后的点位残差加权平方和最小为原则,提出了基于Nelder-Mead单纯形直接搜索的非线性参数求解方法,提高了三维坐标转换参数的求解质量。文献[20]针对非线性最小二乘求解病态问题的不稳定问题,提出了数值收敛解和收敛效率更优的Frozen-Barycentre迭代法。文献[21]针对参数迭代过程中雅可比矩阵计算复杂的问题,结合自动微分和隐式迭代预处理技术,采用最速下降法和信赖域法求解非线性最小二乘问题。文献[22]依赖对精度水平的控制,当检测到精度太低无法进行优化时,对函数逼近方法进行改进,提出了一种基于动态精度评价函数和梯度函数的大规模非线性最小二乘的LM迭代算法,并证明了该算法的全局和局部收敛性。文献[23]对基于变量投影算法参数分离的非线性最小二乘问题,提出采用LM优化方法对非线性参数进行求解以及采用线性最小二乘或基于L-曲线的谱修正迭代方法对线性参数进行估计的混合算法,丰富了可分离非线性最小二乘的参数估计方法,但对基于变量投影算法参数分离的目标函数中残差向量雅可比矩阵的计算方法并未进行深入研究。综上分析可知,非线性参数估计的研究主要针对模型的构建和参数优化过程进行改进,取得了很好的结果[24-25],但很少有考虑函数模型可分离的特殊结构,并且将所有待求参数均作为非线性参数进行解算时,对参数初值的要求较高[26]。
本文从测绘领域中非线性函数模型的特殊结构出发,首先,将线性参数通过变量投影算法用非线性函数表示,基于Moore-Penrose广义逆矩阵微分和立体矩阵理论推导了残差向量雅可比矩阵的计算过程;然后,对参数分离后的非线性最小二乘问题利用LM优化方法进行求解,得到非线性参数的迭代方向和最优估值,进而采用最小二乘方法计算线性参数的最优解;最后,通过模拟试验和LiDAR波形参数求解试验验证了基于Moore-Penrose广义逆矩阵微分的可分离非线性最小二乘方法的有效性。
1 可分离非线性最小二乘法原理设测量平差中的非线性函数模型和随机模型为
 (1)
(1)
式中,f(x) 为非线性函数向量;x为待求参数向量;L为观测值向量;σ2为单位权方差;矩阵Q和P分别为观测向量协因数阵和权阵。在非线性最小二乘准则下建立目标函数为
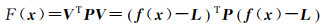 (2)
(2)
为便于讨论,假设等精度观测,权阵为单位阵(P=I),参数求解问题则等价于求解非线性最小二乘优化问题[27-28],即通过式(3)来确定最优参数
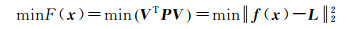 (3)
(3)
式中,‖·‖表示欧氏范数。
在式(1)的非线性函数模型中,若待求参数x由线性参数向量a和非线性参数向量b两部分组成,且fi(x)为非线性函数的线性组合,将其可以写成以下形式
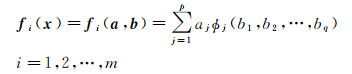 (4)
(4)
式中,p是线性参数a的维数;q是非线性参数b的维数;令n=p+q,n表示待求参数的总个数;m表示观测次数。
令Φ(b)的列对应的是与参数向量b相关的非线性函数ϕj(b), (j=1, 2, …, p)。那么,非线性函数模型写成矩阵形式为
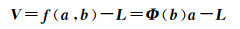 (5)
(5)
则式(5)的非线性最小二乘优化问题为
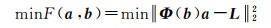 (6)
(6)
若给定非线性参数b,则线性参数a的最小二乘最小范数解为
 (7)
(7)
式中,Φ+(b)是Φ(b)的Moore-Penrose广义逆[29]。
令向量L在Φ(b)列向量张成的线性空间上的正交投影为PΦ(b)=Φ(b)Φ+(b),其正交补空间为PΦ(b)⊥=I-PΦ(b),将式(7)代入式(6)可得
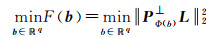 (8)
(8)
则原问题转化为仅含有非线性参数的最小二乘问题。基于式(8)的算法也称为变量投影算法[9]。
经参数分离后的平差函数模型为
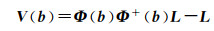 (9)
(9)
根据最小二乘准则,待求参数的最优值通过求极值方法得到[30],其可分离非线性最小二乘的目标函数F(b)的一阶导数为
 (10)
(10)
因此,只需计算变量投影算子PΦ(b)的一阶导数
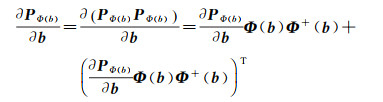 (11)
(11)
又由于PΦ(b)Φ(b)=Φ(b),因此
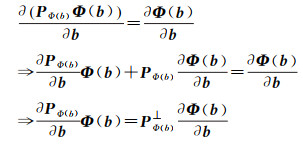 (12)
(12)
将式(12)代入式(11),得变量投影算子的一阶偏导为
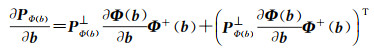 (13)
(13)
式中,
 (14)
(14)
那么,
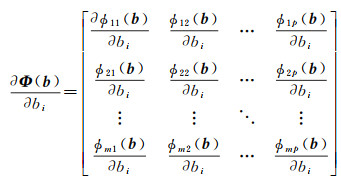 (15)
(15)
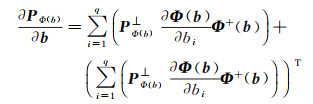 (16)
(16)
最终式(10)的目标函数一阶导数为
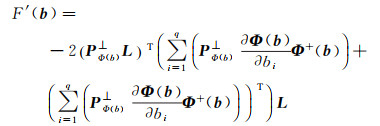 (17)
(17)
则残差向量的Jacobian矩阵J(b) 为
 (18)
(18)
对目标函数F(b)用泰勒级数公式展开,并取至二阶项,由以下优化模型来得到迭代方向
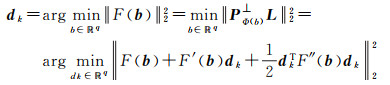 (19)
(19)
由极值条件可得
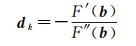 (20)
(20)
式中
 (21)
(21)
因此,式(20)迭代方向dk为
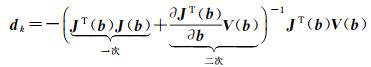 (22)
(22)
由于矩阵J(b)对参数b求导计算复杂,对于小残差问题,常用Gauss-Newton算法通过忽略式(22)中的二次项信息,但对于大残差的问题,二次项信息的省略,导致该算法不能很好收敛。因此,为了兼顾计算量和算法的收敛性,LM算法通过增加μI项,其中μ>0,保证了JT(b)J(b)+μI始终为正定的,并且正参数μ的引入也避免了矩阵JT(b)J(b) 接近奇异时,搜索方向的模‖dk‖过大的问题。
设第k次迭代的非线性参数向量为bk,从而基于变量投影的可分离非线性最小二乘LM算法的迭代方向dk为
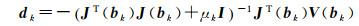 (23)
(23)
式中,μk>0,J(bk)是残差向量V(bk)(式(9))关于bk的一阶偏导构成的矩阵。
令V =[V1 V2 … Vm]T,Vi的梯度为
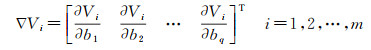 (24)
(24)
残差向量的雅可比矩阵J(b) 的每一行由相应向量函数的梯度转置得到,即
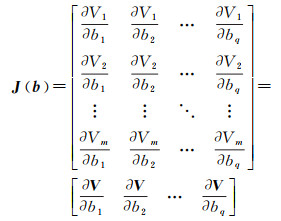 (25)
(25)
直接由式(13)可得
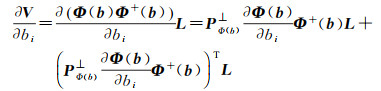 (26)
(26)
然后计算新的迭代点
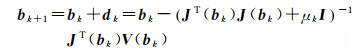 (27)
(27)
直到目标函数满足迭代终止条件,求解得到非线性参数向量b的最优解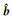
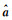
 (28)
(28)
令系数矩阵
 (29)
(29)
设观测值向量L的协因数阵为QLL,单位权中误差为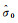
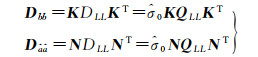 (30)
(30)
结合以上参数求解过程,基于变量投影算法参数分离的LM优化方法步骤如下。
(1) 给定非线性参数初值b0以及阈值0 < ε < < 1,并置迭代次数k=0。
(2) 计算非线性函数矩阵Φ(bk)和雅可比矩阵J(bk)。
(3) 根据式(23)和式(27)计算可分离非线性参数的迭代方向dk和第k+1次的参数值bk+1。
(4) 若目标函数梯度的范数‖ gk‖22=‖JT(bk)V(bk)‖22≤ε,停止迭代;否则k=k+1,转至步骤(2)。
(5) 根据式(7)计算线性参数的解,进而得到所有参数的最优解(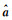
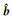
当非线性函数矩阵Φ(bk)为列满秩且良态时,仅含有非线性参数的可分离非线性最小二乘问题(式(8))与原问题(式(6))参数估计结果一致,即,若非线性参数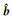
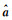
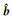
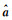
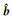
当非线性函数矩阵Φ(bk)秩亏或病态时,则需要通过解算不适定问题的方法进行求解[35-36],参数收敛结果也会有所不同。
3 试验分析为了验证基于Moore-Penrose广义逆矩阵微分的可分离非线性最小二乘方法在参数估计中的有效性,采用指数函数拟合的模拟试验及LiDAR全波形分解试验与传统的参数不分离的非线性最小二乘LM优化方法进行了对比,试验环境为Matlab 2016b,2.80 GHz PC,Windows10系统。
3.1 指数函数模型的拟合模拟试验源于放射性物质的衰变过程,其函数模型表达式为
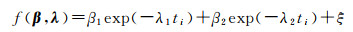 (31)
(31)
式中,β =(β1, β2)T,λ =(λ1, λ2)T是待求衰减因子参数;ti是观测时刻;ξ是观测误差。假设在没有观测误差的影响下,衰减因子的真值为β1*=3.1, β2*=2.8, λ1*=10.1, λ1*=1.4,令ξ是标准差为0.1的高斯噪声,试验随机生成时间t为[0, 2]范围内均匀间隔的201个观测数据yi, i=1, 2, …, m。
为了获得待求参数的最优估计,首先根据实际观测值列出误差方程,并通过变量投影算法将线性参数进行消除,得到基于变量投影算法的误差方程,然后基于Moore-Penrose广义逆矩阵的微分和立体矩阵理论计算目标函数的雅可比矩阵,采用LM算法对非线性参数λ =[λ1 λ2]T进行估计,当目标函数(残差平方和)的梯度小于10-6时,迭代终止。
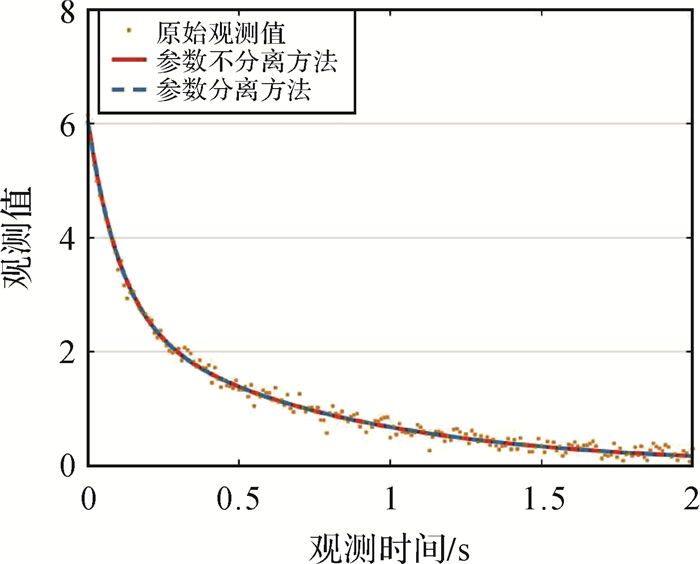
结合衰变模型的结构特点,根据参数初值选择在真值附近或初值选择常用的0和1得到4组不同的参数初值为[3 2 10 1]T、[0 1 10 1]T、[3 2 0 1]T和[0 1 0 1]T,然后采用本文提出的参数分离的LM优化方法对非线性参数进行优化,与参数不分离的LM优化方法进行结果对比。给定4组参数初值,参数分离方法和参数不分离方法得到的衰减因子估值均为[3.30 2.68 9.54 1.32]T。由该参数估值得到的拟合曲线如图 1所示。
|
| 图 1 参数不分离方法和参数分离方法的拟合曲线对比 Fig. 1 Comparison of fitted curves between parameter non-separation method and parameter separation method |
由图 1可知,参数分离方法和参数不分离方法得到的指数函数模型曲线与观测值拟合较好。
从迭代次数、残差平方和、均方根误差、拟合优度、相关系数和最大差值等评价指标对参数分离的LM优化方法得到的结果进行分析,为了减少计算机性能等影响因素对时间的影响,将线性参数和非线性参数初值均在真值附近的试验中参数不分离方法的计算时间设为单位1,其余试验的时间对其进行比值,评价指标结果见表 1。
| 初值 | a0=[3 2]T, b0=[10 1]T | a0=[0 1]T, b0=[10 1]T | a0=[3 2]T, b0=[0 1]T | a0=[0 1]T, b0=[0 1]T | ||||
| 方法 | 不分离 | 分离 | 不分离 | 分离 | 不分离 | 分离 | 不分离 | 分离 |
| 迭代次数 | 23 | 7 | 201 | 7 | 1808 | 15 | 1794 | 15 |
| 迭代时间 | 1 | 1.23 | 20.50 | 1.18 | 294.14 | 2.49 | 193.04 | 2.37 |
| 残差平方和 | 1.941 3 | 1.941 3 | 1.941 3 | 1.941 3 | 1.941 3 | 1.941 3 | 1.941 3 | 1.941 3 |
| 均方根误差 | 0.098 3 | 0.098 3 | 0.098 3 | 0.098 3 | 0.098 3 | 0.098 3 | 0.098 3 | 0.098 3 |
| 拟合优度 | 0.992 5 | 0.992 5 | 0.992 5 | 0.992 5 | 0.992 5 | 0.992 5 | 0.992 5 | 0.992 5 |
| 相关系数 | 0.996 2 | 0.996 2 | 0.996 2 | 0.996 2 | 0.996 2 | 0.996 2 | 0.996 2 | 0.996 2 |
| 最大差值 | 0.284 5 | 0.284 5 | 0.284 5 | 0.284 5 | 0.284 5 | 0.284 5 | 0.284 5 | 0.284 5 |
结合参数最终估值结果和表 2可知,4组试验的评价指标除迭代次数和迭代时间外,其余指标结果相同,并且从拟合优度和相关系数的数值可以看出,参数分离方法和参数不分离方法都能与观测值拟合较好;迭代次数方面,当目标函数(残差平方和)的梯度小于10-6时,由于第1组和第2组的非线性参数初值相同,参数分离的LM优化方法不受线性参数初值的影响,因此迭代次数均为7,参数不分离方法由于线性参数的初值不同,迭代次数分别为23次和201次;第3组和第4组的非线性参数初值相同,参数分离的LM优化方法的迭代次数均为15,参数不分离方法的迭代次数分别为1808次和1794次;迭代时间方面,第1组试验中虽然参数分离的LM优化方法迭代次数少,但是由于迭代过程中目标函数的一阶导数计算复杂,导致计算时间比参数不分离的LM优化方法多了约23%,但第2组、第3组和第4组试验中,参数分离方法的计算时间均比参数不分离方法少,特别是第3组和第4组试验,由于参数分离的LM优化方法比参数不分离的LM优化方法的迭代次数分别减少了1793次和1779次,因此参数分离方法的计算时间明显减少,计算效率得到显著提高。另外,第1组和第2组试验参数分离方法的时间理论上应该完全相同,但是由于计算机实时状态的不同,所以计算时间有少许差别,第3组和第4组试验的计算时间也是如此。
| 方法 | 参数初值 | |||
| a0=[3 2]T,
b0=[10 1]T |
a0=[0 1]T,
b0=[10 1]T |
a0=[3 2]T,
b0=[0 1]T |
a0=[0 1]T,
b0=[0 1]T |
|
| 参数不分离 | 48.70 | 1.55×1018 | 652.84 | 7.43×1018 |
| 参数分离 | 16.66 | 16.66 | 5.35 | 5.35 |
为了验证参数分离方法对原问题病态性的改进,对基于变量投影算法参数分离的残差向量雅可比矩阵的条件数进行分析,其4组初值对应的参数分离方法和参数不分离方法的条件数结果见表 2。
由表 2可知,同一组参数初值的参数分离方法雅克比矩阵的条件数比参数不分离方法更小,特别是第2组和第4组参数初值,原非线性最小二乘问题的雅可比矩阵的条件数均超过1018,存在明显病态问题,而基于变量投影参数分离方法的雅可比矩阵的条件数分别为16.66和5.23,原问题的病态性得到明显改善。
3.2 基于可分离非线性最小二乘的LiDAR波形分解试验采用海南某部分海域2012年12月测量得到的机载LiDAR测深数据进行波形分解,其波形数据采用Optech Aquarius机载测深系统测量得到,激光脉冲频率为70 kHz,以1~2 GHz的高采样率记录各采样点的振幅,采样间隔为1 ns,采样数量为287。由于在反射率低的情况下,电压值会很小,因此,将观测值进行量化,得到数字信号值(digital number),即每一条波形由(ti, DNi), i=1, 2, …,287组成。利用双高斯模型对海面回波和海底回波建立模型,即
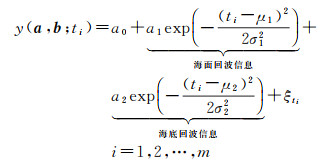 (32)
(32)
式中,a =[a0 a1 a2]T,b =[μ1 μ2 σ1 σ2]T是待求线性参数和非线性参数;ξ是测量误差。
利用极大值检测法及原始观测值的图像特点假设线性参数和非线性参数的近似值为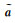
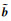
|
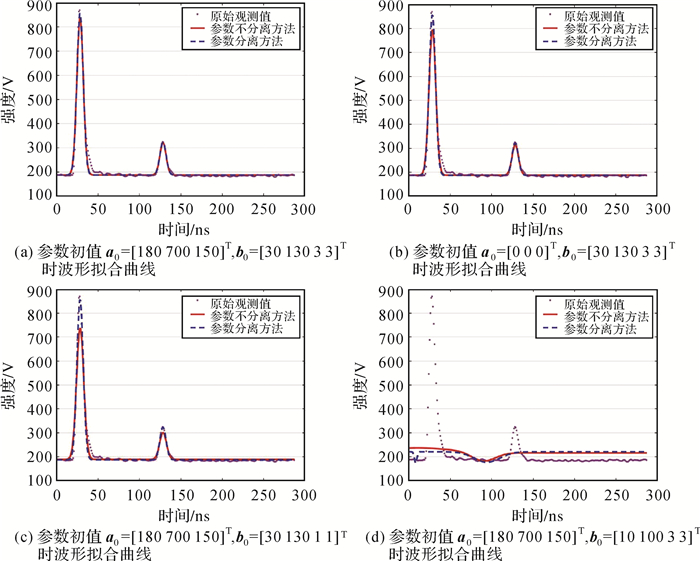
| 图 2 不同参数初值的参数不分离方法和参数分离方法的LiDAR波形拟合曲线 Fig. 2 Comparison of LiDAR waveform fitted curves between parameter non-separation method and parameter separation method with different initial values of parameters |
由图 2可知,参数分离的LM优化方法根据第1、2和3组的参数初值得到LiDAR波形曲线与原始观测值拟合较好;参数不分离的LM优化方法第1组和第2组试验得到的LiDAR波形曲线与参数分离方法相比,在第1个波峰处相差较大,第2个波峰拟合较好,第3组试验得到的LiDAR波形在两个波峰处与参数分离方法得到的拟合曲线都存在差值;第4组试验无论是参数分离方法还是参数不分离方法都未能与观测值进行较好拟合,也说明了两种方法都对参数初值具有一定的依赖性。
从迭代次数、计算时间,残差平方和、均方根误差、拟合优度、相关系数和最大差值等评价指标与参数不分离的非线性最小二乘LM优化方法进行对比,与模拟试验一样,并将第1组参数初值在近似值附近的参数不分离方法的计算时间设为单位1,结果见表 3。
| 参数初值 | 方法 | 迭代次数 | 相对时间 | 残差平方和 | 均方根误差 | 拟合优度 | 相关系数 | 最大差值 |
| [180 700 150 30 130 3 3]T | 不分离 | 10 | 1 | 6.31×104 | 14.823 8 | 0.979 3 | 0.989 8 | 73.65 |
| 分离 | 10 | 1.71 | 6.13×104 | 14.616 5 | 0.979 9 | 0.989 9 | 71.03 | |
| [0 0 0 30 130 3 3]T | 不分离 | 11 | 0.94 | 7.98×104 | 16.671 7 | 0.973 8 | 0.988 9 | 103.24 |
| 分离 | 10 | 1.64 | 6.13×104 | 14.616 5 | 0.979 9 | 0.989 9 | 71.03 | |
| [180 700 150 30 130 1 1]T | 不分离 | 11 | 0.95 | 1.33×105 | 21.523 1 | 0.956 4 | 0.986 1 | 156.00 |
| 分离 | 11 | 1.85 | 6.13×104 | 14.616 6 | 0.979 9 | 0.989 9 | 70.96 | |
| [180 700 150 10 100 3 3]T | 不分离 | 13 | 1.11 | 2.84×106 | 99.433 0 | 0.069 5 | 0.348 5 | 634.96 |
| 分离 | 13 | 2.11 | 3.00×106 | 102.286 4 | 0.015 3 | 0.123 8 | 649.23 |
表 3中加粗的值表示离近似值较远的初值。由表 3可知,当线性参数初值和非线性参数初值都选择在近似值附近时(第1组),参数分离方法和参数不分离方法的迭代次数都是10,迭代终止时,参数不分离方法的残差平方和是6.31×104,参数分离方法的残差平方和是6.13×104,从均方根误差、拟合优度、相关系数和最大偏差4个评价指标也可以看出,参数分离方法得到的参数估计值精度更高,但是相同的迭代次数参数分离方法计算所需的时间更多。
当非线性参数初值选择在最优值附近,线性参数初值任意选择时(第2组),参数分离方法由于只与非线性参数有关,所以与第1组试验结果相同;参数不分离方法与第1组试验相比,迭代次数增加1,均方根误差由14.82增大为16.67,结合其余评价指标可知,参数分离方法的拟合精度更高,但所需计算时间更多。
当线性参数初值选择在最优值附近,非线性的部分参数(波形宽度)初值任意选择时(第3组),参数分离方法仍然可以得到与第1组试验相同的结果;而参数不分离方法均方根误差由第1组的14.82增加为21.52,拟合优度也由0.979 3降至0.956 4,由此可知,参数不分离方法更容易受参数初值的影响。
当线性参数初值选择在最优值附近,非线性的部分参数(波峰位置)初值任意选择时,参数不分离方法和参数分离方法都未得到与第1组精度一致的参数估值,结合图 2可知,参数分离方法和参数不分离方法都对波峰位置参数的初值比较敏感。
对上述4组试验中参数分离方法和参数不分离方法的残差平方和变化过程进行对比,结果如图 3所示。

|
| 图 3 LiDAR波形拟合试验参数不分离方法和参数分离方法残差平方和的变化 Fig. 3 The change of the residual sum of squares between the parameter non-separation method and the parameter separation method in LiDAR waveform fitting experiment |
由图 3可知,第1、2和3组在迭代终止时,参数分离方法的残差平方和更小,也说明了参数分离方法在求解可分离非线性最小二乘问题时的参数估计精度更高,第4组试验在迭代终止时虽然参数不分离方法的残差平方和更小,但结合表 2可知,两种方法得到均方根误差(99.433 0和102.286 4) 都与参数初值在近似值附近(第1组)的结果(14.616 5)相差较大,说明两种方法均未得收敛到待估参数的最优值。
为了更全面地对比参数不分离方法和参数分离方法的收敛结果,根据LiDAR波形分解中常用的峰值探测法得到波峰位置参数和振幅参数的近似初值,波峰宽度参数的近似初值由峰值一半处对应的两点位置得到,然后以近似初值为中心,初值的一半为邻域设定线性参数和非线性参数的取值区间,在均匀分布区间内随机取200组线性参数和非线性参数的初值,进行迭代建模,进而分析200组试验中两种方法的均方根误差、拟合优度、相关系数和最大偏差等指标的分布情况,结果如图 4和表 4所示。

|
| 图 4 LiDAR波形拟合200次试验的效果评价指标分布情况 Fig. 4 The distribution of evaluation indexes in 200 experiments of LIDAR waveform fitting |
| 方法 | 均方根误差 (均值) |
拟合优度 (均值) |
拟合优度 >0.90 |
相关系数 (均值) |
相关系数 >0.90 |
相关系数的标准差 | 最大差值 (均值) |
| 不分离 | 74.068 0 | 0.364 7 | 32.5% | 0.465 4 | 35% | 0.420 0 | 459.954 6 |
| 分离 | 39.346 7 | 0.774 7 | 74.5% | 0.828 1 | 76.5% | 0.298 4 | 226.696 7 |
由图 4和表 4可知,参数分离方法的均方根误差均值比参数不分离方法小34.721 3,说明整体上参数分离方法的精度更高;200次试验中,拟合优度大于0.9的参数分离方法占74.5%,参数不分离方法占32.5%,相关系数大于0.9的参数分离方法占76.5%,参数不分离方法占35%;由两种方法相关系数的标准差数值可知,参数分离方法200次试验的相关系数标准差更小,说明其算法稳定性更好。
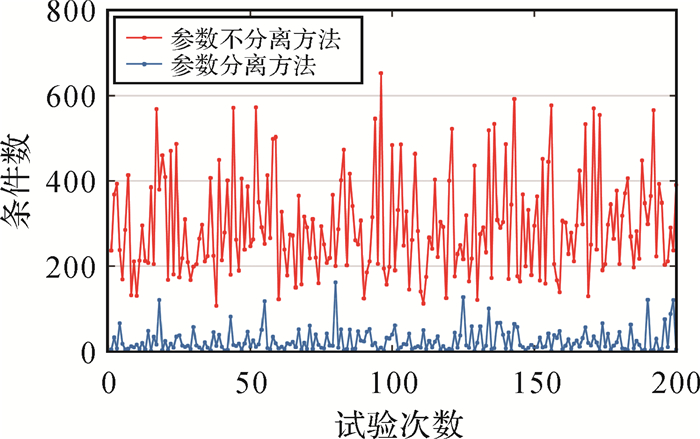
对200次试验中非线性参数初值相同的参数分离方法的残差向量雅可比矩阵的条件数与参数不分离方法进行对比,结果如图 5所示。
|
| 图 5 200次试验中残差向量雅可比矩阵的条件数对比 Fig. 5 The comparison of the condition number of the Jacobian matrix of residual vector in 200 experiments |
综上分析可知:①参数分离的LM优化方法只对非线性参数初值具有一定的依赖性,比传统参数不分离的LM方法对待求参数初值的要求更低;②参数分离的LM优化方法在对参数优化过程中,所需的迭代次数更少,计算效率更高;③若两种方法的迭代次数相同,由于参数分离的LM优化方法在迭代过程中需要对Moore-Penrose广义逆矩阵的微分和立体矩阵进行计算,增加了计算复杂度,因此需要的时间更多。
4 结论基于Moore-Penrose广义逆矩阵微分的可分离非线性最小二乘方法通过利用变量投影算法将原来含有两类参数的优化问题转化为仅含有非线性参数的最小二乘问题,降低了待求参数的维数,迭代过程只依赖非线性参数的初值,避免了线性参数初值导致的病态问题。机载LiDAR测深全波形数据拟合试验结果表明,参数分离后的非线性最小二乘方法在波形参数求解过程中,参数估计精度更高,算法稳定性也更强,为机载LiDAR波形分解参数的求解提供了新的方法,也拓展了可分离非线性最小二乘方法在测绘领域的应用,但基于Moore-Penrose广义逆矩阵的微分和立体矩阵的雅可比矩阵的显式表达增加了计算复杂度,导致得到相同参数估计精度时,计算时间更多,因此如何提高计算效率也是可分离非线性最小二乘解算需要进一步研究的内容。
| [1] |
杨元喜, 张丽萍. 中国大地测量数据处理60年重要进展第二部分: 大地测量参数估计理论与方法的主要进展[J]. 地理空间信息, 2010, 8(1): 1-6. YANG Yuanxi, ZHANG Liping. Progress of geodetic data processing for 60 years in China part 2: progress of parameter estimation theory and methodology[J]. Geospatial Information, 2010, 8(1): 1-6. DOI:10.3969/j.issn.1672-4623.2010.01.001 |
| [2] |
GHILANI C D. Adjustment computations: spatial data analysis [D]. New Jersey: The Pennsylvania State University, 2017.
|
| [3] |
陶本藻. 关于测量中非线性模型估计问题[J]. 测绘通报, 1998(2): 3-5. TAO Benzao. On the estimation problem of nonlinear model in measurement[J]. Bulletin of Surveying and Mapping, 1998(2): 3-5. |
| [4] |
王新洲. 非线性模型参数估计的直接解法[J]. 武汉测绘科技大学学报, 1999(1): 64-67. WANG Xinzhou. A direct solution method of parameter estimation of nonlinear model[J]. Journal of Wuhan Techonical University of Surveying and Mapping, 1999(1): 64-67. |
| [5] |
刘国林. 非线性最小二乘与测量平差[M]. 北京: 测绘出版社, 2002. LIU Guolin. Nonlinear least squares and measurement adjustment[M]. Beijing: Surveying and Mapping Press, 2002. |
| [6] |
XU P, LIU J, SHI C. Total least squares adjustment in partial errors-in-variables models: algorithm and statistical analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675. DOI:10.1007/s00190-012-0552-9 |
| [7] |
GOLUB G H, PEREYRA V. The differentiation of Pseudo-inverses and nonlinear least squares problems whose variables separate[J]. SIAM Journal on Numerical Analysis, 1973, 10(2): 413-432. DOI:10.1137/0710036 |
| [8] |
GAN M, CHEN C L P, CHEN G Y, et al. On some separated algorithms for separable nonlinear least squares problems[J]. IEEE Transactions on Cybernetics, 2018, 48(10): 2866-2874. DOI:10.1109/TCYB.2017.2751558 |
| [9] |
魏木生. 广义最小二乘问题的理论和计算[M]. 北京: 科学出版社, 2006. WEI Musheng. Theory and calculation of generalized least squares problem[M]. Beijing: Science Press, 2006. |
| [10] |
王滨辉, 宋沙磊, 龚威, 等. 全波形激光雷达的波形优化分解算法[J]. 测绘学报, 2017, 46(11): 1859-1867. WANG Binhui, SONG Shalei, Gong Wei, et al. Optimization decomposition method of full-waveform LiDAR[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1859-1867. DOI:10.11947/j.AGCS.2017.20170045 |
| [11] |
WAGNER W, ULLRICH A, DUCIC V, et al. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(2): 100-112. DOI:10.1016/j.isprsjprs.2005.12.001 |
| [12] |
AKYILMAZ O. Total least squares solution of coordinate transformation[J]. Survey Review, 2007, 39(303): 68-80. DOI:10.1179/003962607X165005 |
| [13] |
LU Z P, WEI Z Q, LI J, et al. Grid model for high-accuracy coordinate transformation of China geodetic coordinate system 2000[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 17-25, 36. |
| [14] |
GAN M, LI H X, PENG H. A variable projection approach for efficient estimation of RBF-ARX model[J]. IEEE Transactions on Cybernetics, 2015, 45(3): 476-485. |
| [15] |
PALANCZ B, AWANGE J L, ZALETNYIK P, et al. Linear homotopy solution of nonlinear systems of equations in geodesy[J]. Journal of Geodesy, 2010, 84(1): 79-95. DOI:10.1007/s00190-009-0346-x |
| [16] |
张勤, 陶本藻. 基于同伦法的非线性最小二乘平差统一模型[J]. 武汉大学学报(信息科学版), 2004(8): 708-710. ZHANG Qin, TAO Benzao. Uniform model of nonlinear least squares adjustment based on homotopy method[J]. Geomatics and Information Science of Wuhan University, 2004(8): 708-710. |
| [17] |
HOFTON M A, MINSTER J B, BLAIR J B. Decomposition of laser altimeter waveforms[J]. IEEE Transactions on Geoscience & Remote Sensing, 2000, 38(4): 1989-1996. |
| [18] |
郭锴, 刘焱雄, 徐文学, 等. 机载激光测深波形分解中LM与EM参数优化方法比较[J]. 测绘学报, 2020, 49(1): 117-131. GUO Kai, LIU Yanxiong, XU Wenxue, et al. Comparison of LM and EM parameter optimization method for airborne laser bathymetric full-waveform decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(1): 117-131. DOI:10.11947/j.AGCS.2020.20180242 |
| [19] |
郭迎钢, 李宗春, 何华, 等. 三维坐标转换公共点最优权值的单纯形搜索算法[J]. 测绘学报, 2020, 49(8): 1004-1013. GUO Yinggang, LI Zongchun, HE Hua, et al. Asimplex search algorithm for the optimal weight of common point of 3D coordinate transformation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 1004-1013. DOI:10.11947/j.AGCS.2020.20190409 |
| [20] |
孙振, 曲国庆, 苏晓庆, 等. 测距定位方程参数估计的Frozen-Barycentre算法[J]. 武汉大学学报(信息科学版), 2020, 45(9): 1478-1484. SUN Zhen, QU Guoqing, SU Xiaoqing, et al. Frozen-Barycentre algorithm for solving distance equations[J]. Geomatics and Information Science of Wuhan University, 2020, 45(9): 1478-1484. |
| [21] |
XU W, ZHENG N, HAYAMI K. Jacobian-free implicit inner-iteration preconditioner for nonlinear least squares problems[J]. Journal of Scientific Computing, 2016, 68(3): 1055-1081. |
| [22] |
BELLAVIA S, GRATTON S, RICCIETTI E. A Levenberg-Marquardt method for large nonlinear least-squares problems with dynamic accuracy in functions and gradients[J]. Numerische Mathematik, 2018, 140(3): 791-825. |
| [23] |
WANG K, LIU G L, TAO Q X, et al. Efficient parameters estimation method for the separable nonlinear least squares problem[J]. Complexity, 2020(1): 1-16. |
| [24] |
方兴, 曾文宪, 刘经南, 等. 基于非线性高斯-赫尔默特模型的混合整体最小二乘估计[J]. 测绘学报, 2016, 45(3): 291-296. FANG Xing, ZENG Wenxian, LIU Jingnan, et al. Mixed LS-TLS estimation based on nonlinear Gauss-Helmert model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 291-296. DOI:10.11947/j.AGCS.2016.20150157 |
| [25] |
姚宜斌, 黄书华, 张良, 等. 求解三维坐标转换参数的整体最小二乘新方法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 853-857. YAO Yibin, HUANG Shuhua, ZHANG Liang, et al. A new method of TLS for solving the parameters of three-dimensional coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 853-857. |
| [26] |
XUE Shugiang, YANG Yuanxi. Adjustment model and colored noise compensation of continuous observation system[J]. Journal of Geodesy and Geoinformation Science, 2018, 1(1): 39-45. |
| [27] |
JIATIAN LI C W, CHENGLIN JIA, YIRU NIU, et al. A hybrid conjugate gradient algorithm for solving relative orientation of big rotation angle stereo pair[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 62-70. |
| [28] |
吕志鹏, 隋立芬. 基于非线性高斯-赫尔默特模型的结构总体最小二乘法[J]. 武汉大学学报(信息科学版), 2019, 44(12): 1808-1815. LV Zhipeng, SUI Lifen. A structured total least squares method based on nonlinear Gauss-Helmert model[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1808-1815. |
| [29] |
STOJANOVIC K S, MOSIC D. Generalization of the Moore-Penrose inverse[J]. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 2020, 114(4): 1-16. |
| [30] |
吕志鹏, 隋立芬. 基于变量投影的结构总体最小二乘算法[J]. 武汉大学学报(信息科学版), 2021, 46(3): 388-394. LV Zhipeng, SUI Lifen. Structured total least squares method based on variable projection[J]. Geomatics and Information Science of Wuhan University, 2021, 46(3): 388-394. |
| [31] |
张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2013. ZHAN Xianda. Matrix analysis and application[M]. Beijing: Tsinghua University Press, 2013. |
| [32] |
韦博成. 近代非线性回归分析[M]. 南京: 东南大学出版社, 1989. WEI Bocheng. Modern nonlinear regression analysis[M]. Nanjing: Southeast University Press, 1989. |
| [33] |
SHI Y, XU P, PENG J, et al. Adjustment of measurements with multiplicative errors: error analysis, estimates of the variance of unit weight, and effect on volume estimation from LiDAR-type digital elevation models[J]. Sensors, 2014, 14(1): 1249-1266. |
| [34] |
XU P, LIU J. Variance components in errors-in-variables models: estimability, stability and bias analysis[J]. Journal of Geodesy, 2014, 88(8): 719-734. |
| [35] |
鲁铁定, 吴光明, 周世健. 病态不确定性平差模型的岭估计算法[J]. 测绘学报, 2019, 48(4): 403-411. LU Tieding, WU Guangming, ZHOU Shijian. Ridge estimation algorithm to ill-posed uncertainty adjustment model[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4): 403-411. DOI:10.11947/j.AGCS.2019.20180044 |
| [36] |
唐利民. 非线性最小二乘问题的不适定性及算法研究[J]. 测绘学报, 2012, 41(4): 630. TANG Limin. Research on the ill-posed and solving methods of nonlinear least squares problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 630. |



