2. 福建经纬测绘信息有限公司, 福建 福州 350001
2. Fujian Jingwei Surveying Information Co., Ltd., Fuzhou 350001, China
随着世界经济和城市化快速发展,许多城市都面临空气污染问题[1-2]。PM2.5是指在空气中直径小于2.5 μm的悬浮颗粒,是造成空气污染的主要来源,PM2.5浓度的增加会严重危害人体的身体健康和生态环境[3-6]。实现全国大范围区域内的大气污染物浓度的高精度时空预报和分析对大气污染物的联防联控和公众环境大气质量信息服务具有重要的现实意义。
目前,大气污染物浓度时空预报的方法主要包括物理模型的方法和统计模型的方法。物理模型的方法是基于大气污染物形成的机制和原理,进行演化、模拟从而通过数学的方式构建模型从而推演出污染物的时空分布[7-8]。然而,该方法难以基于物理方程准确描述大气污染浓度与外部特征之间的关系,且计算量巨大等问题使其难以用于大范围区域的空间化模拟[9]。统计模型的方法主要以统计学为基础,通过拟合历史的污染物数据与外部特征的定量关系,从而预测未来大气污染的分布,此类方法精度较高且相对于物理模型易于实现,应用更加广泛[10],常用的统计模型包括机器学习模型[11-14]和人工神经网络模型[15-16],基于机器学习模型的方法能很好地拟合大气污染物与外部特征间的数值关系,但是其更适用于小样本数据致使无法充分捕捉大气污染物自身的时空依赖特征[17]。
随着计算机能力的增强,人工神经网络的模型逐渐应用于大气污染物浓度的时空预报任务中,特别是基于深度学习的模型(含有两层或两层以上的隐藏层)由于其自适应、自组织、自学习能力决定了其在空间预测任务中能表现良好的性能[18-19]。其中,反向传播神经网络(BPNN)通过并入气象因素(例如,相对湿度、温度和风速)、土地使用类型、人口、道路网络等多种外源的变量能很好地实现PM2.5浓度空间化展示[20-22],但是,此模型空间化的精度有待改善,难以广泛应用于未来实时的预测。研究发现基于长短期记忆(LSTM)网络的模型擅长捕获时间序列数据中的长时间依赖性[23-24]。LSTM模型是循环神经网络(RNN)的变体,能有效解决RNN产生的梯度爆炸或者梯度消失等问题,使其能更有效地学习长时间序列数据的特征[25]。许多研究者通过建立基于长短期记忆(LSTM)网络的模型来预测未来时刻监测站点的PM2.5浓度的变化,并取得不错的预测结果[26-29]。目前基于LSTM的模型一般能在未来1 h的PM2.5浓度预测任务中表现优秀,但长期预测的精度普遍较低。目前的研究预测PM2.5浓度的范围大都为区域小尺度范围,很少有对全国大尺度范围实现较高精度的PM2.5浓度预测,并且大多研究预测的是各个空气质量监测站未来PM2.5浓度的变化,很少有全国大范围精细空间化的预报结果,仅仅对PM2.5浓度的区域预测和分析难以获取全国尺度的PM2.5浓度时空分布状况从而为整个中国的宏观监测提供足够的信息。
针对以上问题,本文通过构建基于深度学习的多层LSTM迭代预报模型和改进的S-BPNN空间化模型实现全国大范围内精细空间化的PM2.5浓度预报。主要贡献如下:①在PM2.5的时空相关性和影响因素分析基础上,将全国范围内PM2.5监测站进行自适应分区并分别构建非线性和自适应的多层LSTM迭代预测模型,该模型结合最佳时滞,利用迭代的方式通过多层双向LSTM捕获PM2.5浓度的长时间依赖特征,从而可以保持较高的时间相关性,从而预测各个监测站点未来24 h PM2.5浓度的变化;②结合预报模型,再利用改进的空间反向传播神经网络(S-BPNN)空间化模型,该模型通过顾及监测站点的空间相关性对预报模型的预报结果进行全国大范围精细化制图,实现PM2.5浓度的空间预报;③基于预测模型和空间化模型搭建大气污染物浓度预报的智能化在线信息原型系统从而发布全国大范围的PM2.5浓度时空预报。
1 研究区域与数据分析 1.1 研究区域本文获取了2016-01-01—2019-12-31共4年全国范围内1286个空气质量监测站点的PM2.5监测数据(http://106.37.208.233:20035/),相应的辅助数据包括气象数据(CMDC: http://data.cma.cn/en),建筑用地数据(http://www.dsac.cn/),道路长度数据(http://www.openstreetmap.org/),人口密度数据(https://web.ornl.gov/sci),归一化的植被指数(NDVI)(https://web.ornl.gov/sci)数据和高程(DEM)(http://www.gscloud.cn/)数据。图 1显示了所有空气质量监测站点地理位置分布和对应2019年的平均PM2.5浓度。如图 1所示,我国PM2.5浓度较高的区域集中在京津冀及周边地区、汾渭平原和西北部的一些城市,京津冀及周边地区和汾渭平原的人口数量密集,是我国重工业集中区域,区域性的大气污染问题较为严重,而西北地区如乌鲁木齐、伊犁等城市风沙较大,沙尘天气较多,以及城市特殊的地理位置导致污染物难以散去,导致PM2.5浓度较高。

|
| 图 1 研究区域内空气质量监测站点的分布 Fig. 1 Distribution of air quality monitoring stations in the study area |
首先,基于PM2.5站点的空间相关性对所有监测站点进行自适应分区,再利用历史时刻的实测PM2.5监测数据和气象数据基于深度学习的方法分别建立预报模型,从而预测各个监测站未来时刻的PM2.5浓度值,其中气象数据包括降水量(PRE)、气压(PRS)、相对湿度(RHU)、日照(SSD)、温度(TEM)及风向风速(WIN),气象数据通过反距离加权空间插值的方式匹配到各个PM2.5监测站点。然后,结合气象数据,建筑用地数据,道路长度数据,人口密度数据,NDVI数据和DEM数据进行空间化建模,对PM2.5浓度预报结果进行精细化制图,从而实现全国大范围尺度的PM2.5浓度空间预报,以实时评估全国的PM2.5浓度空间分布特征。最后,基于研究的大气污染物预报模型和空间化模型,初步生成大气污染物浓度预报平台原型系统,从而发布大气污染物浓度的预报结果。表 1列出了选取数据的统计特征。
| 变量 | 取值范围 | 均值 | 标准差 |
| PM2.5/(μg/m3) | [1.00, 894.00] | 42.84 | 42.21 |
| 降水量/mm | [0.00, 410.42] | 2.95 | 9.18 |
| 气压/hPa | [593.16, 1047.13] | 968.30 | 66.67 |
| 相对湿度/(%) | [0.00, 100.00] | 51.94 | 22.65 |
| 日照/(MJ/m2) | [0.00, 25.38] | 5.48 | 4.05 |
| 温度/℃ | [-38.75, 42.16] | 15.07 | 10.96 |
| 风向风速/(m/s) | [0.00, 19.69] | 2.22 | 1.05 |
| 建筑用地/万km2 | [23.5, 1998] | 731 | 1426 |
| 道路长度/万km | [393.77, 41.50] | 43.72 | 49.16 |
| 人口密度/人/km2 | [0.25, 470.55] | 89.03 | 79.38 |
| NDVI | [0.21, 0.92] | 0.53 | 0.13 |
| DEM/m | [1.00, 3678.00] | 329.74 | 516.93 |
| 季节/NA | [1, 4] | - | - |
| 月份/NA | [1, 12] | - | - |
| 天/NA | [1, 31] | - | - |
1.2 PM2.5浓度预报模型的影响因子
气象条件是影响大气污染物浓度的重要因素,并且大气污染物浓度具有一定的时间特征[30-31]。图 2展示了2016-01-01—2019-12-31全国日均PM2.5浓度值。由图 2可知,PM2.5浓度具有明显的季节特征,由于受到污染源排放和气象条件影响,PM2.5浓度一年表现为“冬季普遍偏高,春秋次之,夏季最轻”。冬季,温度的降低会致使大气污染不易扩散从而累积,并且釆暖期的燃煤量需求变大也导致污染物的排放增加;夏季,气象条件的变化如温度的增高、降水量的增加等,有利于降低PM2.5浓度。因此在进行PM2.5浓度预测中,本文考虑将大气污染的时间特征(季节特征、月份特征、天特征)的独热编码(one-hot)作为预测模型的辅助输入。图 3展示了2019-01-01—2019-12-31所有监测站日均PM2.5浓度、降水量、气压、相对湿度、日照、温度及风向风速值,通过PM2.5浓度与同时期的气象数据进行对比分析,可以发现PM2.5浓度值与降水量、湿度、气压、温度呈现明显的负相关,气象条件是大气污染关键的影响外因,当风速很小,大气静稳,近地面逆温,湿度较高等情况容易产生重污染,在本文中将归一化的气象数据和时间数据的one-hot编码作为PM2.5预测模型的辅助数据,增加这些辅助数据能提高模型的预测能力。
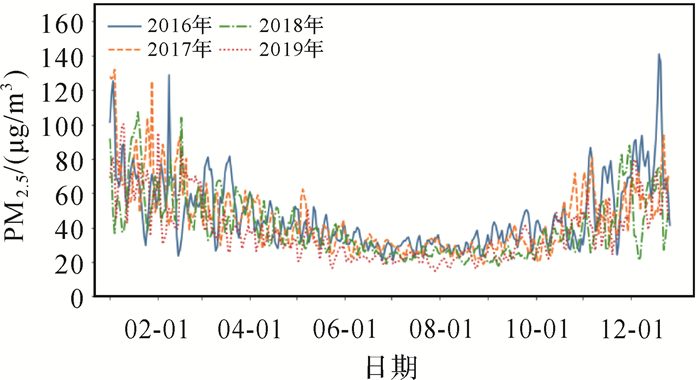
|
| 图 2 1月1日—12月31日全国日均PM2.5浓度值(2016—2019年) Fig. 2 Daily average PM2.5 concentration values in China from January 1 to December 31 (2016—2019) |

|
| 图 3 2019-01-01—2019-12-31日平均观测PM2.5浓度值与降水量,气压量,湿度,日照量,温度和风速的关系 Fig. 3 The relationship diagram of daily averaged observed PM2.5 and PRE, PRS, RHU, SSD, TEM, WIN from January 1 to December 31 (2016—2019) |
1.3 时空相关性分析 1.3.1 时间相关性分析
利用最大互信息系数分析PM2.5数据的时间相关性,最大互信息系数(maximal information coefficient, MIC)是用来度量两个变量之间线性或非线性关联强度[32],其公式为
 (1)
(1)
式中,x和y分别代表时滞前后的PM2.5数据;a和b分别为x和y方向上的网格数量;B为可变变量,一般设置为数据量的0.6次方。
图 4显示了全国范围为内随机选取的100个空气质量监测站0~20 h时间间隔的最大信息相关系数变化情况。由图 4可知,相关系数随时滞的增大而减小,时滞越小,相关程度越强,这说明了PM2.5数据具有显著的时间相关性,这些发现同样可为预测任务选择合适的时滞。
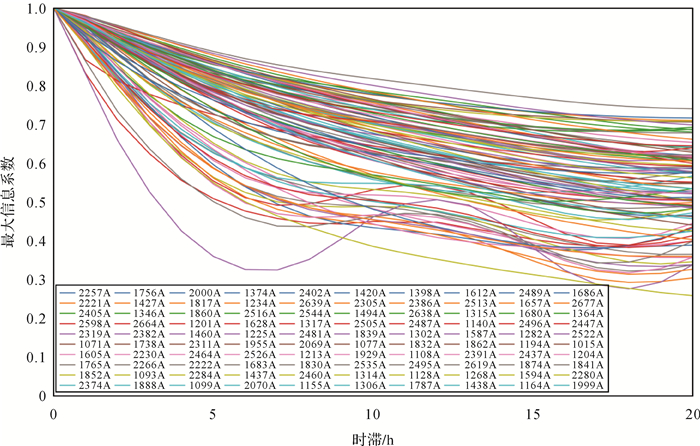
|
| 图 4 100个随机选择站点之间的最大信息相关系数 Fig. 4 MIC between 100 randomly selected stations |
1.3.2 空间相关性分析
单个站点的PM2.5浓度监测值往往会受到区域范围内污染物的影响,距离较近的PM2.5监测站点之间往往空间相关程度较强[22]。本文综合考虑全国范围内各个站点的PM2.5污染程度和地理位置,以自相关系数为衡量标准,研究最佳相关分区,将所有站点划分到68个区域,再分别进行建模预测未来的PM2.5浓度。
利用莫兰指数(Moran’s I)评估各个分区内的PM2.5监测站的空间相关性,以下分别为全局莫兰指数I和全局莫兰检验数Z的计算公式
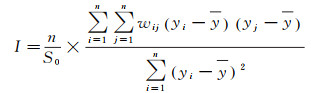 (2)
(2)
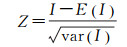 (3)
(3)
式中,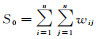
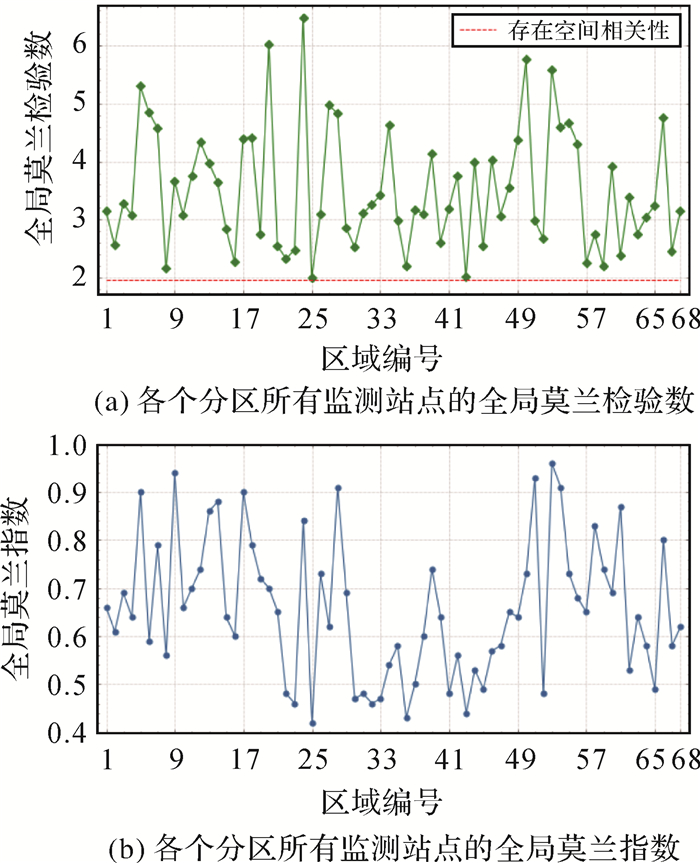
以各个监测站2016—2019年PM2.5平均值作为观测矩阵,区域内各个监测站点之间距离的倒数作为空间权重矩阵从而计算全局莫兰指数和显著性检验值。图 5(a)和(b)分别显示了每个分区的全局莫兰指数和显著性检验值。由图 5可知,每个区域在显著性为0.05水平下,全局莫兰指数Z都大于1.96,莫兰指数皆大于0.4,且大部分区域都大于0.5,个别区域甚至大于0.9,表明了PM2.5浓度具有一定区域效应,在一定区域范围内的PM2.监测站之间具有显著的空间相关性。
|
| 图 5 各个分区的空间相关性统计情况 Fig. 5 Spatial correlation statistics of each partition |
2 研究方法 2.1 PM2.5浓度预报模型
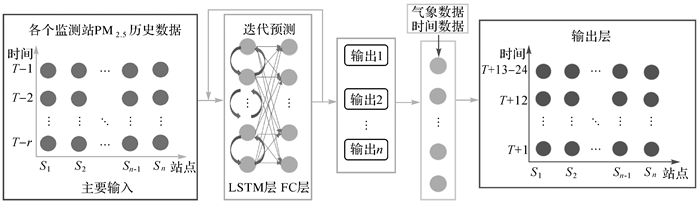
长短期记忆(LSTM)网络是通过门控机制和状态变量控制循环信息的传递。本文基于在68个分区区域分别建立多层LSTM迭代预测模型,该预测模型能够同时对同一个区域内的多个PM2.5监测站进行协同训练,并一次性得到该区域内各个监测站未来24 h的PM2.5预测值。该模型的总体结构如图 6所示,此模型以各个区域内的所有监测站PM2.5时滞历史数据作为模型的主要输入,结合合适的时滞r,然后通过双向LSTM层和全连接层的组合进行迭代预测,将预测未来24 h的时间段分为24/r个区间, 以时滞r=8为例,将进行3次迭代预测任务(输出1:未来1~8 h, 输出2:未来9~16 h, 输出3:未来17~24 h),每次输出作为下一次迭代预测的输入,直到迭代任务结束,其中r=12时,预测结果最好(具体试验见3.1节)。另外,为了减少迭代预测中的误差累积,最后一个输出为该时间段预测的平均值。将迭代预测的所有输出结果再结合辅助输入(气象数据和时间数据)通过全连接层训练,最后输出该区域各个监测站未来1~12 h实时,13~24 h的平均PM2.5预测值。
|
| 图 6 多层LSTM迭代模型的网络结构 Fig. 6 The network structure of multi-layer LSTM iterative model |
预测模型整体流程图如图 7所示,主要包括3个步骤。
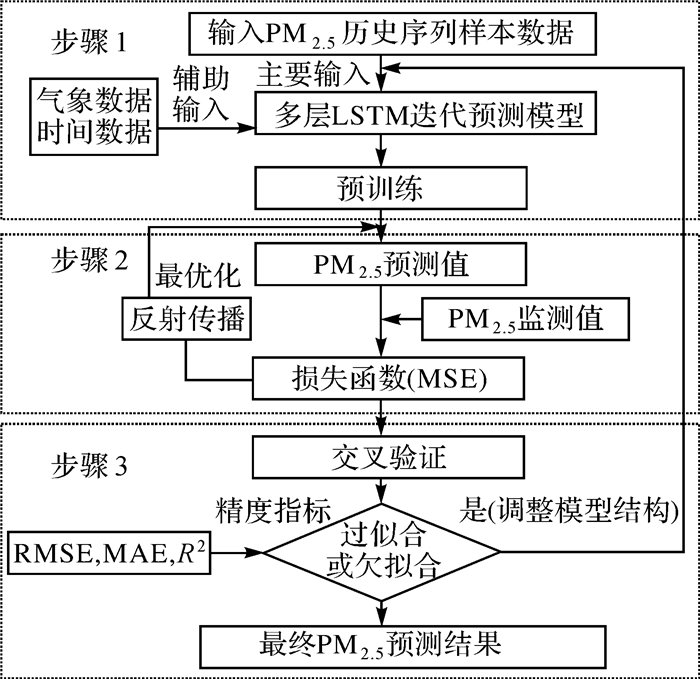
|
| 图 7 预测模型整体流程 Fig. 7 Overall flow chart of prediction model |
(1) 由于考虑PM2.5监测站点间显著的时空相关性,以每个区域各个PM2.5监测站点的历史序列数据作为模型的主要输入,以气象数据和时间数据作为辅助输入,通过多层LSTM迭代预测模型进行训练,得到未来24 h PM2.5浓度的预测值。
(2) 通过模型的预训练得出初步的PM2.5预测值,结合PM2.5观测值,计算损失函数,这里以均方误差作为损失函数,损失函数的公式为式(4),再通过反向传播的方式调整网络的权重参数,使结果最优化。
(3) 将样本数据集以75%和25%划分为训练数据集和测试数据集,以RMSE, MAE, R2作为精度指标,评估预测模型是否存在过拟合或者欠拟合的现象,若是的话,则回到步骤1,调整预测模型的网络结构。通过上述3个步骤得到68个分区内各个监测站点最终的PM2.5预测值。
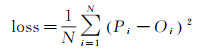 (4)
(4)
式中,N表示总的样本数目;i表示当前样本;Pi表示当前样本的预测值;Oi表示当前样本的观测值。
2.2 PM2.5浓度空间化模型基于多层LSTM迭代模型预测的PM2.5监测站点值难以在空间上进行展示,因此,应采用相应的模型进行空间化建模从而对PM2.5预报结果进行精细化制图,以实时评估区域的PM2.5空间分布特征。相关研究表明空气质量的空间分布会受到气象特征、地理环境以及人类活动等多重影响[33],本文考虑输入影响特征时,分别考虑了气象因素、空间相关因素和物理因素。
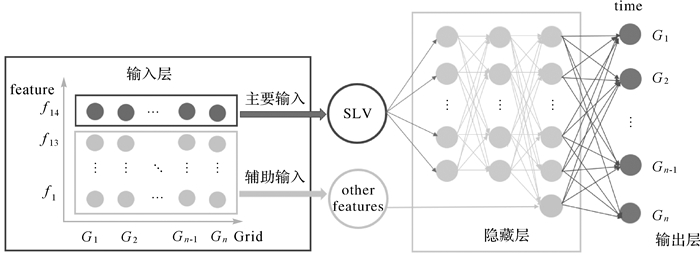
本文在空间化神经网络(S-BPNN)模型[22]的基础上做出进一步改进,改进的空间化模型的结构如图 8所示。
|
| 图 8 空间化模型网络结构 Fig. 8 Network framework of the spatial model |
该模型网络结构主要由输入层、隐藏层和输出层组成,其中输入层是由每个网格点的所有特征组成的,包括主要输入和辅助输入。首先,将全国划分将近为10万个10 km×10 km的网格点。由PM2.5浓度时空分析可知,PM2.5浓度具有高度的空间相关性,对于每个网格单元的PM2.5浓度与其空间距离最近的m个网格单元的PM2.5浓度具有显著的相关性,所以将各个网格点的空间滞后变量(SLV)特征作为主要输入,计算公式见式(5)
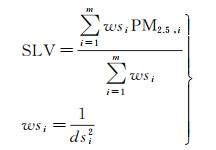 (5)
(5)
式中,m表示空间邻近网格单元数;wsi表示第i个邻近网格的权重;ds表示空间距离。
基于相关研究证明,当m=3时,模型性能表现最佳[22, 33-34]。然后,将主要输入变量输入到隐藏层,通过两层全连接层的训练后,结合辅助输入再通过一层全连接层进行训练,其中辅助输入由站点的经纬度、DEM、NDVI、建筑面积、人口密度、道路长度以及6个气象特征数据共13个特征数据组成。最后,输出各个网格点在t时刻的PM2.5预测值。
3 试验结果与讨论 3.1 PM2.5预测结果本文获取了2016—2019年共35 064 h的数据,基于PM2.5浓度显著的时空相关性,利用时间序列填补法和邻近站点填补法处理缺失值。基于时间相关性分析,并且为保证每次迭代预测的时间间隔一致,本文随机选取5个分区模型分别在[3, 4, 6, 8, 12]中选择时滞r进行试验,得到每个时滞下各个分区模型试验精度指标的平均值结果,由表 2可知,当r=12时,模型预测性能表现最好。
| 时滞r | RMSE/(μg/m3) | MAE/(μg/m3) | R2 |
| 3 | 11.28 | 8.44 | 0.76 |
| 4 | 10.56 | 7.83 | 0.79 |
| 6 | 8.01 | 5.76 | 0.86 |
| 8 | 7.88 | 5.46 | 0.87 |
| 12 | 6.45 | 4.23 | 0.93 |
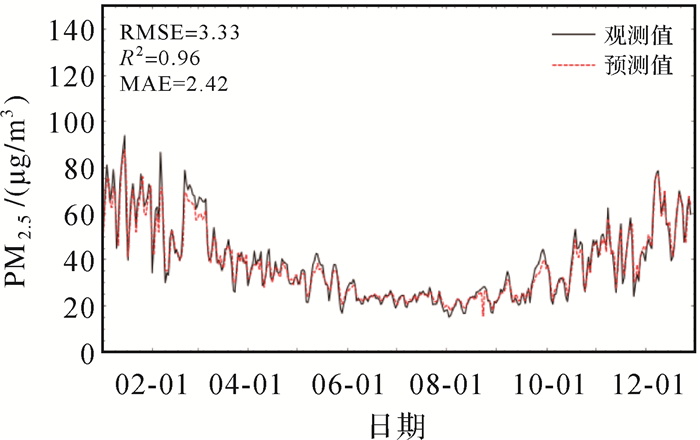
为了验证预测模型的性能以及捕捉时间序列的能力,图 9展示了全国地区2019年1月1日—12月31日的日均PM2.5观测值和多层LSTM迭代模型预测的PM2.5浓度的变化曲线。由图 9可知,PM2.5预测值与观测值的时间变化趋势之间存在一致性,表明多层LSTM迭代模型能很好地预测未来PM2.5浓度的时间序列变化。
|
| 图 9 基于多层LSTM迭代模型的预测结果 Fig. 9 Forecast results based on multi-layer LSTM iterative model |
PM2.5预测值和观测值的回归图如图 10所示。本文不仅预测了2019年365天的PM2.5日均值(图 10(a)),也预测了基于每小时样本未来24 h的PM2.5平均值(图 10(b))。图 10(c)—(f)为1年4个时间段基于每小时样本的回归评价图,其中图 10(a)和图 10(b)的R2分别为0.96和0.88,并且从图 10(c)—(f)和表 3可以看出,PM2.5浓度具有明显的时间特征,表 3为预测模型的时段精度评价,可知预测模型在4个时间段总体表现良好,其中每年1—2月和9—12月R2值在0.90以上,这表明多层LSTM迭代模型总体能实现较高精度的PM2.5浓度预测。由图 9和图 10可知,模型的预测能力随时间的变化很明显,在6—8月期间,存在明显的PM2.5浓度低值高估的现象,如图 10所示,PM2.5浓度预测值和观测值之间的线性回归方程的斜率小于1并且截距大于0,可以推断出预报结果有低估高浓度和高估低浓度的趋势,其预测结果的区间往往小于观测值的区间,从侧面也反映了PM2.5浓度预测的复杂性。
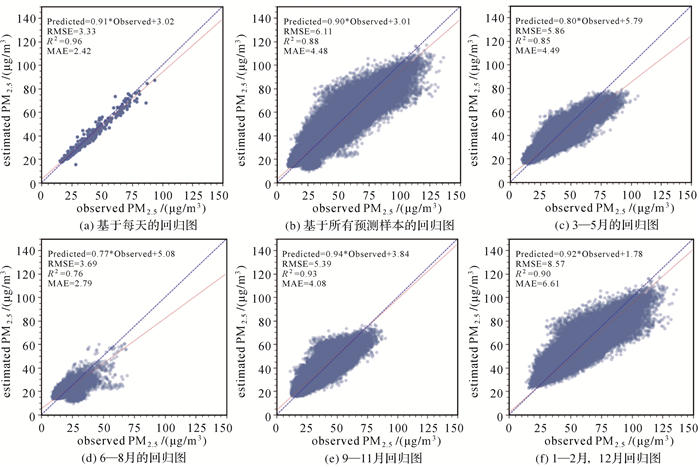
|
| 图 10 PM2.5浓度预测值和观测值的回归图 Fig. 10 Correlation between the observed and estimated PM2.5 concentrations |
| 时间段 | RMSE/(μg/m3) | MAE/(μg/m3) | R2 |
| 3—5月 | 5.86 | 4.49 | 0.85 |
| 6—8月 | 3.69 | 2.79 | 0.76 |
| 9—11月 | 5.39 | 4.08 | 0.93 |
| 1—2月,12月 | 8.57 | 6.61 | 0.90 |
3.2 PM2.5预测结果空间化
利用2016—2019年每个PM2.5监测站实时的数据,采用十折交叉验证的方式评估模型的性能。表 4为改进的S-BPNN空间化模型和S-BPNN模型十折交叉验证结果。由表 4可知,S-BPNN模型训练数据集和测试数据集的平均R2分别为0.77和0.75,而改进的S-BPNN模型R2分别为0.88和0.87,RMSE和MAE值都小于S- BPNN模型的值,RMSE和MAE的值分别提高了24.31%和25.33%,而且对比改进的S-BPNN模型和S-BPNN模型误差的标准差,可以发现改进的S-BPNN模型各项误差的波动较小,表明了改进的S-BPNN模型通过改变模型的网络结构,将空间滞后变量作为主要输入,其他特征数据作为辅助输入,可以实现更高的精度和稳定性,且适当增加隐藏层的层数可以提高模型的预测性能。本文基于预报模型预测的2020年7月29日未来24 h的PM2.5浓度,结合改进的S-BPNN空间化模型绘制了中国在空间分辨率为10 km时未来1~12 h、13~24 h和1~24 h PM2.5浓度的平均分布图,图 11展示了基于改进的S-BPNN模型全国大范围PM2.5预测值的空间分布(未来1 h、6 h、12 h、13~24 h平均和1~24 h平均)。如图 11所示,从季节上看,全国在夏季的PM2.5浓度值普遍偏低,全国大范围地区的PM2.5浓度值都低于30 μg/m3。从时间上看,PM2.5浓度值具有显著的时间相关性,相隔时间越短,其PM2.5浓度变化较小。从空间上看,我国PM2.5浓度值偏高地区主要集中于华北地区,这与该地区的产业发展,地理位置与气候条件等密切相关。
| 模型 | 指标 | 训练数据集 | 测试数据集 | |||||
| RMSE /(μg/m3) |
MAE /(μg/m3) |
R2 | RMSE /(μg/m3) |
MAE /(μg/m3) |
R2 | |||
| S-BPNN | Mean | 21.43 | 11.58 | 0.77 | 21.96 | 11.96 | 0.75 | |
| Std | 2.34 | 1.06 | 0.03 | 2.74 | 0.91 | 0.03 | ||
| 改进的S-BPNN | Mean | 15.77 | 8.48 | 0.88 | 16.62 | 8.93 | 0.87 | |
| Std | 1.86 | 0.78 | 0.02 | 2.13 | 0.76 | 0.02 | ||
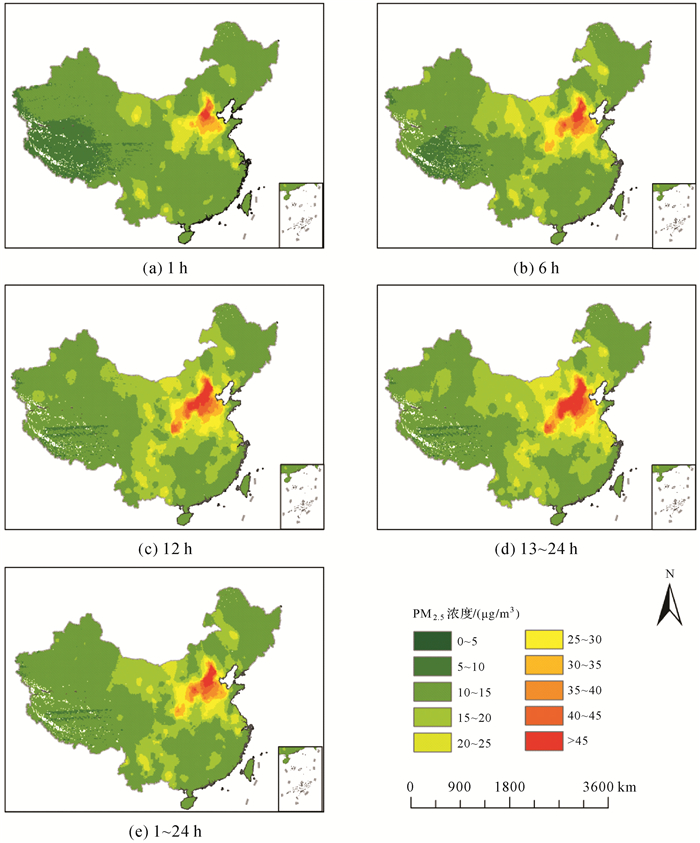
|
| 图 11 基于改进的S-BPNN模型的全国大范围PM2.5预测值空间分布 Fig. 11 Spatial distribution of predicted PM2.5 concentrations in large-scale area based on improved S-BPNN model |
3.3 大气污染物浓度预报原型系统
基于预报模型和空间化模型,建立大气污染物浓度预报原型系统,以此发布全国连续空间PM2.5浓度的预报结果。基于MySQL数据库为运行核心,原型系统主要包括数据管理、模型预测、实时预警及可视化展示4个模块,其中,数据管理模块用于实时大气污染物浓度、气象等数据实时的录入、管理等;模型预测模块主要基于多层LSTM迭代预报模型和改进的S-BPNN网络空间化模型,实现未来时刻大气污染物的时空预报;实时预警模块主要基于大气污染物预报的结果,实时评估大气污染物浓度的污染程度;可视化模块主要实时展示一定时期内的大气污染物浓度信息,实现相关信息的统计分析。图 12为大气污染物浓度预报原型系统的架构图,包括以下3个步骤。

|
| 图 12 大气污染物浓度预报原型系统架构 Fig. 12 Architecture diagram of the prototype system of atmospheric pollutant concentration forecast |
(1) 基于爬虫程序分别在全国城市空气质量实时发布平台(http://113.108.142.147:20035/)和中央气象台(http://www.nmc.cn/publish/forecast/)爬取小时尺度的大气污染监测站点数据以及未来7天的气象站点数据,并将爬取的数据入库。
(2) 利用2016年1月1日—2019年12月31日的实时PM2.5监测数据和气象数据,将全国各个站点分为68个区域并分别建模,训练得到满足监测精度的多层LSTM迭代预测模型,通过读取数据库中实时更新的站点数据,将数据输入已训练的多层LSTM迭代预测模型库中,其中输入的气象数据是基于GDAL进行实时空间插值的数据。同时借助于武汉大学超算中心(http://hpc.whu.edu.cn/),从而实时预测出未来24 h的PM2.5浓度变化,并将PM2.5预测值实时存储到数据库内,其中,采用武汉大学超算中心作为模型计算的平台,可提升模型的运行效率和稳定性。
(3) 读取数据库存储的预测数据,将数据传入应用层,并结合改进的S-BPNN空间化模型,生成实时预报结果的空间化影像图,应用层主要包括B/S网站,B/S网站(http://218.85.23.37:20104/)是基于ArcGIS API将模型预测的结果数据进行发布。B/S网站的重要功能包括预测结果的实时发布、数据的统计分析等,基本功能包括底图切换、地名和地名快捷选择等。预测结果也可以发布至移动端,方便用户用移动终端获取相关信息。
以上步骤如此循环,可以实现监测站点未来时刻的PM2.5预报以及对预测结果的空间化展示,并可实时在线发布区域的PM2.5空间分布特征数据以及统计后的PM2.5浓度变化的特征数据。
3.4 讨论本文通过全国内1286个空气质量站点的PM2.5历史数据,通过分析PM2.5浓度的时空相关性和影响因素,通过结合多层LSTM迭代预测模型和改进的S-BPNN模型从而实现全国大范围PM2.5浓度空间化预报,由于如PM10、O3、SO2等大气污染物都为长时间序列数据,且皆具有显著的时空相关性,并且会受到气象等特征的影响,本文的方法可以根据实际情况选择合适的影响因素和时滞,也适用于全国大范围其他大气污染物(PM10、O3、SO2等)的时空预报。对全国大范围大气污染进行实时的时空预报可以提前有针对性地治理环境污染,降低大气污染物治理成本,从而提升大气污染物治理的效率。
本文构建的预报模型和空间化模型精度RMSE分别为6.11 μg/m3和16.62 μg/m3,相比于国家发布的《环境质量标准》 (http://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/dqhjbh/dqhjzlbz/201203/W020120410330232398521.pdf)中的PM2.5二级24 h平均浓度限值为75 μg/m3,模型的误差较小,在可接受的误差范围之内,并不会影响模型的应用。但提出的模型也存在一定的局限性,如各个站点的PM2.5浓度预测值会存在高值低估和低值高估的现象,由于西藏地区监测站点数量较少,该地区的PM2.5浓度空间化预报存在一定的偏差等。大气污染空间化预报是一个复杂的问题,地面排放数据、遥感AOD(aerosol optical depth)数据等对PM2.5浓度预报也具有重要的作用。因此在未来的研究中,将应用这些数据建立基于深度学习的模型去改善存在的问题,从而提高全国大气污染时空预报的精度。
4 结论本文利用深度学习的方法分别构建了多层LSTM迭代预报模型和改进的S-BPNN空间化模型,不仅可以提供各个站点未来的PM2.5浓度预报结果,而且能发布空间大范围连续覆盖的未来实时PM2.5浓度预报结果。本文基于PM2.5监测站的历史数据,考虑PM2.5浓度具有一定的区域效应,在一定范围内的各个监测站点间PM2.5浓度具有显著的时空相关性,将所有站点进行自适应分区并分别建立预报模型,同时结合空间化模型将预报结果空间化,以此搭建大气污染浓度预报原型系统从而实现全国PM2.5浓度高时空精度的实时预报,与此同时,根据监测的结果可实时更新预报模型和空间化模型的数据输入与输出,进一步优化PM2.5浓度预报结果。本文研究可对区域的大气污染物浓度进行实时预警,辅助相关政府部门制定相关大气污染物联防联控预案,并可以对公众环境空间质量信息服务提供有力的支持。
| [1] |
李伟, 郑新奇. 结合VIIRS和监测数据插值的北京雾霾监测方法[J]. 测绘学报, 2015, 44(S1): 123-128. LI Wei, ZHENG Xinqi. A haze monitoring method combined VIIRS images with real-time observation data interpolation in Beijing[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(S1): 123-128. DOI:10.11947/j.AGCS.2015.F022 |
| [2] |
LI Can, HSU N C, TSAY S C. A study on the potential applications of satellite data in air quality monitoring and forecasting[J]. Atmospheric Environment, 2011, 45(22): 3663-3675. DOI:10.1016/j.atmosenv.2011.04.032 |
| [3] |
沈焕锋, 李同文. 大气PM2.5遥感制图研究进展[J]. 测绘学报, 2019, 48(12): 1624-1635. SHEN Huanfeng, LI Tongwen. Progress of remote sensing mapping of atmospheric PM2.5[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(12): 1624-1635. DOI:10.11947/j.AGCS.2019.20190456 |
| [4] |
KAMPA M, CASTANAS E. Human health effects of air pollution[J]. Environmental Pollution, 2008, 151(2): 362-367. DOI:10.1016/j.envpol.2007.06.012 |
| [5] |
KURT A, OKTAY A B. Forecasting air pollutant indicator levels with geographic models 3 days in advance using neural networks[J]. Expert Systems with Applications, 2010, 37(12): 7986-7992. DOI:10.1016/j.eswa.2010.05.093 |
| [6] |
DENG Xuejiao, TIE Xuexi, WU Dui, et al. Long-term trend of visibility and its characterizations in the Pearl river delta (PRD) region, China[J]. Atmospheric Environment, 2008, 42(7): 1424-1435. DOI:10.1016/j.atmosenv.2007.11.025 |
| [7] |
KIM Y, FU J S, MILLER T L. Improving ozone modeling in complex terrain at a fine grid resolution: partⅠ: examination of analysis nudging and all PBL schemes associated with LSMs in meteorological model[J]. Atmospheric Environment, 2010, 44(4): 523-532. DOI:10.1016/j.atmosenv.2009.10.045 |
| [8] |
GENG Guannan, ZHANG Qiang, MARTIN R V, et al. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model[J]. Remote Sensing of Environment, 2015, 166: 262-270. DOI:10.1016/j.rse.2015.05.016 |
| [9] |
PAN Lin, SUN Baosheng, WANG Wei. City air quality forecasting and impact factors analysis based on grey model[J]. Procedia Engineering, 2011(12): 74-79. |
| [10] |
ENGEL-COX J, OANH N T K, VAN DONKELAAR A, et al. Toward the next generation of air quality monitoring: particulate matter[J]. Atmospheric Environment, 2013, 80: 584-590. DOI:10.1016/j.atmosenv.2013.08.016 |
| [11] |
ZHU Suling, LIAN Xiuyuan, WEI Lin, et al. PM2.5 forecasting using SVR with PSOGSA algorithm based on CEEMD, GRNN and GCA considering meteorological factors[J]. Atmospheric Environment, 2018, 183: 20-32. DOI:10.1016/j.atmosenv.2018.04.004 |
| [12] |
STADLOBER E, HÖRMANN S, PFEILER B. Quality and performance of a PM10 daily forecasting model[J]. Atmospheric Environment, 2008, 42(6): 1098-1109. DOI:10.1016/j.atmosenv.2007.10.073 |
| [13] |
付倩娆. 基于多元线性回归的雾霾预测方法研究[J]. 计算机科学, 2016, 43(S1): 526-528. FU Qianrao. Research on haze prediction based on multivariate linear regression[J]. Computer Science, 2016, 43(S1): 526-528. |
| [14] |
HU Xuefei, BELLE J H, MENG Xia, et al. Estimating PM2.5 concentrations in the conterminous united states using the random forest approach[J]. Environmental Science & Technology, 2017, 51(12): 6936-6944. |
| [15] |
PEREZ P, REYES J. An integrated neural network model for PM10 forecasting[J]. Atmospheric Environment, 2006, 40(16): 2845-2851. DOI:10.1016/j.atmosenv.2006.01.010 |
| [16] |
FENG Yu, ZHANG Wenfang, SUN Dezhi, et al. Ozone concentration forecast method based on genetic algorithm optimized back propagation neural networks and support vector machine data classification[J]. Atmospheric Environment, 2011, 45(11): 1979-1985. DOI:10.1016/j.atmosenv.2011.01.022 |
| [17] |
MAO Wenjing, WANG Weilin, JIAO Limin, et al. Modeling air quality prediction using a deep learning approach: method optimization and evaluation[J]. Sustainable Cities and Society, 2021, 65(2): 102-118. |
| [18] |
KOLEHMAINEN M, MARTIKAINEN H, RUUSKANEN J. Neural networks and periodic components used in air quality forecasting[J]. Atmospheric Environment, 2001, 35(5): 815-825. DOI:10.1016/S1352-2310(00)00385-X |
| [19] |
VOUKANTSIS D, KARATZAS K, KUKKONEN J, et al. Intercomparison of air quality data using principal component analysis, and forecasting of PM10 and PM2.5 concentrations using artificial neural networks, in Thessaloniki and Helsinki[J]. Science of the Total Environment, 2011, 409(7): 1266-1276. DOI:10.1016/j.scitotenv.2010.12.039 |
| [20] |
WANG Xinpeng, SUN Wenbin. Meteorological parameters and gaseous pollutant concentrations as predictors of daily continuous PM2.5 concentrations using deep neural network in Beijing-Tianjin-Hebei, China[J]. Atmospheric Environment, 2019, 211: 128-137. DOI:10.1016/j.atmosenv.2019.05.004 |
| [21] |
ZHAN Yu, LUO Yuzhou, DENG Xunfei, et al. Spatiotemporal prediction of continuous daily PM2.5 concentra-tions across China using a spatially explicit machine learning algorithm[J]. Atmospheric Environment, 2017, 155: 129-139. DOI:10.1016/j.atmosenv.2017.02.023 |
| [22] |
WANG Weilin, ZHAO Suli, JIAO Limin, et al. Estimation of PM2.5 concentrations in China using a spatial back propagation neural network[J]. Scientific Reports, 2019, 9(1): 1378-1387. DOI:10.1038/s41598-018-37499-2 |
| [23] |
MA Jun, DING Yuexiong, CHENG J C P, et al. A Lag-FLSTM deep learning network based on Bayesian optimization for multi-sequential-variant PM2.5 prediction[J]. Sustainable Cities and Society, 2020, 60(9): 1022-1037. |
| [24] |
XU Fulong, LI Zishen, ZHANG Kefei, et al. An investigation of optimal machine learning methods for the prediction of ROTI[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 1-15. DOI:10.11947/j.JGGS.2020.0201 |
| [25] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [26] |
LI Xiang, PENG Ling, YAO Xiaojing, et al. Long short-term memory neural network for air pollutant concentration predictions: method development and evaluation[J]. Environmental Pollution, 2017, 231: 997-1004. DOI:10.1016/j.envpol.2017.08.114 |
| [27] |
ZHAO Jiachen, DENG Fang, CAI Yeyun, et al. Long short-term memory-Fully connected (LSTM-FC) neural network for PM2.5 concentration prediction[J]. Chemosphere, 2019, 220: 486-492. DOI:10.1016/j.chemosphere.2018.12.128 |
| [28] |
PAK U, KIM C, RYU U, et al. A hybrid model based on convolutional neural networks and long short-term memory for ozone concentration prediction[J]. Air Quality, Atmosphere & Health, 2018, 11(8): 883-895. |
| [29] |
WEN Congcong, LIU Shufu, YAO Xiaojing, et al. A novel spatiotemporal convolutional long short-term neural network for air pollution prediction[J]. Science of the Total Environment, 2019, 654: 1091-1099. DOI:10.1016/j.scitotenv.2018.11.086 |
| [30] |
BAI Yun, LI Yong, WANG Xiaoxue, et al. Air pollutants concentrations forecasting using back propagation neural network based on wavelet decomposition with meteorological conditions[J]. Atmospheric Pollution Research, 2016, 7(3): 557-566. DOI:10.1016/j.apr.2016.01.004 |
| [31] |
ZHANG Boen, JIAO Limin, XU Gang, et al. Influences of wind and precipitation on different-sized particulate matter concentrations (PM2.5, PM10, PM2.5-10)[J]. Meteorology and Atmospheric Physics, 2018, 130(3): 383-392. DOI:10.1007/s00703-017-0526-9 |
| [32] |
RESHEF D N, RESHEF Y A, FINUCANE H K, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334(6062): 1518-1524. DOI:10.1126/science.1205438 |
| [33] |
LI Tongwen, SHEN Huanfeng, ZENG Chao, et al. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: methods and assessment[J]. Atmospheric Environment, 2017, 152: 477-489. DOI:10.1016/j.atmosenv.2017.01.004 |
| [34] |
LI Tiantian, GUO Yuming, LIU Yang, et al. Estimating mortality burden attributable to short-term PM2.5 exposure: a national observational study in China[J]. Environment International, 2019, 125: 245-251. DOI:10.1016/j.envint.2019.01.073 |



