高精度位置服务依赖模糊度固定的毫米级精度的载波相位观测值,而城市复杂遮挡环境导致的频繁相位周跳和中断给模糊度固定带来巨大挑战,因此有效地探测和修复相位周跳和中断能大大地减轻模糊度固定的负担,从而提升高精度定位的连续性和可用性。
在GPS应用之初,诸多学者便针对GPS双频信号开展了基于组合观测值探测周跳的研究,提出了基于Melbourne-Wübbena(MW)组合[1-2]和无几何组合(geometry free, GF)的TurboEdit方法[3],该方法具有程序实现简单、大周跳探测准确的优点,但依然无法准确地确定周跳发生频率和具体数值,因此该方法通常只用来探测而不修复。在此基础上,文献[4-6]在特定应用场景下改进了TurboEdit方法,使其具备探测并修复双频小周跳的能力。三频信号的推出为周跳探测和修复提供了更多更优的组合观测值。文献[7]从成功概率角度公式推导并分析了单台接收机的多频相位周跳检测能力。文献[8]从理论和试验上论证了三频信号对周跳探测模型的改善和探测效果的提升。文献[9]以周跳估值方差最小为准则,选取了探测周跳的GPS三频最优组合,并推导了周跳探测的阈值条件。为了提升窄巷周跳探测与修复效果,文献[10]给出了一种三频无几何相位组合探测周跳方案。文献[11]采用联合伪距和相位无几何组合的周跳分步检测和修复方法。以上方法对高采样的周跳探测与修复效果良好,但当采样间隔较大时,效果依然不佳,其原因在该情景下的电离层变化剧烈,简单地忽略电离层会导致周跳探测错误。为此,如何削弱电离层对周跳探测影响得到了广泛关注,基于无周跳或周跳修复的历元数据计算电离层延迟变化量,在此基础上采用线性模型[12]或二阶模型[13]预报模型补偿当前历元的电离层延迟变化量,从而提高了电离层活跃期的周跳修复。文献[14-15]构建了观测卫星联合周跳处理的几何模型,充分利用了“干净”卫星数据辅助其他卫星的周跳处理,有效解决了大采样间隔下连续周跳问题。
北斗三号系统(BDS-3)已开通了全球服务,可向全球播发四频甚至五频观测值(表 1),为用户提供了更多更优的组合观测值方案[16-18],这在理论上和实践上为准确估计复杂环境下的相位周跳和中断提供了保障。因此,本文研究BDS-3的四频和五频相位周跳探测和修复方法,研究适用于周跳探测的最优无几何组合观测值,建立联合GF组合观测值和电离层补偿的滤波模型,从而实现低采样和数分钟间隔的周跳实时探测和修复。在城市复杂的遮挡环境下,除了频繁的历元间周跳外,数分钟的载波相位频繁中断导致模糊度频繁初始化是影响城市高精度定位的瓶颈,因此,本文方法有效实现数分钟的周跳修复有望解决该瓶颈。
| 频点 | 四频 | 五频 |
| B1C | f1=1 575.420 | f1=1 575.420 |
| B1I | f2=1 561.098 | f2=1 561.098 |
| B3I | f3=1 268.520 | f3=1 268.520 |
| B2b | - | f4=1 207.140 |
| B2a | f4=1 176.450 | f5=1 176.450 |
1 多频相位周跳及中断探测和修复模型 1.1 无几何组合周跳探测模型
由于周跳的继承性,通常利用历元差分观测值探测周跳,历元差分的相位Δϕj和伪距Δpj观测方程为[15]
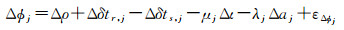 (1)
(1)
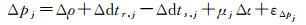 (2)
(2)
式中,下标j、r和s分别表示第j个频率、测站和卫星;Δρ为包含卫地距和对流层信息的几何距离变化量;Δι和μj=f12/fj2分别为历元间电离层延迟及其系数;Δδtr和Δdtr分别为相位和伪距的接收机钟差的历元差;Δδts和Δdts表示相位和伪距的卫星钟差历元差;Δaj为潜在的周跳;εΔϕj和εΔpj表示相位和伪距对应的随机噪声。
为不失一般性,令任意f个频率的组合系数为z=[z1, z2, …, zf]T,则组合观测值Δϕz为
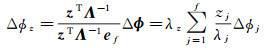 (3)
(3)
式中,矩阵Λ=diag(λ1, λ2, …, λf);ef为元素全为1的f维列向量。组合波长λz、组合电离层系数μz和组合模糊度az为
 (4)
(4)
若取所有频率的相位观测值等精度σϕ,则组合观测值的方差为
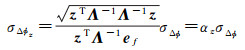 (5)
(5)
类似地,令伪距的组合系数为w=[w1, w2, …, wf]T,则伪距组合观测值为
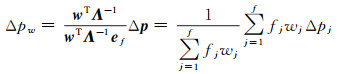 (6)
(6)
在非差观测值中,不同频率的相位和伪距接收机钟差可分别表示为
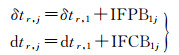 (7)
(7)
相同频率的相位和伪距接收机钟差可表示为
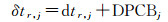 (8)
(8)
式中,IFPB1j和IFCB1j分别表示频间相位和伪距偏差;DPCBj表示相位和伪距的通道延迟。对于卫星钟差,有完全类似的关系。大量文献研究表明,这些偏差和延迟量在短时间内非常稳定以至于可以视为常数[19-21],因此,单差后的接收机钟差和卫星钟差为
 (9)
(9)
在相位和伪距组合观测值的基础上,可构成GF组合观测模型
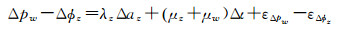 (10)
(10)
类似地,两个组合相位观测值之间也可以构成GF组合观测模型,令两个相位组合观测值为Δϕz1和Δϕz2,则
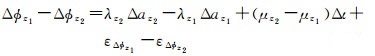 (11)
(11)
显然,GF模型消掉了卫地距、对流层延迟、卫星钟差和接收机钟差,只剩余组合周跳和电离层延迟,因此可用于探测周跳。
1.2 伪距-相位GF模型的超宽巷周跳探测式(11)包含了两个相位组合周跳,显然需事先确定其中一个组合周跳,才有可能确定另外一个组合周跳。而式(10)中只包含了一个相位组合周跳,但受到历元间电离层变化量和伪距组合噪声的影响。考虑到f个频率信号可构造f-1个独立的超宽巷(extra-wide-lane, EWL)或宽巷(wide-lane, WL)观测值[22],超宽巷的波长可达到数米,以至于式(10)中的历元间电离层变化量和伪距噪声对周跳的整数影响较小,从而正确固定周跳,即伪距-相位GF模型计算的周跳浮点解及精度为
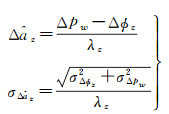 (12)
(12)
对应的偏差为
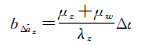 (13)
(13)
通过给定不同的整数系数得到不同的组合。为了实现最优的周跳效果,系数组合应具有长组合波长,尽量小的电离层延迟因子和组合噪声系数。国内外众多学者提出了许多挑选组合系数的方法,但基本都是通过平衡波长和电离层延迟因子来枚举得到。本文以周跳四舍五入固定解的成功概率最大为准则选取最优EWL/WL组合,考虑周跳浮点解偏差的影响,则周跳固定解的成功概率为[23]
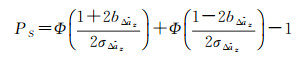 (14)
(14)
式中,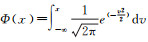
| ϕz | Ρw | λz/m | μz+μw | 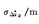 |
PS/(%) | ||
| Δι=0.1 m | Δι=0.2 m | Δι=1 m | |||||
| ϕ(1, -1, 0, 0) | Ρ(1, 1, 0, 0) | 20.932 3 | 0 | 0.024 4 | 100 | 100 | 100 |
| ϕ(0, 0, 1, -1) | Ρ(0, 0, 1, 1) | 3.256 1 | 0 | 0.067 4 | 100 | 100 | 100 |
| ϕ(2, -1, -4, 3) | Ρ(1, 1, 0, -1) | 6.66 | 1.955 | 0.092 | 100 | 100 | 99 |
| ϕ(1, -1, 0, 0, 0) | Ρ(1, 1, 0, 0, 0) | 20.932 3 | 0 | 0.024 4 | 100 | 100 | 100 |
| ϕ(0, 0, 0, 1, -1) | Ρ(0, 0, 0, 1, 1) | 9.768 4 | 0 | 0.027 4 | 100 | 100 | 100 |
| ϕ(0, 0, 1, -1, 0) | Ρ(0, 0, 1, 1, 0) | 4.884 2 | 0.126 8 | 0.046 8 | 100 | 100 | 100 |
| ϕ(-1, 2, -4, 1, 2) | Ρ(1, 1, 1, 0, 0) | 9.157 8 | 2.796 7 | 0.069 7 | 100 | 100 | 99.7 |
由表 2可以看出,由于EWL具有几米甚至20 m长的波长,电离层误差和伪距误差对其影响极小,EWL周跳的固定成功率在所有的情景下几乎都是100%。只有当历元间电离层变化量达到1 m时,四频和五频最差的EWL组合固定率分别为99%和99.7%。事实上,通常历元间的电离层变化远小于1 m,因此,采用伪距-相位GF组合模型固定EWL周跳是可行的。
1.3 相位-相位GF模型的窄巷周跳探测为了恢复每个频率的周跳,除了固定f-1个EWL/WL组合周跳外,还需要固定一个窄巷(narrow-lane,NL)组合的周跳。根据上文所述,由于电离层和伪距噪声的共同影响,采用式(10)固定NL周跳显然是不合适的。周跳固定的EWL观测值,其噪声远小于伪距观测值,因此可采用式(11)相位-相位GF组合模型来固定NL周跳,设z1为EWL组合系数,其对应的组合周跳已固定为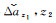
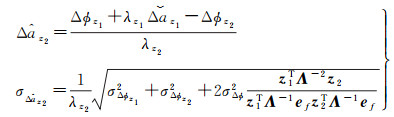 (15)
(15)
对应的偏差为
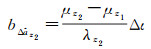 (16)
(16)
同样,以基于式(11)计算的成功概率最大为准则,选取了不同电离层延迟情况下的NL最优组合,表 3给出了这些组合对应NL周跳固定的成功概率。显然,NL周跳固定对电离层延迟非常敏感,只有当Δι≤0.02 m时,才能获得100%的固定成功概率;当Δι=0.04 m时,成功概率锐减至约50%。因此,为了可靠地固定NL周跳,就必须对电离层延迟进行有效补偿。
| Δϕz1 | Δϕz2 | λz2/m | μz2-μz1 | 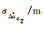 |
PS/(%) | ||
| Δι=0.02 m | Δι=0.04 m | Δι=0.05 m | |||||
| ϕ(0, 1, 0, -1) | ϕ(-1, 1, 0, 1) | 0.258 0 | 3.179 2 | 0.059 0 | 100 | 54 | 2 |
| Δϕ(0, -1, 0, 0, 1) | ϕ(-1, 1, 0, 1, 0) | 0.251 3 | 3.087 2 | 0.052 9 | 100 | 56 | 1 |
2 顾及电离层影响的窄巷周跳探测滤波模型
如果两个连续历元的相位观测值没有周跳或其周跳已被成功修复,则历元间电离层变化量可用式(17)计算
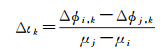 (17)
(17)
式中,下标k表示第k-1和k历元的差分值。一般而言,电离层历元间变化相对比较平稳,即使在复杂的情况下,采用二阶模型足以刻画其复杂变化,因此,电离层时间变化的动力学模型可表示为
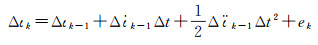 (18)
(18)
式中,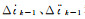
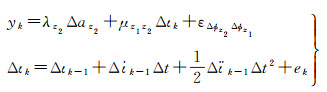 (19)
(19)
式中,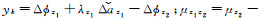
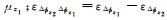
式(19)只利用了一个EWL观测值。事实上,所有的EWL周跳都较为容易固定,因此,为了充分利用(f-1)个EWL/WL观测值信息,可将(19)中的第1个方程改造为
 (20)
(20)
式中,zf表示NL组合系数;z1, z2, …, zf-1为f-1个EWL/WL组合系数。
值得说明的是,①考虑到采用式(17)求解电离层延迟时,频率越近噪声越大,故建议选择[B1C, B3I]、[B1I, B3I]、[B1C, B2a]或者[B1I, B2a]组合计算,或者同时采用这4个组合采用最小二乘计算电离层延迟的加权平均值。②由于电离层在短时间内的变化较为缓慢,计算的电离层变化较小,即当电离层非常平静期时,可以忽略其影响以简化模型提高计算效率。③当无周跳发生时,保持计算模型式(18)以持续预报电离层延迟,以便后续使用。④当发生数据中断时,只需将历元间隔调整为中断时长即可实现中断期间电离层延迟预测和中断修复后的模糊度连接。
一旦f-1个EWL/WL周跳及NL周跳固定,则可通过逆变换求得各个频率的周跳
 (21)
(21)
在周跳探测中尽管EWL探测不出周跳,而NL探测出周跳的极端情况发生概率几乎为零。但在实际应用中,一旦出现此类情况,将重新初始化模糊度。
3 试验分析使用Trimble-Alloy接收机采集3 d静态数据(2021年4月18日-2021年4月20日),采样频率为30 s,试验中截至高度角设置为10°。为了统计分析周跳探测效果,本文模拟试验对6颗MEO卫星(C23、C25、C28、C34、C41、C43)和3颗IGSO卫星(C38、C39、C40)进行周跳和数据中断模拟,分析不同模型的周跳探测效果。
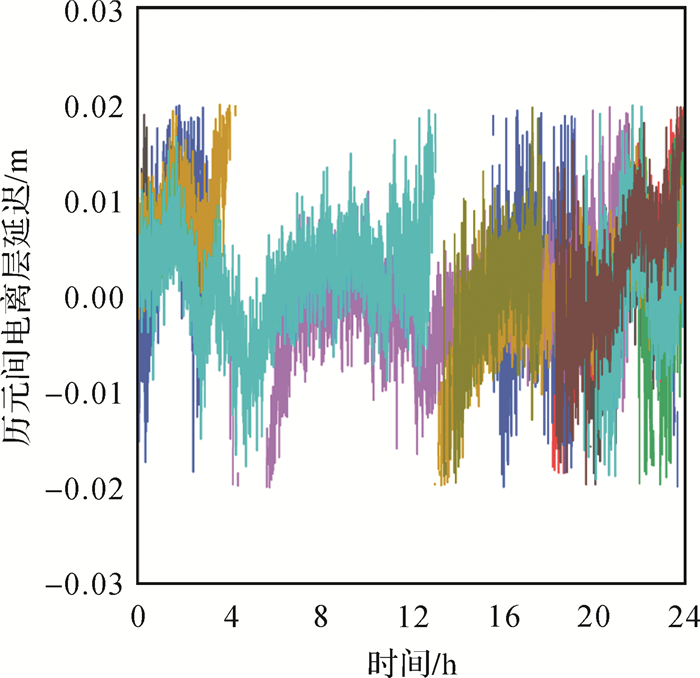
3.1 周跳探测和修复分析采用伪距-相位GF模型探测EWL周跳和基于相位-相位GF模型探测NL周跳的效果。图 1给出了所有卫星历元间电离层延迟变化量,不同颜色代表不同卫星,30 s间隔的电离层延迟变化量在2 cm范围内波动,显然本次试验处于电离层平静期。(根据上文分析,如此小的电离层延迟变化量所引起的EWL偏差式(13)和NL偏差式(16)不会对周跳成功探测造成影响,因此可直接采用伪距-相位GF模型式(12)求解EWL周跳、采用相位-相位GF模型式(15)求解NL周跳。)
|
| 图 1 2021年4月18日30 s采样的历元间电离层延迟 Fig. 1 Between-epoch ionospheric delay for the 30 s sampling on April 18, 2021 |
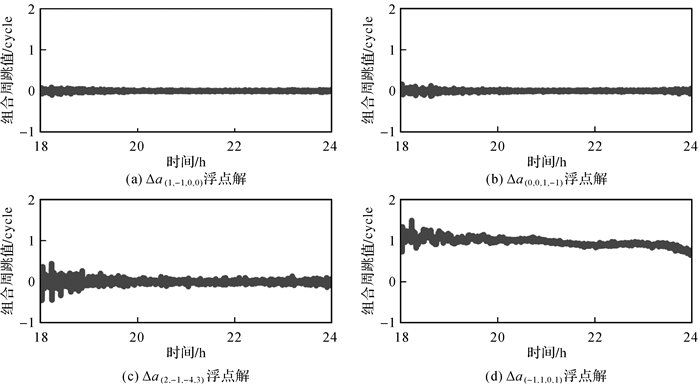
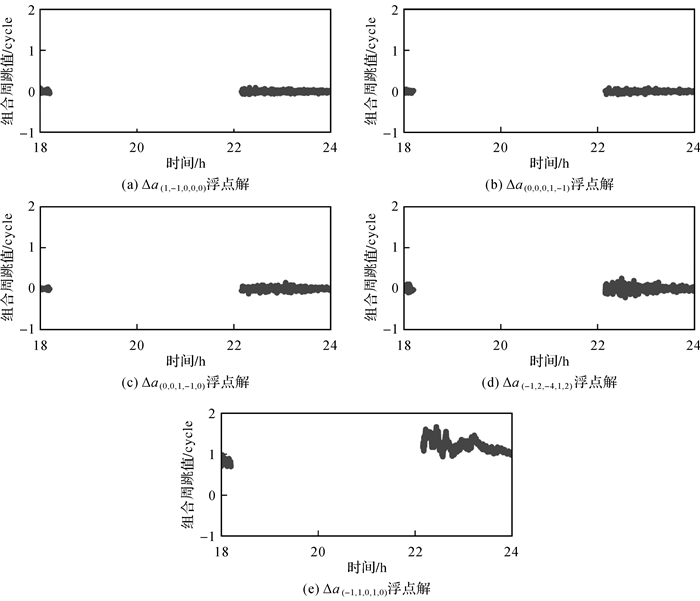
在所有卫星的所有频点都模拟1周的周跳,由于EWL组合系数之和等于0,因此EWL周跳真值等于0;而NL组合系数之和等于1,因此NL周跳真值为1。以18号数据为例,图 2和图 3分别给出了C41卫星四频信号和C40五频信号基于GF模型的EWL和NL周跳浮点解。结果表明,四频和五频EWL组合的周跳浮点解均非常接近0,且其噪声非常小,说明伪距-相位GF模型能有效探测EWL小周跳;NL组合的周跳浮点解均在真值1处波动,且大部分噪声波动小于0.5周,这也说明基于相位-相位GF模型在电离层变化较小的情况下也有能力探测出小周跳。
|
| 图 2 基于伪距-相位GF模型求解的C41卫星四频信号的EWL和NL组合周跳浮点解 Fig. 2 The cycle slip float solutions of combined EWL and NL for the C41 satellite quad-frequency based on the pseudorange-phase GF model |
|
| 图 3 基于相位-相位GF模型求解的C40卫星五频信号的EWL和NL组合周跳浮点解 Fig. 3 The cycle slip float solutions of combined EWL and NL for the C40 satellite penta-frequency based on the phase-phase GF model |
为了统计GF模型固定周跳的性能,本文引入固定率Pfix和固定成功率Psuc评价指标[24]
 (22)
(22)
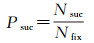 (23)
(23)
式中,Ntotal、Nfix和Nsuc分别表示所有周跳个数、固定的周跳个数及正确固定的周跳个数。实际应用中,为了提高固定的可靠性,本文在四舍五入法中给定0.3周作为阈值,即周跳浮点解与其四舍五入整数解的偏差大于阈值0.3周时,则标记该周跳固定失败。
分别计算3 d四频数据和五频数据的周跳探测结果,其统计结果如图 4所示。所有卫星的固定率大于93%以上,且固定成功率大于94%,所有卫星的固定率均值和固定成功率均值都大于96%。此外,对比四频和五频信号,五频的固定率和固定成功率都比四频有所提升。在有些历元,五频能固定四频因舍入误差而无法固定的周跳。表 4给出了测试时间段内每颗卫星五频固定成功而四频失败的总次数。
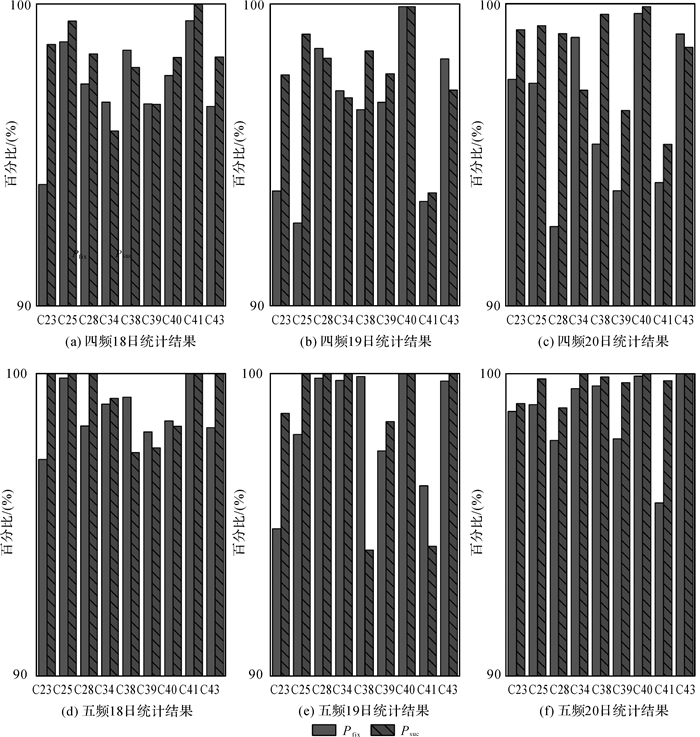
|
| 图 4 四频和五频信号周跳固定率Pfix和固定成功率Psuc Fig. 4 The cycle slip fixed rate Pfix and fixed success rate Psuc of quad-frequency and penta-frequency |
| 卫星编号 | 日期 | ||
| 4月18日 | 4月19日 | 4月20日 | |
| C23 | 31 | 24 | 9 |
| C25 | 5 | 40 | 13 |
| C28 | 13 | 21 | 27 |
| C34 | * | 21 | * |
| C38 | 21 | 18 | 7 |
| C39 | 35 | 29 | 15 |
| C40 | 20 | 2 | 7 |
| C41 | 4 | 49 | 14 |
| C43 | * | * | 17 |
| 注:*表示因五频信号缺失而失败。 | |||
3.2 数据中断修复
本文进一步测试数据中断修复,所谓数据中断是指在城市复杂遮挡环境下,卫星数据被短时间遮挡导致重新接收到信号时需要探测这中断情况下卫星是否发生周跳。在原始数据中,每个历元对每颗卫星分别模拟3 min数据中断,且当在信号重新跟踪的历元模拟1周的周跳。3 min的数据中断将带来电离层变化显著,若不对电离层延迟变化量进行补偿,难以用相位-相位的GF模型直接探测NL周跳,结果如图 5所示。在不对电离层延迟变化量修正情况下,周跳的平均固定率仅为约50%,这显然难以满足实际应用的需求,这也恰恰说明必须对电离层延迟变化量予以补偿。
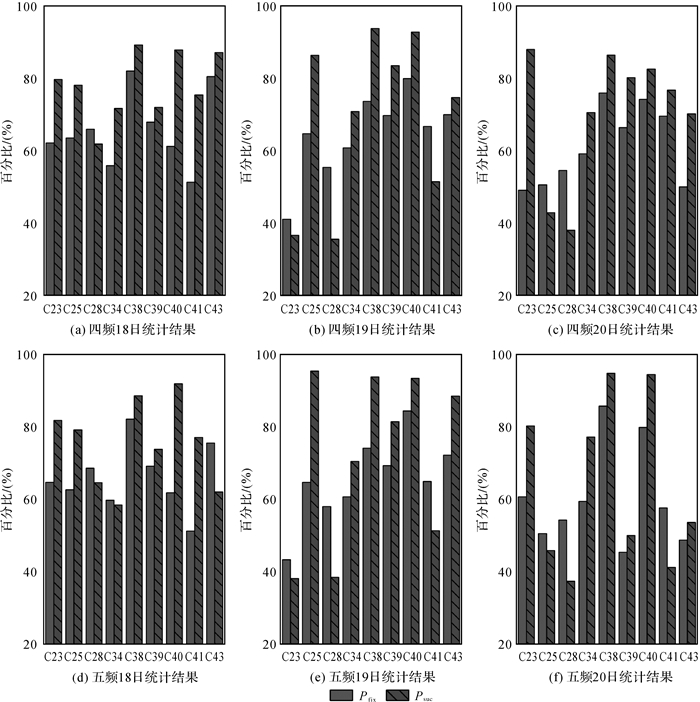
|
| 图 5 采用GF模型探测四频和五频数据中断的固定率Pfix和固定成功率Psuc Fig. 5 The data gap fixed rate Pfix and fixed success rate Psuc of quad-frequency and penta-frequency |
分析基于顾及电离层的滤波模型探测数据中断的效果,此时通过卡尔曼滤波对电离层变化量进行预报。试验统计结果如图 6所示。大部分卫星四频平均固定率和固定成功率分别在94%、96%以上,卫星C34、C41、C43的固定率和固定成功率相对较低,但也达到了92%、91%、91%和93%、88%、93%,然而大部分卫星五频平均固定率、固定成功率在97%、98%以上,仅卫星C34的固定率和固定成功率为95%和96%。考虑到模拟中断时长在3 min,即使个别卫星最低成功率在88%,这样的结果依然是可观的。

|
| 图 6 采用顾及电离层的滤波模型探测四频和五频数据中断的固定率Pfix和固定成功率Psuc Fig. 6 The data gap fixed rate Pfix and fixed success rate Psuc of quad-frequency and penta-frequency by the filtering model taking into account the ionosphere |
4 结论
针对北斗三号系统,本文提出了一种多频相位周跳及中断实时探测和修复方案,包括基于伪距-相位无几何组合模型探测f-1个超宽巷周跳,以及基于电离层延迟补偿的相位-相位无几何窄巷周跳,通过理论和试验分析得出以下结论。
(1) 伪距-相位无几何组合超宽巷周跳探测模型简单易操作,即使在电离层延迟变化量达到1 m时的周跳成功固定率也几乎达到100%。
(2) 相位-相位无几何组合窄巷周跳探测模型受电离层延迟变化量影响较大,在30 s的采样间隔下电离层延迟变化不显著时,四频和五频的固定率和固定成功率分别在93%、94%以上;但在3 min数据中断情况下,电离层延迟变化量显著影响窄巷周跳探测效果,成功率仅为约50%。
(3) 本文提出的顾及电离层延迟变化量的相位-相位无几何组合的卡尔曼滤波模型能有效抑制电离层对窄巷周跳探测的影响,可将3 min数据中断的探测成功率从50%提升至90%以上。
| [1] |
MELBOURNE W. The case for ranging in GPS-based geodetic systems[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, USA: [s. n. ], 1985: 373-386.
|
| [2] |
WUBBENA G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, USA: [s. n. ], 1985: 403-412.
|
| [3] |
BLEWITT G. An automatic editing algorithm for GPS data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. DOI:10.1029/GL017i003p00199 |
| [4] |
王振杰, 聂志喜, 欧吉坤. 一种基于TurboEdit改进的GPS双频观测值周跳探测方法[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1017-1021. WANG Zhenjie, NIE Zhixi, OU Jikun. An improved GPS dual-frequency observation cycle slips detection method based on TurboEdit[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1017-1021. |
| [5] |
吴继忠, 施闯, 方荣新. TurboEdit单站GPS数据周跳探测方法的改进[J]. 武汉大学学报(信息科学版), 2011, 36(1): 29-33. WU Jizhong, SHI Chuang, FANG Rongxin. Improvement of cycle slips detection method for TurboEdit single station GPS data[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 29-33. |
| [6] |
刘宁, 熊永良, 徐韶光. 利用改进的TurboEdit算法与Chebyshev多项式探测与修复周跳[J]. 武汉大学学报(信息科学版), 2011, 36(12): 1500-1503. LIU Ning, XIONG Yongliang, XU Shaoguang. Detection and repair of cycle slips using improved TurboEdit algorithm with Chebyshev polynomials[J]. Geomatics and Information Science of Wuhan University, 2011, 36(12): 1500-1503. |
| [7] |
TEUNISSEN P J G, DE BAKKER P F D. Single-receiver single-channel multi-frequency GNSS integrity: outliers, slips, and ionospheric disturbances[J]. Journal of Geodesy, 2013, 87(2): 161-177. DOI:10.1007/s00190-012-0588-x |
| [8] |
ZHANG Xiaohong, LI Pan. Benefits of the third frequency signal on cycle slip correction[J]. GPS Solutions, 2015, 20(3): 451-460. |
| [9] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722. LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time cycle-slip detection and repair based on code-phase combinations for GNSS triple-frequency undifferenced observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722. |
| [10] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768. HUANG Lingyong, SONG Lijie, WANG Yan, et al. BeiDou triple-frequency geometry-free phase combination for cycle-slip detection and correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768. |
| [11] |
LACY M, REGUZZONI M, SANSÒ F. Real-time cycle slip detection in triple-frequency GNSS[J]. GPS Solutions, 2012, 16(3): 353-362. DOI:10.1007/s10291-011-0237-5 |
| [12] |
LIU Zhitao. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver [J]. Journal of Geodesy, 85(3): 171-183.
|
| [13] |
LI Bofeng, QIN Yanan, LI Zhen, et al. Undifferenced cycle slip estimation of triple-frequency BeiDou signals with ionosphere prediction[J]. Marine Geodesy, 2016, 39(5): 348-365. DOI:10.1080/01490419.2016.1207729 |
| [14] |
ZHANG Xiaohong, LI Xingxing. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing[J]. GPS Solutions, 2012, 16(3): 315-327. DOI:10.1007/s10291-011-0233-9 |
| [15] |
LI Bofeng, QIN Yanan, LIU Tianxia. Geometry-based cycle slip and data gap repair for multi-GNSS and multi-frequency observations[J]. Journal of Geodesy, 2019, 93: 399-417. DOI:10.1007/s00190-018-1168-5 |
| [16] |
YANG Yuanxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system: data analysis based on BDS-3 demonstration system[J]. Science China Earth Sciences, 2018, 61(5): 614-624. DOI:10.1007/s11430-017-9186-9 |
| [17] |
ZHANG Zhiteng, LI Bofeng, NIE Liangwei, et al. Initial assessment of BeiDou-3 global navigation satellite system: signal quality, RTK and PPP[J]. GPS Solutions, 2019, 23(4): 111-123. DOI:10.1007/s10291-019-0905-4 |
| [18] |
LI Bofeng, ZHANG Zhiteng, MIAO Weikai, et al. Improved precise positioning with BDS-3 quad-frequency signals[J]. Satellite Navigation, 2020, 1(1): 328-337. |
| [19] |
LIU Xianglin, TIBERIUS Christian, JONG KD. Modelling of differential single difference receiver clock bias for precise positioning[J]. GPS Solutions, 2004, 7(4): 209-221. DOI:10.1007/s10291-003-0079-x |
| [20] |
ZHOU Zebo, LI Bofeng. Optimal Doppler-aided smoothing strategy for GNSS navigation[J]. GPS Solutions, 2017, 21(1): 197-210. DOI:10.1007/s10291-015-0512-y |
| [21] |
ZANG Nan, LI Bofeng, NIE Liangwei, et al. Inter-system and inter-frequency code biases: simultaneous estimation, daily stability and applications in multi-GNSS single-frequency precise point positioning[J]. GPS Solutions, 2020, 24(1): 18-30. DOI:10.1007/s10291-019-0926-z |
| [22] |
LI Bofeng, LI Zhen, ZHANG Zhiteng, et al. ERTK: extra-wide-lane RTK of triple-frequency GNSS signals[J]. Journal of Geodesy, 2017, 91(9): 1031-1047. DOI:10.1007/s00190-017-1006-1 |
| [23] |
TEUNISSEN P J G. Integer estimation in the presence of biases[J]. Journal of Geodesy, 2001, 75(7): 399-407. |
| [24] |
LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS ambiguity resolution with controllable failure rate for long baseline network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112. |


