2. 辽宁工程技术大学电子与信息工程学院, 辽宁 葫芦岛 125105
2. School of Electronic and Information Engineering, Liaoning Technical University, Huludao 125105, ChinaAbstract
移动网络的迅速发展和智能设备的迅速普及使得基于位置的服务在社交网络中得到广泛关注。兴趣点推荐作为基于位置的社交网络的重要服务之一,逐渐成为地理信息系统、web信息检索等领域的研究热点[1]。协同过滤是最早采用的兴趣点推荐方法,通过学习用户和兴趣点的潜在特征,以向量的形式表示用户和兴趣点,再基于向量预测用户对兴趣点的偏好度。矩阵分解方法利用用户的ID信息作为用户的表示向量,但是随着词嵌入的出现,研究人员开始将用户和兴趣点的特征信息进行嵌入来表示用户和兴趣点。然而,该类方法无法捕获用户-兴趣点交互记录中的协作信息。为此,文献[2-4]提出图神经网络来学习图数据中的向量表示,该方法能够整合图中的节点信息、边信息及拓扑结构,在学习向量表示上获得很大进步。本文深入分析兴趣点推荐的影响因素和发展历程,提出一种基于LBSN和多图融合的兴趣点推荐方法,主要有以下贡献。
(1) 改进了传统的K-means聚类,并用改进的聚类算法对兴趣点进行聚类,得到兴趣点在位置空间的潜在向量。
(2) 将图神经网络应用到兴趣点推荐中,根据用户-兴趣点的评分记录构造出用户-兴趣点交互图,根据用户在社交网络中的朋友信息构造出用户社交图,通过图神经网络学习两个图中的信息获得用户和兴趣点的外部表征向量。
(3) 提出了一种基于LBSN和多图融合的兴趣点推荐方法,同时对用户和兴趣点的内部特征与外部特征建模,获得更准确的用户和兴趣点的向量表示。
(4) 在真实数据集上开展了试验,对所提算法进行效果与性能试验评价,验证了所提算法的有效性和优越性。
1 POI推荐相关工作近些年,深度学习凭借其强大的学习能力在遥感影像处理、轨迹预测和推荐系统等方面得到了广泛应用[5-7]。但是神经网络只适合处理空间结构有规则的欧氏数据,而实际生活中存在很多空间结构不规则的非欧氏数据(如图数据)。图神经网络的出现为图数据的处理带来了新思路,它能够有效建模图数据中的节点信息、边信息及拓扑结构。推荐问题本质上是矩阵补全问题,也可以理解为二部图中的链接预测问题[8-9],因此可以将推荐系统中用到的数据集转换为图数据,使图神经网络与推荐系统相结合,利用图神经网络对这些图数据进行学习来提升推荐系统的性能。GC-MC模型将用户和项目的关系表示成二部图,采用两个多连接的图卷积层聚合用户和项目的特征信息,得到较好的推荐效果[9]。但是GC-MC使用one-hot编码表示节点,导致输入向量的维度过大,无法应用到大型数据集中。与GC-MC不同,文献[10]将用户和项目进行嵌入获得其低维表征向量输入网络,首先屏蔽部分用户和项目的嵌入向量,然后再利用图编码-解码器重构被屏蔽的向量,以缓解冷启动现象。文献[11]将用户-项目交互记录转换成二部图,利用图神经网络在用户-项目二部图上分别学习用户和项目的嵌入向量,并以传播的方式注入协作信息。文献[12]在分析用户-项目二部图中节点信息的同时考虑边的信息(如评分等),依据用户社交信息构建社交图,将社交信息融入用户的向量表征。文献[13]提出一种基于动态图注意力网络的推荐算法,将用户节点与项目节点进行嵌入,输出用户对项目的喜爱程度。AGCN[14]通过图卷积网络和注意力机制学习评分数据和辅助信息的低秩稠密向量表示,进而预测项目评分。文献[15]利用双图注意力网络协同学习双重社交影响,将用户领域的社会效应扩展到产品领域,借助相关产品的信息缓解数据的稀疏性。文献[16]提出一种基于会话的推荐,将会话序列建模成图数据,再利用图神经网络捕获项目间的复杂转换。KGAT[17]从邻居节点中递归传播嵌入信息,通过注意力机制判别邻居节点的重要性。文献[18]提出一种注意力模型GARG,自适应地区分序列中的兴趣点与预测的相关性,基于图实现对兴趣点的推荐。
2 问题定义和解决方案 2.1 问题定义定义1:用户-兴趣点交互图。由用户和兴趣点构成的二部图,用G(P, E)表示,其中P表示节点集合(包括用户集U和兴趣点集V),E表示边集合(代表用户和兴趣点的交互)。
定义2:用户社交图。用户社交图用A(U, S)表示,其中U是用户集合,S是边集合(代表用户和用户之间的社交关系)。
此外,U={u1, u2, …, um}和V={v1, v2, …, vn}分别为用户和兴趣点的集合,m为用户的数量,n为兴趣点的数量。
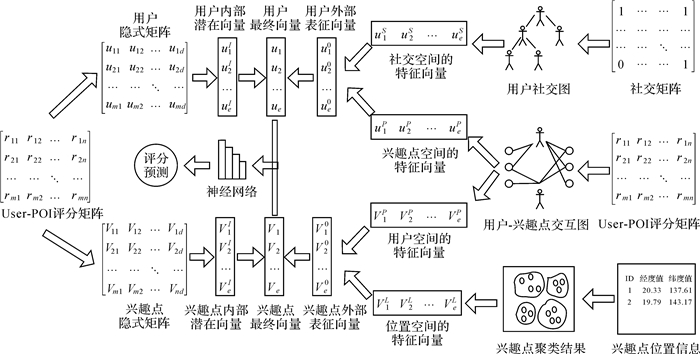
2.2 解决方案基于LBSN和多图融合的兴趣点推荐整体解决方案如图 1所示。
|
| 图 1 整体解决方案 Fig. 1 Overall framework |
(1) 对用户-兴趣点评分矩阵进行矩阵分解操作,学习用户和兴趣点的d维潜在特征,获得用户和兴趣点的内部潜在向量。
(2) 将用户社交矩阵转换成用户社交图,使用社交聚合器在社交图上学习用户在社交空间的特征向量。对兴趣点根据其地理位置进行聚类,将其嵌入到向量中得到兴趣点在位置空间的特征向量。
(3) 将用户-兴趣点评分矩阵转换成用户-兴趣点交互图,通过交互聚合器学习并产生用户在兴趣点空间的特征向量以及兴趣点在用户空间的特征向量。将用户在社交空间的特征向量与兴趣点空间的特征向量进行融合形成用户的外部表征向量。将兴趣点在位置空间的特征向量和用户空间的特征向量进行融合形成兴趣点的外部表征向量。
(4) 分别连接用户和兴趣点的内部潜在向量与外部表征向量获得用户和兴趣点的最终表征向量。将用户和兴趣点的最终表征向量输入到神经网络模型中进行评分预测,进而得到更为理想的推荐结果。
3 用户和兴趣点的内部特征建模矩阵分解(MF)是推荐系统中使用最广泛的方法,其主要思想是将用户-兴趣点评分矩阵分解为用户和兴趣点两个矩阵的乘积[19],使用隐式语义(潜在特征)表达用户和兴趣点,用它们的乘积近似表示原用户-兴趣点评分矩阵。这些潜在特征表示用户和兴趣点共享的特征,这些特征表示为用户的偏好特征和兴趣点的属性特征。因此,推荐问题可以转化为如何获得两个最优子矩阵问题。
MF将高维评分矩阵分解为两个低维隐式矩阵,并对它们进行乘积运算,优化原始矩阵和乘积矩阵之间的均方误差,进而得到两个最优隐式矩阵。以最小化式(1)为目标进行优化
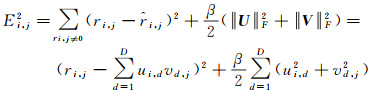 (1)
(1)
式中,U和V分别是用户和兴趣点嵌入后得到的d维隐式矩阵;d是隐式矩阵的维度;ri, j是用户ui对兴趣点vj进行评分的真实数据;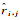
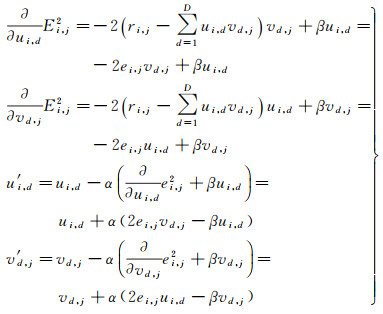 (2)
(2)
式中,α和β是算法优化过程中需要学习的参数,在试验中,根据文献[20]设定α=20,β=0.2。
通过对一个m行n列的评分矩阵R进行如上所述分解过程,可以得到两个最优子矩阵:用户矩阵Um×d和兴趣点矩阵Vn×d,这里m为评分矩阵中的用户数目,n为评分矩阵中的兴趣点数目。分别将用户和兴趣点映射到一个d维的空间中,U矩阵中的m行d维向量其实就是m个用户在d维空间上的投影,反映了用户对这d个潜在特征的偏好程度。因此,每行的d维数据构成了每个用户的内部潜在向量uiI。V矩阵中的n行d维向量其实就是n个兴趣点在d维空间上的投影,反映了兴趣点对这d个潜在特征的贴近程度。因此,每行的d维数据构成了每个兴趣点的内部潜在向量vjI。
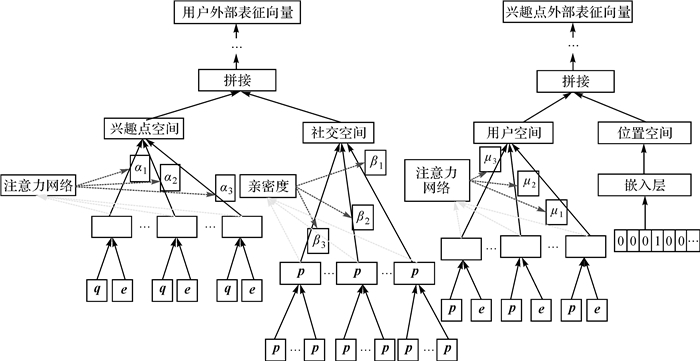
4 用户和兴趣点的外部特征建模外部特征建模大致分为两部分,如图 2所示,左部构成了用户外部表征向量的建模过程,右部构成了兴趣点外部表征向量的建模过程,共包含兴趣点聚合、社交关系聚合、用户聚合及兴趣点位置建模4个模块。在用户外部表征的建模过程中,分别聚合了用户在兴趣点空间和社交空间的信息;在兴趣点外部建模中则分别聚合了兴趣点在用户空间和位置空间的信息。
|
| 图 2 外部特征建模结构 Fig. 2 External feature modeling structure diagram |
4.1 用户外部表征模型的构建
(1) 兴趣点聚合。用户-兴趣点交互图包含用户与兴趣点的交互以及用户对兴趣点的评价。通过共同捕获交互图中交互和评价的方法学习用户在兴趣点空间的潜在向量uiP,具体表示方法为
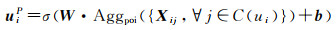 (3)
(3)
式中,Aggpoi为兴趣点聚合函数;C(ui)为用户ui交互过的兴趣点集合;Xij为用户ui和兴趣点vj之间评价感知的交互向量;σ为非线性激活函数;W和b为神经网络的权重和偏置。
评价信息体现用户对兴趣点的偏好,可以有效捕获用户-兴趣点交互图中的协作信息。本文将评价信息r嵌入为稠密向量er∈Rd。对于用户ui和兴趣点vj的带有评价信息r的交互,利用多层感知器结合兴趣点初始嵌入向量qj和评价嵌入向量er为评价感知的交互向量Xij,多层感知器将qj和er的连接向量作为输入,输出是ui和vj之间评价感知的交互向量Xij,计算如下
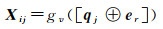 (4)
(4)
式中,⊕表示两个向量的连接操作;gv代表多层感知器。
受注意力机制的启发[21-22],为缓解基于均值的聚合器的局限,本文为每个交互(ui, vj)分配个性化权重,允许每个交互对用户在兴趣点空间的特征向量做出不同贡献
 (5)
(5)
式中,αij代表ui交互过的兴趣点vj的注意力权重,即对计算用户ui在兴趣点空间的特征向量的贡献。本文使用两层神经网络对αij进行参数化,称之为注意力网络。注意力网络的输入为Xij和目标用户ui的初始嵌入向量pi,注意力网络定义如下
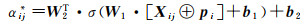 (6)
(6)
通过Softmax函数将注意力得分归一化得到注意力权重,以此代表交互对用户在兴趣点空间的特征向量的贡献
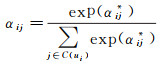 (7)
(7)
(2) 社交关系聚合。用户的偏好往往会受其朋友的影响,朋友间的亲密程度进一步影响用户的决策行为[23-24]。因此,通过注意力网络对用户与其朋友的亲密度建模,体现不同亲密度的朋友对用户嵌入向量的不同贡献。社交关系聚合考虑了用户社交图中的邻居节点,即用户社交网络中的朋友,获得用户社交空间的特征向量uiS,表达式如下
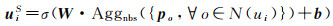 (8)
(8)
式中,N(ui)为ui的邻居节点集合;po为ui邻居节点的嵌入向量;Aggnbs为用户邻居节点的聚合函数。引入注意力网络βi建模用户之间的亲密度,为用户的每个朋友个性化分配亲密度,允许每个朋友对用户社交空间的特征向量做出不同的贡献,如下所示
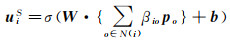 (9)
(9)
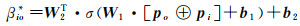 (10)
(10)
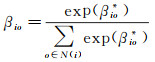 (11)
(11)
式中,βio为用户ui和用户uo之间的亲密度。
(3) 用户外部表征向量。用户-兴趣点交互图和社交图提供不同方面的信息,将已经获得的用户在兴趣点空间的特征向量uiP和社交空间的特征向量uiS输入到多层感知机(MLP)中得到用户的外部表征向量uiO,定义如下
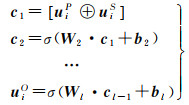 (12)
(12)
式中,l为隐藏层的索引。
4.2 兴趣点外部表征模型的构建(1) 用户聚合。不同用户对同一个兴趣点可能具有不同的评价,这些来自不同用户的评价可以捕捉兴趣点的特征,因此对于每个兴趣点vj,可以从交互过该兴趣点的用户中聚合信息。记用户的聚合函数为Agguser,则兴趣点在用户空间的特征向量vjU可由式(13)获得
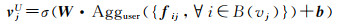 (13)
(13)
式中,B(vj)为交互过兴趣点vj的用户集合;fij=gu([pi⊕er])是评价感知的交互向量,对于具有评价信息r的用户ui与兴趣点vj的交互,将用户的初始嵌入向量pi和评价信息的嵌入向量er输入到多层感知器gu中,gu融合了用户对兴趣点的交互和评价。
为缓解基于均值的聚合器的局限,对每项交互(ui, vj)个性化分配权重,允许不同交互对兴趣点在用户空间的特征向量做出不同的贡献
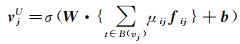 (14)
(14)
式中,μij是用户ui与兴趣点vj交互的注意力权重,表明用户ui对vj在用户空间的特征向量的贡献。本文使用两层的神经网络对μij进行参数化,称之为注意力网络。注意力网络的输入为fij和目标兴趣点vj的初始嵌入向量qj,注意力网络定义如下
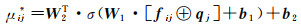 (15)
(15)
通过Softmax函数将注意力得分归一化得到注意力权重,以此代表交互对兴趣点在用户空间的特征向量的贡献
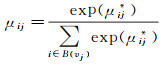 (16)
(16)
(2) 位置信息建模。位置信息建模主要依据兴趣点的地理位置对兴趣点进行聚类,K-means聚类是最经典的聚类算法,以距离为基准,适合对具有位置坐标的对象进行聚类,符合兴趣点的特点,因此本文采用K-means聚类算法实现聚类。
传统的K-means算法随机初始聚类中心,而聚类的结果往往对初始类心有一定的依赖性[25],导致传统的K-means算法无法满足人们的聚类需求。为此,本文提出一种改进的K-means聚类方法,通过概率密度估计法选取聚类的初始中心,替代传统的随机生成初始类心,使聚类尽快稳定下来,得到更理想的聚类结果。采用基于高斯核函数的概率密度估计方法,给定一个兴趣点集合POI={v1, v2, …, vn},兴趣点vj的典型程度可用概率密度函数f(v)定义
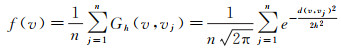 (17)
(17)
式中,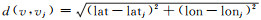
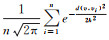
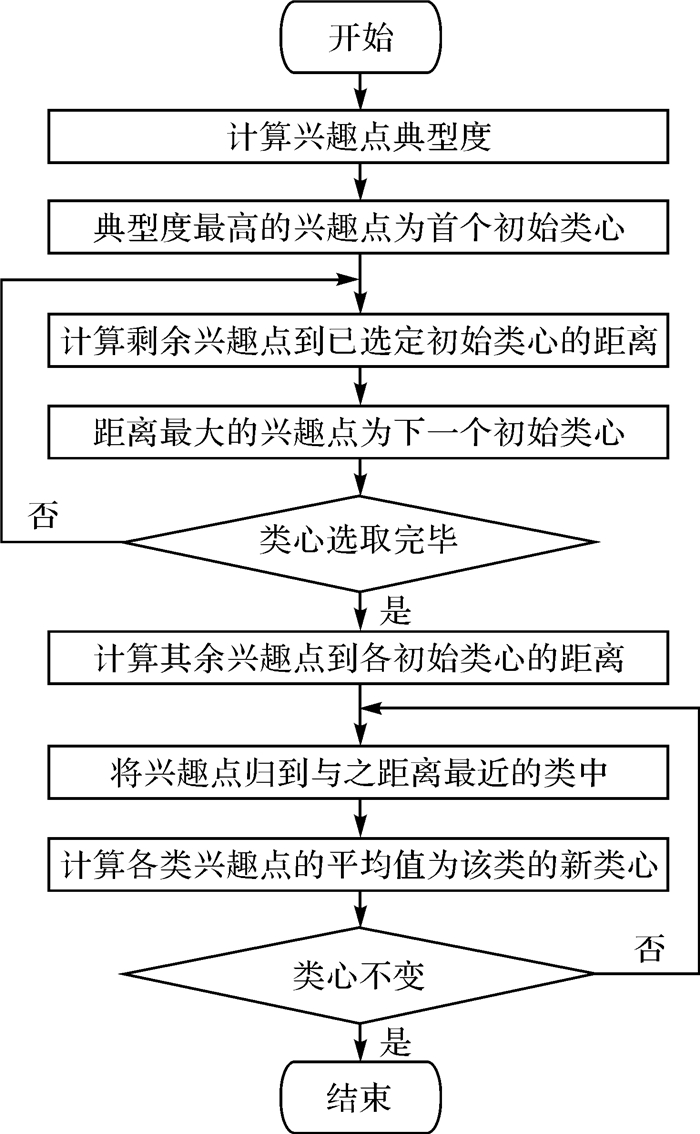
通过上述过程逐个计算兴趣点集合中每个兴趣点的典型程度,选取典型度最高的兴趣点作为首个初始聚类中心。然后从剩余的兴趣点中选取与当前选中聚类中心距离最大的兴趣点,作为下一个初始聚类中心,以此类推,直到找出所有的初始聚类中心。初始聚类中心确定好后,分别计算剩余兴趣点到k个聚类中心的距离(k代表聚类个数),将其归到与之最近的类中,全体兴趣点划分完毕则第1轮聚类结束。在每个类中,分别计算该类中兴趣点的平均值,作为该类新的聚类中心。依次计算各兴趣点到新聚类中心的距离,再次将兴趣点归到与之最近的类中,完成第2轮聚类。以此类推,不断地在每个类中产生新类心,并按照新类心对兴趣点进行归类,直到相邻两次聚类结果相同(聚类中心不变),则聚类达到稳定。该过程具体流程如图 3所示。聚类终止后,每个兴趣点将会获得一个类标签,将兴趣点的聚类标签嵌入到向量中,即可得到兴趣点在位置空间的特征向量vjL。
|
| 图 3 改进K-means聚类算法流程 Fig. 3 Flowchart of improved K-means clustering |
(3) 兴趣点外部表征向量。集成兴趣点在用户空间的特征向量vjU和位置空间的特征向量vjL,将其输入到MLP中得到兴趣点外部表征向量vjO
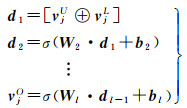 (18)
(18)
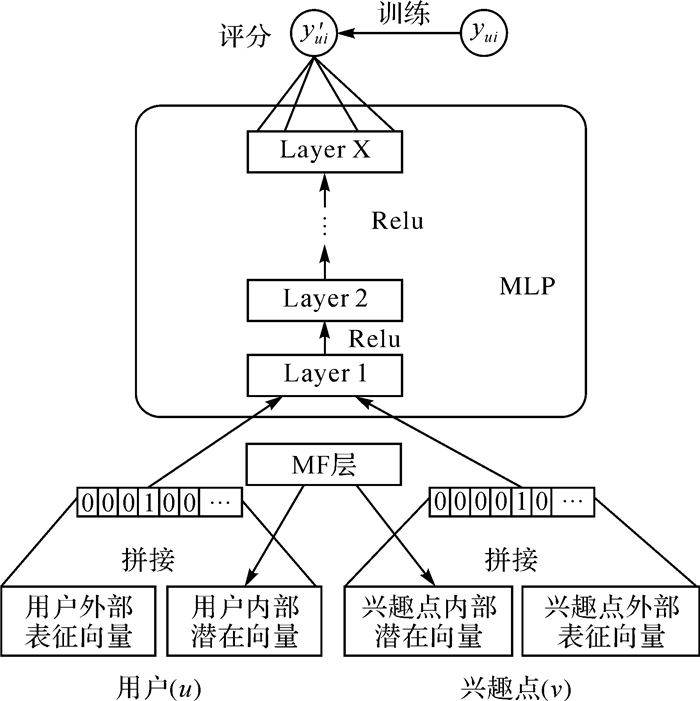
评分预测阶段需要构建用户和兴趣点的交互函数,文献[26]提出使用神经网络建模交互函数,证明了神经网络在建模交互函数上的有效性。评分预测结构如图 4所示。
|
| 图 4 评分预测结构 Fig. 4 Structure of rating prediction |
首先,拼接用户的内部潜在向量和外部表征向量,获得用户最终表征向量ui;拼接兴趣点的内部潜在向量和外部表征向量,获得兴趣点最终表征向量vj。具体的拼接过程同用户与兴趣点的外部表征向量的获取方式相同。然后,将用户和兴趣点的最终表征向量ui和vj输入MLP中进行评分预测,采用Relu激活函数,计算方法如式(19)所示
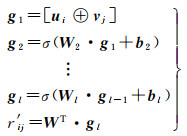 (19)
(19)
以式(20)为目标函数学习模型的参数
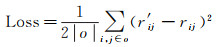 (20)
(20)
式中,|o|为数据集中用户对兴趣点评分的数量;rij为用户ui对兴趣点vj的真实评分;r′ij为模型预测出的用户ui对兴趣点vj的评分。
6 试验与评估 6.1 试验设置采用Yelp(全球最大的点评网站之一)数据集,截取经度在-112.0°和-111.9°之间、纬度在33.3°和33.45°之间的数据作为实验数据,为了保证数据质量,过滤掉用户评分次数少于5次、兴趣点被评分次数少于5次的用户和兴趣点。社交图中的节点代表用户,边代表用户和用户之间存在朋友关系。用户-兴趣点交互图中的节点由用户和兴趣点组成,边代表用户和兴趣点之间存在评分行为,边上的信息为用户对兴趣点的评分。表 1-表 3分别给出了本文试验数据、用户社交网络信息格式、兴趣点地理信息格式。
| 用户编号 | Yelp |
| 用户ID | QGgWWhEi5R4SLAKN-xwtNQ |
| 朋友1 | CCK6WHhMmGqxgmt0vAfRBw |
| 朋友2 | Hnkoajgonagioagjgojjkajio878ja |
| 项目 | Yelp |
| 兴趣点编号 | FYWN1wneV18bWNgQjJ2GNg |
| 纬度 | 33.330 690 2° |
| 经度 | -111.978 599 2° |
试验采用均方根误差RMSE和平均绝对误差MAE作为评价指标对兴趣点推荐方法的准确性进行评估。两者数值越小,代表结果越好
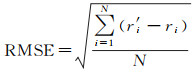 (21)
(21)
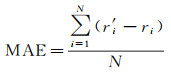 (22)
(22)
式中,r′i为预测值;ri为真实值。
6.2 试验结果为验证本文改进的K-means聚类算法的有效性,将改进K-means聚类算法与传统K-means聚类进行对比。首先对两种聚类算法的聚类结果进行对比,之后又将两种聚类算法应用到具体的推荐系统中进行推荐性能的对比。
在对比两种聚类算法的聚类结果试验中,以簇内变差Einner和簇间变差Einter两种常用指标为依据,其中簇内变差代表位于同一类簇内的数据点之间的差异性,簇内变差越小越好;簇间变差代表位于不同类簇间的数据点之间的差异性(通过不同类簇的类心间距离来体现),簇间变差越大越好。两者计算公式如下
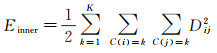 (23)
(23)
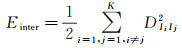 (24)
(24)
式中,C(i)=k代表第k个类中包含的数据点集合;Dij代表数据点i和j之间的距离;Ii和Ij代表第i个类心和第j个类心。
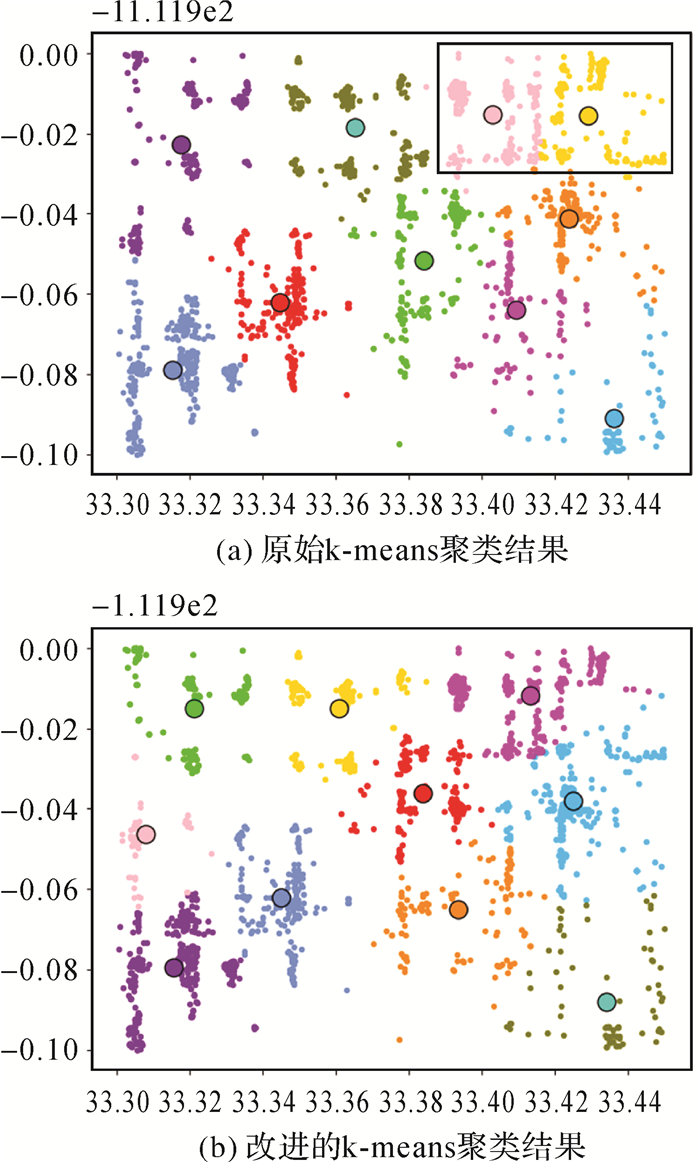
分别用两种聚类算法将yelp数据集聚为10类,聚类结果如图 5所示,其中图 5(a)为原始K-means聚类算法的聚类结果图,图 5(b)为改进的K-means聚类算法的聚类结果图。同时按照式(23)和式(24)分别计算出两种聚类算法的簇内变差和簇间变差,结果见表 4。
|
| 图 5 Yelp数据集的聚类结果 Fig. 5 Clustering results in yelp dataset |
| 算法 | K-means聚类 | 改进K-means聚类 |
| 簇内变差 | 0.006 178 | 0.004 677 |
| 簇间变差 | 6.184 703 | 6.360 483 |
由图 5中可以看出,改进的K-means聚类(图 5(b))每个类心都选在了该类中比较集中、典型的位置,而原始K-means聚类(图 5(a))绿色数据点和黄色数据点两个类中的类心位置比较稀疏,说明该类数据比较分散。此外原始K-means聚类中粉色和黄色数据点过于紧密,导致这两类数据的簇间变差过小。
从试验结果中可以发现,改进后的K-means聚类算法得到的结果中簇内变差更小,簇间变差更大,这说明改进后的K-means聚类能够使得同一类簇内的数据点更相似,不同类簇间的兴趣点区别更大,由此也可以证明改进的K-means聚类得到的聚类结果更合理,效果更好。
在对比两种聚类算法的推荐性能试验中,随机选取80%、60%的数据作为训练集,其余20%、40%的数据作为测试集,考虑不同比例下的训练集和测试集对推荐结果的影响。本文沿用了文献[27]的参数进行试验,即嵌入层数为64,聚类个数为50。试验结果见表 5。
| 数据 | 模型 | RMSE | MAE |
| Yelp(80%) | K-means | 1.043 9 | 0.815 3 |
| 改进K-means | 1.032 2 | 0.809 7 | |
| Yelp(60%) | K-means | 1.053 2 | 0.824 9 |
| 改进K-means | 1.049 9 | 0.818 8 |
由表 5结果可以看出,无论训练集占比80%还是60%,采用改进后的K-means聚类算法得到的推荐模型性能更好,这是因为改进后的K-means算法能够更合理地确定初始聚类中心,而聚类结果很大程度依赖于初始类心,因此改进后的K-means算法能够得到更准确的聚类结果,这对后期计算兴趣点在位置空间的特征向量有着积极的作用。
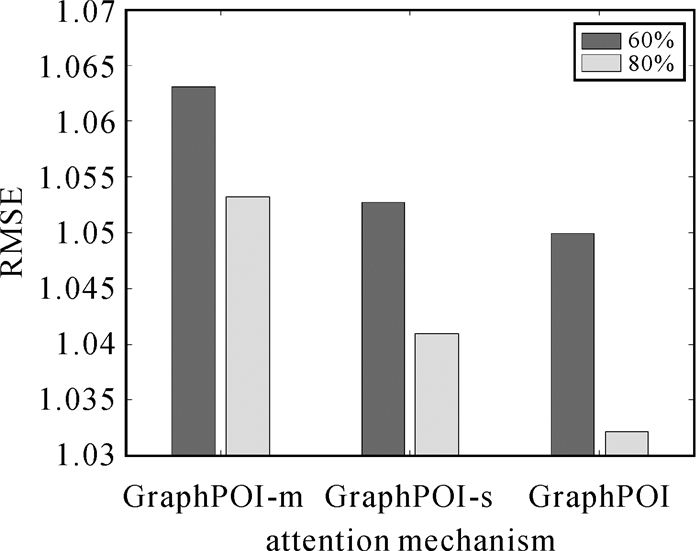
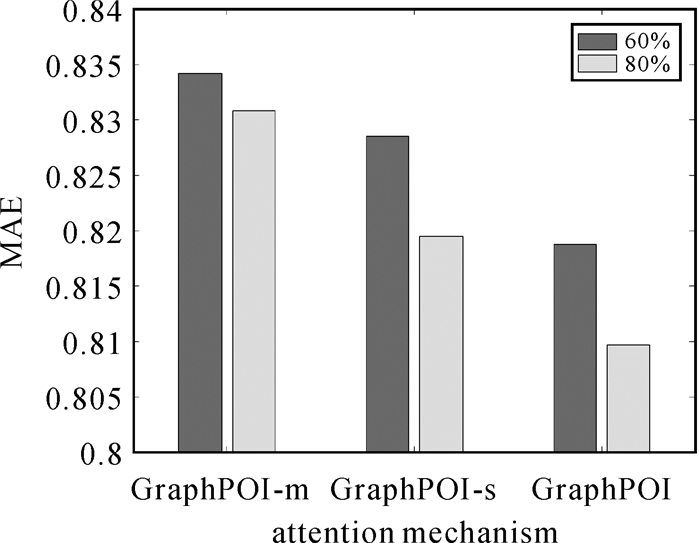
在计算用户和兴趣点的外部表征向量时,用注意力机制代替传统的均值操作,为验证注意力机制的有效性,记录了不同情况的RMSE和MAE结果,如图 6和图 7所示。其中,GraphPOI-m中的全体聚合器均采用均值操作;GraphPOI-s在GraphPOI-m的基础上考虑了用户的亲密度,其余聚合器仍采用均值操作;GraphPOI在考虑用户亲密度的同时采用注意力机制(即认为用户/兴趣点对与其有交互行为的兴趣点/用户贡献不同)。
|
| 图 6 注意力机制对RMSE的影响 Fig. 6 The impact of attention mechanism on RMSE |
|
| 图 7 注意力机制对MAE的影响 Fig. 7 The impact of attention mechanism on MAE |
从RMSE和MAE的结果值看来,显然,GraphPOI-m的推荐性能远小于GraphPOI-s,说明考虑朋友之间的亲密度对推荐结果有着积极的影响。同时GraphPOI-s的性能低于加入了注意力机制的GraphPOI模型,也体现出注意力机制的有效性。
此外,将本文基于LBSN和多图融合的兴趣点推荐方法(GraphPOI)与以下6个模型进行对比。
PMF[28]:概率矩阵分解。基于用户-项目评分矩阵,利用高斯分布对用户和项目的潜在因素建模进行推荐。
GraphRec[12]:近年提出的图神经网络推荐模型。考虑了用户社交图中的朋友关系以及用户-项目交互图中的评分和交互信息。
NeuMF[26]:一种利用多层神经网络实现矩阵分解的推荐算法,设定多个隐藏层捕获用户和项目的非线性交互,捕捉其中的隐式关系,是经典的推荐模型。
GCMC[9]:通过图自编码器GCN获得用户和项目的向量表征,从链接预测的视角分析并处理推荐中的得分预测问题。
NGCF[11]:基于用户和项目的交互数据构建用户-项目二部图,在二部图上进行传播嵌入。将协作信息添加到传播嵌入过程中,进而获得用户和项目的向量表征。
UPC-POIR[27]:基于用户和兴趣点间的耦合关系进行兴趣点推荐。采用传统的K-means算法对兴趣点聚类,没有考虑用户之间的朋友关系。
表 6和表 7描述了GraphPOI等7种推荐算法在Yelp数据集上的RMSE和MAE结果。
| Yelp(80%) | RMSE | MAE |
| PMF | 1.514 4 | 1.236 4 |
| GraphRec | 1.053 3 | 0.837 5 |
| NeuMF | 1.160 2 | 0.911 3 |
| GCMC | 1.087 4 | 0.932 6 |
| NGCF | 1.240 3 | 1.052 1 |
| UPC-POIR | 1.096 2 | 0.933 7 |
| GraphPOI | 1.032 2 | 0.809 7 |
| Yelp(60%) | RMSE | MAE |
| PMF | 1.612 6 | 1.325 3 |
| GraphRec | 1.060 8 | 0.841 8 |
| NeuMF | 1.184 1 | 0.945 4 |
| GCMC | 1.071 9 | 0.874 6 |
| NGCF | 1.182 7 | 0.923 5 |
| UPC-POIR | 1.087 4 | 0.889 3 |
| GraphPOI | 1.049 9 | 0.818 8 |
由表 6和表 7中可以看出,GraphPOI降低了评分预测误差,可以有效提高推荐的准确率。以表 6为例,GraphPOI比GraphRec的RMSE和MAE分别降低了2.0%和3.32%,这是因为GraphRec没有考虑用户和兴趣点各自的内在特征,而GraphPOI不仅捕获了用户和兴趣点的内部因素,同时对兴趣点的位置信息进行嵌入建模,获得了更准确的用户和兴趣点向量表征。算法NGCF、GCMC和NeuMF没有考虑用户的社交信息,因此试验结果不如GraphRec,体现出建模用户社交信息对推荐性能的积极作用。与PMF和NeuMF算法相比,采用了图神经网络的GraphRec、GCMC、NGCF和GraphPOI算法效果更好,体现出图神经网络在兴趣点推荐中的有效性。PMF和NeuMF都只考虑了用户对兴趣点的评分,但是NeuMF的预测误差小于PMF,表明神经网络能够一定程度提升兴趣点推荐的性能。另外,采用了改进K-means算法的GraphPOI模型与采用传统K-means算法的UPC-POIR模型相比,RMSE和MAE分别降低了5.84%和13.28%,说明改进K-means算法的有效性。
7 结论本文充分利用用户-兴趣点评分矩阵和用户社交矩阵,分别获得用户和兴趣点的内部潜在向量和外部表征向量,将其进行拼接得到用户和兴趣点的最终向量表征。构建图神经网络模型,将用户和兴趣点的向量表征输入网络中捕获其非线性交互,并进行评分预测。试验结果表明本文方法能够有效降低推荐误差,提升推荐结果的准确性。本文将图神经网络应用到兴趣点推荐中,为兴趣点推荐提供了新思路,具有实际意义。
兴趣点推荐是基于位置的服务的典型应用,有很大的研究价值,未来将从以下两方面进行深入研究:①K-means算法聚类个数k的确定。聚类个数对聚类结果有很大影响,下一步将考虑根据不同数据集自动调整聚类个数。②对图像信息的捕获。基于位置的社交网络中包含丰富的图像信息,借助图像领域的技术提取图像特征应用到兴趣点推荐中是笔者努力尝试的另一项挑战。
| [1] |
张国明, 王俊淑, 江南, 等. 关注点推荐算法的霍克斯过程法[J]. 测绘学报, 2018, 47(9): 1261-1269. ZHANG Guoming, WANG Junshu, JIANG Nan, et al. A point-of-interest recommendation method based on hawkes process[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1261-1269. DOI:10.11947/j.AGCS.2018.20170552 |
| [2] |
LI Yang, QIAN Buyue, ZHANG Xianli, et al. Graph neural network-based diagnosis prediction[J]. Big Data, 2020, 8(5): 379-390. DOI:10.1089/big.2020.0070 |
| [3] |
ZHOU Fan, YANG Qing, ZHANG Kunpeng, et al. Reinforced spatiotemporal attentive graph neural networks for traffic forecasting[J]. IEEE Internet of Things Journal, 2020, 7(7): 6414-6428. DOI:10.1109/JIOT.2020.2974494 |
| [4] |
MA Yao, WANG Suhang, AGGARWAL C C, et al. Multi-dimensional graph convolutional networks[C]//Proceedings of 2019 SIAM International Conference on Data Mining. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2019: 657-665.
|
| [5] |
FAN Dazhao, DONG Yang, ZHANG Yongsheng. Satellite image matching method based on deep convolutional neural network[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 90-100. |
| [6] |
陆川伟, 孙群, 陈冰, 等. 车辆轨迹数据的道路学习提取法[J]. 测绘学报, 2020, 49(6): 692-702. LU Chuanwei, SUN Qun, CHEN Bing, et al. Road learning extraction method based on vehicle trajectory data[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(6): 692-702. DOI:10.11947/j.AGCS.2020.20190305 |
| [7] |
UNGER M, TUZHILIN A, LIVNE A. Context-aware recommendations based on deep learning frameworks[J]. ACM Transactions on Management Information Systems, 2020, 11(2): 1-15. DOI:10.1145/3386243 |
| [8] |
ZHU Xiaoyan, YANG Xiaomei, YING Chenzhen, et al. A new classification algorithm recommendation method based on link prediction[J]. Knowledge-Based Systems, 2018, 159: 171-185. DOI:10.1016/j.knosys.2018.07.015 |
| [9] |
YING R, HE Ruining, CHEN Kaifeng. Graph convolutional neural networks for web-scale recommender systems[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, NY, USA: ACM, 2018: 10-21.
|
| [10] |
ZHANG Jiani, SHI Xingjian, ZHAO Shenglin, et al. STAR-GCN: stacked and reconstructed graph convolutional networks for recommender systems[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao, China: International Joint Conferences on Artificial Intelligence Organization, 2019: 4264-4270.
|
| [11] |
WANG Xiang, HE Xiangnan, WANG Meng, et al. Neural graph collaborative filtering[C]//Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. Paris, France: ACM, 2019: 165-174.
|
| [12] |
FAN Wenqi, MA Yao, LI Qing, et al. Graph neural networks for social recommendation[C]//Proceedings of 2019 World Wide Web Conference. New York, NY, USA: ACM, 2019: 417-426.
|
| [13] |
SONG Weiping, XIAO Zhiping, WANG Yifan, et al. Session-based social recommendation via dynamic graph attention networks[C]//Proceedings of the 12th ACM International Conference on Web Search and Data Mining. New York, NY, USA: ACM, 2019: 555-563.
|
| [14] |
FENG Chenyuan, LIU Zuozhu, LIN Shaowei, et al. Attention-based graph convolutional network for recommendation system[C]//Proceedings of 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Brighton, UK: IEEE, 2019: 7560-7564.
|
| [15] |
WU Qitian, ZHANG Hengrui, GAO Xiaofeng, et al. Dual graph attention networks for deep latent representation of multifaceted social effects in recommender systems[C]//Proceedings of 2019 World Wide Web Conference. San Francisco CA USA. New York, NY, USA: ACM, 2019: 2091-2102.
|
| [16] |
WU Shu, TANG Yuyuan, ZHU Yanqiao, et al. Session-based recommendation with graph neural networks[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 346-353. |
| [17] |
WANG Xiang, HE Xiangnan, CAO Yixin, et al. KGAT: knowledge graph attention network for recommendation[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage, AK, USA: ACM, 2019: 950-958.
|
| [18] |
WU Shiwen, ZHANG Yuanxing, GAO Chengliang, et al. GARG: anonymous recommendation of point-of-interest in mobile networks by graph convolution network[J]. Data Science and Engineering, 2020, 5(4): 433-447. DOI:10.1007/s41019-020-00135-z |
| [19] |
HAN Peng, SHANG Shuo, SUN Aixin, et al. AUC-MF: point of interest recommendation with AUC maximization[C]//Proceedings of 2019 IEEE 35th International Conference on Data Engineering (ICDE). Macao, China: IEEE, 2019: 1558-1561.
|
| [20] |
孟祥福, 张霄雁, 唐延欢, 等. 基于地理-社会关系的多样性与个性化兴趣点推荐[J]. 计算机学报, 2019, 42(11): 2574-2590. MENG Xiangfu, ZHANG Xiaoyan, TANG Yanhuan, et al. A diversified and personalized recommendation approach based on geo-social relationships[J]. Chinese Journal of Computers, 2019, 42(11): 2574-2590. DOI:10.11897/SP.J.1016.2019.02574 |
| [21] |
YANG Zichao, YANG Diyi, DYER C, et al. Hierarchical attention networks for document classification[C]//Proceedings of 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. San Diego, California. Stroudsburg, PA, USA: Association for Computational Linguistics, 2016: 1480-1489.
|
| [22] |
CHEN Chong, ZHANG Min, LIU Yiqun, et al. Neural attentional rating regression with review-level explanations[C]//Proceedings of 2018 World Wide Web Conference on World Wide Web. New York, NY, USA: ACM, 2018: 1583-1592.
|
| [23] |
CHEN Jiawei, WANG Can, SHI Qihao, et al. Social recommendation based on users' attention and preference[J]. Neurocomputing, 2019, 341(14): 1-9. DOI:10.1016/j.neucom.2019.02.045 |
| [24] |
WANG Hao, TERROVITIS M, MAMOULIS N. Location recommendation in location-based social networks using user check-in data[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Orlando Florida, USA: ACM, 2013: 364-373.
|
| [25] |
彭晏飞, 方金凤, 訾玲玲, 等. 多视觉特征与K-centroid聚类的高分辨率遥感图像检索[J]. 测绘科学技术学报, 2017, 34(5): 496-500. PENG Yanfei, FANG Jinfeng, ZI Lingling, et al. High resolution remote sensing image retrieval based on multi-visual feature and K-centroid clustering[J]. Journal of Geomatics Science and Technology, 2017, 34(5): 496-500. |
| [26] |
HE Xiangnan, LIAO Lizi, ZHANG Hanwang, et al. Neural collaborative filtering[C]//Proceedings of the 26th International Conference on World Wide Web. Perth, Australia: Steering Committee, 2017: 173-182.
|
| [27] |
孟祥福, 齐雪月, 张全贵, 等. 用户-兴趣点耦合关系的兴趣点推荐方法[J]. 智能系统学报, 2021, 16(2): 228-236. MENG Xiangfu, QI Xueyue, ZHANG Quangui, et al. A POI recommendation approach based on user-POI coupling relationships[J]. CAAI Transactions on Intelligent Systems, 2021, 16(2): 228-236. |
| [28] |
SALAKHUTDINOV R, MNIH A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo[C]//Proceedings of the 25th international conference on Machine learning (ICML 2008). Helsinki, Finland: ACM, 2008: 880-887.
|



