2. 武汉大学中国南极测绘研究中心, 湖北 武汉 430079
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
月球记录了太阳系过去40~45亿年的演化历史。月球形状和外部重力场与月球的演化历史、外部天体相互作用密切相关,是月球研究的重要组成部分。高精度月球形状与重力场模型为月球构造特征和内部结构研究提供了重要的几何与物理信息及统一的参考基准[1-2]。同时,月球作为深空探测的首选目标,其形状是探月任务中开展着陆区评估与选择、着陆点定位与巡视器导航等工作的重要依据。月球重力场是绕月卫星精密定轨及探测器着陆的重要力源,也是决定探测器装备载荷的一个重要设计指标。
早期望远镜的发明使人们能够清晰地观察到月球的形貌。1608—1610年,伽利略发现月面存在明暗对比区域和坑洼的凹地,并将这些凹坑取名为“环形山”。1610年,伽利略绘制了第1张月球正面图画,以描述观测到的景象。1645年,Rheita将月面图进一步精化和清晰化,着重描绘了第谷辐射、哥白尼、开普勒、迪莫察利及朗格林诺斯等撞击坑[3]。探月卫星发射以前,人类通过地月观测与天文学计算,粗略获取了月球椭球长短半径、总质量、角速度等,月球的重力值主要是将这些已知的物理参数代入Clairaut定理计算得到[4]。
随着卫星技术的快速发展,1969—1976年,苏联Luna计划和美国Apollo计划均获取了大量的月球影像,并采回了约381.7 kg的岩石样品[5],这使得人类对于月球空间环境、地质地貌、月球的起源等有了进一步的研究和认识。
20世纪90年代至今,月球探测进入第2次高潮。美国、中国、日本、印度、欧盟等国家和地区相继发射了众多月球探测器,获取了大量月球探测数据,并取得了众多成果:从低精度和低分辨率高轨卫星遥感观测到高精度和高分辨率的低轨卫星遥感观测;从单颗卫星的观测到卫卫跟踪模式的观测;从单波束激光测高观测到多波束激光测高观测;从X波段多普勒测速求定重力场到星间Ka波段测距信息求定重力场。从发展态势而言,对月球的研究已从概貌走向具体、从局部走向整体、从单一目标走向综合分析、从定性走向定量,人类对月表的形状与重力特征、内部结构与演化历史、月球的起源和地月系的相互作用和影响等方面都有了全新的认识[6]。
本文从测绘科学与技术在月球探测中的应用角度,综述月球表面形貌、几何形状、月球重力场的研究及主要成果,并针对目前研究的不足进行分析,对研究前景进行展望。
1 月球形状 1.1 月球表面形态月球是一个赤道略鼓、南北稍扁的椭球体。月球表面广泛分布着山脊、谷地、断层等地貌,这些地貌特征的形成与月球曾经经历过的热演化史密切相关。月球正背面存在明显的二分性,如月海多集中在月球正面,而背面以高地为主;月球正面月壳比背面的月壳更薄[7]。
与地球相比,月面整体较为平坦,坡度在15°以下的区域占总面积的90%,其中坡度在2°以下的区域主要分布在月球正面的月海,而平均坡度大于7°的高地相较月海起伏明显,但是月球上的最大高差却与地球相近,达19 901 m[8](如图 1所示,参考半径为1 737.4 km)。最低点位于安东尼亚第环形山附近(图 1中白色三角形,-172.58°E,70.43°S,-9115 m);最高点位于恩格尔伽特陨石坑附近(图 1中黑色三角形,-158.63°E,5.41°N,10 786 m)。月面可分为两个主要地理单元,即月海与高地。根据明暗(反照率)的不同,亮色部分称为高地(Highland)、暗色部分称为月海(Mare),而遍布月表的圆环凹坑构造称为月坑。

|
| 图 1 月球全球数字高程模型 Fig. 1 Lunar global DEM |
月海并非海洋,而是月面肉眼可见的暗色区域,约占月球表面积的17%,主要分布在月球正面。月海的平均地势较之高地单元明显低,且地势起伏较小,与地球上的盆地类似,大多数月海被山脉包围且呈现的形状为封闭的圆形或椭圆形。
月面上亮色部分称为高地(也称月陆)。与月海集中在月球正面不同,月球背面的高地面积大于月球正面[9]。通过对撞击坑密度的计算可得知其形成的时间比月海要早很多。
月坑是指布满月球表面的圆环凹坑构造,包括与环形山、辐射线、撞击坑有关的隆起构造。月坑的大小不一,小到岩屑表面的微坑,大到直径几百千米的月海盆地。据统计,月球表面直径大于1 km的月坑总数在3.3万个以上,且月面没有风、水的侵蚀,使其能够得到完整的保存。月坑主要分布在月陆地区,以小规模的碗形为主,在月海地区的分布则较为稀疏,且撞击坑的数量随直径的增加而显著减少。此外,月球上存在撞击坑、月球古代火山口及构造盆地3种环形构造。对于撞击坑的分类,不断有学者提出新方法。文献[10]基于边界侵蚀程度将撞击坑分为5类;文献[11]根据撞击坑有无主峰、多环盆地等将其分为3类;文献[12]采用以形态为主的定量多指标方法对撞击坑类型判定进行了完善。
1968年,文献[13]解释了第1个绕月运行的航天器撞击盆地受到更为强大的引力这一现象,进而发现了月球质量瘤。质量瘤是月球的质量密集区。月球正面的质量瘤通常为,中间区域存在很大的正重力异常,而周围被负的重力异常所环绕,同时地形却为负值。月球背面质量瘤与正面质量瘤有明显的不同,通常由数值较大的正重力异常环包围内侧的负重力异常环,在负重力异常环中又出现正的重力异常峰,这也是月球二分性的一个表现。
自1919年,国际天文联合会又将月貌细分为月湾、月沼、月岬、山地、穹丘、皱脊、月谷、月溪等。这些地貌特征的形成与月球曾经历过的热演化史密切相关。月球火山活动是月幔物质部分熔融产生岩浆后喷发的过程,是研究月球的地质历史、热演化的重要窗口。31亿年来,月球没有发生过显著的火山活动和板块构造运动[9],因此保留了早期形成的地质条件,为研究地月系的演化及地球内部构造提供了最佳环境。近些年来,人类对月球的认识进入全新的阶段,月球基地建设的呼声也越来越高,其中月面熔岩管洞穴被列为月球基地优先考虑和选择的区域之一。自2010年来,美国的LRO(lunar reconnaissance orbiter)任务利用窄角相机高分辨率成像仪,已经发现了越来越多的熔岩管天窗。从形态和重力特征上识别月球熔岩管对开展月球科学研究及资源与环境利用具有重大意义[14]。
1.2 月球三轴椭球与地球的正常椭球类似,在确定月球大地水准面时,理论上也需要构建一个月球正常椭球。虽然月球的扁率很小,只有0.001 2,目前的研究中,往往用月球平均半径所对应的球体近似代表月球的正常椭球。但随着测量精度的提高,月球扁率的影响会逐渐突出,获取准确的月球正常椭球的意义将会越来越重要。
同时,从描述月球几何形状的角度而言,也需要一个最为接近月球的平均椭球。从月球形状的研究历程看,对应月球正常椭球和平均椭球的研究,主要是以构建月球三轴椭球的结果予以体现。
天然卫星的形状主要由两个因素确定:卫星的自转和行星的引潮力。前者使得卫星的赤道部分隆起,后者使得卫星在向行星的方向上被拉长,使卫星成为三轴椭球体的形状。
早在20世纪60年代,苏联科学家就基于月球上1185个参考点的位置,使用最小二乘原理估算了不同情况下月球三轴椭球体的3个主轴长度,主要结果为:主轴a的长度为1 739.53±0.07 km,主轴b的长度为1 736.72±0.05 km,主轴c的长度为1 736.37±0.07 km[15]。文献[16]利用月球天平动参数及LPl50Q重力场模型计算了月球椭球体3个向径a、b、c的值,表明月球3个主轴的长半径是不同的,向地球方向的长半径a最大,极向的c最小;进而结合月球的平衡潮形状推断出月球现在的形状基本保留了约30亿年前月球凝结时的状态。文献[17]凭借我国“嫦娥一号”自主获取的激光测高数据,采用地形逼近算法获取了月球主惯性矩、主惯性轴指向,月球赤道半径、极半径、平均半径,月球形状扁率及质心与形心偏移量等大地测量参数,得到地形逼近的三轴几何椭球体CE-1-LAM-GEO和三轴水准椭球体CE-1-LAM-LEVEL模型。高精度高分辨LRO测高数据和GRAIL(gravity recovery and interior laboratory)重力场模型的公布,为进一步精确建立三轴椭球体模型提供了有利条件。文献[18]结合最新数据,计算了新的月球三轴几何椭球体和三轴水准椭球体。表 1为具有代表性的月球三轴椭球模型的3个主轴长度。
1.3 月球大地水准面
地球上大地水准面是指与静止海水面相重合的重力等位面,它是地面高程系统的基准,也是代表地球形状的一个封闭曲面。此外,大地水准面起伏与内部密度分布密切相关。然而月球表面并无海洋,因此对于月球大地水准面的诠释有别于地球大地水准面。
文献[20]利用Apollo 11登陆点的实测重力值计算得到重力位,并把通过该点的等势面定义为月球大地水准面。然而仅使用一个点的数据作为约束不够严谨。随着全月地形模型的建立,文献[21]定义月球大地水准面为一等势面,其平均半径与采用激光测高得到的月球地形平均半径相等。由于月球内部质量分布不均匀,其水准面也是一个极不规则的曲面,因此需要寻找一个与月球大地水准面较吻合,且能用数学公式表达的规则曲面代替大地水准面,作为测量计算的基准面。文献[22—24]建立了重力位系数与大地水准面、三轴椭球参考面的关系式。文献[25]对月球水准面方程和物理参数等进行了研究,并就物理参数的选取提出了具体建议。这些研究的不足之处在于:一是在推算月球水准面的过程中未考虑地球、太阳和其他天体的引潮力作用,实际计算表明地球引潮力不可忽略;二是用三轴椭球最佳拟合月球水准面时,不一定满足表面是等势面;三是未顾及水准面外质量的影响。文献[26]进一步考虑地球引潮力和月球大地水准面外部质量对大地水准面的影响,利用月球重力场模型CEGM02和地形模型LRO_LTM02,构建了一个尽可能与月球几何表面贴近的参考等势面,定义为月球大地水准面,其重力位W0=2 822 327.8±16.2 m2/s2。
1.4 月球控制网建立月面控制网是月球大地测量的主要任务之一,通过高精度控制网可以精确测定月球上点的坐标,对于后续月球基地建设和月球制图意义重大。月面控制网的建立首先需要确定一些月球表面的控制点。美国Apollo 11、Apollo 14、Apollo 15任务在月球表面共安置了3个激光反射器,苏联的Luna 17和Luna 21相继安置了Lunakhod 1号和Lunakhod 2号激光后向反射器,通过50余年月球激光测距观测,目前5个激光发射棱镜的绝对测量精度可达厘米级[27]。我国“嫦娥三号”着陆器也进行过无线电相位测距试验,获取了着陆器的高精度绝对位置[28]。在确定控制点的前提下,基于月球轨道器获取的影像,采用摄影测量的方法可以逐步构建月球全球控制网,如ULCN(the unified lunar control network)、CLCN(the clementine lunar control network)、ULCN2005(the unified lunar control network 2005)[29]。目前广泛应用的月球统一控制网ULCN2005由1994年的克莱门汀影像与之前的遥感数据联合平差构建,其平面精度在100 m至数百米之间,垂直精度在100 m量级。
21世纪以来,海量的高精度、高分辨率月球遥感影像和激光测高数据为全新的月球控制网建立带来了契机。文献[30]提出利用新近多探测任务获取的多源数据,包括嫦娥系列任务、LRO和GRAIL任务数据等,构建新一代月球控制网的方案。其关键技术包括:轨道器影像几何模型构建、多任务影像与激光高度计数据构网、多重覆盖下最优影像选择、全球多任务数据的平差等,整体技术方案如图 2所示。据初步估算,全月整体平差后绝对定位精度有望达到20~30 m水平,将远超ULCN 2005控制网的精度。不过构建新一代LGCN涉及集成各种摄影测量处理技术及海量数据的处理,难度大,需要多团队特别是国际团队的密切合作。

|
| 图 2 月球控制网整体技术方案 Fig. 2 The overall technical scheme of lunar control network |
值得一提的是,目前有绝对精度的5个激光反射棱镜和“嫦娥三号”着陆器均分布在月球正面的北半球,如果在月球南极布设新的激光反射棱镜或着陆器,有望获得南半球的高精度控制点,同时也有利于月球天平动的优化,目前国际上多个团体已提出相关构想[31]。此外,通过四程中继测量构型,可以克服月球的遮挡,获取远月面着陆器的绝对位置,为月球背面控制网提供更高精度的约束[32]。
1.5 月球DEM月球DEM是对月球表面地形地貌的一种离散数字表达。早期的月球地形是通过地基观测得到的,如地基摄影测量、月球边缘测量等;其精度相对较低,且由于月球自转周期与公转周期相等,地基观测仅能针对月球正面。随着航天技术的发展,星载激光测高和摄影测量技术成为获取高精度、全覆盖月球DEM的主要手段。1971年,激光测高技术在美国Apollo 15号上进行了首次应用,随后在各国的探月任务中得到广泛应用。尤其是近10年来,中国“嫦娥一号”(CE-1)、日本SELENE(SELenological and ENgineering Explorer)、美国LRO等各国绕月卫星探测任务中,均搭载了不同类型的激光高度计和地形相机,获取了大量的月球地形数据。相关科研组织开展了星载激光测高和摄影测量技术在月球DEM研制方面的工作,并研制了不同分辨率月球全球或局部区域的DEM产品(表 2)。
| 任务时间 | 任务名称 | 数据来源 | 覆盖范围 | 分辨率/精度 | 国家 |
| 1971 | Apollo 15至Apollo 17 | 星载激光测高计 | 26°S—26°N | 径向精度只有400 m | 美国 |
| 1994 | Clementine卫星 | 激光高度计(laser image detection and ranging,LIDAR) | 79°S—81°N | 分辨率为2.5°、径向精度100 m | 美国 |
| 紫外和可见光波段相机(ultraviolet-visible,UVVIS) | 月球两极 | 1 km | |||
| 2007 | SELENE卫星 | 激光高度计(laser altimeter,LALT) | 全月DEM | 分辨率为0.062 5° | 日本 |
| 地形相机(terrain camera,TC) | 全月DEM | 径向精度为10 m、分辨率为10 m | |||
| 2007 | CE-1卫星 | 激光高度计(laser altimeter,LAM) | 全月DEM | 0.25°, 水平精度约445 m, 径向精度约60 m | 中国 |
| 立体影像数据 | 全月DEM | 分辨率500 m | |||
| 2008 | Chandrayaan-1探测器 | 地形相机获取的立体影像数据 | 局部区域 | 印度 | |
| 2009至今 | LRO卫星 | 激光测高仪(lunar orbiter laser altimeter,LOLA) | 月球南极地区 | 400 km×400 km DTM | 美国 |
| 激光测高仪(LOLA)SELENE卫星地形相机 | 60°S—60°N | 水平分辨率512像素/(°) 垂直精度为3~4 m | |||
| 月球轨道器相机(lunar reconnaissance orbiter camera,LROC)激光测高仪(LOLA) | 80°S至极点 | 5~80 m/像素 | |||
| 75°S至极点 | 30~120 m/像素 | ||||
| 60°S至极点 | 30~120 m/像素 | ||||
| 45°S至极点 | 100~400 m/像素 |
构建DEM后,结合日、地、月轨道参数,可以准确地模拟分析受地形特征影响的光照条件与通信条件,即通过计算判断月面待计算点与目标方向之间是否被地形阻挡。从“克莱门汀”任务开始,历次环月遥感任务均通过光学相机和激光高度计获得了极区影像和高程数据,且识别出永久阴影区和长时间持续光照区,月表光照与通信条件的研究为月球着陆探测提供了数据支撑。着陆区的光照条件是设计着陆器太阳翼需要考虑的重要因素之一,也影响着陆期间光学敏感器的效果;同时,光照条件对月球上探究水冰也具有指示作用。通信条件则直接关系到着陆器的正常测控与工作[33]。目前,对月表光照与通信条件的研究大多集中在两极地区。文献[34]基于LOLA的240 m分辨率的极区DEM,对月球极区光照条件进行了模拟,给出阴影区的范围,并确定了光照率最高的位置。文献[35]基于LOLA数据,使用一种新的数据处理方法研制了月球南极地区的高分辨率高精度DEM,重点分析了4个高优先级的月球南极备选着陆点的光照条件等因素。
2 月球重力场的探测及应用获取月球重力场信息最直接的方法就是开展就位测量,但是在地球以外的其他天体上开展就位测量十分困难。目前,仅有Apollo任务进行过数次月面重力测量试验,但其测量精度十分有限。
获取天体重力场有很多方法。对于没有绕飞探测器的天体,可以通过影像数据得到的天体形状,结合天体GM正演估算其重力场;对于有绕飞探测器的天体,一般通过解算探测器在绕飞过程中的轨道扰动,精确求解其重力场。月球作为距地球最近的天体,也可以通过激光测月数据求解月球自转轴的惯性矩,进而解算月球正常重力场的球谐系数J2、J4。但是随着卫星技术的发展,特别是月球重力卫星GRAIL任务的实施,解算绕月卫星的轨道摄动量从而获取月球重力场,成为最主要和最有效的月球重力场获取方法。目前月球重力场模型已经高达1500阶次,分辨率可达3.6 km,其包含整个月球重力场从低频到高频的大部分信号。目前的月球重力场模型研究主要针对绕月卫星摄动,围绕改进跟踪方式、提高跟踪精度展开。
月球具有体积小、密度低、自转速度慢等特点,因此月球重力场相对地球重力场而言是一个弱重力场。在地球重力场中,低阶项系数占明显优势,其中C20项起主导作用;而月球重力场的高阶项、低阶项量级差距并不显著。此外,月球重力场球谐系数的收敛情况也略差于地球。
图 3(a)为月球自由空气重力异常,其分布与地形相关性高,由撞击盆地引起的重力异常显示为正-负-正的“牛眼”重力模式;图 3(b)为月球布格重力异常(月壳平均密度取2560 kg/m3,半径取1738 km),质量瘤的分布显示出明显的正背面二分性,具体表现为正面质量瘤多,远月面质量瘤少;图 3(c)为基于GRAIL重力场模型的全月球布格重力异常梯度的特征值,揭示了月球全球分布的线状重力异常。

|
| 图 3 月球重力异常(绘图时月球正面在中央,1 Eotvos= 10-8/s2) Fig. 3 The gravity anomaly of the Moon(These figures are centered on the lunar near side, 1 Eotvos=10-8/s2) |
高精度的月球重力场模型为深入了解月球提供了契机。重力场模型中低阶次项反映了深部、大尺度的质量异常,利用重力场位系数中的二阶项,结合自转参数,可以确定星球的极惯性矩,从而对深部结构进行约束。重力场模型中高阶次项反映了浅部、小尺度的密度异常,为揭示月球浅层结构提供了有效途径,利用短波重力异常与地形的相关性,也可以对壳层的密度进行估计。同时,月球重力场作为月球高程系统的基准,对于精确确定月球形状具有重要意义。
2.1 月球重力场的表达与求解方法地球重力场可以借助多种重力测量手段获取,但对于月球而言,人类尚无法有效开展就位重力测量,而是主要通过对绕月卫星的轨道跟踪,解算轨道摄动量,构建重力场模型[2]。
目前月球重力场模型一般采用球谐系数的形式表达。位于球面上某点(r,φ,λ)的重力位U(r,φ,λ)的球谐级数的表达形式为
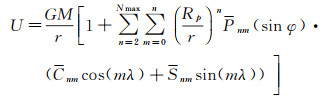 (1)
(1)
式中,GM为月球引力质量;Rp为月球参考半径;(r,φ,λ)为探测器在月球固连坐标系下的球坐标;n与m分别为球谐级数的阶与次;Pnm为正规化连带勒让德级数;Cnm与Snm为月球重力场模型的球谐系数[36]。
利用绕月卫星轨道摄动数据求解月球重力场的基本步骤为:首先根据先验月球重力场理论模型,同时考虑大气校正、地球自转、月球自转及测站坐标改正等因素的影响,并结合行星历表等,应用理论模型对探测器进行轨道预报,获取观测值的理论计算值;然后将此理论计算值与实测数据进行对比,得到两者之间的残差;最后根据残差迭代结果对理论模型进行修正,直至理论观测值与实际观测值符合程度满足期望值,从而获得最终的重力场模型。流程如图 4所示。

|
| 图 4 求定月球重力场的流程 Fig. 4 Flowchart of the lunar gravity field determination |
2.2 代表性月球重力场模型
以月球重力场为主要科学目标的探测任务包括Clementine[37]、LP(lunar prospector)[38]、SELENE[39]及GRAIL[40],其他对月球重力场模型产生显著贡献的探测任务还包括中国嫦娥任务[41]。
Clementine任务最终得到了70阶次的重力场模型GLGM-2[42]。此后,LP任务于1998年发射,采用轨道高度为100 km的极轨和更为稳定的轨道调整策略,更有利于重力场模型的解算。通过LP跟踪数据解算的月球重力场模型包括LP100J、LP165P及LP150Q[43]。
SELENE任务的实施对月球重力场的发展做出了显著贡献,其采用高-低卫卫跟踪模式,能够获取绕月卫星在月球背面的轨道摄动量。利用SELENE任务前3个月的跟踪数据解算的90阶次模型SGM90d[44],首次揭示了月球背面的大尺度重力场特征。中国“嫦娥一号”任务也获取了包含丰富重力场信息的轨道跟踪数据,综合SELENE、“嫦娥一号”及历史探测数据,文献[41]计算了100阶次的月球重力场模型CEGM02,该模型对重力场模型低阶项有所改进。
2011年,美国发射了GRAIL探测任务。GRAIL任务采用类似地球重力卫星GRACE的星间低-低跟踪模式,其平均轨道高度为50 km。文献[45]利用GRAIL任务3个月测量数据,解算了420阶次的月球重力场模型GL0420A,相比之前的月球重力场模型,不论是精度还是分辨率均有了显著提升。GRAIL任务的科学团队持续发布了660阶、900阶、1200阶与1500阶模型[46-48]。
目前对月球重力场的应用主要着眼于绕月卫星的精密定轨和对月球内部结构的反演。随着探测技术的发展,月球重力场在形状及高程基准中的作用将会越来越大。
2.3 月球正常重力场实际应用中往往将重力场表达为正常重力和重力异常(或扰动重力)。由于正常重力场与实际重力场相差很小,在实际重力场中分离出正常部分后,剩下的一小部分重力异常或重力扰动的确定则较简单。关于月球正常重力的研究目前仍不够充分,但已有研究发现:月球正常重力与地球正常重力具有不同的特征。
月球与地球类似,也是一个旋转的、赤道半径略大于极半径的椭球体。但已有的重力场模型计算表明,月球赤道重力与两极重力并没有体现出明显的大小差距。更为有趣的是,1962年Grushinskii和Sagitov通过计算发现,月球上两极正常重力值小于赤道正常重力值[3],但两者的差距较小,约为0.2 Gal。这与在地球上计算的规律完全相反,地球上两极正常重力值大于赤道正常重力,差值约为5 Gal。图 5为月球和地球的正常重力随纬度的变化,可以看出二者相反的趋势。
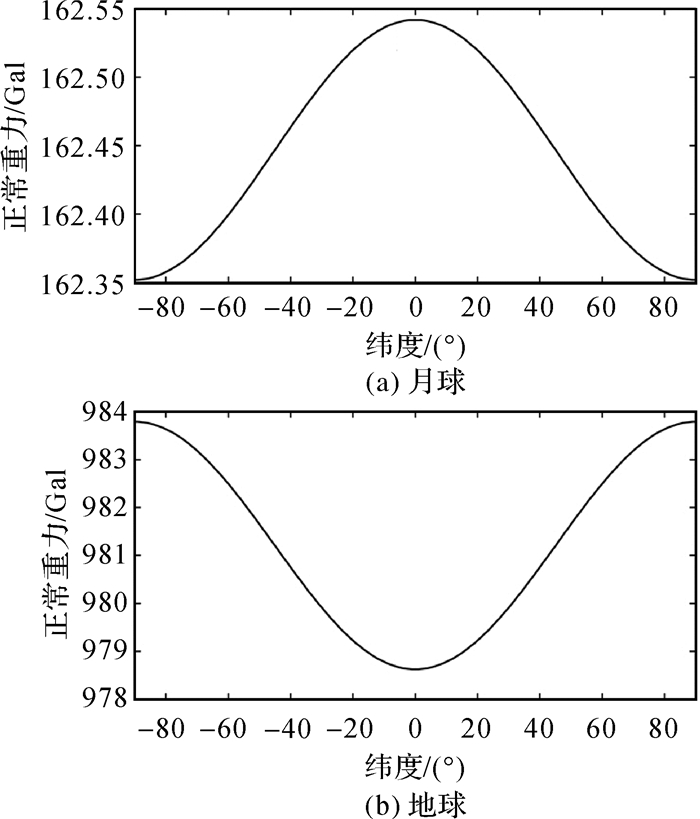
|
| 图 5 月球和地球的正常重力随纬度的变化关系 Fig. 5 Normal gravity variation of the Moon and the Earth with different latitudes |
文献[49]采用新近获取的重力数据及其他月球参数,从截断误差、椭球形状、自转角速度的协调关系出发,详细分析了月球和地球正常重力随纬度变化产生相反趋势的原因,发现月球的椭球扁率与自转角速度之间的数值关系不满足行星流体静力学平衡条件,即利用Clairaut定理求解正常重力并不严格适用于月球,需要探索一种新的计算理论准确地表达月球的正常重力。
2.4 月球重力场解算软件月球重力场模型的构建与探测器的精密定轨密不可分,而探测器精密轨道的计算完全依赖于定轨软件平台的支撑,因此,行星探测器精密定轨软件系统的研制在深空探测中具有重要的工程和科学意义。深空探测器精密定轨技术主要集中在一些欧美航天机构,如喷气推进实验室(Jet Propulsion Laboratory,JPL)、戈达德航天飞行中心(Goddard Space Flight Center,GSFC)、欧洲航天中心(European Space Agency,ESA)等,具有代表性的软件包括DPTRAJ/ODP、MONTE、GEODYN-Ⅱ、GINS等。我国在开展嫦娥系列任务和火星任务中,北京航天飞行控制中心、上海天文台等单位也分别研制了其定轨定位软件系统,以满足工程需求。武汉大学自主研发的深空探测器精密定轨与重力场解算软件系统WUDOGS[50]目前也已经具备月球、火星、木星、太阳系小天体探测器高精度定轨和重力场解算能力,并被指定为火星任务定轨的备份软件。表 3列出了国内外典型的深空定轨软件系统及部分重力场产品。
| 软件名 | 国家 | 研制机构与时间 | 主要开发语言 | 典型深空探测任务 | 部分重力场产品 |
| GEODYN-Ⅱ/SOLVE | 美国 | NASA/GSFC1984年至今 | Fortran | LP、SELENE、GRAIL、DAWN等 | 月球LP、SELEN和GRAIL系列重力场模型,火星MGS系列重力场模型等 |
| DPTRAJ/ODP | 美国 | NASA/JPL1963—2005年 | Fortran | Pioneer、Viking、Voyager、Magellan、Cassini等 | 月球LP、SELEN和GRAIL系列重力场模型,火星MGS系列重力场模型等 |
| MONTE | 美国 | NASA/JPL1998年至今 | C++/Python | CASSINI、JUNO、BepiColombo等 | 土星、木星系列重力场模型等 |
| GINS | 法国 | CNES1970s至今 | Fortran | MGS、MEX、ODY、INSIGHT | 火星、金星重力场模型 |
| ORBIT14 | 意大利 | 比萨大学2007年至今 | Fortran | MESSENGER、JUNO、JUICE、BepiColombo | 木星、水星重力场模型 |
| WUDOGS | 中国 | 武汉大学2011年至今 | Fortran | CE、MEX、Rosetta | 月球重力场CEGM03、火卫Phobos重力场、小行星(21) Lutetia等 |
3 面临的问题及解决途径
随着空间探测技术的发展,月球形状与重力场的确定有了长足的进展。但是,由于月面就位探测的缺乏,月球形状与重力场的精确获取及其可靠性仍然面临诸多挑战,代表性的问题如下。
3.1 测高数据的空缺与条带问题自2011年LRO卫星调轨后,LOLA在月球北半球采集数据存在很大局限,导致很多区域没有有效的数据分布或数据质量不高。对于撞击坑、峭壁及陡坡等特殊地形地貌,无法通过插值技术解决数据空白或质量不高的问题。目前,主要是通过其他探测任务的测高数据(如LAM、LAIT数据)和立体影像数据进行填充融合。
由于观测卫星的运行轨道类型较为单一,且不同时期测高数据的精度存在差异,因此月球地形模型的构建过程产生了呈南北走向的条带状误差。目前,解决条带误差的途径主要是对测高数据进行交叉点处理和滤波技术处理。文献[51]对测高数据进行交叉点平差与滤波处理后,局部月球数字高程模型的条带状误差得到一定程度的缓解。但是,滤波技术只是对获取的月球数字高程模型进行一些粗差的剔除,并不能从根本上解决问题。因此,未来仍需要对探测器激光测高数据进行交叉点平差方法的改进和优化,以处理由轨道数据精度不同引起的误差。
随着月球着陆和载人探测的不断深入,可以考虑在月面布设卫星激光测高定标场,安置光子检测靶标,用于月球卫星测高仪参数的校准与月面数字高程模型的检核。
3.2 重力场模型的可靠性JPL与GSFC发布的重力场模型分别为GL0900D与GRGM900C,被认为是目前精度最高的重力场模型,并被广泛应用。但是它们的二阶项C20却存在不一致性,其中GRGM900C的C20项为-9.088 661 636 134 390 5E-05,GL0900D的C20项为-9.088 124 807 048 000E-05,其差值为5.369 290 863 905E-09,而该系数的观测误差仅在10~11量级,它们之间的差值高出误差两个数量级。这导致由它们反演而来的月球惯性矩等地球物理参数存在不确定性。
解算重力场模型高阶项时使用了更多观测数据,这导致高阶项中包含更多噪声。图 6为具有代表性的重力场模型的误差功率谱。可以发现,模型误差功率随阶次的升高而迅速升高。其中,660阶次与900阶次的模型在高阶次时,其误差功率甚至会高于系数功率;1200阶次模型的误差功率虽然并未超过系数功率,但当阶次超过1000时,误差与系数本身的功率已经极为接近。为了保证数据的可靠性,使用这些模型时会截去一部分误差功率较大的阶次。

|
| 图 6 典型月球重力场模型功率谱 Fig. 6 The spectrum of some representative lunar gravity field models |
月球重力场模型中的重力值实际是由轨道高度处的重力值向下延拓后得到。而向下延拓属于不适定问题[37],这导致解的不稳定性;同时向下延拓具有高通滤波的属性,放大了其中的局部干扰与误差。通过比较Apollo时期的月面观测值与典型重力场模型值,可以发现其符合结果并不理想(表 4)。其中,基于GRAIL观测量解算的GRGM660PRIM的符合程度最差,而一些早期的重力场模型符合程度反而更好。尽管Apollo时期观测值的精度和可靠性很差,但对比的结果仍然提示重力场模型延拓至月面时所存在的不确定性。
| Apollo任务 | Sagitov16 | LP100K | SGM100h | GRGM660PRIM |
| Apollo 11 | 20 | 26 | 19 | 81 |
| Apollo 12 | 56 | 8 | 31 | 35 |
| Apollo 14 | 87 | 10 | 41 | 16 |
| Apollo 17 | 257 | 104 | 100 | 26 |
关于模型可靠性问题,目前一个可行的解决方案是通过融合多源卫星轨道观测数据予以改善。如“嫦娥5T”的轨道倾角在18°~68°之间变化,与其他极轨卫星摄动量的相关性较低。文献[52]利用“嫦娥5T”数据解算的CEGM03模型表明,该数据改进了基于SELENE观测数据解算得到的月球重力场模型的低阶项(图 7);而在月面上直接进行高精度重力测量,以月面实测重力值对重力场模型进行检核,有望从实质上解决上述问题。

|
| 图 7 月球重力场CEGM模型与SGM模型功率谱 Fig. 7 The spectrum of CEGM series and SGM100h lunar gravity field models |
4 结语
对月球形状与重力场的研究,对于人类了解月球、走向深空具有重要意义。虽然我们可以借鉴地球上的很多技术与方法,但是针对月球探测中的特殊性,仍需要不断地探索与创新。21世纪以来已有美国、欧盟、日本、印度、中国实施了多项探月任务,尤其是中国已经实现了月球探测的“绕”“落”“回”,为更加深入、全面研究月球形状和重力场提供了丰富数据和有利条件。当前,许多国家都在加紧实施深空探测计划,抢占深空领域的战略制高点。如欧盟在未来将实施“月球村”计划[53],为月球长期观测站建立提供契机;美国计划于2024年发射Artemis Ⅲ任务,计划在月球上进行包括重力测量在内等一系列地球物理观测;日本计划实施SLIM(smart lander for investigating Moon)任务[54],将提供新的月球控制点。中国也将深空作为国家的战略新疆域之一。面对挑战和机遇,需要我们积极作为,乘势而上。随着我国嫦娥任务的推进,建立月面基地的计划也将实施,开展更多月球表面的大地测量和地球物理就位探测将成为现实,月球形状与重力场的研究也将迈上一个新的台阶。
| [1] |
李斐, 鄢建国. 月球重力场的确定及构建我国自主月球重力场模型的方案研究[J]. 武汉大学学报(信息科学版), 2007, 32(1): 6-10. LI Fei, YAN Jianguo. Principle and method of lunar gravity field determination and project on self-determinational lunar gravity field[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 6-10. |
| [2] |
李斐, 鄢建国, 平劲松. 月球探测及月球重力场的确定[J]. 地球物理学进展, 2006, 21(1): 31-37. LI Fei, YAN Jianguo, PING Jingsong. Lunar exploration and lunar gravity field determination[J]. Progress in Geophysics, 2006, 21(1): 31-37. DOI:10.3969/j.issn.1004-2903.2006.01.006 |
| [3] |
欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005. OUYANG Ziyuan. Introduction to lunar science[M]. Beijing: China Aerospace Publishing House, 2005. |
| [4] |
GRUSHINSKⅡ N P, SAGITOV M U. Some considerations on the lunar gravitational field[J]. Soviet Astronomy, 1962, 6(1): 113-117. |
| [5] |
ZEIGLER R A, MOSIE A B, CORRIGAN C, et al. The Apollo sample collection: 50 years of solar system insight[J]. Elements, 2019, 15(4): 286-287. DOI:10.2138/gselements.15.4.286 |
| [6] |
李斐, 郝卫峰, 鄢建国, 等. 空间跟踪技术的发展对月球重力场模型的改进[J]. 地球物理学报, 2016, 59(4): 1249-1259. LI Fei, HAO Weifeng, YAN Jianguo, et al. Advancement of lunar gravity model due to the development of space tracking techniques[J]. Chinese Journal of Geophysics, 2016, 59(4): 1249-1259. |
| [7] |
姚美娟, 陈建平, 徐彬, 等. 月球正面与背面的差异对比与演化分析[J]. 地球科学与环境学报, 2017, 39(3): 428-438. YAO Meijuan, CHEN Jianping, XU Bin, et al. Difference comparison and evolution analysis of lunar nearside and farside[J]. Journal of Earth Sciences and Environment, 2017, 39(3): 428-438. DOI:10.3969/j.issn.1672-6561.2017.03.011 |
| [8] |
周增坡, 程维明, 周成虎, 等. 基于"嫦娥一号"的月表形貌特征分析与自动提取[J]. 科学通报, 2011, 56(1): 18-26. ZHOU Zengbo, CHENG Weiming, ZHOU Chenghu, et al. Characteristic analysis of the lunar surface and automatically extracting of the lunar morphology based on CE-1[J]. Chinese Science Bulletin, 2011, 56(1): 18-26. |
| [9] |
HEAD Ⅲ J W, WILSON L. Lunar mare volcanism: stratigraphy, eruption conditions, and the evolution of secondary crusts[J]. Geochimica et Cosmochimica Acta, 1992, 56(6): 2155-2175. DOI:10.1016/0016-7037(92)90183-J |
| [10] |
BALDWIN R B. Ranger Ⅷ and gravity scaling of lunar craters[J]. Science, 1967, 157(3788): 546-547. DOI:10.1126/science.157.3788.546 |
| [11] |
HEIKEN G, VANIMAN D, FRENCH B M. Lunar sourcebook: a user's guide to the moon[M]. Cambridge: Cambridge University Press, 1991.
|
| [12] |
王娇, 程维明, 周成虎. 全月球撞击坑识别、分类及空间分布[J]. 地理科学进展, 2015, 34(3): 330-339. WANG Jiao, CHENG Weiming, ZHOU Chenghu. A global inventory of lunar craters: identification, classification, and distribution[J]. Progress in Geography, 2015, 34(3): 330-339. |
| [13] |
MULLER P M, SJOGREN W L. Mascons: lunar mass concentrations[J]. Science, 1968, 161(3842): 680-684. DOI:10.1126/science.161.3842.680 |
| [14] |
肖龙, 黄俊, 赵佳伟, 等. 月面熔岩管洞穴探测的意义与初步设想[J]. 中国科学: 物理学力学天文学, 2018, 48(11): 119602. XIAO Long, HUANG Jun, ZHAO Jiawei, et al. Significance and preliminary proposal for exploring the lunar lava tubes[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2018, 48(11): 119602. |
| [15] |
GAVRILOV I V. The geometric figure and dimensions of the moon[J]. Soviet Astronomy, 1968, 12: 319-325. |
| [16] |
高布锡. 对月球形状的估算[J]. 天文学报, 2008, 49(4): 425-433. GAO Buxi. The estimate on lunar figure[J]. Acta Astronomica Sinica, 2008, 49(4): 425-433. DOI:10.3321/j.issn:0001-5245.2008.04.009 |
| [17] |
王文睿, 李斐, 刘建军, 等. 基于嫦娥一号激光测高数据的月球三轴椭球体模型[J]. 中国科学: 地球科学, 2010, 40(8): 1022-1030. WANG Wenrui, LI Fei, LIU Jianjun, et al. Triaxial ellipsoid models of the moon based on the laser altimetry data of Chang'E-1[J]. Science China Earth Sciences, 2010, 40(8): 1022-1030. |
| [18] |
李蓉, 李斐, 鄢建国, 等. 基于LRO测高数据和GRAIL重力数据解算的月球三轴椭球体模型[J]. 测绘地理信息, 2016, 41(3): 8-11, 24. LI Rong, LI Fei, YAN Jianguo, et al. Lunar tri-axial ellipsoid model based on LRO Altimetry data and GRAIL gravity data[J]. Journal of Geomatics, 2016, 41(3): 8-11, 24. |
| [19] |
SMITH D E, ZUBER M T, NEUMANN G A, et al. Topography of the Moon from the clementine lidar[J]. Journal of Geophysical Research, 1997, 102(E1): 1591-1611. DOI:10.1029/96JE02940 |
| [20] |
BURŠA M, BUCHAR E. Determination of the parameters of a selenocentric reference system and the deflections of the vertical at the lunar surface[J]. Studia Geophysica et Geodaetica, 1971, 15(3): 210-227. |
| [21] |
MARTINEC Z, PĚČ K. A determination of the parameters of the level surface of lunar gravity[J]. Earth, Moon, and Planets, 1988, 43(1): 21-31. DOI:10.1007/BF00056475 |
| [22] |
BURŠA M. Potential of the geoidal surface, the scale factor for lengths and Earth's figure parameters from satellite observations[J]. Studia Geophysica et Geodaetica, 1969, 13(4): 337-358. DOI:10.1007/BF02587793 |
| [23] |
BURŠA M. Best-fitting tri-axial earth ellipsoid parameters derived from satellite observations[J]. Studia Geophysica et Geodaetica, 1970, 14(1): 1-9. DOI:10.1007/BF02585546 |
| [24] |
BURŠA M. Distortions of the Moon's figure due to the Earth[J]. Earth, Moon, and Planets, 1994, 64(3): 265-271. DOI:10.1007/BF00572152 |
| [25] |
张承志. 月球的力学形状以及月球物理参数的研究[J]. 南京大学学报, 1993, 29(4): 569-580. ZHANG Chengzhi. A study of dynamical figure and of physical parameters for the moon[J]. Journal of Nanjing University, 1993, 29(4): 569-580. |
| [26] |
丰海, 李建成, 李大炜, 等. 新的月球大地水准面模型与参考三轴水准椭球[J]. 大地测量与地球动力学, 2013, 33(4): 133-136. FENG Hai, LI Jiancheng, LI Dawei, et al. A new selenoid model and reference triaxial level ellipsoid[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 133-136. |
| [27] |
FOLKNER W M, WILLIAMS J G, BOGGS D H, et al. The planetary and lunar ephemerides DE430 and DE431[R]. [S. l. ]: Interplanetary Network Progress Report, 2014: 1-81.
|
| [28] |
曹建峰, 胡松杰, 张宇, 等. 嫦娥三号着陆器统计定位精度分析[J]. 飞行器测控学报, 2014, 33(3): 244-249. CAO Jianfeng, HU Songjie, ZHANG Yu, et al. Analysis of the accuracy of statistical positioning for Chang'E-3 lunar lander[J]. Journal of Spacecraft TT & C Technology, 2014, 33(3): 244-249. |
| [29] |
ARCHINAL B A, ROSIEK M R, KIRK R L, et al. Final completion of the unified lunar control network 2005 and topographic model[C]//Proceedings of the 38th Lunar and Planetary Science Conference. League: LPI, 2007.
|
| [30] |
邸凯昌, 刘斌, 彭嫚, 等. 利用多探测任务数据建立新一代月球全球控制网的方案与关键技术[J]. 武汉大学学报(信息科学版), 2018, 43(12): 2099-2105. DI Kaichang, LIU Bin, PENG Man, et al. Scheme and key techniques for construction of new-generation lunar global control network using multi-mission data[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2099-2105. |
| [31] |
VISWANATHAN V, MAZARICO E, CREMONS D, et al. Scientific exploration of the lunar south pole with retro-reflectors[C]//Proceedings of Lunar Surface Science Workshop. Denver: LPI, 2020: 5070.
|
| [32] |
叶茂. 月球探测器精密定轨软件研制与四程中继跟踪测量模式研究[J]. 测绘学报, 2016, 45(9): 1132. YE Mao. Development of lunar spacecraft precision orbit determination software system and research on a four-way relay tracking measurement mode[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1132. DOI:10.11947/j.AGCS.2016.20160339 |
| [33] |
郝卫峰, 李斐, 叶茂, 等. 基于嫦娥一号卫星获取的DEM研究月球车通信的可达性[J]. 宇航学报, 2012, 33(10): 1453-1459. HAO Weifeng, LI Fei, YE Mao, et al. The communication accessibility of the lunar rover based on DEM derived from Chang'E-1[J]. Journal of Astronautics, 2012, 33(10): 1453-1459. DOI:10.3873/j.issn.1000-1328.2012.10.013 |
| [34] |
MAZARICO E, NEUMANN G A, SMITH D E, et al. Illumination conditions of the lunar polar regions using LOLA topography[J]. Icarus, 2011, 211(2): 1066-1081. DOI:10.1016/j.icarus.2010.10.030 |
| [35] |
BARKER M K, MAZARICO E, NEUMANN G A, et al. Improved LOLA elevation maps for south pole landing sites: error estimates and their impact on illumination conditions[J]. Planetary and Space Science, 2021, 203: 105119. DOI:10.1016/j.pss.2020.105119 |
| [36] |
海斯卡涅, 莫里斯, 卢福康, 等. 物理大地测量学[M]. 胡国理, 译. 北京: 测绘出版社, 1979. HEISKANEN W A, MORITZ H, LU Fukang, et al. Physical geology[M]. HU Guoli, trans. Beijing: Surveying and Mapping Press, 1979. |
| [37] |
NOZETTE S, RUSTAN P, PLEASANCE L P, et al. The clementine mission to the moon: scientific overview[J]. Science, 1994, 266(5192): 1835-1839. DOI:10.1126/science.266.5192.1835 |
| [38] |
HUBBARD G S, BINDER A B, FELDMAN W. The lunar prospector discovery mission: mission and measurement description[J]. IEEE Transactions on Nuclear Science, 1998, 45(3): 880-887. DOI:10.1109/23.682655 |
| [39] |
SASAKI S, ⅡJIMA Y, TANAKA K, et al. The SELENE mission: goals and status[J]. Advances in Space Research, 2003, 31(11): 2335-2340. DOI:10.1016/S0273-1177(03)00543-X |
| [40] |
ZUBER M T, SMITH D E, ASMAR S W, et al. Gravity recovery and interior laboratory (GRAIL) mission: status at the initiation of the science mapping phase[C]//Proceedings of the 43rd Lunar and Planetary Science Conference. Woodlands: LPI, 2012: 1489.
|
| [41] |
YAN Jianguo, GOOSSENS S, MATSUMOTO K, et al. CEGM02: an improved lunar gravity model using Chang'E-1 orbital tracking data[J]. Planetary and Space Science, 2012, 62(1): 1-9. DOI:10.1016/j.pss.2011.11.010 |
| [42] |
LEMOINE F G R, SMITH D E, ZUBER M T, et al. A 70th degree lunar gravity model (GLGM-2) from Clementine and other tracking data[J]. Journal of Geophysical Research, 1997, 102(E7): 16339-16359. DOI:10.1029/97JE01418 |
| [43] |
KONOPLIV A S, ASMAR S W, CARRANZA E, et al. Recent gravity models as a result of the Lunar Prospector mission[J]. Icarus, 2001, 150(1): 1-18. DOI:10.1006/icar.2000.6573 |
| [44] |
NAMIKI N, IWATA T, MATSUMOTO K, et al. Farside gravity field of the Moon from four-way Doppler measurements of SELENE (Kaguya)[J]. Science, 2009, 323(5916): 900-905. DOI:10.1126/science.1168029 |
| [45] |
ZUBER M T, SMITH D E, LEHMAN D H, et al. Gravity Recovery and Interior Laboratory (GRAIL): mapping the lunar interior from crust to core[J]. Space Science Reviews, 2013, 178(1): 3-24. DOI:10.1007/s11214-012-9952-7 |
| [46] |
KONOPLIV A S, PARK R S, YUAN D N, et al. The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL primary mission[J]. Journal of Geophysical Research, 2013, 118(7): 1415-1434. DOI:10.1002/jgre.20097 |
| [47] |
GOOSSENS S, SABAKA T J, WIECZOREK M A, et al. High-resolution gravity field models from GRAIL data and implications for models of the density structure of the Moon's crust[J]. Journal of Geophysical Research, 2020, 125(2): e2019JE006086. |
| [48] |
PARK R S, KONOPLIV A S, YUAN D N, et al. A high-resolution spherical harmonic degree 1200 lunar gravity field from the GRAIL mission[C]//Proceedings of American Geophysical Union. [S. l. ]: AGU Fall Meeting Abstracts, 2015.
|
| [49] |
郝卫峰, 叶茂, 鄢建国, 等. 月球和地球正常重力特征差异及成因探讨[J]. 地球物理学报, 2021, 64(7): 2417-2425. HAO Weifeng, YE Mao, YAN Jianguo, et al. Difference of normal gravity characteristics between the Moon and the Earth and its causes[J]. Chinese Journal of Geophysics, 2021, 64(7): 2417-2425. |
| [50] |
叶茂, 李斐, 鄢建国, 等. 国内外深空探测器精密定轨软件研究综述及WUDOGS简介[J]. 飞行器测控学报, 2017, 36(1): 45-55. YE Mao, LI Fei, YAN Jianguo, et al. Review of deep space orbit determination software and introduction to WUDOGS[J]. Journal of Spacecraft TT&C Technology, 2017, 36(1): 45-55. |
| [51] |
HAO Weifeng, ZHU Chang, LI Fei, et al. Illumination and communication conditions at the Mons Rümker region based on the improved Lunar Orbiter Laser Altimeter data[J]. Planetary and Space Science, 2019, 168: 73-82. DOI:10.1016/j.pss.2019.01.010 |
| [52] |
YANJianguo, LIU Shanhong, XIAO Chi, et al. A degree-100 lunar gravity model from the Chang'e 5T1 mission[J]. Astronomy & Astrophysics, 2020, 636: A45. |
| [53] |
CASINIA E M, MITTLER P, COWLEY A, et al. Lunar analogue facilities development at EAC: the LUNA project[J]. Journal of Space Safety Engineering, 2020, 7(4): 510-518. DOI:10.1016/j.jsse.2020.05.002 |
| [54] |
TOUKAKU Y. JAXA space science program and international collaboration[EB/OL]. [2022-01-20]. https://www.essc.esf.org/wp-content/uploads/2021/09/55th_Geneva18_ISAS_Program_Overview_May-2018.pdf.
|


