激光(雷达)测高作为一种主动式遥感技术,是现代雷达探测技术从厘米波和毫米波向光波探测技术的延伸。具有测量精度高、时空分辨率高、垂直分辨率高等特点,广泛应用于三维成像、地球观测和行星探测等领域[1]。特别是近几年,随着激光技术、光电探测技术和计算机控制技术的进一步发展,星载激光探测技术也有了长足的发展[2]。激光雷达、光谱成像技术和合成孔径雷达技术被列为地球观测系统的核心信息技术[3]。鉴于机载激光测高的应用已经十分普遍,本文主要讨论星载激光测高技术,但在工作原理和数据处理的方法上两者往往是相通的。
早期的激光测高仪采用离散记录方式,通过采样获得多个回波信号的三维空间位置。美国火星轨道器激光测高仪(Mars Orbiter Laser Altimeter, MOLA)和月球轨道器激光测高仪(Lunar Orbiter Laster Altimeter, LOLA)是离散激光的典型例子。与离散激光雷达不同,全波形激光测高仪向地面发射激光,接收地面反射的激光脉冲信号,并记录激光全波形回波信号; ICESat(Ice, Cloud and land Elevation Satellite)卫星上搭载的地球科学激光测高系统(Geoscience Laster Altimeter, GLAS)是全波形激光测高仪的典型例子。在2018年美国国家宇航局NASA发射的ICESat-2(Ice, Cloud and land Elevation Satellite-2)卫星上,首次搭载了光子计数激光雷达[4]。光子计数激光雷达的发射器具有低能量、高脉冲重复频率的特点,并且采用高灵敏度的单光子探测器(即接收器),可以获取光斑(足印)更小、密度更高的光子点云数据,进而实现更精细的地表三维信息获取[5-6]。
与机载激光雷达测高技术相比,星载激光具有覆盖范围广和运行轨道高的特点,被广泛应用于制作全球控制点库、监测极地冰川和湖中水位的变化,以及估算森林生物量、碳储量等[7]。需要指出的是,机载激光雷达测高技术能同时沿飞行方向和其垂直飞行方向进行扫描,目前星载激光测高技术只能实现沿轨方向扫描,但就基本原理而言两者都是激光测距(测高)。目前已有多颗对地观测卫星搭载了激光测高系统,其中包括2003年的美国NASA发射的ICESat,其上搭载的地球科学激光测高系统GLAS是世界上第一个对地球进行连续观测的激光系统,主要用于监测南极洲和格陵兰冰盖的高程变化、测量全球范围内云层高度和云/气溶胶垂直结构以及森林垂直结构信息[8]。2009年ICESat失效后,NASA于2018年先后发射ICESat-2和GEDI(Global Ecosystem Dynamics Investigation),前者搭载了光子计数激光测高仪,后者则是全波形激光雷达载荷[6]; 2019年中国发射的高分七号卫星,同时搭载了全波形激光测高仪和双线阵立体相机[9]。
本文对星载激光测高系统的工作原理,数据处理方法以及应用进行详细讨论和归纳,并对未来的研究方向进行了展望。
1 星载激光测高原理星载激光测高的发展历史可以追溯至R.W.Hellwarth和F.J.McClung于1962年发明的调Q(又称“Q开关”)脉冲激光器。由于其产生的巨脉冲激光有足够高的峰值功率,使得远距离脉冲激光测距成为可能。早在1971年阿波罗15号就搭载了调Q脉冲激光器并完成了多次绕月激光测距探测[10]; 此后,星载激光测高仪被广泛应用于对地球及其他星体的探测。经过半个多世纪的探索,星载激光测高技术得到了极大的发展,目前已有多个搭载了激光测高仪的卫星发射升空。根据探测原理的不同,将分两类针对迄今为止的几个典型的星载激光测高系统进行讨论。
1.1 线性探测激光测高系统从原理来看,激光测高技术的核心是激光测距。传统激光测高仪主要采用线性探测原理(即按线性关系进行光电转换),通过测量自激光脉冲发射至接收到目标回波信号的时间间隔,计算光在该时间间隔内所经过距离的一半,即为探测器至目标的距离[11]。典型的星载激光雷达系统主要由三部分组成,即发射系统、接收系统和位置姿态系统。
1.1.1 激光发射系统由于作用距离较远,星载激光测高仪的发射系统只能采用脉冲激光。到20世纪80年代,星载激光测距仪一直使用氪灯或氙灯泵浦固体激光器作为发射系统的光源[2]。20世纪90年代,搭载了第一代应用于空间探测的半导体泵浦固体激光器(Diode-pumped solid-state lastor, DPSSL)的火星轨道器激光测高仪(MOLA)于1996年由美国国家宇航局发射。因其寿命长、质量轻、体积小和功耗低等优点,半导体泵浦固体激光器自此取代了氪灯或氙灯泵浦固体激光器的主导地位,逐渐成为各国星载激光测高仪的首选光源。NASA于2003年发射的第一颗主要用于冰、云和陆地测量的卫星(ICESat)所搭载的地球科学激光测高系统(GLAS)配备了3台半导体泵浦Nd: YAG激光器(其中2台为备份激光器)[12]。GLAS的激光器采用了二极管泵浦调Q结构,能同时输出1064 nm基频和532 nm倍频激光脉冲,前者用于开展地表高程探测,后者则用于开展气溶胶、云垂直分布廓线的探测[12]。作为中国星载激光测高仪的首次应用,2007年和2013年分别发射的对月观测嫦娥(CE)一号、二号上所搭载的激光器也均采用了半导体泵浦Nd: YAG激光器作为发射系统的光源,发射的1064 nm基频激光用于高精度量测月球表面的高程[2]。中国首个对地试验激光测高仪随着2016年资源三号02卫星的升空正式开展对地测高探索,这台试验激光测高仪也采用了半导体泵浦Nd: YAG激光器。
以上所讨论的激光测高仪的发射系统均使用单波束发射系统,即单个半导体泵浦Nd: YAG激光器。单波束激光器的劣势在于为了实现在扫描方式下高密度、高覆盖的目标采样,单个激光器的重复频率需要足够高。但是星载激光测高仪的重复频率受制于系统体积、质量和功耗等因素,高功率脉冲激光器的重复频率无法做得非常高。因此多波束激光器的推帚式探测是如今颇具优势和潜能的激光发射系统[2]。美国用于对月观测的LOLA即为采用了多波束激光器的测高仪。搭载在国际空间站(International Space Station, ISS)上的全球生态系统动态检测(GEDI)激光雷达于2018年成功发射。GEDI拥有3台同时工作的半导体泵浦Nd: YAG激光器,是第一个实现多波束对地观测的星载激光雷达[13]。中国随后在2019年发射的对地立体测绘卫星高分七号上也搭载了多波束激光发射系统,该系统配备了4台半导体泵浦Nd: YAG激光器,采取2主2备的形式,在任意时刻都有2台激光器同时工作,实现了双波束对地激光测高[10]。
1.1.2 信号接收系统线性探测激光测高仪的接收系统主要由一个雪崩光电二极管(Avalanche photodiode, APD)和一个模拟数字转换器(ADC)组成。信号接收系统先由APD将接收到的回波转换成模拟信号,再由ADC将模拟信号转换为数字信号。线性探测原理的“线性”正是体现在APD的输入光信号和输出的模拟信号线性相关[14]。目前在空间激光测高仪接收系统中占主导地位的是硅APD,其灵敏度高,且具有响应度高、响应速度快的特点[15]。
对接收到的回波信号,线性探测原理有两种不同的数据记录方式。因而,线性探测原理下的激光雷达也经常分为两类:离散激光雷达和全波形激光雷达。前者记录若干离散的回波信号,后者则以很小的时间间隔对目标接收到激光脉冲后返回的能量进行完整的采样记录[16]。
早期的星载线性探测激光测高仪都为离散记录方式,通常不超过4个回波信号记录。虽然离散激光雷达的确能采集到高精度的测高数据,但是它的劣势也非常明显。由于记录回波信号个数的限制,离散激光雷达无法记录茂密高大的树林,因此难以对这类区域进行精准测量。此外,其离散的记录方式会造成高达2.0 m的盲区(dead zone effect),也就是说当两个邻近目标的垂直距离小于2.0 m时,离散激光雷达无法检测到第二个目标的存在[17]。对非地球观测或对小行星观测来说,由于不受植被影响,因此常采用离散激光雷达探测。例如1994年NASA发射的对月观测卫星Clementine上的LiDAR测高仪,NASA 1996年的火星探测卫星MGS(Mars Global Surveyor)上的MOLA测高仪,2009年的月球探测卫星LRO(Lunar Reconnaissance Orbiter)上的LOLA测高仪,以及近些年中国发射的月球观测卫星嫦娥一号(CE-1)、嫦娥二号(CE-2)搭载的激光测高仪[18]均为离散激光雷达。
与离散激光雷达不同,全波形激光雷达对完整回波波形按时间间隔进行记录。除了能提供高精度点云数据,全波形激光雷达的每个数据点还涵括了许多其他信息,包括回波波形特征和回波的强度,因此它能对地表和地表植被结构采集到丰富全面的数据[17, 19]。研究表明,无论是从测距精度、目标特征,还是目标辨别能力来看,全波形激光雷达相比离散激光雷达都有着更大的潜能和优势[17]。2003年ICESat卫星所搭载的GLAS就是由NASA发射的第一颗星载全波形激光测高仪,其采集到的数据被广泛应用于反演区域尺度的森林高度和生物量等参数[7]。2019年发射的高分七号卫星搭载的激光测高仪是中国首台全波形星载激光测高仪,其主要目标是为实现1∶10 000的测绘提供高精度的地面高程控制点。结合其双波束激光器的特点,高分七号激光测高数据将能提供密集的地面点,因此能为全球气候变化和海洋监测提供有效的数据源,同时也能在植被高度提取、植被特征分类和全球生物量估计方面进行多学科研究[18, 20]。
1.2 光子计数激光雷达光子计数激光雷达系统的研究发展可以追溯到20世纪90年代,文献[21]提出用光子计数激光雷达来进行距离测量。近些年,因其独特的优势,光子计数激光雷达受到越来越多的研究学者和机构的关注。不论是离散激光雷达还是全波形激光雷达,线性探测激光雷达需要通过光子流(500~1000个光子)来记录返回的信号,只有足够大的激光发射能量才能产生大流量光子流并记录散射回来的波形信号[22]。不同于线性探测激光雷达,光子计数激光雷达系统每秒发射数千个激光脉冲,并记录后向散射和漫反射到接收器的单个光子的传播时间。单个光子的飞行距离则可以通过记录的光子到达时间得出,从而实现对地表高度的测量。因光子计数激光雷达可对单个光子敏感,其激光发射能量要远低于线性探测激光雷达。作为对比,采用全波形探测技术的GLAS,其发射的激光能量约为70 mJ[23]; 而作为世界首个采用微脉冲多波束光子计数激光雷达技术的星载激光雷达测高仪ATLAS,其强激光束发射的激光能量约为48~172 uJ,弱激光束的能量约为12~43 uJ,从而在实现了500 km距离下的对地测高的同时,也大大减小了对激光发射器的激光能量的要求[24]。此外,光子计数激光雷达在低能量消耗下的高灵敏度的特点使得光子计数激光雷达系统有望延长激光寿命,并能够在更高的高度飞行,从而提供更大的覆盖范围。
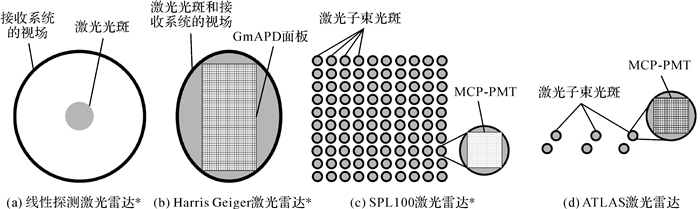
需要指出的是,线性探测激光雷达系统体系已颇为成熟,而光子计数激光雷达的民用测量系统还比较少,其中有3个代表性的系统在光子计数激光雷达体系中尤为重要。一是由Harris公司开发的Geiger模式激光雷达系统GmLiDAR,二是由Leica公司旗下的Sigma Space开发的单光子激光雷达系统(SPL100)[5, 25-26],三是搭载在美国NASA于2018发射的ICESat-2卫星上的ATLAS(advanced topographic laser altimeter system)。前两个系统目前都只实现了机载测量(具有在垂直于飞行方向上的扫描功能),而第三个是目前首个应用单光子探测技术的星载激光测高仪。这3个系统从激光发射系统和接收系统来看都有着很大的差别,如果把传统线性探测激光雷达描述为点发射-点接收的话,Harris的GmLiDAR可以被描述为点发射-面接收,而SPL100和ATLAS则为面发射-面接收。图 1从原理上简略描述了线性探测激光雷达图 1(a)和3个不同的光子计数激光雷达的激光发射系统和信号接收系统(图 1(b)、(c)、(d))。图 1(b)、图 1(c)目前尚未有相应的星载激光雷达。下文将从激光发射系统和信号接收系统两方面详细介绍光子计数激光雷达系统。
1.2.1 激光发射系统
大部分光子计数激光雷达的激光发射光源同线性探测激光雷达一样,都采用半导体泵浦Nd: YAG激光器作为发射系统的光源[14],只有星载的ATLAS略有不同,其采用的是半导体泵浦Nd: YVO4激光器作为光源[24]。Nd: YAG晶体是目前半导体泵浦激光器中最成熟的晶体材料,它具有良好的导热特性和光学特性,但由于它的晶体吸收谱较窄,导致激光器电光转换效率较低。而Nd: YVO4晶体在808 nm附近的吸收谱宽高达15 nm,是Nd: YAG晶体(3 nm)的5倍宽,大大提高了激光器的电光转换效率[27]。
如图 1所示,传统线性探测激光雷达的发射系统向地面发射单个激光束,而光子计数激光雷达既可有单个激光束发射系统,也可有激光子束阵列发射系统(不同于由多台激光器组成的多波束系统)。Harris的Geiger激光雷达系统与线性探测激光雷达一样,向地面发射单束激光束[22],而SPL100和ATLAS的发射系统额外装配了一个衍射光学元件(diffractive optical element, DOE),通过这个DOE将激光发射器的单个激光束分成激光子束阵列[28]。SPL100的激光子束阵列为10×10,每个激光子束的能量均等[26],而ATLAS的激光束通过DOE被分成3对激光子束,每对激光子束包含了一个强激光束和一个弱激光束,强弱激光束的能量比为4∶1[24]。
需要说明的是,在这3种光子计数激光雷达中,Geiger激光雷达由于接收系统的设置,使得它对视场内扫描重复率要求很高[29],因此,目前的机载Geiger激光雷达系统采用Palmer(即椭圆形状)扫描机制,而不是传统线性探测系统使用的Z形扫描机制[15]。SPL100虽然对视场内扫描重复率的要求比Geiger激光雷达略低,它采用的也是Palmer扫描机制[14]。而目前唯一的星载光子计数激光雷达ATLAS采用的是推帚式扫描[24],其在垂直于轨道方向的分辨率是很低的(约3.3 km[4])。
1.2.2 信号接收系统光子计数激光雷达与传统线性探测激光雷达最大的区别在于其信号接收系统采用了单光子敏感的探测元件。对于单光子敏感探测元件,当其接收到单个光子时就能触发二极管的光电效应,从而输出电信号[14]。而通常线性探测激光雷达使用的APD需要接收到一连串的光子流才会触发光电效应,且这样的光子流所含的光子数目一般不少于250个光子[15]。目前光子计数激光雷达使用的接收系统有两类,一类是Harris Geiger激光雷达使用的GmAPD,另一类是SPL100和ATLAS使用的微通道板光电倍增器(Microchannel plate-photomultipier, MCP-PMT)[30]。
线性探测激光雷达的信号接收系统由单个探测元件APD组成,而光子计数激光雷达往往采用多个探测元件组成的面板。例如Harris Geiger激光雷达的接收系统为由128×32个GmAPD组成的GmAPD面板[22],对于这个面板上的每个GmAPD,在被散射回来的第一个单光子触发后,GmAPD会自行关闭并停止接收后续的光子信息,直至下次整个GmAPD面板被重置[14]。GmAPD这样的工作原理尽管能大幅降低所需激光束的能量,但是由于它只能记录一束脉冲里最先散射回来的单个光子,它的穿透能力在植被覆盖地区有着很大的局限性。如果系统发射的激光束只能单次照亮地面目标物的话,对地面目标的成功探测率将会非常低。为了保证Geiger激光雷达系统对地面目标物有更高的成功探测率,需要对地面目标物进行多次照亮,即上文所讨论的,它要求更高的视场覆盖率[29]。
SPL100和ATLAS采用的是MCP-PMT,每个MCP-PMT都包含了数百个对单光子敏感的探测元件[14, 30]。相较于Geiger激光雷达系统较长的恢复时间,这两个激光雷达系统的恢复时间极短,SPL100只有1.6 ns,换算成距离为24 cm[22]; ATLAS的恢复时间为3.1~3.3 ns,约为48 cm[30]。因此每个光子探测器都能探测到从多个目标物散射回来的多个光子。这样的特点使得SPL100和ATLAS对植被、薄雾和稀薄云层都有一定的穿透性,而且在白天太阳背景噪声大的情况下依然能进行工作。
2 星载激光测高数据处理方法根据记录回波信号的方式,星载激光测高系统可获取离散、全波形和光子计数三类数据。目前尚未形成成熟的数据处理流程和规范。需要说明的是,数据处理方法的适应性主要由数据获取方式和原理来决定,与数据获取的平台并无必然联系,因此,这里介绍的方法在许多方面也适合于多种数据采集平台。
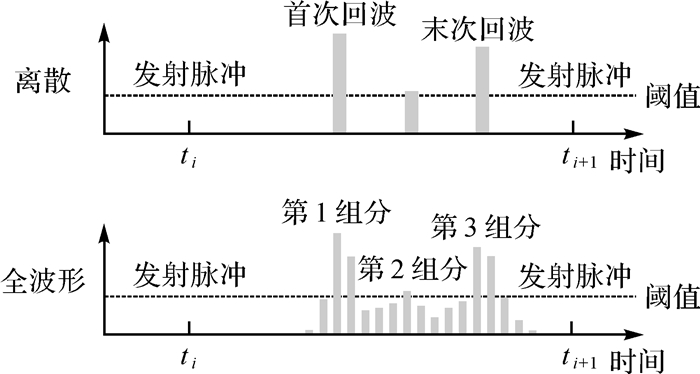
2.1 离散激光雷达数据处理离散激光雷达系统通过采样得到多个回波信号的三维空间位置。通常除了记录激光从离开到返回系统的时间外,回波强度也会被记录下来。如图 2所示,当回波强度超过某个设定的阈值时,传感器会记录此回波,直到达到传感器允许的最大回波记录数。一般情况下,每个脉冲会记录有3-5个回波。目前对地观测的离散激光雷达系统主要是机载的,光斑较小,能够提供高密度的点云数据。与机载离散激光雷达相比,星载激光雷达的光斑较大[31],测距精度可到分米级; 此外,由于卫星高度较高,星载激光雷达相邻光斑之间的距离可达到百米甚至千米,给其几何定标带来了很大的挑战[32]。
|
| 图 2 离散和全波形激光雷达回波波形 Fig. 2 Return signals of discrete LiDAR and full waveform LiDAR |
离散激光雷达点云数据中会存在各种噪声,斑点噪声、太阳背景噪声、探测器噪声,以及与时间和温度相关的噪声等,因此,点云去噪是离散激光雷达数据处理的重要步骤。首先要去除数值异常的数据点。例如,在月面测高的应用中,月球表面的高程范围在-10至+11 km之间[33],则在这个范围之外的数据点均被视为异常值而被去除。对于在正常范围内的激光点云数据,可以通过滤波的方式处理噪声。文献[34]基于均值和标准差设置阈值,先后沿着单个轨道和在局部区域内进行滤波。但基于均值的滤波会导致在大块平坦区域的少数凸起或者凹陷的数据点被消除,在去噪的同时也损失了一些信息,并且无法滤除连续分布的噪声。文献[35]提出了一种结合了滤波和聚类方法的去噪算法,计算数据点和均值的插值并通过K均值(K-means)聚类区分出信号点和噪声点,一定程度上克服了基于均值滤波的缺点。
由于卫星发射过程的震动和工作环境的变化,星载激光雷达测高仪的系统参数会较发射前的地面测量值有所改变,从而导致系统误差[36]。激光测高仪几何定标的目的就是减少或消除这些系统误差的影响。此类定标方法可以分为两种。一是与已知的自然地形相比较[37-38]。然而,这种方法要求卫星具有较为灵活的姿态机动能力,能够按要求完成对该自然地形的测量。二是基于地面控制点进行定标。这种方法需要布设大量的室外探测器(如激光靶标器)来捕捉来自卫星的激光信号,确定控制点的精确位置; 然后根据计算激光雷达所观测的光斑坐标和控制点坐标的差异,计算出几何定标参数,从而得到高精度的几何定位和测距结果[39]。使用定标场的方法能够得到较高的几何定标精度,但是地面定标场的建立耗时耗力。因此,提出了一些不依赖于定标场的几何定标方法。文献[40-41]利用已经公开的数字地形数据, 使用金字塔搜索将资源三号02星的激光数据与参考数据进行匹配,估计了激光测高仪的指向误差。文献[42]使用测距和轨道精度更高的月球轨道器激光测高仪(LOLA)数据作为基准,对嫦娥一号离散激光数据可能存在的系统误差进行校正。此外,测绘卫星,如美国的火星和月球观测卫星、中国的高分七号等卫星上通常既有测高仪也有摄影机,因此,两种数据的精确地理配准也成为一个基本的研究内容[43-44]。
星载离散激光测高仪获取的大量点云数据可以通过内插计算生成DEM。目前常见的离散点数据插值方法包括克里金(Kriging)插值法[45]、改进谢别德(Shepard)法(即距离反比加权平均法[46])、径向基(核)函数法(Radial Basis Function)[47]、移动最小二乘法[48]等。例如从嫦娥一号(CE-1)的激光点云中,可以提取整个月球的DEM。文献[34]提出了分层多节点样条估计法,利用CE-1点云数据生成了0.625°×0.625°分辨率的月球全球DEM。文献[49]首先对离散点云数据进行合并和简化,筛选出曲率变化较快的点,然后通过曲面蒙皮(surface skinning)重构算法生成DEM,该方法能够保留更多的细节信息。
2.2 全波形激光雷达数据处理全波形激光雷达系统采用波形的形式记录接收到的后向散射能量随时间的变化。在激光光斑覆盖范围内,具有复杂空间结构的目标与雷达发射的脉冲相互作用。全波形激光雷达系统接收目标的后向散射脉冲,以极短时间间隔对该脉冲的强度进行采样和量化,从而采集到波形数据。与离散激光雷达系统记录的点云数据相比,全波形数据所探测的目标信息更加丰富[50]。如图 2所示,离散激光雷达能够采集的回波脉冲及其强度信息比较有限,而全波形激光雷达则可以得到完整的回波形态。激光雷达系统发射的脉冲波形一般为高斯函数形式[51],结合激光雷达方程,接收的回波Pr(t)可视为描述散射体的后向散射特性的方程与所发射脉冲的卷积[52],即
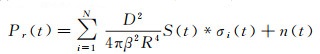 (1)
(1)
式中,N表示光斑范围内目标的个数; R是接收机到目标的距离; β为发射器波束宽度; D为接收器光学元件的光圈直径; S(t)是激光雷达系统贡献的部分,即为发射脉冲与接收器脉冲响应方程的卷积; σi(t)为第i个目标的散射特性描述函数; n(t)为噪声信号。激光雷达光斑覆盖区域的每个散射目标分别贡献出不同的波形分量,雷达最终接收到的回波可视为不同波形分量叠加的结果。通过对波形的分解,可以提取出每个波形的振幅、脉冲宽度和时间、峰值位置、峰值之间的距离以及后向散射截面等信息[53-54]。
为了提高后续波形分解方法的准确度,需要对波形数据进行预处理。其包括3个步骤,即:背景噪声的估计与去除、波形数据平滑和信号起始点和终止点估计[55-56]。首先,全波形激光雷达系统对后向散射回波进行采样和数字量化,记录后向散射回波脉冲的强度。由于该强度值会受到噪声的影响,需对其进行滤波处理。噪声来源主要有两方面,一是由于采样导致的强度信息量丢失,进而引起振铃噪声; 二是光电探测器中的暗电流[57],会降低信噪比。因此,为了能够准确地分解回波波形信息,需要先对噪声进行估计和去除。通常可通过设定阈值的方法来区分回波信号和噪声,回波强度低于阈值的部分被视为噪声去除,高于阈值的部分则作为信号保留下来。波形粗糙的形状容易导致分解出很多低强度窄波段的分量,因此需要对波形进行平滑处理,例如使用宽度与发射激光脉冲宽度近似的高斯滤波[58]。平滑后即可获取信息起始点和终止点的位置,回波强度大于背景噪声阈值的首个和最后一个位置即为该波形的起始点和终止点,常见的阈值设置为均值加标准差的3~4.5倍[59]。如同离散激光雷达一样,全波形激光雷达也需要进行定标。由于在森林茂密地区很难有可见的地面标志点,定标尤其困难; 为此,文献[60]研究了仅利用已知的数字地面模型,通过对由全波形数据动态产生的数字表面模型实施多次迭代滤波,来标定全波形激光扫描仪的自检校方法。
对于理想的平坦区域,激光雷达可以接收到近似于单个高斯回波波形。然而,在星载激光雷达光斑范围内,目标往往具有多样的垂直结构,使得后向散射回波的波形变得复杂且具有多个峰值,因此波形分解是提取各个目标后向散射回波信息的必要步骤,对捕捉雷达覆盖区域内每个目标的垂直结构信息至关重要。目前比较常见的波形分解方法包括直接分解法和基于反卷积的方法。
(1) 直接分解法。此类方法将回波波形视为多个核函数叠加的结果,其中高斯核函数、小波变换最为常用,并通过拟合各个核函数分量的方式进行回波分解。尽管基于高斯函数的回波分解在平坦区域有较好的表现,然而,回波波形的分量也可能不符合高斯函数,尤其是对于目标的垂直空间结构复杂的区域,或激光照射到非平面或者有倾斜平面的目标时。这一问题可以通过使用广义高斯模型来解决
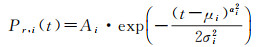 (2)
(2)
式中,Ai是第i个回波波形分量Pr, i(t)的振幅; μi为其均值,表示波形分量的位置; σi为标准差,决定了脉冲的宽度; αi为形状参数, 对于高斯函数,αi=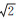
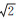
文献[61]提出了分解机载激光雷达回波数据的方法,假设各个分量均为高斯模型,根据连续拐点位置估计得到高斯模型系数的初值并进行参数优化。这个方法被NASA用于GLAS星载激光雷达波形的分解,得到GLA14产品。文献[62]分别使用高斯和广义高斯核函数来分解回波波形,并比较它们的分解效果; 研究表明,其不仅能够测量树冠高度,同时还可以捕捉到树冠内部和低层植被的结构信息。对于植被密集的区域,广义高斯函数能够取得比高斯函数更好的结果,减少对树高的低估。此外,还有研究用小波变换来分解回波波形。文献[63]提出了一种基于多尺度小波分析的波形分解算法,并应用于ICESat卫星获取的GLAS数据,最后从分解的波形各个分量中估算平均树高。与从采用高斯函数拟合的GLA14产品[61]中估算的平均树高对比表明,对于双峰或者多峰的波形,基于小波变换的分解方法得到的平均树高估计比高斯核函数拟合的方法更加准确。
目前,较为常用的核函数拟合方法包括极大似然估计法和非线性最小二乘法,例如期望值最大化(Expectation-Maximization)算法[64]、列文伯格-马夸尔算法(Levenburg-Marquardt)[61]等。这两种方法均需要预先估计回波波形的性质,如波形分量的个数、各个分量的强度和波形宽度等。文献[65]使用基于熵的赤池信息量准则(Akaike's Information Criterion)来估计回波组分的数量,文献[66]提出了一种渐进式波形分解法来自动检测出每个波峰的位置,从而得到回波组分的个数,然后进行逐一拟合,避免了初始化。然而在缺乏叠加的回波波形的先验知识的前提下,难以对这些波形分量参数做出准确的估计, 尤其是对于组分复杂的回波波形更是如此。除了会受到严格的初始化条件的限制,直接分解法还难以处理无法采用高斯函数等核函数进行建模的复杂波形分量,并且没有考虑探测器系统对波形的影响,不能反映目标的真实截面信息[67]。文献[19]用模糊统计聚类的方法对全波形数据进行分解和确定散射目标, 获得了比常规高斯函数分解更好的结果。
(2) 反卷积法。该方法试图解决上述直接分解法存在的问题。如前所述,激光雷达接收器接收到的回波信号可以视作为系统发射的脉冲信号、接收器脉冲响应和目标后向散射截面相互卷积的结果。在已知回波信号和系统贡献的情况下,反卷积法考虑回波信号中发射脉冲和系统脉冲响应部分的共同作用,即式(1)中的S(t),进而得到目标的后向散射截面σ(t)[52, 68]。从反卷积的结果中可以提取特征并用其进行分类,例如文献[69]将主成分分析法用于反卷积得到的波形,对草本植物的生物量进行分类。文献[67]采用自动波峰检测等方法对反卷积结果进一步分解,提取每个波形分量的振幅、位置和拐点。3种最为常用的反卷积算法为:Richardson-Lucy方法[70-71]、维纳滤波[72]和非负最小二乘法[73]。
Richardson-Lucy算法最初是为图像恢复而设计的,通过迭代来解求反卷积问题。该反卷积方法基于贝叶斯定理,将激光雷达回波看作大小为1×L(L为回波波形的总时间长度)的影像,对给定时刻t,利用系统贡献项S(t)和接收的回波信号Pr(t),通过以下迭代计算σ(t)最可能的估计值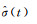
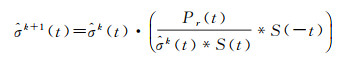 (3)
(3)
式中,k是迭代次数,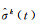
Richardson-Lucy算法对于低信噪比的回波信号有较好的分解效果,可以有效避免产生负值,然而,该算法收敛速度慢,迭代的求解方式较为耗时,并且无法防止噪声的扩大。基于噪声和信号在统计上相互独立的假设,维纳滤波在频率域对发射和接收的回波信号比值进行滤波处理,并使得到的目标散射截面估计值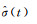
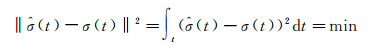 (4)
(4)
维纳滤波反卷积算法的优势在于计算速度快,但容易导致振铃噪声,无法避免无意义的负信号值的产生,并且需要噪声的功率谱密度[75]。基于非负最小二乘法的反卷积算法可以描述为
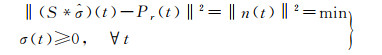 (5)
(5)
该算法不需要关于目标散射截面σ(t)和噪声信号n(t)的任何先验知识,可以通过迭代使得目标函数收敛求解σ(t),结果较为准确,但缺点是迭代会造成较高的时间计算代价。
2.3 光子计数激光雷达数据处理光子计数激光雷达的接收器能够灵敏地探测到单个光子,得到密度较高的光子点云,从而能够获取更加精细的三维信息。与线性探测激光雷达相比,光子计数激光雷达具有低能量、高灵敏度、高重复频率的优势[76],降低了高脉冲能量对于系统的损耗,为解决能量传输和高重复频率之间的矛盾提供了新的解决思路。然而,低脉冲能量和高灵敏度同时也会带来一些问题,如光子计数激光雷达发射和接收的信号都比较弱,非常容易受到各种噪声的影响,如系统噪声、大气散射引起的噪声以及太阳背景光[4]。光子噪声在空间中随机分布且数量众多,给光子计数激光雷达数据的处理和垂直结构信息的精确提取带来了挑战[77]。因此,需要采用有效的去噪方法,将信号从噪声中分离出来。去噪是光子计数激光点云数据处理的关键步骤,常见的去噪方法可以被分为基于密度聚类的算法、基于栅格化的算法及基于局部统计量的算法。
基于密度聚类的算法利用激光雷达探测到的光子的空间分布特点。目标散射的信号光子往往比噪声光子的分布更加密集,由此可以通过对光子进行空间聚类来将其与噪声分开。可以使用的空间聚类方法包括:DBSCAN(density-based spatial clustering of applications with noise)[78-79]、OPTICS(ordering points to identify the clustering structure)[80]、贝叶斯决策理论等。文献[81]将DBSCAN算法应用于光子点云去噪,对于点云中的每个点,采用椭圆邻域进行聚类,以便更适用于光子计数雷达点云在沿轨方向分布较密集的特征,从而使得计算代价大幅降低。尽管DBSCAN算法在平坦的区域能够有效去噪,但对陡峭的区域的效果则较差; 并且,DBSCAN算法需要指定搜索半径和最少点数,这两个参数对聚类结果影响很大。OPTICS算法是DBSCAN算法的扩展,与DBSCAN不同的是,OPTICS不直接产生聚类结果,而是计算得到所有光子的簇排序和距离值来表示光子的内在聚类结果。注意到光子点云的数据特点,文献[82]在应用OPTICS聚类算法时进行了改进,使用椭圆邻域,并根据大津法[83]选取阈值区分信号和噪声光子,在模拟和真实的ICESat-2数据上的试验表明该方法比同样使用椭圆邻域的DBSCAN算法的效果更好,并且对聚类参数不敏感,但是仍然需要指定搜索区域的大小。文献[84]提出了一种基于贝叶斯理论单光子激光雷达去噪算法,考虑近邻距离的概率分布并通过贝叶斯决策理论计算光子属于噪声的概率,该方法在地形陡峭地区的去噪效果优于改进的DBSCAN算法,但是需要预先估计信噪比。总体来说,基于密度聚类的方法需要预先指定一些输入参数,并对参数敏感、时间代价往往较大。
基于栅格化的算法先将光子计数激光雷达的点云剖面内插成栅格图像,然后使用数字图像处理中的去噪方法去除噪声光子。文献[77]提出了基于改进的Canny边缘检测的去噪方法,对栅格化的光子点云提取边缘特征,根据数据内部的差异确定梯度阈值,结果表明该算法能够有效地去除森林区域的噪声。从而更准确地提取地面和树冠。然而,从光子点云到栅格图像的转化过程会导致部分信息的损失[85]。同时,基于密度和栅格的去噪算法还存在一些问题,如在点云密度较小或者噪声光子的位置和信号光子比较接近的时候,信号可能会作为噪声被去除或者不能有效地区分信号与噪声[86]。
基于局部统计量的方法从光子点云数据中提取一些局部统计量,例如特征向量、点云的密度、高程等,并根据这些统计量的分布特征(如直方图)来设置区分信号和噪声的阈值。文献[87]使用一系列统计量,包括径向基函数、几何各向异性、特征向量、点云密度,以及地学统计学分类参数和超参数等,来检测地面和冠层覆盖信号以及噪声。文献[88]基于光子的高程设置阈值来检测噪声。文献[89-90]提出的光子点云去噪算法从高程和密度两方面计算局部统计量,并且考虑到了表面坡度。该方法首先建立高程直方图来消除明显的噪声光子,然后根据光子在沿轨方向和高程方向的距离来确定用于密度统计的椭圆邻域的参数(如椭圆的方向),最后通过密度直方图去除剩下的噪声。与基于栅格化的算法相比,基于局部统计量的算法在大型数据集上的计算更加鲁棒,适用于多种地形环境,但是去噪过程中的阈值需要考虑到地表特征、点云密度、地形等因素来设置,并且阈值对去噪结果的影响较大[6]。
3 星载激光测高应用星载激光雷达搭载在卫星平台上,具有运行轨道高、观测视野广的特点,适合林业、海洋、极地、月球、火星和小行星探测等[91]。需要说明的是,由于星载激光雷达的地面分辨率限制,在全球地表测绘中,主要作用是为其他光学遥感数据提供控制信息[92]; 与其他遥感手段相比,星载激光雷达目前其尚不能提供具有优势且满足要求的数字地面模型产品。因此,将针对星载激光雷达在林业生态、极地海洋和行星探测三个领域的应用进行讨论。
3.1 在林业生态测量中的应用(1) 树高估算。ICESat上的GLAS是第一个用于全球连续对地观测的星载激光雷达测高仪。GLAS记录从其光斑路径上返回的激光能量[93],可以获取大范围的垂直数据信息,因此在大区域尺度对森林参数进行定量反演具有优势[7]。在平坦地区(0~5°),坡度对回波信号造成的影响较小。因此在平坦地区树高可以直接使用GLAS的波形数据进行估测。然而,当GLAS激光较大的光斑(直径约为70 m[94])照亮在倾斜表面上的植被时,接收到的脉冲回波波形会变宽[95],因此从ICESat数据中估计可靠的森林高度变得复杂[96]。文献[96]基于GLAS波形数据提出了地形指数模型,以期对大坡度上的树高度反演获得好的效果。考虑到波形前缘长度(即从信号开始到第一个波峰的波形长度),其使用了以下修正后的模型
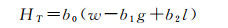 (6)
(6)
式中,HT是测量的树冠高度; b0是当根据地形指数进行校正时的综合系数; w是波形长度; b1是应用于地形指数的系数; g是地形指数,即在DEM数据中的N×N采样窗口内的地表高程差值; b2为波形前缘调整系数; l为波形前缘长度。
文献[97]基于GLAS完整波形在吉林长白山林区以激光波形长度和地形指数为变量,在不同地形坡度范围内建立了森林冠层高度反演模型。在ArcGIS平台上利用1∶50 000 DEM数据计算地形指数:计算以激光光斑中心点所在像元为中心的矩形3×3窗内最大高程与最小高程之差,并将这个差值赋给该窗口的中心像元,作为该像元对应的地形指数g。模型参数b0和b1采用Levenberg-Marquardt (LM)算法求解。研究结果表明,在0~5°坡度范围内建立的模型与90%的冠层高度相吻合; 但随着坡度的增加,该模型的反演精度会显著下降。
(2) 郁闭度估算。森林郁闭度(crown density)是指林冠垂直投影面积与林地面积的比值[98]。它是森林资源调查的一个重要因子,通过该因子可以区分有林地、疏林地和无林地。
GLAS发射的激光脉冲穿过大气层后首先会到达森林冠层,一部分被反射回传感器,另一部分会继续向下传播,透过叶片缝隙到达地面,并被地面反射。因此可以通过计算植被回波能量与回波总能量的比值来对森林郁闭度进行估测[95]
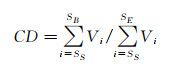 (7)
(7)
式中,CD为从GLAS波形中提取的比值能量参数,用于估测森林郁闭度; SS为信号开始位置; SE为信号结束位置; SB为冠层回波和地面回波的界限位置; Vi为第i帧对应的回波能量值。
(3) 森林地上生物量估算。森林生物量按来源的部位不同可分为根、干、枝和叶生物量。其中, 干、枝、叶生物量合称为森林地上生物量[99]。森林地上生物量的估算对于陆地生态系统碳循环机制的研究具有重要意义[100]。目前大区域生物量研究采用的数据主要有光学遥感数据,激光雷达数据和微波数据等。星载激光雷达数据可以获取森林冠层高度信息,在大区域森林地上生物量研究方向上发挥了很大作用。从反演方法来看,目前研究所采用的方法以非参数化的训练方法为主[101]。文献[102]在印度西北喜马拉雅山使用随机森林算法,结合ICESat-2和Sentinel-1数据获取森林冠层高度,并将森林冠层高度信息与Sentinel-2数据结合对森林地上生物量(AGB)进行估测。文献[103]通过构建神经网络模型,利用MODIS和ICESat/GLAS数据估算西伯利亚北部森林地上生物量。文献[104]结合GLAS数据和HSI数据,使用支持向量回归机算法构建森林地上生物量估测模型,绘制吉林省汪清林业局经营区的森林地上生物量分布图。
3.2 在极地海洋测量中的应用(1) 海冰厚度估算。极地地区是全球最为重要的冷源,也是海冰分布最广泛的区域[105]。海冰覆盖可以阻隔海水和大气中的水汽交换等环节,对极地乃至全球的气候都会产生重要影响[106],故此计算海冰厚度是目前的一个重要研究内容[107]。
海冰可以视为由两部分组成,一部分为海面下的冰,另一部分为露出海面的部分。露出海面的冰层可以通过观测数据直接计算,而隐藏在海面下的冰,无法根据观测数据直接测量。因此对于整体海冰厚度的测量是根据阿基米德原理和浮出海面的冰层体积进行估算的。对露出海面的冰层计算海冰干舷高度HF,即海冰表面高与海面的差异[108],文献[109]使用ICESat-2数据对海冰干舷高度F进行计算,计算公式如下
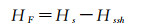 (8)
(8)
式中,Hs是由ICESat-2激光测高仪测量的海冰表面高程; Hssh是海面高,可以通过文献[110]提出的最低面滤波法来计算。其过程为,假设海面高程总是低于海冰表面高程,选取区域内测量高程值最低的部分作为海面高程值,通过使用ICESat潮汐修正后的测高数据减去大地水准面高后,按照10 km的轨迹长度选取其中最低的高程值作为海面高程。
计算出海冰干舷高度HF后,根据阿基米德原理,海冰厚度可以使用式(9)进行计算[111]
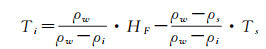 (9)
(9)
式中,Ti为海冰厚度; Ts为雪层深度; ρi为海冰密度; ρs为雪密度; ρw为海水密度。值得注意的是,式(9)考虑了露出海面的冰层有雪层覆盖的情况,是比较完整的海冰厚度估算的模型。
(2) 冰盖高程变化率估算。测高卫星绕地球一周产生的运动轨迹可分为上升弧段(自南向北)和下降弧段(自北向南),上升弧段和下降弧段的运动轨迹会产生交叉点。此外,测高卫星的运动轨迹还具有周期性重复的特点,即运行一段时间后,会出现重复的地面轨迹。因此,利用测高卫星在交叉点上或同一区域的重复观测,便可估算冰盖高程的变化率。
基于在交叉点重复观测得到的高程值,文献[112-113]应用最佳线性无偏估计与季节周期参数联合计算交叉点处的高程变化率
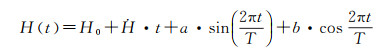 (10)
(10)
式中,H(t)表示在时间t时, 由ICESat观测值内插成的交叉点处高程; H0为t=0时交叉点的高程; 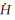
此外,也可以利用周期性重复的地面轨迹来计算冰面表面高程变化率。由于卫星受到轨道摄动等因素影响,不同周期的轨道并不会完全重复,为了避免重复轨道地面光斑不重合造成的误差,可以将各个重复轨道数据内插到同一位置进行计算。考虑到内插点和地面光斑之间的坡度,应当对内插点的高程进行坡度改正[114]。
(3) 水深估测。ICESat-2携带的ATLAS是具有绿色波段(532 nm)和10 kHz脉冲重复率的光子计数激光雷达。ATLAS提供了一种主动探测水深的方式,它能够沿地球轨道方向以高分辨率穿透水体[115]。但是生成光子测高数据的算法并未考虑到空气-水界面处发生的折射和水柱中光速的影响,因此ATL03中记录的数据会产生水平和垂直上的误差,需要进行折射校正,如式(11)所示[116]
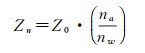 (11)
(11)
式中,Zn是经折射校正后的水深; Z0是无折射改正时计算的水深; na(1.000 29)、nw(1.341 16)分别是光在空气和海水中的折射率。文献[116]结合Sentinel-2光学数据和折射校正后的ICESat-2数据,使用半经验函数对水深进行拟合,得出南海六个岛礁的浅水深度(深度 < 20 m)。
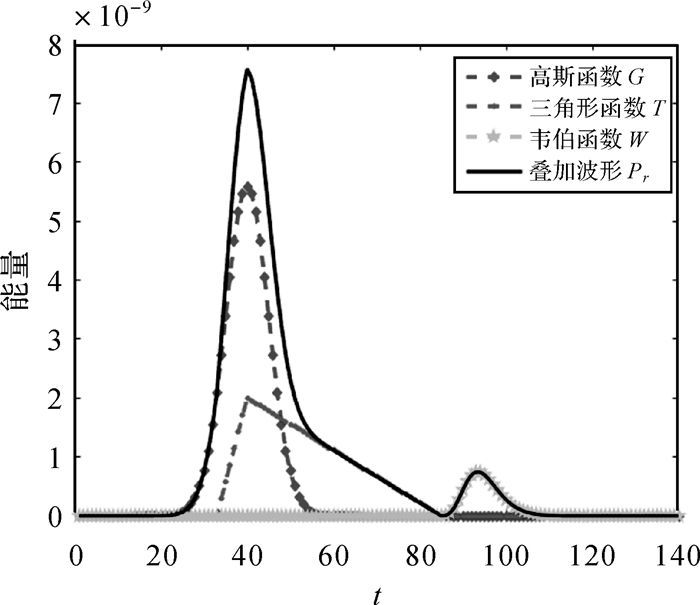
水深也可以使用全波形数据进行检测。如图 3所示,文献[117]用高斯函数、三角形函数和韦伯(Weibull)函数的叠加来拟合发射脉冲经过水体反射的回波波形Pr(t)
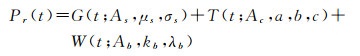 (12)
(12)
式中,G(t; As, μs, σs)为高斯函数; As是振幅; μs是发射脉冲到达水面的时刻; σs是标准差
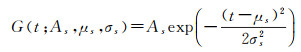 (13)
(13)
T(t; Ac, a, b, c)为由参数Ac, a, b, c定义的三角形函数
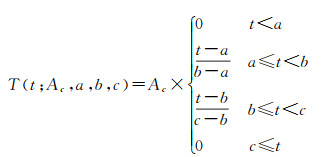 (14)
(14)
W(t; Ab, kb, λb)是振幅为Ab的韦伯函数
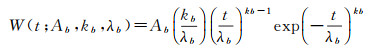 (15)
(15)
式中,λb为韦伯函数的比例参数,描述发射脉冲到达水底的时刻; kb为韦伯函数的形状参数。使用非线性最小二乘法对式(15)进行求解得到拟合参数。然后利用拟合参数对水深De进行计算,计算方法如下[61]
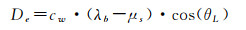 (16)
(16)
式中,cw为光在水中的速度; (λb-μs)描述的是发射脉冲从水面到达水底的时间; θL为局部入射角,其值取决于传感器的入射角、水的折射率以及水面和底面的坡度。
3.3 在行星测绘中的应用尽管星载激光测高可以用于对地观测的高程测量中,但由于其在垂直轨道方向尚无常规意义下的扫描功能,分辨率较低,再加之有很多基于星载和机载的光学和微波成像测量手段,因此,目前利用星载激光测高的地形测绘和数字地面模型的建立主要集中在对行星(含月球)进行测量。
行星测量往往是由月球测量开始的。月球地形是描述月球基本特征的重要参数。月面高程值主要是根据激光测高、轨道和姿态数据来进行计算。首先要计算观测时刻光斑中心点的位置,计算公式为[118]
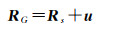 (17)
(17)
式中,RG表示光斑在月心坐标系中的位置矢量; Rs表示观测时刻卫星在月心坐标系下的位置矢量,可由卫星高精度轨道给出; u由激光测高仪的测距值和姿态数据确定,表示观测时刻激光测高仪的观测矢量。利用上述得到的RG值,可以对月面光斑中心点对应的月面高程值进行计算,公式为
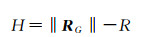 (18)
(18)
式中,H为月面高程值; R为月球参考半径, 如选择半径为1738 km的正球作为参考球体,将该正球体表面定义为月面高程基准面。
在月球探测方面,各国利用激光测高数据生成了若干数字高程模型。文献[118]利用嫦娥一号第一次正式飞行阶段获取的约300多万个有效激光测高数据点, 得到了月球全球地形模型CLTM-s01。文献[119]利用嫦娥一号获取的数据制作了空间分辨率为3 km的全月DEM模型。文献[120]应用高分辨率的GRAIL(Gravity Recovery and Interior Laboratory)重力场模型和LOLA激光测高数据对月球岩石圈有效弹性厚度进行估计。文献[121]利用选取的嫦娥一号测高地形数据及Lunar Prospector月球重力场模型作为数据源建立了月球三轴椭球体模型。文献[122]使用日本月球探测器Selenological and Engineering Explorer (SELENE或Kaguya)上的激光高度计(LALT)的测高数据,获得了空间分辨率优于0.5°的全球月球地形图。文献[123]使用SELENE上的激光测高仪数据制作的数字高程模型来估计月球极地地区的日照条件。文献[124]使用LOLA获得的高分辨率测高数据来表征月球极地地区的光照条件,并展示了两个极点在很长一段时间内的平均太阳照度模拟结果。
在火星探测方面,MOLA测高仪[125]可以测量地形、表面反射率和后向散射激光回波宽度,非常适合计算火星表面地形和粗糙度。文献[126]利用火星全球测绘卫星(MGS)上的激光测高仪MOLA数据,通过交叉点法确定行星表面高程变化来研究火星以前是否存在海洋。文献[127]利用MOLA在一个火星年内收集的地形数据来测量火星表面海拔随时间的变化。文献[128]通过自动配准后的MOLA剖面绘制火星极地季节性二氧化碳雪盖和二氧化碳冰盖高度随时间的变化图。
在水星探测方面,文献[129]通过测量水星激光测高仪(MLA)在1064 nm处的表面反射率,证明水星在其两极附近的永久阴影区域(PSR)内存在水冰。文献[130]使用均方根差来计算水星表面粗糙度。
在获得行星表面数字高程后,可以进而计算地形的一些数字特征。表面粗糙度是在去除大尺度坡度的影响后,在某个给定水平尺度上,表面高度变化的统计量度,可用于了解地质过程如何在不同尺度上形成和改变行星的地形特征。文献[131]提出了中位差坡度的测量方法,目的是分出小尺度和大尺度坡度对表面粗糙度的影响。对于一定的水平基线L,通过减去该给定基线两倍处的坡度来分离出基线L上的粗糙度特征sd(L)
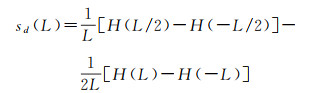 (19)
(19)
式中,H(L)和H(-L)分别为兴趣点两侧距离为L处的高程。
4 总结与展望20世纪70年代以来,作为一种主动卫星遥感技术,星载激光雷达的发展与应用一直都得到了各国的关注。尤其是近些年来,随着各科学领域对高精度测量需求的日益增长,星载激光测高技术因其独特的特点与优势得到了迅猛的发展。经过多年的探索,美国在对地观测以及对行星探测方面都有着较为成熟的应用,在星载和机载光子计数激光雷达测高技术领域更是处于领先地位。日本和欧洲在对行星探测领域也都有多年的积累,如日本航天局(JAXA)在2007年对月观测的SELENE激光测高仪,以及欧洲航天局(ESA)于2018年开展的水星探测计划用的BepiColombo激光测高仪(BELA)。从2007年嫦娥一号对月成功观测开始,到2019年高分七号成功获取数据,中国的星载激光测高技术在一系列国家重大科学研究和工程应用中取得了令人瞩目的成就,并且对当前和未来的深空探测计划和对地观测重大基础设施建设提供了宝贵的经验。
可以预见的是,星载激光雷达测高技术将会朝着更高的空间分辨率、更高的测量精度以及更高的量测效率发展; 与此同时,测绘和探测的对象也会更加多样。归纳起来,有以下几个方面。
(1) 研制新型星载激光器和探测器。①研制高能量窄脉宽的新型激光器,更有效地抑制背景噪声光子,提高激光增益、重复频率和电光转换的效率,降低量子亏损以及对激光器的体积和重量的需求。②研制单个激光器的多波束激光并行发射技术,增加波束数量,减小波束地面光斑的大小和其间的距离,增大幅宽,提高空间分辨率和观测效率; 研究采用阵列探测器同时接收多波束激光的回波,提高阵列探测器的灵敏度和响应,降低单个波束的所需的能量。③研制高效的多波段(多光谱)激光器,丰富激光器发射脉冲的频域特性,实现在多个光谱波段的同时探测,从而更有效地识别目标及其属性; 提高探测器在不同波长下的量子效率,研发基于新型材料的探测器,将单光子探测器所能够探测的可见光波段扩展为1~2 μm的近红外波段; 由于波长的增大,在相同能量下发射的脉冲可以包含更多的光子,在近红外波段目标反射回去的光子一般也会更多,使得同等灵敏度的探测器对单波束的能量需求将降低,有利于进一步增加波束数。④研究星载量子激光雷达,结合量子特性和量子力学原理,将已有的光子计数激光雷达与量子调控相结合,利用纠缠光子对进行量子测距,突破激光雷达在激光器信噪比、探测器灵敏度、在复杂环境中的抗干扰性能等方面的瓶颈,并逐步将单纯的距离测量扩展到全息测量,如物体的速度、相位和形变等。
(2) 发展卫星组网激光测高增强方法。①由于星载多波束的光子计数激光雷达探测到的噪声较多,不仅需要大量存储资源,也会受到传输效率限制无法及时传至地面站,因此有必要和其他卫星,如气象和环境卫星组网,测高卫星实时获得这些卫星上的相关数据进行测高信号检测和噪声去除,减小存储和下传数据,同时获得更可靠更有效的观测数据。②为提高星载激光雷达的测距精度,需要发展更加有效的方法来消除光行差和噪声的影响,提高激光雷达卫星本身的位置精度; 为此可以利用在低轨道平台运行的其他卫星系统,比如通信卫星,消除GNSS的系统误差,从而提高激光雷达卫星的定位精度,提升卫星到地面的测距精度, 以期将星载测距精度提高到厘米级,位置精度提高到分米级。
(3) 拓展星载激光测高的科学和工程应用。①星载激光雷达可快速获取大规模高精度的海面测高数据,结合海面地形精确计算大地水准面高程,同时提高该高程估算值的时间和空间分辨率,通过反演得到更精细准确的海洋和全球重力场,同时为重力异常的监测和重力分布数据的及时更新提供有效途径。②尽管目前的激光雷达卫星可以提供大量的观测数据,然而单个激光雷达测高卫星的时间、空间分辨率和覆盖率都是有限的,无法实现全球范围内的重复和高分辨率测量。因此,有必要研究不同星载激光雷达测高数据的联合处理以及数据同化技术,研发相应的数据配准和融合方法,消除不同激光雷达卫星之间的系统差异,从而提供一致和完整的数据产品,实现更高频率的全球测高。另外,也有必要融合星载激光雷达数据与光学、微波观测数据,发挥各自的优势,利用多源信息的融合实现对目标更全面和准确的描述。③尽管星载激光雷达发射的信号强度是固定的,由于大气分子和具有不同特性的目标的散射和吸收,返回激光雷达接收器的能量强度会存在差异。目前的光子计数激光雷达仅记录了从目标返回的光子数,而忽略了后向散射的强度信息。然而,后向散射强度能够反应目标的空间结构、几何形态、材料等特性,是值得关注和挖掘的信息。可以从两个方面实现对激光后向散射强度的度量,一是对同一区域返回的光子进行累积,通过累计的光子密度反映该目标的后向散射性质; 二是发展量子激光雷达,测量后向散射激光振幅和相位,并用纠缠光子对间的强度相关性表示目标的后向散射性质。④星载激光测高技术目前已应用于月球、火星、水星,还可以进一步开发其在深空探测领域的应用潜力,如对其他行星的观测,获取行星表面的地形和粗糙度信息。此外,星载激光雷达还可以应用于太空碎片的探测,迅速对太空碎片进行定位,满足远距离、高精度的探测需求。
| [1] |
SHAN J, TOTH C K. Topographic laser ranging and scanning: Principles and processing[M]. 2nd ed. Boca Raton: CRC Press, 2018.
|
| [2] |
于真真, 侯霞, 周翠芸. 星载激光测高技术发展现状[J]. 激光与光电子学进展, 2013, 50(2): 020006. YU Zhenzhen, HOU Xia, ZHOU Cuiyun. Progress and current state of space-borne laser altimetry[J]. Laser & Optoelectronics Progress, 2013, 50(2): 020006. |
| [3] |
唐新明, 李国元, 高小明, 等. 卫星激光测高严密几何模型构建及精度初步验证[J]. 测绘学报, 2016, 45(10): 1182-1191. TANG Xinming, LI Guoyuan, GAO Xiaoming, et al. The rigorous geometric model of satellite laser altimeter and preliminarily accuracy validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1182-1191. DOI:10.11947/j.AGCS.2016.20150357 |
| [4] |
TIAN Xiangxi, SHAN Jie. Comprehensive evaluation of ICESat-2 ATL08 terrain product[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(10): 8195-8209. DOI:10.1109/TGRS.2021.3051086 |
| [5] |
LI Qinghua, DEGNAN J J, BARRETT T, et al. First evaluation on single photon-sensitive LiDAR data[J]. Photogrammetric Engineering and Remote Sensing, 2016, 82(7): 455-463. DOI:10.14358/PERS.82.7.455 |
| [6] |
朱笑笑, 王成, 习晓环, 等. ICESat-2星载光子计数激光雷达数据处理与应用研究进展[J]. 红外与激光工程, 2020, 49(11): 20200259. ZHU Xiaoxiao, WANG Cheng, XI Xiaohuan, et al. Research progress of ICESat-2/ATLAS data processing and applications[J]. Infrared and Laser Engineering, 2020, 49(11): 20200259. |
| [7] |
庞勇, 李增元, 陈博伟, 等. 星载激光雷达森林探测进展及趋势[J]. 上海航天, 2019, 36(3): 20-27. PANG Yong, LI Zengyuan, CHEN Bowei, et al. Status and development of spaceborne LiDAR applications in forestry[J]. Aerospace Shanghai, 2019, 36(3): 20-27. |
| [8] |
岳春宇, 郑永超, 邢艳秋, 等. 星载激光遥感林业应用发展研究[J]. 红外与激光工程, 2020, 49(11): 20200235. YUE Chunyu, ZHENG Yongchao, XING Yanqiu, et al. Technical and application development study of space-borne LiDAR in forestry remote sensing[J]. Infrared and Laser Engineering, 2020, 49(11): 20200235. |
| [9] |
唐新明, 刘昌儒, 张恒, 等. 高分七号卫星立体影像与激光测高数据联合区域网平差[J]. 武汉大学学报(信息科学版), 2021, 46(10): 1423-1430. TANG Xinming, LIU Changru, ZHANG Heng, et al. GF-7 satellite stereo images block adjustment assisted with laser altimetry data[J]. Geomatics and Information Science of Wuhan University, 2021, 46(10): 1423-1430. |
| [10] |
舒嵘, 黄庚华, 孔伟. 空间激光测高技术发展及展望[J]. 红外与激光工程, 2020, 49(11): 20201047. SHU Rong, HUANG Genghua, KONG Wei. Development and review of space-based laser altimetry technology[J]. Infrared and Laser Engineering, 2020, 49(11): 20201047. |
| [11] |
郭商勇, 胡雄, 闫召爱, 等. 国外星载激光雷达研究进展[J]. 激光技术, 2016, 40(5): 772-778. GUO Shangyong, HU Xiong, YAN Zhaoai, et al. Research development of space-borne LiDAR in foreign countries[J]. Laser Technology, 2016, 40(5): 772-778. |
| [12] |
SCHUTZ B E, ZWALLY H J, SHUMAN C A, et al. Overview of the ICESat mission[J]. Geophysical Research Letters, 2005, 32(21). |
| [13] |
COYLE D B, STYSLEY P R, POULIOS D, et al. Laser transmitter development for NASA's Global Ecosystem Dynamics Investigation (GEDI) LiDAR[C]//Proceedings of 2015 SPIE of 9612, LiDAR Remote Sensing for Environmental Monitoring XV. San Diego, CA: SPIE, 2015: 961208.
|
| [14] |
MANDLBURGER G, LEHNER H, PFEIFER N. A comparison of single photon and full waveform LiDAR[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2019, Ⅳ-2/W5: 397-404. |
| [15] |
ULLRICH A, PFENNIGBAUER M. Linear LIDAR versus Geiger-mode LIDAR: Impact on data properties and data quality[C]//Proceedings of 2016 SPIE 9832, Laser Radar Technology and Applications XXI. Baltimore, MD: SPIE, 2016: 983204.
|
| [16] |
USSYSHKIN V, THERIAULT L. Airborne LiDAR: advances in discrete return technology for 3D vegetation mapping[J]. Remote Sensing, 2011, 3(3): 416-434. DOI:10.3390/rs3030416 |
| [17] |
WANG Cheng, LUO Shezhou, XI Xiaohuan, et al. Influence of voxel size on forest canopy height estimates using full-waveform airborne LiDAR data[J]. Forest Ecosystems, 2020, 7: 31. DOI:10.1186/s40663-020-00243-2 |
| [18] |
郭金权, 李国元, 左志强, 等. 高分七号卫星激光测高仪全波形数据质量及特征分析[J]. 红外与激光工程, 2020, 49(S2): 20200387. GUO Jinquan, LI Guoyuan, ZUO Zhiqiang, et al. Full waveform data quality and characteristic analysis of GF-7 satellite laser altimeter[J]. Infrared and Laser Engineering, 2020, 49(S2): 20200387. |
| [19] |
LI Qinghua, URAL S, ANDERSON J, et al. A fuzzy mean-shift approach to LiDAR waveform decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7112-7121. DOI:10.1109/TGRS.2016.2596105 |
| [20] |
TANG Xinming, XIE Junfeng, LIU Ren, et al. Overview of the GF-7 laser altimeter system mission[J]. Earth and Space Science, 2020, 7(1): e2019EA000777. |
| [21] |
PRIEDHORSKY W C, SMITH R C, HO C. Laser ranging and mapping with a photon-counting detector[J]. Applied Optics, 1996, 35(3): 441-452. DOI:10.1364/AO.35.000441 |
| [22] |
STOKER J M, ABDULLAH Q A, NAYEGANDHI A, et al. Evaluation of single photon and Geiger mode LiDAR for the 3D elevation program[J]. Remote Sensing, 2016, 8(9): 767. DOI:10.3390/rs8090767 |
| [23] |
SUN Xiaoli, ABSHIRE J B, BORSA A A, et al. ICESat/GLAS altimetry measurements: received signal dynamic range and saturation correction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5440-5454. DOI:10.1109/TGRS.2017.2702126 |
| [24] |
MARTINO A J, NEUMANN T A, KURTZ N T, et al. ICESat-2 mission overview and early performance[C]//Proceedings of 2019 SPIE 11151, Sensors, Systems, and Next-Generation Satellites XXⅢ. Strasbourg, France: SPIE, 2019: 111510C.
|
| [25] |
Harris. Website of Harris Geiger-mode LiDAR[EB/OL]. [2022-02-15]. https://www.harris.com/solution/geiger-mode-lidar.
|
| [26] |
Leica. Leica SPL100 single photon LiDAR sensor data sheet[EB/OL]. [2022-02-15]. https://leica-geosystems.com/en-us/products/airborne-systems/topographic-lidar-sensors/leica-spl100.
|
| [27] |
屈鹏飞, 王石语, 邵新征, 等. Nd: YAG/Nd: YVO4组合晶体激光器温度稳定性研究[J]. 光学学报, 2017, 37(6): 0614001. QU Pengfei, WANG Shiyu, SHAO Xinzheng, et al. Temperature Stability of Nd: YAG/Nd: YVO4 Combination Crystals Laser[J]. Acta Optica Sinica, 2017, 37(6): 0614001. |
| [28] |
DEGNAN J J. Scanning, multibeam, single photon lidars for rapid, large scale, high resolution, topographic and bathymetric mapping[J]. Remote Sensing, 2016, 8(11): 958. DOI:10.3390/rs8110958 |
| [29] |
FRIED D G. Fast, Cost-Efficient Airborne 3D Imaging with Geiger-mode Detector Arrays[J]. MIT RLE & 3DEO, Inc. ILMF 2015, Denver, CO.
|
| [30] |
YANG Guangming, MARTINO A J, LU Wei, et al. IceSat-2 ATLAS photon-counting receiver: initial on-orbit performance[C]//Proceedings of 2019 SPIE 10978, Advanced Photon Counting Techniques XⅢ. Baltimore, MD: SPIE, 2019: 109780B.
|
| [31] |
岳春宇, 孙世君, 何红艳. 一种星载激光测高仪光斑内定位方法[J]. 武汉大学学报(信息科学版), 2019, 44(4): 586-592. YUE Chunyu, SUN Shijun, HE Hongyan. A positioning method in footprint of space-borne laser altimeter[J]. Geomatics and Information Science of Wuhan University, 2019, 44(4): 586-592. |
| [32] |
SHAN Jie, YOON J S, LEE D S, et al. Photogrammetric analysis of the mars global surveyor mapping data[J]. Photogrammetric Engineering and Remote Sensing, 2005, 71(1): 97-108. DOI:10.14358/PERS.71.1.97 |
| [33] |
SMITH D E, ZUBER M T, NEUMANN G A, et al. Summary of the results from the lunar orbiter laser altimeter after seven years in lunar orbit[J]. Icarus, 2017, 283: 70-91. DOI:10.1016/j.icarus.2016.06.006 |
| [34] |
CAI Zhanchuan, ZHENG Caimu, TANG Zesheng, et al. Lunar digital elevation model and elevation distribution model based on Chang'e-1 LAM data[J]. Science China Technological Sciences, 2010, 53(9): 2558-2568. DOI:10.1007/s11431-010-3180-8 |
| [35] |
HAO Weifeng, ZHU Chang, LI Fei, et al. Illumination and communication conditions at the Mons Rümker region based on the improved lunar orbiter laser altimeter data[J]. Planetary and Space Science, 2019, 168: 73-82. DOI:10.1016/j.pss.2019.01.010 |
| [36] |
岳春宇, 何红艳, 鲍云飞, 等. 星载激光高度计几何定位误差传播分析[J]. 航天返回与遥感, 2014, 35(2): 81-86. YUE Chunyu, HE Hongyan, BAO Yunfei, et al. Study on error propagation of space-borne laser altimeter geometric positioning[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(2): 81-86. DOI:10.3969/j.issn.1009-8518.2014.02.012 |
| [37] |
易洪, 李松, 翁寅侃, 等. 自然地表测距残差对激光测高系统的在轨检校[J]. 华中科技大学学报(自然科学版), 2016, 44(8): 58-61. YI Hong, LI Song, WENG Yinkan, et al. On-orbit calibration of spaceborne laser altimeter using natural surface range residuals[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(8): 58-61. |
| [38] |
谢俊峰, 刘仁, 王宗伟, 等. 高分七号星载激光测高仪在轨几何检校与精度评估[J]. 红外与激光工程, 2021, 50(8): 20200396. XIE Junfeng, LIU Ren, WANG Zongwei, et al. In-orbit geometric calibration and accuracy evaluation of GaoFen-7 spaceborne laser altimeter[J]. Infrared and Laser Engineering, 2021, 50(8): 20200396. |
| [39] |
XIE Junfeng, TANG Xinming, MO Fan, et al. ZY3-02 laser altimeter footprint geolocation prediction[J]. Sensors, 2017, 17(10): 2165. DOI:10.3390/s17102165 |
| [40] |
TANG Xinming, XIE Junfeng, GAO Xiaoming, et al. The in-orbit calibration method based on terrain matching with pyramid-search for the spaceborne laser altimeter[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(3): 1053-1062. DOI:10.1109/JSTARS.2018.2890552 |
| [41] |
张过, 李少宁, 黄文超, 等. 资源三号02星对地激光测高系统几何检校及验证[J]. 武汉大学学报(信息科学版), 2017, 42(11): 1589-1596. ZHANG Guo, LI Shaoning, HUANG Wenchao, et al. Geometric calibration and validation of ZY3-02 satellite laser altimeter system[J]. Geomatics and Information Science of Wuhan University, 2017, 42(11): 1589-1596. |
| [42] |
HUANG Yong, CHANG Shengqi, QIN Songhe, et al. A new lunar DEM based on the calibrated Chang'E-1 laser altimeter data[J]. Advances in Astronomy, 2018, 2018: 5363797. |
| [43] |
YOON J S, SHAN Jie. Combined adjustment of MOC stereo imagery and MOLA altimetry data[J]. Photogrammetric Engineering and Remote Sensing, 2005, 71(10): 1179-1186. DOI:10.14358/PERS.71.10.1179 |
| [44] |
方勇, 曹彬才, 高力, 等. 激光雷达测绘卫星发展及应用[J]. 红外与激光工程, 2020, 49(11): 20201044. FANG Yong, CAO Bincai, GAO Li, et al. Development and application of lidar mapping satellite[J]. Infrared and Laser Engineering, 2020, 49(11): 20201044. |
| [45] |
OLIVER M A, WEBSTER R. Kriging: a method of interpolation for geographical information systems[J]. International Journal of Geographical Information Systems, 1990, 4(3): 313-332. DOI:10.1080/02693799008941549 |
| [46] |
NOUISSER O, ZERROUDI B. Modified Shepard's method by six-points local interpolant[J]. Journal of Applied Mathematics and Computing, 2021, 65(1): 651-667. |
| [47] |
HARDY R L. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research, 1971, 76(8): 1905-1915. DOI:10.1029/JB076i008p01905 |
| [48] |
LANCASTER P, SALKAUSKAS K. Surfaces generated by moving least squares methods[J]. Mathematics of Computation, 1981, 37(155): 141-158. DOI:10.1090/S0025-5718-1981-0616367-1 |
| [49] |
ZHANG Xiaobin, ZHANG Wuming. Dem extraction from Chang'e-1 lam data by surface skinning technology[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2011, XXXVⅢ-4/W25: 159-162. |
| [50] |
王滨辉, 宋沙磊, 龚威, 等. 全波形激光雷达的波形优化分解算法[J]. 测绘学报, 2017, 46(11): 1859-1867. WANG Binhui, SONG Shalei, GONG Wei, et al. Optimization decomposition method of full-waveform LiDAR[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1859-1867. DOI:10.11947/j.AGCS.2017.20170045 |
| [51] |
杜松, 李晓辉, 刘照言, 等. 激光雷达回波强度数据辐射特性分析[J]. 中国科学院大学学报, 2019, 36(3): 392-400. DU Song, LI Xiaohui, LIU Zhaoyan, et al. Radiometric characteristics of the intensity data of laser scanner[J]. Journal of University of Chinese Academy of Sciences, 2019, 36(3): 392-400. |
| [52] |
WAGNER W, ULLRICH A, DUCIC V, et al. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner[J]. ISPRS journal of Photogrammetry and Remote Sensing, 2006, 60(2): 100-112. DOI:10.1016/j.isprsjprs.2005.12.001 |
| [53] |
黄冬梅, 徐基衡, 宋巍, 等. GLAS全波形数据的高斯分解与高斯小波基分解对比分析[J]. 激光与光电子学进展, 2018, 55(11): 112801. HUANG Dongmei, XU Jiheng, SONG Wei, et al. Comparison and analysis of Gaussian decomposition and gaussian wavelet decomposition for GLAS full waveform data[J]. Laser & Optoelectronics Progress, 2018, 55(11): 112801. |
| [54] |
段乙好, 张爱武, 刘诏, 等. 一种用于机载LiDAR波形数据高斯分解的高斯拐点匹配法[J]. 激光与光电子学进展, 2014, 51(10): 102801. DUAN Yihao, Zhang Aiwu, LIU Zhao, et al. A Gaussian inflexion points matching method for Gaussian decomposition of airborne LiDAR waveform data[J]. Laser & Optoelectronics Progress, 2014, 51(10): 102801. |
| [55] |
ZHEN Ying, XIE Junfeng, ZHU Hong, et al. Land cover classification method considering the contribution of waveform characteristic parameters and the pooling scale[J]. Journal of Applied Remote Sensing, 2019, 13(4): 044529. |
| [56] |
XIE Junfeng, HUANG Genghua, LIU Ren, et al. Design and data processing of China's first spaceborne laser altimeter system for earth observation: GaoFen-7[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 1034-1044. DOI:10.1109/JSTARS.2020.2977935 |
| [57] |
ABEDIN M N, REFAAT T F, SULIMA O V, et al. Recent development of Sb-based phototransistors in the 0.9- to 2.2-μm wavelength range for applications to laser remote sensing[J]. International Journal of High Speed Electronics and Systems, 2006, 16(2): 567-582. DOI:10.1142/S0129156406003850 |
| [58] |
FAYAD I, IENCO D, BAGHDADI N, et al. A CNN-based approach for the estimation of canopy heights and wood volume from GEDI waveforms[J]. Remote Sensing of Environment, 2021, 265: 112652. DOI:10.1016/j.rse.2021.112652 |
| [59] |
DUBAYAH S L R, LUTHCKE S, BLAIR J, et al. GEDI L1B geolocated waveform data global footprint level V001[Z]. Washington, DC, USA: National Aeronautics and Space Administration, 2020.
|
| [60] |
LI Qinghua, SHAN Jie. Georeferencing with self-calibration for airborne full-waveform Lidar data using digital elevation model[J]. Photogrammetric Engineering & Remote Sensing, 2021, 87(1): 43-52. |
| [61] |
HOFTON M A, MINSTER J B, BLAIR J B. Decomposition of laser altimeter waveforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(4): 1989-1996. DOI:10.1109/36.851780 |
| [62] |
CHAUVE A, VEGA C, DURRIEU S, et al. Advanced full-waveform lidar data echo detection: Assessing quality of derived terrain and tree height models in an alpine coniferous forest[J]. International Journal of Remote Sensing, 2009, 30(19): 5211-5228. DOI:10.1080/01431160903023009 |
| [63] |
WANG Cheng, TANG Fuxin, LI Liwei, et al. Wavelet analysis for ICESat/GLAS waveform decomposition and its application in average tree height estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 115-119. DOI:10.1109/LGRS.2012.2194692 |
| [64] |
DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1977, 39(1): 1-22. DOI:10.1111/j.2517-6161.1977.tb01600.x |
| [65] |
PERSSON Å, SÖDERMAN U, TÖPEL J, et al. Visualization and analysis of full-waveform airborne laser scanner data[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2005, 36(3/W19): 103-108. |
| [66] |
ZHU J, ZHANG Z, HU X, et al. Analysis and application of LiDAR waveform data using a progressive waveform decomposition method[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2011, XXXVⅢ-5-W12: 31-36. |
| [67] |
ZHOU Tan, POPESCU S C, KRAUSE K, et al. Gold-A novel deconvolution algorithm with optimization for waveform LiDAR processing[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 129: 131-150. DOI:10.1016/j.isprsjprs.2017.04.021 |
| [68] |
NEUENSCHWANDER A L. Evaluation of waveform deconvolution and decomposition retrieval algorithms for ICESat/GLAS data[J]. Canadian Journal of Remote Sensing, 2008, 34(S2): S240-S246. |
| [69] |
WU Jiaying, VAN AARDT J A N, ASNER G P. A comparison of signal deconvolution algorithms based on small-footprint LiDAR waveform simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2402-2414. DOI:10.1109/TGRS.2010.2103080 |
| [70] |
RICHARDSON W H. Bayesian-based iterative method of image restoration[J]. Journal of the Optical Society of America, 1972, 62(1): 55-59. DOI:10.1364/JOSA.62.000055 |
| [71] |
LUCY L B. An iterative technique for the rectification of observed distributions[J]. The Astronomical Journal, 1974, 79: 745. DOI:10.1086/111605 |
| [72] |
WIENER N. Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications[M]. Vol. 8. Cambridge, MA: MIT Press, 1964.
|
| [73] |
LAWSON C L, HANSON R J. Solving least squares problems[M]. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1995.
|
| [74] |
JUTZI B, STILLA U. Range determination with waveform recording laser systems using a Wiener filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 61(2): 95-107. DOI:10.1016/j.isprsjprs.2006.09.001 |
| [75] |
NORDIN L. Analysis of waveform data from airborne laser scanner systems[D]. Luleå: Luleå University of Technology, 2006.
|
| [76] |
侯利冰, 郭颖, 黄庚华, 等. 光子计数激光雷达时间-数字转换系统[J]. 红外与毫米波学报, 2012, 31(3): 243-247. HOU Libing, GUO Ying, HUANG Genghua, et al. A time-to-digital converter used in photon-counting LiDAR[J]. Journal of Infrared and Millimeter Waves, 2012, 31(3): 243-247. |
| [77] |
MAGRUDER L A, WHARTON M E Ⅲ, STOUT K D, et al. Noise filtering techniques for photon-counting ladar data[C]//Proceedings of SPIE 8379, Laser Radar Technology and Applications XVⅡ. Baltimore, MD: SPIE, 2012: 83790Q.
|
| [78] |
WANG W T, WU Y L, TANG C Y, et al. Adaptive density-based spatial clustering of applications with noise (DBSCAN) according to data[C]//Proceedings of 2015 International Conference on Machine Learning and Cybernetics (ICMLC). Guangzhou, China: IEEE, 2015: 445-451.
|
| [79] |
ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland, OR: AAAI Press, 1996: 226-231.
|
| [80] |
ANKERST M, BREUNIG M M, KRIEGEL H P, et al. OPTICS: Ordering points to identify the clustering structure[J]. ACM SIGMOD Record, 1999, 28(2): 49-60. DOI:10.1145/304181.304187 |
| [81] |
ZHANG Jiashu, KEREKES J. An adaptive density-based model for extracting surface returns from photon-counting laser altimeter data[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 726-730. DOI:10.1109/LGRS.2014.2360367 |
| [82] |
ZHU Xiaoxiao, NIE Sheng, WANG Cheng, et al. A noise removal algorithm based on OPTICS for photon-counting LiDAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(8): 1471-1475. DOI:10.1109/LGRS.2020.3003191 |
| [83] |
OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66. DOI:10.1109/TSMC.1979.4310076 |
| [84] |
WANG Xiao, PAN Zhigang, GLENNIE C. A novel noise filtering model for photon-counting laser altimeter data[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 947-951. DOI:10.1109/LGRS.2016.2555308 |
| [85] |
HUANG Jiapeng, XING Yanqiu, YOU Haotian, et al. Particle swarm optimization-based noise filtering algorithm for photon cloud data in forest area[J]. Remote Sensing, 2019, 11(8): 980. DOI:10.3390/rs11080980 |
| [86] |
谢锋, 杨贵, 舒嵘, 等. 方向自适应的光子计数激光雷达滤波方法[J]. 红外与毫米波学报, 2017, 36(1): 107-113. XIE Feng, YANG Gui, SHU Rong, et al. An adaptive directional filter for photon counting LiDAR point cloud data[J]. Journal of Infrared and Millimeter Waves, 2017, 36(1): 107-113. |
| [87] |
HERZFELD U C, MCDONALD B W, WALLIN B F, et al. Algorithm for detection of ground and canopy cover in micropulse photon-counting lidar altimeter data in preparation for the ICESat-2 mission[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 2109-2125. DOI:10.1109/TGRS.2013.2258350 |
| [88] |
夏少波, 王成, 习晓环, 等. ICESat-2机载试验点云滤波及植被高度反演[J]. 遥感学报, 2014, 18(6): 1199-1207. XIA Shaobo, WANG Cheng, XI Xiaohuan, et al. Point cloud filtering and tree height estimation using airborne experiment data of ICESat-2[J]. Journal of Remote Sensing, 2014, 18(6): 1199-1207. |
| [89] |
ZHU Xiaoxiao, NIE Sheng, WANG Cheng, et al. A ground elevation and vegetation height retrieval algorithm using micro-pulse photon-counting lidar data[J]. Remote Sensing, 2018, 10(12): 1962. DOI:10.3390/rs10121962 |
| [90] |
NIE Sheng, WANG Cheng, XI Xiaohuan, et al. Estimating the vegetation canopy height using micro-pulse photon-counting LiDAR data[J]. Optics Express, 2018, 26(10): A520-A540. DOI:10.1364/OE.26.00A520 |
| [91] |
胡国军, 方勇, 张丽. 星载激光雷达的发展与测绘应用前景分析[J]. 测绘技术装备, 2015, 17(2): 34-37. HU Guojun, FANG Yong, ZHANG Li. Development and application prospect analysis of spaceborne LiDAR[J]. Geomatics Technology and Equipment, 2015, 17(2): 34-37. DOI:10.3969/j.issn.1674-4950.2015.02.010 |
| [92] |
赵瑞山, 张过, 杨帆. 利用光学遥感影像进行星载SAR影像正射纠正[J]. 测绘通报, 2016(10): 16-20, 38. ZHAO Ruishan, ZHANG Guo, YANG Fan. Ortho-rectification of space-borne SAR image based on optical remote sensing image[J]. Bulletin of Surveying and Mapping, 2016(10): 16-20, 38. DOI:10.13474/j.cnki.11-2246.2016.0320 |
| [93] |
SUN G, RANSON K J, KIMES D S, et al. Forest vertical structure from GLAS: An evaluation using LVIS and SRTM data[J]. Remote Sensing of Environment, 2008, 112(1): 107-117. DOI:10.1016/j.rse.2006.09.036 |
| [94] |
庞勇, 孙国清, 李增元. 林木空间格局对大光斑激光雷达波形的影响模拟[J]. 遥感学报, 2006, 10(1): 97-103. PANG Yong, SUN Guoqing, LI Zengyuan. Large footprint LiDAR waveform modelling of forest spatial patterns[J]. Journal of Remote Sensing, 2006, 10(1): 97-103. |
| [95] |
HARDING D J, CARABAJAL C C. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure[J]. Geophysical Research Letters, 2005, 32(21): L21S10. |
| [96] |
LEFSKY M A, HARDING D J, KELLER M, et al. Estimates of forest canopy height and above-ground biomass using ICESat[J]. Geophysical Research Letters, 2005, 32(22): L22S02. |
| [97] |
邢艳秋, 王立海. 基于ICESat-GLAS完整波形的坡地森林冠层高度反演研究—以吉林长白山林区为例[J]. 武汉大学学报(信息科学版), 2009, 34(6): 696-700. XING Yanqiu, WANG Lihai. ICESat-GLAS full waveform-based study on forest canopy height retrieval in sloped area-a case study of forests in Changbai Mountains, Jilin[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 696-700. |
| [98] |
NEUENSCHWANDER A L, URBAN T J, GUTIERREZ R, et al. Characterization of ICESat/GLAS waveforms over terrestrial ecosystems: implications for vegetation mapping[J]. Journal of Geophysical Research: Biogeosciences, 2008, 113(G2): G02S03. |
| [99] |
娄雪婷, 曾源, 吴炳方. 森林地上生物量遥感估测研究进展[J]. 国土资源遥感, 2011, 23(1): 1-8. LOU Xueting, ZENG Yuan, WU Bingfang. Advances in the estimation of above-ground biomass of forest using remote sensing[J]. Remote Sensing for Land & Resources, 2011, 23(1): 1-8. |
| [100] |
林晓娟. 基于ICESat-2和GEDI森林冠层高度和森林地上生物量遥感诊断[D]. 北京: 中国科学院空天信息创新研究院, 2021. LIN Xiaojuan. Remote sensing diagnosis of forest canopy height and forest above-ground biomass based on ICESat-2 and GEDI[D]. Beijing: Aerospace Information Research Institute, Chinese Academy of Sciences, 2021. |
| [101] |
刘茜, 杨乐, 柳钦火, 等. 森林地上生物量遥感反演方法综述[J]. 遥感学报, 2015, 19(1): 62-74. LIU Qian, YANG Le, LIU Qinhuo, et al. Review of forest above-ground biomass inversion methods based on remote sensing technology[J]. Journal of Remote Sensing, 2015, 19(1): 62-74. |
| [102] |
NANDY S, SRINET R, PADALIA H. Mapping forest height and aboveground biomass by integrating ICESat-2, Sentinel-1 and Sentinel-2 data using random forest algorithm in northwest Himalayan foothills of India[J]. Geophysical Research Letters, 2021, 48(14): e2021GL093799. |
| [103] |
NELSON R, RANSON K J, SUN G, et al. Estimating Siberian timber volume using MODIS and ICESat/GLAS[J]. Remote Sensing of Environment, 2009, 113(3): 691-701. DOI:10.1016/j.rse.2008.11.010 |
| [104] |
邱赛, 邢艳秋, 徐卫华, 等. 星载大光斑LiDAR与HJ-1A高光谱数据联合估测区域森林地上生物量[J]. 生态学报, 2016, 36(22): 7401-7411. QIU Sai, XING Yanqiu, XU Weihua, et al. Estimation of regional forest aboveground biomass combining spaceborne large footprint LiDAR and HJ-1A hyperspectral images[J]. Acta Ecologica Sinica, 2016, 36(22): 7401-7411. |
| [105] |
梁爽. 极地海冰密集度和厚度遥感反演方法研究[D]. 北京: 中国科学院空天信息创新研究院, 2021. LIANG Shuang. Research on polar sea ice concentration and thickness retrieval using remote sensing observation[D]. Beijing: Aerospace Information Research Institute, Chinese Academy of Sciences, 2021. |
| [106] |
季青, 庞小平, 许苏清, 等. 极地海冰厚度探测方法及其应用研究综述[J]. 极地研究, 2016, 28(4): 431-441. JI Qing, PANG Xiaoping, XU Suqing, et al. Review of technology and application research on polar sea ice thickness detection[J]. Chinese Journal of Polar Research, 2016, 28(4): 431-441. |
| [107] |
PEACOCK N R. Arctic sea ice and ocean topography from satellite altimetry[D]. London: University of London, 1998.
|
| [108] |
袁乐先, 李斐, 张胜凯, 等. 利用ICESat/GLAS数据研究北极海冰干舷高度[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1176-1182. YUAN Lexian, LI Fei, ZAHNG Shengkai, et al. A study of arctic sea ice freeboard heights from ICESat/GLAS[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1176-1182. |
| [109] |
KWOK R, KACIMI S, WEBSTER M A, et al. Arctic snow depth and sea ice thickness from ICESat-2 and CryoSat-2 freeboards: a first examination[J]. Journal of Geophysical Research: Oceans, 2020, 125(3): e2019JC016008. |
| [110] |
FORSBERG R, SKOURUP H. Arctic ocean gravity, geoid and sea-ice freeboard heights from ICESat and GRACE[J]. Geophysical Research Letters, 2005, 32(21): L21502. DOI:10.1029/2005GL023711 |
| [111] |
KWOK R, CUNNINGHAM G F. ICESat over Arctic sea ice: estimation of snow depth and ice thickness[J]. Journal of Geophysical Research: Oceans, 2008, 113(C8): C08010. |
| [112] |
SLOBBE D C, LINDENBERGH R C, DITMAR P. Estimation of volume change rates of Greenland's ice sheet from ICESat data using overlapping footprints[J]. Remote Sensing of Environment, 2008, 112(12): 4204-4213. DOI:10.1016/j.rse.2008.07.004 |
| [113] |
TEUNISSEN P J G. Network quality control, series on mathematical geodesy and positioning[M]. Delft, The Netherlands: Delft University of Technology, 2006.
|
| [114] |
李斐, 袁乐先, 张胜凯, 等. 利用ICESat数据解算南极冰盖冰雪质量变化[J]. 地球物理学报, 2016, 59(1): 93-100. LI Fei, YUAN Lexian, ZHANG Shengkai, et al. Mass change of the Antarctic ice sheet derived from ICESat laser altimetry[J]. Chinese Journal of Geophysics, 2016, 59(1): 93-100. |
| [115] |
PARRISH C E, MAGRUDER L A, NEUENSCHWANDER A L, et al. Validation of ICESat-2 ATLAS bathymetry and analysis of ATLAS's bathymetric mapping performance[J]. Remote Sensing, 2019, 11(14): 1634. DOI:10.3390/rs11141634 |
| [116] |
HSU H J, HUANG C Y, JASINSKI M, et al. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: a case study in the South China Sea[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 178: 1-19. DOI:10.1016/j.isprsjprs.2021.05.012 |
| [117] |
ABDALLAH H, BAILLY J S, BAGHDADI N N, et al. Potential of space-borne LiDAR sensors for global bathymetry in coastal and inland waters[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(1): 202-216. DOI:10.1109/JSTARS.2012.2209864 |
| [118] |
平劲松, 黄倩, 鄢建国, 等. 基于嫦娥一号卫星激光测高观测的月球地形模型CLTM-s01[J]. 中国科学(G辑: 物理学力学天文学), 2008, 38(11): 1601-1612. PING Jinsong, HUANG Qian, YAN Jianguo, et al. Lunar topographic model CLTM-s01 from Chang'e-1 laser Altimeter[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2008, 38(11): 1601-1612. |
| [119] |
李春来, 任鑫, 刘建军, 等. 嫦娥一号激光测距数据及全月球DEM模型[J]. 中国科学: 地球科学, 2010, 40(3): 281-293. LI Chunlai, REN Xin, LIU Jianjun, et al. Laser altimetry data of Chang'e-1 and the global lunar DEM model[J]. Science China Earth Sciences, 2010, 40(3): 281-293. |
| [120] |
熊德永, 钟振, 刘高福. 高分辨率卫星重力和激光测高数据的月球岩石圈有效弹性厚度估计的分析及应用[J]. 地球物理学进展, 2016, 31(2): 622-628. XIONG Deyong, ZHONG Zhen, LIU Gaofu. Analysis and application in the estimation of the lunar effective elastic thickness based on the high-resolution gravity and topography data[J]. Progress in Geophysics, 2016, 31(2): 622-628. |
| [121] |
王文睿, 李斐, 刘建军, 等. 基于嫦娥一号激光测高数据的月球三轴椭球体模型[J]. 中国科学: 地球科学, 2010, 40(8): 1022-1030. WANG Wenrui, LI Fei, LIU Jianjun, et al. Triaxial ellipsoid models of the Moon based on the laser altimetry data of Chang'E-1[J]. Science China Earth Sciences, 2010, 40(8): 1022-1030. |
| [122] |
ARAKI H, TAZAWA S, NODA H, et al. Lunar global shape and polar topography derived from Kaguya-LALT laser altimetry[J]. Science, 2009, 323(5916): 897-900. DOI:10.1126/science.1164146 |
| [123] |
NODA H, ARAKI H, GOOSSENS S, et al. Illumination conditions at the lunar polar regions by KAGUYA (SELENE) laser altimeter[J]. Geophysical Research Letters, 2008, 35(24): L24203. DOI:10.1029/2008GL035692 |
| [124] |
SMITH D E, ZUBER M T, NEUMANN G A, et al. Initial observations from the lunar orbiter laser altimeter (LOLA)[J]. Geophysical Research Letters, 2010, 37(18): L18204. |
| [125] |
ZUBER M T, SMITH D E, SOLOMON S C, et al. The Mars Observer laser altimeter investigation[J]. Journal of Geophysical Research: Planets, 1992, 97(E5): 7781-7797. DOI:10.1029/92JE00341 |
| [126] |
SMITH D E, ZUBER M T, FREY H V, et al. Topography of the Northern Hemisphere of Mars from the Mars Orbiter Laser Altimeter[J]. Science, 1998, 279(5357): 1686-1692. DOI:10.1126/science.279.5357.1686 |
| [127] |
SMITH D E, ZUBER M T, FREY H V, et al. Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars[J]. Journal of Geophysical Research: Planets, 2001, 106(E10): 23689-23722. DOI:10.1029/2000JE001364 |
| [128] |
XIAO Haifeng, STARK A, STEINBRVGGE G, et al. Prospects for mapping temporal height variations of the seasonal CO2 snow/ice caps at the Martian Poles by Co-registration of MOLA profiles[J]. Planetary and Space Science, 2022, 214: 105446. DOI:10.1016/j.pss.2022.105446 |
| [129] |
CAVANAUGH J F, SMITH J C, SUN Xiaoli, et al. The mercury laser altimeter instrument for the MESSENGER mission[J]. Space Science Reviews, 2007, 131(1): 451-479. |
| [130] |
SUSORNEY H C M, BARNOUIN O S, ERNST C M, et al. The surface roughness of Mercury from the Mercury Laser Altimeter: Investigating the effects of volcanism, tectonism, and impact cratering[J]. Journal of Geophysical Research: Planets, 2017, 122(6): 1372-1390. DOI:10.1002/2016JE005228 |
| [131] |
KRESLAVSKY M A, HEAD J W. Kilometer-scale roughness of Mars: Results from MOLA data analysis[J]. Journal of Geophysical Research: Planets, 2000, 105(E11): 26695-26711. DOI:10.1029/2000JE001259 |