2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
我们生活的地球是太阳系中唯一生机盎然的行星,地球内部发生许多动力学过程,如构造活动、地震等,表面受到大气、海洋等的负荷作用,同时也会受到来自太阳系其他天体的引潮力作用,以及太阳的热辐射等。伴随这些过程与力的作用,地球会产生形变。有些形变是能够直观地感受到的,比如地震产生的破坏性错动;有些形变只有通过高精度仪器设备才能探测到,如潮汐形变,尽管它在地面的垂向位移幅度有数十厘米之大[1],但因为没有相对运动,所以人们站在地表是无法感知到这种形变的。实际上,人们对于地球形变的研究,不仅仅局限于狭义的几何量(或运动学变量),如地面的位移、倾斜、应变等,而且拓展到了许多物理量,如外部重力场的变化、内部的应力场变化等动力学变量。随着针对不同观测量的仪器观测精度的提高,对于地球形变的研究不仅可以检验形变理论的正确性,还可以进一步完善地球模型与分析和认知不同的动力学过程。实际上,这些不同的动力学过程都可以用等效的力源来表示,如地震的等效体力源、火山的Mogi源、流体运动的膨胀源等。因此,研究地球的形变就与不同力源的作用紧密联系在了一起。
研究地球形变通常基于两种坐标系统:柱坐标系和球坐标系。前者通常适用于研究小范围形变,如中小地震引起的近场形变;后者适用于研究全球范围内的大尺度形变,如大地震引起的中远场形变、海潮负荷引起的全球形变等。关于地球受力形变的研究理论最早可能要追溯到对平面半无限空间负荷问题的系统工作,该理论主要涉及平衡方程与本构关系方程[2]。随着观测精度的提高,对理论的发展也提出了新的要求。如GNSS、InSAR、DAS(分布式声速传感器)可以探测毫米级乃至更微小的形变信息;重力测量的精度也达到了μgal量级,如FG-5重力仪,特别是超导重力仪的探测精度甚至要再高2个数量级。此外,倾斜仪、应变仪等观测精度也越来越高。因此,通常在研究全球性的大尺度形变时,除了需要采用球坐标系外[3-4],还需要考虑地球的分层结构、自引力及由变形导致的质量调整产生的附加引力位等。因此,在平衡方程中需要考虑重力及引入泊松方程[5-6]。地震反演研究表明,地球更加接近于一个弹性的分层球体[7]。因此,现今地球形变的研究大多以此为基本模型。
为了方便研究,通常假设地球是球对称、不自转、完全弹性和各向同性的,也就是所谓的SNREI(spherically symmetric, non-rotating, elastic and isotropic)地球[8],如目前常用的PREM地球模型,除了考虑地幔的各向异性外,也给出了一个等效的各向同性模型[7]。此外,采用该类模型研究地球形变常常隐含地包括地球的可压缩性与自引力。采用SNREI模型的一个方便之处在于球型形变与环型形变的解耦,从而简化数值计算。然而对于研究动态的形变问题,特别是地球自由振荡问题,常常需要考虑地球的椭率与自转[8-10],这两个因素不仅会导致球型形变与环型形变的耦合,还会引起振型的谱峰发生分裂,即所谓的正常谱峰分裂,相关内容可以参考文献[11—12]。
地球表面的动力过程主要体现为全球水循环,它导致水在大气、海洋与地表和地下不停运移与交换。在地球的表面,约70%是海洋,在引潮力作用下,海洋产生潮起潮落现象,即海洋潮汐,简称海潮。而海潮产生的海水质量的时空变化会改变固体地球表面的荷载,由此导致的影响称为海潮负荷效应。此外,大气中的水汽含量、温度、气压等导致其密度产生变化,也就是质量的时空变化,它也会使地球发生形变。同时大气在地表的温度、气压的变化也会使地球发生形变。与海潮负荷类似,地表的河流、地下水等也会产生负荷效应。
不管是地球外部、表面或内部的力源,地球变形过程都可以用基本的物理方程与地球介质的弹性参数来描述,因此,可以建立相应的初边值问题,从而模拟出变形量的大小。地球的形变通常用无量纲的勒夫数来描述[3, 13],它是一个比值,反映了地球在力的作用下的反应强度。勒夫数大,说明单位力作用下的变形量也大。因此,对于地球形变问题的研究,基础的工作就是基于一个给定的地球模型,计算不同的勒夫数与相应的格林函数,并结合实测数据进行模拟计算与分析。鉴于地球固体潮的研究已经非常成熟,相关改正方法和参数可以参考IERS规范。本文着重介绍地表质量和热负荷与地震引起的地球形变方面的理论模拟研究进展情况。
1 地球形变理论初边值问题求解初边值问题涉及泛定方程与边界条件和初始条件[14],泛定方程通常是用数学方法对基本的物理定理或定律进行描述所获得的一组微分方程。对于地球而言,主要包括由牛顿第二定律描述的运动方程,对于不考虑惯性力时的静态形变问题也称为平衡方程;联系弹性体(即地球介质)应力和应变的本构关系,即虎克定律;描述扰动位与扰动密度的泊松方程。如果要考虑与温度场有关的热效应,需要考虑热传导方程。对于SNREI地球来说,可以将所有变量展开为球函数级数。在理论研究中,采用点力源是非常方便的,并将这个力源置于球坐标的极轴上,如地表负荷源置于北极点,内部位错源的震中置于北极点。同时,对力源同样做球谐展开,这样就可以得到关于球谐展开系数的微分方程,这些方程最后都可以写成如下统一的形式
 (1)
(1)
式中,r是球坐标系下的矢径;Y是由不同变量构成的矢量;A是系数矩阵;F是(等效的)单位体积力的球谐展开系数。对于力源在地表的负荷问题,可直接用F建立地表边界条件[6, 15-16];对于力源在内部的地震位错问题,可将F转换为内部震源处的不连续边界条件[5]。因此,最终只需要求解齐次的微分方程组,即式(1)右边不再出现F。在地心处,满足正则条件,即位移场、附加引力位和温度梯度为零。如果地表没有力源,则需要满足自由边界条件,即正应力与剪应力为零。此外,如果方程涉及时间,还需要初始条件。这样通过求解这个初边值问题就可以得到任意位置的Y,从而得到勒夫数
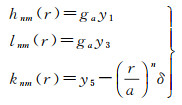 (2)
(2)
式中,y1、y3、y5分别表示Y中的垂直位移、水平位移和附加引力位分量,对于有直接引力项的力源δ=1(如地表质量负荷),其他力源δ=0,n和m分别是球谐展开的阶和次。对于地表负荷问题,m=0;对于位错问题,m=0, 1, 2。这样,就可得到格林函数
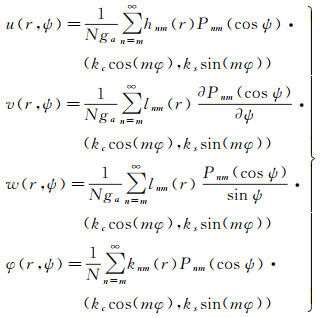 (3)
(3)
式中,u、v、w、ϕ分别为垂直位移、切向位移、横向位移、附加引力位;N为构建边界条件时的规格化系数;Pnm为Legendre函数;ψ是计算点到源点的角距离;φ是方位角;最右边的括号适用于位错问题,kc和ks是某个常数,至于是取余弦还是正弦取决于不同位移场分量与位错模式[17-18]。
对于SNREI模型,传统的研究地球纯弹性形变的方法是采用四阶Runge-Kutta方法[19-20]。需要注意的是,变量之间的相关性会随着球谐阶数的增大而增强,因此,当球谐阶数非常大时,会导致最后确定待定系数的矩阵奇异。文献[20]注意到变量包含因子rn,因此,先从变量中扣除rn再进行计算,再结合积分过程中的归一化方法,可有效改善相关性问题。
对上述的初边值问题,可采用有限元方法的思路直接进行数值求解,或者从最基本的方程出发构造弱解形式。文献[21]在有限元方法的基础上发展了谱有限元方法,在球面上采用球谐函数展开,在矢径方向采用有限元,但该方法没有考虑地球的可压缩性及液态的外核。文献[22—23]将该方法扩展到可压缩地球模型,但同样没有考虑液态的外核。文献[24]借鉴文献[19]的方法,引入势函数并假设液核初始模型满足Adams-Williamson条件,推导出液核中平衡方程及其对应的弱解形式,使谱有限元方法能够应用于更加真实的地球模型。
文献[25]提出了一种近似解析解方法,通过合理假设地球介质分层参数随r的变化关系,得到了常系数矩阵A,从而得到了每一层的解析解,然后通过传播矩阵方法与边界条件得到最终的解。文献[26]曾经也给出一个解析解,但它的假设与真实地球不太符合。不同于文献[26]的假设,文献[25]的假设更加合理,只要层厚足够小,通过这种假设所得模型与最初模型是完全一致的。数值试验表明,实际上层厚可以取得很大,就能得到满意的结果,因此这种方法非常高效,但对球谐展开的高阶项存在数值溢出问题。文献[27]采用传播矩阵中的刚度矩阵方法解决了溢出问题。文献[28]对比了多种高效的传播矩阵方法。关于不同求解方法的讨论可参考文献[29]。
2 研究进展 2.1 地表质量负荷在年际以下的时间尺度上,地球表面的质量调整主要是全球的水循环,体现在海洋、大气与陆地水的变化中,其中海洋的影响又分为潮汐与非潮汐效应。海洋与陆地水的影响可用式(4)表示(以地表的垂直位移为例)
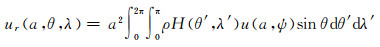 (4)
(4)
式中,a是地球半径;θ和λ分别是计算点的余纬与经度;θ′和λ′分别是源点(即负荷作用点)的余纬与经度;ρ是海水或陆地水密度;H是海潮潮高或海面高变化量或等效水高;u称为垂直位移的格林函数;ψ与源点和计算点的坐标满足式(5)
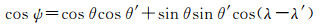 (5)
(5)
除了采用式(4)的数值积分外,还可以采用球谐展开方法。球谐展开方法就是将H展开为球谐级数,u采用式(3)中的形式,根据球谐函数的正交关系,得到式(6)
 (6)
(6)
式中,ρe是地球平均密度(来自于N),带上标C和S的Hnm表示H的球谐展开系数,注意这里为了方便计算,采用了大地测量学中使用的完全规格化的球函数(以上横线加以区别),并且N的值为单位引力位。文献[30]讨论了重力负荷计算中关于直接引力项系数的选取问题。文献[31]提出了一种加速式(6)收敛的方法,并指出由于负荷质量分布不连续引起的吉布斯效应在沿海地区对结果会有很大的影响。文献[32]采用该方法研究了海潮负荷对垂直位移的影响。数值积分方法的计算量大、精度高,而球谐展开方法由于比较简单,计算量小但精度相对低。鉴于此,文献[33]提出了近区采用数值积分、远区采用球谐展开的方法。文献[34]对这两种方法进行了比较,计算了海潮负荷导致的垂直位移,指出在沿海区域由两种方法得到的结果平均差异为3 mm,最大达到10 mm。文献[35]给出了比较完整的计算重力、位移、倾斜和应变的球谐展开方法的计算公式,通过对两种方法计算的结果的比较(表 1),也指出该方法只适合于内陆地区。
| 截断阶数 | 球谐展开方法 | 数值积分方法 | ||||||
| 720阶 | 1440阶 | - | ||||||
| 振幅 | 相位 | 振幅 | 相位 | 振幅 | 相位 | |||
| g/(10-8 m/s2) | 2.418 9 | 152.01 | 2.418 9 | 152.01 | 1.905 2 | 156.65 | ||
| U/mm | 8.647 9 | 153.50 | 8.647 9 | 153.50 | 6.641 1 | 158.97 | ||
| Vew/mm | 2.146 0 | 20.73 | 2.146 0 | 20.73 | 2.077 3 | -4.88 | ||
| Vns/mm | 3.070 6 | -158.22 | 3.070 6 | -158.22 | 3.324 8 | -155.82 | ||
| Vew/(10-9 rad) | 45.255 4 | -32.69 | 45.255 5 | -32.69 | 54.001 7 | -62.62 | ||
| Vns/(10-9 rad) | 51.681 2 | -151.71 | 51.666 0 | -151.72 | 45.505 4 | -147.71 | ||
| eθθ/(10-9) | 1.766 9 | 112.96 | 1.760 7 | 113.18 | 4.474 5 | 163.67 | ||
| eθλ/(10-9) | 6.380 9 | -140.36 | 6.381 1 | -140.36 | 10.752 4 | -134.47 | ||
| eλλ/(10-9) | 5.637 2 | 85.60 | 5.637 2 | 85.60 | 9.300 4 | -36.96 | ||
随着计算机技术的发展,数值计算效率得到了很大的提高,因此应选择用式(4)进行数值计算。目前,有许多开放软件可以计算式(4),如文献[36]编写的SPOTL包中的nloadf函数,该方法采用了文献[37]提出的积分格林函数方法,有效提高了计算效率,同时考虑了不同海洋区域的海水密度变化影响。文献[38]在GOTIC基础上发布的改进版本GOTIC2;Bos和Scherneck提供的计算海潮负荷的网页版(http://holt.oso.chalmers.se/loading/)。文献[39]发布的SGOTL,随着Python的流行,也出现了Python版本的软件[40]。
由式(4)可知,两个关键的量是H和u,前者对应着负荷源模型,如海潮模型,后者对应着地球模型。实际上,H中隐含一个关于海陆边界的信息,由于海潮或海面变化只存在于海洋,而陆地水和大气负荷(考虑反变气压计效应)只存在于陆地。因此,在研究陆地水的负荷效应时,只需要改变海洋和陆地的判断就可以直接使用计算海潮负荷的程序进行计算。STRM地形数据为确定高空间分辨率的海陆边界提供了直接的资料,利用分辨率为90 m的地形数据优化计算点周边的海陆边界。文献[41]计算了沿海台站的海潮负荷效应对重力的影响,对比了由不同海陆边界获得的结果,并指出了高精度海陆边界对于准确计算海潮负荷的重要性(图 1)。后来在计算中对中国沿海全域的海陆边界进行了优化,构建了我国沿海和岛屿的海潮负荷模型[42]。
得益于卫星测高技术的发展,流体动力学模拟与验潮站资料的增多,海潮模型的精度得到了很大的提高,特别是近海潮汐模型,已广泛应用于海潮负荷效应的模拟。全球有多家机构从事全球大气、海洋和陆地水模型的构建工作,如FES系列的全球海潮模型[43],ECCO模型(www.ecco-group.org)、CPC模型(www.cpc.ncep.noaa.gov/products/GODAS)和GLDAS模型(earth.gsfc.nasa.gov)等。通过这些模型,开展了许多负荷效应的模拟应用工作[44-53]。文献[54—55]研究了海潮模型在重力海潮负荷改正中的适定性问题。文献[56]研究了利用不同海潮模型用于重力改正对解算的自由核章动参数的影响。这些研究为海潮模型的选择提供了重要的参考。近年来,InSAR技术广泛应用于地球形变的研究,文献[57]研究了海潮负荷对InSAR视线方向形变的影响。文献[58—59]比较了香港地区部分GPS站得到的海潮负荷和模型的比较,类似的工作也用于新西兰GPS站观测数据的开展。
由不同地球模型计算获得的格林函数是不同的。如果考虑不同区域地壳的参数,如CRUST1.0,则格林函数在近区会有很大的不同[41, 60-61]。图 2显示了两种地球模型计算的重力负荷格林函数在近场随角距的变化,从中可以看出很明显的差异。
在模拟大气对重力观测影响时,不同于研究海洋的影响,由于大气的垂向分布范围较广,不能将其看成单层,而需要考虑大气的垂向分布来计算直接引力。文献[62]采用一个服从指数分布的大气模型计算了直接引力项,并与计算点的局部大气压强进行比较得到了一个大气重力导纳值(直接引力/局部压强),发现结果比用平面大气模型小7%~8%,说明了考虑地球曲率的必要性。文献[63]指出,大气负荷产生的重力变化达到30 μgal,其中90%由计算点周边50 km的大气引起,同时地表的大气温度发挥很大的作用。文献[64]通过标准大气模型计算了大气重力格林函数,为进行全球大气重力负荷效应的积分计算奠定了基础。文献[16]也计算了大气重力格林函数,但采用不同的方法处理直接引力项,即除了对地表的大气压强产生的正应力负荷作用外,将大气的引力看成是固体地球之外的作用(实际上该力可看成引潮力),然后根据大气的空间分布进行积分得到直接引力项的格林函数。实际上,由于采用的是基于小形变的线性理论,因此地球对地表质量负荷的响应等价于潮汐响应与地表正压力响应的叠加。因此,文献[16]的结果与以前的结果是一致的。然而实际研究中,由于三维大气观测资料的缺乏,常采用大气重力导纳值进行大气负荷效应的扣除。大气负荷除了引起重力变化外,同样会引起位移、倾斜和应变等变化,而模拟它们的方法与海潮负荷中的方法是一致。
2.2 地表热负荷由于四季变化与日夜扭转,地表的温度是时刻变化的。热胀冷缩对于地球也不例外,关于温度与应变的关系在材料力学领域研究得比较多,因此在半无限空间体系下比较成熟。虽然人们对地球上典型岩石的热力学参数都有很好的了解[65],但是整个地球在地表热负荷作用下的形变问题研究并不多。文献[66]研究了分层球体的热弹性变形问题,并用差分方法进行了数值计算,但跟平面半空间模型下的理论一样,没有考虑任何的体力。文献[67]研究了均匀球的热弹性变形问题,同样也没有考虑体力项。并且为了方便,在理论推导过程中作了一定的假设,因此,在球谐阶数超过一定的值之后会有较大误差。采用球谐展开的方法计算了地表温度的周年变化对位移场的影响,发现与采用平面半无限空间模型得到的结果有较大的差异,进一步说明了采用球坐标系的必要性。对于地球来说,自引力是不容忽视的。文献[68]利用全耦合的方程,考虑预应力和自引力,并采用文献[25]的近似解析解方法及DVP传播矩阵方法,求得了任意球谐展开阶数的热负荷勒夫数。并且在不作任何假设的情况下,给出了不考虑自引力的均匀球的严格解析解,其中热负荷勒夫数是以球贝塞尔函数表示的。该理论为研究SNREI地球的地球热源引起的地球形变,特别是重力场变化,奠定了理论基础。
2.3 同震形变最早关于地球地震位错形变的研究采用的是平面柱坐标,如经典的Okada解析公式[69]。采用柱坐标系的主要原因可能源于材料或工程研究领域的理论传承。文献[70—71]将相关理论拓展到球形地球模型并给出了解析解,但采用的模型没有考虑重力场耦合,即自引力效应。文献[72]采用了1个考虑预应力、自引力、液态外核,径向非均匀等更接近真实地球的模型开展了相关工作。文献[17, 73—74]在此基础上作了深入的系统性研究,采用文献[5]的方法模拟了点源位错引起的位移场和重力场等变化。通过将有限断层离散化,将每个子断层认为是点源,得到了有限断层产生的同震形变[75]。相关的理论体系可参考文献[76]。
文献[4]比较了由平面模型和球模型所得结果,说明在近场二者是一致的。但是后续的研究表明,在中远场二者的差异较明显,说明了使用球形地球模型的必要性,这一点也被后来的研究进一步强调[77-78]。
文献[79]提出了计算同震形变的互换定理,即内部的位错源产生的地表形变可以用3种地表力源作用下在位错源所在位置产生的形变的组合来表示,这使得同震形变的计算更加简单,因为这使得位错形变问题只涉及3组在地心正则的解,或者说只需要解齐次的微分方程组而不需要考虑力源项(从力源转化的内部不连续性或特解项)。文献[80]给出了上述3种地表力源引起的地球变形的渐近解。因此利用互换定理,文献[81—83]研究了同震形变的渐近解,该方法也被用来计算断层在地表时的位错勒夫数渐近值[84]。文献[85]也用该方法加速内部同震体应变格林函数计算的收敛,说明渐近值在格林函数计算中的作用。文献[3]给出了均匀球的3组在地心正则的解。因此,可以直接运用互换定理计算均匀球内的位错产生的地表形变,并且采用文献[80]的渐近解可确保格林函数的收敛[86]。但是,对于一个更加真实的分层地球,均匀球的渐近值无法被应用。
文献[18]利用文献[25]的近似解析解方法和DVP传播矩阵法研究了位错勒夫数的计算问题,他们的方法解决了以前的方法在超高阶的计算中的变量相关导致矩阵奇异的问题,因此,可以计算到很高的阶数。由于用不同于文献[74]的位错勒夫数定义,能够通过观察高阶位错勒夫数值和球谐阶数的关系直观地发现二者之间的联系,并确定了拟合公式与位错勒夫数渐近值,从而克服了特殊情形下格林函数不收敛的计算难题[87]。渐近值加速格林函数收敛的作用可从式(7)看出,同样以垂直位移为例
 (7)
(7)
式中,第1个求和的差值随着阶数n的增大衰减更快,而第2个求和有严格的解析式[87-88],因此,能够很快得到收敛的格林函数。文献[89]也对地震引起内部变形进行了研究,同样获得了收敛的格林函数。当球谐阶数很高时,重力的影响越来越不明显,因此,通过忽略自引力并运用DVP传播矩阵的特殊性质。文献[90]在理论上获得了位错勒夫数的渐近值,从而彻底解决了位错格林函数的计算问题。
最近十几年,发生了多次震级较大的地震,这些大地震引起了全球尺度的显著变形[91],同时也对地球自转[92-93]、地球参考框架[94-95]、地球的体积变化[96](图 3),以及地球内部能量的转换产生了较大影响[97-99]。这些研究是对地震形变模拟理论的重要应用。
3 总结与展望
本文回顾了地球弹性变形的理论、地表负荷和地震位错引起形变的理论模拟方面的主要研究进展,地球弹性变形理论发展至今,可以说已经非常完善,相关的研究成果也非常多。然而随着技术的发展,观测精度越来越高,地球变形的理论也需要得到更进一步的发展。
在短时间尺度下,地球表现出显著的弹性特征,因此,地球的弹性形变模拟在目前大地测量和地球物理学的研究中发挥着非常重要的作用。因为地球的形变模拟提供了联系力源与形变的纽带——格林函数,因此一方面可以确定不同力源导致的地球形变,另一方面也可以在反演地球内部结构、物性参数,以及力源参数、甚至动力过程中发挥重要作用。地球是一个复杂的系统,有太多的因素会导致地球的形变。随着高精度观测资料的获取,会发现更多观测与理论不相符合的情形,或用现有理论无法解释的现象。比如越来越多的证据表明,在地热开采区或注水区的地震具有明显的非双力偶特征,并认为这可能与流体有关[100],然而具体的机制仍不明确,对震后孔隙弹性回弹的认识仍有待加强,因此,需要发展孔隙弹性位错理论;地温观测发现了明显的温度场同震变化[101]和温度的潮汐变化信号[102],前者与构造活动的关系及后者与引潮力的联系都是值得深入研究的课题,因此,需要发展地球的热弹性变形理论,包括引潮力作用与地震位错作用的相应理论。热弹性理论不仅可用于计算由于温度场变化导致的地球形变,还可以研究变形引起的温度场变化,尽管人们一直认为后者的效应是很小的,通常采用所谓单向耦合的理论,但是地球内部温度的测量目前已经能够达到非常高的精度(0.1 mK),因此,需要发展双向耦合的热弹性理论及开展相关的应用研究。
在长时间尺度上,地球表现出滞弹性的特征,相关的研究涉及冰后均衡调整与震后黏弹性松弛,根据对应性原理,其在拉普拉斯域的边值问题与弹性边值问题是一致的,因此,相关的弹性理论可以直接应用,只需要最后对结果实施反拉普拉斯变化即可。相关的黏弹性形变的研究进展可参考文献[103]。
我国正大力发展非常规能源的开采(如页岩气和地热等)及水电开发,要评估这类活动对环境的影响就涉及流体与温度场,即孔隙弹性与热弹性的问题,或将二者统一的孔隙热弹性的问题。现在也有一些基于柱坐标系统理论的研究,但是现有理论可能已经不能满足当今观测精度越来越高的需求。因为这些理论没有考虑预应力与地球的自引力,然而这些会影响最终的计算结果[104]。考虑自引力后,由于平面半无限空间模型天然的缺陷,需要作某种假设[105]。因此,作为多学科交叉的地球形变问题,有必要发展球坐标系统下的相应理论对观测结果或现象作客观的描述与解释,同时也有必要开展观测网络的建设获取更加丰富的高精度观测数据,以增强我们对地球动力过程的认知。
| [1] |
许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010. XU Houze. Solid Earth's tides[M]. Wuhan: Hubei Science and Technology Press, 2010. |
| [2] |
BOUSSINESQ J. Équilibre d'élasticité d'un sol isotrope sans pesanteur, supportant différents poids[J]. Comptes Rendus de l'Académie des Sciences, 1878, 86: 1260-1263. |
| [3] |
LOVE A E H. Some problems of geodynamics[M]. London: Cambridge University Press, 1911.
|
| [4] |
SUN W K, OKUBO S. Effects of Earth's spherical curvature and radial heterogeneity in dislocation studies-for a point dislocation[J]. Geophysical Research Letters, 2002, 29(12): 1605. DOI:10.1029/2001GL014497 |
| [5] |
TAKEUCHI H, SAITO M. Seismic surface waves[J]. Methods in Computational Physics: Advances in Research and Applications, 1972, 11: 217-295. |
| [6] |
郭俊义. 地球物理学基础[M]. 北京: 测绘出版社, 2001. GUO Junyi. Fundamentals of geophysics[M]. Beijing: Surveying and Mapping Press, 2001. |
| [7] |
DZIEWONSKI A M, ANDERSON D L. Preliminary reference earth model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356. DOI:10.1016/0031-9201(81)90046-7 |
| [8] |
DAHLEN F A. The normal modes of a rotating, elliptical Earth[J]. Geophysical Journal International, 1968, 16(4): 329-367. DOI:10.1111/j.1365-246X.1968.tb00229.x |
| [9] |
SMITH M L. Translational inner core oscillations of a rotating, slightly elliptical Earth[J]. Journal of Geophysical Research, 1976, 81(17): 3055-3065. DOI:10.1029/JB081i017p03055 |
| [10] |
WAHR J M. A normal mode expansion for the forced response of a rotating Earth[J]. Geophysical Journal International, 1981, 64(3): 651-675. DOI:10.1111/j.1365-246X.1981.tb02689.x |
| [11] |
BACKUS G, GILBERT F. The rotational splitting of the free oscillations of the Earth[J]. Proceedings of the National Academy of Sciences of the United States of America, 1961, 47(3): 362-371. DOI:10.1073/pnas.47.3.362 |
| [12] |
DAHLEN F A, SAILOR R V. Rotational and elliptical splitting of the free oscillations of the Earth[J]. Geophysical Journal International, 1979, 58(3): 609-623. DOI:10.1111/j.1365-246X.1979.tb04797.x |
| [13] |
SHIDA T. On the elasticity of the Earth and the Earth's crust[M]. Memoirs of the College of Science and Kyoto: Kyoto Imperial University, 1912.
|
| [14] |
梁昆淼. 数学物理方法[M]. 北京: 人民教育出版社, 1979. LIANG Kunmiao. Mathematical methods for physics[M]. Beijing: People's Education Press, 1979. |
| [15] |
SUN W K, SJÖBERG L E. Gravitational potential changes of a spherically symmetric Earth model caused by a surface load[J]. Geophysical Journal International, 1999, 137(2): 449-468. |
| [16] |
GUO J Y, LI Y B, HUANG Y, et al. Green's function of the deformation of the Earth as a result of atmospheric loading[J]. Geophysical Journal International, 2004, 159(1): 53-68. DOI:10.1111/j.1365-246X.2004.02410.x |
| [17] |
SUN W K, OKUBO S, VANÍČEK P. Global displacements caused by point dislocations in a realistic Earth model[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B4): 8561-8577. DOI:10.1029/95JB03536 |
| [18] |
ZHOU J, PAN E, BEVIS M. A point dislocation in a layered, transversely isotropic and self-gravitating Earth. Part Ⅰ: analytical dislocation Love numbers[J]. Geophysical Journal International, 2019, 217(3): 1681-1705. DOI:10.1093/gji/ggz110 |
| [19] |
LONGMAN I M. A Green's function for determining the deformation of the earth under surface mass loads: 2. Computations and numerical results[J]. Journal of Geophysical Research, 1963, 68(2): 485-496. DOI:10.1029/JZ068i002p00485 |
| [20] |
汪汉胜, 许厚泽, 李国营. SNREI地球模型负荷勒夫数数值计算的新进展[J]. 地球物理学报, 1996, 39(S1): 182-189. WANG Hansheng, XU Houze, LI Guoying. Improvement of computations of load Love numbers of SNREI Earth model[J]. Chinese Journal of Geophysics, 1996, 39(S1): 182-189. |
| [21] |
MARTINEC Z. Spectral-finite element approach to three-dimensional viscoelastic relaxation in a spherical Earth[J]. Geophysical Journal International, 2000, 142(1): 117-141. DOI:10.1046/j.1365-246x.2000.00138.x |
| [22] |
TANAKA Y, KLEMANN V, FLEMING K, et al. Spectral finite element approach to postseismic deformation in a viscoelastic self-gravitating spherical Earth[J]. Geophysical Journal International, 2009, 176(3): 715-739. DOI:10.1111/j.1365-246X.2008.04015.x |
| [23] |
TANAKA Y, KLEMANN V, MARTINEC Z, et al. Spectral-finite element approach to viscoelastic relaxation in a spherical compressible Earth: application to GIA modelling[J]. Geophysical Journal International, 2011, 184(1): 220-234. DOI:10.1111/j.1365-246X.2010.04854.x |
| [24] |
廖彬彬, 徐建桥, 孙和平, 等. 利用谱元法计算SNREI地球的表面负荷变形[J]. 地球物理学报, 2019, 62(7): 2382-2393. LIAO Binbin, XU Jianqiao, SUN Heping, et al. Spectral element method to load deformation in a SNREI Earth[J]. Chinese Journal of Geophysics, 2019, 62(7): 2382-2393. |
| [25] |
PAN E, CHEN J Y, BEVIS M, et al. An analytical solution for the elastic response to surface loads imposed on a layered, transversely isotropic and self-gravitating Earth[J]. Geophysical Journal International, 2015, 203(3): 2150-2181. DOI:10.1093/gji/ggv432 |
| [26] |
GILBERT F, BACKUS G. Elastic-gravitational vibrations of a radially stratified sphere[M]//HERRMANN G. Dynamics of Stratified Solids. New York: American Society of Mechanical Engineers, 1968: 82-95.
|
| [27] |
CHEN J Y, PAN E, BEVIS M. Accurate computation of the elastic load Love numbers to high spectral degree for a finely layered, transversely isotropic and self-gravitating Earth[J]. Geophysical Journal International, 2018, 212(2): 827-838. |
| [28] |
PAN E. Green's functions for geophysics: a review[J]. Reports on Progress in Physics, 2019, 82(10): 106801. DOI:10.1088/1361-6633/ab1877 |
| [29] |
周江存, 潘尔年, 孙和平, 等. 地球变形近似解析解的构建及应用[J]. 地球物理学报, 2021, 64(10): 3521-3531. ZHOU Jiangcun, PAN Ernian, SUN Heping, et al. The construction of an approximated analytical solution to Earth's deformation and its application[J]. Chinese Journal of Geophysics, 2021, 64(10): 3521-3531. DOI:10.6038/cjg2021P0642 |
| [30] |
PEKERIS C L. The bodily tide and the yielding of the Earth due to tidal loading[J]. Geophysical Journal International, 1978, 52(3): 471-478. DOI:10.1111/j.1365-246X.1978.tb04244.x |
| [31] |
MERRIAM J B. The series computation of the gravitational perturbation due to an ocean tide[J]. Physics of the Earth and Planetary Interiors, 1980, 23(2): 81-86. DOI:10.1016/0031-9201(80)90003-5 |
| [32] |
RAY R D, SANCHEZ B V. Radial deformation of the Earth by oceanic tidal loading[R]. NASA Technical Memorandum 100743, Greenbelt: NASAC, 1989.
|
| [33] |
许厚泽, 陈振邦, 杨怀冰. 海洋潮汐对重力潮汐观测的影响[J]. 地球物理学报, 1982, 25(2): 120-129. XU Houze, CHEN Zhenbang, YANG Huaibing. The effect of oceanic tides on the gravity tidal observations[J]. Chinese Journal of Geophysics, 1982, 25(2): 120-129. DOI:10.3321/j.issn:0001-5733.1982.02.003 |
| [34] |
SCHRAMA E J O. Three algorithms for the computation of tidal loading and their numerical accuracy[J]. Journal of Geodesy, 2005, 78(11): 707-714. |
| [35] |
周江存, 孙和平, 徐建桥, 等. 海潮负荷计算的球谐展开方法[C]//2014年大地测量研究进展学术研讨会论文集. 武汉: 湖北科学技术出版社, 2014: 343-351. ZHOU Jiangcun, SUN Heping, XU Jianqiao, et al. Spherical harmonic expansion method to computation of ocean tide loading[C]//Proceedings of 2014 Progress in Geodesy and Geodynamics. Wuhan: Hubei Science and Technology Press, 2014: 343-351. |
| [36] |
AGNEW D C. NLOADF: a program for computing ocean-tide loading[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5109-5110. DOI:10.1029/96JB03458 |
| [37] |
GOAD C C. Gravimetric tidal loading computed from integrated Green's functions[J]. Journal of Geophysical Research: Solid Earth, 1980, 85(B5): 2679-2683. DOI:10.1029/JB085iB05p02679 |
| [38] |
MATSUMOTO K, SATO T, TAKANEZAWA T, et al. GOTIC2:a program for computation of oceanic tidal loading effect[J]. Journal of the Geodetic Society of Japan, 2001, 47(1): 243-248. |
| [39] |
HWANG C, HUANG Jiufu. SGOTL: a computer program for modeling high-resolution, height-dependent gravity effect of ocean tide loading[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2012, 23(2): 219-229. DOI:10.3319/TAO.2011.10.06.02(Oc) |
| [40] |
MARTENS H R, RIVERA L, SIMONS M. LoadDef: a Python-based toolkit to model elastic deformation caused by surface mass loading on spherically symmetric bodies[J]. Earth and Space Science, 2019, 6(2): 311-323. DOI:10.1029/2018EA000462 |
| [41] |
ZHOU J C, HWANG C, SUN H P, et al. Precise determination of ocean tide loading gravity effect for absolute gravity stations in coastal area of China: effects of land-sea boundary and station coordinate[J]. Journal of Geodynamics, 2013, 68: 29-36. DOI:10.1016/j.jog.2013.03.003 |
| [42] |
王继刚, 周江存. 沿海和岛屿重力海潮负荷改正模型——以马祖岛为例[J]. 大地测量与地球动力学, 2020, 40(8): 794-798. WANG Jigang, ZHOU Jiangcun. Correction model of ocean tide loading on gravity over coastal area and islands: a case study of Matzu Island[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 794-798. |
| [43] |
LEFōVRE F, LYARD F H, LE PROVOST C, et al. FES99:a global tide finite element solution assimilating tide gauge and altimetric information[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(9): 1345-1356. DOI:10.1175/1520-0426(2002)019<1345:FAGTFE>2.0.CO;2 |
| [44] |
BOY J P, GEGOUT P, HINDERER J. Reduction of surface gravity data from global atmospheric pressure loading[J]. Geophysical Journal International, 2002, 149(2): 534-545. DOI:10.1046/j.1365-246X.2002.01667.x |
| [45] |
BOY J P, HINDERER J. Study of the seasonal gravity signal in superconducting gravimeter data[J]. Journal of Geodynamics, 2006, 41(1-3): 227-233. DOI:10.1016/j.jog.2005.08.035 |
| [46] |
NEUMEYER J, BARTHELMES F, DIERKS O, et al. Combination of temporal gravity variations resulting from superconducting gravimeter (SG) recordings, GRACE satellite observations and global hydrology models[J]. Journal of Geodesy, 2006, 79(10): 573-585. |
| [47] |
周江存, 孙和平, 徐建桥. 用地表和空间重力测量验证全球水储量变化模型[J]. 科学通报, 2009, 54(9): 1282-1289. ZHOU Jiangcun, SUN Heping, XU Jianqiao. Validating global hydrological models by ground and space gravimetry[J]. Chinese Science Bulletin, 2009, 54(9): 1282-1289. |
| [48] |
ZHOU Jiangcun, SUN Heping, XU Jianqian, et al. Estimation of local water storage change by space-and ground-based gravimetry[J]. Journal of Applied Geophysics, 2016, 131: 23-28. DOI:10.1016/j.jappgeo.2016.05.007 |
| [49] |
周江存, 徐建桥, 孙和平. 中国大陆精密重力潮汐改正模型[J]. 地球物理学报, 2009, 52(6): 1474-1482. ZHOU Jiangcun, XU Jianqiao, SUN Heping. Accurate correction models for tidal gravity in Chinese continent[J]. Chinese Journal of Geophysics, 2009, 52(6): 1474-1482. DOI:10.3969/j.issn.0001-5733.2009.06.008 |
| [50] |
WILLIAMS S D P, PENNA N T. Non-tidal ocean loading effects on geodetic GPS heights[J]. Geophysical Research Letters, 2011, 38(9): L09314. |
| [51] |
FU Yuning, FREYMUELLER J T, VAN DAM T. The effect of using inconsistent ocean tidal loading models on GPS coordinate solutions[J]. Journal of Geodesy, 2012, 86(6): 409-421. DOI:10.1007/s00190-011-0528-1 |
| [52] |
SHE Yawen, FU Guangyu, LIU Tai. Effect of earth models on coulomb stress change caused by surface load[J]. Pure and Applied Geophysics, 2021, 178(4): 1235-1251. DOI:10.1007/s00024-021-02706-1 |
| [53] |
XUE Liang, FU Yuning, MARTENS H R. Seasonal hydrological loading in the Great Lakes region detected by GNSS: a comparison with hydrological models[J]. Geophysical Journal International, 2021, 226(2): 1174-1186. DOI:10.1093/gji/ggab158 |
| [54] |
孙和平, DUCARME B, 许厚泽, 等. 基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J]. 中国科学D辑: 地球科学, 2005, 35(7): 649-657. SUN Heping, DUCARME B, XU Houze, et al. Adaptability of the ocean and Earth tidal models based on global observations of the superconducting gravimeters[J]. Science in China Series D: Earth Science, 2005, 35(7): 649-657. |
| [55] |
孙和平, 许厚泽, 周江存, 等. 武汉超导重力仪观测最新结果和海潮模型研究[J]. 地球物理学报, 2005, 48(2): 299-307. SUN Heping, XU Houze, ZHOU Jiangcun, et al. Latest observation results from superconducting gravimeter at station Wuhan and investigation of the ocean tide models[J]. Chinese Journal of Geophysics, 2005, 48(2): 299-307. DOI:10.3321/j.issn:0001-5733.2005.02.010 |
| [56] |
SUN H P, JENTZSCH G, XU J Q, et al. Earth's free core nutation determined using C032 superconducting gravimeter at station Wuhan/China[J]. Journal of Geodynamics, 2004, 38(3-5): 451-460. DOI:10.1016/j.jog.2004.07.007 |
| [57] |
李鹏, 李振洪, 冯万鹏, 等. 海潮负荷对沿海地区宽幅InSAR形变监测的影响[J]. 地球物理学报, 2019, 62(8): 2845-2857. LI Peng, LI Zhenhong, FENG Wanpeng, et al. Impacts of ocean tidal loading on coastal deformation mapping with wide-swath InSAR observations[J]. Chinese Journal of Geophysics, 2019, 62(8): 2845-2857. |
| [58] |
YUAN L G, DING X L, SUN H P, et al. Determination of ocean tide loading displacements in Hong Kong using GPS technique[J]. Science China Earth Sciences, 2010, 53(7): 993-1007. DOI:10.1007/s11430-010-3076-2 |
| [59] |
LIU Z G, YUAN L G, HAN K Y, et al. Comparison of GPS-derived ocean tide loading displacements with models in New Zealand[J]. New Zealand Journal of Marine and Freshwater Research, 2021. DOI:10.1080/00288330.2021.1993276 |
| [60] |
WANG H S, XIANG L W, JIA L L, et al. Load Love numbers and Green's functions for elastic Earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2.0[J]. Computers & Geosciences, 2012, 49: 190-199. |
| [61] |
MARTENS H R, RIVERA L, SIMONS M, et al. The sensitivity of surface mass loading displacement response to perturbations in the elastic structure of the crust and mantle[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(5): 3911-3938. DOI:10.1002/2015JB012456 |
| [62] |
NIBAUER T M. Correction gravity mearsurements for the effect of local air pressure[J]. Journal of Geophysics, 1988, 53: 155-162. |
| [63] |
MERRIAM J B. Atmospheric pressure and gravity[J]. Geophysical Journal International, 1992, 109(3): 488-500. DOI:10.1111/j.1365-246X.1992.tb00112.x |
| [64] |
孙和平. 大气重力格林函数[J]. 科学通报, 1997, 42(15): 1640-1646. SUN Heping. Atmospheric gravity Green's functions[J]. Chinese Science Bulletin, 1997, 42(15): 1640-1646. DOI:10.3321/j.issn:0023-074X.1997.15.017 |
| [65] |
CHENG A H D. Poroelasticity[M]. Switzerland: Springer, 2016.
|
| [66] |
LEE Z Y. Coupled problem of thermoelasticity for multilayered spheres with time-dependent boundary conditions[J]. Journal of Marine Science and Technology, 2004, 12(2): 93-101. |
| [67] |
FANG Ming, DONG Danan, HAGER B H. Displacements due to surface temperature variation on a uniform elastic sphere with its Centre of mass stationary[J]. Geophysical Journal International, 2014, 196(1): 194-203. DOI:10.1093/gji/ggt335 |
| [68] |
ZHOU Jiangcun, PAN Ernian, BEVIS M. Deformation due to surface temperature variation on a spherically layered, transversely isotropic and self-gravitating Earth[J]. Geophysical Journal International, 2021, 225(3): 1672-1688. DOI:10.1093/gji/ggab056 |
| [69] |
OKADA Y. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1135-1154. DOI:10.1785/BSSA0750041135 |
| [70] |
BEN-MENAHEM A, SINGH S J, SOLOMON F. Static deformation of a spherical Earth model by internal dislocations[J]. Bulletin of the Seismological Society of America, 1969, 59(2): 813-853. DOI:10.1785/BSSA0590020813 |
| [71] |
BEN-MENAHEM A, SINGH S J, SOLOMON F. Deformation of a homogeneous Earth model by finite dislocations[J]. Reviews of Geophysics, 1970, 8(3): 591-632. DOI:10.1029/RG008i003p00591 |
| [72] |
SMYLIE D E, MANSINHA L. The elasticity theory of dislocations in real Earth models and changes in the rotation of the earth[J]. Geophysical Journal International, 1971, 23(3): 329-354. DOI:10.1111/j.1365-246X.1971.tb01824.x |
| [73] |
SUN W K. Potential and gravity changes raised by dislocations in spherically symmetric Earth models[D]. Tokyo: The University of Tokyo, 1992.
|
| [74] |
SUN W K, OKUBO S. Surface potential and gravity changes due to internal dislocations in a spherical Earth-Ⅰ. Theory for a point dislocation[J]. Geophysical Journal International, 1993, 114(3): 569-592. DOI:10.1111/j.1365-246X.1993.tb06988.x |
| [75] |
SUN W K, OKUBO S. Surface potential and gravity changes due to internal dislocations in a spherical Earth-Ⅱ. Application to a finite fault[J]. Geophysical Journal International, 1998, 132(1): 79-88. |
| [76] |
孙文科. 地震位错理论[M]. 北京: 科学出版社, 2012. SUN Wenke. Theory on seismic dislocation[M]. Beijing: Science Press, 2012. |
| [77] |
DONG J, SUN W K, ZHOU X, et al. Effects of Earth's layered structure, gravity and curvature on coseismic deformation[J]. Geophysical Journal International, 2014, 199(3): 1442-1451. DOI:10.1093/gji/ggu342 |
| [78] |
DONG J, SUN W K, ZHOU X, et al. An analytical approach to estimate curvature effect of coseismic deformations[J]. Geophysical Journal International, 2016, 206(2): 1327-1339. DOI:10.1093/gji/ggw215 |
| [79] |
OKUBO S. Reciprocity theorem to compute the static deformation due to a point dislocation buried in a spherically symmetric earth[J]. Geophysical Journal International, 1993, 115(3): 921-928. DOI:10.1111/j.1365-246X.1993.tb01501.x |
| [80] |
OKUBO S. Asymptotic solutions to the static deformation of the Earth-Ⅰ. Spheroidal mode[J]. Geophysical Journal International, 1988, 92(1): 39-51. DOI:10.1111/j.1365-246X.1988.tb01119.x |
| [81] |
SUN W K. Asymptotic theory for calculating deformations caused by dislocations buried in a spherical Earth: geoid change[J]. Journal of Geodesy, 2003, 77(7-8): 381-387. DOI:10.1007/s00190-003-0335-4 |
| [82] |
SUN W K. Short Note: asymptotic theory for calculating deformations caused by dislocations buried in a spherical earth-gravity change[J]. Journal of Geodesy, 2004, 78(1-2): 76-81. |
| [83] |
SUN W K. Asymptotic solution of static displacements caused by dislocations in a spherically symmetric Earth[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B5): B05402. |
| [84] |
SUN W K, DONG J. Relation of dislocation Love numbers and conventional Love numbers and corresponding Green's functions for a surface rupture in a spherical Earth model[J]. Geophysical Journal International, 2013, 193(2): 717-733. DOI:10.1093/gji/ggt030 |
| [85] |
TAKAGI Y, OKUBO S. Internal deformation caused by a point dislocation in a uniform elastic sphere[J]. Geophysical Journal International, 2017, 208(2): 973-991. DOI:10.1093/gji/ggw424 |
| [86] |
TANG H, SUN W K. Asymptotic expressions for changes in the surface co-seismic strain on a homogeneous sphere[J]. Geophysical Journal International, 2017, 209(1): 202-225. |
| [87] |
ZHOU J, PAN E, BEVIS M. A point dislocation in a layered, transversely isotropic and self-gravitating Earth-Part Ⅱ: accurate Green's functions[J]. Geophysical Journal International, 2019, 219(3): 1717-1728. DOI:10.1093/gji/ggz392 |
| [88] |
TANG H, SUN W K. Analytical equations for an infinite series involving loworder associated Legendre functions in geoscience[J]. Journal of Geodesy, 2021, 95(7): 86. DOI:10.1007/s00190-021-01527-3 |
| [89] |
ZHOU J, PAN E, BEVIS M. A point dislocation in a layered, transversely isotropic and self-gravitating Earth-Part Ⅲ: internal deformation[J]. Geophysical Journal International, 2020, 223(1): 420-443. DOI:10.1093/gji/ggaa319 |
| [90] |
ZHOU J C, PAN E, BEVIS M. A point dislocation in a layered, transversely isotropic and self-gravitating Earth. Part Ⅳ: exact asymptotic solutions of dislocation Love numbers for the special case of isotropy[J]. Geophysical Journal International, 2021, 225(1): 664-683. DOI:10.1093/gji/ggaa612 |
| [91] |
FU G Y, SUN W K. Global co-seismic displacements caused by the 2004 Sumatra-Andaman earthquake (Mw 9.1)[J]. Earth, Planets and Space, 2006, 58(2): 149-152. DOI:10.1186/BF03353371 |
| [92] |
ZHOU J C, SUN W K, SUN H P, et al. Reformulation of co-seismic polar motion excitation and low degree gravity changes: applied to the 2011 Tohoku-Oki earthquake (Mw9.0)[J]. Journal of Geodynamics, 2013, 63: 20-26. DOI:10.1016/j.jog.2012.09.004 |
| [93] |
ZHOU J C, SUN W K, SUN H P, et al. Co-seismic change of length of day based on the point dislocation theory for a SNREI Earth[J]. Journal of Geodynamics, 2014, 79: 18-22. DOI:10.1016/j.jog.2014.04.012 |
| [94] |
ZHOU J C, SUN W K, DONG J. A correction to the article"Geo-center movement caused by huge earthquakes"by Wenke Sun and Jie Dong[J]. Journal of Geodynamics, 2015, 87: 67-73. DOI:10.1016/j.jog.2015.02.003 |
| [95] |
ZHOU J C, SUN W K, JIN S G, et al. Rotation change in the orientation of the centre-of-figure frame caused by large earthquakes[J]. Geophysical Journal International, 2016, 206(2): 999-1008. DOI:10.1093/gji/ggw182 |
| [96] |
XU C Y, SUN W K. Earthquake-origin expansion of the Earth inferred from a spherical-Earth elastic dislocation theory[J]. Geophysical Journal International, 2014, 199(3): 1655-1661. DOI:10.1093/gji/ggu364 |
| [97] |
周江存, 孙和平, 徐建桥, 等. 重力位能同震变化及其构造意义——以青藏高原地区为例[J]. 地球物理学报, 2017, 60(6): 2493-2499. ZHOU Jiangcun, SUN Heping, XU Jianqiao, et al. Co-seismic change of gravitational potential energy and its tectonic implications: a case study of the Tibetan Plateau[J]. Chinese Journal of Geophysics, 2017, 60(6): 2493-2499. |
| [98] |
XU C Y, CHAO B F. Coseismic changes of gravitational potential energy induced by global earthquakes based on spherical-Earth elastic dislocation theory[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(5): 4053-4063. DOI:10.1002/2017JB014204 |
| [99] |
XU C Y. Coseismic changes in the kinetic rotational energy of the Earth from 1976 to 2019[J]. Geophysical Journal International, 2021, 224(2): 1127-1132. |
| [100] |
YU C P, VAVRYČUK V, ADAMOVÁ P, et al. Moment tensors of induced microearthquakes in the Geysers geothermal reservoir from broadband seismic recordings: implications for faulting regime, stress tensor, and fluid pressure[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(10): 8748-8766. DOI:10.1029/2018JB016251 |
| [101] |
CHEN S Y, LIU P X, GUO Y S, et al. Co-seismic response of bedrock temperature to the Ms6.3 Kangding earthquake on 22 November 2014 in Sichuan, China[J]. Pure and Applied Geophysics, 2019, 176(1): 97-117. DOI:10.1007/s00024-018-1933-7 |
| [102] |
JAHR T, BUNTEBARTH G, SAUTER M. Earth tides as revealed by micro-temperature measurements in the subsurface[J]. Journal of Geodynamics, 2020, 136: 101718. DOI:10.1016/j.jog.2020.101718 |
| [103] |
唐河, 孙文科. 黏弹地球地震变形理论研究进展和展望[J]. 地球与行星物理论评, 2021, 52(1): 11-26. TANG He, SUN Wenke. Progress and prospect of deformation theory in the viscoelastic Earth[J]. Reviews of Geophysics and Planetary Physics, 2021, 52(1): 11-26. |
| [104] |
GÓMEZ D D, BEVIS M, PAN E, et al. The influence of gravity on the displacement field produced by fault slip[J]. Geophysical Research Letters, 2017, 44(18): 9321-9329. DOI:10.1002/2017GL074113 |
| [105] |
WANG R J. The dislocation theory: a consistent way for including the gravity effect in (visco) elastic plane-earth models[J]. Geophysical Journal International, 2005, 161(1): 191-196. DOI:10.1111/j.1365-246X.2005.02614.x |





