2. 中国科学院上海天文台, 上海 200030;
3. 湘潭大学土木工程学院, 湖南 湘潭 411105
2. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
3. School of Civil Engineering, Xiangtan University, Xiangtan 411105, China
全球导航卫星系统(GNSS)可以向全球用户提供高精度定位、导航和授时(PNT)服务[1]。早期GNSS仅能提供米级的伪距单点定服务,现阶段可以提供厘米级甚至毫米级的精密单点定位服务。精密单点定位(PPP)是20世纪发展起来的空间定位技术,即利用GNSS测站伪距和载波相位观测值及精密卫星轨道和种差产品获得高精度的位置信息, 其定位方式灵活,因此广泛应用于导航定位、精密授时和灾害监测等领域[2-3]。相比传统的双差相对定位,PPP一般采用非差相位和伪距观测值,一般不需要其他参考站观测值[4],可以精确估计接收机绝对位置信息、接收机钟差、天顶对流层延迟和电离层延迟等参数[4-5]。20多年来,PPP技术先后经历了从静态到动态、从单系统到多系统、从模糊度浮点解到固定解、从双频到单频和多频、从后处理到实时定位,以及从PPP到PPP-RTK(精密单点实时动态定位),已成为卫星导航定位领域的前沿热点方向,具有重要和广泛的应用前景[6]。
随着多频多系统GNSS的快速发展,包括中国的北斗卫星导航系统(BDS)、美国的GPS、俄罗斯的GLONASS、欧洲的Galileo系统,以及日本的准天顶卫星导航系统(QZSS)和印度区域导航卫星系统(IRNSS)等,优化了导航卫星几何构型,给用户提供更多频率和更多系统的伪距、相位和多普勒观测数据,为数据处理带来更多的选择和思路,如周跳探测、定位模型、模糊度固定、钟差估计和电离层建模等[7]。众多学者研究不同频率、不同系统GNSS观测组合和提高多频多系统GNSS PPP模糊度收敛时间、定位精度和可靠性等。近几年,GNSS PPP技术主要侧重于高采样率卫星钟差实时估计、多频多系统PPP、PPP增强及PPP-RTK等方面,取得一系列进展。如分析和评估了单频到三频GNSS PPP模型的定位性能,并与传统单频和双频PPP定位结果相比,三频观测值的加入能提高定位精度[8]。此外,BDS和Gaileo系统还提供四频到五频的观测值,研究结果表明多频多系统GNSS PPP显著缩短模糊度收敛时间和提高定位精度[9-10]。
另外,多频多系统GNSS观测也扩大了GNSS应用,如共视、全视、PPP等多种高精度时频传递,以及确定两地重力位差等[11-12]。联合多频多系统GNSS可获得更多视线方向的可降水汽量和电离层总电子含量,提高了GNSS气象学和空间天气监测的时间空间分辨率等。但同时多频多系统GNSS观测也带来了诸多的问题和挑战,如多频多系统GNSS PPP模型、周跳探测、模糊度固定、频间偏差、差分码偏差、钟差、对流层延迟、电离层延迟等[13-16]。例如GPS、BDS、Galileo和QZSS等卫星导航系统采用的是码分多址(CDMA)技术,而GLONASS系统采用的是频分多址(FDMA)技术,不同卫星信号在接收机内部产生的伪距和相位硬件延迟是不同的,即频间偏差(IFB)。不同频点观测值估计得到的卫星钟差不一致,即卫星钟差频间偏差(IFCB),以及BDS-2和BDS-3两个系统采用不同的信号接收和处理单元,存在时间延迟偏差(TDB)等,需要合理估计和消除[10, 15]。
为此,针对当前多频多系统GNSS PPP模型、参数估计及其应用,本文系统性地给出了单频到五频多系统GNSS PPP模型,评估了单频到五频多系统GNSS PPP定位、钟差、对流层延迟、电离层延迟和硬件延迟估计性能,并展示了最新多频多系统GNSS PPP气象学、电离层模拟、时频传递、建筑物安全和地震监测等应用进展,最后讨论了多频多系统GNSS PPP应用前景与展望。
1 GNSS PPP模型对于GNSS单系统单历元观测值,接收机r在历元t时刻观测到的卫星s原始非差伪距和相位观测值可以表示为[17]
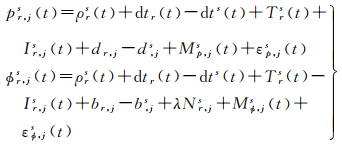 (1)
(1)
式中,pr, js(t)和ϕr, js(t)分别表示伪距和相位观测值;ρrs(t)表示接收机与卫星之间几何距离;dtr(t)和dts(t)表示接收机和卫星钟差延迟;Trs(t)表示对流层延迟;Ir, js(t)表示GNSS单系统第j频点上的电离层斜延迟;dr, j和d, js分别表示接收机和卫星伪距未校准硬件延迟(UCD);br, j和b, js分别表示接收机和卫星相位未校准硬件延迟(UPD);Nr, js表示第j频点上的整周模糊度;Mp, js(t)和Mϕ, js(t)分别表示伪距和相位观测多路径;εp, js(t)和εϕ, js(t)分别表示伪距和相位观测值噪声。
PPP随机模型反映了观测值的统计特性,最常采用的是基于高度角的函数模型。GNSS卫星的高度角越低,GNSS观测值受到的大气延迟和多路径效应影响就越大。因此,高度角随机模型将观测值测量噪声描述为卫星高度角的函数,一般可表示为σ=a/sin E,其中,E为卫星高度角,a为不同系统伪距和相位观测值的特定系数。假设不同频率观测值之间不相关且噪声相同,则原始观测值(非差非组合)PPP模型对应的方差协方差可以表示为
 (2)
(2)
式中,I为单位矩阵,其阶数与非差非组合PPP的频率数有关,如三频则为6阶单位矩阵。需要说明的是,其他PPP模型的随机模型可以由式(2) 扩充表示为
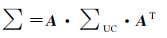 (3)
(3)
式中,A为模型的系数矩阵。
为了消除某些系统误差的影响,通常对GNSS原始观测值进行线性组合,包括几何无关组合、无电离层组合、宽巷组合和窄巷组合等[18]。无论哪种组合都涉及观测函数模型的改变,GNSS PPP函数模型描述相应观测量与待估参数之间的函数关系。根据当前多系统GNSS频率数,可以将GNSS PPP模型分为单频、双频、三频、四频和五频PPP模型。表 1概括了相应GNSS PPP模型的类型[19-25],包括单频到五频电离层浮点非差非组合,即接收机UCD被接收机钟差和电离层延迟等参数吸收,将电离层延迟等作未知参数估计;无电离层组合,即通过无电离层组合来消除各观测值电离层一阶项的影响;电离层改正,即电离层延迟通过电离层模型直接改正,如采用全球电离层格网模型(GIM)进行改正等;电离层加权PPP模型,即增加了电离层外部虚拟观测值及其对应约束方差的电离层加权非差非组合PPP模型。
| 频率 | 模型1 | 模型2 | 模型3 | 模型4 |
| 单频 | SF1 (电离层浮点非差非组合)[19] |
SF2 (无电离层组合)[20] |
SF3 (电离层改正)[21] |
SF4 (电离层加权)[22] |
| 双频 | DF1 (电离层浮点非差非组合)[22] |
DF2 (无电离层组合)[21] |
DF3 (UofC)[23] |
DF4 (电离层加权)[24] |
| 三频 | TF1 (电离层浮点非差非组合)[21] |
TF2 (无电离层双组合)[24] |
TF3 (无电离层组合)[24] |
TF4 (电离层加权)[24] |
| 四频 | QF1 (电离层浮点非差非组合)[24] |
QF2 (无电离层双组合)[2] |
QF3 (无电离层组合)[21] |
QF4 (电离层加权)[2] |
| 五频 | FF1 (电离层浮点非差非组合)[25] |
FF2 (无电离层四组合)[25] |
FF3 (无电离层组合)[25] |
FF4 (电离层加权)[25] |
2 参数估计与评估
为了分析多频多系统GNSS PPP定位、钟差、硬件延迟偏差和大气延迟估计性能,本文选择多系统GNSS试验(MGEX)提供的多频多系统GNSS观测数据,估计和分析了台站坐标、钟差、对流层和电离层延迟等参数,并评论了相关国内外研究进展。
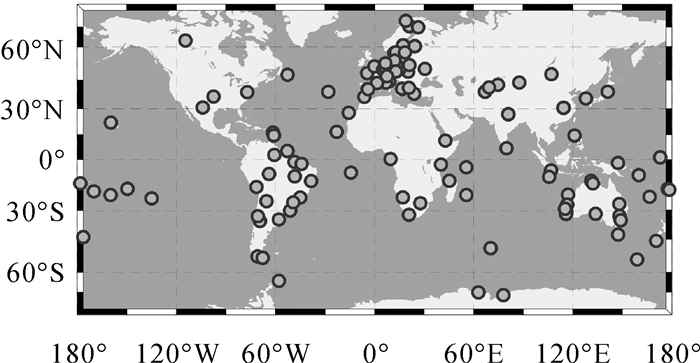
2.1 GNSS观测数据图 1为本文所选取的MGEX单频到五频多系统GNSS测站分布图,均可观测到GPS、BDS、Galileo和GLONASS数据[24]。其中,70个测站可观测到BDS-2数据,77个测站可以观测到BDS-3 B1I/B3I/B1C/B2a数据,20个测站可以观测到BDS-3 B1I/B3I/B1C/B2a/B2/B2b数据。
|
| 图 1 MGEX测站地理分布 Fig. 1 Geographical distribution of MGEX stations |
2.2 定位精度
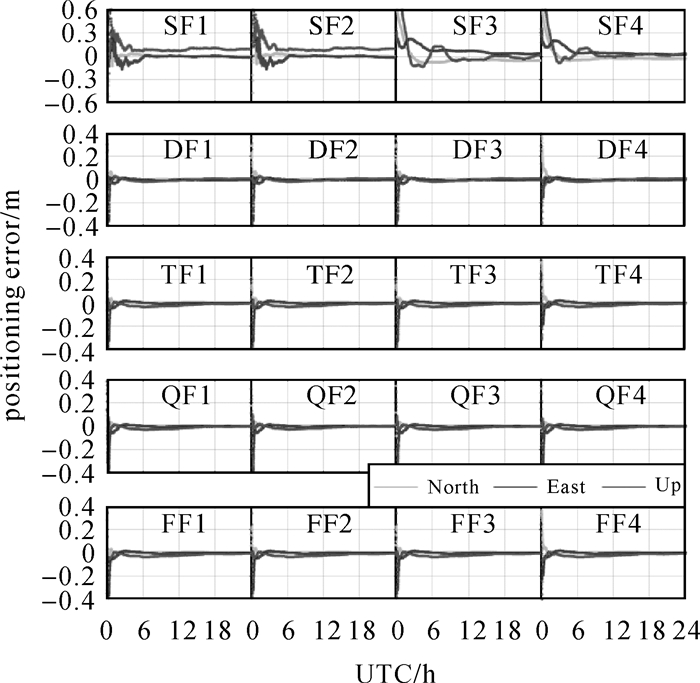
利用IGS精密卫星轨道、卫星钟差产品及单频到五频MGEX多系统GNSS观测数据基于PPP可以精确估计测站坐标。图 2给出了2020年DOY 275 FFMJ测站BDS-3 B1I单频、B1I+B3I双频、B1I+B3I+B2a三频、B1I+B3I+B1C+B2a四频和B1I+B3I+B2b+B2a+B2五频静态PPP定位误差[24]。BDS静态单频PPP定位误差收敛后在北、东和垂直方向定位精度为厘米到分米级,多频PPP定位误差收敛后三维坐标精度达到厘米甚至毫米级,明显优于单频PPP定位精度,但双频到五频PPP定位精度比较接近。
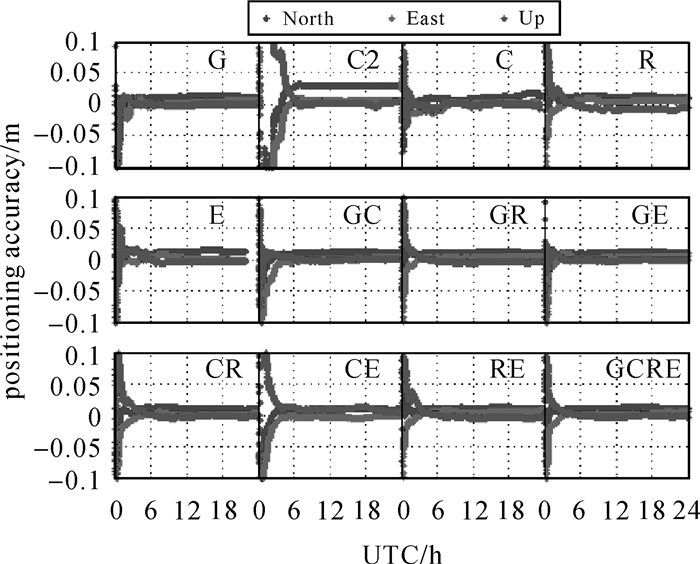
为了进一步比较不同系统GNSS PPP定位性能,分别估计和比较了GPS(G)、BDS-2(C2)、BDS-2/3(C)、GLONASS(R)、Galileo(E)、GPS+BDS-2/3(GC)、GPS+GLONASS(GR)、GPS+Galileo(GE)、BDS-2/3+GLONASS(CR)、BDS-2/3+Galileo(CE)、GLONASS+Galileo(RE)和GPS+BDS-2/3+GLONASS+Galileo(GCRE)静态PPP定位结果。除了BDS-2可见卫星少和星座分布差,结果稍差一点,其他均达到厘米级定位结果,而多系统GNSS相比单系统,极大降低了模糊度收敛时间和提高定位精度,甚至达到了毫米级。如图 3给出了2019年DOY 024 BRCH站单系统和多系统双频无电离层组合PPP定位误差,明显看出多系统GNSS PPP定位结果好于单系统[26]。
2.3 接收机钟差
接收机钟差是GNSS PPP误差源之一,利用多频多系统GNSS PPP可以估计接收机钟差。文献[21]估计了2019年DOY 017 BRCH-XIA3时间链路BDS B1I单频、B1I+B3I双频、B1I+B3I+B2a三频和B1I+B3I+B1C+B2a四频PPP接收机钟差之差(图 4)。单频PPP接收机钟差之差噪音较大,双频到四频PPP结果基本一致,多频PPP接收机钟差之差明显好于单频PPP结果。文献[27]进一步利用Galileo双频(DF)、三频(TF)、四频(QF)和五频(FF)PPP模型估计了2020年DOY 190—DOY 196 BRUX-CEBR、BRUX-PTBB、BRUX-ROAG和BRUX-USN7时间链路钟差平均偏差,双频到五频PPP结果平均偏差基本一致。例如BRUX-PTBB时间链路双频到五频PPP钟差平均偏差均为0.01 ps,RMS分别为7.02、6.88、6.97和6.87 ps,表明五频PPP相比双频钟差估计并没有明显提高。
2.4 对流层延迟
对流层天顶湿延迟(ZWD)在GNSS PPP中一般当作未知参数估计,求得ZWD后可进一步计算对流层天顶总延迟(ZTD)。文献[24]利用BDS单频、双频、三频、四频和五频观测估计了2020年DOY 288 FFMJ测站ZTD时间序列,对应的ZTD误差RMS分别为(1.1,1.1,3.2,1.2)、(0.5,0.5,0.5,0.5)、(0.5,0.5,0.5,0.5)、(0.5,0.5,0.5,0.5)和(0.5,0.5,0.5,0.5) cm。相比于单频GNSS PPP,多频GNSS PPP显著提高ZTD估计精度,且多频结果比较接近。为了进一步分析不同系统GNSS PPP估计ZTD精度,GPS(G)、BDS-2(C2)、BDS-2/3(C)、GLONASS(R)、Galileo(E)、GPS+BDS-2/3(GC)、GPS+GLONASS(GR)、GPS+Galileo(GE)、BDS-2/3+GLONASS(CR)、BDS-2/3+Galileo(CE)、GLONASS+Galileo(RE)和GPS+BDS-2/3+GLONASS+Galileo(GCRE)静态PPP分别估计ZTD,并与iGMAS产品进行比较。图 5给出了2019年DOY 024 BRCH站单系统和多系统双频无电离层组合PPP估计ZTD和iGMAS产品差[26],当模糊度收敛后,单系统和多系统GNSS PPP估计ZTD基本上接近,但多系统GNSS PPP极大提高ZTD估计速度和精度。
2.5 硬件延迟和频间偏差
在多频多系统GNSS PPP模型中,单系统GNSS接收机硬件延迟(DCB)和不同系统GNSS卫星信号频间偏差(IFB)被当成未知参数估计。利用DF4、TF4、QF4和FF4模型估计了FFMJ和WUH2测站接收机BDS C2I-C6I DCB时间序列,并给出了TF1、TF2、TF4、QF1、QF4、FF1、FF2和FF4模型估计的IFB时间序列,总体DCB和IFB时间序列比较稳定[24]。本文进一步估计和分析了GPS、GLONASS、BDS和Galileo卫星DCB及其精度。传统的方法采用电离层建模或使用GIM模型来消除TEC参数,然后估计各接收机和卫星硬件延迟。为了减小电离层建模和GIM不确定性影响,使用电离层浮点非差非组合PPP模型直接估计VTEC获取卫星和接收机的DCB,然后基于卫星DCB零均值约束来分离卫星和接收机DCB,进而获取多频多系统GNSS卫星和接收机DCB。对于BDS系统,只有两种类型的DCB被估计(C2I-C7I和C2I-C6I,其中BDS-3只有可用的C2I-C6I观测数据)。本文估计的多频多系统GNSS接收机和卫星DCB与CAS和DLR产品具有较好的一致性,接收机DCB一般没有卫星DCB稳定。表 2列出了多频多系统GNSS卫星DCB相对于MGEX产品的平均RMS(ns),GPS、GLONASS、BDS和Galileo卫星DCB相对于CAS和DLR产品的RMS均值分别为0.12、0.23、0.21和0.13 ns[28],表明非差非组合PPP模型能够较好地估计多频多系统GNSS接收机和卫星DCB。
| 系统 | DCB类型 | CAS | DLR |
| GPS | C1C-C2W | 0.07 | 0.10 |
| C1W-C2W | 0.10 | 0.20 | |
| C1C-C5X | 0.12 | 0.14 | |
| C1C-C5Q | 0.10 | 0.10 | |
| GLONASS | C1C-C2P | 0.12 | 0.17 |
| C1P-C2P | 0.27 | 0.33 | |
| C1C-C2C | 0.16 | 0.21 | |
| Galileo | C1X-C5X | 0.11 | 0.11 |
| C1X-C7X | 0.11 | 0.11 | |
| C1X-C8X | 0.11 | 0.12 | |
| C1C-C5Q | 0.13 | 0.13 | |
| C1C-C7Q | 0.12 | 0.12 | |
| C1C-C8Q | 0.12 | 0.12 | |
| BDS | C2I-C7I | 0.25 | 0.14 |
| C2I-C6I | 0.24 | 0.22 |
3 多频多系统GNSS PPP应用 3.1 GNSS PPP气象学应用
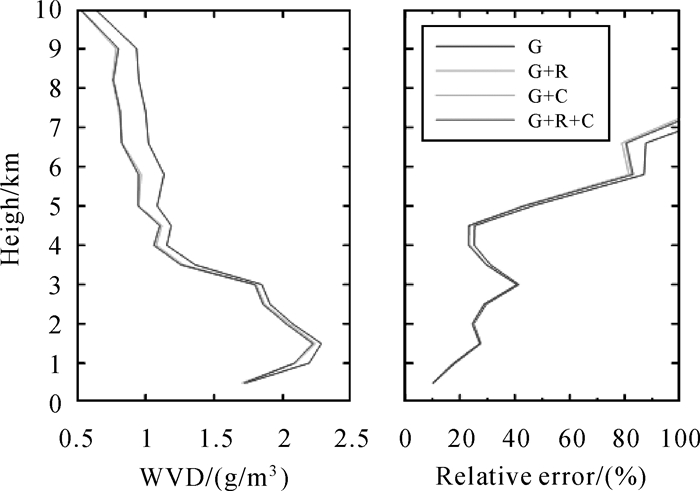
利用GNSS PPP技术可以估计GNSS测站对流层天顶总延迟和可降水汽量,但无法获取水汽的垂直分布信息。目前无线电探空仪广泛用于探测大气水汽垂直分布,但是时空分辨率低。多频多系统GNSS全球跟踪站和区域综合CORS网为三维水汽层析提供了更多的观测数据源,可以进一步提高分辨率和精度。例如利用2014年DOY 170—176武汉CORS网7个测站多系统GNSS(GPS/GLONASS/BDS)观测数据进行水汽层析,并利用GPS系统和多系统水汽层析廓线与对应ERA5廓线间的平均皮尔森相关性分析,统计7 d不同层析高度的水汽密度和ERA5再分析数据的RMS和相对误差,多系统GNSS平均皮尔森相关性均为96.4%,GPS系统为95.9%[29]。由图 6(a)可知,不同高度处RMS值总体上呈现出随高度递减的趋势,而随着高度的增加,三系统与GPS单系统间RMS值偏差在递增,这是由于近地表水汽密度随高度的增加而递减。进一步利用该地区探空站(站号:57494)观测结果进行比较,结果表明,多系统GNSS层析水汽密度剖面更接近于探空气球观测,好于单一系统GNSS水汽层析结果,但提高有限。
3.2 电离层模拟
电离层延迟是GNSS导航定位重要的误差源之一,反过来利用双频及以上GNSS观测可以估计电离层总电子含量。GNSS电离层建模的关键是精确提取电离层斜路径总电子含量(STEC),常用方法主要有两种,即载波相位平滑伪距方法(CCL)和PPP[30]。最近研究结果表明,相对于CCL,PPP提取电离层STEC精度更高[31]。基于PPP提取电离层STEC可以分为单频和多频,其中单频是采用单频电离层浮点解非差非组合GNSS PPP模型估计电离层STEC参数,或采用单频半消电离层组合GNSS PPP模型来估计电离层STEC[31]。多频GNSS PPP可以直接估计STEC和卫星加接收机差分码偏差,常采用双频电离层浮点解非差非组合PPP模型(表 1的DF1),评估发现估计的STEC观测值噪声相比CCL降低了超过70%[32]。此外,DF1也与双频无电离层组合PPP(表 1中DF2)和双频UofC PPP(表 1中DF3)提取的STEC基本上一致[33-35]。以上双频PPP模型也可以扩展到多频(表 1),同样可用于估计电离层STEC[30]。通过映射函数可将STEC转化为垂直总电子含量(VTEC),以及建立二维电离层格网模型,应用于GNSS导航定位电离层延迟改正和空间天气变化监测,例如利用GNSS估计TEC监测磁暴期间电离层扰动特征[36]。
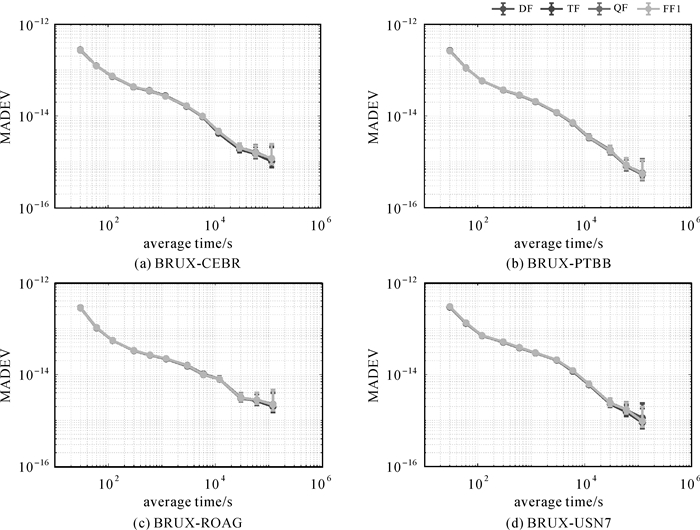
3.3 时间频率传递多频多系统GNSS PPP可以估计接收机钟差,当接收机配备了高精度原子钟,可以进一步用于精密时间频率传递。分析了BDS PPP模型BRCH-XIA3时间链路BDS-3单频、双频、三频和四频PPP时间传递的阿伦方差[21],结果表明,BDS单频、双频、三频和四频PPP时间传递10 000 s频率稳定度要优于1.6×10-14。文献[27]进一步利用Galileo双频(DF)、三频(TF)、四频(QF)和五频(FF)PPP模型估计了2020年DOY 190—196 BRUX-CEBR(a)、BRUX-PTBB(b)、BRUX-ROAG(c)和BRUX-USN7(d)时间链路的时间传递改进阿伦方差(MADEV)[27],结果表明双频到五频PPP估计的频率稳定度基本一致(图 7)。时间传递120 000 s频率稳定度双频估计平均为1.23×10-15,三频估计平均为1.15×10-15,四频估计平均为1.23×10-15,五频估计平均为1.23×10-15。
|
| 图 7 2020年DOY 190—196 BRUX-CEBR、BRUX-PTBB、BRUX-ROAG和BRUX-USN7时间链路Galileo双频(DF)、三频(TF)、四频(QF)和五频(FF)PPP模型估计的时间传递改进阿伦方差(MADEV)[27] Fig. 7 MADEV of the Galileo dual-frequency (DF), triple-frequency (TF), quad-frequency (DF) and five-frequency (FF) PPP time transfer using the time-link BRUX-CEBR, BRUX-PTBB, BRUX-ROAG and BRUX-USN7 on DOY 190—196, 2020[27] |
3.4 建筑物安全监测
高层建筑物、桥梁、水库大坝、道路等形变和地面沉降需要高精度近实时地监测与健康评估。传统技术成本高,劳动强度大,无法连续监测,而GNSS PPP能够连续、全天候、高精度、近实时地监测建筑物形变,提升了自动化程度和监测效率,为监测、评估和预警建筑物安全与健康状态提供重要的保障。由于大型桥梁和高层建筑物等经常遮挡GNSS信号,多频多系统GNSS可以提供监测系统更多观测数据,从而提高定位精度和可靠性。文献[37]提出了一种联合GPS、GLONASS、BDS等实时动态PPP监测方法,并在高层建筑、大坝、桥梁等工程中验证了其可靠性。文献[38]提出了双频载波相位GPS与北斗系统相结合的变形监测数据处理策略,提高了GNSS PPP桥梁动态监测的可靠性。文献[39]利用双频单系统和多系统GNSS高采样率观测数据估计了工程结构形变行为和振荡频率,与差动变压位移传感器(LVDT)观测相比,GLONASS、GPS和GPS+GLONASS PPP估计的振荡频率幅度偏差分别不超过6.0、4.5、3.9 mm,多系统GNSS PPP相比单系统PPP结果更接近实测数据,更好地监测工程结构振荡频率幅度。
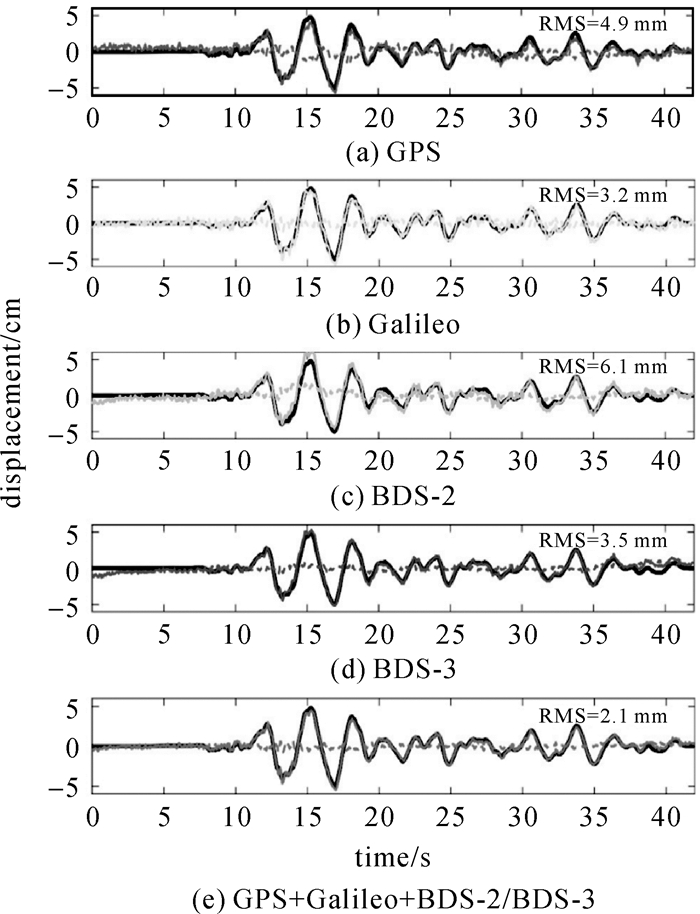
3.5 地震监测与预警传统地震监测利用地震仪或加速度计,但地震仪观测数据存在饱和和数据缺失等问题,不能完全地记录地震同震位移振幅。加速度计数据不会缺失,但数据积分得到的地震位移可能会因仪器的倾斜和旋转而失真[40]。如今GNSS能够近实时高精度精密单点定位,可以快速估计绝对地震位移和震级等。为了验证单系统和多系统GNSS估计地震波形性能,文献[41]利用0.5 Hz GPS、Galileo、BDS-2、BDS-3和GPS+Galileo+BDS-2/3观测数据基于PPP分别估计了形变位移,并与2010年4月4日7.2级El Mayor-Cucapah地震奇瓦瓦站强震仪模拟地震波东西方向分量进行比较,两者差异均方根(RMS)分别为4.9、3.1、6.1、3.5和2.1 cm,其中联合多系统GNSS PPP估计地震波形精度最高(图 8)。
|
| 图 8 2010年7.2级El Mayor-Cucapah地震奇瓦瓦站强震仪模拟地震波东西方向分量(黑色)和GNSS PPP估计结果比较[40] Fig. 8 Simulated seismic waveforms by the embedded encoder of the shake table in the east-west component at Chihuahua station for the 2010 Mw 7.2 El Mayor-Cucapah earthquake (black) and the displacement derived from GNSS PPP[40] |
利用北斗试验跟踪站(BETS)提供的LASA测站1 Hz GPS、BDS、GLONASS和Galileo观测数据估计了2015年4月25日尼泊尔Mw 7.8级地震位移,包括动态PPP(DPPP)、常速度(CV)动态PPP(CVDPPP)和常加速度(CA)动态PPP(CADPPP)模型BDS、GPS、BDS+GPS、BDS+GLONASS和BDS+GPS+GLONASS+Galileo在地震发生初始时刻300 s期间相应的加速度、速度和位移时间序列,与西藏地区附近的LSA强震仪站记录结果对比,具有较好的一致性[24]。联合多系统GNSS PPP估计的速度和加速度波更平滑,验证了多系统GNSS PPP监测地震同震位移的优势。
4 总结与展望本文概括了单频到五频多系统GNSS精密单点定位(PPP)模型,详细估计和分析了单频到五频多系统GNSS PPP定位、钟差、对流层延迟、接收机和卫星硬件延迟、频间偏差等性能,最后给出了GNSS PPP在GNSS气象学、电离层模拟、时间频率传递、建筑物安全和地震监测等最新应用进展。结果表明,多频多系统GNSS极大地提高了GNSS PPP参数估计精度和应用可靠性。
随着多频多系统GNSS星座增多、测站增加、算法完善及卫星轨道与钟差产品精度的提高,GNSS PPP在大地测量、时频传递和灾害监测预警等方面发挥重要的作用。例如,利用实时多频多系统GNSS PPP获得高精度的台站位移、可降水汽量和电离层电子含量等,可应用和提高滑坡、地震、海啸、气象和空间天气监测与预警能力。在爱因斯坦提出的引力红移理论的基础上,所有精密时钟在最接近平均海面的封闭表面运行速度相同,也称为等时率大地水准面。通过高精度多频多系统GNSS PPP时间频率比对技术或可能确定两地的重力位差和高程差等[12],具有重要的应用前景。但GNSS PPP仍存在诸多问题和局限性,如需要实时高精度的卫星轨道和钟差信息,以及较难模拟多路径延迟、映射函数存在较大误差[42]、模糊度收敛时间过长、地面测站仍然有限和GNSS接收信号失锁等。随着地球低轨卫星(LEO)的迅速发展,搭载多频GNSS接收机提供更高的空间分辨率观测数据,且不受对流层和地面多路径等影响,联合LEO低轨卫星和地面GNSS观测将为卫星定轨以及大气监测等提供更多有效的观测数据,带来新的机遇。同时LEO播发导航信号和误差改正信息,实现LEO导航定位和导航增强,有助于提高GNSS PPP模糊度收敛时间和导航定位精度。
另外,基于LEO卫星观测数据可以估计顶部电离层和等离子体层的变化特性及理解电离层与等离子层之间的耦合过程。联合LEO卫星GNSS和地基GNSS观测可以更详细地分析电离层和等离子层的变化特性及其各自贡献[43]。此外,相比于地基GNSS观测,LEO卫星GNSS观测数据受电离层变化影响较小,联合LEO卫星和地基GNSS观测数据估计GNSS伪距时变观测值特定信号偏差(OSB)特性成为新的可能。
| [1] |
杨元喜, 杨诚, 任夏. PNT智能服务[J]. 测绘学报, 2021, 50(8): 1006-1012. YANG Yuanxi, YANG Cheng, REN Xia. PNT intelligent services[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(8): 1006-1012. DOI:10.11947/j.AGCS.2021.20210051 |
| [2] |
ZUMBERGE J, HEFLIN M, JEFFERSON D, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [3] |
KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [4] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013. LI Xingxing. Rapid ambiguity resolution in GNSS precise point positioning[D]. Wuhan: Wuhan University, 2013. |
| [5] |
杨旭海, 李孝辉, 华宇, 等. 卫星授时与时间传递技术进展[J]. 导航定位与授时, 2021, 8(4): 1-10. YANG Xuhai, LI Xiaohui, HUA Yu, et al. Technical progress of satellite time service and time transfer[J]. Navigation Positioning and Timing, 2021, 8(4): 1-10. DOI:10.19306/j.cnki.2095-8110.2021.04.001 |
| [6] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100. ZHANG Xiaohong, HU Jiahuan, REN Xiaodong. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100. DOI:10.11947/j.AGCS.2020.20200328 |
| [7] |
葛玉龙. 多频多系统精密单点定位时间传递方法研究[D]. 西安: 中国科学院大学(中国科学院国家授时中心), 2020. GE Yulong. Research on methodology of multi-frequency and multi-GNSS precise point positioning time transfer[D]. Xi'an: University of Chinese Academy of Sciences (National Time Service Center, Chinese Academy of Sciences), 2020. |
| [8] |
GUO Fei, ZHANG Xiaohong, WANG Jinling, et al. Modeling and assessment of triple-frequency BDS precise point positioning[J]. Journal of Geodesy, 2016, 90(11): 1223-1235. DOI:10.1007/s00190-016-0920-y |
| [9] |
苏珂, 金双根. BDS/Galileo四频精密单点定位模型性能分析与比较[J]. 测绘学报, 2020, 49(9): 1189-1201. SU Ke, JIN Shuanggen. Analysis and comparisons of the BDS/Galileo quad-frequency PPP models performances[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1189-1201. DOI:10.11947/j.AGCS.2020.20200236 |
| [10] |
SU Ke, JIN Shuanggen, JIAO Guoqiang. Assessment of multi-frequency global navigation satellite system precise point positioning models using GPS, BeiDou, GLONASS, Galileo and QZSS[J]. Measurement Science and Technology, 2020, 31(6): 064008. DOI:10.1088/1361-6501/ab69d5 |
| [11] |
QIN Weijin, GE Yulong, ZHANG Zhe, et al. Accounting BDS3-BDS2 inter-system biases for precise time transfer[J]. Measurement, 2020, 156: 107566. DOI:10.1016/j.measurement.2020.107566 |
| [12] |
李纯. 多系统GNSS精密单点定位时间传递与高程差估计[D]. 湘潭: 湘潭大学, 2020. LI Chun. Time frequency transfer and elevation difference from multi-GNSS precise point positioning[D]. Xiangtan: Xiang Tan University, 2020. |
| [13] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018. ZHOU Feng. Theory and methodology of multi-GNSS undifferenced and uncombined precise point positioning[D]. Shanghai: East China Normal University, 2018. |
| [14] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-407. ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1399-1407. DOI:10.11947/j.AGCS.2017.20170327 |
| [15] |
汪奇生. 多模多频GNSS差分码偏差估计及电离层建模研究[D]. 武汉: 中国地质大学, 2021. WANG Qisheng. Study of differential code bias estimation and ionosphere modeling using multi-mode and multi-frequency GNSS observations[D]. Wuhan: China University of Geosciences, 2021. |
| [16] |
LI Pan, JIANG Xinyuan, ZHANG Xiaohong, et al. GPS+Galileo+BeiDou precise point positioning with triple-frequency ambiguity resolution[J]. GPS Solutions, 2020, 24(3): 78. DOI:10.1007/s10291-020-00992-1 |
| [17] |
LEICK A, RAPOPORT L, TATARNIKOV D. GPS satellite surveying[M]. 4th ed. Hoboken: John Wiley & Sons, 2015.
|
| [18] |
张宝成, 欧吉坤. 论精密单点定位整周模糊度解算的不同策略[J]. 测绘学报, 2011, 40(6): 710-716. ZHANG Baocheng, OU Jikun. On the different strategies for integer ambiguity resolution in precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 710-716. |
| [19] |
STERLE O, STOPAR B, PREŠEREN P. Single-frequency precise point positioning: an analytical approach[J]. Journal of Geodesy, 2015, 89(8): 793-810. DOI:10.1007/s00190-015-0816-2 |
| [20] |
LI Bofeng, ZANG Nan, GE Haibo, et al. Single-frequency PPP models: analytical and numerical comparison[J]. Journal of Geodesy, 2019, 93(12): 2499-2514. DOI:10.1007/s00190-019-01311-4 |
| [21] |
JIN Shuanggen, SU Ke. PPP models and performances from single-to quad-frequency BDS observations[J]. Satellite Navigation, 2020, 1(1): 16. DOI:10.1186/s43020-020-00014-y |
| [22] |
GAO Zhouzheng, GE Maorong, SHEN Wenbin, et al. Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements[J]. Journal of Geodesy, 2017, 91(11): 1351-1366. DOI:10.1007/s00190-017-1029-7 |
| [23] |
XIANG Yan, GAO Yang, SHI Junbo, et al. Consistency and analysis of ionospheric observables obtained from three precise point positioning models[J]. Journal of Geodesy, 2019, 93(8): 1161-1170. DOI:10.1007/s00190-019-01233-1 |
| [24] |
苏珂. 北斗/GNSS精密单点定位模型及应用[D]. 上海: 中科院上海天文台, 2021. SU Ke. Models and applications of BeiDou/GNSS precise point positioning[D]. Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences, 2021. |
| [25] |
SU Ke, JIN Shuanggen. Analytical performance and validations of the Galileo five-frequency precise point positioning models[J]. Measurement, 2021, 172: 108890. DOI:10.1016/j.measurement.2020.108890 |
| [26] |
JIAO Guoqiang, SONG Shuli, GE Yulong, et al. Assessment of BeiDou-3 and multi-GNSS precise point positioning performance[J]. Sensors, 2019, 19(11): 2496. DOI:10.3390/s19112496 |
| [27] |
XU Wei, SHEN Wenbin, CAI Chenghui, et al. Modeling and performance evaluation of precise positioning and time-frequency transfer with Galileo five-frequency observations[J]. Remote Sensing, 2021, 13(15): 2972. DOI:10.3390/rs13152972 |
| [28] |
WANG Qisheng, JIN Shuanggen, YE Xianfeng. A novel method to estimate multi-GNSS differential code bias without using ionospheric function model and global ionosphere map[J]. Remote Sensing, 2022, 14(9): 2002. DOI:10.3390/rs14092002 |
| [29] |
DONG Zhounan, JIN Shuanggen. 3D water vapor tomography in Wuhan from GPS, BDS and GLONASS observations[J]. Remote Sensing, 2018, 10(1): 62. |
| [30] |
LIU Teng, ZHANG Baocheng, YUAN Yunbin, et al. On the application of the raw-observation-based PPP to global ionosphere VTEC modeling: an advantage demonstration in the multi-frequency and multi-GNSS context[J]. Journal of Geodesy, 2020, 94(1): 1. DOI:10.1007/s00190-019-01332-z |
| [31] |
SU Ke, JIN Shuanggen. A novel GNSS single-frequency PPP approach to estimate the ionospheric TEC and satellite pseudorange observable-specific signal bias[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5801712. |
| [32] |
ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning[J]. Science China Earth Sciences, 2012, 55(11): 1919-1928. DOI:10.1007/s11430-012-4454-8 |
| [33] |
CHENLiang, YI Wenting, SONG Weiwei, et al. Evaluation of three ionospheric delay computation methods for ground-based GNSS receivers[J]. GPS Solutions, 2018, 22(4): 125. DOI:10.1007/s10291-018-0788-9 |
| [34] |
XIANG Yan, GAO Yang, SHI Junbo, et al. Consistency and analysis of ionospheric observables obtained from three precise point positioning models[J]. Journal of Geodesy, 2019, 93(8): 1161-1170. DOI:10.1007/s00190-019-01233-1 |
| [35] |
SU Ke, JIN Shuanggen. Three dual-frequency precise point positioning models for the ionospheric modeling and satellite pseudorange observable-specific signal bias estimation[J]. Remote Sensing, 2021, 13(24): 5093. DOI:10.3390/rs13245093 |
| [36] |
JIN Shuanggen, JIN Rui, KUTOGLU H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations[J]. Journal of Geodesy, 2017, 91(6): 613-626. DOI:10.1007/s00190-016-0988-4 |
| [37] |
TU Rui, LIU Jinhai, LU Cuixian, et al. Cooperating the BDS, GPS, GLONASS and strong-motion observations for real-time deformation monitoring[J]. Geophysical Journal International, 2017, 209(3): 1408-1417. DOI:10.1093/gji/ggx099 |
| [38] |
XI Ruijie, CHEN Hua, MENG Xiaolin, et al. Reliable dynamic monitoring of bridges with integrated GPS and BeiDou[J]. Journal of Surveying Engineering, 2018, 144(4): 04018008. DOI:10.1061/(ASCE)SU.1943-5428.0000263 |
| [39] |
OKU TOPAL G, AKPINAR B. High rate GNSS kinematic PPP method performance for monitoring the engineering structures: shake table tests under different satellite configurations[J]. Measurement, 2022, 189: 110451. DOI:10.1016/j.measurement.2021.110451 |
| [40] |
BILICH A, CASSIDY J F, LARSON K M. GPS seismology: application to the 2002 Mw 7.9 Denali Fault earthquake[J]. Bulletin of the Seismological Society of America, 2008, 98(2): 593-606. DOI:10.1785/0120070096 |
| [41] |
FANG Rongxin, LÜ Huanghui, SHU Yuanming, et al. Improved performance of GNSS precise point positioning for high-rate seismogeodesy with recent BDS-3 and Galileo[J]. Advances in Space Research, 2021, 68(8): 3255-3267. DOI:10.1016/j.asr.2021.06.012 |
| [42] |
SU Ke, JIN Shuanggen, JIANG Jintao, et al. Ionospheric VTEC and satellite DCB estimated from single-frequency BDS observations with multi-layer mapping function[J]. GPS Solutions, 2021, 25(2): 68. DOI:10.1007/s10291-021-01102-5 |
| [43] |
JIN Shuanggen, GAO Chao, YUAN Liangliang, et al. Long-term variations of plasmaspheric total electron content from topside GPS observations on LEO satellites[J]. Remote Sensing, 2021, 13(4): 545. DOI:10.3390/rs13040545 |