1957年,苏联首颗人造地球卫星Sputnik的成功发射,标志着人类正式进入航天时代,并揭开了人类利用卫星来开发导航定位系统的序幕。美国于1960年建立了由6颗卫星组成的子午卫星系统(Transit),这是世界上第一个成功运行的卫星导航系统,并在此基础上进一步建立了全球定位系统(GPS)。作为重要的时空信息基础设施,导航卫星系统不仅在防灾减灾、变形监测、海上搜救等领域发挥着举足轻重的作用,而且对于经济、政治、军事也具有极其重要的意义,是大国核心竞争力的体现[1]。除美国外,各大国也纷纷组建了自己的导航卫星系统,如俄罗斯的GLONASS,欧盟的Galileo系统和中国的北斗卫星导航系统(BDS),这4大系统并称为全球导航卫星系统(GNSS)[2]。此外,日本和印度也建立了本国的区域导航卫星系统(QZSS、IRNSS)[3]。
作为GNSS卫星空间基准信息来源,精密的卫星轨道产品是GNSS卫星为用户提供连续精确的导航、定位和授时(PNT)服务的先决条件和必要前提。20世纪70年代末,第一颗GPS卫星的问世使得针对GPS卫星精密定轨的研究开始出现,由于早期的GPS星座建设尚不完善,地面测站数量有限,GPS卫星定轨主要基于区域观测网的数据,定轨精度仅能达到米级。随着GPS星座的不断建设及地面测站的增加,GPS卫星定轨精度逐渐提升,特别是1994年国际GPS/GNSS服务(IGS)组织的出现进一步推动了GPS卫星定轨精度迈向厘米级[4]。伴随着GPS的现代化及GLONASS、Galileo、BDS等全球导航卫星系统的出现,可用的GNSS信号和频点也越来越多,而科学研究和实际应用领域对于多系统GNSS卫星精密轨道/钟差产品的需求也愈发强烈。因此,IGS组织于2011年进一步发起了多GNSS实验(MGEX)项目,致力于提供多系统GNSS卫星的精密产品。目前有多个分析中心提供多模GNSS卫星精密轨道/钟差产品,除了BDS GEO卫星,各分析中心提供的GNSS卫星事后精密轨道产品精度均能达到厘米级[5]。
GNSS卫星精密定轨精度由米级提升至厘米级,这既是卫星/测站数量增加和GNSS量测精度提升的共同结果,也离不开全球范围内各大研究机构的学者在GNSS卫星精密定轨领域所做出的不懈努力,主要有:①函数模型的精化,内容包括观测值模型由双频无电离层组合扩展至多频非差非组合、相位模糊度由浮点解逐步提升为双差/非差固定解、偏航姿态与天线相位中心改正的精确建模。②动力学模型的精化,主要是针对太阳光压、地球反照、天线推力和热辐射等非保守力的建模和精细化处理。③随机模型的精化,主要是针对不同GNSS观测定权策略的改进。④观测数据来源的多样化,由仅依靠地面观测数据的地基定轨发展为低轨卫星星载GNSS数据及星间链路数据增强的联合定轨。这些方面一直都是GNSS卫星精密定轨研究领域的热点问题,同时也是本文梳理GNSS卫星精密定轨研究的主要脉络。
1 GNSS星座和跟踪数据当前,全球的导航定位系统已呈现出百花齐放的局面(表 1),目前在轨正常运行的导航卫星已达134颗,并且拥有丰富的信号资源。其中,GPS、GLONASS和Galileo星座均由中轨道卫星(MEO)组成,而BDS则开创性地使用了包含地球同步轨道(GEO)卫星、倾斜地球同步轨道(IGSO)卫星和MEO卫星的混合异构星座。当前北斗系统(包括BDS-2和BDS-3)共有45颗在轨卫星,可为全球用户提供PNT服务。
| 导航卫星系统 | 轨道类型 | 卫星数量 | 信号 |
| GPS | MEO | 31 | L1C/A, L2C, L5 |
| GLONASS | MEO | 22 | L1C/A, L2C/A, L3 |
| Galileo | MEO | 24 | E1, E5a, E5b, E5ab, E6 |
| BDS | BDS-2 GEO | 5 | B1I, B2I, B3I |
| BDS-2 IGSO | 7 | B1I, B2I, B3I | |
| BDS-2 MEO | 3 | B1I, B2I, B3I | |
| BDS-3 GEO | 3 | B1I, B3I | |
| BDS-3 IGSO | 3 | B1I, B3I, B1C, B2a, B2b | |
| BDS-3 MEO | 24 | B1I, B3I, B1C, B2a, B2b | |
| QZSS | GEO | 1 | L1C/A, L1C, L2C, L5 |
| IGSO | 3 | L1C/A, L1C, L2C, L5 | |
| IRNSS | GEO | 3 | L5, S |
| IGSO | 5 | L5, S |
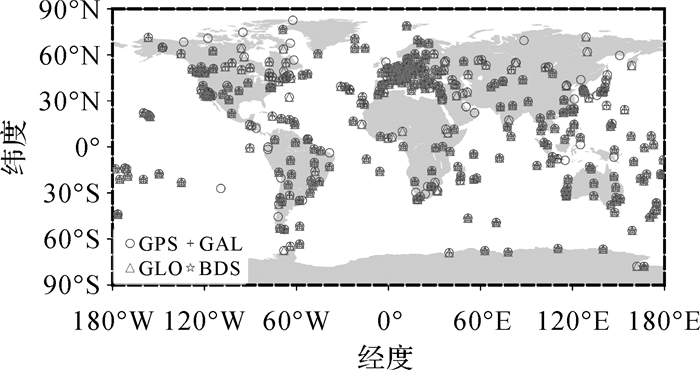
伴随着各大GNSS星座的不断完善,GNSS卫星地面跟踪站的数量也在不断增加,其分布也更加均匀。尤其是MGEX项目成立以来,多模GNSS地面跟踪站的数量显著增加。截至2022年1月,全球范围内的IGS跟踪站已达504个,测站分布如图 1所示,其中,能够跟踪GPS、GLONASS、Galileo、BDS、QZSS和IRNSS卫星信号的测站数量分别为504、437、365、297、163及76。这些IGS测站均搭载有测地型接收机(如Javad、Leica、NovAtel、Trimble、Septentrio等),可以接收双频甚至多频的多模GNSS卫星信号。除IGS外,由我国发起并主导的国际GNSS监测评估系统(iGMAS)也在全球范围内建立了30个跟踪站,可提供四系统GNSS观测数据(http://www.igmas.org/)。
|
| 图 1 IGS测站分布 Fig. 1 Distribution of all IGS stations |
除地面测站外,不少低轨(LEO)卫星上也搭载有能够接收GNSS信号的高精度星载接收机。由于早期GNSS星座建设尚不完善,大部分LEO卫星上搭载的接收机仅能接收GPS信号,如CHAMP、GRACE、MetOp、Swarm等卫星。随着我国BDS的建设,能够接收GPS+BDS双系统信号的LEO卫星也开始出现,如FY-3C/3D、LING QIAO、Luojia-1A、Tianping-1B等。此外,美国于2019年6月发射的6颗COSMIC2卫星上均搭载了接收GPS+GLONASS双系统信号的接收机,欧洲空间局(ESA)于2020年11月发射的Sentinel-6A卫星上则搭载了能够接收GPS+Galileo双系统信号的接收机。这些LEO卫星的星载GNSS数据同样能够应用于GNSS卫星精密定轨中,目前大部分的LEO星载GNSS数据均已在各自任务的官方网站上公开发布。
地面测站与LEO卫星接收的均是GNSS卫星L波段信号,除此之外,基于Ka波段的星间链路(ISL)数据也是精密定轨中的重要数据来源。星间链路技术最早在GPS Block ⅡR卫星上得到验证,我国的BDS-3星座也采用了星间链路技术,主要用于卫星间通信、时间同步及精密定轨等,并且可以显著改善卫星的自主导航性能[6]。BDS-3卫星上搭载了Ka波段的相控阵天线,采用时分多址双向测距模式,在整个星座内建立动态链路。L波段和Ka波段信号均是GNSS卫星信号的重要组成部分,同时也是精密定轨中的重要数据来源。图 2为GNSS卫星跟踪数据示意图,可以看出,GNSS卫星跟踪网涵盖地基、星基、星间等多源观测,这为GNSS精密定轨提供了充足的观测数据。

|
| 图 2 GNSS卫星多源观测网络 Fig. 2 Multi-source observation network of GNSS satellites |
2 GNSS精密定轨的数学模型 2.1 函数模型
在基于L波段伪距和相位观测值的GNSS卫星精密定轨中,基本函数模型可以表示为
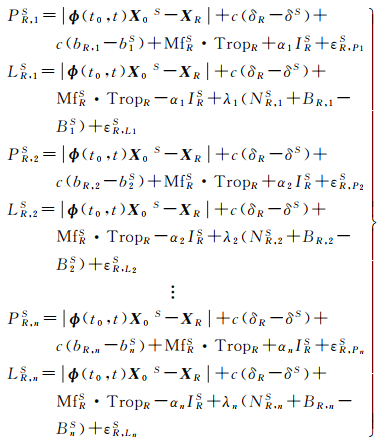 (1)
(1)
式中,PR, iS和LR, iS分别表示伪距和载波相位观测值,上标S表示卫星,下标R表示测站,i表示第i个频点;n表示频点总数;ϕ(t0, t)为卫星轨道状态转移矩阵;X0S为卫星参考历元轨道参数;XR为测站坐标;c为真空中的光速;δR和δS分别表示接收机和卫星钟差,bR, i和biS分别表示接收机和卫星伪距硬件延迟,MfRS表示对流层延迟投影函数;TropR表示对流层延迟;αi表示电离层映射因子;IRS表示电离层延迟;λi表示波长;NR, iS表示载波相位模糊度;BR, i和BiS分别表示接收机和卫星载波相位硬件延迟;εSR, Pi和εSR, Li分别表示伪距和载波相位观测值噪声。
由式(1)可知,GNSS观测值涉及卫星端、接收机端、传播路径上等多种类型误差,如何准确识别、分离以及消除各类误差影响,是实现GNSS精密定轨的基础。同时,在当前观测值频率由双频扩充至多频的背景下,需要采取合适的组合方式对不同频率的观测数据进行处理,以充分利用多频观测数据。
2.1.1 观测值组合从GNSS原始观测方程出发,可以构建不同的GNSS精密定轨函数模型。根据观测值组合方式的不同,常用的函数模型可以分为无电离层组合模型(IF)和非差非组合模型(UDUC)。无电离层组合模型通过不同频点观测值线性组合消除电离层一阶项误差的影响,其中双频无电离层组合模型实现简单,参数较少,被广泛应用于GNSS定轨和定位[7-8]。但是无电离层组合丢失了观测值中的一些可用信息,并且放大了观测值的噪声,于是有学者提出并研究了基于原始观测值的非组合模型[9],并在此基础上采用GPS精密单点定位(PPP)模型推导了电离层延迟及差分码偏差等误差的估计方法,进一步拓展了非组合模型的应用空间[10]。相比于无电离层组合模型,非组合模型虽然待估参数更多,但是在以下4个方面具有明显优势:①避免组合观测值放大观测噪声和未模型化误差;②模型可扩展性强,可以容易地由双频扩展至多频;③估计了电离层参数,能够为电离层建模与反演、差分码偏差(DCB)估计提供电离层观测量,同时可以引入外部电离层信息约束法方程[11-12]。
随着BDS和Galileo系统的建设,以及GPS和GLONASS的现代化,可用的GNSS卫星信号频率资源越来越丰富。其中,我国BDS-2提供3频观测信号(B1I、B2I、B3I),BDS-3在B1I和B3I的基础上新增了B1C、B2a、B2b与B2a+b信号;Galileo系统提供5频观测信号(E1、E5a、E5b、E5a+b、E6);GPS从Block ⅡF型号卫星开始提供3频信号(L1、L2、L5);GLONASS从GLONASS-M+型号开始在频分多址的L1、L2信号基础上新增码分多址的L3信号。如何充分利用GNSS多频信号资源,构建合理的观测值函数模型,进一步提升GNSS定轨定位精度,成了亟须解决的问题。多频无电离层组合模型通常可分为两类,一类是在多频观测值之间两两组合,形成多组无电离层组合观测值;另一类则综合多频观测数据,构造一个噪声最小的无电离层组合。但是这两种模型都存在频率组合繁杂、可扩展性差的问题,难以适应当前信号频率资源日趋丰富的环境。非组合模型灵活性高、可扩展性强、避免了频率选择问题,在处理多频数据时优势更加突出。近年来越来越多的学者基于非组合模型开展多频精密单点定位(PPP)、信号偏差估计、电离层建模等研究[13-17]。
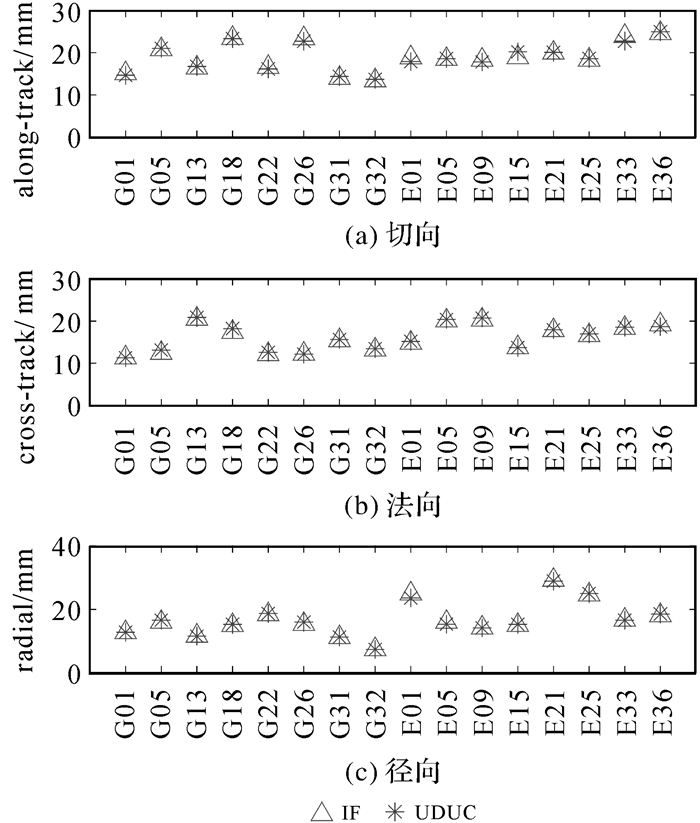
受限于非组合模型中参数数量增加而导致的计算效率降低问题,目前GNSS精密轨道确定依然主要采用双频无电离层组合模型[18-19]。在定轨精度方面,格拉茨技术大学(TUG)采用非组合模型计算了2003—2018年的GPS轨道并与IGS综合轨道产品对比,二者轨道差异为9.5 mm,定轨精度优于大部分IGS分析中心的轨道产品,验证了非组合模型定轨可以达到无电离层组合相当甚至更优的精度[20]。文献[21]利用Galileo多频资源,评估了双频、三频无电离层组合和非组合模型的定轨精度,结果表明非组合模型和无电离层组合模型定轨精度差异在1 mm以内。图 3示例性地给出了部分GPS和Galileo卫星无电离层组合(IF)与非差非组合(UDUC)定轨结果,可以看出二者的定轨精度基本相当。
|
| 图 3 无电离层组合与非差非组合定轨外部检核结果 Fig. 3 POD results of IF model and UC model |
为提升非差非组合模型的计算效率,文献[22]提出了一种“站-星-历元”消除电离层参数的策略,可将GPS三频非组合定轨的计算效率提升数倍甚至数十倍,但对于成倍增加的模糊度参数快速固定的问题仍有待解决。除参数消去法,在大规模GNSS网解中,还可应用AMBIZAP方法[23]和Carrier-range方法[24]提升计算效率,其本质均是通过提高模糊度固定的计算速率进而实现高效数据处理,而文献[19]则将Carrier-range方法与PPP及其模糊度固定紧密融合,提出了一套新的快速解算方法,应用该方法可提高近两倍的计算效率。以上方法均属于处理策略层面的改进,除此之外,文献[25]从软件层面采用OpenBLAS库加速算法进行GPS实时滤波定轨,在100个测站条件下,参数估计耗时约为2 s,显著提升了定轨解算效率。随着计算机技术的不断发展,利用CPU+GPU异构混合并行计算、矩阵块消参和高性能矩阵库等加速方法,有望突破非组合模型定轨的效率瓶颈,并取得更高精度的定轨结果。
2.1.2 模糊度固定技术在GNSS数据处理中,载波相位模糊度参数由于受到卫星端和接收机端相位小数偏差(UPD)的影响不再具备整周特性,因此只能作为浮点数估计,限制了参数解算精度。如果模糊度被固定为整数值,将显著提升定轨精度和可靠性。传统的双差模糊度固定方法通过在不同测站和卫星间两两差分,消除卫星端和接收机端的相位偏差,得到具有整数特性的双差模糊度[26]。由于无电离层组合模糊度难以直接固定,通常将其分解为宽巷(WL)和窄巷(NL)模糊度依次固定。其中,WL模糊度可以通过无电离层无几何距离组合(HMW)得到,NL模糊度则可以通过整数WL模糊度和无电离层组合模糊度计算。在恢复双差模糊度整数特性之后,可以采用基于假设检验的取整法或者LAMBDA搜索方法将其固定为整数值,然后在法方程上施加约束。由于GNSS卫星精密定轨时参与解算的测站/卫星数量较多,可组合的双差模糊度数量巨大,导致计算负担较大,如何高效选取最大独立模糊度集是双差模糊度固定的关键。目前广泛采用的双差模糊度搜索算法有模糊度方差排序法、独立基线法、分层选取法以及Gram-Schmidt正交化等[27-28]。
为了适应卫星导航从单GPS到多GNSS,从双频到多频,从无电离层组合模型到非差非组合模型的发展趋势,模糊度固定技术也在不断发展。在多GNSS方面,针对BDS-2卫星受星上伪距偏差(SCB)影响导致宽巷模糊度固定率低的问题,通过建立SCB高度角相关的经验模型并改正,可以显著改善BDS-2模糊度固定率[29]。而新一代的BDS-3卫星伪距信号质量更优,不受SCB影响[30]。针对GLONASS卫星采用频分多址技术导致其模糊度参数受到频率间偏差(IFB)的影响而难以固定的问题,文献[31]通过估计并改正每条基线的相位IFB,将GLONASS的固定率提升到90%。在多频信号资源方面,充分利用目前GPS、BDS和Galileo的多频观测值,可以构建超宽巷(EWL)等受电离层影响较小、噪声水平低、波长较长的线性组合,按照先易后难的顺序,依次固定组合模糊度。研究表明在地面测站分布不均匀的条件下,三频固定解轨道精度可以提升14%[21-22]。在非组合模型方面,可以利用非组合模糊度参数(N1、N2、N3)的估计值组成波长更长的EWL、WL和NL模糊度并依次固定。相比于无电离层组合模型中利用HMW组合观测值计算EWL和WL模糊度的方式,非组合模型可以直接根据模糊度参数得到WL和EWL模糊度而不需要引入伪距观测值,噪声更小,同时可获得EWL、WL模糊度协方差信息,便于模糊度的取整和搜索。
随着国内外学者对UPD产生机理与时空特性的研究不断深入,估计并分离UPD,进而固定非差模糊度逐渐成为可能。文献[32]提出利用最小二乘方法将参考网解算的模糊度作为观测值估计卫星端和接收机端的UPD,发现WL UPD和NL UPD分别能够在数天内和数十分钟内保持稳定,而文献[33]则进一步实现了GPS、BDS、GLONASS和Galileo的UPD估计。利用参考网估计得到的卫星端UPD产品,PPP用户可以通过星间单差实现单接收机模糊度固定,显著提高定位的收敛速度、精度和可靠性[34]。IGS分析中心CNES/CLS从2009年开始生成并提供基于非差模糊度固定方法的GPS轨道和钟差产品[35],并在2018年扩展到GPS+Galileo[36]。不同于双差模糊度整数约束通常施加在非差函数模型的法方程域,非差模糊度整数约束可以直接作用在GNSS相位观测值域,即直接标定相位观测值中的整周模糊度。这种改正了整周模糊度的相位观测值成为和伪距类似的距离观测量,但精度可达到毫米级,也被称为载波距[24]。文献[37]提出了利用PPP非差模糊度固定来生成载波距产品的方法,实现了基于载波距的GPS精密定轨,由于消除了模糊度,待估参数大大减少,参数解算效率显著提升。此外,相位偏差无法进入模糊度参数,只能被接收机和卫星钟差参数吸收,得到的包含卫星端UPD的钟差产品被称为整数钟,可以使PPP用户在无须额外UPD产品的条件下直接实现非差模糊度固定。整数钟和UPD方法在数学上等价,可以达到同等的定位效果[38]。基于载波距方法,文献[39]实现了GPS、BDS、GLONASS和Galileo的实时整数钟快速估计。
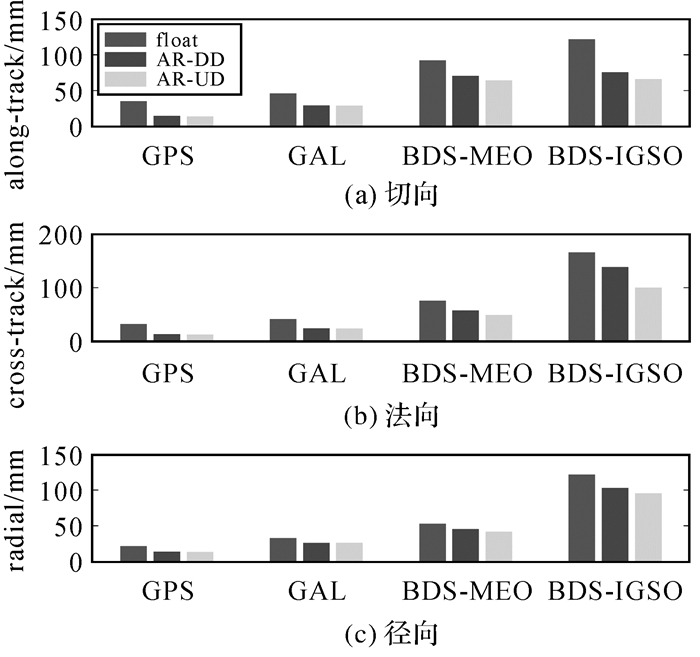
从质量控制的角度来看,双差模糊度固定是利用一个星间单差模糊度的小数部分检校另一个星间单差模糊度,其固定的准确性取决于该星间单差模糊度的精度,而非差模糊度固定是利用参考网估计的精密UPD产品来检校模糊度,UPD产品的精度显然优于某个星间单差模糊度。一旦双差模糊度固定到错误的整数值,它的影响可能被整个参考网中互相耦合的所有双差模糊度均匀吸收,难以查找和剔除;而非差模糊度固定只作用于一个测站-卫星对,质量控制更加容易。图 4给出了GPS、Galileo、BDS IGSO和MEO卫星浮点解(Float)、双差固定解(AR-DD)及非差固定解(AR-UD)定轨结果,可以看出,固定模糊度能够显著提升GNSS卫星精密定轨的精度。
|
| 图 4 浮点解、双差固定解及非差固定解定轨外部检核结果 Fig. 4 POD results of "float" solution, "AR-DD" solution, and "AR-UD" solution |
2.1.3 姿态模型
偏航姿态变化对卫星精密定轨的影响主要体现在3个方面:①天线相位中心偏差(PCO)改正[40];②相位缠绕误差改正;③太阳光压等非保守力的精确建模。其中,①所引起的误差与PCO的量级相关,②引起的误差最大为1周,而③主要是源于姿态变化所导致的卫星受照面变化。因此,对GNSS卫星偏航姿态进行精确建模,是实现高精度定轨的重要前提与保障。
为满足任务需求,GNSS卫星姿态控制一般需要满足2个条件:信号发射天线指向地球,以便地面测站能够接收到GNSS信号;太阳帆板垂直于太阳入射方向,以便卫星能接收到足够的太阳能。这种姿态控制模式也被称为“动偏”(YS),被GPS、GLONASS和Galileo等卫星采用[41-43]。但该模式存在一定的缺陷,即当太阳高度角较小时,卫星在轨道“正午”和“午夜”附近所需的偏航速率将超出自身姿控系统的极限速率。此时,卫星需要进行“正午机动”和“午夜机动”。目前,GPS Block ⅡA/ⅡR/ⅡF与GLONASS-M卫星的正午/午夜机动均已得到较好建模[41-42],而Galileo、QZSS IGSO卫星的正午/午夜姿态机动法则也由系统官方发布[44-45]。此外,GPS的Block Ⅱ/ⅡA和Block ⅡF卫星进入地影后星敏感器无法获取太阳的位置,导致姿态控制失效,还会产生地影机动[18]。我国BDS-3 IGSO与MEO卫星也采用动偏模式,其正午机动和午夜机动发生在太阳高度角±3°期间[46]。
除“动偏”模式外,部分卫星还会采用“零偏”(ON)姿态模式。在ON模式下,卫星太阳能帆板旋转轴始终保持和轨道面垂直,并且星固系X轴始终指向卫星速度方向[47]。BDS-2/3 GEO卫星及QZSS GEO卫星均采用此种姿态控制模式。BDS-2 IGSO、MEO卫星及QZSS首颗卫星QZS-1则采用了动偏-零偏混合姿态模型,两种模式之间的切换主要取决于太阳高度角的大小。对于BDS-2卫星,当太阳高度角绝对值小于约4°时采用零偏模式,反之采用为动偏模式[48]。对于QZS-1卫星,相应太阳高度角绝对值阈值为20°[49]。此外,近年来有学者利用逆动态精密单点定位(RTPPP)方法估计了BDS-2卫星的偏航姿态,结果表明,C06、C13、C14这3颗卫星已从动偏-零偏混合姿态模型切换为了类似BDS-3卫星的连续动偏模式[50]。各GNSS卫星的姿态控制模式均已在表 2中给出。
| 导航卫星系统 | 轨道类型 | 姿态控制模式 |
| GPS | MEO | YS |
| GLONASS | MEO | YS |
| Galileo | MEO | YS |
| BDS | BDS-2 GEO | ON |
| BDS-2 IGSO | C06, C13: YS[50];其余卫星:YS/ON混合模式(姿态切换发生于|β|≈4°) | |
| BDS-2 MEO | C14: YS;其余卫星:YS/ON混合模式(姿态切换发生于|β|≈4°) | |
| BDS-3 GEO | ON | |
| BDS-3 IGSO | YS | |
| BDS-3 MEO | YS | |
| QZSS | GEO | ON |
| IGSO | QZS-1:YS/ON混合模式(姿态切换发生于|β|≈20°);QZS-2/4:YS[51] | |
| IRNSS | GEO | Biased YS |
| IGSO | Biased YS |
对卫星偏航姿态的精确建模,可以有效减小卫星天线相位中心改正及天线相位缠绕误差对于GNSS精密定轨的影响,减小定轨中因误差改正所引起的系统性偏差,提升卫星钟差和模糊度参数估计精度,进而提升精密定轨精度。另一方面,偏航姿态改正可以有效改善太阳光压等非保守力建模精度,减小力模型误差对于定轨的影响,进而改善定轨精度。文献[48]指出通过对BDS IGSO和MEO卫星姿态的精确建模,可以显著减小“零偏”模式下的重叠轨道误差,尤其是对于IGSO卫星轨道径向和MEO卫星轨道切向,精度提升幅度分别可达50%和60%左右。
2.1.4 天线相位中心改正模型GNSS信号测量的是卫星发射天线相位中心到地面接收天线相位中心之间的几何距离,而在导航卫星精密定轨中,卫星精密轨道是以卫星质心为参考点的。为实现参考点的统一,需要引入一个卫星天线相位中心相对于卫星质心的坐标改正向量,这便是卫星天线相位中心改正(PCC),主要包含相位中心偏差(PCO)与相位中心变化(PCV)两部分[40]。对于大部分GNSS卫星,其PCO可达到米级,而PCV最大也能达到分米级,因此在高精度GNSS卫星定轨中,卫星天线相位中心改正需要被精确标定。
在早期的GNSS数据处理中,IGS采用的是相对天线相位中心模型,该模型仅采用与类型相关的卫星PCO改正,并认为天线中心较为稳定且不受PCV的影响。采用该模型进行长基线处理时会产生系统性偏差[52]。自2006年11月6日起,IGS开始使用绝对天线相位中心模型,其中地面接收天线相位中心模型主要由德国Geo++ GmbH公司采用自动机器人标定得到,而卫星端相位中心模型则主要采用地面跟踪数据估计得到。需要指出,由于卫星Z向PCO与地面测站坐标、卫星钟差、对流层等参数强相关,必须将地面尺度固定至特定框架下,才能实现卫星Z向PCO估计[53]。IGS天线模型igs08.atx和igs14.atx中的GPS和GLONASS卫星端PCO便是分别将尺度固定到ITRF2008和ITRF2014而得到[54-55]。除了地面观测数据外,低轨星载数据也可用于标定GPS卫星PCV,并能够将PCV天底角覆盖范围由0°~14°至0°~17°[56]。
除GPS和GLONASS卫星外,近年来Galileo和BDS的快速发展也使得精密定轨领域对其天线相位中心改正的需求愈发迫切。有些学者对Galileo和BDS卫星端相位中心模型进行了深入研究,主要包括Galileo卫星的PCO估计[57]、BDS-2卫星B1I/B2I频率的PCO与PCV估计[58]、BDS-2/3卫星B1I/B3I频率的PCO与PCV估计[59-60]。由于缺少接收天线相位中心信息,上述研究中Galileo E1/E5a、BDS B1I/B2I以及B1I/B3I频率的接收机天线相位中心模型均使用GPS L1/L2近似代替[61-62]。使用估计的天线相位中心模型,能将卫星的定轨精度提升最大30%。同时,欧洲GNSS服务中心(EGSC)、日本内阁府(CAO)和中国卫星导航系统管理办公室(CSNO)也分别发布了Galileo、QZSS和BDS的卫星天线相位中心改正地面标定元数据[44-45, 63]。
表 3给出了最新的igs14_2194.atx天线文件中各导航卫星天线相位中心改正信息。该文件提供了GPS卫星、GLONASS卫星、Galileo卫星及大部分QZSS卫星的相位中心改正信息,同时提供了BDS和IRNSS卫星的PCO信息,但对于BDS、IRNSS及QZSS J01卫星PCV改正,该文件并未给出。可以预见的是,随着对GNSS天线相位中心建模研究的深入,导航卫星相位中心模型将会进一步完善与精化,而在其支撑下GNSS精密定轨精度也将进一步得到提升。
| 导航卫星系统 | PCV天底角范围 | PCV来源 | PCO来源 |
| GPS | 0°~17° | 0°~14°: 地基数据在轨标定 14°~17°: 星基数据在轨标定 |
X, Y:卫星生产商提供(Block IIR:地面标定) Z: 地基数据在轨标定 |
| GLONASS | 0°~15° | 地基数据在轨标定 | X, Y:卫星生产商提供 Z: 地基数据在轨标定 |
| Galileo | Galileo-1: 0°~14° Galileo-2: 0°~20° |
发射前地面标定 | 发射前地面标定[44] |
| BDS | - | - | BDS-2:多个文献中的结果取平均[63] BDS-3:CSNO提供[64] |
| QZSS | J01: 无 其他:0°~10° |
发射前地面标定 | 发射前地面标定[45] |
| IRNSS | - | - | ISRO提供 |
2.2 动力学模型
为获取高精度的导航卫星轨道产品,需要采用动力学精密定轨的方法,即在已知卫星初始轨道的前提下,通过对卫星所受各种保守摄动力和非保守摄动力进行建模与分析,根据牛顿运动定律以及万有引力定律计算卫星受摄运动的加速度,再通过积分的方法获取卫星的位置、速度以及相应的偏导信息。卫星运动方程可以表示为
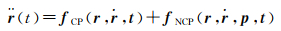 (2)
(2)
式中,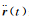
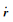
太阳光辐射直接作用在导航卫星上所产生的摄动力可以描述为卫星星体及太阳能帆板表面吸收的太阳光子施加到卫星的作用力及反射的太阳光子产生的反作用力之和,而这两部分作用力的大小主要取决于太阳辐射通量、卫星有效的受照面积、卫星表面的吸收率和反射率及太阳光线的入射角等因素[65]。在GNSS卫星所受非保守摄动力中,太阳光压摄动力对卫星产生的影响最大,其产生的加速度可达到所有非保守摄动力产生加速度的95%以上[66]。因此,对于太阳光压的精细化建模也成为导航卫星精密定轨研究中的核心内容。
根据建模方式的不同,可以将现有的光压模型分为3类:经验型光压模型、分析型光压模型及半分析半经验型光压模型[47]。其中,经验型光压模型可以在没有卫星面板光学属性等先验信息的条件下使用,模型相对更为简洁,但模型参数的物理意义不直观。一种常用的经验型光压模型是ECOM系列模型(包括ECOM-1、ECOM-2),ECOM-1模型为[67]
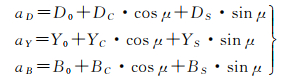 (3)
(3)
ECOM-1模型分别在卫星D(卫星-太阳方向)、Y(太阳帆板旋转轴方向)和B(与D、Y方向构成右手系)方向引入3个加速度(常量部分、正弦部分及余弦部分)来描述卫星所受光压摄动[67],对应式(3)中的9个光压参数,μ表示轨道角。GPS卫星采用ECOM-1模型能够获得较高的精密定轨精度,但对于其他GNSS卫星,由于卫星结构的差异,该模型无法精确描述光压摄动[68]。文献[69]进一步提出ECOM-2模型,相比于ECOM-1模型,ECOM-2模型能够有效提升GLONASS、Galileo和QZSS卫星精密定轨精度,但对于BDS卫星精密定轨精度改善不显著。近年来,学者们还研究了经验型光压模型在“零偏”姿态下的适用性。结果表明,在ECOM-1基础上引入切向加速度偏差参数能将BDS-2 IGSO/MEO卫星在ON模式下的重叠轨道精度提升87.7%和95.8%[47, 61];采用六参数ECOM-1模型可将BDS-2 GEO卫星的SLR检核精度提升37.4%[70]。文献[71]则在新坐标系TERM上构建了一系列适用于零偏姿态的经验型光压模型,并自2018年起用于CODE的定轨处理中。
与经验型光压模型不同,分析型光压模型根据卫星几何与光学属性,通过严格的物理表达式建模光压摄动力[72]。分析型光压模型主要包括“ROCK”系列模型、“Box-wing”模型、“Ray-tracing”模型等。其中,“Box-wing”模型将卫星简化为长方体/圆柱体星体与太阳帆板的组合,卫星本体与太阳帆板的光压加速度分别表达为
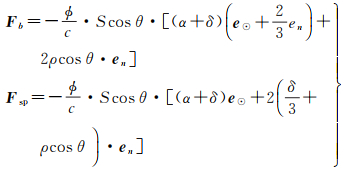 (4)
(4)
式中,ϕ为太阳辐射通量;S为受照面积;c为真空中的光速;e⊙和en分别表示为太阳光入射方向单位向量和受照面法向单位向量;θ为e⊙和en的夹角;α、ρ和δ分别表示吸收系数、镜面反射系数和漫反射系数。与“Box-wing”不同,“Ray-tracing”模型采用光线追踪的方法,以像素点为单位对卫星本体各种载荷所受光压力进行建模,并且还考虑了不同星体部件之间的相互遮挡影响[73],该模型已在GLONASS IIv以及BDS卫星精密定轨中成功应用[73-74]。
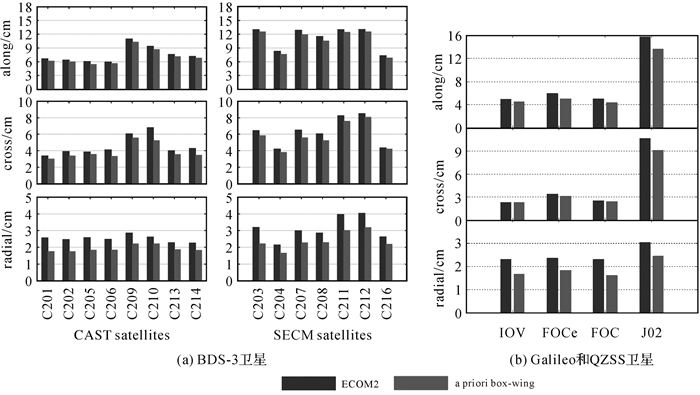
由于卫星表面材料老化、几何光学属性不精确等条件的限制,分析型光压模型的精度一般较为有限[47]。为弥补分析型光压模型的不足,有学者提出了半分析半经验型光压模型。文献[73]在Box-wing的基础上,通过估计星体表面光学参数、太阳帆板尺度因子、太阳帆板旋转滞后角等参数,在定轨的同时实现对卫星光学信息的重构,这便是可校正Box-wing模型。该模型可以有效改善GPS和GLONASS卫星在地影期间的定轨精度[75],并且能够减小BDS IGSO卫星太阳高度角相关和轨道角相关的轨道误差[47]。此外,Box-wing模型还常作为先验光压模型,在定轨中同时估计经验参数吸收未模型化光压误差,此类模型被称为先验Box-wing模型。图 5给出了BDS-3卫星和Galileo/QZSS卫星分别应用ECOM2模型和先验Box-wing模型的定轨结果,可以看出,与ECOM2模型相比,在先验Box-wing+ECOM1模型的应用下,BDS-3、Galileo和QZSS卫星定轨精度均有所提升,精度提升幅度分别约为8%、12%和13%[51, 75]。
表 4总结了各导航卫星采用几种常用的光压模型进行精密定轨的精度结果。可以看出,对于各GNSS卫星,采用不同的光压模型的定轨结果有一定差异。表中列出的3种模型中,采用先验Box-wing+5参数ECOM-1的半分析半经验型模型可以获得相对更高的定轨精度。
| 导航卫星系统 | 光压模型 | 定轨精度 | |
| 轨道比较 | SLR检核 | ||
| GPS | ECOM-1(5参数) | 轨道比较3D 4 cm[76] | - |
| ECOM-2 | 轨道比较3D 3.6 cm[76] | - | |
| 先验Box-wing+5参数ECOM-1 | 轨道比较3D 3.7 cm[76] | - | |
| GLONASS | ECOM-1 | 轨道比较3D 3.6 cm[77] | SLR检核残差标准差5.4 cm[77] |
| ECOM-2 | 轨道比较3D 4.2 cm[77] | SLR检核残差标准差5.7 cm[77] | |
| 先验Box-wing+5参数ECOM-1 | 轨道比较3D 3.5 cm[77] | SLR检核残差标准差4.5 cm[77] | |
| Galileo | ECOM-1 | - | SLR检核残差标准差9.2 cm[78] |
| ECOM-2 | 轨道比较3D 3.5 cm[21] | - | |
| 先验Box-wing+5参数ECOM-1 | - | SLR检核残差标准差5.2 cm[78] | |
| BDS | ECOM-1 | 轨道比较3D 6.9 cm[79] | - |
| ECOM-2 | 轨道比较3D 7.8 cm[79] | - | |
| 先验Box-wing+5参数ECOM-1 | 轨道比较3D 4.9 cm[79] | - | |
| QZSS | ECOM-1 | - | SLR检核残差标准差15.2 cm[49] |
| ECOM-2 | - | SLR检核残差标准差7.0 cm[49] | |
| 先验Box-wing+5参数ECOM-1 | - | SLR检核残差标准差5.5 cm[49] | |
2.2.2 地球反照
与太阳光压摄动类似,卫星所受地球反照摄动也是由于外部辐射所产生的摄动力,但其辐射源来自地球,主要分为两部分:太阳辐射照到地球表面的可见光被反射的部分,以及地球自身产生的红外辐射。地球反照辐射压主要受云层覆盖率、季节、轨道高度及卫星太阳与地球间的几何关系(SSE)等因素的影响,并且计算过程中需要卫星结构及光学属性等信息。在所有非保守摄动力中,地球反照辐射压对导航卫星的影响仅次于太阳光压,可占到总非保守摄动力的2.5%左右[66],计算表达式为
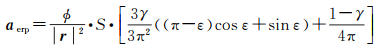 (5)
(5)
式中,ϕ为地球反照辐射通量;S为受照面积;r为卫星位置矢量;γ为辐射参数;ε为太阳方位角。对于地球反照辐射的建模关键在于对辐射通量的建模,一种常用的模型是数值型模型。文献[80]通过对辐射通量建模的深入研究,指出为建立更为精确的数值型模型,需要用到云层及地球辐射能量系统(CERES)数据。CERES数据的公开极大地推动了地球反照辐射模型的发展,文献[81]基于CERES数据集对Galileo卫星地球反照辐射压进行建模,通过应用相应的模型可以有效提升卫星轨道精度。地球反照辐射对于GNSS卫星精密定轨的影响主要体现在卫星轨道径向方向,在考虑地球反照辐射的前提下GPS Block ⅡA卫星精密定轨径向精度可提高约1 cm[80]。在Galileo卫星精密定轨中,地球反照辐射对于卫星轨道最大的影响体现在D方向的加速度,并且不能被ECOM2模型所吸收[66]。
地球反照辐射能够影响卫星精密定轨精度,并且会对地心参数估计以及测站坐标估计产生系统性偏差,因此,目前大多数IGS分析中心在确定卫星轨道时均将地球反照辐射作为一项重要的摄动力加以考虑。
2.2.3 热辐射和天线推力卫星在吸收太阳光辐射后,其星体表面温度会有一定程度的升高,而根据斯特藩-玻尔兹曼定律,受热的卫星表面将向外辐射热量,产生热辐射压。卫星所受热辐射压主要与卫星表面绝对温度、卫星表面辐射率相关,具体表达式为
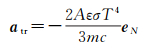 (6)
(6)
式中,A为等效作用面积;ε为辐射率;σ为斯特藩-玻尔兹曼常数;T为热辐射表面绝对温度;m为卫星质量;c为真空中的光速;eN为热辐射面法向矢量。
与太阳光压建模方法类似,对于导航卫星热辐射压建模一般也有两种方法:分析型模型和经验型模型。其中,分析型热辐射模型依赖卫星表面绝对温度、辐射率、星体结构等多种精确信息,模型各参数具有明确的物理意义[82]。在卫星信息缺失的情况下,经验型热辐射模型则更为适用。在经验型热辐射压建模中,往往先引入一个先验模型,在精密定轨解算的同时估计先验模型的尺度因子或增强参数,然后通过多次迭代对先验模型进行修正[82]。经验热辐射模型已被成功应用于GNSS卫星精密定轨中,并被证实能够提升定轨精度[83]。目前,部分GNSS卫星精密定轨中考虑了热辐射压的影响[66, 84]。文献[85]考虑了Galileo卫星-X面因星载原子钟散热而产生的热辐射,得到了X方向的常量加速度,以此减弱热辐射的影响。文献[76—77, 79]则在可校正Box-wing模型中增加X方向加速度参数来弥补GLONASS/BDS卫星热辐射的影响。文献[65]同样利用可校正Box-wing模型获得热辐射加速度,并将其作为先验加速度引入ECOM-1模型,使BDS-2卫星的SLR检核残差RMS降低了1.5 cm。
在导航卫星天线向地面发射信号时,还会产生一个径向上的反作用力,这便是天线推力。天线推力加速度的计算如下式所示,其大小主要取决于发射信号的功率及卫星的质量[86]
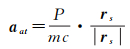 (7)
(7)
式中,P为发射信号功率;m为卫星质量;c为真空中光速;rs为卫星位置矢量。对于卫星天线推力建模的关键在于获取卫星天线发射信号的实际功率。一般来说,可以通过:①卫星发射前对天线进行测试;②在轨测试信号功率;③在地面通过高增益天线接收信号等方法确定天线信号功率[87]。其中,文献[88]采用第1种方法确定GPS Block ⅡR卫星天线发射功率,指出对于L1和L2信号功率分别为50 W和11 W,而文献[89]则综合比较了第1种方法和第2种方法所确定GPS Block ⅡR卫星信号功率的结果,指出L1和L2信号功率范围分别为29~60 W及9~22 W。文献[87]采用30 m长的抛物面天线对不同GNSS卫星的信号能量进行标定,指出对于GPS,BDS-2,Galileo和GLONASS卫星而言,其信号功率范围分别为50~240 W,130~185 W,95~265 W及20~135 W,将标定结果应用于精密定轨中,可以实现卫星轨道径向1~27 mm的精度提升。各卫星具体的信号功率可见IGS整理的卫星元数据文件(https://igs.org/mgex/metadata/#metadata)。
2.3 随机模型在GNSS精密定轨中,对于同一导航系统,相位观测值精度要远高于伪距观测值精度,不同历元、不同卫星之间的观测值精度与可靠性也有所差异,而对于不同系统的观测数据其精度也不相同。为充分利用不同类型、不同历元、不同卫星及不同系统的观测数据,需要在定轨处理中选择适当的随机模型,对相应的观测数据设置一定的权重,以达到观测数据的最优融合,实现高精度GNSS卫星定轨。
随机模型的选取需要充分考虑实际观测数据的噪声水平、精度等特性,在此基础上对其设置合理的权重。常用的定权方法有等权法、高度角三角函数定权法、高度角指数函数定权法、信噪比定权法等。其中,最早出现并被广泛应用的等权法处理简单,认为观测值精度不随时间变化,但在某些复杂场景下缺乏合理性。由于卫星信号在大气层中传播的延迟误差随着高度角的增大而逐渐减小,并且在低高度角时卫星信号受多路径效应影响较为严重,因此卫星高度角的大小能够在一定程度上反映观测数据的质量,文献[90—91]以此为依据分别提出高度角三角函数模型和高度角指数函数模型,通过建立卫星高度角与观测值方差之间的函数关系实现不同观测数据的权重设置。目前国际上知名的大地测量数据处理软件Bernese、GAMIT及PANDA所采用的随机模型主要是基于高度角的指数函数模型与三角函数模型[28, 92-93]。除卫星高度角外,信噪比也能够较好地反映卫星信号的质量,当卫星信号受多路径影响较为严重时,信噪比会出现剧烈变化,常用的信噪比定权模型包括SIGMA-Δ模型及CALMS算法等[94-95]。文献[96]则对比分析了高度角定权法和信噪比定权法,并指出在GPS基线解算中,采用信噪比定权法可以实现更高的平面精度,而在减小高程方向误差方面,高度角三角函数定权法则更具有优势。
上述随机模型主要依据观测数据质量与某些因素之间的联系而建立,属于经验模型,在单系统处理中被广泛应用。而在多模GNSS联合处理中,还需要考虑到不同系统观测数据质量的差异,调整系统间的相对权比,常用的方法有经验定权法和方差分量估计方法。其中,经验定权法是依据大量数据处理经验对不同系统观测进行定权,但不具备理论依据。方差分量估计方法则是基于验后残差数据,采用合适的统计方法并通过迭代的方式进行估计,最终获得受多种不同因素影响的观测值的单位权方差,属于验后随机模型,常用的方法包括Helmert方差分量估计定权法以及最小二乘方差分量估计(LS-VCE)定权法等,被广泛应用于多模GNSS联合精密定位/定轨中[7, 97-98]。方差分量估计方法需要大量冗余数据,计算量较大,因此一般适用于静态GNSS处理。而对于动态GNSS处理,文献[99]则提出直接利用伪距和载波相位观测值实时估计观测数据的先验方差-协方差矩阵,进而反映实际观测数据的误差特性,该方法可被应用于实时/事后、静态/动态等多种测量模式[100]。此外,在GNSS多频观测数据定权方面,文献[101—102]基于三频无几何距离无电离层组合的方法对单站BDS三频非差观测数据的方差进行估计,实现了对单站多频数据的合理定权。
3 多源观测数据增强的GNSS精密定轨数量足够且分布良好的地面测站网是实现GNSS卫星高精度定轨的必要前提。坐标信息准确的地面测站不仅是定轨过程中的空间基准来源,同时其数量及分布也决定了最终的定轨精度。早期的GNSS卫星定轨研究主要采用少量区域跟踪站的观测数据,只能实现米级的定轨精度。随着地面测站数量的增加,GNSS卫星定轨精度也逐渐提升,在上百个均匀分布的全球测站参与下,GPS卫星定轨精度可以达到2 cm以内。但是对于BDS、Galileo等新兴系统,其全球测站数量相对较少且分布不均匀,这在一定程度上不利于精密轨道的获取。另一方面,以BDS GEO和IGSO为主要代表的区域覆盖卫星,其独特的轨道特性使得仅利用地面测站数据,无法获得足够的几何观测信息,从而限制了此类卫星的定轨精度。低轨卫星星载GNSS技术的快速发展以及GNSS卫星星间链路技术的出现为打破地面观测条件的制约提供了新的思路。
3.1 低轨卫星增强GNSS精密定轨不同于地面静态测站,低轨卫星高动态、全球覆盖的特性赋予了其观测值数据在改善导航卫星几何观测结构方面的独特优势[103]。同时,由于低轨卫星通常飞行于300~1500 km的轨道高度,远高于对流层,使得其星载GNSS观测数据不受对流层误差的影响。
GNSS与LEO卫星联合定轨思想的提出、概念的形成以及技术的运用最早出现在T/P卫星的精密定轨研究中。为了提高T/P卫星的定轨精度,文献[104]同时联合地面测站和T/P卫星数据估计了GPS卫星和T/P卫星的轨道参数,试验证明了联合定轨对于GPS卫星轨道精度的增强效果。此后,众多学者分别基于不同数量的低轨卫星和地面测站网深入研究了地面测站分布、卫星数量、轨道组合等因素对于LEO卫星增强GNSS定轨效果的影响,并取得一系列研究成果。当前,针对LEO卫星增强GNSS精密定轨的研究主要围绕3方面展开:①通过引入尽可能多的低轨卫星观测数据,降低导航卫星精密定轨对于地面测站网的依赖,以实现在区域参考网或稀疏全球网等地面观测受限条件下的高精度轨道确定[105-106];②借助低轨卫星的高动态特性,改善BDS GEO、IGSO等区域覆盖卫星的几何观测结构,从而提升其定轨精度[107-109];③分析制约联合定轨精度提高的各类因素,优化GNSS/LEO联合定轨处理方法与策略[110-111]。
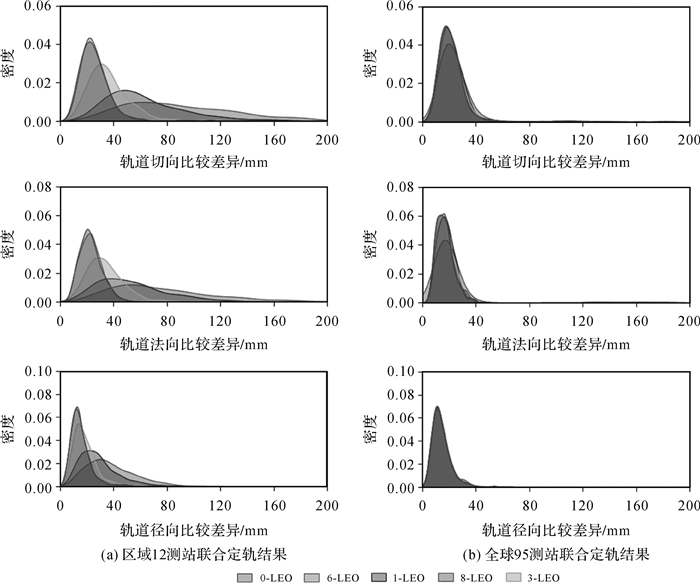
图 6给出了在区域12测站和全球95测站条件下不同数量LEO卫星与GPS卫星联合定轨结果与CODE精密轨道产品比较差异,可以发现,在区域12测站条件下,随着LEO卫星数量的增加,GPS卫星定轨精度能够得到显著改善,在加入8颗LEO卫星时,GPS卫星轨道1D精度可达2 cm左右。而在全球95测站条件下,LEO卫星的加入仍能够在一定程度上提升GPS卫星定轨精度,但提升幅度微小,且LEO卫星数量的增加对GPS卫星定轨精度几乎没有影响。由此说明LEO卫星对导航卫星轨道的增强效果是随着地面测站数量的增加及分布的优化而逐渐递减的,在测站数量足够且分布较好的情况下,加入LEO卫星对导航卫星轨道精度并无显著改善效果,反而大大增加了定轨解算中的计算负荷。
|
| 图 6 区域12测站与全球95测站条件下加入不同数量LEO卫星后GPS卫星定轨结果比较密度曲线 Fig. 6 Density curve of GPS POD comparison results with the inclusion of different LEO satellites under the condition of 12 regional stations and 95 global stations |
3.2 星间链路增强GNSS精密定轨
与地面测站及低轨卫星提供的“高-低观测”数据不同,星间链路提供了GNSS卫星之间的高精度测距信息,即“高-高观测”。星间链路在设计之初,是为了在长时间缺少地面测控系统支持的情况下,赋予导航卫星的自主定轨的能力[112]。通过在导航卫星上搭载星间链路收发设备,进行星间纳秒级精度的时间测量以及厘米级精度的星间测距,进而有效弥补地面测站数量及分布上的不足,提升导航卫星系统的抗破坏性以及卫星自主导航性能。
基于星间链路的导航星座自主定轨与时间同步的思想最早来自于美国对GPS BLOCK ⅡR卫星的设计[113],我国在建设北斗卫星系统的过程中,充分利用了这一思想,并使之真正实践成为一种可能。我国的BDS-3卫星上搭载了星间链路收发设备,可以实现MEO卫星之间及MEO与IGSO卫星之间高精度测距与通信[6]。星间链路解决了我国无法全球均匀布站的难题,使得BDS系统可以在国内区域建站的条件下,实现卫星的全弧段跟踪测量。星间链路数据的加入也让BDS卫星观测网络更加立体,有利于进一步提高BDS卫星的定轨精度。此外,星间链路还能够解决海外卫星广播星历无法及时注入和更新的问题,通过星间链路实现海外注入和更新[114-116]。
当前利用星间链路增强GNSS卫星精密轨道的研究可以总结为以下3方面:①联合地面测站L波段数据以及星间链路Ka波段观测数据确定GNSS卫星精密轨道时,星间链路数据对于定轨精度的增强效果的有效性评估[6];②针对星间链路数据各类误差和偏差的准确识别、估计与分离[117];③联合处理中随机模型、处理策略、计算效率等方面的优化提升[118-119]。
表 5对比了低轨增强GNSS与星间链路增强GNSS两种精密定轨增强技术。可以看到,两种方法利用了针对GNSS卫星的不同路径上的观测信息。低轨卫星星载观测值数据丰富,可提供更多的几何观测变化信息,而星间链路数据则提供了独特的高轨卫星间的几何观测,使得卫星观测网络更为立体。总而言之,两种数据各有优势与劣势,在应用于GNSS精密定轨时,需要综合考虑其优缺点,充分发挥多层次观测数据的优势,削弱其负面影响,实现数据的最优融合,提升GNSS卫星定轨精度。
| 参数 | 低轨增强GNSS | 星间链路增强GNSS |
| 观测路径 | 低轨卫星至导航卫星(高-低观测) | 导航卫星至导航卫星(高-高观测) |
| 支持系统 | GPS、BDS及Galileo | BDS |
| 信号频段 | L波段 | Ka波段 |
| 主要优点 | ①星载数据较为丰富,且支持多系统观测 ②低轨卫星高速飞行,观测几何变化快 ③星载观测值不受对流层延迟误差的影响 |
①具备星间通信、数据传输、星间测距和星间测控等功能,授时测距精度相对较高 ②星间链路一般距离地面较远,不受大气误差影响,误差模型简单,建模相对容易 ③可支持导航卫星自主定轨 |
| 主要缺点 | ①低轨卫星摄动力建模复杂,需额外估计大量模型参数,影响估计效率 ②依赖地面锚固站,单独定轨存在星座整体漂移的问题 ③无法支持导航卫星自主定轨 |
①依赖地面锚固站,单独定轨存在星座整体漂移的问题 ②当前可用数据量有限,仅支持单个系统 |
4 GNSS精密轨道产品
高质量的GNSS卫星精密轨道钟差产品是实现GNSS高精度定位、导航和授时的重要前提,直接影响GNSS的服务性能。GNSS广播星历轨道和钟差精度通常在分米级和纳秒级,难以满足GNSS高精度应用的需求。以IGS等为代表的国际组织和国内外科研机构利用全球大量跟踪站数据生成精密轨道钟差产品并公开发布,为广大用户和科研人员开展研究和生产活动提供了便利。
4.1 精密轨道产品现状目前,提供GNSS卫星精密轨道与钟差产品的IGS分析中心主要包括欧洲定轨中心(CODE)、德国地学研究中心(GFZ)、法国国家空间研究中心(CNES/CLS)、中国科学院上海天文台(SHAO)、俄罗斯GLONASS应用中心(IAC)、武汉大学(WHU)、欧洲航天局(ESA)、慕尼黑工业大学(TUM)及日本宇航研究中心(JAXA)。表 6总结了截至2022年1月各大分析中心的精密轨道与钟差产品基本信息,其中,CODE、GFZ、IAC、WHU及ESA均提供包含GPS、GLONASS、Galileo、BDS、QZSS(GRECJ)在内的5系统精密产品[61, 120],而CNES/CLS、JAXA和TUM则分别提供支持GRE、GRJ和ECJ 3系统的精密产品[121]。所有精密轨道产品采样间隔为5 min/15 min,钟差采样间隔为30 s/5 min。值得注意的是,在所有提供BDS精密产品的分析中心中,SHAO与TUM所发布产品中只包含BDS-2卫星;CODE与ESA则提供包含BDS-2和BDS-3卫星的精密产品,但不包含GEO卫星;只有GFZ和WHU能够提供包含BDS-2和BDS-3完整星座的精密轨道/钟差产品。
| 分析中心 | 缩写 | 产品系统 | 产品采样间隔 | 定轨软件 | 备注 | |
| 轨道 | 钟差 | |||||
| CODE | COD | GRECJ | 5 min | 30 s | Bernese | 不包括GEO |
| GFZ | GFZ | GRECJ | 15 min | 30 s | EPOS | 包括GEO |
| CNES/CLS | GRG | GRE | 15 min | 30 s | GINS/DYNAMO | - |
| JAXA | JAX | GRJ | 5 min | 30 s | MADOCA | - |
| SHAO | SHA | GREC | 15 min | 30 s | PANDA | 不包括BDS-3 |
| TUM | TUM | ECJ | 5 min | 5 min | Bernese | 不包括BDS-3 |
| IAC | IAC | GRECJ | 5 min | 30 s | STARK | - |
| WHU | WUM | GRECJ | 15 min | 5 min | PANDA | 包括GEO |
| ESA | ESA | GRECJ | 5 min | 30 s | NAPEOS | 不包括GEO |
除IGS外,iGMAS也建立了包含武汉大学、中国科学院上海天文台、中国科学院测量与地球物理研究所、中国科学院国家授时中心等在内的13家数据分析中心(http://www.igmas.org/Product/Cpdetail/detail/nav_id/4/cate_id/36.html),以及武汉大学测绘学院iGMAS创新中心(http://igmas.users.sgg.whu.edu.cn/products),均对外提供GNSS精密轨道/钟差产品。
为满足实时用户需求,IGS于2000年开始提供超快轨道产品(IGU),经多次策略调整,目前产品时延为3 h,轨道加权RMS优于5 cm[25]。此外,包括WHU、GFZ、CODE、ESA在内的多家分析中心也提供相应的GNSS超快轨道产品。超快轨道产品主要基于事后观测数据,通过轨道预报的方式获得,轨道精度受外推弧段长度的限制。为提供实时更新的精密轨道产品,IGS于2013年起提供实时服务(RTS),通过接收实时数据流实时更新GNSS精密轨道/钟差产品,主要RTS分析中心信息见表 7。其中,01IGS1、02IGS1和03IGS1为综合产品,即综合多家分析中心的实时轨道/钟差产品后的结果,01IGS1为单历元综合解,02IGS1和03IGS1为卡尔曼滤波综合解[122],表中列出所有轨道产品均包含以质心为参考点的轨道产品(SSRC)和以天线相位中心为参考点的轨道产品(SSRA)。各分析中心确定实时轨道均采用滤波算法,即逐历元求解卫星轨道参数及动力学参数以实现实时定轨,主要包括卡尔曼滤波[123]和均方根信息滤波(SRIF)[124]。
| 分析中心 | 产品系统 | 先验轨道 | 定轨软件 | 滤波算法 | NTRIP挂载点 |
| ESA/ESOC | G | IGU轨道产品 | - | - | 01IGS1 |
| G | IGU轨道产品 | RETINA+BNC | 卡尔曼滤波 | 00ESA1/01ESA1 | |
| BKG | GRE | IGU轨道产品 | - | - | 02IGS1 |
| GREC | CODE超快轨道产品 | - | - | 03IGS1 | |
| GRE | CODE超快轨道产品 | RTNet+BNC | 均方根信息滤波 | 00BKG1 | |
| DLR/GSOC | GRECJ | IGV/CODE/DLR超快轨道产品 | RETICLE | 卡尔曼滤波 | 00DLR1 |
| CAS | GREC | GFZ超快轨道产品 | - | - | 00CAS1 |
| CNES | GREC | GFZ超快轨道产品 | PPP-Wizard+BNC | 卡尔曼滤波 | 00CNE1 |
| GFZ | GREC | GFZ超快轨道产品 | EPOS-RT+BNC | 均方根信息滤波 | 00GFZ1/01GFZ1 |
| GMV | GREC | GMV超快轨道产品 | magicGNSS | 卡尔曼滤波 | 00GMV1 |
| NRCan | G | NRCan超快轨道产品 | HPGPSC | 卡尔曼滤波 | 00NRC1 |
| WHUAN | GREC | IGU/WUM超快轨道产品 | PANDA+BNC | 均方根信息滤波 | 00WHU1 |
| SHAO | GEC | IGU轨道产品 | - | - | 00SHA1 |
| 注:“ESOC”为欧洲航天局空间运营中心;“BKG”为德国联邦制图与大地测量局;“DLR/GSOC”为德国宇航中心;“CAS”为中国科学院大地测量与地球物理研究所;“NRCan”为加拿大自然资源部;“NTRIP”为通过互联网进行RTCM网络传输协议;“BNC”为BKG NTRIP客户端。 | |||||
4.2 精度评估
GNSS精密轨道产品的精度评估方法主要有3种:与外部参考轨道比较、重叠轨道比较及SLR检核。其中,与外部参考轨道比较主要用于检验轨道产品与外部产品之间的一致性,通常需要选择足够精确的外部轨道产品作为参考轨道,利用轨道产品与参考轨道的差异大小衡量轨道产品的精度。重叠轨道比较则通过比对两个定轨弧段重叠部分的差异对轨道内符合性进行检验。SLR技术提供了一种独立的由地面测站到卫星的厘米级距离观测量,通过分析SLR观测值减去各项误差以及利用精密轨道产品计算的卫地距得到的SLR残差,可以有效检核精密轨道产品的精度。由于SLR测量方向与卫星轨道径向较为接近,SLR检核对轨道径向的偏差尤其敏感。目前BDS、GLONASS、Galileo等卫星均搭载有SLR反射棱镜,这也为相应的轨道产品SLR检核提供了条件。
由于各分析中心发布的单个轨道产品文件仅包含一天的轨道信息,不存在重叠轨道,因此本文主要采用与外部参考轨道比较以及SLR检核两种方式对轨道产品进行评估。其中,与外部参考轨道比较选择的是武汉大学测绘学院iGMAS创新中心所发布的快速轨道产品为参考轨道,该轨道产品基于武汉大学测绘学院自主研发的GREAT软件解算得到,支持GRECJ 5系统,产品时延为37 h,采样间隔为5 min,产品缩写为“GRT”。选取了应用较为广泛的CODE、WHU、GFZ、CNES/CLS 4家分析中心所发布的精密轨道产品进行评估。
图 7给出了4家分析中心所发布的精密轨道产品与“GRT”轨道产品的比较结果,轨道比较时仅选取了各个产品共有的卫星,“GRG”产品未参与BDS的结果统计。由图 7可以看出,GPS、GLONASS、Galileo和BDS卫星轨道3D RMS分别在2.5、4.0、8.5及9.0 cm左右。对于不同分析中心的轨道产品,轨道比较结果也存在差异,以Galileo卫星为例,COD、WUM、GBM和GRG与GRT轨道比较3D RMS分别为4.0、5.0、4.6及4.8 cm。表 8给出了各分析中心精密轨道产品SLR检核残差平均值与标准差(STD)统计结果,对于Galileo和GLONASS卫星,各轨道产品SLR残差STD整体差异不大,分别在2.8和4.0 cm左右,BDS2-IGSO卫星SLR检核残差STD相对略大,为5~6 cm,而BDS2-MEO卫星SLR残差STD则在3~4 cm。相比于BDS-2 MEO卫星,BDS-3 MEO卫星SLR残差相对更小,STD在3 cm左右。值得注意的是,CASC与SECM生产的BDS-3 MEO卫星轨道SLR检核结果存在较大差异,这主要与卫星星体结构差异有关[125],其中CASC生产的MEO卫星星体沿星固系Z轴方向拉伸,而SECM生产的MEO卫星星体则沿星固系X轴方向拉伸[75],星体结构差异导致太阳光压建模精度不同,进而影响卫星轨道误差特性。

|
| 图 7 各分析中心精密轨道产品与iGMAS创新中心轨道产品比较结果 Fig. 7 Comparison results between orbit products from different analysis centers and orbit products from iGMAS innovation center |
| 导航卫星 | 统计值 | COD | WUM | GBM | GRG | GRT |
| GAL | 平均值 | -8.7 | 5.3 | 6.2 | 12.4 | -15.7 |
| 标准差 | 26.1 | 26.8 | 27.6 | 28.0 | 27.4 | |
| GLO | 平均值 | 12.1 | -2.1 | 1.6 | 13.2 | -5.4 |
| 标准差 | 38.4 | 39.5 | 42.6 | 40.0 | 42.0 | |
| BDS2-IGSO (CASC) |
平均值 | 8.0 | -8.9 | 3.4 | - | 1.4 |
| 标准差 | 60.0 | 49.0 | 52.7 | - | 47.0 | |
| BDS2-MEO (CASC) |
平均值 | -8.8 | -6.1 | -25.7 | - | -21.8 |
| 标准差 | 40.2 | 33.5 | 33.7 | - | 31.1 | |
| BDS3-MEO (CASC) |
平均值 | 43.0 | 36.7 | 26.0 | - | 27.7 |
| 标准差 | 27.7 | 31.4 | 35.3 | - | 33.6 | |
| BDS3-MEO (SECM) |
平均值 | -31.6 | -1.8 | -49.0 | - | -53.2 |
| 标准差 | 24.0 | 33.0 | 33.5 | - | 35.3 | |
| 注:“CASC”为中国航天科技集团有限公司;“SECM”为上海微型卫星研究院。 | ||||||
5 挑战与机遇
在过去的数十年间,GNSS技术发展迅猛,与此同时,GNSS卫星精密定轨理论与方法也在不断完善并且逐渐成熟。伴随着当前GNSS信号频率日益丰富,观测数据趋于多样及精度需求不断提高,GNSS卫星精密定轨也面临着诸如模型精化、效率提升等一系列挑战。同时,低轨星座、光原子钟、激光链路等新技术的出现与快速发展,也为GNSS卫星的高精度轨道获取提供了新的机遇。GNSS卫星精密定轨研究由此迈向了挑战与机遇并存的新局面。
5.1 当前面临的挑战(1) 多频多系统下的GNSS大网快速解算。近年来,随着各导航系统卫星数的逐渐增加、多频信号资源的不断丰富及地面跟踪站数量的快速增长,海量数据下轨道解算的耗时指数级增长、传统的单机集中式处理模式难以满足效率需求等问题日益突出。如何充分利用并行计算、分布式计算等现代高性能计算技术来提升GNSS定轨的解算效率,挖掘多频多系统观测数据对GNSS卫星精密定轨的贡献,是亟待解决的问题。
(2) 多层次观测数据融合的GNSS卫星精密定轨。目前,以地面测站为基础,以各类地球同步卫星、中轨道卫星、低轨道卫星等空间平台为载体的多源立体空间观测网络正在加速形成,这为GNSS卫星定轨提供了丰富的多层次观测数据。各类数据观测原理不同,误差特性各异。如何充分利用各类观测信息,挖掘各层次观测数据对GNSS定轨精度提升的最大潜力,实现多源数据间的优势互补,进一步提升GNSS卫星轨道确定精度和可靠性,值得深入研究。
(3) 太阳光压等非保守力模型的进一步精化。当前Galileo、BDS等卫星的轨道精度与GPS相比仍有一定差距,非保守力模型仍是制约这些卫星定轨精度的最主要问题。尤其是我国BDS系统,由于星座类型多、卫星型号多、星上载荷多,太阳光压等非保守力的物理来源、影响大小、建模方法也各有不同,必须针对不同卫星类型甚至不同卫星个体进行精细处理。除了定轨精度以外,还需要综合考虑动力学参数对于地球自转、地心运动、测站坐标等大地测量参数的影响,以构建综合表现最优的非保守力模型。
(4) 基于实时滤波的高精度GNSS定轨。人工智能、自动驾驶、智慧城市等技术的兴起对位置信息服务的精准性、时效性和可靠性提出了更高的要求,而高精度实时GNSS卫星精密轨道是提供实时精密时空服务的关键。目前,基于预报模式的实时轨道极易受到地影、偏航姿态切换、轨道机动等“非平稳”运动的影响,导致动力学模型的精度退化或不可用,无法满足高精度位置服务的需求。因此,需要深入探究和完善卫星运动状态异常变化期间实时定轨的动力学补偿方法,实现实时滤波系统的稳健处理,进一步提升多系统GNSS实时轨道的精度与可靠性。
5.2 未来机遇(1) 大规模低轨星座的建设带来了新数据。为了克服GNSS的脆弱性和局限性,以“星网”,CentiSpace等为代表的低轨导航增强星座近年来得到了飞速发展。这些由成百上千颗卫星组成的低轨星座,可为GNSS卫星提供海量的星载观测数据,可以在降低GNSS定轨地面依赖、改善观测几何等方面充分发挥其特有优势,同时,也可为精密定轨过程中天线相位中心准确标定等问题的解决提供新的可能。
(2) 光钟技术的发展与应用提供了新机遇。GNSS卫星原子钟的性能直接决定着精密定轨的精度,当前GNSS卫星搭载的原子钟均是基于微波频率,其稳定性有所限制,而近十年来光钟技术的发展则为GNSS精密定轨带来了新的机遇。相比于传统的微波钟,光钟振荡频率更高,其稳定性也要高出几个数量级[126]。在不久的将来GNSS卫星若能搭载光钟,卫星钟差对于精密定轨影响将大大减小,定轨精度有望进一步提高。
(3) 激光链路的出现与推广赋予了新思路。当前的GNSS卫星星间链路主要基于Ka波段信号,即微波链路,由于频率资源有限,微波链路难以满足高速数据传输的要求,并且微波通讯的抗干扰能力不足,关键信息容易被探测并拦截。近年来激光技术的发展使得采用激光进行GNSS卫星星间通讯成为可能。与微波链路相比,激光链路能够实现高速数据传输,具有极强的抗干扰性,并且激光信号不易衰减,具有更高的测量精度[127]。未来激光链路应用于GNSS卫星上,将实现高效、安全、可靠、低耗的星间通信,并且能够提供高精度的星间激光链路数据应用于GNSS卫星精密定轨中,进一步提升GNSS精密定轨的精度。
致谢: 本论文的数值计算得到了武汉大学超级计算中心的计算支持和帮助。
| [1] |
陈俊勇. GPS技术进展及其现代化[J]. 大地测量与地球动力学, 2010, 30(3): 1-4. CHEN Junyong. On progress in technology and modernization of GPS[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 1-4. |
| [2] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, contribution and challenges of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [3] |
KOGURE S, GANESHAN A S, MONTENBRUCK O. Regional systems[M]//TEUNISSEN P J G, MONTENBRUCK O. Springer Handbook of Global Navigation Satellite Systems. Cham: Springer, 2017: 305-338.
|
| [4] |
赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. ZHAO Qile. Research on precise orbit determination theory and software of both GPS navigation constellation and LEO satellites[D]. Wuhan: Wuhan University, 2004. |
| [5] |
LI Xingxing, ZHU Yiting, ZHENG Kai, et al. Precise orbit and clock products of Galileo, BDS and QZSS from MGEX Since 2018:comparison and PPP validation[J]. Remote Sensing, 2020, 12(9): 1415. DOI:10.3390/rs12091415 |
| [6] |
YANG Daoning, YANG Jun, LI Gang, et al. Globalization highlight: orbit determination using BeiDou inter-satellite ranging measurements[J]. GPS Solutions, 2017, 21(3): 1395-1404. DOI:10.1007/s10291-017-0626-5 |
| [7] |
李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min. Research on multi-GNSS precise orbit determination theory and application[D]. Wuhan: Wuhan University, 2011. |
| [8] |
袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉: 中国科学院研究生院(测量与地球物理研究所), 2002. YUAN Yunbin. Study on theories and methods of correcting ionospheric delay and monitoring ionosphere based on GPS[D]. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2002. |
| [9] |
LE A Q, KESHIN M O, VAN DER MAREL H. Single and dual-frequency precise point positioning: approaches and performances[C]//Proceedings of the 3rd ESA Workshop on Satellite Navigation User Equipment Technologies. Noordwijk, Wederland: ESA Publications, 2007.
|
| [10] |
LEANDRO R F. Precise point positioning with GPS: a new approach for positioning, atmospheric studies, and signal analysis[D]. Fredericton: University of New Brunswick, 2009.
|
| [11] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099-1099. ZHANG Baocheng. Study on the theoretical methodology and applications of precise point positioning using undifferenced and uncombined GNSS data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099-1099. DOI:10.13485/j.cnki.11-2089.2014.0155 |
| [12] |
LIU Teng, ZHANG Baocheng. Estimation of code observation-specific biases (OSBs) for the modernized multi-frequency and multi-GNSS signals: an undifferenced and uncombined approach[J]. Journal of Geodesy, 2021, 95(8): 97. DOI:10.1007/s00190-021-01549-x |
| [13] |
LI Xingxing, GE Maorong, ZHANG Hongping, et al. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning[J]. Journal of Geodesy, 2013, 87(5): 405-416. DOI:10.1007/s00190-013-0611-x |
| [14] |
LI Xin, LI Xingxing, LIU Gege, et al. BDS multi-frequency PPP ambiguity resolution with new B2a/B2b/B2a+b signals and legacy B1I/B3I signals[J]. Journal of Geodesy, 2020, 94(10): 107. DOI:10.1007/s00190-020-01439-8 |
| [15] |
辜声峰. 多频GNSS非差非组合精密数据处理理论及其应用[D]. 武汉: 武汉大学, 2013. GU Shengfeng. Research on the zero-difference un-combined data processing model for multi-frequency GNSS and its applications[D]. Wuhan: Wuhan University, 2013. |
| [16] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018. ZHOU Feng. Theory and methodology of multi-GNSS undifferenced and uncombined precise point positioning[D]. Shanghai: East China Normal University, 2018. |
| [17] |
SCHÖNEMANN E. Analysis of GNSS raw observations in PPP solutions[M]. Darmstadt: Technische Universität Darmstadt, 2013.
|
| [18] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014. GUO Jing. The impacts of attitude, solar radiation and function model on precise orbit determination for GNSS satellites[D]. Wuhan: Wuhan University, 2014. |
| [19] |
陈华. 基于原始观测值的GNSS统一快速精密数据处理方法[D]. 武汉: 武汉大学, 2015. CHEN Hua. An efficient and unified GNSS raw data processing strategy[D]. Wuhan: Wuhan University, 2015. |
| [20] |
STRASSER S, MAYER-GVRR T, ZEHENTNER N. Processing of GNSS constellations and ground station networks using the raw observation approach[J]. Journal of Geodesy, 2019, 93(7): 1045-1057. DOI:10.1007/s00190-018-1223-2 |
| [21] |
李星星, 黄健德, 袁勇强, 等. Galileo三频非组合精密定轨模型及精度评估[J]. 测绘学报, 2020, 49(9): 1120-1130. LI Xingxing, HUANG Jiande, YUAN Yongqiang, et al. Galileo triple-frequency uncombined precise orbit determination: model and quality assessment[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1120-1130. DOI:10.11947/j.AGCS.2020.20200320 |
| [22] |
曾添. 多频GNSS精密定轨及低轨卫星增强研究[D]. 郑州: 信息工程大学, 2020. ZENG Tian. Research on multi-frequency GNSS precise orbit determination and low earth orbit satellite enhancement[D]. Zhengzhou: Information Engineering University, 2020. |
| [23] |
BLEWITT G. Fixed point theorems of GPS carrier phase ambiguity resolution and their application to massive network processing: ambizap[J]. Journal of Geophysical Research, 2008, 113(B12): B12410. DOI:10.1029/2008JB005736 |
| [24] |
BLEWITT G, BERTIGER W, WEISS J P. Ambizap3 and GPS carrier-range: a new data type with IGS applications[C]//Proceedings of 2010 IGS Workshop and Vertical Rates. Newcastle: [s.n.], 2010: 28.
|
| [25] |
匡开发. GNSS卫星实时精密定轨技术研究[D]. 武汉: 武汉大学, 2019. KUANG Kaifa. Research on GNSS satellite real-time precise orbit determination technique[D]. Wuhan: Wuhan University, 2019. |
| [26] |
TEUNISSEN P J G, JOOSTEN P, TIBERIUS C C J M. A comparison of TCAR, CIR and LAMBDA GNSS ambiguity resolution[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR, USA: Institute of Navigation, 2002: 2799-2808.
|
| [27] |
BEUTLER G, BOCK H, DACH R, et al. Bernese GPS software version 5.0[R]. Bern: Astronomical Institute, University of Bern, 2007.
|
| [28] |
GE M, GENDT G, DICK G, et al. Improving carrier-phase ambiguity resolution in global GPS network solutions[J]. Journal of Geodesy, 2005, 79(1): 103-110. DOI:10.1007/s00190-005-0447-0 |
| [29] |
GENG Tao, XIE Xin, ZHAO Qile, et al. Improving BDS integer ambiguity resolution using satellite-induced code bias correction for precise orbit determination[J]. GPS Solutions, 2017, 21(3): 1191-1201. DOI:10.1007/s10291-017-0602-0 |
| [30] |
LOU Yidong, GONG Xiaopeng, GU Shengfeng, et al. Assessment of code bias variations of BDS triple-frequency signals and their impacts on ambiguity resolution for long baselines[J]. GPS Solutions, 2017, 21(1): 177-186. DOI:10.1007/s10291-016-0514-4 |
| [31] |
LIU Yang, GE Maorong, SHI Chuang, et al. Improving integer ambiguity resolution for GLONASS precise orbit determination[J]. Journal of Geodesy, 2016, 90(8): 715-726. DOI:10.1007/s00190-016-0904-y |
| [32] |
GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 401. DOI:10.1007/s00190-007-0208-3 |
| [33] |
LI Xingxing, LI Xin, YUAN Yongqiang, et al. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo[J]. Journal of Geodesy, 2018, 92(6): 579-608. DOI:10.1007/s00190-017-1081-3 |
| [34] |
LI Xingxing, LI Xin, LIU Gege, et al. Triple-frequency PPP ambiguity resolution with multi-constellation GNSS: BDS and Galileo[J]. Journal of Geodesy, 2019, 93(8): 1105-1122. DOI:10.1007/s00190-019-01229-x |
| [35] |
LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS ambiguity resolution at CNES-CLS IGS analysis center[J]. Journal of Geodesy, 2012, 86(11): 991-1003. DOI:10.1007/s00190-012-0559-2 |
| [36] |
LOYER S, PEROSANZ F, VERSINI L, et al. CNES/CLS IGS Analysis center: recent activities[C]//Proceedings of 2018 IGS Workshop. Wuhan: [s.n.], 2018.
|
| [37] |
CHEN Hua, JIANG Weiping, GE Maorong, et al. An enhanced strategy for GNSS data processing of massive networks[J]. Journal of Geodesy, 2014, 88(9): 857-867. DOI:10.1007/s00190-014-0727-7 |
| [38] |
GENG Jianghui, MENG Xiaolin, DODSON A H, et al. Integer ambiguity resolution in precise point positioning: method comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581. DOI:10.1007/s00190-010-0399-x |
| [39] |
LI Xingxing, XIONG Yun, YUAN Yongqiang, et al. Real-time estimation of multi-GNSS integer recovery clock with undifferenced ambiguity resolution[J]. Journal of Geodesy, 2019, 93(12): 2515-2528. DOI:10.1007/s00190-019-01312-3 |
| [40] |
SCHMID R, ROTHACHER M, THALLER D, et al. Absolute phase center corrections of satellite and receiver antennas: impact on global GPS solutions and estimation of azimuthal phase center variations of the satellite antenna[J]. GPS Solutions, 2005, 9(4): 283-293. DOI:10.1007/s10291-005-0134-x |
| [41] |
KOUBA J. A simplified yaw-attitude model for eclipsing GPS satellites[J]. GPS Solutions, 2009, 13(1): 1-12. DOI:10.1007/s10291-008-0092-1 |
| [42] |
DILSSNER F, SPRINGER T, GIENGER G, et al. The GLONASS-M satellite yaw-attitude model[J]. Advances in Space Research, 2011, 47(1): 160-171. DOI:10.1016/j.asr.2010.09.007 |
| [43] |
MONTENBRUCK O, SCHMID R, MERCIER F, et al. GNSS satellite geometry and attitude models[J]. Advances in Space Research, 2015, 56(6): 1015-1029. DOI:10.1016/j.asr.2015.06.019 |
| [44] |
EGSC (European GNSS Service Centre). Galileo satellite metadata[DB/OL]. [2022-01-08]. https://www.gsc-europa.eu/support-to-developers/galileo-satellite-metadata.
|
| [45] |
CAO (Cabinet Office, Government of Japan). QZSS satellite information[DB/OL]. [2022-05-01]. https://qzss.go.jp/en/technical/qzssinfo/.
|
| [46] |
GUO Jing, ZHAO Qile. Analysis of precise orbit determination for BeiDou satellites during yaw maneuvers[C]//Proceedings of 2014 China Satellite Navigation Conference. Nanjing: [s.n.], 2014.
|
| [47] |
GUO Jing, CHEN Guo, ZHAO Qile, et al. Comparison of solar radiation pressure models for BDS IGSO and MEO satellites with emphasis on improving orbit quality[J]. GPS Solutions, 2017, 21(2): 511-522. DOI:10.1007/s10291-016-0540-2 |
| [48] |
DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the yaw-attitude of BDS IGSO and MEO satellites[J]. Journal of Geodesy, 2015, 89(10): 1005-1018. DOI:10.1007/s00190-015-0829-x |
| [49] |
YUAN Yongqiang, Li Xingxing, ZHU Yiting, et al. Improving QZSS precise orbit determination by considering the solar radiation pressure of the L-band antenna[J]. GPS Solutions, 2020, 24(2): 50. DOI:10.1007/s10291-020-0963-7 |
| [50] |
刘宇玺, 贾小林, 阮仁桂. 北斗系统IGSO卫星新姿态控制模式下定轨精度分析[J]. 大地测量与地球动力学, 2017, 37(6): 614-617. LIU Yuxi, JIA Xiaolin, RUAN Rengui. BeiDou IGSO Satellite orbit determination precision analysis based on new attitude control mode[J]. Journal of Geodesy and Geodynamics, 2017, 37(6): 614-617. DOI:10.14075/j.jgg.2017.06.012 |
| [51] |
LI Xingxing, YUAN Yongqiang, HUANG Jiande, et al. Galileo and QZSS precise orbit and clock determination using new satellite metadata[J]. Journal of Geodesy, 2019, 93(8): 1123-1136. DOI:10.1007/s00190-019-01230-4 |
| [52] |
MADER G L. GPS antenna calibration at the national geodetic survey[J]. GPS Solutions, 1999, 3(1): 50-58. DOI:10.1007/PL00012780 |
| [53] |
GE Maorong, GENDT G, DICK G, et al. Impact of GPS satellite antenna offsets on scale changes in global network solutions[J]. Geophysical Research Letters, 2005, 32(6): L06310. DOI:10.1029/2004gl022224 |
| [54] |
REBISCHUNG P, GRIFFITHS J, RAY J, et al. IGS08:the IGS realization of ITRF2008[J]. GPS Solutions, 2012, 16(4): 483-494. DOI:10.1007/s10291-011-0248-2 |
| [55] |
REBISCHUNG P, SCHMID R. IGS14/igs14. atx: a new framework for the IGS products[C]//Proceedings of 2016 American Geophysical Union, Fall Meeting. San Francisco, CA, USA: IGS, 2016.
|
| [56] |
JÄGGI A, DILSSNER F, SCHMID R, et al. Extension of the GPS satellite antenna patterns to nadir angles beyond 14°[C]//Proceedings of 2012 EGU General Assembly. Vienna, Austria: EGU, 2012: 14.
|
| [57] |
STEIGENBERGER P, FRITSCHE M, DACH R, et al. Estimation of satellite antenna phase center offsets for Galileo[J]. Journal of Geodesy, 2016, 90(8): 773-785. DOI:10.1007/s00190-016-0909-6 |
| [58] |
HUANG Guanwen, YAN Xingyuan, ZHANG Qin, et al. Estimation of antenna phase center offset for BDS IGSO and MEO satellites[J]. GPS Solutions, 2018, 22(2): 49. DOI:10.1007/s10291-018-0716-z |
| [59] |
DILSSNER F, SPRINGER T, SCHÖNEMANN E, et al. Estimation of satellite antenna phase center corrections for BeiDou[C]//Proceedings of 2014 IGS Workshop. Pasadena, CA, USA: ESA, 2014: 23-27.
|
| [60] |
YAN Xingyuan, HUANG Guanwen, ZHANG Qin, et al. Estimation of the antenna phase center correction model for the BeiDou-3 MEO satellites[J]. Remote Sensing, 2019, 11(23): 2850. DOI:10.3390/rs11232850 |
| [61] |
GUO Jing, XU Xiaolong, ZHAO Qile, et al. Precise orbit determination for quad-constellation satellites at Wuhan University: strategy, result validation, and comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159. DOI:10.1007/s00190-015-0862-9 |
| [62] |
LI Xingxing, YUAN Yongqiang, ZHU Yiting, et al. Precise orbit determination for BDS-3 experimental satellites using iGMAS and MGEX tracking networks[J]. Journal of Geodesy, 2019, 93(1): 103-117. DOI:10.1007/s00190-018-1144-0 |
| [63] |
VILLIGER A. igs14_2056: update including BeiDou-3S and BeiDou-3 satellites[DB/OL]. [2019-06-04]. https://lists.igs.org/pipermail/igsmail/2019/007778.html.
|
| [64] |
CSNO (China Satellite Navigation Office). Satellite antenna phase center of BDS[DB/OL]. [2019-06-10]. http://en.beidou.gov.cn/SYSTEMS/Officialdocument/201912/P020200323536112807882.atx.
|
| [65] |
王晨. 北斗导航卫星光压模型构建与精化研究[D]. 武汉: 武汉大学, 2019. WANG Chen. Solar radiation pressure modelling for BeiDou navigation satellites[D]. Wuhan: Wuhan University, 2019. |
| [66] |
BURY G, SOŚNICA K, ZAJDEL R, et al. Toward the 1-cm Galileo orbits: challenges in modeling of perturbing forces[J]. Journal of Geodesy, 2020, 94(2): 16. DOI:10.1007/s00190-020-01342-2 |
| [67] |
BEUTLER G, BROCKMANN E, GURTNER W, et al. Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): theory and initial results[J]. Manuscripta Geodaetica, 1994, 19(6): 367-386. |
| [68] |
MONTENBRUCK O, STEIGENBERGER P, PRANGE L, et al. The multi-GNSS experiment (MGEX) of the International GNSS service (IGS)-achievements, prospects and challenges[J]. Advances in Space Research, 2017, 59(7): 1671-1697. DOI:10.1016/j.asr.2017.01.011 |
| [69] |
ARNOLD D, MEINDL M, BEUTLER G, et al. CODE's new solar radiation pressure model for GNSS orbit determination[J]. Journal of Geodesy, 2015, 89(8): 775-791. DOI:10.1007/s00190-015-0814-4 |
| [70] |
LIU Junhong, GU Defeng, JU Bing, et al. A new empirical solar radiation pressure model for BeiDou GEO satellites[J]. Advances in Space Research, 2016, 57(1): 234-244. DOI:10.1016/j.asr.2015.10.043 |
| [71] |
PRANGE L, BEUTLER G, DACH R, et al. An empirical solar radiation pressure model for satellites moving in the orbit-normal mode[J]. Advances in Space Research, 2020, 65(1): 235-250. DOI:10.1016/j.asr.2019.07.031 |
| [72] |
FLIEGEL H F, GALLINI T E, SWIFT E R. Global positioning system radiation force model for geodetic applications[J]. Journal of Geophysical Research, 1992, 97(B1): 559-568. DOI:10.1029/91jb02564 |
| [73] |
FENG Weidong, GUO Xiangyu, QIU Hongxing, et al. A study of analytical solar radiation pressure modeling for BeiDou navigation satellites based on raytracing method[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC)2014 Proceedings: Volume Ⅱ. Berlin, Heidelberg: Springer, 2014: 425-435.
|
| [74] |
ZIEBART M. Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape[J]. Journal of Spacecraft and Rockets, 2004, 41(5): 840-848. DOI:10.2514/1.13097 |
| [75] |
LI Xingxing, YUAN Yongqiang, ZHU Yiting, et al. Improving BDS-3 precise orbit determination for medium earth orbit satellites[J]. GPS Solutions, 2020, 24(2): 53. DOI:10.1007/s10291-020-0967-3 |
| [76] |
DUAN Bingbing, HUGENTOBLER U. Enhanced solar radiation pressure model for GPS satellites considering various physical effects[J]. GPS Solutions, 2021, 25(2): 42. DOI:10.1007/s10291-020-01073-z |
| [77] |
DUAN Bingbing, HUGENTOBLER U, HOFACKER M, et al. Improving solar radiation pressure modeling for GLONASS satellites[J]. Journal of Geodesy, 2020, 94(8): 72. DOI:10.1007/s00190-020-01400-9 |
| [78] |
MONTENBRUCK O, STEIGENBERGER P, HUGENTOBLER U. Enhanced solar radiation pressure modeling for Galileo satellites[J]. Journal of Geodesy, 2015, 89(3): 283-297. DOI:10.1007/s00190-014-0774-0 |
| [79] |
DUAN Bingbing, HUGENTOBLER U, SELMKE I, et al. BeiDou satellite radiation force models for precise orbit determination and geodetic applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022. DOI: 10.1109/TAES.2021.3140018.
|
| [80] |
RODRIGUEZ-SOLANO C J, HUGENTOBLER U, STEIGEN-BERGER P. Impact of albedo radiation on GPS satellites[M]//KENYON S, PACINO M C, MARTI U. Geodesy for Planet Earth. Berlin, Heidelberg: Springer, 2012: 113-119.
|
| [81] |
BURY G, ZAJDEL R, SOŚNICA K. Accounting for perturbing forces acting on Galileo using a box-wing model[J]. GPS Solutions, 2019, 23(3): 74. DOI:10.1007/s10291-019-0860-0 |
| [82] |
SVEHLA D. Model of solar radiation pressure and thermal re-radiation[M]//SVEHLA D. Geometrical Theory of Satellite Orbits and Gravity Field. Cham: Springer, 2018: 269-295.
|
| [83] |
COLOMBO O L. The dynamics of global positioning system orbits and the determination of precise ephemerides[J]. Journal of Geophysical Research, 1989, 94(B7): 9167-9182. DOI:10.1029/jb094ib07p09167 |
| [84] |
WANG Chen, GUO Jing, ZHAO Qile, et al. Empirically derived model of solar radiation pressure for BeiDou GEO satellites[J]. Journal of Geodesy, 2019, 93(6): 791-807. DOI:10.1007/s00190-018-1199-y |
| [85] |
SIDOROV D, DACH R, POLLE B, et al. Adopting the empirical CODE orbit model to Galileo satellites[J]. Advances in Space Research, 2020, 66(12): 2799-2811. DOI:10.1016/j.asr.2020.05.028 |
| [86] |
ZIEBART M, SIBTHORPE A, CROSS P, et al. Cracking the GPS-SLR orbit anomaly[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation. Fort Worth, TX, USA: Fort Worth Convention Center, 2007: 2033-2038.
|
| [87] |
STEIGENBERGER P, THOELERT S, MONTENBRUCK O. GNSS satellite transmit power and its impact on orbit determination[J]. Journal of Geodesy, 2018, 92(6): 609-624. DOI:10.1007/s00190-017-1082-2 |
| [88] |
EDGAR C, PRICE J, ITEIGH D. GPS Block ⅡA and ⅡR received signal power measurements[C]//Proceedings of 1998 National Technical Meeting of the Institute of Navigation. Long Beach, CA, USA: Westin Long Beach Hotel, 1998: 401-411.
|
| [89] |
WU A. Predictions and field measurements of the GPS Block ⅡR L1 and L2 ground powers[C]//Proceedings of 2002 National Technical Meeting of the Institute of Navigation. San Diego, CA, USA: The Catamaran Resort Hotel, 2002: 931-938.
|
| [90] |
GERDAN G P. A comparison of four methods of weighting double difference pseudorange measurements[J]. Australian Surveyor, 1995, 40(4): 60-66. DOI:10.1080/00050334.1995.10558564 |
| [91] |
HAN S. Quality-control issues relating to instantaneous ambiguity resolution for real-time GPS kinematic positioning[J]. Journal of Geodesy, 1997, 71(6): 351-361. DOI:10.1007/s001900050103 |
| [92] |
KING R W, BOCK Y. Documentation for the GAMIT GPS analysis software[R]. Cambridge: Massachusetts Institute of Technology, 1995.
|
| [93] |
LIU Jingnan, GE Maorong. PANDA software and its preliminary result of positioning and orbit determination[J]. Wuhan University Journal of Natural Sciences, 2003, 8(2): 603-609. DOI:10.1007/bf02899825 |
| [94] |
SATIRAPOD C. Stochastic models used in static GPS relative positioning[J]. Survey Review, 2006, 38(299): 379-386. DOI:10.1179/sre.2006.38.299.379 |
| [95] |
LAU L, MOK E. Improvement of GPS relative positioning accuracy by using SNR[J]. Journal of Surveying Engineering, 1999, 125(4): 185-202. DOI:10.1061/(asce)0733-9453(1999)125:4(185) |
| [96] |
刘志强. 基于随机模型精化的GPS精密定位算法研究与实现[D]. 南京: 河海大学, 2007. LIU Zhiqiang. Research and implementation of precise GPS positioning data processing algorithm based on refined stochastic model[D]. Nanjing: Hohai University, 2007. |
| [97] |
刘金海, 涂锐, 张睿, 等. Helmert方差分量估计在GPS/GLONASS/BDS组合定位权比确定中的应用[J]. 大地测量与地球动力学, 2018, 38(6): 568-570, 576. LIU Jinhai, TU Rui, ZHANG Rui, et al. Application of helmert variance component estimation in GPS/GLONASS/BDS combined positioning weight determination[J]. Journal of Geodesy and Geodynamics, 2018, 38(6): 568-570, 576. DOI:10.14075/j.jgg.2018.06.004 |
| [98] |
杨汀, 陈宜金, 陈浩男. 最小二乘方差分量估计在GNSS差分定位随机模型精化中的应用[J]. 大地测量与地球动力学, 2017, 37(2): 196-199, 204. YANG Ting, CHEN Yijin, CHEN Haonan. Least-squares variance component estimation applied to stochastic model refinement of GNSS difference positioning[J]. Journal of Geodesy and Geodynamics, 2017, 37(2): 196-199, 204. DOI:10.14075/j.jgg.2017.02.018 |
| [99] |
何海波, 杨元喜. GPS观测量先验方差-协方差矩阵实时估计[J]. 测绘学报, 2001, 30(1): 42-47. HE Haibo, YANG Yuanxi. Real-time estimation of a prior variance-covariance for GPS observations[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 42-47. |
| [100] |
杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报(信息科学版), 2003, 28(6): 714-718. YANG Yuanxi, XU Tianhe. An adaptive Kalman filter combining variance component estimation with covariance matrix estimation based on moving window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714-718. |
| [101] |
WANG Yongchao, FENG Yanming, ZHENG Fu. Geometry-free stochastic analysis of BDS triple frequency signals[C]//Proceedings of 2016 International Technical Meeting of the Institute of Navigation. Monterey, CA, USA: The Institute of Navigation, 2016: 956-969.
|
| [102] |
黄令勇, 吕志平, 吕浩, 等. 北斗三频伪距相关随机模型单站建模方法[J]. 测绘学报, 2016, 45(S2): 165-171. HUANG Lingyong, LÜ Zhiping, LÜ Hao, et al. The BDS triple frequency pseudo-range correlated stochastic model of single station modeling method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 165-171. DOI:10.11947/j.AGCS.2016.F038 |
| [103] |
张小红, 马福建. 低轨导航增强GNSS发展综述[J]. 测绘学报, 2019, 48(9): 1073-1087. ZHANG Xiaohong, MA Fujian. Review of the development of LEO navigation-augmented GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1073-1087. DOI:10.11947/j.AGCS.2019.20190176 |
| [104] |
RIM H J, SCHUTZ B E, ABUSALI P A M, et al. Effect of GPS orbit accuracy on GPS-determined Topex/Poseidon orbit[C]//Proceedings of 1995 ION GPS-95. [S. l. ]: Institute of Navigation, 1995: 613-617.
|
| [105] |
ZHU Shengyuan, REIGBER C, KÖNIG R. Integrated adjustment of CHAMP, GRACE, and GPS data[J]. Journal of Geodesy, 2004, 78(1): 103-108. DOI:10.1007/s00190-004-0379-0 |
| [106] |
GENG Jianghui, SHI Changhong, ZHAO Qile, et al. Integrated adjustment of LEO and GPS in precision orbit determination[C]//Proceedings of 2008 VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy. Wuhan: Springer, 2008: 133-137.
|
| [107] |
LI Xingxing, ZHANG Keke, MENG Xiangguang, et al. LEO-BDS-GPS integrated precise orbit modeling using FengYun-3D, FengYun-3C onboard and ground observations[J]. GPS Solutions, 2020, 24(2): 48. DOI:10.1007/s10291-020-0962-8 |
| [108] |
LI Xingxing, ZHANG Keke, MA Fujian, et al. Integrated precise orbit determination of multi-GNSS and large LEO constellations[J]. Remote Sensing, 2019, 11(21): 2514. DOI:10.3390/rs11212514 |
| [109] |
ZHAO Qile, WANG Chen, GUO Jing, et al. Enhanced orbit determination for BeiDou satellites with FengYun-3C onboard GNSS data[J]. GPS Solutions, 2017, 21(3): 1179-1190. DOI:10.1007/s10291-017-0604-y |
| [110] |
LI Bofeng, GE Haibo, GE Maorong, et al. LEO enhanced global navigation satellite system (LeGNSS) for real-time precise positioning services[J]. Advances in Space Research, 2019, 63(1): 73-93. DOI:10.1016/j.asr.2018.08.017 |
| [111] |
HUANG Wen, MÄNNEL B, SAKIC P, et al. Integrated processing of ground-and space-based GPS observations: improving GPS satellite orbits observed with sparse ground networks[J]. Journal of Geodesy, 2020, 94(10): 96. DOI:10.1007/s00190-020-01424-1 |
| [112] |
石立国. 分布式卫星系统星间链路关键技术研究[D]. 北京: 中国科学院国家空间科学中心, 2016. SHI Liguo. Research on key technologies of inter satellite links for distributed satellites system[D]. Beijing: National Space Science Center, the Chinese Academy of Sciences, 2016. |
| [113] |
ANANDA M P, BERNSTEIN H, CUNNINGHAM K E, et al. Global positioning system (GPS) autonomous navigation[C]//Proceedings of 1990 IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences. Las Vegas, NV, USA: IEEE, 1990: 497-508.
|
| [114] |
WANG Haihong, XIE Jun, ZHUANG Jianlou, et al. Performance analysis and progress of inter-satellite-link of BeiDou system[C]//Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR, USA: Oregon Convention Center, 2017: 1178-1185.
|
| [115] |
XU Hongliang, WANG Jinling, ZHAN Xingqun. Autonomous broadcast ephemeris improvement for GNSS using inter-satellite ranging measurements[J]. Advances in Space Research, 2012, 49(6): 1034-1044. DOI:10.1016/j.asr.2012.01.001 |
| [116] |
REN Xia, YANG Yuanxi, ZHU Jun, et al. Orbit determination of the next-generation BeiDou satellites with intersatellite link measurements and a priori orbit constraints[J]. Advances in Space Research, 2017, 60(10): 2155-2165. DOI:10.1016/j.asr.2017.08.024 |
| [117] |
阮仁桂, 冯来平, 贾小林. 导航卫星星地/星间链路联合定轨中设备时延估计方法[J]. 测绘学报, 2014, 43(2): 137-142, 157. RUAN Rengui, FENG Laiping, JIA Xiaolin. Equipment delay estimation for GNSS satellite combined orbit determi-nation with satellite-ground link and inter-satellite link observations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 137-142, 157. DOI:10.13485/j.cnki.11-2089.2014.0020 |
| [118] |
冯来平. 低轨卫星与星间链路增强的导航卫星精密定轨研究[D]. 郑州: 信息工程大学, 2017. FENG Laiping. Study of precise orbit determination for GNSS enhanced by LEO satellite and inter-satellite ranging[D]. Zhengzhou: Information Engineering University, 2017. |
| [119] |
ZHANG Rui, TU Rui, ZHANG Pengfei, et al. Orbit determination of BDS-3 satellite based on regional ground tracking station and inter-satellite link observations[J]. Advances in Space Research, 2021, 67(12): 4011-4024. DOI:10.1016/j.asr.2021.02.027 |
| [120] |
PRANGE L, ARNOLD D, DACH R, et al. CODE product series for the IGS-MGEX project[R]. [S.l.]: Astronomical Institute, University of Bern, 2020.
|
| [121] |
SELMKE I, DUAN Bingbing, HUGENTOBLER U. Status of the TUM MGEX orbit and clock products[C]//Proceedings of 2018 IGS Workshop. Wuhan: [s.n.], 2018.
|
| [122] |
AGROTIS L, SCHÖNEMANN E, ENDERLE W, et al. The IGS real time service[C]//Proceedings of 2017 GNSS 2017-Kompetenz für die Zukunft. Potsdam, Germany: [s.n.], 2017.
|
| [123] |
LAURICHESSE D, CERRI L, BERTHIAS J P, et al. Real time precise GPS constellation and clocks estimation by means of a Kalman filter[C]//Proceedings of 2013 ION-GNSS. Nashville, TN, USA: Institute of Navigation, 2013: 1155-1163.
|
| [124] |
戴小蕾. 基于平方根信息滤波的GNSS导航卫星实时精密定轨理论与方法[D]. 武汉: 武汉大学, 2016. DAI Xiaolei. Real-time precise GNSS satellite orbit determination using the SRIF method: theory and implemencation[D]. Wuhan: Wuhan University, 2016. |
| [125] |
ZHAO Qile, GUO Jing, WANG Chen, et al. Precise orbit determination for BDS satellites[J]. Satellite Navigation, 2022, 3(1): 2. DOI:10.1186/s43020-021-00062-y |
| [126] |
SCHULDT T, GOHLKE M, OSWALD M, et al. Optical clock technologies for global navigation satellite systems[J]. GPS Solutions, 2021, 25(3): 83. DOI:10.1007/s10291-021-01113-2 |
| [127] |
GIORGI G, SCHMIDT T D, TRAINOTTI C, et al. Advanced technologies for satellite navigation and geodesy[J]. Advances in Space Research, 2019, 64(6): 1256-1273. DOI:10.1016/j.asr.2019.06.010 |