2. 南京信息工程大学遥感与测绘工程学院, 江苏 南京 210044
2. Nanjing University of Information Science and Technology, Nanjing 210044, China
地表形变是一种由自然因素或人为原因导致的地质现象,其致灾过程缓慢且不可逆,同时也是一种破坏力较强的地质灾害[1]。近年来,伴随经济飞速发展、地下资源开采及地下空间开发等,地表沉降和基础设施形变问题日益严重,不仅影响和破坏了地面人工建筑物,还极大危害了人类的生命安全与经济活动,破坏了发展资源和生态环境。仅我国长江和珠江三角洲经济区、汾渭断陷盆地、华北平原等地区,就有90多个城市发生过严重地面沉降和地裂缝灾害,还引发了土地盐碱化、洪涝、海水倒灌等次生灾害,给当地造成了极大的经济损失[2]。地表形变监测是重大基础设施安全评价的基础和重要组成,对探测潜在风险和保障安全具有至关重要的作用。传统的工程测量监测手段,如水准测量、全站仪测量等,虽然测量精度足够高,但监测范围小,易受外界观测环境的影响,耗费大量的人力与物力,且不能连续作业,因而导致监测效率低,无法及时有效地更新形变信息,难以适应现代化建设的需求。
全球导航卫星系统(GNSS)作为重要的时空信息基础设施,在国民经济建设和国防安全领域发挥着十分重要的作用。2020年7月31日我国北斗三号全球导航卫星系统(BeiDou System,BDS)全面建成开通,进一步推动了北斗/GNSS应用的深度和广度。除了导航、定位与授时等基本服务外,GNSS技术因其可全天时全天候、站间无须通视、可获取高精度三维绝对坐标信息等优点,已被广泛应用于地表形变监测领域[3]。作为一种点观测系统,GNSS技术需要在待监测区布设台站,受接收机数量和密度限制,无法获取高空间密度的地表形变信息。在工程实践中,受限于诸如水电工程高山深谷、高位隐蔽性滑坡体等复杂环境,仅在重点部位布设分散、不连续的单个监测点,利用全站仪、GNSS等测量手段按以点代面、以局部代替整体的方法采集离散点形变信息进行数据处理,难免遗漏一些重大的安全隐患,严重时将造成人员伤亡、经济损失,带来负面的社会影响。
合成孔径雷达干涉测量(InSAR)作为一种主动式空间对地微波遥感技术,少受云雨等条件影响,可以大范围、低成本及高空间分辨率获取地面高程或形变信息,在过去近30年间得到迅猛发展,已被广泛应用于地震形变研究[4]、城市沉降监测[5-6]、滑坡监测[7-8]、矿山形变监测[9-10]、水利工程安全监测[11]等多个领域。许多国家和组织近年来已经发射或将要发射多颗SAR卫星,将进一步带动InSAR技术和应用的发展。然而,InSAR也有自身固有限制,如易受大气延迟误差和时空失相干噪声等影响,严重时混淆真实形变信号,导致对InSAR形变结果的误判;其获取的形变结果为地表形变沿卫星视线向(line of sight, LOS)上的投影,难以准确评估真实形变的大小和方向[12]。
地表形变成因机制复杂、持续时间长、涉及范围广且诱发因素多,使得利用单一技术手段监测地表形变存在较多难题。考虑InSAR与GNSS两种技术的特点及互补性(见表 1),综合InSAR与北斗/GNSS技术方法,能够同时在空间和时间上提升地表形变监测能力。但如何更好、更深层次地综合两种技术服务于地表形变灾害监测,一直是国内外学界重点研究的课题。本文将重点介绍综合InSAR与北斗/GNSS技术在地表形变监测方面的技术发展和应用情况。
| 指标 | InSAR技术 | GNSS技术 |
| 观测量 | 视线向(一维) | 水平、垂直向(三维) |
| 时间分辨率 | 周期性(数天~数十天) | 近连续(采样率可达200 Hz) |
| 空间分辨率 | 空间连续、面状覆盖 | 离散点 |
| 获取形变量 | 相对量 | 绝对量和相对量 |
| 垂直方向形变敏感度 | 敏感 | 相对不敏感 |
| 现场作业 | 无须 | 需布设接收机 |
1 概述 1.1 InSAR技术基本原理
InSAR技术利用覆盖同一地区不同时刻的两景或多景复数影像,通过共轭相乘得到干涉信号,最初被用于地形测图及三维地表地形数据的获取[13]。InSAR干涉信号除了与高程相关,还与形变相关,因此在去除地形相位贡献的基础上,可用于获取微小地表形变信息,该技术称为差分InSAR(differential InSAR,D-InSAR)技术。1992年,文献[14]基于该技术得到Landers地震的同震形变场,引起了世界学者的广泛关注。但失相干噪声和大气延迟等误差严重降低了D-InSAR技术监测的可靠性,因此其应用场景主要限制在地震、地质构造运动、火山等形变量级较大的监测区域,精度一般只能达到分米至厘米级[12]。
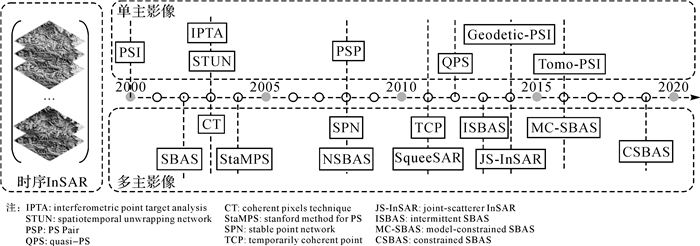
为了克服传统D-InSAR技术的局限性,提高InSAR技术地表形变精细化监测能力,国内外众多学者在D-InSAR技术的基础上发展了一系列时序InSAR(time-series InSAR,TS-InSAR)技术,又称为多时相InSAR(multi-temporal InSAR,MT-InSAR)(如图 1所示),并成为InSAR领域研究的热点。该技术的核心思想主要是利用同一区域的差分缠绕或解缠干涉图集,提取散射特性稳定的高相干性点,然后基于最小范数理论重构形变速率和形变时间序列。当前TS-InSAR技术根据主影像的数量可以划分为两大类,最具代表性的是单一主影像的永久散射体(persistent scatterer InSAR,PS-InSAR)技术[15]和多主影像的小基线集(small baseline subset,SBAS)技术[16]。其中PS-InSAR技术主要是针对自然环境中的基础设施和裸露岩石等强反射的永久散射体(persistent scatterer, PS)目标进行建模,故该类技术往往在人工建筑较密集的城市区域应用效果较好。而多主影像SBAS技术主要是针对分布式目标(distributed scatterer,DS)进行建模分析。该技术提出初期,主要是使用多视滤波抑制噪声,同时也提升了数据处理效率,但代价是损失了空间分辨率,因此它主要适用于广域地表探测,如震源机理、大型断裂带研究。但面对复杂场景和精细化监测目标时,多视SBAS技术不利于捕获形变细节特征。为此,基于全分辨率(单视)的SBAS技术逐步发展起来。特别的,自文献[17]提出第2代永久散射体SqueeSAR技术以来,分布式目标InSAR(distributed scatterer InSAR,DS-InSAR)技术成为国际时序InSAR领域新的研究热点之一。
|
| 图 1 各种时序InSAR技术的发展 Fig. 1 The development of various time-series InSAR technologies |
以上探讨的时序InSAR技术仅使用单一极化数据进行地表形变反演。随着新一代SAR卫星大多具备多极化数据获取能力,一些学者在上述时序InSAR技术的基础上延伸了新的技术分支——极化时序InSAR(polarimetric PSI,PolPSI)技术[18]。该技术的提出进一步减弱了城市区域多种散射机制混叠或建构筑物朝向等因素导致的失相干,提高了形变监测点的密度。
除上述几种应用较为广泛的InSAR技术,近些年也发展了其他一些高级InSAR技术,如像素偏移量追踪(pixel offset tracking,POT)技术[19]、多孔径InSAR(multi-aperture InSAR,MAI)技术[20]、SAR层析成像(SAR tomography)技术[21]及哨兵数据方位向子带重叠区域干涉(burst overlap interferometry,BOI)技术[22]。需要指出的是,理论上POT技术是基于振幅数据而非干涉相位信息,因此本不应属于InSAR技术。但为了便于描述,本文也将POT归于InSAR技术范畴。由于其技术原理不同,监测精度也略有差异,因此在实际应用中需要视情况而定。
1.2 北斗/GNSS技术形变监测基本原理相较于传统全站仪测量,以及以三维激光扫描、InSAR、近景摄影测量技术为代表的遥感技术,GNSS技术在监测的时效性和连续性上具有巨大优势,因此在高精度地表形变监测领域得到了大量应用[23-24]。目前,将GNSS应用于高精度地表形变监测主要采用的技术有静态差分技术、实时动态载波相位差分(real time kinematic,RTK)技术和精密单点定位(precise point positioning,PPP)技术等[25-26]。其中PPP技术可实现绝对单点定位,不依赖基准站,但易受误差改正不彻底或未模型化误差影响,因此该技术的定位精度往往难以满足高精度形变监测的需求。而静态差分技术又称为相对定位[27],一般利用2台以上GNSS接收机进行同步观测,通过对不同接收机之间的有效观测值进行差分处理,最终确定接收机之间的相对坐标。最常见的静态差分方式是双差定位,即利用站间单差和星间单差组成双差的方式进行定位,这种方式可以减少双差伪距和载波相位观测方程中的误差项。当被监测目标的形变速率较缓慢时,在一定空间域和时间域上被认作是稳定的,即可以利用GNSS静态差分技术进行形变监测。因此,大坝、边坡、矿山、铁路、码头等形变缓慢及对实时性要求不高的对象普遍采用该技术,在一些公网通信不便的区域也常有应用。GNSS静态差分技术虽然可以通过消除误差和增加观测时长等策略获得毫米级的监测精度,但其时效性难以满足实时性监测要求。
随着形变信息由静态周期性向动态实时性转变,RTK技术应运而生。早期RTK技术的主要技术难点是模糊度固定,但随着快速模糊度求解LAMBDA算法[28]及后续几个版本的升级,RTK技术逐渐走向成熟并被广泛应用于精密工程测量、大坝桥梁形变监测、工程放样及地形测图等领域。由于常规RTK技术需要设置基准站,作用范围小且可靠性差,因此基于双差模式的网络RTK技术成为实时动态定位的主要发展方向。依据大气误差模型等差分信息播发方式的不同,双差网络RTK技术又分为主辅站(master auxiliary concept,MAC)技术[29]、区域改正数(flachen korrektur parameter, FKP)技术[30]和虚拟参考站(virtual reference station, VRS)技术[31]。RTK技术多适用于快速形变或缓慢形变中存在突变情况的监测对象,对监测点实时变化要求较高时也常采用该技术。但该技术对于GNSS数据通信的时延性能要求较高,需保证数据的实时连续稳定传输,以获取连续可靠的形变监测结果。GNSS静态差分和RTK技术通常采用的双差差分相对定位观测模型为
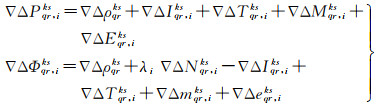 (1)
(1)
式中,上下标k和s分别代表参考卫星和公视卫星;q和r分别代表参考站和移动站;∇ΔPqr, iks和∇ΔΦqr, iks分别为双差伪距和载波相位观测值;∇Δρqrks为接收机至卫星间的双差卫地距;∇ΔIqr, iks为双差电离层延迟;∇ΔTqr, iks为双差对流层延迟;∇ΔMqr, iks和∇Δmqr, iks分别为双差伪距和载波相位多路径误差;λi为频率i信号的波长;∇ΔNqr, iks为双差整周模糊度;∇ΔEqr, iks和∇Δeqr, iks分别为双差伪距和载波相位噪声及非模型化误差等。这种方式可以消除接收机钟差、卫星钟差、接收机和卫星端的硬件延迟,以及削弱卫星轨道误差、对流层延迟、电离层延迟等误差,被广泛应用于高精度地表形变监测领域中。
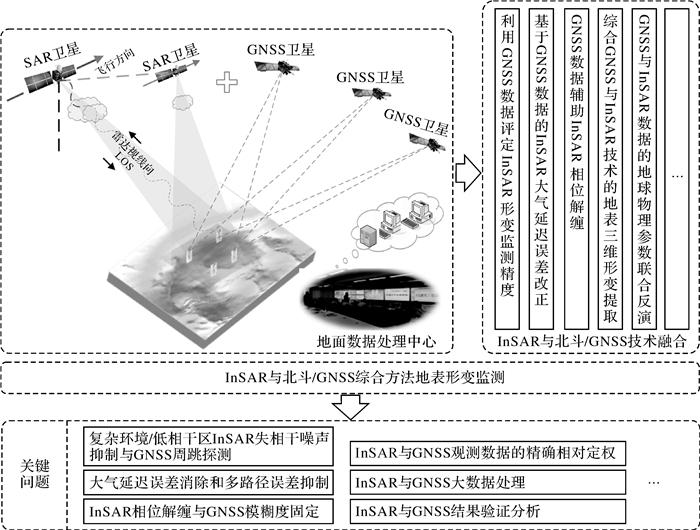
2 现有InSAR与北斗/GNSS技术融合研究分析InSAR技术与GNSS技术是目前获取地表形变应用最为广泛的两种空间大地测量手段,通过比较表 1可知,二者具有很好的互补性。因此,关于GNSS与InSAR的数据融合一直是一个重要的研究热点。继1997年文献[32]首次提出两种技术融合的思想后,国内学者分析了GPS与InSAR数据融合的必要性与可行性,并探讨了数据融合存在的主要问题[33]。经过20多年的不断探索,目前针对两种技术已在以下几个方面开展了大量的融合研究工作,其研究总体思路如图 2所示。
|
| 图 2 InSAR与GNSS综合方法地表形变监测的总体思路 Fig. 2 The overall framework of the integration of InSAR and GNSS for monitoring deformation |
2.1 利用GNSS数据评定InSAR形变监测精度
分析InSAR数据中存在的各种误差及其传播规律并构建误差模型,对InSAR技术的数学模型完善具有重要作用,同时对参数的估计和精度评估有着重要意义[34]。如何准确、客观地进行精度评定是目前InSAR技术真正发展成为一门应用更为广泛的高精度测量技术的主要挑战之一。目前对InSAR测量结果的精度分析一般包括理论分析和与实地数据对比分析。而GNSS精密定位技术已在大地测量、地壳形变监测、精密工程测量等诸多领域得到了广泛的应用和普及。大量研究证明,GNSS技术在水平位移的监测精度可达1 mm,高程方向的测量误差约为水平位移误差的2倍[35],这为融合InSAR与GNSS数据、研究精度评定模型和方法提供了契机。目前GNSS测量结果也成为验证InSAR结果可靠性的主要外部数据之一,如文献[7]将InSAR观测结果与GPS观测资料进行对比,验证了InSAR处理方法的有效性;文献[36]利用同时期BDS观测数据对InSAR得到的线性形变速率和时序位移序列进行了精度评估。
2.2 基于GNSS数据的InSAR大气延迟误差改正大气延迟是所有电磁波测量技术中的主要误差源之一。1994年,文献[37]首次在InSAR干涉图中发现了大气误差引起的干涉条纹;随后文献[38]表明20%的相对湿度时空变化可导致10~14 cm的形变观测值误差。GNSS技术可精确测定测站周边天顶对流层延迟参数,为InSAR大气延迟误差改正提供依据。文献[32]通过模拟试验证明了大气误差遵循幂律模型,并提出结合GPS对流层参数和空间拟合模型改正InSAR干涉图中的大气影响。文献[39]基于GPS地形相关湍流模型有效改善了InSAR干涉图中长波信号的大气水汽影响和与地形相关的短波大气延迟。文献[40]采用基于“凝固流”假设的大气传输模型和回归估计方法,通过对稀疏分布的GPS站点上的大气延迟估计值进行插值,获取了空间上加密的大气延迟场。文献[41—42]基于EMCWF和GNSS站点数据,通过迭代对流层模型,生成了通用型大气延迟改正产品(generic atmospheric correction online service for InSAR, GACOS),并逐渐成为InSAR大气误差改正的首选方法。此外,文献[43]融合InSAR和GPS观测数据重构获得了高分辨率的大气可降水量分布。
2.3 GNSS数据辅助InSAR相位解缠相位解缠是InSAR数据处理中的关键步骤,也是目前数据处理中的难点和热点问题。随着GNSS技术,尤其是连续运行参考站(continuously operating reference stations,CORS)技术的不断发展,引入GNSS观测信息辅助InSAR相位解缠成为可能。该类方法的思想主要是利用GNSS技术得到的高精度的三维信息反算InSAR绝对相位值,从而进一步确定最优积分路径和相位孤岛之间的解缠相位关系。2002年,文献[44]首次提出了一种基于马尔可夫随机场的GPS辅助InSAR相位解缠算法,该算法的本质为利用GPS获取的解缠相位初值指导解缠,其目标函数f表示为
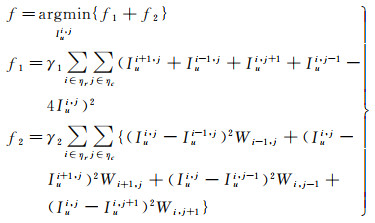 (2)
(2)
式中,ηr和ηc分别为干涉图在行和列方向上的像元数;Iui, j为第i行j列的解缠相位值;γ1和γ2为常数;W为计算掩码,当W在GPS固定域内时值为1,否则为0。
文献[45]在该算法的基础上,提出了一种基于多个GPS控制点的多解缠起算点枝切线综合相位解缠算法,提高了相位解缠精度和范围。此后,文献[46]进一步给出了一种可将GNSS及激光雷达(light detection and ranging,LiDAR)等外部数据作为先验约束的二维相位解缠框架,有效保证了相位边缘一致性。
2.4 综合GNSS与InSAR技术的地表三维形变提取由于SAR卫星是侧视成像系统,InSAR技术实际观测到的是真实形变在雷达视线上一维投影,而非地表在垂直、东西和南北方向的真实三维形变,这一缺陷极大限制了InSAR技术的实际应用前景。而GNSS技术可以连续实时获取高精度地表三维矢量形变和位置信息。因此,国内外学者开展了大量综合GNSS技术重构InSAR三维形变和预计研究工作。2002年,文献[47]首次提出基于马尔可夫随机场的GPS和InSAR综合方法,建立了Gibbs能量方程,其能量函数U可以表示为
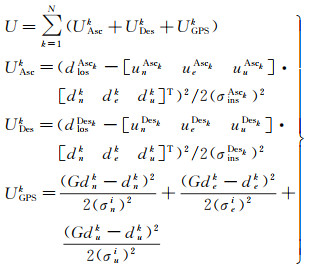 (3)
(3)
式中,N为像元数量;UAsc、UDes及UGPS分别代表InSAR升、降轨及GPS观测值约束;[dndedu]T为地表在南北、东西、垂直向上的形变矢量;σn、σe、σu为GPS对应方向上的地表形变的标准差;σe和σu为InSAR升、降轨获得的地表形变的标准差;[unkuekuuk]为InSAR视线向上的单位投影矢量;[GunGueGuu]T为由GPS形变场内插得到形变矢量。
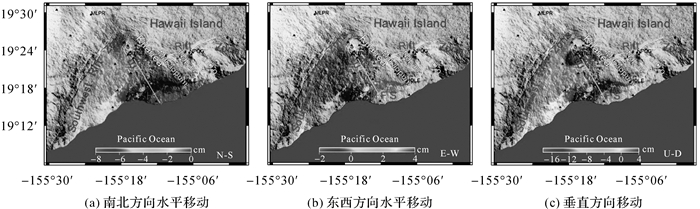
针对Gibbs能量方程,文献[47]借助模拟退火算法进行求解。由于模拟退火法计算复杂且有时无法收敛,因而近年来对能量方程的求解成为一个研究热点,并发展了一些行之有效的方法,主要包括解析优化法[48]、直接分解法[49]、拟Newton法(BFGS方法)[50]、插值法[51]、蚁群算法[52]等。图 3显示了基于蚁群算法的综合GPS与DInSAR技术获取的基拉韦厄火山南翼地区的三维形变场。此外,对于随机模型的确定,文献[53]也提出了一种基于方差分量估计的验后估计法,更加精确地确定权比,从而进一步提高了三维形变场的反演精度。
2.5 GNSS与InSAR数据的地球物理参数联合反演
利用大地测量技术获取的高精度地表形变场是目前地球物理参数反演研究的一种重要手段。如利用InSAR技术获得的同震形变可用于研究地震震源机制和发震断层滑动分布。在相干性较好的区域,InSAR技术能够精确测量地震中断层片段的几何分布。此外,联合其他技术,如POT、BOI、MAI技术等,可直接获取地表破裂几何长度等关键信息。在此基础上,通过简单弹性位错模型,可获取形变图的特定特征与地震震源参数的关系,进一步反演出地震的断层几何参数和断层面上的滑动分布。相比于InSAR对地表垂直运动的高敏感性,GNSS技术在水平位移监测方面更具优势。因此,联合InSAR与GNSS观测资料不仅可以弥补InSAR视线向对南北向形变不敏感和GNSS数据空间点位分布稀疏的不足,更有利于研究破裂机制和提高反演结果的可靠性,进而提高发现孕震形变的可能性。2020年,文献[54]联合运用2008汶川大地震前后GNSS和InSAR技术观测获得的同震位移,结合断层位错模型开展了汶川大地震断层几何参数和断层面上的滑动分布的反演研究,进而分析了地震发生的破裂机制。除用于震源参数反演,InSAR与GNSS获取的高分辨率地表形变资料还可用于火山岩浆囊参数、地下水文学参数反演等。如通过建立地表形变与地下水变化的函数和物理模型,可以探测地下水变化的物理特征及与地表沉降间的耦合关系[55]。文献[56]在获取GNSS和InSAR长时序形变的基础上,结合有限元模型,捕捉到了Okmok火山岩浆系统的时间演化规律。
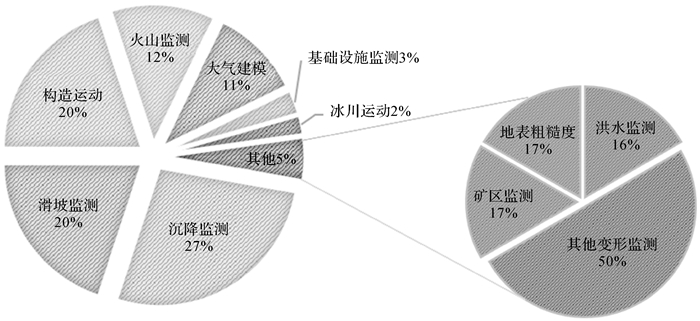
3 InSAR与北斗/GNSS技术在地表形变监测应用中关键问题近年来,国内外已有众多学者将InSAR和北斗/GNSS技术应用于大型工程的施工、运营及维护等各个建设阶段,并积累了一定的工程应用经验。图 4显示了截至2021年,欧洲地区综合InSAR与GNSS技术在各个领域的应用情况。为了充分明确两种技术在探测和监测各类地表形变灾害方面的优势和不足,本文总结了实际应用过程中的几大关键问题。
3.1 复杂环境/低相干区InSAR失相干噪声抑制与GNSS周跳探测
高精度形变信息的获取是保障工程安全监测的重要前提,但在实际应用中无论GNSS还是InSAR技术均会面临复杂观测环境等影响,造成监测结果精度和可靠性降低。在复杂环境或低相干场景下,GNSS高精度定位需要解决周跳、粗差、多路径误差等关键问题,而InSAR技术则面临干涉失相干、衰落信号误差等影响。
对于GNSS周跳问题的处理,根据对卫地距处理方式可归纳为几何无关(geometry-free,GF)和基于几何(geometry-based,GB)两类模型。文献[58]基于GF组合提出了一种经典的TurboEdit算法,被广泛应用于周跳处理中。文献[59—60]利用伪距和相位观测值并基于GF组合实现了三频数据的周跳探测与修复。其中基于GF等组合观测值理论的周跳算法的关键是解决电离层延迟和观测噪声等影响。为此,文献[61]构造了一种无几何无电离层组合(geometry-free and ionospheric-free, GFIF)模型;文献[62]在GB模型的基础上联立多系统多频观测值提出了一种有效的周跳处理算法;文献[63]联立多历元观测值并基于GB模型提出了一种周跳探测与修复方法,特别适用于监测场景中。此外,还可以考虑将GF和GB模型进行结合应用[64]。针对粗差问题,目前主要可采用两类思想进行处理。一种是基于均值漂移的思想并从函数模型出发,如经典的(detection identification and adaptation,DIA)方法[65];另一种是基于方差膨胀的思想并从随机模型出发,如经典的选权迭代方法[66]。复杂观测环境下,GNSS观测值中往往会包含更多样性的粗差和更显著的多路径等误差,如非模型化误差[67]。因此,研究复杂环境下北斗/GNSS高精度定位技术成为地表形变监测中亟须解决的关键问题之一。此外,随着GNSS的现代化建设和北斗不同类型星座特点及5频信号的出现,多系统多频信号的周跳探测与修复理论也是今后研究的一个重要内容。
而对于InSAR失相干噪声抑制,常用方法主要包括以下几种:①选用长波段SAR数据。长波段SAR数据对植被具有较强的穿透能力,在成像过程中受植被覆盖的影响也小[68],从而可以更好地保证干涉相位质量。目前常用的长波段SAR数据主要是L波段的ALOS-1/2卫星数据,未来美国国家航空航天局发射的具备双频(L和S频段)的NISAR和我国在研的L波段差分SAR卫星将会不断丰富数据源。②选用高空间分辨率SAR数据有助于保证分辨单元内的影像质地更为单一,在一定程度上提升干涉对的相干性。③利用成像时间间隔较短的干涉对也可以削弱时间失相干的影响,其思路主要源于小基线集方法,假设时间间隔越短地物变化越不显著。但此处值得注意的是,最新研究发现,尽管利用短时间间隔的多视SAR数据会削弱失相干噪声,但也会伴随“衰落”信号的出现,又称作Fading Signal[69]。该信号的特性不同于失相干引起的随机噪声,它会引入系统偏差并随时间衰减。以上3种策略受限于研究区现有的SAR数据条件,其可行性和普适性不强。④应用相位优化方法。该方法本质上是一种时域滤波技术,其主要思想是对现有数据集进行全组合干涉,然后利用统计特征进行最大似然估计得到优化后的时序相位[70-71]。该方法是现有SAR数据条件下可行性最强、发展性最好的解决措施,但占据大量的计算资源,计算效率也是制约其推广应用的一个重要因素[72]。目前考虑到失相干噪声是制约InSAR测量精度的瓶颈,因此如何通过定量分析这些因素与干涉测量间的关系,并采取有效的措施减小或避免这种影响仍是今后InSAR领域研究的重点内容。
3.2 大气延迟误差改正和多路径误差抑制前文所述,大气延迟误差对InSAR和GNSS监测结果的影响不可忽略,因而在数据处理和干涉影像解译的过程中,必须研究和分析大气的影响并加以处理。目前就两种技术本身的发展而言,GNSS数据处理领域中已有诸多成熟的模型和解算策略可以很好地估计或削弱大气延迟误差的影响,然而对于InSAR技术还存在诸多挑战。
在InSAR领域,关于大气延迟误差的改正方法大致可分为两类:第1类方法是采用外部数据集或气象模型去除干涉图中的大气相位。例如,文献[73]基于MERIS水汽数据,构建了一种局部均值可变的简单克里金与Onn模型算法,对美国南加州地区的InSAR干涉图进行改正;文献[74]利用大气数值模型(weather research and forecasting model,WRF)、文献[75]利用气象模型(NARR、ECMWF、MERRA)估计大气相位及大气延迟中的垂直分层误差,并评估了其在预测横向大气、长波大气,以及在提取长波形变信号中的潜力。第2类方法主要是基于InSAR干涉图中大气误差本身特征进行建模估计,包括线性组合法[76]、堆叠(Stacking)法[77]、时序InSAR分析中常用的时空滤波法,以及文献[78]提出的类似Stacking策略的共同主影像方法、文献[79]提出的干涉图组合方法。此外,对InSAR大气延迟误差改正效果的评估也值得引起重视,文献[80]讨论了大气延迟误差改正效果的评价指标,文献[81]基于大气的物理特性建立了统计指标体系,并为InSAR大气延迟误差改正的统计评估提供了指南,解决了先前分析中因使用的干涉图数量有限(几幅至几十幅)导致研究结论可能缺乏统计学意义的问题。更多有关大气延迟误差改正的研究进展可参阅文献[82]。
多路径误差则是GNSS定位中一个难以处理的误差源,主要由测站周围物体的信号反射或衍射引起,从而导致信号的相位和幅度不同,理论上多路径误差最大可达载波波长的四分之一[83]。在高精度基线解算中,相对定位可消除或减轻卫星钟、轨道、大气延迟等多种观测误差,但无法消除多路径误差,因此多路径误差成为制约高精度形变监测的主要误差因素。为了克服这一难题,国内外众多学者开发了一系列方法削弱或抑制多路径误差。其中最常用的方法是为GNSS接收机选择一个良好的观测环境。除此之外,目前消除多路径误差的策略主要分为两个方向:基于硬件条件的多路径消除策略和基于软件数据处理的多路径消除策略。硬件改进技术主要包括釆用右旋极化天线削弱左旋极化的反射多路径信号的接收强度;利用扼流圈天线抑制多路径信号;安装抑径板屏蔽地面反射的低于接收机天线的多路径信号及改进接收机的信号处理方式。而基于软件数据处理抑制多路径的方式则只需极少的成本投入,尤其是在大面积的形变监测中具有很高的经济效益,已被国内外众多学者广泛研究。数据处理主要可借助多路径时间重复性的恒星日滤波[84]及空间重复性的半天球模型[85]。此外,还可借助信噪比(signal to noise ratio,SNR)[86]或载噪比(carrrie-to-noise power density ratio, C/N0)的方法[87]及基于时间序列分析手段,如采用Vondrak滤波[88]、经验模式分解(empirical mode decomposition,EMD)[89]、小波分析[90]等方法构建多路径误差改正模型。此外,近年来一些机器学习算法[91-92]也被引入多路径检测算法中。然而,当不存在多路径时,这些算法易产生相位数据被错误地向下加权的问题,其可靠性仍然需要进一步评估,这也是机器学习方法没有在商用GNSS相位处理软件中得到广泛采用的制约因素之一。
随着雷达遥感技术进入高分辨率时代,InSAR技术的精细化监测对于大气延迟误差的改正提出了更高的要求。而当前大气延迟误差的改正面临各种挑战,尤其是对于多云多雨环境。更具挑战的是,我国大部分重大工程设施附近存在河流、湖泊等水体,加上一般地处高海拔山区,大气温度及水汽分布在时空上变化强烈,考虑到卫星成像期间可能存在强对流天气现象,从而极易造成与高程相关的规则信号和不规则扰动信号的耦合,进一步增加了大气的空间异质性。总之,大气效应在不同分辨率SAR影像、不同区域都显示出其独特的特性。因此,如何提出大气改正的稳健性和普适性方法仍是InSAR领域今后研究的重点。对于多路径效应,虽然当前已有较多的模型可以解决该问题,但在工程化应用中仍有许多局限性,如何有效地消除多路径对卫星定位的影响也是一个有待解决的问题。
3.3 InSAR相位解缠与GNSS模糊度固定相位解缠和模糊度固定分别是InSAR和GNSS技术中至关重要的数据处理步骤,也是制约结果可靠性的最关键因素之一,二者虽在技术本质上相似,即均为准确恢复缠绕观测数据的2π模糊度个数,但在具体实施步骤与面临的主要难题略有差异。
在InSAR技术中,相位解缠主要是基于相位连续性假设估算真实相位信息,该条件假设相邻两个待解缠点的真实相位差(相位梯度)绝对值应小于π[93]。基于此前提,目前已发展了一系列的相位解缠方法,按照解缠的维度特性可以划分为二维(2D)相位解缠、分步相位解缠(一维+二维或二维+一维)和整体三维相位解缠(3D)。其中2D相位解缠方法在实际应用中最为广泛,又可进一步细分为3大类:路径跟踪法[93]、Lp范数解缠方法[94]及综合滤波和相位解缠方法[95]。这类方法主要是通过最小化缠绕相位梯度与真实相位梯度的范数距离获得可靠的解缠结果,优势是解缠结果在全局上是稳健的,不会造成“孤岛”现象。最具代表性的方法为基于L2范数的最小二乘(least sqaure,LS)方法、基于L1范数的最小费用流(minimum cost flow,MCF)法[96]及基于压缩感知的稀疏解缠方法[97]。1D+2D相位解缠方法主要是在实施二维解缠之前,先对相干点形成的弧段上相位进行建模估计,然后基于空间上冗余网络扩展到全局获得稳健的解缠结果。此外,先空间维解缠,再利用时间维相位三角闭合进行误差探测与补偿也逐渐成为新的研究思路[98-99]。而整体3D相位解缠技术则是利用时间和空间维度上的三角相位闭合差优化无旋性约束,逼近相位连续性假设,从而获得较稳健的解缠结果[100-101]。更多关于相位解缠的研究进展可参阅文献[102]。
尽管目前在InSAR领域中相位解缠方法已经由一维拓展到三维空间,也逐步解决了相位积分路径单一的问题,降低了相位不连续区域出现的概率,提高了相位解缠结果的可靠性。但是这些方法都是基于相位连续性假设,在强相位噪声和地形起伏较大的地区,如高海拔山区、跨海大桥及高型大坝等区域,很难保证相位连续性假设在实际的干涉图中处处得到满足,导致错误解缠并进而影响InSAR监测结果。利用POT或距离分频InSAR技术与常规InSAR技术组合,在一定程度上可以解决相位不连续导致的解缠错误,但POT或距离分频InSAR较低的测量精度限制了该方法的应用。尽管人工智能和深度学习方法(如基于PGNet[103]和PUNet[104]等深度学习网络)的引入,使得相位解缠突破相位连续性这一假设成为可能,但是如何获取海量和可靠的训练数据集是当前一个首需解决的问题,此外作为近两年新兴的研究内容,智能解缠的可靠性和普适性需要进一步研究。
而整周模糊度固定是北斗/GNSS技术高精度形变监测应用的关键,如何快速可靠且有效地进行整周模糊度固定一直是高精度定位的研究热点。通常而言,整周模糊度固定包括以下步骤:首先,采用一定的估计方法求解浮点模糊度及其方差-协方差阵;其次,基于估计的浮点模糊度及其方差-协方差阵应用整数估计方法进行整周模糊度固定;最后,采用有效性检验方法进行整周模糊度检验。其中,高精度浮点模糊度是整周模糊度固定的重要前提,如文献[105]采用正则化等方法解决浮点模糊度法中的方程病态性问题,以提高浮点模糊度的精度和可靠性;文献[106]采用部分约束条件改善浮点模糊度解。而高效的模糊度搜索算法是整周模糊度固定的关键,文献[28]首次提出了一种整数最小二乘降相关平差(LAMBDA)方法,以提高搜索速度,其他降相关方法可参考文献[107—108]。此外,合理的有效性检验是正确固定整周模糊度的重要保障,通常可采用显著性检验和成功概率指标评定整周模糊度的有效性[109]。而GNSS多频信号的出现,可以形成波长更长、电离层延迟和观测误差影响较小的组合观测值,有利于突破传统整周模糊度复杂搜索方法的界限和快速固定多频整周模糊度,如基于三频相位模糊度解算(triple-frequency carrier ambiguity resolution,TCAR)方法[110]或基于GIF模型的TCAR方法[111],以及基于四频的FCAR方法[112],甚至多频的MCAR方法[113]等。文献[114]也详尽回顾了众多整周模糊度固定理论,并基于北斗三频实测数据评估不同整周模糊度固定方法的性能。尽管GNSS多频信号能为整周模糊度固定提供更多更优的线性组合,但面临的主要挑战是如何快速准确地固定窄巷模糊度[113]。此外,当较难固定正确的整周模糊度时,尤其是在复杂的监测环境中,如何确定和融合备选组值得进一步研究。
3.4 InSAR与GNSS观测数据的精确相对定权GNSS与InSAR数据融合能够实现GNSS高时间分辨率与InSAR数据高空间分辨率的有效统一,但作为两种异源观测系统,如何准确地确定GNSS与InSAR观测数据集间的相对权比是实现有效融合研究的关键[53, 115]。对于GNSS而言,主要采用插值方差评定插值精度。对于InSAR系统而言,常用的定权方法主要有3种。第1种是直接利用InSAR相干性计算方差进行定权,但相干性只能反映失相干噪声,无法有效反映非失相干信号(如大气延迟)导致的影响。第2种是使用滑动窗口估计形变观测值的先验方差,但该方法需要观测值在有限范围内满足各态历经性,此条件在现实应用中难以满足。第3种是采用赫尔默特方差分量估计法,该方法的基本思想是先将观测量分类并定初始权,通过迭代平差至各类观测量的单位权中误差相等为止。但该方法要求有足够多的多余观测数,并且当InSAR受时空失相干、解缠错误等影响时,定权过程会出现负单位权中误差的情况。针对此问题,目前可通过使用地表应力应变模型增加多余观测个数,以提高方差分量估计精度[53, 116]。
3.5 InSAR与GNSS大数据处理随着GNSS卫星和频率资源的显著增加及SAR卫星数据获取能力的大幅提升,目前可获取的观测数据规模正呈指数级增长,尤其对于InSAR技术,其地表形变监测能力已经由传统的静态D-InSAR进入动态时序InSAR时代。面对如此海量的观测数据,如何对InSAR与GNSS/北斗观测数据进行快速可靠地处理是实现综合形变监测的关键,也是近几年InSAR与GNSS融合领域新兴的一个热点问题。针对传统的集中式存储方法难以满足大规模监测数据存储需求的问题,云存储是解决海量数据存储瓶颈的一种有效途径。而针对大数据的处理,目前国内外学者已经针对InSAR和GNSS大数据处理独立开展了一些研究,主要集中在计算机硬件和数据处理算法两个层面。在计算机硬件层面,主要借助分布式计算、并行计算及云计算等高性能计算技术。如文献[117]开发了GNSS分布式处理软件GNSSer;文献[118]在常规SBAS算法的基础上设计了一种可并行计算的SBAS(parallel SBAS, P-SBAS)处理流程;文献[119]提出了综合定位、导航与授时(PNT)概念,将云端化运控(云平台控制体系)作为其核心关键技术。而在数据处理算法层面上,当前研究主要通过改进模型算法,如文献[120]提出了一种基于数据压缩和极大似然估计的时序InSAR序贯估计方法;文献[121]将序贯平差思想引入时序InSAR参数解算,初步实现了动态形变参数的连续估计;文献[122]构建了一套适合并行计算的大型GNSS观测网解算方法。
尽管目前大数据获取、存储、管理、处理、分析等相关的技术已有了初步进展,但面对数据量呈现出的爆炸式增长,现有技术体系仍难以满足大数据应用需求,同时大数据理论与技术还远未成熟。因此,对于InSAR与GNSS大数据协同处理和分析等方面的基础理论,以及高性能、高时效、高吞吐等硬件设施亟待进一步研究和技术攻关。
3.6 InSAR与GNSS结果验证分析InSAR与GNSS监测结果可以在时间和空间上相互补充和验证,尤其GNSS结果是评定InSAR形变监测精度最常用的手段之一。由于GNSS技术本身可以获取高精度三维地理绝对坐标信息,而InSAR影像处于雷达坐标系下,因此,精确实现二者测量坐标的统一是后续验证分析和数据融合的前提。该过程主要涉及将InSAR雷达坐标系投影至地理坐标系下,又称为地理编码。目前主要是通过外部DEM数据模拟SAR影像和真实SAR影像匹配特征点实现[123],此外也可借助外部数据实现高精度匹配,如LiDAR点云数据、高分光学影像等[124]。在实际工程应用中,相干点的定位精度对于后续的形变解译和质量评估至关重要,也是利用GNSS结果有效评定InSAR形变监测精度的关键因素之一。尤其是对于某些线状人工设施的重点部位监测,定位精度过低会引发InSAR结果的“移位”,造成误判和漏检。总体而言,目前对于星载InSAR地理编码的研究相对较少,对相关数据处理的重视程度不高,面对相干点偏离真实相应地物,有时会直接出现人为“拖拽”的现象,极易引起外界对监测结果可靠性的质疑。
4 未来应用展望综合InSAR和北斗/GNSS技术为解决传统地表形变监测的局限带来了全新的契机。近年来,随着相关理论与方法均取得重要进展,InSAR技术与北斗/GNSS技术在大范围区域沉降和基础设施安全监测领域已经有了诸多成功案例。结合笔者所在团队有关研究,本文提出以下展望。
4.1 深化综合InSAR与北斗+智慧行业建设应用随着我国自主研发的北斗三号全球导航卫星系统全球组网的完成,北斗已迈进了全球服务的新时代。除了兼容其他3大定位系统实现多模多频融合定位外,BDS在时间可用性和空间可用性上更强,尤其特有的IGSO卫星设计使得中国区域局部增强,卫星信号更优。“十三五”期末北斗技术已进入以创新为主题的新技术融合、新产品开发、新服务应用、新模式推广的高质量发展阶段。以智慧水利应用为例,未来仍需要把水利建设工程数字信息化建设作为北斗产业运用创新的切入点,打造水利数字经济。此外,得益于国内外SAR数据陆续开放政策及商业SAR卫星产业的快速发展,InSAR快速精细化监测能力得以大大提升。同时将InSAR技术纳入智慧水利服务市场中,成为面向水利安全监管领域不可或缺的技术,有助于补充北斗在空间监测能力方面的不足。通过运用综合InSAR与北斗监测系统,可对中小型水库、山塘水库等水利工程进行数字化转型,进一步提升信息化管理水平,实现安全监控覆盖,有效降低水利工程安全隐患,打造服务、辐射全国的时空信息大数据应用服务生态。
4.2 构建天-空-地-内多源协同监测与其他地质灾害不同,缓慢型地表形变具有范围广、多尺度及动态的特性,形变类型复杂多样。特别场景下,综合InSAR与北斗/GNSS技术监测模式和指标单一,难以满足需求。为有效克服复杂条件下地表形变监测的难题,可以结合其他平台的测量手段,如天基(卫星高分遥感、InSAR等)、空基(无人机等)、地基(热成像、GNSS、LiDAR、雨量计等)、内部测量(位移计等),实现点—面监测融合、监测—数值模拟耦合、形变—温度场与水文数据综合等多源异质数据融合,在空间、时间、监测参数和功能上达到协同优势互补。
4.3 InSAR和北斗/GNSS监测与云平台融合未来地表形变监测的发展趋势具有即时化、智能化、网络化等特点,而当前无论是GNSS接收机设备,还是InSAR数据的处理能力均有限,监测精度容易受复杂环境等有色噪声影响,监测结果不可靠。目前各种云已成为平台服务(PaaS)、数据服务(DaaS)及软件服务(SaaS)的必争之地,因此,可将常规的GNSS和InSAR监测数据转移到云平台上进行存储和数据处理,平台通过挖掘利用通信网络、大数据、云计算等技术优势,创新基础设施安全监测模式,变革传统安全监测系统针对单点、单业务或单目标的“烟囱式”建设思路,提高安全监测系统建设效率,降低监测成本,为多行业决策管理者提供丰富可靠的数据和服务。
4.4 借助AI技术进行地表形变监测与高精度数据处理随着人工智能(artificial intelligence,AI)技术的迅速发展及其在海量数据自动化批处理方面应用的逐渐成熟,InSAR相位解缠领域已逐渐引入深度卷积神经网络等方法恢复相位梯度,从而达到非病态InSAR相位解缠快速处理。此外,机器学习与AI算法也为解决GNSS多路径检测和InSAR大气延迟误差改正问题提供了必要条件,甚至训练衰减信号与土壤植被与湿度的关系,从而削弱InSAR长时间序列处理中的系统偏差,实现高精度数据处理。未来将人工智能纳入InSAR与GNSS/北斗数据处理流程,是实现数据快速式处理、地表形变大面积快速分析非常重要的方面。
| [1] |
殷跃平, 张作辰, 张开军. 我国地面沉降现状及防治对策研究[J]. 中国地质灾害与防治学报, 2005, 16(2): 1-8. YIN Yueping, ZHANG Zuochen, ZHANG Kaijun. Land subsidence and countermeasures for its prevention in China[J]. The Chinese Journal of Geological Hazard and Control, 2005, 16(2): 1-8. DOI:10.3969/j.issn.1003-8035.2005.02.001 |
| [2] |
何庆成, 叶晓滨, 李志明, 等. 我国地面沉降现状及防治战略设想[J]. 高校地质学报, 2006, 12(2): 161-168. HE Qingcheng, YE Xiaobin, LI Zhiming, et al. The status and prevention strategy of land subsidence in China[J]. Geological Journal of China Universities, 2006, 12(2): 161-168. DOI:10.3969/j.issn.1006-7493.2006.02.002 |
| [3] |
白正伟, 张勤, 黄观文, 等. "轻终端+行业云"的实时北斗滑坡监测技术[J]. 测绘学报, 2019, 48(11): 1424-1429. BAI Zhengwei, ZHANG Qin, HUANG Guanwen, et al. Real-time BeiDou landslide monitoring technology of "light terminal plus industry cloud"[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(11): 1424-1429. DOI:10.11947/j.AGCS.2019.20190167 |
| [4] |
刘洋, 许才军, 温扬茂. 温扬茂. 门源Mw5.9级地震形变InSAR观测及区域断裂带深部几何形态[J]. 武汉大学学报(信息科学版), 2019, 44(7): 1035-1042. LIU Yang, XU Caijun, WEN Yangmao. InSAR observation of Menyuan Mw5.9 earthquake deformation and deep geometry of regional fault zone[J]. Geomatics and Information Science of Wuhan University, 2019, 44(7): 1035-1042. |
| [5] |
SHI Guoqiang, MA Peifeng, HU Xie, et al. Surface response and subsurface features during the restriction of groundwater exploitation in Suzhou (China) inferred from decadal SAR interferometry[J]. Remote Sensing of Environment, 2021, 256: 112327. DOI:10.1016/j.rse.2021.112327 |
| [6] |
林珲, 马培峰, 王伟玺. 监测城市基础设施健康的星载MT-InSAR方法介绍[J]. 测绘学报, 2017, 46(10): 1421-1433. LIN Hui, MA Peifeng, WANG Weixi. Urban infrastructure health monitoring with spaceborne multi-temporal synthetic aperture radar interferometry[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1421-1433. DOI:10.11947/j.AGCS.2017.20170339 |
| [7] |
赵超英, 刘晓杰, 张勤, 等. 甘肃黑方台黄土滑坡InSAR识别、监测与失稳模式研究[J]. 武汉大学学报(信息科学版), 2019, 44(7): 996-1007. ZHAO Chaoying, LIU Xiaojie, ZHANG Qin, et al. Research on loess landslide identification, monitoring and failure mode with InSAR technique in Heifangtai, Gansu[J]. Geomatics and Information Science of Wuhan University, 2019, 44(7): 996-1007. |
| [8] |
史绪国, 张路, 许强, 等. 黄土台塬滑坡变形的时序InSAR监测分析[J]. 武汉大学学报(信息科学版), 2019, 44(7): 1027-1034. SHI Xuguo, ZHANG Lu, XU Qiang, et al. Monitoring slope displacements of loess terrace using time series InSAR analysis technique[J]. Geomatics and Information Science of Wuhan University, 2019, 44(7): 1027-1034. |
| [9] |
杨泽发, 朱建军, 李志伟, 等. 基于单个雷达成像几何学SAR影像的矿区三维时序形变监测方法: 中国, 201610546270.1[P]. 2016-12-14. YANG Zefa, ZHU Jianjun, LI Zhiwei, et al. Based on the timing of individual mines dimensional radar imaging geometry SAR image deformation monitoring methods: China, 201610546270.1[P]. 2016-12-14. |
| [10] |
陈洋, 陶秋香, 刘国林, 等. InSAR与概率积分法联合的矿区地表沉降精细化监测方法[J]. 地球物理学报, 2021, 64(10): 3554-3566. CHEN Yang, TAO Qiuxiang, LIU Guolin, et al. Detailed mining subsidence monitoring combined with InSAR and probability integral method[J]. Chinese Journal of Geophysics, 2021, 64(10): 3554-3566. DOI:10.6038/cjg2021O0421 |
| [11] |
肖儒雅, 何秀凤. 时序InSAR水库大坝形变监测应用研究[J]. 武汉大学学报(信息科学版), 2019, 44(9): 1334-1341. XIAO Ruya, HE Xiufeng. Deformation monitoring of reservoirs and dams using time-series InSAR[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1334-1341. |
| [12] |
朱建军, 杨泽发, 李志伟. InSAR矿区地表三维形变监测与预计研究进展[J]. 测绘学报, 2019, 48(2): 135-144. ZHU Jianjun, YANG Zefa, LI Zhiwei. Recent progress in retrieving and predicting mining-induced 3D displacements using InSAR[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(2): 135-144. DOI:10.11947/j.AGCS.2019.20180188 |
| [13] |
BAMLER R, HARTL P. Synthetic aperture radar interferometry[J]. Inverse Problems, 1998, 14(4): R1-R54. DOI:10.1088/0266-5611/14/4/001 |
| [14] |
MASSONNET D, ROSSI M, CARMONA C, et al. The displacement field of the landers earthquake mapped by radar interferometry[J]. Nature, 1993, 364(6433): 138-142. DOI:10.1038/364138a0 |
| [15] |
FERRETTI A, PRATI C, ROCCA F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2202-2212. DOI:10.1109/36.868878 |
| [16] |
BERARDINO P, FORNARO G, LANARI R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375-2383. DOI:10.1109/TGRS.2002.803792 |
| [17] |
FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks: SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460-3470. DOI:10.1109/TGRS.2011.2124465 |
| [18] |
ZHAO Feng, MALLORQUI J J. Coherency matrix decomposition-based polarimetric persistent scatterer interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 7819-7831. DOI:10.1109/TGRS.2019.2916649 |
| [19] |
MICHEL R, AVOUAC J P, TABOURY J. Measuring ground displacements from SAR amplitude images: application to the Landers earthquake[J]. Geophysical Research Letters, 1999, 26(7): 875-878. DOI:10.1029/1999GL900138 |
| [20] |
BECHOR N B D, ZEBKER H A. Measuring two-dimensional movements using a single InSAR pair[J]. Geophysical Research Letters, 2006, 33(16): L16311. DOI:10.1029/2006GL026883 |
| [21] |
ZHU Xiaoxiang, MONTAZERI S, GISINGER C, et al. Geodetic SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 18-35. DOI:10.1109/TGRS.2015.2448686 |
| [22] |
GRANDIN R, KLEIN E, MÉTOIS M, et al. hree-dimensional displacement field of the 2015 Mw8.3 Illapel earthquake (Chile) from across- and along-track Sentinel-1 TOPS interferometry[J]. Geophysical Research Letters, 2016, 43(6): 2552-2561. DOI:10.1002/2016GL067954 |
| [23] |
QIU Dongwei, WANG Laiyang, LUO Dean, et al. Landslide monitoring analysis of single-frequency BDS/GPS combined positioning with constraints on deformation characteristics[J]. Survey Review, 2019, 51(367): 364-372. DOI:10.1080/00396265.2018.1467075 |
| [24] |
韩军强. 高精度GNSS实时滑坡变形监测技术及环境建模分析研究[J]. 测绘学报, 2020, 49(3): 397. HAN Junqiang. Research on high precision GNSS real time landslide deformation monitoring technology and environmental modeling[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3): 397. DOI:10.11947/j.AGCS.2020.20190177 |
| [25] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [26] |
张宝成, 欧吉坤, 袁运斌. 基于精选基准消秩亏的GNSS参考网数据处理方法[J]. 测绘学报, 2014, 43(9): 895-901. ZHANG Baocheng, OU Jikun, YUAN Yunbin. Method of processing GNSS reference network data with refined datum definition for rank-deficiency elimination[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 895-901. DOI:10.13485/j.cnki.11-2089.2014.0164 |
| [27] |
段举举, 沈云中. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报, 2012, 41(6): 825-830, 917. DUAN Juju, SHEN Yunzhong. An algorithm of combined GPS/GLONASS static relative positioning[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 825-830, 917. |
| [28] |
TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. DOI:10.1007/BF00863419 |
| [29] |
BROWN N, GEISLER I, TROYER L. RTK rover performance using the master-auxiliary concept[J]. Journal of Global Positioning Systems, 2006, 5(1-2): 135-144. |
| [30] |
WVBBENA G, BAGGE A, SCHMITZ M. Network based techniques for RTK applications[C]//Proceedings of the GPS Symposium, Japan Institute of Navigation. Tokyo: [s. n. ], 2001.
|
| [31] |
WANNINGER L. The performance of virtual reference stations in active geodetic GPS-networks under solar maximum conditions[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation. Nashville, TN, 1999: 1419-1428.
|
| [32] |
BOCK Y, WILLIAMS S. Integrated satellite interferometry in southern California[J]. Eos, Transactions American Geophysical Union, 1997, 78(29): 293-300. |
| [33] |
许才军, 王华, 黄劲松. GPS与INSAR数据融合研究展望[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 58-61, 78. XU Caijun, WANG Hua, HUANG Jinsong. Prospect on the integration of GPS and INSAR data[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 58-61, 78. |
| [34] |
许才军, 何平, 温扬茂, 等. InSAR技术及应用研究进展[J]. 测绘地理信息, 2015, 40(2): 1-9. XU Caijun, HE Ping, WEN Yangmao, et al. Recent advances InSAR interferometry and its applications[J]. Journal of Geomatics, 2015, 40(2): 1-9. |
| [35] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100. ZHANG Xiaohong, HU Jiahuan, REN Xiaodong. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100. |
| [36] |
何秀凤, 高壮, 肖儒雅, 等. 多时相Sentinel-1A InSAR的连盐高铁沉降监测分析[J]. 测绘学报, 2021, 50(5): 600-611. HE Xiufeng, GAO Zhuang, XIAO Ruya, et al. Monitoring and analysis of subsidence along Lian-Yan railway using multi-temporal Sentinel-1A InSAR[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(5): 600-611. |
| [37] |
MASSONNET D, FEIGL K, ROSSI M, et al. Radar interferometric mapping of deformation in the year after the Landers earthquake[J]. Nature, 1994, 369(6477): 227-230. DOI:10.1038/369227a0 |
| [38] |
ZEBKER H A, ROSEN P A, HENSLEY S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B4): 7547-7563. DOI:10.1029/96JB03804 |
| [39] |
LI Zhenhong, FIELDING E J, CROSS P, et al. Interferometric synthetic aperture radar atmospheric correction: GPS topography-dependent turbulence model[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B2): B02404. |
| [40] |
宋小刚, 李德仁, 单新建, 等. 基于GPS和MODIS的ENVISAT ASAR数据干涉测量中大气改正方法研究[J]. 地球物理学报, 2009, 52(6): 1457-1464. SONG Xiaogang, LI Deren, SHAN Xinjian, et al. Correction of atmospheric effect in ASAR interferogram using GPS and MODIS Data[J]. Chinese Journal of Geophysics, 2009, 52(6): 1457-1464. DOI:10.3969/j.issn.0001-5733.2009.06.006 |
| [41] |
YU Chen, PENNA N T, LI Zhenhong. Generation of real-time mode high-resolution water vapor fields from GPS observations[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(3): 2008-2025. DOI:10.1002/2016JD025753 |
| [42] |
YU Chen, LI Zhenhong, PENNA N T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model[J]. Remote Sensing of Environment, 2018, 204: 109-121. DOI:10.1016/j.rse.2017.10.038 |
| [43] |
CAO Yunmeng, LI Zhiwei, DUAN Meng, et al. High-resolution water vapor maps obtained by merging interferometric synthetic aperture radar and GPS measurements[J]. Journal of Geophysical Research: Atmospheres, 2021, 126(1): e2020JD033430. |
| [44] |
GUDMUNDSSON S, CARSTENSEN J M, SIGMUNDSSON F. Unwrapping ground displacement signals in satellite radar interferograms with aid of GPS data and MRF regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1743-1754. DOI:10.1109/TGRS.2002.802516 |
| [45] |
罗海滨, 何秀凤. GPS控制点辅助InSAR相位解缠算法研究[J]. 武汉大学学报(信息科学版), 2017, 42(5): 630-636. LUO Haibin, HE Xiufeng. InSAR phase unwrapping algorithms with the aid of GPS control points[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 630-636. |
| [46] |
YU Hanwen, HU Xie. Knowledge-aided InSAR phase unwrapping approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5209508. DOI:10.1109/TGRS.2021.3081039 |
| [47] |
GUDMUNDSSON S, SIGMUNDSSON F, CARSTENSEN J M. Three-dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10): 2250. |
| [48] |
SAMSONOV S, TIAMPO K, RUNDLE J, et al. Application of DInSAR-GPS optimization for derivation of fine-scale surface motion maps of southern California[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(2): 512-521. DOI:10.1109/TGRS.2006.887166 |
| [49] |
罗海滨, 何秀凤, 刘焱雄. 利用DInSAR和GPS综合方法估计地表3维形变速率[J]. 测绘学报, 2008, 37(2): 168-171. LUO Haibin, HE Xiufeng, LIU Yanxiong. Estimation of three-dimensional surface motion velocities using integration of DInSAR and GPS[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 168-171. DOI:10.3321/j.issn:1001-1595.2008.02.007 |
| [50] |
胡俊, 李志伟, 朱建军, 等. 基于BFGS法融合InSAR和GPS技术监测地表三维形变[J]. 地球物理学报, 2013, 56(1): 117-126. HU Jun, LI Zhiwei, ZHU Jianjun, et al. Measuring three-dimensional surface displacements from combined InSAR and GPS data based on BFGS method[J]. Chinese Journal of Geophysics, 2013, 56(1): 117-126. DOI:10.3969/j.issn.1672-7940.2013.01.024 |
| [51] |
王霞迎, 张菊清, 张勤, 等. 升降轨InSAR与GPS数据集成反演西安形变场[J]. 测绘学报, 2016, 45(7): 810-817. WANG Xiaying, ZHANG Juqing, ZHANG Qin, et al. Inferring multi-dimensional deformation filed in Xi'an by combining InSAR of ascending and descending orbits with GPS data[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 810-817. DOI:10.11947/j.AGCS.2016.20150485 |
| [52] |
SHI Guoqiang, HE Xiufeng, XIAO Ruya. Acquiring three-dimensional deformation of Kilauea's South Flank From GPS and DInSAR integration based on the ant colony optimization[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2506-2510. DOI:10.1109/LGRS.2015.2489243 |
| [53] |
汪友军, 胡俊, 刘计洪, 等. 融合InSAR和GNSS的三维形变监测: 利用方差分量估计的改进SISTEM方法[J]. 武汉大学学报(信息科学版), 2021, 46(10): 1598-1608. WANG Youjun, HU Jun, LIU Jihong, et al. Measurements of three-dimensional deformations by integrating InSAR and GNSS: An improved SISTEM method based on variance component estimation[J]. Geomatics and Information Science of Wuhan University, 2021, 46(10): 1598-1608. |
| [54] |
伍吉仓, 宋鑫友, 胡凤鸣, 等. 联合GNSS和InSAR观测位移反演2008年汶川大地震断层位错模型参数[J]. 中国地震, 2020, 36(4): 767-779. WU Jicang, SONG Xinyou, HU Fengming, et al. Fault slip distribution of 2008 Wenchuan earthquake by jointed coseismic displacements from GPS and InSAR[J]. Earthquake Research in China, 2020, 36(4): 767-779. |
| [55] |
CASTELLAZZI P, MARTEL R, GALLOWAY D L, et al. Assessing groundwater depletion and dynamics using GRACE and InSAR: Potential and limitations[J]. Groundwater, 2016, 54(6): 768-780. DOI:10.1111/gwat.12453 |
| [56] |
WANG Jiahui, LU Zhong, GREGG P M. Inflation of Okmok volcano during 2008-2020 from PS analyses and source inversion with finite element models[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(10): e2021JB022420. |
| [57] |
DEL SOLDATO M, CONFUORTO P, BIANCHINI S, et al. Review of works combining GNSS and InSAR in Europe[J]. Remote Sensing, 2021, 13(9): 1684. DOI:10.3390/rs13091684 |
| [58] |
BLEWITT G. An automatic editing algorithm for GPS data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. DOI:10.1029/GL017i003p00199 |
| [59] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722, 729. LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time cycle-slip detection and repair based on code-phase combinations for GNSS triple-frequency un-differenced observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722, 729. |
| [60] |
刘柳, 吕志伟, 于晓东, 等. GNSS三频周跳探测与修复算法[J]. 测绘学报, 2017, 46(4): 453-459. LIU Liu, LÜ Zhiwei, YU Xiaodong, et al. Real-time cycle-slip detection and repair algorithm of GNSS triple-frequency observations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 453-459. DOI:10.11947/j.AGCS.2017.20160532 |
| [61] |
张晨晰, 党亚民, 薛树强, 等. BDS三频GIF组合非显著周跳探测与修复[J]. 测绘学报, 2018, 47(S0): 38-44. ZHANG Chenxi, DANG Yamin, XUE Shuqiang, et al. Detection and repair of the non-significant cycle slip in BDS triple-frequencies GIF combination[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S0): 38-44. DOI:10.11947/j.AGCS.2018.20180314 |
| [62] |
LI Bofeng, QIN Yanan, LIU Tianxia. Geometry-based cycle slip and data gap repair for multi-GNSS and multi-frequency observations[J]. Journal of Geodesy, 2019, 93(3): 399-417. DOI:10.1007/s00190-018-1168-5 |
| [63] |
ZHANG Wenhao, WANG Jinglin. A real-time cycle slip repair method using the multi-epoch geometry-based model[J]. GPS Solutions, 2021, 25(2): 60. DOI:10.1007/s10291-021-01098-y |
| [64] |
徐天扬, 章浙涛, 何秀凤, 等. 一种适用于单频GNSS数据的多周跳探测与修复方法[J/OL]. 武汉大学学报(信息科学版): 1-17[2021-11-20]. http://kns.cnki.net/kcms/detail/42.1676.TN.20211105.1147.005.html. XU Tianyang, ZHANG Zhetao, HE Xiufeng, et al. A new multi-cycle slips detection and repair method for a single-frequency GNSS receive[J/OL]. Geomatics and Information Science of Wuhan University: 1-17[2021-11-20]. http://kns.cnki.net/kcms/detail/42.1676.TN.20211105.1147.005.html. |
| [65] |
TEUNISSEN P J G. Distributional theory for the DIA method[J]. Journal of Geodesy, 2018, 92(1): 59-80. DOI:10.1007/s00190-017-1045-7 |
| [66] |
杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95-99. YANG Yuanxi, SONG Lijie, XU Tianhe. Robust parameter estimation for geodetic correlated observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99. DOI:10.3321/j.issn:1001-1595.2002.02.001 |
| [67] |
章浙涛. GNSS非模型化误差处理理论与方法[J]. 测绘学报, 2020, 49(7): 936. ZHANG Zhetao. Theory and method for processing the GNSS unmodeled errors[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(7): 936. DOI:10.11947/j.AGCS.2020.20190345 |
| [68] |
SINGLETON A, LI Z, HOEY T, et al. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain[J]. Remote Sensing of Environment, 2014, 147: 133-144. DOI:10.1016/j.rse.2014.03.003 |
| [69] |
ANSARI H, DE ZAN F, PARIZZI A. Study of systematic bias in measuring surface deformation with SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(2): 1285-1301. DOI:10.1109/TGRS.2020.3003421 |
| [70] |
蒋弥, 丁晓利, 李志伟. 时序InSAR同质样本选取算法研究[J]. 地球物理学报, 2018, 61(12): 4767-4776. JIANG Mi, DING Xiaoli, LI Zhiwei. Homogeneous pixel selection algorithm for multitemporal InSAR[J]. Chinese Journal of Geophysics, 2018, 61(12): 4767-4776. DOI:10.6038/cjg2018L0490 |
| [71] |
ANSARI H, DE ZAN F, BAMLER R. Efficient phase estimation for interferogram stacks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(7): 4109-4125. DOI:10.1109/TGRS.2018.2826045 |
| [72] |
李振洪, 宋闯, 余琛, 等. 卫星雷达遥感在滑坡灾害探测和监测中的应用: 挑战与对策[J]. 武汉大学学报(信息科学版), 2019, 44(7): 967-979. LI Zhenhong, SONG Chuang, YU Chen, et al. Application of satellite radar remote sensing to landslide detection and monitoring: Challenges and solutions[J]. Geomatics and Information Science of Wuhan University, 2019, 44(7): 967-979. |
| [73] |
许文斌, 李志伟, 丁晓利, 等. 利用MERIS水汽数据改正ASAR干涉图中的大气影响[J]. 地球物理学报, 2010, 53(5): 1073-1084. XU Wenbin, LI Zhiwei, DING Xiaoli, et al. Correcting atmospheric effects in ASAR interferogram with MERIS integrated water vapor data[J]. Chinese Journal of Geophysics, 2010, 53(5): 1073-1084. DOI:10.3969/j.issn.0001-5733.2010.05.007 |
| [74] |
XIONG Siting, ZENG Qiming, JIAO Jian, et al. Improvement of PS-InSAR atmospheric phase estimation by using WRF model[C]//2014 IEEE Geoscience and Remote Sensing Symposium. Quebec City, QC, Canada: IEEE, 2014: 2225-2228.
|
| [75] |
JOLIVET R, AGRAM P S, LIN N Y, et al. Improving InSAR geodesy using global atmospheric models[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(3): 2324-2341. DOI:10.1002/2013JB010588 |
| [76] |
MASSONNET D, FEIGL K L. Discrimination of geophysical phenomena in satellite radar interferograms[J]. Geophysical Research Letters, 1995, 22(12): 1537-1540. DOI:10.1029/95GL00711 |
| [77] |
SANDWELL D T, SICHOIX L. Topographic phase recovery from stacked ERS interferometry and a low-resolution digital elevation model[J]. Journal of Geophysical Research: Solid Earth, 2000, 105(B12): 28211-28222. DOI:10.1029/2000JB900340 |
| [78] |
TYMOFYEYEVA E, FIALKO Y. Mitigation of atmospheric phase delays in InSAR data, with application to the eastern California shear zone[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(8): 5952-5963. DOI:10.1002/2015JB011886 |
| [79] |
LUO Heng, WANG Teng, WEI Shengji, et al. Deriving centimeter-level coseismic deformation and fault geometries of small-to-moderate earthquakes from time-series Sentinel-1 SAR images[J]. Frontiers in Earth Science, 2021, 9: 636398. DOI:10.3389/feart.2021.636398 |
| [80] |
MURRAY K D, BEKAERT D P S, LOHMAN R B. Tropospheric corrections for InSAR: Statistical assessments and applications to the Central United States and Mexico[J]. Remote Sensing of Environment, 2019, 232: 111326. DOI:10.1016/j.rse.2019.111326 |
| [81] |
XIAO Ruya, YU Chen, LI Zhenhong, et al. Statistical assessment metrics for InSAR atmospheric correction: Applications to generic atmospheric correction online service for InSAR (GACOS) in Eastern China[J]. International Journal of Applied Earth Observation and Geoinformation, 2021, 96: 102289. DOI:10.1016/j.jag.2020.102289 |
| [82] |
LI Zhiwei, DUAN Meng, CAO Yunmeng, et al. Mitigation of time-series InSAR turbulent atmospheric phase noise: A review[J]. Geodesy and Geodynamics, 2022, 13(2): 93-103. DOI:10.1016/j.geog.2021.12.002 |
| [83] |
LAU L, CROSS P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling[J]. Journal of Geodesy, 2007, 81(11): 713-732. DOI:10.1007/s00190-007-0139-z |
| [84] |
YE Shirong, CHEN Dezhong, LIU Yanyan, et al. Carrier phase multipath mitigation for BeiDou navigation satellite system[J]. GPS Solutions, 2015, 19(4): 545-557. DOI:10.1007/s10291-014-0409-1 |
| [85] |
王亚伟, 邹璇, 唐卫明, 等. 削弱GNSS多路径效应的半天球格网点建模方法[J]. 测绘学报, 2020, 49(4): 461-468. WANG Yawei, ZOU Xuan, TANG Weiming, et al. A method for mitigating GNSS multipath effect based on multi-point hemispherical grid model[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 461-468. DOI:10.11947/j.AGCS.2020.20190184 |
| [86] |
COMP C J, AXELRAD P. Adaptive SNR-based carrier phase multipath mitigation technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 264-276. DOI:10.1109/7.640284 |
| [87] |
ZHANG Zhetao, LI Bofeng, GAO Yang, et al. Real-time carrier phase multipath detection based on dual-frequency C/N0 data[J]. GPS Solutions, 2019, 23(1): 7. DOI:10.1007/s10291-018-0799-6 |
| [88] |
ZHENG D W, ZHONG P, DING X L, et al. Filtering GPS time-series using a Vondrak filter and cross-validation[J]. Journal of Geodesy, 2005, 79(6-7): 363-369. DOI:10.1007/s00190-005-0474-x |
| [89] |
戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321-327. DAI Wujiao, DING Xiaoli, ZHU Jianjun, et al. EMD filter method and its application in GPS multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327. DOI:10.3321/j.issn:1001-1595.2006.04.005 |
| [90] |
SOUZA E M, MONICO J F G. Wavelet Shrinkage: High frequency multipath reduction from GPS relative positioning[J]. GPS Solutions, 2004, 8(3): 152-159. DOI:10.1007/s10291-004-0100-z |
| [91] |
CHEN Liang, ALI-LÖYTTY S, PICHÉ R, et al. Mobile tracking in mixed line-of-sight/non-line-of-sight conditions: algorithm and theoretical lower bound[J]. Wireless Personal Communications, 2012, 65(4): 753-771. DOI:10.1007/s11277-011-0294-7 |
| [92] |
QUAN Yiming, LAU L, ROBERTS G W, et al. Convolutional neural network based multipath detection method for static and kinematic GPS high precision positioning[J]. Remote Sensing, 2018, 10(12): 2052. DOI:10.3390/rs10122052 |
| [93] |
马张烽, 蒋弥, 李桂华, 等. 空间网络对时序InSAR相位解缠的影响: 以Delaunay与Dijkstra网络为例[J]. 测绘学报, 2022, 51(2): 248-257. MA Zhangfeng, JIANG Mi, LI Guihua, et al. Effects of spatial network on time series InSAR phase unwrapping: take the Delaunay and Dijkstra networks for example[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(2): 248-257. DOI:10.11947/j.AGCS.2022.20200469 |
| [94] |
COSTANTINI M. A novel phase unwrapping method based on network programming[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 813-821. DOI:10.1109/36.673674 |
| [95] |
XIE Xianming, ZENG Qingning. Efficient and robust phase unwrapping algorithm based on unscented Kalman filter, the strategy of quantizing paths-guided map, and pixel classification strategy[J]. Applied Optics, 2015, 54(31): 9294-9307. DOI:10.1364/AO.54.009294 |
| [96] |
GHIGLIA D C, ROMERO L A. Minimum LP-norm two-dimensional phase unwrapping[J]. Journal of the Optical Society of America A, 1996, 13(10): 1999-2013. DOI:10.1364/JOSAA.13.001999 |
| [97] |
MANUNTA M, MUHAMMAD Y. A novel algorithm based on compressive sensing to mitigate phase unwrapping errors in multitemporal DInSAR approaches[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5207520. |
| [98] |
XU Xiaohua, SANDWELL D T. Toward absolute phase change recovery with InSAR: Correcting for earth tides and phase unwrapping ambiguities[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 726-733. DOI:10.1109/TGRS.2019.2940207 |
| [99] |
MA Zhangfeng, JIANG Mi, KHOSHMANESH M, et al. Time series phase unwrapping based on graph theory and compressed sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5204412. DOI:10.1109/TGRS.2021.3066784 |
| [100] |
LI Rui, LU Xiaolei, YUN Ye. A network-optimization-based L1-norm Sparse 2-D phase unwrapping method for persistent scatterer interferometry[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(5): 709-713. DOI:10.1109/LGRS.2018.2806005 |
| [101] |
LIU Fei, PAN Bin. A new 3-D minimum cost flow phase unwrapping algorithm based on closure phase[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 1857-1867. DOI:10.1109/TGRS.2019.2949926 |
| [102] |
YU Hanwen, LAN Yang, YUAN Zhihui, et al. Phase unwrapping in InSAR: a review[J]. IEEE Geoscience and Remote Sensing Magazine, 2019, 7(1): 40-58. DOI:10.1109/MGRS.2018.2873644 |
| [103] |
ZHOU Lifan, YU Hanwen, LAN Yang. Deep convolutional neural network-based robust phase gradient estimation for two-dimensional phase unwrapping using SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 4653-4665. DOI:10.1109/TGRS.2020.2965918 |
| [104] |
WU Zhipeng, WANG Teng, WANG Yingjie, et al. Deep learning for the detection and phase unwrapping of mining-induced deformation in large-scale interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5216318. DOI:10.1109/TGRS.2021.3121907 |
| [105] |
王振杰, 欧吉坤, 柳林涛. 单频GPS快速定位中病态问题的解法研究[J]. 测绘学报, 2005, 34(3): 196-201. WANG Zhenjie, OU Jikun, LIU Lintao. Investigation on solutions of ill-conditioned problems in rapid positioning using single frequency GPS receivers[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 196-201. DOI:10.3321/j.issn:1001-1595.2005.03.002 |
| [106] |
李博峰, 沈云中. 顾及基线先验信息的GPS模糊度快速解算[J]. 测绘学报, 2008, 37(4): 423-427, 432. LI Bofeng, SHEN Yunzhong. Prior baseline information based fast GPS ambiguity resolution[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 423-427, 432. DOI:10.3321/j.issn:1001-1595.2008.04.004 |
| [107] |
范龙, 翟国君, 柴洪洲. 模糊度降相关的整数分块正交化算法[J]. 测绘学报, 2014, 43(8): 818-826. FAN Long, ZHAI Guojun, CHAI Hongzhou. Ambiguity decorrelation with integer block orthogonal ization algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 818-826. |
| [108] |
卢立果, 刘万科, 鲁铁定, 等. GNSS模糊度降相关性能的条件方差平稳度评价法[J]. 测绘学报, 2020, 49(8): 955-964. LU Liguo, LIU Wanke, LU Tieding, et al. Conditional variance stationarity evaluation method for GNSS ambiguity decorrelation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 955-964. DOI:10.11947/j.AGCS.2020.20190417 |
| [109] |
WANG Jun, FENG Yanming. Reliability of partial ambiguity fixing with multiple GNSS constellations[J]. Journal of Geodesy, 2013, 87(1): 1-14. DOI:10.1007/s00190-012-0573-4 |
| [110] |
FENG Yanming. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy, 2008, 82(12): 847-862. DOI:10.1007/s00190-008-0209-x |
| [111] |
LI Bofeng, FENG Yanming, SHEN Yunzhong. Three carrier ambiguity resolution: distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J]. GPS Solutions, 2010, 14(2): 177-184. DOI:10.1007/s10291-009-0131-6 |
| [112] |
ZHANG Zhetao, LI Bofeng, HE Xiufeng, et al. Models, methods and assessment of four-frequency carrier ambiguity resolution for BeiDou-3 observations[J]. GPS Solutions, 2020, 24(4): 96. DOI:10.1007/s10291-020-01011-z |
| [113] |
ZHANG Zhetao. Code and phase multipath mitigation by using the observation-domain parameterization and its application in five-frequency GNSS ambiguity resolution[J]. GPS Solutions, 2021, 25(4): 144. DOI:10.1007/s10291-021-01179-y |
| [114] |
ZHANG Xiaohong, HE Xiyang. Performance analysis of triple-frequency ambiguity resolution with BeiDou observations[J]. GPS Solutions, 2016, 20(2): 269-281. DOI:10.1007/s10291-014-0434-0 |
| [115] |
吴学雨, 李明峰, 董思学, 等. 利用基于抗差垂直向方差分量估计的GPS-InSAR数据融合方法反演三维形变场[J]. 测绘通报, 2021(12): 38-43. WU Xueyu, LI Mingfeng, DONG Sixue, et al. GPS-InSAR data fusion method with robust vertical variance component estimation for 3D deformation field[J]. Bulletin of Surveying and mapping, 2021(12): 38-43. DOI:10.13474/j.cnki.11-2246.2021.369 |
| [116] |
刘计洪, 胡俊, 李志伟, 等. InSAR三维同震地表形变监测——窗口优化的SM-VCE算法[J]. 测绘学报, 2021, 50(9): 1222-1239. LIU Jihong, HU Jun, LI Zhiwei, et al. Estimation of 3D coseismic deformation with InSAR: an improved SM-VCE method by window optimization[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9): 1222-1239. DOI:10.11947/j.AGCS.2021.20200610 |
| [117] |
GNSSer. GNSS数据处理服务与交流平台[EB/OL]. 2021-22-20. http://www.gnsser.com. GNSSer. GNSS data processing service and exchange platform[EB/OL]. 2021-22-20. http://www.gnsser.com. |
| [118] |
CASU F, ELEFANTE S, IMPERATORE P, et al. SBAS-DInSAR parallel processing for deformation time-series computation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(8): 3285-3296. DOI:10.1109/JSTARS.2014.2322671 |
| [119] |
杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505-510. YANG Yuanxi. Concepts of comprehensive PNT and related key technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505-510. DOI:10.11947/j.AGCS.2016.20160127 |
| [120] |
ANSARI H, DE ZAN F, BAMLER R. Sequential estimator: toward efficient InSAR time series analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5637-5652. DOI:10.1109/TGRS.2017.2711037 |
| [121] |
WANG Baohang, ZHAO Chaoying, ZHANG Qin, et al. Sequential estimation of dynamic deformation parameters for SBAS-InSAR[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 1017-1021. DOI:10.1109/LGRS.2019.2938330 |
| [122] |
吕志平, 许国昌, 陈正生, 等. 大型GNSS观测网的并行计算[J]. 测绘科学技术学报, 2021, 38(1): 1-8. LÜ Zhiping, XU Guochang, CHEN Zhengsheng, et al. Parallel resolution of huge GNSS networks[J]. Journal of Geomatics Science and Technology, 2021, 38(1): 1-8. |
| [123] |
AUER S, GERNHARDT S, BAMLER R. Investigations on the nature of persistent scatterers based on simulation methods[C]//Proceedings of 2011 Joint Urban Remote Sensing Event. Munich, Germany: IEEE, 2011: 61-64.
|
| [124] |
WANG Yuanyuan, ZHU Xiaoxiang, ZEISL B, et al. Fusing meter-resolution 4D InSAR point clouds and optical images for semantic urban infrastructure monitoring[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 14-26. DOI:10.1109/TGRS.2016.2554563 |