2. 中国资源卫星应用中心, 北京 100094;
3. 中南林业科技大学土木工程学院, 湖南 长沙 410018
2. China Centre For Resources Satellite Data and Application, Beijing 100094, China;
3. School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410018, China
自然因素或人类活动可使地球表层或内部应力发生变化,进而导致地震、火山活动、滑坡、泥石流、基础设施损毁等一系列地质灾害。在地质灾害预警与防控体系中,获取灾害事件与灾害过程的关键地学参数是至关重要的。然而,受限于技术手段或观测空间,部分关键地学参数难以直接测量(如地震震源参数)。地质灾害事件的第一表征往往是地表形变,通过卫星遥感获取的地表形变数据间接反演地学参数是目前获取关键地学参数的主要途径之一。通过反演获得的关键地学参数对于准确理解灾变过程、科学解释灾变机制、正确拟定应对策略具有重要意义。受观测成本高、工作范围小、空间分辨率低等因素的限制,传统GNSS、水准等测量手段监测的地表形变通常是局部且离散的,难以宏观、精细地反映地表真实形变场,限制了地学参数反演的精度和可靠性。
星载合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)是一种主动微波遥感技术。自1989年,文献[1]首次提出差分InSAR(differential InSAR,D-InSAR)技术以来,InSAR已成为地表形变监测的重要工具之一[2-6]。相较于传统大地测量手段,InSAR在形变监测上具有全天时、全天候、空间上连续覆盖、分辨率高、数据处理效率高等优势。此外,InSAR可利用存档影像回溯地表历史形变(最早可到1991年),从而为已发生的形变事件参数反演提供观测资料基础。鉴于此,InSAR已被广泛应用于自然因素或人类活动导致的灾害事件的参数反演。
为了更系统地阐述InSAR地学参数反演领域的研究进展,本文梳理分析了目前该领域的主要研究现状和挑战。
1 InSAR卫星及测量原理 1.1 InSAR卫星发展现状作为一种新兴的对地观测手段,InSAR技术具有全天时、全天候、大范围、高精度、低成本的优势,在地震、火山、滑坡等地质灾害的快速响应,城市、矿区、人工建构筑物形变的长期监测,以及冰川运动、冻土冻融、地下水开采等活动的动态监测中得到了广泛应用。随着硬件技术的日益发展,几十年间InSAR观测平台实现了从空基向星基的跨越,多元化成像方式、多极化信号收发及高时空分辨率观测已成为SAR卫星发展的新趋势。本节将从在轨SAR卫星和即将发射的SAR卫星两个方面,对星载InSAR平台的发展历程进行介绍。
1.1.1 在轨SAR卫星21世纪,航天工业的蓬勃发展极大地推动了SAR卫星技术的发展和进步。SAR卫星系统朝着广域覆盖、星座联合、超高分辨率、多模式、全极化的方向发展。由表 1可知,所有在轨SAR卫星均采用了多种成像模式,以此满足高分辨率或广域覆盖的监测需求。特别地,为满足广域覆盖需求,除小型SAR卫星ICEYE-X1/X2外,其他在轨卫星均具备扫描式成像模式,特别是Sentinel-1A/B宽幅成像模式采用的TOPS技术,能更好地满足常态化的广域地表观测需要。此外,为提高SAR卫星的时间分辨率,实现对突发事件的快速响应,很多SAR卫星采用了多星联合的星座运行模式。例如,RadarSat-2在与RCM串联组成星座后,最快4 d即可实现地面重访观测;在欧洲等重点监测区域,COSMO-SkyMed四星星座可实现24 h内的快速重访;TerraSAR-X/TanDEM-X星座采用单发双收模式,时间基线几乎为0,最大限度地降低了时间去相关和大气对干涉相位的影响。
| 卫星/传感器 | 发射时间/年 | 波段(极化) | 成像模式(分辨率) | 幅宽/km | 国家/机构 |
| TerraSAR-X/TanDEM-X/PAZ | 2007、2010、2018 | X(全极化) | ST SL(25 cm) | 5 | 德国、西班牙 |
| HR SL(1 m) | 10 | ||||
| SL(2 m) | 10 | ||||
| SM(3 m) | 35 | ||||
| Scan(26 m) | 100 | ||||
| COSMO-SkyMed | 2007 | X(双极化) | SL(1 m) | 10 | 意大利 |
| SM(3 m) | 35 | ||||
| Scan(30 m) | 100 | ||||
| RadarSat-2/RCM | 2007、2019 | C(全极化) | SL(< 1 m) | 8 | 加拿大 |
| UF(3 m) | 20 | ||||
| Fine(8 m) | 50 | ||||
| Standard(25 m) | 100 | ||||
| Scan(50~100 m) | 300~500 | ||||
| ALOS-2 | 2014 | L(全极化) | SL(1 m) | 25 | 日本 |
| UF(3 m) | 50 | ||||
| Fine(10 m) | 70 | ||||
| Scan(60 m) | 490 | ||||
| Sentinel-1A/1B | 2014、2016 | C(双极化) | WV(5 m×20 m) | 20 | 欧洲空间局 |
| SM(5 m) | 80 | ||||
| IW(5 m×20 m) | 250 | ||||
| EW(20 m×100 m) | 450 | ||||
| GF-301星 | 2016 | C(全极化) | ST(1 m) | 10 | 中国 |
| UF(3 m) | 30 | ||||
| Standard(25 m) | 130 | ||||
| Scan(100 m) | 500 | ||||
| GF-3 02星 | 2022 | C(全极化) | ST(1 m) | 10 | 中国 |
| UF(3 m) | 30 | ||||
| Standard(25 m) | 130 | ||||
| Scan(100 m) | 500 | ||||
| Saocom-1A/1B | 2018、2020 | L(双极化) | SM(< 10 m) | > 40 | 阿根廷 |
| TOPS(< 30 m) | > 150 | ||||
| ICEYE-X1/X2 | 2018 | X(VV) | SL(1 m) | 5 | 芬兰 |
| SM(3 m) | 30 | ||||
| Hisea-1 | 2020 | C(VV) | SL(1 m) | 5 | 中国 |
| SM(3 m) | 20 | ||||
| Narrow Scan(10 m) | 50 | ||||
| Extra Scan(20 m) | 100 | ||||
| LT-1A/B星 | 2022 | L(全极化) | SM(3 m) | 50 | 中国 |
| SM(12 m) | 100 | ||||
| SM(6 m) | 30 | ||||
| SM(24 m) | 160 | ||||
| Scan(30 m) | 400 |
1.1.2 即将发射的SAR卫星
当今时代,SAR卫星观测刈幅越来越宽,重访周期越来越短,全极化、简缩极化已成为多数SAR系统的标准配置,亚米级分辨率已实现常规化。星载SAR平台的巨大潜力和广阔前景引起各国广泛关注,政府、军方甚至商业遥感公司均在计划投资运营新的SAR卫星。除传统X、C、L波段的SAR卫星外,P和S波段的SAR卫星的研发也在持续深入(见表 2)。欧空局预计于2022年发射的BIOMASS卫星有望成为全球第1颗P波段SAR卫星;美国NASA与印度合作研发的NISAR将成为全球第1颗L和S双频段SAR卫星。在NISAR与德国宇航局的下一代TanDEM-L任务中,SAR凝视成像模式有望得到进一步发展。承继ALOS-2卫星、搭载新一代PALSAR-3传感器的ALOS-4,将具备更高的观测性能。
| 卫星/传感器 | 预计发射时间/年 | 计划波段(极化) | 国家/机构 |
| NISAR | 2022 | L(全极化) | 美国、印度 |
| S(全极化) | |||
| BIOMASS | 2022 | P(全极化) | 欧洲空间局 |
| GF-3 03星 | 2022 | C(全极化) | 中国 |
| ALOS-4 | 未定 | L(全极化) | 日本 |
| TanDEM-L | 未定 | L(全极化) | 德国 |
1.2 InSAR高程测量原理
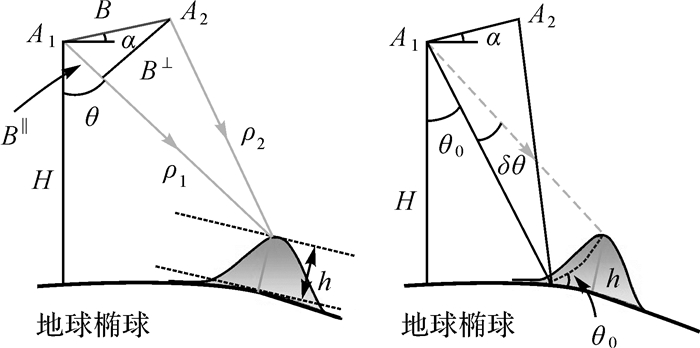
DEM获取是InSAR技术的一个重要应用,通过两次在不同位置对同一地面区域进行观测,InSAR可以解算大范围的地表高程[7-10]。图 1为InSAR高程测量的成像几何。其中,A1、A2分别为两次成像的位置,B为空间基线,B‖、B⊥分别为平行基线和垂直基线,ρ1、ρ2为雷达天线到地面点的距离,α为基线倾角,θ为地面点的入射角,θ0为参考椭球面上点的入射角,δθ=θ-θ0,h为该地面点的椭球高,H为卫星高度。
|
| 图 1 InSAR高程测量成像几何 Fig. 1 Imaging geometry of InSAR elevation measurements |
设Ψ1为地面点在A1处的观测相位,Ψ2为同一地面点在A2处的观测相位,则干涉相位Φinf由平地相位(Φflat)、地形相位(Φtopo)、形变相位(Φdef)、大气相位(Φatm)和噪声相位(Φnoi组成,可以表示为
 (1)
(1)
在InSAR高程测量中,需满足两次成像期间没有地表形变发生、大气状态一致(如双天线或双星绕飞观测),或地表形变、大气相位可以被很好地扣除或抑制的前提,根据成像几何关系,高程h可以近似表示为
 (2)
(2)
式中,λ为雷达波长。通过式(2)可以计算地表相对高程,其中地形相位可以通过相位去平地处理并解缠得到。
2000年,美国国家航空航天局采用航天飞机携带C波段和X波段雷达干涉仪在11 d内对全球80%的地表进行了至少一次观测,获取了第1个InSAR全球DEM产品SRTM(shuttle radar topography mission),提供30 m和90 m两种分辨率产品,相对高程精度约为10 m[9]。单轨双天线的设计使得相位测量中的环境误差被极大削弱。其生产的全球DEM数据已有多个版本,部分开放获取。
2007和2010年,德国宇航局与空客防务公司发射了TerraSAR-X和TanDEM-X卫星。两颗卫星参数配置一致,以250~500 m的基线距离进行双星绕飞,可实现交轨或沿轨干涉测量。该任务陆续发布了12、30、90 m分辨率的3种全球DEM产品,绝对高程精度可达10 m,相对高程精度可达2 m,很好地展示了星载InSAR获取高精度DEM的可行性和优越性[10]。
1.3 InSAR形变测量原理 1.3.1 D-InSAR基本原理在重轨InSAR系统中,假设获取了两景覆盖同一地区的单视复数影像,通过配准和干涉生成一幅干涉图[11],其干涉相位则同时包含地表高程和形变信息,可以表示为[12]
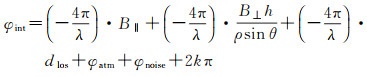 (3)
(3)
式中,dlos代表LOS(line of sight)向的形变量;等号右侧分别表示平地相位分量、地形相位分量、形变相位分量、大气相位分量、噪声分量及整周相位,其中k为整周模糊度。
D-InSAR技术是对形变相位分量除外的其他相位分量进行估算并去除,或通过滤波等抑制至很低水平以获取dlos。地形相位分量和平地相位分量可以利用外部DEM产品提供的较高精度高程h和准确估计的基线B从干涉相位去除[13];通过多视处理和滤波可以抑制失相干噪声φnoise;通过二维空间解缠方法可以估计整周模糊度k[14];大气相位分量可以通过外部数据辅助或滤波方法进行改正[15]。
1.3.2 MT-InSAR基本原理为了克服D-InSAR技术的局限性,MT-InSAR(multi-temporal InSAR)技术应运而生,凭借能够有效抑制失相干噪声、大气延迟、高程残余误差及提供时间序列形变等优点,一系列时序算法相继被提出,如永久散射体干涉法(persistent scatterer,PS)[16-18]、短基线集方法(small baseline subsets,SBAS)[19]、部分时域相干点法(temporarily coherent point, TCP)[20]、干涉点目标分析法(interferometric point target analysis, IPTA)[21]及分布式散射体干涉(SqueeSAR)[22]等。MT-InSAR技术对选取的反射相位稳定点进行建模和时序分析,能够更加精确地获取地表形变速率和时间序列。其中,相干点目标选取、形变参数估计及大气误差改正是MT-InSAR的3大关键技术环节。
相干点目标选取在MT-InSAR技术中占据非常重要的地位[23-24],其质量和密度直接影响形变参数的提取精度。目前主流的方法主要有相干系数阈值法、振幅离差指数法、相位稳定性分析法、偏移量估计法等。选取相干点目标后,将对相干点的形变参数进行估计,MT-InSAR形变参数解算的关键就是如何解算或避免相位模糊度[25-26],目前已有的方法主要包括最小二乘法、解空间搜索法、LAMBDA方法、三维解缠法、模糊度探测法等。随着MT-InSAR技术的发展,大气延迟误差改正的精度决定着InSAR形变监测的精度,目前主流方法主要包括采用外部数据辅助法(如GNSS、MODIS、MERIS及数值天气模型等提供的大气数据[15])和时空滤波法[19]进行改正。
2 InSAR参数反演 2.1 地震震源参数反演地震震源参数是指地震发生时震源处的一些特征量(如空间位置、强度等)或震源物理过程的一些物理量(如发震断层的几何特性、地震位错的空间展布、震源时间函数等)。震源参数是制定地震应急救援策略和开展救援工作的关键震情信息,也是研究发震断层机制及其破裂特征、分析区域应力触发与危险性评估的重要基础。随着卫星遥感技术的日新月异及处理能力的不断提高,震源参数反演由基于单一观测数据的反演逐渐发展为基于多源观测数据的联合反演,大大推动了震源参数反演进程。水准测量、GNSS、光学、InSAR等大地测量形变数据是震源参数反演的重要数据源。利用InSAR数据进行地震震源参数反演源于文献[5],利用两景ERS-1 SAR影像对1992年美国加州Landers Mw7.3级地震的同震形变进行研究。随着InSAR技术在同震形变监测方面的理论与方法日趋成熟,国内外越来越多的学者开始利用InSAR地表形变反演震源参数。文献[27]首次利用二轨D-InSAR技术提取的视线向同震形变场为数据约束,基于Okada模型[28]反演得到了Landers地震的震源机制解。文献[29]率先在国内利用InSAR数据反演了1998年张北-尚义Mw6.2级地震的震源机制解。迄今,InSAR技术已成功应用于诸多同震、震后、震间地表形变监测与震源参数反演案例中[30-34]。
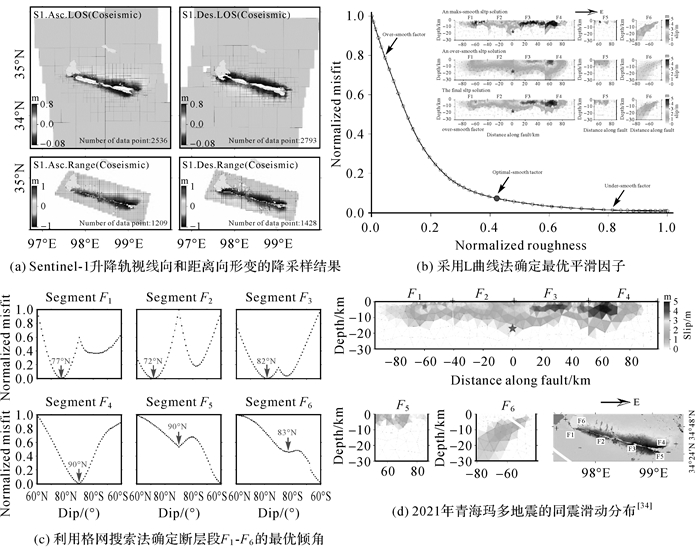
大地测量震源参数反演的方法主要包括解析法与数值法两大类。其中解析法一般适用于反演线性问题和简单的非线性问题,震源参数反演研究主要集中在数值模拟算法方面。对于由断层错动而引发的构造地震而言,震源参数即为断层参数。通过对大地测量数据、地震波资料等进行地球物理反演,即可获得更具细节的震源描述,包括发震断层的长度、宽度、深度、倾角、走向角、震源位置等几何参数,以及滑动角和滑动量等运动参数。其中,断层几何参数的非线性反演通常采用模拟退火算法、遗传算法、神经网络法、粒子群算法、贝叶斯法等搜索算法[35-36],断层运动参数的线性反演通常可以采用附加光滑约束的非负约束最小二乘法[37]、总体最小二乘法等进行求解。图 2为2021年青海玛多Mw7.4级地震的震源反演结果[34]。利用Sentinel-1升降轨SAR数据获取了该地震的视线向和距离向同震形变场,采用四叉树降采样算法对形变数据进行了降采样,构建了变走向及倾角的6段断层几何,引入了二阶拉普拉斯平滑算子进行平滑约束,同时采用L曲线法和格网搜索法分别确定了最优平滑因子和6个断层分段的最优倾角,最后采用非负最小二乘方法求解了该地震的最优同震滑动分布。
|
| 图 2 青海玛多地震的震源反演结果 Fig. 2 The earthquake source inversion results of Maduo earthquake |
InSAR震源参数反演中,简化的断层几何、断层面的离散化方法与平滑因子的选取、约束数据的多源性、数据定权方法与降采样方法及位错模型的选取(如弹性半空间位错模型与球体分层位错模型)等,是制约地震震源参数反演精度的重要因素。另外,Okada位错模型是基于各向同性、均匀半空间体假设的,是对真实地球空间结构的粗糙近似,并未考虑地壳横向和纵向分层结构,这也会导致断层滑移参数估计不可避免地存在偏差。如何准确确定不同观测数据集之间的相对权比与平滑因子、发展顾及地壳横向分层结构的地震震源参数反演仍然值得进一步研究。
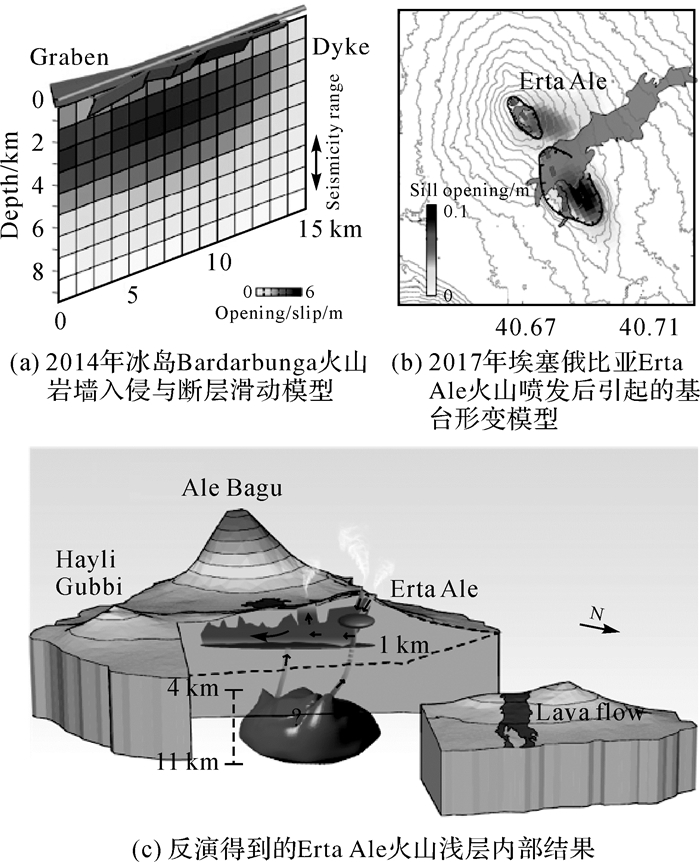
2.2 火山活动参数反演InSAR可以监测火山浅部岩浆运动、岩浆补给和亏损引起的地表变形。通过地表形变和模型反演得到的岩浆囊参数有助于识别火山喷发的前兆,跟踪火山喷发的演变,能够深化对火山岩浆活动的理解,有利于减轻火山活动及伴随的次生灾害带来的危害[3]。Mogi模型是最早用于解释火山形变的几何模型,由日本火山学家Mogi于1914年提出并用于Sakurajima火山的重复水准观测建模[38]。文献[6]首次利用InSAR技术发现了埃特纳火山的收缩现象,并利用Mogi模型反演了岩浆囊的位置和体积变化。Mogi模型假设在地壳的弹性半空间中嵌入一个球形源(源半径α远小于源深度d),球形源内静水压力变化产生的地表位移和体积变化为
 (4)
(4)
式中,u、v、w为地表(x,y,0)处的位移;球形源的腔体中心为(0,0,-d);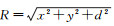
然而,解析模型是对研究对象进行高度抽象后的建模,因此揭示的规律也相对模糊。数值模型为更准确地理解火山事件的构造过程提供了可能性。数值模型可以将岩浆房建模为有限大小的任意形状及由不同力学性能的岩层组成的复合火山,还可以引入各种类型的断层,使结果更逼真。在数值模型中,容纳岩浆囊的地壳被分为许多离散单元,采用适当的本构方程(描述岩石的流变性质),结合质量守恒定律(连续性方程)和动量守恒定律(动量方程)建立微分方程,通过联立代数方程近似求解。目前最常用的数值模型求解方法是有限元法和边界元法。此外,构建多种地球物理手段结合的火山监测系统有助于更清晰地呈现岩浆系统的构造形态和运动状态;综合岩石学、地球化学和地球物理的观点处理有关岩浆管道系统的问题也有利于加深对岩浆系统演化的认识[44]。
2.3 地下水文学参数反演地下水超采导致的地面沉降、地裂缝、海水侵入等灾害,影响工农业生产和城市可持续发展,造成供水、粮食、生态安全等一系列问题。对地下水资源进行科学管理和开展相关防灾减灾工作,需准确估计含水层的参数。InSAR能够获取高分辨率地表形变场,建立地表形变与地下水变化的函数模型,探测地下水变化的物理特征及反演相应的含水层参数,为地下水文学应用提供了崭新的视角[45-46]。文献[47]首次利用InSAR技术和含水层压缩模型证明了加州羚羊谷地下水开采与地表沉降间的耦合关系。随后,在拉斯维加斯、内华达州等具有良好观测条件的区域相继开展了含水层地表形变及参数反演的InSAR研究[48]。在我国华北平原、汾渭盆地、长江三角洲等重点区域,InSAR技术被用于分析地下水开采引起的地表沉降的时空分布特征和形变规律[49]。利用InSAR观测的季节/年际形变数据和一定数量的地下水测井数据,结合土力学、应力应变等理论模型,可识别和反演一系列地下水文学参数[50-53]:①含水层的边界和内部特征;②含水层储量(含水层厚度、储量);③含水层贮水参数(贮水度、弹性/非弹性骨架贮水系数);④含水层响应状态(渗透系数、滞后系数);⑤地下水载荷应力变化;⑥水头及采水量估计。这些参数可应用于:①提取含水层空间-时间分布的异质性,弥补水位测井网络的分布;②校正已有的地下水流动模型,用于地下水流动模拟及地表沉降预测;③评估地下水储量变化,及其对构造活动和地震风险的影响;④精化区域含水层和岩石圈结构。
如前文所述,利用InSAR开展地下水文学参数的反演研究,可以获得高空间分辨率的地下水文学参数,有效弥补地面观测数据不足难以估计空间上详细的水文参数的问题,对探测含水层物理结构、校正地下水文学模型及开展地面沉降模拟具有良好的应用前景。然而,利用InSAR观测反演地下水参数仍存在以下两大问题。
(1) 承压含水层模型简化对参数反演的影响。目前,以InSAR地表形变作为观测值反演水文学参数主要基于Terzaghi有效应力原理所导出的线弹性模型[41]。在数值求解中一般采用“两步法”,即将三维地下水流动和一维垂向固结过程进行分步计算(如MODFLOW-SUB方法)[40]。文献[54]研究表明,这一类简化土体骨架水平位移模型,在含水层边界或采水井周边等存在水平形变的区域会造成明显误差,并且利用线弹性模型进行参数反演时,往往忽略含水层参数随时间的变化特性(如渗透系数随有效应力增加而减小),造成反演结果无法准确反映含水层的动态变化。除了线弹性形变,含水层土体也可能存在塑性和黏弹性等非线性形变(如弱透水层的塑形形变)[55],如何准确结合InSAR观测结果与不同本构关系,是反演地下水参数的关键问题。
(2) 不同地质结构对参数反演的影响。除了地下水储量变化对承压含水层带来的直接影响,断层结构与不透水层/半透水层的夹层结构等低渗透率地质单元的分布会降低含水层系统的地表响应,从而减弱InSAR对含水层形变的捕获能力,增加参数反演的不确定性[40, 44]。文献[44]利用InSAR资料估计了边界断层的平均水平传导率,然而由于含水层与断层结构的非均一性,在断层两侧存在明显的拟合残差。文献[56]利用贝叶斯估计方法和最大后验概率的准则,基于单个测井数据和InSAR观测资料,成功反演了含水层渗透率的侧向空间分布,为识别含水层中不同地质结构提供了新的思路。但采用贝叶斯估计和最大后验概率的方法计算效率不高,且未对多变量进行联合反演,限制了对含水层中不同地质单元影响的评估与模型的准确性。
如何融合InSAR水平形变(如含水层边缘、采水井周边)与不同的含水层变形机制进行地下水文学参数反演,获取含水层的动态响应、应力场各向异性等参数,以及如何分离和重建微小的地表响应信号,联合反演获得不同场景下水文参数的时空分布,仍值得进一步研究。
2.4 地下采空区几何参数反演地下矿产资源开采后留下的采空区容易引发一系列灾害事故。例如,采空区上覆岩体因失去支撑容易产生移动形变,从而引发地表塌陷、基础设施破坏等地质灾害;上覆岩体破裂后,地表或地下水容易通过裂缝流入废弃采空区并形成“老窑水”,一旦“老窑水”在未知情况下被导通,极易引发矿井突水等重大安全事故。因此,精确探测或反演地下采空区几何参数(如位置、深度、长度、宽度、厚度、倾角、方位角等),对于减少采空区灾害事故至关重要。传统方法大都以物探等接触式手段为主[57],虽精度较高,但工作范围小,且费时费力。
矿山地表移动形变与地下采空区几何参数密切相关[58]。因此,若能精确监测地表移动形变,理论上便可反演地下采空区几何参数。如前文所述,InSAR可低成本、大范围、高空间分辨率地获取地表形变值,其在地下采空区几何参数反演中具有较大的应用潜力。近年来,国内外学者在该领域展开了探索,并发展了多种算法。根据反演依据不同,算法大致可分为两大类。
(1) 联合InSAR观测与形变几何特征反演法。2013年,有学者首次以InSAR视线向形变观测值为基础,根据煤矿区地表沉降盆地中心位置、沉降梯度变化等形变几何特征反演了大范围地下采空区的中心位置,但该研究未能反演深度、长度、宽度等其他关键几何参数。为克服该局限,文献[59—62]提出引入开采沉陷盆地半径、拐点偏移距、开采影响传播角等变形几何特征参数反演地下采空区深度、长度、宽度等其他几何参数。该方法计算工作量小,但因其仅利用了部分(如中心点、走向或倾向剖面等)InSAR观测值,导致采空区几何参数反演精度对InSAR观测误差较为敏感。
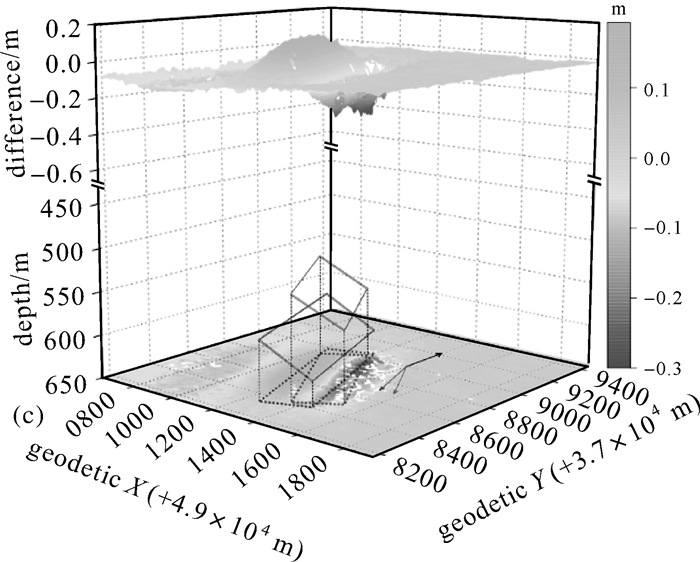
(2) 联合InSAR观测与理论模型反演法。2018年,文献[63]引入概率积分法(我国最常用的开采沉陷理论预计模型之一),建立了采空区几何参数与InSAR视线向形变的函数模型,并通过非线性搜索率先实现了基于InSAR观测值的地下采空区几何参数定量反演。图 4为安徽某矿区实测采空区几何参数(蓝色矩形)与InSAR反演的几何参数(红色矩形)。由图 4可看出InSAR实测形变与基于反演参数和概率积分法模型预测的形变的差异。2021年,文献[64]引入反向学习法提高了采空区参数反演的效率和精度。相较于联合形变几何特征方法,联合理论模型反演法能充分利用InSAR整体观测(对误差敏感性较前者低),且理论基础更坚实;但因该方法涉及大量非线性搜索,反演效率不佳。
总体而言,虽然两类算法在一定程度推动了采空区几何参数InSAR反演研究,但目前的反演精度都不高。此外,现有研究大都集中于煤矿规则采空区(如长壁采煤),而甚少关注非规则工作面参数反演。因此,面向更复杂的开采场景,并提出全新算法以提升采空区参数反演精度,是未来的重要研究方向。
2.5 冻土活动层厚度反演随着全球气候变暖,多年冻土已经发生明显且持续的退化,对碳循环、水循环、生物多样性、工程安全等产生了重大影响。多年冻土区活动层是多年冻土与大气圈层进行物质交换的纽带,它随着气温的变化冬季发生冻结、夏季发生融化,引发地表产生周期性形变[65-70]。活动层厚度是冻土的重要物理参数,其变化直接反映多年冻土的存继及其退化或变化情况[65, 70]。大面积获取和反演活动层厚度对冻土科学研究、冻土区工程建设和防灾具有非常重要的意义。传统获取活动层厚度的方法主要有实地测量方法、解析模型反演法[70-73]。随着遥感技术的发展,基于遥感数据的深度学习方法[73-74]也可被用于估计冻土区活动层厚度,但受不同条件的制约。近年来,具有高分辨率、高精度、大范围、长时段优势的InSAR技术可以准确获取冻土区地表形变,为大范围、高精度反演冻土物理参数(如融化深度、活动层厚度)提供了观测基础。国内外学者通过建立冻土区InSAR地表形变与活动层厚度之间的函数关系,估计多年冻土活动层厚度,相关研究大致可以分为以下两类。
(1) 基于活动层变化与InSAR形变观测量之间的函数关系。文献[66]采用时序InSAR技术探究了冻土区地表形变与活动层厚度之间的关系,其假设冻土区地表沉降形变是由活动层融化引起的,并基于水质量守恒定律,建立了形变和活动层厚度之间的积分函数模型,通过逆运算可以求得研究区域的活动层厚度。但该模型水质量守恒的假设在实际中并不能满足。文献[68, 75]简化文献[66]模型中的土壤孔隙、土壤湿度饱和度,用于反演青藏高原多年冻土区的活动层厚度。文献[69]建立了活动层土壤水分含量模型,得到不同深度土壤水分含量的分布,将其代入文献[66]反演模型中估算活动层厚度;但该方法在建立冻土土壤含水量沿土壤深度方向的分布模型时,依赖实测的土壤含水量数据,影响了活动层厚度反演结果的精度。除此之外,文献[76]在文献[66]模型基础之上,采用L波段InSAR结果和P波段极化SAR数据联合估计土壤湿度和活动层厚度,解算过程实际为求解联合目标函数最小值问题。该方法减少了土壤湿度信息不准确对活动层厚度估计的影响,但目前P波段数据获取困难。文献[67]将工程应用中采用的土壤分层模型引入活动层厚度反演研究中,提出了一种基于InSAR形变与土壤分层模型反演活动层厚度的方法,该模型假设冻土区地表融化形变由两部分组成,即冻土融化产生的下沉量和压缩变形,在反演过程中土壤的热参数采用经验值,并且假设活动层下多年冻土刚性不可压缩,因而导致反演精度对这些假设较为敏感。
(2) 基于土壤一维热传导方程。文献[68]提出了基于InSAR形变及土壤一维热传导方程反演活动层厚度的方法。该方法首先利用时序InSAR获取多年冻土区的地表时间序列形变数据,分析冻土时序形变与温度之间的时间延迟关系;然后根据土壤一维热传导方程推导并建立活动层厚度与延迟时间之间的函数关系;最后利用冻土区融化沉降形变曲线计算地表温度和融化深度达到最大时的延迟时间,进而可以估算多年冻土区土壤的最大融化深度,即活动层厚度。该方法间接建立了InSAR观测值和冻土活动层厚度之间的函数关系,反演精度对InSAR形变结果的变化趋势依赖性较高。
基于InSAR技术反演活动层厚度具有全天时、全天候、大范围、高空间分辨率等优势,在冻土物理参数反演研究中具有很好的应用前景。但通过建立活动层厚度与冻土区InSAR形变量之间的函数模型反演活动层厚度,受InSAR形变结果为相对形变量的影响,反演结果多为相对活动层厚度,其结果的精度受形变测量精度的影响。建立活动层厚度与冻土形变时间延迟(相对温度)之间的函数关系反演活动层厚度的方法,可以得到绝对的活动层厚度,但其精度受模型采用的土壤热参数经验值精度及只考虑土壤热变化的影响。实际中,冻土变化机理与过程复杂,如何准确地建立InSAR观测量和活动层厚度的函数关系,是限制InSAR反演冻土相关物理参数的关键问题。在未来研究中,利用InSAR技术监测获取准确的活动层厚度需要全面考虑实际冻土变化的机理,实现高精度InSAR冻土物理参数可靠反演方法仍需深入研究。
2.6 冰川跃动参数反演近年来,高亚洲发生的一系列与冰川跃动相关的灾害引起了全世界对气候变暖背景下冰川动态的关注。冰川跃动是由冰川内部压力状态发生突破性变化而触发的[77]。在不同的内外因素作用下,跃动会使冰川发生多种几何形态变化,包括冰面高程变化、流速变化、边界变化、表面形态特征变化[78]。观测这些几何参数的时空演化是反演冰川跃动持续时间、转移物质当量、触发机理等信息的关键所在,而这些跃动信息又是灾害防范和应急救援的科学基础。冰川边界、表面形态特征变化可以通过光学遥感分类解译的方法获取,方法相对成熟。观测的难点在于冰川的表面高程变化和流速变化。利用InSAR技术估计冰川表面高程变化主要有两种方法:一是利用多轨SAR数据估计冰川三维形变,然后结合冰面局部坡度估计冰川表面高程变化[77-78];二是利用InSAR技术生成多期冰面DEM,对多期DEM进行配准后再进行差分[79-83]。DEM差分法依赖于InSAR DEM的生产能力,但应用更广。由于冰面散射特征变化较快,SAR冰川流速变化估计一般采用偏移量跟踪技术(offest tracking),即影像匹配技术,包括斑点匹配(speckle tracking)[80]和强度匹配(intensity tracking)[81]。以SAR影像匹配技术获取的多轨多时相像素偏移量为基础观测值,通过时序形变处理和三维形变模型可以反演冰川三维时序流速[82-83]。
为提高冰川跃动参数反演的可信度,学者们一般综合利用InSAR和其他手段(光学遥感和激光测高等)的多项观测结果。文献[84]率先利用SAR影像匹配估计的冰川流速变化和光学影像解译的冰川形态变化,反演喀喇昆仑地区冰川跃动机理,认为该地区冰川跃动是由内部温度环境的改变引起的。此后,文献[85]利用同样手段获取的冰川流速变化和形态变化,反演了西昆仑山地区冰川跃动机理,认为该地区冰川跃动行为受到了热力学条件改变和内部水文系统季节性变化的共同作用。文献[86]结合SAR影像匹配和光学影像匹配获取的冰川二维流速序列和InSAR DEM差分技术估计的冰川多时段表面高程变化,反演了帕米尔高原Bivachny冰川近期跃动物质转移量、跃动体移动速度及跃动触发机制,认为该冰川跃动由内部水文条件变化引起。文献[83]通过基于匹配偏移量的SAR多维小基线集技术估计喀喇昆仑山Hispar冰川的三维时序流速,同时利用InSAR DEM差分技术估计该冰川的多时段表面高程变化,再结合光学影像匹配技术估计的冰川二维时序流速、光学遥感解译获取的冰川表面形态变化和冰川边界变化,反演了该冰川近期跃动的起止时间、跃动体分布范围、跃动体移动速度、跃动中物质转移量及跃动触发机制,结果表明该冰川跃动主要由冰川底部水压突破极限而触发,北部支流先于主干开始跃动。需要注意的是,光学遥感的星下点成像方式相比SAR的斜距成像方式受地形影响更小,在地形特别复杂的地区应该将两种手段的优势互补,以实现长时序高精度冰川流速和高程变化观测,更好地服务于冰川跃动参数反演和跃动触发机制解译。
2.7 大气水汽参数反演水汽是地球大气中变化最快的组分,在大气辐射平衡、能量转换、云的形成,以及降雨、气候研究等过程中发挥着重要的作用[87]。高分辨率精确获取大气水汽的空间分布对大气动力学的研究也十分重要。InSAR技术作为一种新的大气水汽估计手段,可以弥补传统气象学水汽监测方法成本高、空间分辨率低、受天气影响较大等不足。文献[88]率先发现InSAR干涉图可以提供空间分辨率高至米级的高精度差分大气水汽,从而开启了InSAR气象学研究。更进一步,文献[89]推导了常用SAR传感器反演差分水汽的理论精度,计算结果表明,该理论精度可达1 mm。然而,InSAR获取的是主、辅SAR影像成像时刻对应的水汽差分值,难以直接应用于中尺度气象学和数值天气预报等。
文献[17]通过时空域滤波的方法首次将大气水汽作为副产品从InSAR干涉图中估计出来。虽然时空域滤波的方法被广泛应用,然而目前还没有研究可以提供统一的标准以实现不同试验条件下最优滤波器和滤波窗口的自适应选择。随后,文献[90]创新性地利用最小二乘配置方法将大气水汽作为参数,与地表形变同时进行估计,然而该方法仅适用于稳定且渐进的地表形变。在忽略地表形变影响的前提下,文献[91]通过假设湍流大气在时序上的统计均值为零,获取了莱茵河上游地区17景ASAR影像成像时刻的非差分水汽分布结果。虽然这种附加假设条件的方法便于计算,但其需要大量SAR数据确保统计意义,且反演的水汽结果精度受极端天气的影响较大。为了克服这些限制,文献[92]以时序水汽均值不变作为约束条件,获取了沙特阿拉伯地区的5景SAR影像成像时刻对应的非差分水汽,试验结果如图 5所示;同时证明了利用时序水汽均值为零的约束条件反演的水汽结果在时序上整体存在一个固定的偏差,且该偏差等于时序上的水汽均值。虽然时序水汽均值不变的约束条件可以确保反演的时序水汽的整体精度,然而由于大部分地区难以在反演之前获取研究区域时序上的水汽均值,因此一定程度上限制了该方法的应用。除此之外,融合各种外部气象数据(如GPS、MERIS)和气象模型(如WRF模型)的InSAR非差分水汽反演方法被不断发展和优化[93-95]。然而,目前外部气象数据的空间分辨率普遍较低,且受云、雨等条件的影响较大,该方法反演的非差分水汽精度直接取决于输入数据的质量。
尽管InSAR技术已经成功反演了特定试验区的大气水汽,但是如何发展一种通用的、高精度的水汽反演方法仍然是InSAR在气象学研究中亟须解决的瓶颈问题之一。随着SAR卫星的不断发展,可用于水汽反演的InSAR干涉图越来越多,如何在充分利用海量InSAR数据的基础上,结合数理统计的知识较好地解决时序InSAR非差分水汽反演中的秩亏问题,是未来重要的研究方向之一。同时,伴随着获取的非差分水汽数据的不断丰富,如何将这些高精度、高分辨率的水汽数据与气象资料同化,提高气象预报特别是降水预报的准确性,是未来InSAR气象学研究的重要方向。
2.8 地下流体体积变化参数反演地下流体(石油、天然气、地热等)的承载、卸载、运移及开采等会引发显著的地表形变,从而导致地面沉降、坍陷等地质灾害,已经成为影响区域经济和社会可持续发展的重要因素。国内外学者为了准确理解地下流体灾变过程并科学解释地下流体灾变机制,将地下流体与地表作用机理进行耦合研究,构建出一系列物理解析模型,将地表形变与模型相结合,以反演地下流体几何参数、体积变化参数及静力压强参数,已取得较好的应用效果。其中,地下流体的体积变化可以解译地下流体活动、评估地下流体活动造成的灾害严重程度等,是地下流体反演中最重要的参数之一。
反演地下流体参数需要精确获取地下流体活动导致的地表形变,而InSAR技术能低成本、大范围、高空间分辨率地获取地表面域形变值,因此在地下流体参数反演中具有巨大应用潜力。国内外学者在地下流体体积变化参数反演领域构建了多种模型,大致可分为如下两大类。
(1) 基于确定几何形状的地下流体体积反演。基于地下流体的先验信息(勘探资料、地质构造等),将地下流体真实形状近似为一个确定的几何形状,从而进行单一源的体积反演,获得地下流体体积变化。这种反演方法称为基于确定几何形状的地下流体体积反演。简化为简单的几何形状,降低了参数反演的复杂程度。此类反演模型包括Mogi模型、Okada模型、CDM(compound dislocation model)模型、Yang's模型和扁椭球模型等。1995年文献[6]首次利用InSAR技术和Mogi模型发现了埃特纳火山的收缩现象,并获得了埃特纳火山岩浆囊位置及体积变化。2017年,文献[40]发展了一种自由度更高的CDM,并应用于卡尔布科火山,基于InSAR观测实现了地表三维形变及岩浆囊体积变化反演。2021年,文献[96]利用InSAR技术监测呼图壁储气库注/采气过程,并引入CDM模型实现了地下储气库的体积变化反演和地表三维形变估计,为我国战略储气库的安全监测和体积反演提供了科学参考。这些模型在进行地下流体体积反演时依赖于先验的源形状,因此,假定的与真实的地下流体几何形状是否一致是地下流体反演的关键。然而,实际中地下流体几何形状一般是不规则的,难以获得准确的反演结果。
(2) 基于非确定几何形状的地下流体体积反演。在无须先验假定地下流体几何形状的前提下,基于弹性半空间理论将地下流体储层分为若干个均质单元(如平行六面体、柱体),先对每个单元分别进行地下流体体积反演,最后通过体积可叠加原理获得整个地下流体体积变化。这种反演方法被称为基于非确定几何形状的地下流体体积反演,可以减少由于先验信息不足导致的反演精度不够的问题。此类反演模型包括柱体模型(Geertsma's模型)、分布式点源模型等。2002年,文献[97]首次将InSAR数据用于分布式点源模型的地下流体体积参数反演中,获得了Coso地热田的地下流体体积变化,InSAR数据的使用极大地改善了地下流体参数反演的准确性。随后,文献[98—99]利用该模型与InSAR数据分别反演了加利福尼亚州威尔明顿油田的体积变化和与黄石火山温泉的体积变化。2011年,文献[100]提出了一种将分布式点源模型与椭球体模型相结合的自由几何体建模方案,该方案联合InSAR数据和重力数据,实现了同时反演火山口下方岩浆囊的体积变化分布与重力压力变化。2016年,文献[101]利用InSAR数据、分布式点源模型及PCA技术,实现了基拉韦厄火山口长时序体积变化,以及火山喷发期和休眠期不同深度的体积源分布。2017年,文献[102—103]在分布式点源模型的基础上,提出了基于地下流体模型约束的三维形变模型,将体积变化参数与地表三维形变联合求解,并成功反演了涩北气田的动态体积变化。
以上反演模型皆为高度非线性模型,在实际应用中需假定地下流体几何参数(如地下流体深度、厚度等),使非线性问题转化为线性问题,这些简化在地下流体反演参数中会导致一定的不确定性。因此,通过利用非线性反演算法(模拟退火法、粒子群算法、遗传算法等)搜索得到模型的最优反演参数将是未来研究的重点。其次,地下流体活动与断层活动导致的地表形变常常出现混叠现象,如何从形变结果中区分断层活动地表形变与地下流体活动引起的地表形变,从而获得更准确的地下流体体积变化,未来也需要进一步研究。以上基于弹性半空间理论的解析模型是高度抽象化后的模型,因此揭示出的地下流体体积变化规律相对不够全面,而数值模型(有限元法和边界元法)可将地下流体形状建模为有限大小的任意形状并结合不同的力学性质,采用适当的本构方程(描述地下流体的流变性质)联立求解地下流体参数。因此,如何高效准确地建立地下流体反演的数值模型,也是未来进一步研究的方向。
3 InSAR参数反演面临的问题和挑战 3.1 InSAR观测误差与单一观测几何制约参数反演精度 3.1.1 低相干区InSAR观测降低参数反演精度利用InSAR技术可以获得高空间分辨率的地表形变信息,可为与地表形变相关的潜在致灾过程参数反演提供可靠的数据源。然而受时空去相干、观测误差等因素的限制,一些InSAR误差源很难被准确地抑制或去除,从而制约了参数反演的精度。断层区域的植被、水域覆盖往往会导致InSAR相干性降低,严重的失相干会导致InSAR技术无法获取有效的地表形变监测结果。受两次SAR成像时刻电离层和对流层的温度、相对湿度、气压等大气物理参数发生时空变化的影响,InSAR差分干涉相位信息中残留了大气相位,很难对其进行消除,严重制约了InSAR技术监测地表形变的精度和后续参数反演精度。其次,卫星轨道误差、DEM误差、数据解缠误差及数据处理过程中引入的误差等也会影响地表形变获取的精度和参数反演精度。
3.1.2 InSAR一维形变导致部分反演参数不敏感除地学模型的准确和可靠外,观测值能否全面描述地表形变的关键特征也是地学参数精确反演的关键。受SAR斜视成像的影响,单一平台或轨道InSAR仅能监测地表真实三维形变在雷达视线方向的一维投影,难以反映地表真实形变特征。因此,仅利用InSAR一维形变观测值反演地学参数可能出现部分参数对观测值的不敏感现象(即观测值难以有效约束相关参数),降低参数反演的精度和可靠性。例如,在目前SAR卫星近极地轨道场景下,地表南北方向形变分量对InSAR一维视线向形变贡献较小。这就意味着,与南北向形变密切相关的模型参数对InSAR观测不敏感,该模型参数反演的误差会较大,可靠性不高。鉴于此,在InSAR数据允许的前提下,充分利用多视角、多平台及多轨道InSAR形变观测值,有助于提高地学参数反演精度和可靠性。
3.1.3 InSAR几何条件相近引起的病态问题不同卫星成像几何条件相近,会大幅降低观测的图形强度。此外,同一卫星获取的InSAR形变观测数据,也不是完全独立的。这些因素会造成地学参数反演中法方程存在一定的病态问题,导致反演的地学参数不稳定、不精确。目前,主要通过附加约束(如正则化等)稳定待求参数克服病态问题。不同地学反演模型,参数数量及参数间可能存在的相关性也会造成模型求解方程病态,需要通过线性化或有效的非线性估计方法减少模型待估参数,从而减弱病态问题对参数反演精度的影响。针对大地测量地球物理反演中的病态问题,文献[104—105]提出了很多解决方法(如谱修正迭代法、正则化法、岭估计、主成分分析、贝叶斯方法等),在满足结果精度的要求下,评估病态问题对特定地学模型的影响程度将深化对特定病态问题的认识。
3.2 InSAR观测与地学参数之间模型关系不准制约参数反演InSAR观测得到的是地表三维形变沿LOS向的一维投影。地面位移通常发生在三维立体空间内,在某些情况下,如沿南北向的走滑、与LOS向近乎垂直的滑坡等,InSAR观测值可能并不能很好地捕捉这些地表形变,也不能很好地作为形变观测值约束地学模型的参数反演,从而使得既有InSAR观测与模型地学参数之间的关系不准确或约束性弱。另外,由于目前SAR卫星的重返周期仍然较大,部分潜在的致灾事件或地球物理现象,如地震、滑坡、冰崩等,是在极短的时间内发生的,且之后还会出现一些残余的运动或环境因素变化。如果上述灾害事件或地球物理现象发生在InSAR两次观测之间,目前的InSAR形变结果很难区分出主要变形与残余运动和环境因素变化的影响。直接将InSAR观测用于震源参数等模型参数反演过程中,将会导致输入数据中存在非主要形变事件和环境因素变化的形变污染,影响模型参数反演的准确性。此外,对于不同类型的灾害事件或地球物理现象,如果对其发生形变的物理机制认知不准确甚至错误,而运用不合适的物理机制或假设进行建模,将严重影响地学参数与InSAR形变观测值之间的关系。这时,很有可能反演出一组伪地学参数,得到不准确甚至错误的物理解释和结论。
3.3 海量观测数导致的反演效率低InSAR定期重返和高空间分辨率形变监测优势能为地学参数反演提供海量观测数据。例如,面对10 km2的研究区域,3 m空间分辨率的单个InSAR干涉对理想条件下可获得约11万个地表形变观测值。随着时间序列和多平台/多轨道InSAR数据集的加入,观测值数量将呈指数级增长。然而,目前大多地学模型为非线性,且现有方法基本通过非线性搜索反演地学参数。由于非线性反演算法的核心思想是通过解空间搜索寻找最优化地学参数,因此,其面对海量InSAR观测值时反演效率较低。目前,通过四叉树降采样等手段减少观测值数量[106]或使用更高效的反演算法[36],是克服该问题的途径之一,但是如何降采样获得有代表性的观测样本,如何平衡反演精度和效率,仍是需要研究的问题。
3.4 多次地球活动反演的参数可区分性受限于当前SAR卫星较长的重访周期(即低时间分辨率)。两景SAR影像差分得到的InSAR形变场往往包含了影像获取时间内所有地球活动所造成的形变[21]。例如,InSAR同震形变中往往叠加了较大余震和震后早期形变(如余滑、孔隙弹性回弹、非弹性形变等)信号,造成基于InSAR反演的同震震源参数具有一定的不确定性。因此,如何有效区分多次地球活动反演的参数,是限制InSAR技术在地学领域应用和推广的瓶颈之一。为了克服上述难题,除了寄希望于未来高时间分辨率的SAR卫星数据之外,部分学者开始引入特定地球活动形变模型(如将余滑模型引入同震滑动反演模型中),进而构建更为复杂的参数模型以求逼近真实地球物理过程[107],为后续深入研究指明了方向。然而,特定模型的引入并不能解释所有相关地球活动事件(如引入余滑模型并不能解释较大余震、孔隙弹性回弹等活动造成的形变),而且联合模型的复杂性(如强非线性等)增强,造成了模型求解稳定性差、耗时量大等。此外,发展基于特定模型有效融合高频GNSS和InSAR联合模型,将为区分多次地球活动反演参数提供有效解决途径。
3.5 InSAR与其他大地测量观测联合反演问题随着卫星遥感技术的日新月异、计算机数据传输能力与处理能力的不断提高,震源参数反演由基于单一观测数据的反演逐渐发展为基于多源观测数据(水准、GNSS、光学、InSAR等数据)的联合反演,大大推动和加速了震源参数反演进程。联合多源大地测量数据不仅可以提高震源参数解的稳健性,而且具有更好的数据分辨率,进而提高对反演参数的约束能力。InSAR数据具有较高的空间分辨率,可以为浅源地震的反演提供紧约束。GNSS数据具有较高的时间分辨率,可以弥补InSAR技术低时间分辨率的不足。光学影像匹配技术可以监测得到大范围的东西向和南北向水平地表形变场,可以较好地弥补InSAR视线向形变对南北向不敏感和GNSS数据空间上点位稀疏的不足。针对地震产生的大范围、大梯度复杂形变场,综合利用光学影像匹配、InSAR、GNSS等空间对地观测技术各自的优势,对快速恢复地震同震形变场及准确获取震源参数至关重要。利用多源大地测量观测数据联合反演震源参数时,不同观测数据在目标函数中的相对权重决定了各类数据对反演结果的贡献,从而对参数估值的最优性质产生影响。如何准确确定不同观测数据集之间的相对权比是提高震源参数反演精度的关键因素之一。
3.6 InSAR地学参数反演精度评定问题使用有限的地表观测数据约束复杂的地学参数是非常难的反演问题。常规的InSAR地学参数反演主要包含非线性全局最优估计方法和线性最小二乘方法,这样求解得到的地学参数往往是一组全局最优解。任何反演方法的差异都可能导致截然不同的模型参数解。只有充分考虑反演过程中的不确定性,才能更加客观、准确地反演得到震源参数,更好地解译其机制。随着InSAR数据的类别、模式及获取平台的增多,如何有效考虑InSAR大气误差、卫星轨道误差、DEM误差、数据解缠误差,以及数据处理过程中引入的误差、参数先验信息、系数矩阵误差等重要信息,从而定性、定量地分析和解释这些误差对反演参数不确定性的影响,是InSAR地学参数反演需要进一步解决的难题之一。为了克服上述难题,可以考虑将数据误差引入随机模型,联合贝叶斯反演方法和蒙特卡罗马尔科夫链中的抽样方法评估高维参数后验概率分布,解决传统反演方法难以定性、定量评估参数误差分布的问题,并提供参数误差分布的置信区间。
4 结语目前,InSAR已被广泛应用于自然因素或人类活动导致的灾害事件和灾变过程的关键地学参数反演。本文系统介绍了国内外学者在地震震源参数、火山活动参数、地下水文学参数、地下采空区几何参数、冻土活动层厚度、冰川物质平衡变化、冰川跃动参数、大气水汽参数及地下流体体积变化参数等地学参数反演领域的成功应用和经验方法。但是,顾及星载InSAR固有的成像模式、有限的观测条件、亟待发展的反演算法等因素,InSAR地学参数反演仍面临着观测误差复杂与单一观测几何制约反演精度的问题、观测量与地学参数之间模型关系不准确的问题,以及海量观测数据导致的反演效率低、多次地球活动引发的反演参数的不确定性、InSAR与其他大地测量观测联合反演、InSAR地学参数反演精度评定的问题。
| [1] |
GABRIEL A K, GOLDSTEIN R M, ZEBKER H A. Mapping small elevation changes over large areas: differential radar interferometry[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B7): 9183-9191. DOI:10.1029/JB094iB07p09183 |
| [2] |
BVRGMANN R, ROSEN P A, FIELDING E J. Synthetic aperture radar interferometry to measure Earth's surface topography and its deformation[J]. Annual Review of Earth and Planetary Sciences, 2000, 28(1): 169-209. DOI:10.1146/annurev.earth.28.1.169 |
| [3] |
HOOPER A, BEKAERT D, SPAANS K, et al. Recent advances in SAR interferometry time series analysis for measuring crustal deformation[J]. Tectonophysics, 2012, 514-517: 1-13. DOI:10.1016/j.tecto.2011.10.013 |
| [4] |
GOLDSTEIN R M, ENGELHARDT H, KAMB B, et al. Satellite radar interferometry for monitoring ice sheet motion: Application to an antarctic ice stream[J]. Science, 1993, 262(5139): 1525-1530. DOI:10.1126/science.262.5139.1525 |
| [5] |
MASSONNET D, ROSSI M, CARMONA C, et al. The displacement field of the Landers earthquake mapped by radar interferometry[J]. Nature, 1993, 364(6433): 138-142. DOI:10.1038/364138a0 |
| [6] |
MASSONNET D, BRIOLE P, ARNAUD A. Deflation of Mount Etna monitored by spaceborne radar interferometry[J]. Nature, 1995, 375(6532): 567-570. DOI:10.1038/375567a0 |
| [7] |
ROSEN P A, HENSLEY S, JOUGHIN I R, et al. Synthetic aperture radar interferometry[J]. Proceedings of the IEEE, 2000, 88(3): 333-382. DOI:10.1109/5.838084 |
| [8] |
GRAHAM L C. Synthetic interferometer radar for topographic mapping[J]. Proceedings of the IEEE, 1974, 62(6): 763-768. DOI:10.1109/PROC.1974.9516 |
| [9] |
FARR T G, ROSEN P A, CARO E, et al. The shuttle radar topography mission[J]. Reviews of Geophysics, 2007, 45(2): RG2004. |
| [10] |
RIZZOLI P, MARTONE M, GONZALEZ C, et al. Generation and performance assessment of the global TanDEM-X digital elevation model[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 132: 119-139. DOI:10.1016/j.isprsjprs.2017.08.008 |
| [11] |
CURLANDER J C, MCDONOUGH R N. Synthetic aperture radar: systems and signal processing[M]. New York: [s.n.], 1991.
|
| [12] |
ELACHI C. Spaceborne radar remote sensing: applications and techniques[M]. New York: IEEE, 1988.
|
| [13] |
GENS R, VAN GENDEREN J L. Review article SAR interferometry-issues, techniques, applications[J]. International Journal of Remote Sensing, 1996, 17(10): 1803-1835. DOI:10.1080/01431169608948741 |
| [14] |
CHEN C W, ZEBKER H A. Phase unwrapping for large SAR interferograms: statistical segmentation and generalized network models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1709-1719. DOI:10.1109/TGRS.2002.802453 |
| [15] |
LI Zhiwei, CAO Yunmeng, WEI Jianchao, et al. Time-series InSAR ground deformation monitoring: atmospheric delay modeling and estimating[J]. Earth-Science Reviews, 2019, 192: 258-284. DOI:10.1016/j.earscirev.2019.03.008 |
| [16] |
FERRETTI A, PRATI C, ROCCA F. Permanent scatterers in SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8-20. DOI:10.1109/36.898661 |
| [17] |
FERRETTI A, PRATI C, ROCCA F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2202-2212. DOI:10.1109/36.868878 |
| [18] |
HOOPER A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches[J]. Geophysical Research Letters, 2008, 35(16): 96-106. |
| [19] |
BERARDINO P, FORNARO G, LANARI R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375-2383. DOI:10.1109/TGRS.2002.803792 |
| [20] |
ZHANG Lei, DING Xiaoli, LU Zhong. Ground settlement monitoring based on temporarily coherent points between two SAR acquisitions[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(1): 146-152. DOI:10.1016/j.isprsjprs.2010.10.004 |
| [21] |
WERNER C, WEGMULLER U, STROZZI T, et al. Interferometric point target analysis for deformation mapping[C]//Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No. 03CH37477). Toulouse, France: IEEE, 2004: 4362-4364.
|
| [22] |
FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks: SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460-3470. DOI:10.1109/TGRS.2011.2124465 |
| [23] |
DONG Jie, ZHANG Lu, TANG Minggao, et al. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: a case study of Jiaju landslide in Danba, China[J]. Remote Sensing of Environment, 2018, 205: 180-198. DOI:10.1016/j.rse.2017.11.022 |
| [24] |
PERISSIN D, WANG Teng. Time-series InSAR applications over urban areas in China[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2011, 4(1): 92-100. DOI:10.1109/JSTARS.2010.2046883 |
| [25] |
YU Hanwen, LAN Yang, YUAN Zhihui, et al. Phase unwrapping in InSAR: a review[J]. IEEE Geoscience and Remote Sensing Magazine, 2019, 7(1): 40-58. DOI:10.1109/MGRS.2018.2873644 |
| [26] |
COSTANTINI M. A novel phase unwrapping method based on network programming[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 813-821. DOI:10.1109/36.673674 |
| [27] |
FEIGL K L, SERGENT A, JACQ D. Estimation of an earthquake focal mechanism from a satellite radar interferogram: application to the December 4, 1992 Landers aftershock[J]. Geophysical Research Letters, 1995, 22(9): 1037-1040. DOI:10.1029/94GL03212 |
| [28] |
OKADA Y. Internal deformation due to shear and tensile faults in a half-space[J]. Bulletin of the seismological society of America, 1992, 82(2): 1018-1040. DOI:10.1785/BSSA0820021018 |
| [29] |
张红, 王超, 单新建, 等. 基于SAR差分干涉测量的张北-尚义地震震源参数反演[J]. 科学通报, 2001, 46(21): 1837-1841. ZHANG Hong, WANG Chao, SHAN Xinjian, et al. Source parameter inversion of Zhangbei-Shangyi earthquake based on SAR differential interferometry[J]. Chinese Science Bulletin, 2001, 46(21): 1837-1841. DOI:10.3321/j.issn:0023-074X.2001.21.017 |
| [30] |
FIALKO Y, SANDWELL D, AGNEW D, et al. Deformation on nearby faults induced by the 1999 Hector Mine earthquake[J]. Science, 2002, 297(5588): 1858-1862. DOI:10.1126/science.1074671 |
| [31] |
FUNNING G J, PARSONS B, WRIGHT T J, et al. Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B9): B09406. |
| [32] |
FENG Guangcai, HETLAND E A, DING Xiaoli, et al. Coseismic fault slip of the 2008Mw 7.9 Wenchuan earthquake estimated from InSAR and GPS measurements[J]. Geophysical Research Letters, 2010, 37(1): L01302. |
| [33] |
HAMLING I J, HREINSDÓTTIR S, CLARK K, et al. Complex multifault rupture during the 2016Mw 7.8 Kaikōura earthquake, New Zealand[J]. Science, 2017, 356(6334): eaam7194. DOI:10.1126/science.aam7194 |
| [34] |
HE Lijia, FENG Guangcai, WU Xiongxiao, et al. Coseismic and early postseismic slip models of the 2021Mw 7.4 Maduo earthquake (western China) estimated by space-based geodetic data[J]. Geophysical Research Letters, 2021, 48(24): e2021GL095860. |
| [35] |
冯万鹏, 李振洪. InSAR资料约束下震源参数的PSO混合算法反演策略[J]. 地球物理学进展, 2010, 25(4): 1189-1196. FENG Wanpeng, LI Zhenhong. A novel hybrid PSO/simplex algorithm for determining earthquake source parameters using InSAR data[J]. Progress in Geophysics, 2010, 25(4): 1189-1196. DOI:10.3969/j.issn.1004-2903.2010.04.007 |
| [36] |
BAGNARDI M, HOOPER A. Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: a Bayesian approach[J]. Geochemistry, Geophysics, Geosystems, 2018, 19(7): 2194-2211. DOI:10.1029/2018GC007585 |
| [37] |
JÓNSSON S, ZEBKER H, SEGALL P, et al. Fault slip distribution of the 1999Mw 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements[J]. Bulletin of the Seismological Society of America, 2022, 92(4): 1377-1389. |
| [38] |
MOGI K. Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them[J]. Bulletin of the Earthquake Research Institute, 1958, 36: 99-134. |
| [39] |
YANG Xuemin, DAVIS P M, DIETERICH J H. Deformation from inflation of a dipping finite prolate spheroid in an elastic half-space as a model for volcanic stressing[J]. Journal of Geophysical Research: Solid Earth, 1988, 93(B5): 4249-4257. DOI:10.1029/JB093iB05p04249 |
| [40] |
NIKKHOO M, WALTER T R, LUNDGREN P R, et al. Compound dislocation models (CDMs) for volcano deformation analyses[J]. Geophysical Journal International, 2017, 208(2): 877-894. DOI:10.1093/gji/ggw427 |
| [41] |
XU Wenbin, XIE Lei, AOKI Y, et al. Volcano-wide deformation after the 2017 Erta Ale Dike Intrusion, Ethiopia, Observed with Radar Interferometry[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(8): e2020JB019562. |
| [42] |
XU Wenbin, RUCH J, JÓNSSON S. Birth of two volcanic islands in the southern Red Sea[J]. Nature Communications, 2015, 6(1): 7104. DOI:10.1038/ncomms8104 |
| [43] |
RUCH J, WANG Teng, XU Wenbin, et al. Oblique rift opening revealed by reoccurring magma injection in central Iceland[J]. Nature Communications, 2016, 7(1): 12352. DOI:10.1038/ncomms12352 |
| [44] |
BIGGS J, WRIGHT T J. How satellite InSAR has grown from opportunistic science to routine monitoring over the last decade[J]. Nature Communications, 2020, 11(1): 3863. DOI:10.1038/s41467-020-17587-6 |
| [45] |
GALLOWAY D L, BURBEY T J. Review: Regional land subsidence accompanying groundwater extraction[J]. Hydrogeology Journal, 2011, 19(8): 1459-1486. DOI:10.1007/s10040-011-0775-5 |
| [46] |
HOFFMANN J, GALLOWAY D L, ZEBKER H A. Inverse modeling of interbed storage parameters using land subsidence observations, Antelope Valley, California[J]. Water Resources Research, 2003, 39(2): 1031. |
| [47] |
GALLOWAY D L, HUDNUT K W, INGEBRITSEN S E, et al. Detection of aquifer system compaction and land subsidence using interferometric synthetic aperture radar, Antelope Valley, Mojave Desert, California[J]. Water Resources Research, 1998, 34(10): 2573-2585. DOI:10.1029/98WR01285 |
| [48] |
AMELUNG F, GALLOWAY D L, BELL J W, et al. Sensing the ups and downs of Las Vegas: InSAR reveals structural control of land subsidence and aquifer-system deformation[J]. Geology, 1999, 27(6): 483-486. DOI:10.1130/0091-7613(1999)027<0483:STUADO>2.3.CO;2 |
| [49] |
JIANG L, BAI L, ZHAO Y, et al. Combining InSAR and hydraulic head measurements to estimate aquifer parameters and storage variations of confined aquifer system in Cangzhou, North China Plain[J]. Water Resources Research, 2018, 54(10): 8234-8252. DOI:10.1029/2017WR022126 |
| [50] |
CHAUSSARD E, MILILLO P, BVRGMANN R, et al. Remote sensing of ground deformation for monitoring groundwater management practices: application to the Santa Clara Valley during the 2012-2015 California drought[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(10): 8566-8582. DOI:10.1002/2017JB014676 |
| [51] |
PENG Mimi, LU Zhong, ZHAO Chaoying, et al. Mapping land subsidence and aquifer system properties of the Willcox Basin, Arizona, from InSAR observations and independent component analysis[J]. Remote Sensing of Environment, 2022, 271: 112894. DOI:10.1016/j.rse.2022.112894 |
| [52] |
许文斌, 李志伟, 丁晓利, 等. 利用InSAR短基线技术估计洛杉矶地区的地表时序形变和含水层参数[J]. 地球物理学报, 2012, 55(2): 452-461. XU Wenbin, LI Zhiwei, DING Xiaoli, et al. Application of small baseline subsets D-InSAR technology to estimate the time series land deformation and aquifer storage coefficients of Los Angeles area[J]. Chinese Journal of Geophysics, 2012, 55(2): 452-461. |
| [53] |
CHEN Jingyi, KNIGHT R, ZEBKER H A, et al. Confined aquifer head measurements and storage properties in the San Luis Valley, Colorado, from spaceborne InSAR observations[J]. Water Resources Research, 2016, 52(5): 3623-3636. DOI:10.1002/2015WR018466 |
| [54] |
BURBEY T J. Three-dimensional deformation and strain induced by municipal pumping, part 2:numerical analysis[J]. Journal of Hydrology, 2006, 330(3-4): 422-434. DOI:10.1016/j.jhydrol.2006.03.035 |
| [55] |
WU Jichun, SHI Xiaoqing, YE Shujun, et al. Numerical simulation of viscoelastoplastic land subsidence due to groundwater overdrafting in Shanghai, China[J]. Journal of Hydrologic Engineering, 2010, 15(3): 223-236. DOI:10.1061/(ASCE)HE.1943-5584.0000172 |
| [56] |
ALGHAMDI A, HESSE M A, CHEN Jingyi, et al. Bayesian poroelastic aquifer characterization from InSAR surface deformation data. part I: maximum a posteriori estimate[J]. Water Resources Research, 2020, 56(10): e2020WR027391. |
| [57] |
WEN Laifu, CHENG Jiulong, HUANG Shaohua, et al. Review of geophysical exploration on mined-out areas and water abundance[J]. Journal of Environmental and Engineering Geophysics, 2019, 24(1): 129-143. DOI:10.2113/JEEG24.1.129 |
| [58] |
YANG Zefa, LI Zhiwei, ZHU Jianjun, et al. InSAR-based model parameter estimation of probability integral method and its application for predicting mining-induced horizontal and vertical displacements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4818-4832. DOI:10.1109/TGRS.2016.2551779 |
| [59] |
XIA Yuanping, WANG Yunjia, DU Sen, et al. Integration of D-InSAR and GIS technology for identifying illegal underground mining in Yangquan District, Shanxi Province, China[J]. Environmental Earth Sciences, 2018, 77(8): 319. DOI:10.1007/s12665-018-7488-1 |
| [60] |
XIA Yuanping, WANG Yunjia. InSAR-and PIM-based inclined goaf determination for illegal mining detection[J]. Remote Sensing, 2020, 12(23): 3884. DOI:10.3390/rs12233884 |
| [61] |
DU Sen, WANG Yunjia, ZHENG Meinan, et al. Goaf locating based on InSAR and probability integration method[J]. Remote Sensing, 2019, 11(7): 812. DOI:10.3390/rs11070812 |
| [62] |
BU Pu, LI Chaokui, LIAO Mengguang, et al. An approach for estimating underground-goaf boundaries based on combining DInSAR with a graphical method[J]. Advances in Civil Engineering, 2020, 2020: 9375056. |
| [63] |
YANG Zefa, LI Zhiwei, ZHU Jianjun, et al. Locating and defining underground goaf caused by coal mining from space-borne SAR interferometry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 135: 112-126. DOI:10.1016/j.isprsjprs.2017.11.020 |
| [64] |
FAN Hongdong, LI Tengteng, GAO Yantao, et al. Characteristics inversion of underground goaf based on InSAR techniques and PIM[J]. International Journal of Applied Earth Observation and Geoinformation, 2021, 103: 102526. DOI:10.1016/j.jag.2021.102526 |
| [65] |
程国栋, 赵林, 李韧, 等. 青藏高原多年冻土特征、变化及影响[J]. 科学通报, 2019, 64(27): 2783-2795. CHENG Guodong, ZHAO Lin, LI Ren, et al. Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau[J]. Chinese Science Bulletin, 2019, 64(27): 2783-2795. |
| [66] |
LIU Lin, SCHAEFER K, ZHANG Tingjun, et al. Estimating 1992-2000 average active layer thickness on the Alaskan North Slope from remotely sensed surface subsidence[J]. Journal of Geophysical Research: Earth Surface, 2012, 117(F1): F01005. |
| [67] |
赵蓉. 基于SBAS-InSAR的冻土形变建模及活动层厚度反演研究[D]. 长沙: 中南大学, 2014. ZHAO Rong. Permafrost deformation model establishment and active layer thickness inversion based on SBAS-InSAR[D]. Changsha: Central South University, 2014. |
| [68] |
LI Zhiwei, ZHAO Rong, HU Jun, et al. InSAR analysis of surface deformation over permafrost to estimate active layer thickness based on one-dimensional heat transfer model of soils[J]. Scientific Reports, 2015, 5(1): 15542. DOI:10.1038/srep15542 |
| [69] |
WANG Chao, ZHANG Zhengjia, ZHANG Hong, et al. Active layer thickness retrieval of Qinghai-Tibet permafrost using the TerraSAR-X InSAR technique[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(11): 4403-4413. DOI:10.1109/JSTARS.2018.2873219 |
| [70] |
徐晓明, 吴青柏, 张中琼. 青藏高原多年冻土活动层厚度对气候变化的响应[J]. 冰川冻土, 2017, 39(1): 1-8. XU Xiaoming, WU Qingbai, Zhang Zhongqiong. Responses of active layer thickness on the Qinghai-Tibet Plateau to climate change[J]. Journal of Glaciology and Geocryology, 2017, 39(1): 1-8. |
| [71] |
ANISIMOV O A. Changing climate and permafrost distribution in the Soviet Arctic[J]. Physical Geography, 1989, 10(3): 285-293. DOI:10.1080/02723646.1989.10642383 |
| [72] |
SUN Zhe, ZHAO Lin, HU Guojie, et al. Modeling permafrost changes on the Qinghai-Tibetan Plateau from 1966 to 2100:a case study from two boreholes along the Qinghai-Tibet engineering corridor[J]. Permafrost and Periglacial Processes, 2020, 31(1): 156-171. DOI:10.1002/ppp.2022 |
| [73] |
GANGODAGAMAGE C, ROWLAND J C, HUBBARD S S, et al. Extrapolating active layer thickness measurements across Arctic polygonal terrain using LiDAR and NDVI data sets[J]. Water Resources Research, 2014, 50(8): 6339-6357. DOI:10.1002/2013WR014283 |
| [74] |
WIDHALM B, BARTSCH A, LEIBMAN M, et al. Active-layer thickness estimation from X-band SAR backscatter intensity[J]. The Cryosphere, 2017, 11(1): 483-496. DOI:10.5194/tc-11-483-2017 |
| [75] |
JIA Yuanyuan, KIM J W, SHUM C K, et al. Characterization of active layer thickening rate over the northern Qinghai-Tibetan Plateau permafrost region using ALOS interferometric synthetic aperture radar data, 2007-2009[J]. Remote Sensing, 2017, 9(1): 84. DOI:10.3390/rs9010084 |
| [76] |
CHEN R H, MICHAELIDES R J, SULLIVAN T D, et al. Joint retrieval of soil moisture and permafrost active layer thickness using L-band insar and P-band polsar[C]//Proceedings of 2020 IEEE International Geoscience and Remote Sensing Symposium. Waikoloa, HI, USA: IEEE, 2020: 4606-4609.
|
| [77] |
MEIER M F, POST A. What are glacier surges?[J]. Canadian Journal of Earth Sciences, 1969, 6(4): 807-817. DOI:10.1139/e69-081 |
| [78] |
SINGH V P, SINGH P, HARITASHYA U K. Encyclopedia of snow, ice and glaciers[M]. Dordrecht: Springer, 2011.
|
| [79] |
HU Jun, LI Zhiwei, LI Jia, et al. 3D movement mapping of the alpine glacier in Qinghai-Tibetan Plateau by integrating D-InSAR, MAI and offset-tracking: case study of the Dongkemadi Glacier[J]. Global and Planetary Change, 2014, 118: 62-68. DOI:10.1016/j.gloplacha.2014.04.002 |
| [80] |
GRAY A L, SHORT N, MATTAR K E, et al. Velocities and flux of the filchner ice shelf and its tributaries determined from speckle tracking interferometry[J]. Canadian Journal of Remote Sensing, 2001, 27(3): 193-206. DOI:10.1080/07038992.2001.10854936 |
| [81] |
STROZZI T, LUCKMAN A, MURRAY T, et al. Glacier motion estimation using SAR offset-tracking procedures[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2384-2391. DOI:10.1109/TGRS.2002.805079 |
| [82] |
LI Jia, LI Zhiwei, WU Lixin, et al. Deriving a time series of 3D glacier motion to investigate interactions of a large mountain glacial system with its glacial lake: use of Synthetic Aperture Radar Pixel Offset-Small Baseline Subset technique[J]. Journal of Hydrology, 2018, 559: 596-608. DOI:10.1016/j.jhydrol.2018.02.067 |
| [83] |
GUO Lei, LI Jia, LI Zhiwei, et al. The surge of the Hispar glacier, Central Karakoram: SAR 3D flow velocity time series and thickness changes[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(7): e2019JB018945. |
| [84] |
QUINCEY D J, BRAUN M, GLASSER N F, et al. Karakoram glacier surge dynamics[J]. Geophysical Research Letters, 2011, 38(18): L18504. |
| [85] |
YASUDA T, FURUYA M. Dynamics of surge-type glaciers in West Kunlun Shan, Northwestern Tibet[J]. Journal of Geophysical Research: Earth Surface, 2015, 120(11): 2393-2405. DOI:10.1002/2015JF003511 |
| [86] |
WENDT A, MAYER C, LAMBRECHT A, et al. A glacier surge of Bivachny Glacier, Pamir Mountains, observed by a time series of high-resolution digital elevation models and glacier velocities[J]. Remote Sensing, 2017, 9(4): 388. DOI:10.3390/rs9040388 |
| [87] |
TRENBERTH K E, FASULLO J, SMITH L. Trends and variability in column-integrated atmospheric water vapor[J]. Climate Dynamics, 2005, 24(7): 741-758. |
| [88] |
HANSSEN R F, WECKWERTH T M, ZEBKER H A, et al. High-resolution water vapor mapping from interferometric radar measurements[J]. Science, 1999, 283(5406): 1297-1299. DOI:10.1126/science.283.5406.1297 |
| [89] |
MATEUS P, NICO G, CATALÃO J. Can spaceborne SAR interferometry be used to study the temporal evolution of PWV?[J]. Atmospheric Research, 2013, 119: 70-80. DOI:10.1016/j.atmosres.2011.10.002 |
| [90] |
LIU S. Satellite radar interferometry: Estimation of atmospheric delay[D]. Delft: Delft University of Technology, 2012.
|
| [91] |
ALSHAWAF F, HINZ S, MAYER M, et al. Constructing accurate maps of atmospheric water vapor by combining interferometric synthetic aperture radar and GNSS observations[J]. Journal of Geophysical Research: Atmospheres, 2015, 120(4): 1391-1403. DOI:10.1002/2014JD022419 |
| [92] |
DUAN Meng, XU Bing, LI Zhiwei, et al. Non-differential water vapor estimation from SBAS-InSAR[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2020, 204: 105284. DOI:10.1016/j.jastp.2020.105284 |
| [93] |
PICHELLI E, FERRETTI R, CIMINI D, et al. InSAR water vapor data assimilation into mesoscale model MM5:technique and pilot study[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 3859-3875. DOI:10.1109/JSTARS.2014.2357685 |
| [94] |
MATEUS P, TOMÉ R, NICO G, et al. Three-dimensional variational assimilation of InSAR PWV using the WRFDA model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7323-7330. DOI:10.1109/TGRS.2016.2599219 |
| [95] |
CAO Yunmeng, LI Zhiwei, DUAN Meng, et al. High-resolution water vapor maps obtained by merging interferometric synthetic aperture radar and GPS measurements[J]. Journal of Geophysical Research: Atmospheres, 2021, 126(1): e2020JD033430. |
| [96] |
WANG Yuedong, FENG Guangcai, LI Zhiwei, et al. Retrieving the displacements of the Hutubi (China) underground gas storage during 2003-2020 from multi-track InSAR[J]. Remote Sensing of Environment, 2022, 268: 112768. DOI:10.1016/j.rse.2021.112768 |
| [97] |
VASCO D W, WICKS C JR, KARASAKI K, et al. Geodetic imaging: reservoir monitoring using satellite interferometry[J]. Geophysical Journal International, 2002, 149(3): 555-571. DOI:10.1046/j.1365-246X.2002.01569.x |
| [98] |
VASCO D W, FERRETTI A. On the use of quasi-static deformation to understand reservoir fluid flow[J]. Geophysics, 2005, 70(4): O13-O27. DOI:10.1190/1.1993711 |
| [99] |
VASCO D W, PUSKAS C M, SMITH R B, et al. Crustal deformation and source models of the Yellowstone volcanic field from geodetic data[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B7): B07402. |
| [100] |
CAMACHO A G, GONZÁLEZ P J, FERNÁNDEZ J, et al. Simultaneous inversion of surface deformation and gravity changes by means of extended bodies with a free geometry: Application to deforming calderas[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B10): B10401. DOI:10.1029/2010JB008165 |
| [101] |
ZHAI Guang, SHIRZAEI M. Spatiotemporal model of Kīlauea's summit magmatic system inferred from InSAR time series and geometry-free time-dependent source inversion[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(7): 5425-5446. DOI:10.1002/2016JB012953 |
| [102] |
HU Jun, DING Xiaoli, ZHANG Lei, et al. Estimation of 3D surface displacement based on InSAR and deformation modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(4): 2007-2016. DOI:10.1109/TGRS.2016.2634087 |
| [103] |
LIU Xiaoge, HU Jun, SUN Qian, et al. Deriving 3D time-series ground deformations induced by underground fluid flows with InSAR: case study of sebei gas fields, China[J]. Remote Sensing, 2017, 9(11): 1129. DOI:10.3390/rs9111129 |
| [104] |
WANG Leyang, CHEN Tao. Ridge estimation iterative solution of ill-posed mixed additive and multiplicative random error model with equality constraints[J]. Geodesy and Geodynamics, 2021, 12(5): 336-346. DOI:10.1016/j.geog.2021.07.003 |
| [105] |
蒋星达, 张伟, 杨辉. 地球物理反演问题中的贝叶斯方法研究[J]. 地球与行星物理论评, 2022, 53(2): 159-171. JIANG Xingda, ZHANG Wei, YANG Hui. The research on Bayesian inference for geophysical inversion[J]. Reviews of Geophysics and Planetary Physics, 2022, 53(2): 159-171. |
| [106] |
LOHMAN R B, SIMONS M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling[J]. Geochemistry, Geophysics, Geosystems, 2005, 6(1): Q01007. |
| [107] |
LIU Xiaoge, XU Wenbin. Logarithmic model joint inversion method for coseismic and postseismic slip: application to the 2017Mw 7.3 Sarpol Zahāb Earthquake, Iran[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(11): 12034-12052. DOI:10.1029/2019JB017953 |