从1854年Snow医生用手工地图揭示霍乱病例与伦敦市中心的宽街(Broad Street)中的一口井的关联,到1970年代的计算机辅助桌面制图(如使用AutoCAD)及2010年基于Web的空间分析(如ArcGIS),地理信息科学走过了漫长的岁月。随着移动技术、物联网、大数据和人工智能的发展,地理信息科学也从GeoComputation向GeoAI和SpaceTimeAI快速发展。机器学习,特别是近年来深度学习的快速发展,为研究地理和城市问题带来了新的机遇。虽然深度学习因其对栅格数据的自然适用性而在图像处理中取得了巨大成功,但其在其他的空间和时空数据类型中的应用仍在探索之中。
深度学习在地理信息科学中的早期应用是图像理解,如城市目标检测[1]和街景分析[2]。此外,涉及交通、电讯等网络的流量预测工作是将空间数据结构(如网络和点)转换为网格进行[3]。然而,基于网格的方法存在3个潜在问题:①网格化导致原始的矢量数据的点位精度损失,进而导致后续分析结果不准确(arXiv: 1707.03340, 2017)。通常用于时空分析预测的格网尺寸较大,在数百米到数千米之间[4]。这样的网格可能包含多个不同类型的地理目标(如湖泊、道路和火车站)特征。②不同大小的网格可能会导致不同的分析结果,将会出现可变化区域单元问题(modifiable areal unit problem, MAUP)[5]。③网格结构不适合城市应用和管理,如城市交通,因为交通流必须沿着街道网络走,并不是在人为划分的网格中移动[6]。基于网格的方法将流量推向完全没有流量的空间(道路以外的地方),这将导致分析结果无法满足实际使用。
基于网格的方法的劣势正是基于网络的空间表达的优势:①基于网络的时空分析可以提供比基于网格更细粒度和更高精度的分析。基于网络的方法可以更准确地估计局部空间相似度。例如文献[5]证明,基于网络的校准模型在犯罪预测准确性方面大大优于基于网格的方案,这是因为网络作为一种自然的底层结构,比网格空间更能捕捉到精确的空间相关性。②基于网络的表示避免了使用不同大小的网格转化原始的观测值导致的MAUP。③基于网络的时空分析更合理和实用。城市研究中许多时空数据的内在结构是基于网络的,因为道路网络是城市系统的关键决定因素,例如交通、犯罪、电信和能源网络及传感器网络。网络拓扑会影响时空数据的时空相关性[7-8],而这种时空现象的分布受到网络布局的限制[8]。在这种情况下使用欧几里得平面(如网格或区域)可能会扭曲网络上空间分布模式表示及空间距离的计算。考虑到其实用性,基于网络的分析和预测更便于实际应用。例如,基于街道网络的犯罪热点预测可以比基于网格的预测能更直观地指导警察在城市巡逻[9]。因此使用网络作为时空分析的空间基础具有许多潜在优势。
此外,基于图的深度学习已经成为处理非欧几里得空间中不规则数据的最新方法,已在生物学、化学和社会网络分析方面取得了进展。鉴于图的灵活性,所有空间数据都可以表示为图(网络),这为充分利用基于图的深度学习(GNN)进行空间和时空建模提供了启示。因此,本文提出了使用网络(图)作为分析框架来推进SpaceTimeAI的倡议。建议使用网络(图)作为空间结构来表示通常表示为空间单位的时空过程,包括点、线/网络或多边形/区域。本文旨在提供一个系统的理论研究框架,因而未对所有的相关应用文献进行综述,但文中所引用的例子都是基于网络的时空智能方法——预测、聚类和优化的开创性示例。因此,对于相关方法的后续应用及改进,可以参照其他相关文献。
1 基于图的时空数据表达如何通过图来表达时空数据和过程,如何将网络(图)作为一个通用的空间结构来呈现通常以点、线/网络或多边形/区域/网格表达的时空过程。笔者按照时空分析方法的分类来讨论它们基于网络的实现[10],即时空建模和预测、时空聚类和优化。
“网络”与“图”在很大程度上是同义词[11]。然而,网络通常指现实中具有网络结构特征的情况,包括物理网络(如道路网络)和虚拟网络(如互联网网络和社交网络)。网络科学主要旨在解决发现社区及内部关系、量化连通性、确定特定实体相关性等问题[12]。图是表示网络结构特征的抽象数学概念[13],是一种通用的数据表示方法,可以方便地描述复杂网络的几何结构。因此,大多数网络问题可以归结为基于图的问题。
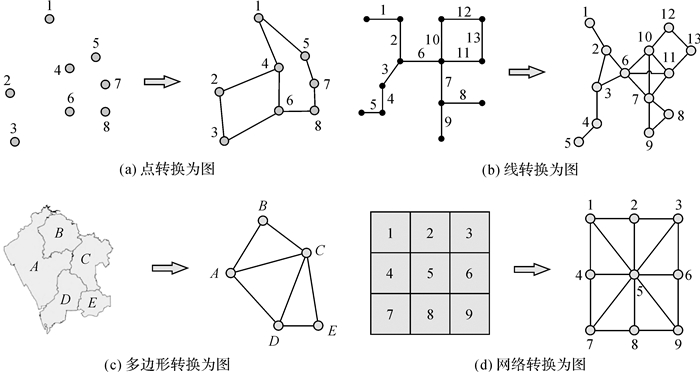
图论提供了一种更好的方法来处理抽象概念,如关系和交互。通常,图的顶点用于表示离散实体(如道路交叉口),而边用于表示实体之间的关系, 其权重通常表示它连接的两个顶点之间的相似性。边的连通性和权重一般来自研究对象的物理特性或者数据特征。例如,可以将道路网络转换为图,用邻接矩阵显示其连通性,也可以将其转换为包含距离(或反距离)的空间权重矩阵。空间权重矩阵可以是一阶或高阶,以表示不同空间阶(距离)的空间关联。此外,网络(或图)可以是无向的和有向的[7]。空间单元如何转换为网络图,如图 1所示。
|
| 图 1 将点、线、多边形及网格等空间表达转换成网络图结构表达 Fig. 1 Using network (graph) structure to express spatial structure (e.g., point, polyline, polygon, and grid) |
这种基于图的表示方式为模拟时空过程带来了数学上的便利。有两种方法可以将时空过程网络转换为图。一是将网络的节点转换为图的顶点,网络的链接转换为图的边;二是将网络的链接转换为图的顶点,将网络的节点作为图的边。图上定义的数据是位于顶点上的数值,称为图信号[13],如图 2所示。

|
| 图 2 基于图的时空网络过程表达 Fig. 2 Graph representation of network-based spacetime processes |
2 基于图的时空深度预测 2.1 时空数据建模的深度学习框架
深度学习是传统机器学习的高级发展。它已经在视频处理、语言翻译、游戏等领域取得了突破[2, 14-15]。此外,深度学习也已成功应用于解决许多城市问题。与传统机器学习方法相比,深度学习模型有3个优点:①深度学习模型实现了“端到端”学习,它可以接受原始格式的输入数据,并自动提取潜在特征以对数据中底层、复杂和非线性关系进行建模,从而生成所需的输出。极大地简化了提取特征的工作量。②具有数千个可训练变量的深层结构能够对输入和输出之间复杂的未知关系进行建模和预测学习。③深度学习模型具有强大的利用非线性激活函数处理非线性关系的能力。
3种最流行的时间序列数据建模的深度学习结构为RNN、LSTM和GRU。
(1) 循环神经网络(recurrert neural network, RNN)。RNN是一类神经网络,其中节点之间的连接沿时间序列形成有向图[16], 以表现出时间动态行为。与经典人工神经网络(artificial neural network, ANN)不同,RNN可以使用其内部状态(记忆)来处理输入序列,这使其适用于语音识别和语言翻译等任务。然而,RNN受到短期记忆的影响,当序列足够长时,将很难将信息从较早的时间步传送到较晚的时间步。RNN还存在梯度消失问题,意味着梯度会随着时间的推移反向传播而缩小。
(2) 长短期记忆(long short time memory, LSTM)。LSTM[17]是RNN的一种变体。LSTM具有与RNN类似的控制流程,但它是作为短期记忆的解决方案而创建的。一个典型的LSTM(arXiv: 1308.0850, 2013)有一个输入、一个遗忘和一个输出门,分别确定是否传递新输入、阻塞当前状态及让当前状态影响每个时间步的输出。其还有一个细胞状态,理论上,它可以携带来自早期时间步长的信息,从而减少短期记忆的影响。
(3) 门控循环单元(gated recurrent unit, GRU)。作为新一代的RNN,GRU与LSTM非常相似,但更简单[18]。GRU使用隐藏状态来传输没有单元状态的早期信息。它只有两个门,一个重置门和一个更新门。重置门是另一个门,用于决定忘记多少过去的信息。更新门决定了要通过哪些信息以及添加哪些新信息,这类似于LSTM的遗忘和输入门。
典型深度学习结构包括用于规则空间的CNN和用于不规则空间的GCN。
(1) 卷积神经网络(convolutional neural network, CNN)。CNN最早由LeCun和Bengio提出[19],主要用于图像处理。CNN通常具有一系列卷积层,将图像视为2D平面。在卷积层中,图像的每个网格(像素)只连接其近邻网格(即局部感知),而不是所有单元格。它使用权重向量提取特征(称为特征图)。位于图像上不同位置的网格具有相同的权重向量(权重共享),堆叠多个卷积层可以从常规欧几里得空间中捕获远距离空间依赖性。
(2) 图卷积网络(graph convolutional network, GCN)。经典的CNN在规则的网格拓扑上运行,缺乏处理网络/图结构数据的能力。图的深度学习,特别是GCN,近年来引起了广泛关注。从广义上讲,有两类GCN:空间方法和谱方法。空间方法中卷积算子聚合相邻节点的特征以进行空间信息提取[20]。空间方法可以在有向图或无向图上工作,但没有简单的方法可以在图的不同位置之间进行权重共享(arXiv: 1506.05163, 2015)。谱方法中通过图拉普拉斯算子上的图傅里叶变换在谱域中定义图卷积[21]。到目前为止,大多数的方法仅限于无向图,因为卷积需要一个对称的拉普拉斯矩阵来获得正交特征分解。
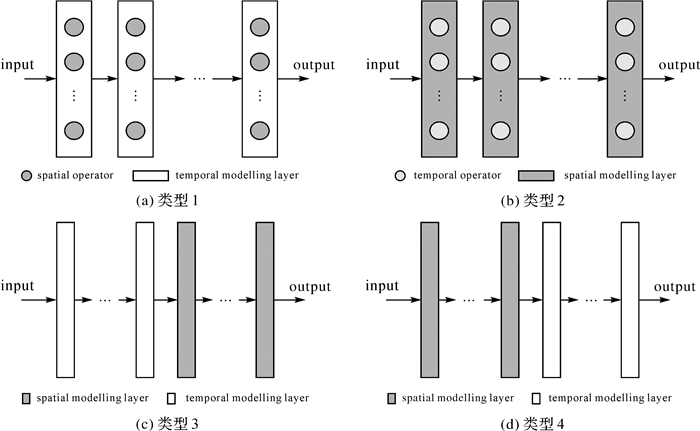
早期开发的深度学习模型通常用于预测基于网格表示的时空数据,这是因为这些深度学习模型使用卷积神经网络(CNN)来捕获空间依赖性,而CNN只能在规则网格化的空间域上工作。然而,在交通、传感器、能源和社交网络等应用中,时空数据自然地存在于网络空间中,网络能既精准又实用地表达时空数据,同时基于图的深度学习也能被用于模型建模,并且广泛适用于密集的和稀疏的时空数据。为了对时空数据的时空相关性进行建模,一种直接且有效的方法是将空间和时间建模组件集成到深度学习模型中, 可以归纳为4种主要类型(图 3)[22]:①将空间算子集成到时间建模结构。一个典型的例子是ConvLSTM[23],它本质上是一个循环层(如LSTM),但是内部的矩阵乘法被卷积运算所取代。它可以通过非线性和卷积结构学习数据集中复杂的时空模式。②将空间算子集成到时间建模结构。这种类型的混合深度学习方法将循环机制集成到空间建模深度学习结构中,如循环CNN(RCNN)将循环连接合并到每个卷积层中[24]。③先时间建模,后空间建模。例如,LSTM-CNN架构通过利用LSTM从其输入序列中查找长关系并通过卷积操作提取局部和密集特征,非常适用于人脸反诈骗[25]。④先空间建模,后时间建模。这一方式通过顺序连接空间和时间深度学习结构以进行时空信息学习。例如,CNN-LSTM结构的组合已被用于智慧城市中PM2.5预测[26]和交通预测[27]。
2.2 基于图的深度学习时空预测案例
时空过程在空间上可以是密集的(无处不在),也可以是稀疏的(仅在某处)。对于空间密集的过程,通常使用时空序列(STS)来表示;对于稀疏的过程,通常被称为时空点过程(STPP)[28]。基于图的时空预测方法在交通、犯罪和健康等方面的应用,可以很好地解释图 3中的深度学习构架,以及基于图的时空智能的优势。
2.2.1 交通流预测——密集型时空序列过程从时间序列(ARIMA)、时空序列(STARIMA及其变体)到基于网格的LSTM建模的交通预测是一个热门的研究课题。早期的深度学习将空间划分为网格,使用CNN对每周中每日和每小时模式进行建模并预测。文献[29]开发了第1个基于网络的深度时空残差神经网络,即第1次将网络链接(路段)直接作为神经网络的建模节点,空间邻接矩阵用于对空间关联进行建模, 即不同的层使用不同的空间邻接顺序。这将全连接的深度学习神经网络转变为一个局部化的深度学习网络。在其后续研究中,文献[30]开发了CNN与LSTM结合的深度学习结构来预测交通流量。文献[15]开发了第一个基于网络和图的时空序列预测-RGC-LSTM网络。由于交通流的时间依赖性强,文献[30—31]都将空间卷积算子集成到时间深度学习模型中。为了处理有向交通流,文献[31]进一步开发了有向图深度学习模型,将基于网络的时空数据表示为具有方向的一系列信号“表现良好”的图,图顶点是网络链接,图的边表示相邻关系。这个表现良好的图使有向网络的拓扑能够被纳入时空预测。然后,网络流的动态被建模为图上的马尔可夫链,其边权重由马尔可夫TPM确定。此外,还设计了一个新颖的时空图卷集STGC算子,该算子通过在加权有向图中结合上游和下游链接路段的影响,实现从多个周期中自适应地提取时间特征并充分利用空间信息,这也很大程度解决了时空异质性问题。此外,这是第一次将初始残差学习技术用于基于网络结构的时空序列预测。该方法在中国成都的一个由4089个路段组成的大型交通网络上进行了10、30、60 min的车流量预测(图 4)。
通过与其他交通预测方法(包括ARIMA、SVR、LSTM、CNN、STGCN和RGC-LSTM)相比较,有向图深度学习模型显著提高了预测精度和效率,并在高峰时段上的表现尤为良好(图 4(d))。此外,对交通事故和堵塞不需要额外的处理,整个预测过程完全自动化。这一算法不须如谷歌公司所采用的将路段人为分割为10 m的小路段,以建立额外的网络节点。因此,具有更高的学习和计算效率,具备良好的应用前景,特别适用于大城市的实时交通预测。
2.2.2 犯罪热点预测——稀疏型时空序列过程时空点过程(spale time point process, STPP)的热点地图能突出显示事件发生率,以及在空间和时间上稀疏分布的区域/位置。热点地图的早期功能主要是回顾、测量和检测稀疏历史时空数据的时空集群,包括公共安全、地震事件、犯罪、流行病学和环境科学等领域。近期,人们越来越关注使用历史数据生成预测热点地图。例如,准确的犯罪热点预测可以帮助警察在高风险地段巡逻以防止犯罪行为,而交通事故预测则可以预警道路安全。
尽管基于网络的结构可以更好地捕捉时空事件的微观变化,但现有的稀疏事件预测深度学习方法均基于区域单元或网格单元。深度学习对基于网络的STPP热点预测的关键挑战在于如何对网络中稀疏事件的复杂时空依赖关系进行建模。难点包括:①时间域中事件计数的序列不是一个可以在传统深度学习模型中近似的连续函数[32]。②空间域中常用的基于图的深度学习模型使用权重共享策略来学习空间依赖关系(arXiv: 1707.03340, 2017)。由于很多链接的观测值为零,如果直接应用该类方法,将导致权重全为零,无法生成预测映射。③预测映射如果直接使用标准回归损失函数进行参数学习会使DL模型容易出现过拟合或全零预测,这将产生不平衡的回归学习场景[36]。
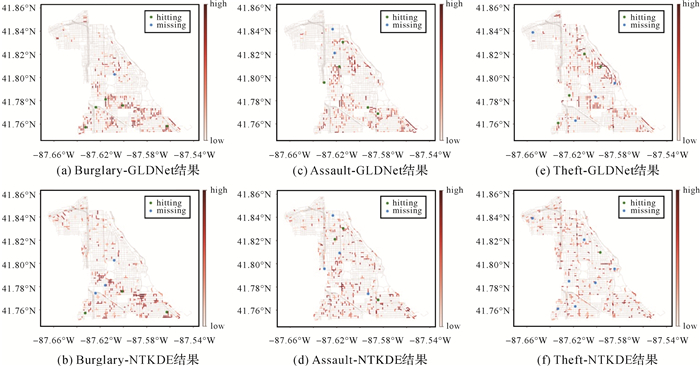
文献[15]开发了一种基于图的深度学习框架,即门控局部扩散网络(GLDNet)。这一方法被用于生成网络空间中STPP的预测热点映射。这个模型使用图 3(d)模式将时空结合在一起。其中,街道网络表示为加权无向图,其中事件计数定义为图顶点集上的值。在GLDNet中,历史事件的时间传播由门控网络建模,相关的空间传播通过网络距离和拓扑的局部扩散网络捕获,以克服空间异质性。在模型训练过程中,采用加权回归损失函数来解决许多零观测值的问题。这一模型使用美国芝加哥市的犯罪数据进行评估,以证明其可行性和有效性。据笔者所知,这是首次尝试开发基于图的深度学习方法来预测网络上稀疏时空数据的热点。
2.2.3 健康——全球COVID-19病例预测COVID-19大流行的早期阶段,有许多统计和流行病模型被用于分析COVID-19的爆发,但这些模型在评估干预计划的影响时存在许多假设,导致了低准确性和不确定的预测(arXiv: 2013.10532, 2020)。因此,需要开发新的框架和方法(arXiv: 2013.09800, 2020)。其中,文献[34]引入了基于变分自动编码器LSTM模型来预测COVID-19病毒在全球的传播,该模型不仅基于病毒传播的时间序列数据,还基于以位置和人口统计(如人口密度、城市人口和生育率等)为城市分析数据,以及当地政府为缓解疫情而采取的应对措施。
该模型使用图结构将139个国家表示为图的节点。通过使用长短期记忆(LSTM),从每个国家/地区预先定义的时间戳中学习,而且还从统一时间戳的其他国家/地区学习。为了了解其在本地和全局级别的输入和输出之间的关系,向LSTM单元引入了自我注意机制学习空间相关性。这一图结构最初是根据所有受疫情影响国家的空间权重进行初始化。但是,自疫情暴发以来,由于各国采取不同的政策和措施,空间权重在中间几天可能看起来完全不同。他们没有为模型提供静态图,而是使用变分自动编码器图来编码、学习并输出可以满足不同国家甚至全球的每日变化。该模型使用了图 3(a)中的框架(图 6)。该模型对一周内的各国的感染数目的预测比其他模型要精准。
3 基于网络结构的时空热点聚类和优化 3.1 基于网络的空间和时空热点聚类
兴趣区域(region of interest, ROI)在人类活动研究中有许多同义词,例如热点和兴趣点等。这一概念被广泛应用于出现模式、犯罪研究和流行病学等研究中,其中事件的发生由空间中的点记录表示,热点是点记录的重要聚合。随着传感器(如GPS设备和智能手机)及社交媒体(GSM)生成的位置点数据越来越多,人们聚集和交互所产生的ROI已成为人类行为研究中的热门研究课题。
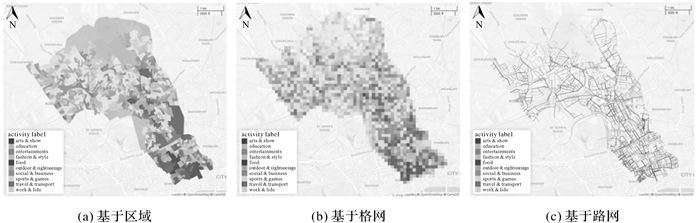
传统的ROI检测方法仅在平面空间中寻找聚合区,从而生成分布在2D笛卡尔空间中的ROI,如图 7(a)和(b)所示的基于小区域和网格的活动热点。相比之下,图 7(c)中基于网络的活动热点则能提供更加精细的表达和分析[35]。
空间热点与时间维度的结合就引申出时空热点区域的问题,研究中常用的方法有spacetime scan statistics和ST-DBSCAN。这些方法都是将时间维度添加到基于空间维度的热点检测分析中。这样不仅可以检测空间中的ROI,还可以在事件的其他非空间属性中找到时间聚合模式(图 8)。
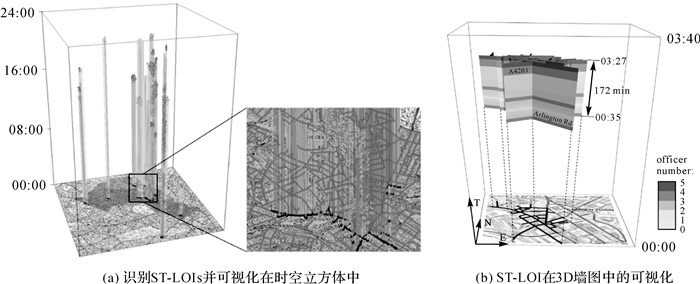
文献[42]开发了一种基于网络的ROI检测方法,命名为ST-LOI[37]。这一方法将时空聚类从笛卡尔空间扩展到基于网络的空间,并且无缝考虑空间和时间维度(图 9)。基于网络的时空热点的空间范围比空间凸包(图 8)的范围精准,更利于结合有具体坐标的兴趣点(point of interests, POIs)及其语义信息,对活动热点类型进行标示,以便于对人群的活动行为画像聚类。
3.2 基于网络的时空优化——设计高效且平衡的警察巡逻区
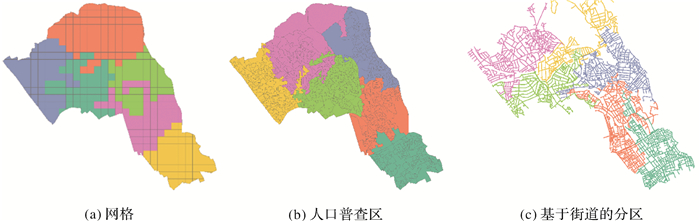
警区划分问题(police districting problem, PDP)需要根据工作量和响应时间等要求将管辖区域划分为若干个合理的巡逻区。传统上,警区划分是在地图上手工制定的,因而难以实现工作量平衡或地理紧凑性的要求[38]。近几十年来,随着地理信息系统和计算机技术的进步,自动定义警区的优化方法越来越受到研究人员和警察部门的关注[39]。继文献[45]对PDP问题进行研究后[40],研究人员开发了不同的PDP数学优化模型,这些模型重点关注区域的连续性和巡逻工作量的平衡分布。
在制定PDP时,第一步是选择可以合并的基本单元。大多数PDP模型使用区域单位或格网作为基本单位[40-41],如图 10(a)、(b)所示。开发基于街道的PDP模型能够获得更优的方案,原因如下:①街道网络的特征既影响长期犯罪模式,也影响犯罪行为的短期动态,这表明街道一级预防犯罪的重要性。②由于街道网络从根本上影响警察的行动,基于网络的模型将产生更好的可用性的分区计划。由于方形网格或人口普查区可能与物理障碍相交并包含未连接的街道段,因此街道比它们更适合运营部署。③由于街道是人类运动和空间认知的基本要素,基于街道的分区解决方案能够减轻基于网格的模型中固有的可变区域单元问题(MAUP)的影响。因此,文献[42—43]提出了基于城市街道网络的警察巡逻区划分方法,如图 10(c)所示。其能设计高效且平衡的警察巡逻区和在线实时优化巡逻路线,并能减少20%紧急事件应急反应时间,使得警员可以有更多的时间在犯罪热点路段上巡逻。该方法可以扩展应用到大型车队的物流调配。
4 总结与讨论
笔者介绍了使用网络和图作为SpaceTimeAI或GeoAI的基本空间结构进行时空分析的多种方法。由于人们的生活和出行大多是沿着城市路网展开,这一框架特别适用于城市问题的研究。相比于传统的基于网格的表达,基于网络的结构更加精确和实用。图能实现对点、线、面/多边形/网格和网络等多种空间结构的表达,通过将这些空间结构转化为(有向或无向)图和图顶点上的信号,使用信号域或谱域对密集或稀疏的时空过程进行建模。
本文旨在提供一个基于网络和图的时空智能分析的理论研究框架,并没有对SpaceTimeAI和GeoAI进行严格的定义。本文通过介绍具有开创性的基于网络的时空分析方法,以阐述时空预测、时空聚类及时空优化等内容。针对相关模型的后续应用及发展,可以参考其他相关文献。
基于图的深度学习和时空预测的发展如火如荼,但大多数是基于静态图结构,即图结构固定不变。如果网络结构变化(节点或节点之间的链接丢失或增加),现有的模型都无法对此类动态图结构进行时空预测。这类动态图模型的发展将有助于研究交通事故、路网优化等问题。由于缺乏历史数据来训练模型,速移学习或强化学习的发展可能有助于解决这个问题。此外,利用多智能体的强化学习进行时空优化也是当前的热点方向,如出租车和用户需求的匹配[44]。
尽管图论相关的研究发展迅速,但其在地理信息科学中的应用仍局限于导航和路径搜索。因此,基于图的知识和基于矩阵的运算能力仍须提高,以进一步辅助图结构在地理信息科学中的应用,并推动SpaceTimeAI和GeoAI的发展。此外,需要开发更多基于图的分析和数据库管理工具等应用,这将有力推动数字孪生和元宇宙的发展。例如,图数据库Neo4J可以灵活地链接几何和语义信息,其路径搜索快捷,在连接室内和室外路径研究中表现出了突出的优越性[45]。
自20世纪80年代以来,网络复杂性的研究方兴未艾,但在地理信息科学研究中仍然局限于单层网络,如道路、电网或社交网络等。由于各个城市核心功能间的联系日趋紧密,交通运输、电信和能源等网络之间的相互作用也日趋紧密。多层网络模型和相关分析也成为推动SpaceTimeAI和GeoAI发展,以及研究地理空间和现实世界实际问题的重要方向。
致谢: 感谢参与各资助课题的合作者和研究人员,尤其是UCL SpaceTimeLab近几年毕业的博士,包括陈焕发博士、沈嘉男博士、赖俊陶博士和Ibrahim博士,以及任沂斌博士和Seula Park博士两位访问学者。他们的研究工作都贡献了本文思想和方法的一部分;此外,SpaceTimeLab的其他成员,尤其是张翔晖博士生对本文的整理给予了大力帮助,也一并致谢。
| [1] |
IBRAHIM M R, HAWORTH J, CHENG Tao. Understanding cities with machine eyes: a review of deep computer vision in urban analytics[J]. Cities, 2020, 96: 102481. DOI:10.1016/j.cities.2019.102481 |
| [2] |
ZHANG Fan, WU Lun, ZHU Di, et al. Social sensing from street-level imagery: a case study in learning spatio-temporal urban mobility patterns[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 153: 48-58. DOI:10.1016/j.isprsjprs.2019.04.017 |
| [3] |
ZHANG Junbo, ZHENG Yu, QI Dekang, et al. Predicting citywide crowd flows using deep spatio-temporal residual networks[J]. Artificial Intelligence, 2018, 259: 147-166. DOI:10.1016/j.artint.2018.03.002 |
| [4] |
OPENSHAW S, TAYLOR P. The modifiable areal unit problem[M]//WRIGLEY N, BENNETT R J. Quantitative Geography: A British View. London: Routledge, 1981: 60-69.
|
| [5] |
ROSSER G, DAVIES T, BOWERS K J, et al. Predictive crime mapping: arbitrary grids or street networks?[J]. Journal of Quantitative Criminology, 2017, 33(3): 569-594. DOI:10.1007/s10940-016-9321-x |
| [6] |
CHENG Tao, HAWORTH J, WANG Jiaqiu. Spatio-temporal autocorrelation of road network data[J]. Journal of Geographical Systems, 2012, 14(4): 389-413. DOI:10.1007/s10109-011-0149-5 |
| [7] |
CHENG Xingyi, ZHANG Ruiqing, ZHOU Jie, et al. Deeptransport: learning spatial-temporal dependency for traffic condition forecasting[C]//Proceedings of 2018 International Joint Conference on Neural Networks. Rio de Janeiro: IEEE, 2018.
|
| [8] |
SHIODE S. Street-level spatial scan statistic and STAC for analysing street crime concentrations[J]. Transactions in GIS, 2011, 15(3): 365-383. DOI:10.1111/j.1467-9671.2011.01255.x |
| [9] |
CHEN Huanfa, CHENG Tao, SHAWE-TAYLOR J. A balanced route design for min-max Multiple-Depot Rural Postman Problem (MMMDRPP): a police patrolling case[J]. International Journal of Geographical Information Science, 2018, 32(1): 169-190. DOI:10.1080/13658816.2017.1380201 |
| [10] |
CHENG Tao, HAWORTH J, ANBAROGLU B, et al. Spatio-temporal data mining[M]//FISCHER M, NIJKAMP P. Handbook of Regional Science. Berlin: Springer, 2019.
|
| [11] |
BOLLOBÁS B. Modern graph theory[M]. New York: Springer, 2019.
|
| [12] |
ORTEGA A, FROSSARD P, KOVAČEVIC'J, et al. Graph signal processing: overview, challenges, and applications[J]. Proceedings of the IEEE, 2018, 106(5): 808-828. DOI:10.1109/JPROC.2018.2820126 |
| [13] |
ESTRADA E. Graph and network theory[J]. Developments in Water Science, 1988, 32: 317-339. DOI:10.1016/S0167-5648(08)70928-6 |
| [14] |
HASHEMI H, ABDELGHANY K. End-to-end deep learning methodology for real-time traffic network management[J]. Computer-Aided Civil and Infrastructure Engineering, 2018, 33(10): 849-863. DOI:10.1111/mice.12376 |
| [15] |
ZHANG Yang, CHENG Tao. Graph deep learning model for network-based predictive hotspot mapping of sparse spatio-temporal events[J]. Computers, Environment and Urban Systems, 2020, 79: 101403. DOI:10.1016/j.compenvurbsys.2019.101403 |
| [16] |
HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the National Academy of Sciences of the United States of America, 1982, 79(8): 2554-2558. DOI:10.1073/pnas.79.8.2554 |
| [17] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [18] |
CHO K, VAN MERRIËNBOER B, BAHDANAU D, et al. On the properties of neural machine translation: encoder-decoder approaches[C]//Proceedings of the 8th Workshop on Syntax, Semantics and Structure in Statistical Translation. Doha: Association for Computational Linguistics, 2014: 103-111.
|
| [19] |
LECUN Y, BENGIO Y. Convolutional networks for images, speech, and time-series[M]//ARBIB M A. The Handbook of Brain Theory and Neural Networks. Cambridge: MIT Press, 1995.
|
| [20] |
MONTI F, OTNESS K, BRONSTEIN M M. Motifnet: a motif-based graph convolutional network for directed graphs[C]//Proceedings of 2018 IEEE Data Science Workshop. Lausanne: IEEE, 2018: 225-228.
|
| [21] |
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[C]//Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview, 2017: 1-14.
|
| [22] |
ZHANG Yang. Graph deep learning models for network-based spatio-temporal data forecasting: from dense to sparse[D]. London: University College London, 2020.
|
| [23] |
SHI Xingjian, CHEN Zhourong, WANG Hao, et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting[C]//Proceedings of Annual Conference on Neural Information Processing Systems 2015. Montreal: [s. n. ], 2015.
|
| [24] |
LIANG Ming, HU Xiaolin. Recurrent convolutional neural network for object recognition[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 3367-3375.
|
| [25] |
XU Zhenqi, LI Shan, DENG Weihong. Learning temporal features using LSTM-CNN architecture for face anti-spoofing[C]//Proceedings of the 20153rd IAPR Asian Conference on Pattern Recognition, Kuala Lumpur: IEEE, 2015: 141-145.
|
| [26] |
HUANG C J, KUO P H. A deep cnn-lstm model for particulate matter (PM2.5) forecasting in smart cities[J]. Sensors, 2018, 18(7): 2220. DOI:10.3390/s18072220 |
| [27] |
LIU Yipeng, ZHENG Haifeng, FENG Xinxin, et al. Short-term traffic flow prediction with conv-LSTM[C]//Proceedings of the 20179th International Conference on Wireless Communications and Signal Processing (WCSP). Nanjing: IEEE, 2017: 1-6.
|
| [28] |
ADEPEJU M, ROSSER G, CHENG Tao. Novel evaluation metrics for sparse spatio-temporal point process hotspot predictions-a crime case study[J]. International Journal of Geographical Information Science, 2016, 30(11): 2133-2154. DOI:10.1080/13658816.2016.1159684 |
| [29] |
REN Yibin, CHENG Tao, ZHANG Yang. Deep spatio-temporal residual neural networks for road-network-based data modeling[J]. International Journal of Geographical Information Science, 2019, 33(9): 1894-1912. DOI:10.1080/13658816.2019.1599895 |
| [30] |
REN Yibin, CHEN Hao, HAN Yong, et al. A hybrid integrated deep learning model for the prediction of citywide spatio-temporal flow volumes[J]. International Journal of Geographical Information Science, 2020, 34(4): 802-823. DOI:10.1080/13658816.2019.1652303 |
| [31] |
ZHANG Yang, CHENG Tao, REN Yibin. A graph deep learning method for short-term traffic forecasting on large road networks[J]. Computer-Aided Civil and Infrastructure Engineering, 2019, 34(10): 877-896. DOI:10.1111/mice.12450 |
| [32] |
MHASKAR H N, POGGIO T. Deep vs. shallow networks: an approximation theory perspective[J]. Analysis and Applications, 2016, 14(6): 829-848. DOI:10.1142/S0219530516400042 |
| [33] |
KRAWCZYK B. Learning from imbalanced data: open challenges and future directions[J]. Progress in Artificial Intelligence, 2016, 5(4): 221-232. DOI:10.1007/s13748-016-0094-0 |
| [34] |
IBRAHIM M R, HAWORTH J, LIPANI A, et al. Variational-LSTM autoencoder to forecast the spread of coronavirus across the globe[J]. PLoS One, 2021, 16(1): e0246120. DOI:10.1371/journal.pone.0246120 |
| [35] |
LAI Juntao. Urban place profiling using geo-referenced social media data[D]. London: University College London, 2019.
|
| [36] |
CHENG Tao, SHEN Jianan. Grouping people in cities: from space-time to place-time based profiling[M]//SHAW S L, SUI D. Human Dynamics Research in Smart and Connected Communities. Cham: Springer, 2018: 181-201.
|
| [37] |
SHEN Jianan. Profiling and grouping space-time activity patterns of urban individuals[D]. London: University College London, 2017.
|
| [38] |
BRUCE C. Districting and resource allocation: a question of balance[J]. Geography&Public Safety, 2009, 1(4): 1-3. |
| [39] |
WANG Fahui. Why police and policing need GIS: an overview[J]. Annals of GIS, 2012, 18(3): 159-171. DOI:10.1080/19475683.2012.691900 |
| [40] |
MITCHELL P S. Optimal selection of police patrol beats[J]. The Journal of Criminal Law, Criminology, and Police Science, 1972, 63(4): 577-584. DOI:10.2307/1141814 |
| [41] |
ZHANG Yue, BROWN D E. Police patrol districting method and simulation evaluation using agent-based model&GIS[J]. Security Informatics, 2013, 2(1): 7. |
| [42] |
CHEN Huanfa, CHENG Tao, YE Xinyue. Designing efficient and balanced police patrol districts on an urban street network[J]. International Journal of Geographical Information Science, 2019, 33(2): 269-290. |
| [43] |
CHEN Huanfa. Developing police patrol strategies based on the urban street network[D]. London: University College London, 2019.
|
| [44] |
ZHOU Ming, JIN Jiarui, ZHANG Weinan, et al. Multi-agent reinforcement learning for order-dispatching via order-vehicle distribution matching[C]//Proceedings of the 28th ACM International Conference on Information and Knowledge Management. Beijing: ACM, 2019: 2645-2653.
|
| [45] |
PARK S. ISPRS WG IV/8(GeoComputation and GeoSimulation) webinar[EB/OL]. [2022-03-01]. https://www.isprs.org/news/announcements/details.aspx?ID=277.
|